河北省保定市定州市八年级(上)期中数学试卷
2024-2025学年八年级数学上学期期中模拟卷(冀教版,八上第12~15章)(考试版A4)

2024-2025学年八年级数学上学期期中模拟卷(冀教版)(满分120分,时间120分钟)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:冀教版八年级上册第十二章~第十五章。
5.难度系数:0.65。
第Ⅰ卷一、选择题(本大题共16个小题,共38分,1~6小题每题3分,7~16小题每题2分.每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.在实数15,0,p )A .1B .2C .3D .42.若分式32x x +-有意义,则x 应满足的条件是( )A .2x =B .2x ¹C .3x =-D .3x ¹-3.下列计算正确的是( )A =B =C D 4=4.某校为了丰富学生的校园生活,准备购买一批陶笛.已知A 型陶笛比B 型陶笛的单价低20元,用2700元购买A 型陶笛与用4500元购买B 型陶笛的数量相同,设A 型陶笛的单价为x 元,根据题意列出正确的方程是( )A .2700450020x x=-B .2700450020x x =-C .2700450020x x =+D .2700450020x x =+5.若23(4)270a b -++=,则2023()a b -+的值为( )A .2-B .1-C .1D .26.用※定义一种新运算:对于任意实数m 和n ,规定2m n m n mn =-※,如:21212120=´-´=※.则(的值为( )A +B -C .D .7.若关于x 的方程311x m x x -=--产生增根,则m 的值是( )A .3-B .2-C .2D .08.若 6的整数部分是m ,小数部分是n ,则n m -为( )A 10B .10C 2D .89.如图,在Rt ABC △中,90C Ð=°,12cm AC =,6cm BC =,一条线段PQ AB =,P ,Q 两点分别在线段AC 和AC 的垂线AX 上移动,若以A 、B 、C 为顶点的三角形与以A 、P 、Q 为顶点的三角形全等,则AP 的值为( )A .6cmB .12cmC .12cm 或6cmD .以上答案都不对10.已知()()341212A B m m m m m -+=----,则常数A ,B 的值分别是( )A .1A =,2B =B .2A =,1B =C .1A =-,2B =-D .2A =-,1B =-11.如图,小虎用10块高度都是3cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC BC =,90ACB Ð=°),点C 在DE 上,点A 和B 分别与木墙的顶端重合,则两堵木墙之间的距离DE 的长度为( )A .30cmB .27cmC .24cmD .21cm12.如图1,已知Rt ABC △、画一个Rt A B C ¢¢¢V ,使得Rt Rt A B C ABC ¢¢¢△≌△.在已有90MB N ¢Ð=°的条件下,图2,图3分别是嘉嘉、琪琪两位同学的画图过程.下列说法错误的是( )A .嘉嘉第一步作图时,是以B ¢为圆心,线段BC 的长为半径画弧B .嘉嘉作图判定两个三角形全等的依据是HLC .琪琪第二步作图时,是以C ¢为圆心、线段AC 的长为半径画弧D .琪琪作图判定两个三角形全等的依据是SAS13.根据分式的性质,可以将分式22211m m M m -+=-(m 为整数)进行如下变形:22211(1)2211111m m m m M m m m m -+-+-====--+++,其中m 为整数.结论Ⅰ:依据变形结果可知,M 的值可以为0;结论Ⅱ:若使M 的值为整数,则m 的值有3个.A .Ⅰ和Ⅱ都对B .Ⅰ和Ⅱ都不对C .Ⅰ不对Ⅱ对D .Ⅰ对Ⅱ不对14.如图,给出下列四组条件:①AB DE =,BC EF =,AC DF =;②AB DE =, B E Ð=Ð,BC EF =;③B E Ð=Ð,BC EF =,C F Ð=Ð;④AB DE =,AC DF =,B E Ð=Ð.其中,能使ABC DEF ≌△△的条件共有( )A .1组B .2组C .3组D .4组15.如图,在ABC V 中,50ABC Ð=°,30C Ð=°,作BD 平分ABC Ð交边AC 于D ,过A 作AE BD ^于E ,延长AE 交边BC 于点F ,连接DF ,则CDF Ð的度数为( )A .50°B .60°C .65°D .70°16.如图,在ABC V 中,45ABC Ð=°,CD AB ^于点D ,BE 平分ABC Ð,且BE AC ^于点E ,与CD 相交于点F ,DH BC ^于点H ,交BE 于点G .下列结论:①BD CD =;②AD CF BD +=;③12CE BF =;④AE CF =.其中正确的是( )A .①②B .①③C .①②③D .①②③④第Ⅱ卷二、填空题(本大题共3个小题,共10分;17小题2分,18~19小题各4分,每空2分,答案写在答题卡上)17.若关于x 的分式方程1322m x x x --=--的解为正数,则m 的取值范围是 .18.我市某中学举办剪纸艺术大赛,要求参赛作品的面积在220dm 以上,如图是小悦同学的参赛作品(单位:dm ).(1)小悦的作品 (填“是”或“否)符合参赛标准;(2)小涵给小悦提出建议:在参赛作品周围贴上金色彩条,这样参赛作品更漂亮,则需要彩条的长度约为 dm 1.41»).19.添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt ABC △中,90ABC Ð=°,BD 是高,E 是ABC V 外一点,BE BA =,E C Ð=Ð,若25DE BD =,16AD =,20BD =,求BDE V 的面积,同学们可以先思考一下……,小颖思考后认为可以这样添加辅助线:在BD 上截取BF DE =.(如图2).同学们,根据小颖的提示,聪明的你可以求得:(1)BDEV≌.(2)BDEV的面积为.三、解答题(本大题共7个小题,共72分,解答应写出文字说明、证明过程或演算步骤)20.(本小题满分9分)计算:221.(本小题满分9分)先化简,再求值:3444x xx x-----,其中x=解:原式34(4)(4)44x xx xx x--=×--×---34x x=-+-1=-(1)求原式正确的化简结果;(2)老师说:“虽然该过程有错误,但最后所求的值是正确的.”求图中被污染的x的值.某校为美化校园,计划对面积为22000m 的区域进行绿化,安排甲、乙两个工程队完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为2480m 区域的绿化时,甲队比乙队少用6天.(1)求甲乙两工程队每天能完成绿化的面积分别是多少2m ?(2)在该次校园绿化工程中,设安排甲队工作y 天①再安排乙队工作_____天,完成该工程(用含有y 的式子表示)②若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.12万元,要使这次的绿化总费用不超过7.6万元,乙队的工作天数不超过34天,如何安排甲队的工作天数?23.(本小题满分10分)如图,在ABC V 中,2AB AC ==,40B Ð=°,点D 在线段BC 上运动(点D 不与点B ,C 重合),连接AD ,作40ADE Ð=°,DE 交线段AC 于点E .(1)当115BDA Ð=°时,EDC Ð=_____ °,AED =∠_____ °.(2)若2DC =,试说明ABD DCE ≌△△.(3)在点D 的运动过程中,ADE V 的形状可以是等腰三角形吗?若可以,求BDA Ð的度数;若不可以,请说明理由.嘉琪在学习《二次根式》时,发现一些含有根号的式子也可以写成完全平方式的形式,如(231+=,善于思考的嘉琪进行了如下探索:设(2a m +=+(其中a ,b ,m ,n 均为正整数),则有2222a m n +=+.所以222,2=+=a m n b mn .这样,嘉琪找到了把类似a +琪的方法探索并解决问题:(1)当a ,b ,m ,n 均为正整数时,若(2a m +=+,用含m ,n 的式子分别表示a 和b ;(2)利用所探索的结论,找一组满足(1)中关系式(2a m +=+的正整数a ,b .m .n ;(3)若(2a m +=+.且a ,b ,m ,n 均为正整数,求a 的值.25.(本小题满分12分)我们给出定义:若一个分式约分后是一个整式,则称这个分式为“巧分式”,约分后的整式称为这个分式的“巧整式”.例如:24842x x x x -=-,则称分式2482x x x --是“巧分式”,4x 为它的“巧整式”.根据上述定义,解决下列问题.(1)下列分式中是“巧分式”的有__________(填序号);①(1)(23)(2)(1)(2)x x x x x --+-+;②253x x ++;③22x y x y-+.(2)若分式24x x m x n-++(m 、n 为常数)是一个“巧分式”,它的“巧整式”为7x -,求m 、n 的值;(3)若分式322x x A -+的“巧整式”为1x -,请判断32242x x x A++是否是“巧分式”,并说明理由.【问题提出】如图1,在ABC V 中,90,BAC AB AC Ð=°=,直线l 经过点A ,分别从点,B C 向直线l 作垂线,垂足分别为,D E .求证:ABD CAE △△≌;【变式探究】如图2,在ABC V 中,AB AC =,直线1经过点A ,点,D E 分别在直线l 上,如果CEA ADB BAC Ð=Ð=Ð,猜想DE BD CE ,,有何数量关系,并给予证明;【拓展应用】小明在科技创新大赛上创作了一幅机器人图案,大致图形如图3所示,以ABC V 的边AB AC ,为一边向外作BAD V 和CAE V ,其中90BAD CAE Ð=Ð=°,,,AB AD AC AE AG ==是边BC 上的高.延长GA 交DE 于点H .(1)求证:点,D E 到直线H G 的距离相等;(2)经测量,50cm DE =,求HE 的长.。
河北省保定市八年级上学期数学期中试卷

河北省保定市八年级上学期数学期中试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)汉字是中华民族的瑰宝,下列图形是轴对称图形的个数是()美洋善祥A . 1个B . 2个C . 3个D . 4个2. (2分)若线段2a+1,a,a+3能构成一个三角形,则a的范围是()A . a>0B . a>1C . a>2D . 1<a<33. (2分)(2018·深圳模拟) 如图,在△ABC中,AB=5,AC=4,BC=3,分别以点A,点B为圆心,大于 AB 的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则CO的长是()A . 1.5B . 2C . 2.4D . 2.54. (2分) (2020八上·临河月考) 如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是()A . 三角形具有稳定性B . 两点之间,线段最短C . 直角三角形的两个锐角互为余角D . 垂线段最短5. (2分)(2019·平江模拟) 下列命题正确的是()A . 矩形对角线互相垂直B . 方程的解为C . 六边形内角和为540°D . 一条斜边和一条直角边分别相等的两个直角三角形全等6. (2分) (2018八下·江门月考) △ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13.其中能判断△ABC是直角三角形的个数有()A . 1个B . 2个C . 3个D . 4个7. (2分) (2017八上·虎林期中) 如图,△ABC中,AD⊥BC,D为BC的中点,以下结论:△ABD≌△ACD;(2)AB=AC;(3)∠B=∠C;(4)AD是△ABC的角平分线。
河北省保定市八年级上学期数学期中考试试卷

河北省保定市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2019九上·丽江期末) 下列图形中,既是轴对称图形,又是中心对称图形的是()A . 平行四边形B . 等边三角形C . 梯形D . 圆2. (2分) (2019八上·普兰店期末) 已知△ABC的三条边长都是整数,其中两条边长分别为则第三条边长等于()A . 1B . 2C . 3D . 1或23. (2分)如图所示,△ABC中,∠C=90°,AB的垂直平分线交BC于点D,连接AD,若∠CAD=20°,则∠B =()A . 20°B . 30C . 35°D . 40°4. (2分) (2018七下·深圳期末) 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC 和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有()A . ①③⑤B . ①③④⑤D . ①②③④⑤5. (2分)在△ABC和△DEF中,已知∠C=∠D,∠B=∠E要判定这两个三角形全等,还需条件()A . AB=EDB . AB=FDC . AC=FDD . ∠A=∠E6. (2分) (2017八上·台州期中) 如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DEF()A . BC=EFB . AC=DFC . AC∥DFD . ∠A=∠D7. (2分) (2019八下·太原期中) 如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为()A . 90°B . 95°C . 105°D . 110°8. (2分)如图所示,某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()B . 带②去C . 带③去D . ①②③都带去9. (2分) (2019八下·锦江期中) 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为()A . 30°B . 45°C . 50°D . 75°10. (2分)(2018·龙东模拟) 如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DA E,其中结论正确的个数有()A . 1个B . 2个C . 3个D . 4个二、填空题 (共10题;共10分)11. (1分)已知△ABC是等腰三角形,其边长为3和7,△DEF≌△ABC,则△DEF的周长是________.12. (1分)根据下面每幅图中的横线和竖线,把你想到的成语写在横线上________ ,________ ,________ ,________13. (1分)如图,已知MN∥PQ,EF与MN,PQ分别交于A、C两点,过A、C两点作两组内错角的平分线,分别交于点B、D,则四边形ABCD是________.14. (1分)如图,△ABC≌△A′B′C′,若BC′=9,B′C=2,则BB′的长度是________.15. (1分)如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是________.16. (1分) (2016九上·温州期末) 如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB 于B,PB交AC于E,若AB=4,BE=2,则PE的长为________.17. (1分) (2017八上·无锡开学考) 已知n边形的内角和是一个五边形的外角和的2倍,则n=________.18. (1分)如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为________.19. (1分)(2017·南充) 如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 ,其中正确结论是________(填序号)20. (1分) (2017七下·苏州期中) 已知a+b=3,,则=________三、解答题 (共7题;共41分)21. (5分)(2019·南陵模拟) 如图,在由边长为1个单位长度的小正方形组成的12×2网格中,给出了格点△ABC和直线l.(1)画出△ABC关于直线l对称的格点△A′B′C;(2)在直线l上选取一格点,在网格内画出格点△DPE,使得△DPE∽△ABC,且相似比为2:1.22. (5分)求证:三角形的外角和等于360° .一般地,n边形的外角和等于360°23. (5分) (2018九上·晋江期中) 如图△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.(1) PH=________cm.(2)△ABC与△DEF重叠部分的面积为________cm2.24. (5分)如图:已知BD=CD,BF⊥AC,CE⊥AB,求证:点D在∠BAC的平分线上.25. (5分)(2017·成都) 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D 为BC的中点,∠BAD= ∠BAC=60°,于是 = = ;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.(1)①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;(2)拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.①证明△CEF是等边三角形;②若AE=5,CE=2,求BF的长.26. (5分)(2017·西安模拟) 如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.27. (11分) (2016八上·泸县期末) 综合题探究发现(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:①∠AEB的度数为________;②线段AD,BE之间的数量关系为________.(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共10题;共10分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共7题;共41分) 21-1、21-2、22-1、23-1、23-2、24-1、25-1、25-2、26-1、27-1、27-2、。
2015-2016年保定市定州市八年级上期中数学试卷含答案解析

22.已知:如图,已知△ABC 中,其中 A(0,﹣ 2),B(2,﹣ 4),C(4,﹣ 1). (1)画出与△ABC 关于 y 轴对称的图形△A1B1C1; (2)写出△A1B1C1 各顶点坐标; (3)求△ABC 的面积.
10.如图,在△ABC 中,AD 是它的角平分线,AB=8cm,AC=6cm,则 S△ABD:
S△ACD=(
)
A.3:4 B.4:3 C.16:9 D.9:16 11.如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若 AE=8,则 DF 等于( )
A.5 B.4 C.3 D.2
12.如图,在 Rt 直角△ABC 中,∠B=45°,AB=AC,点 D 为 BC 中点,直角∠MDN 绕点
23.如图,在等边△ABC 中,点 D,E 分别在边 BC,AC 上,且 DE∥AB,过点 E 作 EF⊥DE,交 BC 的延长线于点 F, (1)求∠F 的度数; (2)若 CD=3,求 DF 的长.
24.如图,∠ABC=90°,D、E 分别在 BC、AC 上,AD⊥DE,且 AD=DE,点 F 是 AE 的中 点,FD 与 AB 相交于点 M. (1)求证:∠FMC=∠FCM; (2)AD 与 MC 垂直吗?并说明理由.
25.如图,四边形 ABCD中,∠B=90°,AB∥CD,M 为 BC 边上的一点,且 AM 平分 ∠BAD,DM 平分∠ADC.求证: (1)AM⊥DM; (2)M 为 BC 的中点.
2015-2016 学年河北省保定市定州市八年级(上)期中数学试卷
河北省定州市2022年八年级上学期《数学》期中试题与参考答案

河北省定州市2022年八年级上学期《数学》期中试题与参考答案一、选择题本大题共12个小题,每小题3分,共36分。
每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题中的括号内。
1.下列标志中,不是轴对称图形的是( )A.B.C.D.【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.解:A、是轴对称图形,故此选项不合题意;B、是轴对称图形,故此选项不合题意;C、是轴对称图形,故此选项不合题意;D、不是轴对称图形,故此选项符合题意;故选:D.2.下列图形具有稳定性的是( )A.正方形B.长方形C.平行四边形D.钝角三角形【分析】根据三角形具有稳定性即可得出答案.解:具有稳定性的是钝角三角形.故选:D.3.有2cm和3cm的两根小棒,请你再找一根小棒,并以这三根小棒为边围成一个三角形,下列长度的小棒不符合要求的是( )A.2cm B.3cm C.4cm D.5cm【分析】根据三角形的三边关系可得3﹣2<第三根小棒的长度<3+2,再解不等式可得答案.解:设第三根小棒的长度为xcm,由题意得:3﹣2<x<3+2,解得:1<x<5,故选:D.4.△ABC中,如果∠A+∠B=∠C,那么△ABC形状是( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定【分析】据在△ABC中,∠A+∠B=∠C,∠A+∠B+∠C=180°可求出∠C的度数,进而得出结论.解:因为在△ABC中,∠A+∠B=∠C,∠A+∠B+∠C=180°,所以2∠C=180°,解得∠C=90°,所以△ABC是直角三角形.故选:B.5.如图,在△ABC中AB=AC,D是BC的中点,∠B=36°,则∠BAD=( )A.108°B.72°C.54°D.36°【分析】根据等腰三角形三线合一的性质可得AD⊥BC,然后利用直角三角形两锐角互余的性质解答.解:因为AB=AC,D是BC的中点,所以AD⊥BC,因为∠B=36°,所以∠BAD=90°﹣36°=54°.故选:C.6.已知图中的两个三角形全等,则∠1等于( )A.70°B.68°C.58°D.52°【分析】先根据全等三角形的对应角相等得出对应角相等,再根据三角形的内角和定理求出即可.解:因为两三角形全等,所以∠1=180°﹣70°﹣52°=58°,故选:C.7.正多边形的一个内角等于144°,则该多边形是正( )边形.A.8B.9C.10D.11【分析】根据正多边形的每个内角相等,可得正多边形的内角和,再根据多边形的内角和公式,可得答案.解:设正多边形是n边形,由题意得(n﹣2)×180°=144°n.解得n=10,故选:C.8.等腰三角形的底角是15°,腰长为10,则其腰上的高为( )A.8B.7C.5D.4【分析】过C作CD⊥BA,交BA的延长线于D,则∠D=90°,根据三角形的外角性质求出∠DAC=30°,求出CD=AC,即可求出答案.解:过C作CD⊥BA,交BA的延长线于D,则∠D=90°,因为AB=AC,∠B=15°,所以∠ACB=∠B=15°,所以∠DAC=∠B+∠ACB=30°,所以CD==,故选:C.9.如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )A.65°B.60°C.55°D.45°【分析】根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.解:由题意可得:MN是AC的垂直平分线,则AD=DC,故∠C=∠DAC,因为∠C=30°,所以∠DAC=30°,因为∠B=55°,所以∠BAC=95°,所以∠BAD=∠BAC﹣∠CAD=65°,故选:A.10.如图,竖直放置一等腰直角三角板,直角顶点C紧靠在桌面,AD⊥DE,BE⊥DE,垂足分别为D、E.下列结论正确的是( )A.DE=AD+BE B.DE=AC+BE C.DE=BC+BE D.DE=AB•BE【分析】根据△ABC是等腰直角三角形,可得∠ACB=90°,AC=BC,然后证明△ADC≌△CEB,进而可得结论.解:因为△ABC是等腰直角三角形,所以∠ACB=90°,AC=BC,所以∠ACD+∠BCE=90°,因为AD⊥DE,BE⊥DE,所以∠ADC=∠CEB=90°,所以∠ACD+∠DAC=90°,所以∠BCE=∠DAC,在△ADC和△CEB中,所以△ADC≌△CEB(AAS),所以DC=EB,所以DE=DC+CE=BE+AD,故选:A.11.如图,直线l是五边形ABCDE的对称轴,其中∠C=100°,∠ABC=130°,那么∠BEA 的度数等于( )A.45°B.50°C.60°D.65°【分析】依据轴对称图形的性质可求得∠AED、∠D的度数,然后用五边形的内角和减去∠AED、∠ABC、∠C、∠D的度数,进而利用三角形内角和解答即可.解:因为直线l是五边形ABCDE的对称轴,所以∠ABC=∠AED=130°,∠C=∠D=100°,AB=AE,所以∠BAE=540°﹣130°×2﹣100°×2=80°.所以∠BEA=故选:B.12.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC 的面积是△PBD面积的2倍,其中结论正确的个数有( )A.4个B.3个C.2个D.1个【分析】过点P作PK⊥AB,垂足为点K.证明Rt△BPK≌Rt△BPD,△PAK≌△PCD,利用全等三角形的性质即可解决问题.解:过点P作PK⊥AB,垂足为点K.因为PK⊥AB,PD⊥BC,∠ABP=∠CBP,所以PK=PD,在Rt△BPK和Rt△BPD中,,所以Rt△BPK≌Rt△BPD(HL),所以BK=BD,因为∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,所以∠KPD=∠APC,所以∠APK=∠CPD,故①正确,在△PAK和△PCD中,所以△PAK≌△PCD(ASA),所以AK=CD,PA=PC,故②正确,所以BK﹣AB=BC﹣BD,所以BD﹣AB=BC﹣BD,所以AB+BC=2BD,故③正确,因为Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),所以S△BPK=S△BPD,S△APK=S△PDC,所以S四边形ABCP=S四边形KBDP=2S△PBD.故④正确.故选:A.二、填空题本大题共6个小题,每小题3分,共18分,把答案直接写在题中的横线上。
河北省定州市八年级数学上学期期中试题(扫描版) 新人教版

河北省定州市2017-2018学年八年级数学上学期期中试题八年级数学参考答案一、选择题1—6: BABBCA; 7—12:BCCBDD.二、填空题13. 35°;14. 80°;15. 15cm或18cm;16. 4; 17.(﹣4,3)或(﹣2,﹣3)或(﹣4,﹣3);18.(1,﹣4)三、解答题19.解:∵在△ABC中,∠B=40°,∠C=70°,∴∠BAC=180°﹣40°﹣70°=70°.∵AD是△BAC的角平分线,∴∠DAC=∠BAC=35°,∴∠ADC=180°﹣∠C﹣∠D AC=180°﹣70°﹣35°=75°.20.(1)如图1,连接AB,作线段AB的垂直平分线,交直线l于点P,则点P即为所求点.(2)如图2,作点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求点.21.解:∵DE∥BC∴∠DOB=∠OBC,又∵BO是∠AB C的角平分线,∴∠DBO=∠OBC,∴∠DBO=∠DOB,∴BD=OD,同理:OE=EC,∴△ADE的周长=AD+OD+OE+AE=AD+BD+AE+EC=AB+AC=14cm.22. 情况之一:题设:①②③;结论:④.(其他情况略)证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF.在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),∴∠1=∠2;23.证明:连BE,∵ED⊥BC,∴∠EDB=90°,在Rt△ABE和Rt△DBE中,∴△ABE≌△DBE (HL),∴DE=AE.∴DE+CE=AC.24. 解:4(1)探究:假若你是该小组的成员,请把你研究的结果填入上表;(2)猜想:随着边数的增加,多边形对角线的条数会越来越多,从n边形的一个顶点出发可引的对角线条数为(n﹣3)),n边形对角线的总条数为(n≥3).(3)==35次,25.证明:∵AC=2AB,D是AC的中点,∵△AED为等腰直角三角形,∴AE=DE,且∠EAD=∠EDA=45°,∴∠BAE=∠CDE=135°,在△ABE和△DCE中∴△ABE≌△DCE(SAS),∴BE=CE,∠AEB=∠DEC,∴∠BED+∠DEC=∠AEB+∠BED=∠AED=90°,∴BE⊥CE,即BE和CE的关系为相等且垂直.26.解:(1)CE=BD,理由如下:∵等腰Rt△ABC,等腰Rt△ADE,∴AE=AD,AC=AB,在△EAC与△DAB中,,∴△EAC≌△DAB(SAS),∴CE=BD;(2)∵△EAC≌△DAB,∴∠ECA=∠DBA,∴∠ECA+∠CBF=∠DBA+∠CBF=45°,∴∠ECA+∠CBF+∠DCB=45°+45°=90°,∴∠BFC=180°﹣90°=90°;(3)成立,∵等腰Rt△ABC,等腰Rt△ADE,∴AE=AD,AC=AB,∠EAD=∠BAC∴∠EAD+∠DAC=∠BAC+∠DAC即∠EAC=∠DAB∴△EAC≌△DAB(SAS),∵△EAC≌△DAB,∴∠ECA=∠DBA,∴∠ECA+∠CBF=∠DBA+∠CBF=45°,∴∠ECA+∠CBF+∠A CB=45°+45°=90°,∴∠BFC=180°﹣90°=90°.。
河北省定州市2021年八年级上学期《数学》期中试题与参考答案
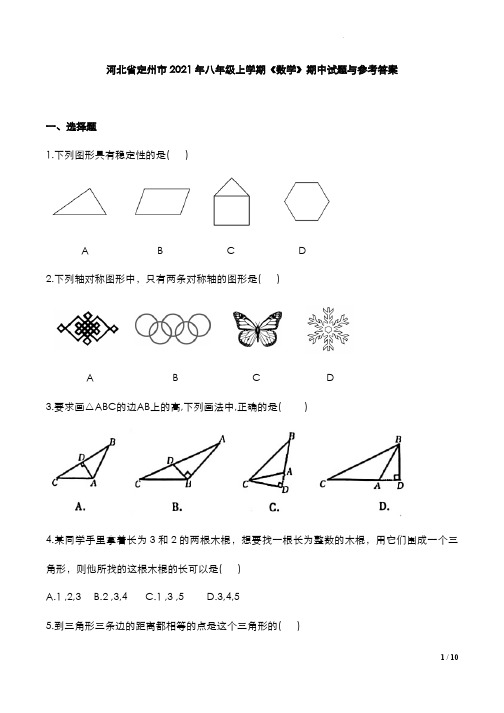
河北省定州市2021年八年级上学期《数学》期中试题与参考答案一、选择题1.下列图形具有稳定性的是( )A B C D2.下列轴对称图形中,只有两条对称轴的图形是( )A B C D3.要求画△ABC的边AB上的高,下列画法中,正确的是( )4.某同学手里拿着长为3和2的两根木棍,想要找一根长为整数的木棍,用它们围成一个三角形,则他所找的这根木棍的长可以是( )A.1 ,2,3B.2 ,3,4C.1 ,3 ,5D.3,4,55.到三角形三条边的距离都相等的点是这个三角形的( )A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点6.如图,△ABC中,AB=AC,AD⊥BC,下列结论中不正确的是( ).A.∠B=∠CB. D是BC中点C. AD平分∠BACD. AB=2BD7.某同学把一块三角形的玻璃打碎成了3 块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )A.带①去B.带②去C.带③去D.带①②③去8.如图,图中x的值为( ).A.80B.70C.60D.509.等腰三角形一个角的度数为50°,则顶角的度数为( )A.50°B.80°C.65°D.50°或80°10.下列各组条件中,能判定△ABC≌△DEF的是( ).A.∠A=∠D,∠B=∠E,∠C=∠FB.∠A=∠D,∠C=∠F,AC=EFC. AB=DE,BC=EF,∠A=∠DD. AB=DE,BC=EF,∠C=∠F=90°11.如图,在△ABC中,AD 是∠BAC的角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )A.6B.5C.4D.312.如图,把长方形纸片ABCD 沿对角线折叠,设重叠部分为△EBD,那么有下列说法:①△EBD是等腰三角形,EB =ED;②折叠后∠ABE=∠CBD和一定相等;③折叠后得到的图形是轴对称图形;④△EBA和△EDC一定是全等三角形,其中正确的有( )A.1个B.2个C.3个D.4个二、填空题13.将一副三角板如图叠放,则图中∠α的度数为.14.如图,在△ABC中,∠ABC=90°,∠A=50°,BD∥AC,则∠CBD的度是 °.15.如图,射线OP 平分∠AOB,PC∥OB,PD⊥OB于点D,∠AOP=15°,PD=5,则PC等于 .16.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件。
河北省保定市定州市2023-2024学年八年级上学期期中数学试题
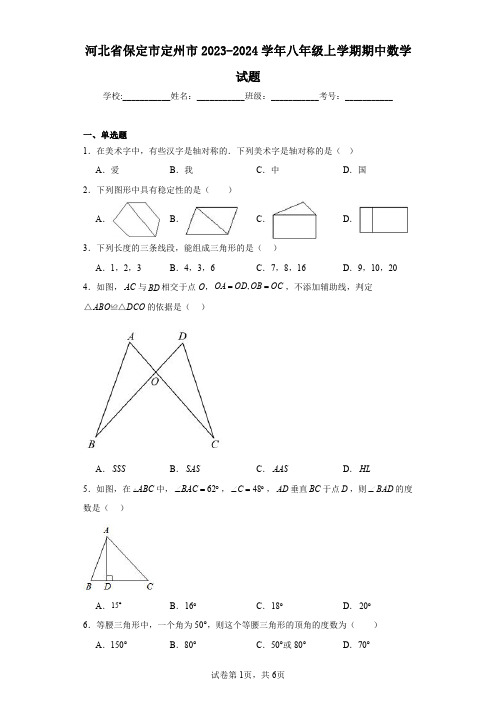
河北省保定市定州市2023-2024学年八年级上学期期中数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.在美术字中,有些汉字是轴对称的.下列美术字是轴对称的是()A .爱B .我C .中D .国2.下列图形中具有稳定性的是()A .B .C .D .3.下列长度的三条线段,能组成三角形的是()A .1,2,3B .4,3,6C .7,8,16D .9,10,204.如图,AC 与BD 相交于点O ,,OA OD OB OC ==,不添加辅助线,判定ABO DCO △≌△的依据是()A .SSSB .SASC .AASD .HL5.如图,在ABC 中,62∠=︒BAC ,48C ∠=︒,AD 垂直BC 于点D ,则BAD ∠的度数是()A .15︒B .16︒C .18︒D .20︒6.等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为()A .150°B .80°C .50°或80°D .70°7.如图,将三角形纸片剪掉一角得四边形,设△ABC 与四边形BCDE 的外角和的度数分别为α,β,则正确的是()A .0αβ-=B .0αβ-<C .0αβ->D .无法比较α与β的大小8.如图,Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则∠A ′DB =()A .40°B .30°C .20°D .10°9.在三条公路AB ,AC ,BC 围成的一块平地上修建一个物流服务中心(如图所示),若要使物流服务中心到三条公路的距离相等,则这个物流服务中心应修建在()A .ABC 三条高线的交点处B .ABC 三条角平分线的交点处C .ABC 三条中线的交点处D .ABC 三边垂直平分线的交点处10.如图,在△ABC 中,AB =AC ,∠A =36°,由图中的尺规作图得到的射线与AC 交于点D ,则以下推断错误的是()二、填空题18.如图为6个边长相等的正方形的组合图形,则三、解答题19.如图,在平面直角坐标系中,ABC 的三个顶点的坐标分别为()0,2A -,()2,4B -,()4,1C -.(1)请在图中画出ABC 关于x 轴对称的111A B C △;(2)求ABC 的面积.20.如图,ABC 中,45B ∠=︒,38C ∠=︒,E 是BC 边上一点,ED 交CA 的延长线D ,交AB 于点F ,32D ∠=︒.求AFE ∠的大小.四、填空题21.如图1,AD 是ABC 的中线.求证:2AB AC AD +>.图1请将下面的推理过程补充完整:证明:如图2,延长AD 到点E ,使DE AD =,连接BE .∵AD 是ABC 的中线,∴BDCD =.在ADC △和EDB △中,()______AD ED CD BD =⎧⎪⎨⎪=⎩,∴ADC EDB V V ≌(______)∴______(全等三角形的对应边相等).∴在ABE 中,AB BE AE +>(______),∴AB AC AD DE +>+.即2AB AC AD +>.图2五、解答题22.如图,线段AC 与线段BD 相交于点E ,A D ∠=∠,AE DE =.求证:BD AC =.23.如图,在∆ABC 中,AB =AC ,AD 是BC 边上的中线,BE ⊥AC 于点E.求证:∠CBE=∠BAD .24.如图,点D 是等边ABC 边AB 上的一点,3AB AD =,DE BC ⊥于点E ,AE 、CD相交于点F .(1)求证:ACD BAE ≌;(2)请你过点C 作CG AE ⊥,垂足为点G ,探究CF 与FG 之间的数量关系,并证明.25.如图90DAB D ∠=∠=︒,E 是AD 的中点,CE 平分BCD ∠,CE 的延长线与BA 的延长线交于点F .(1)若50DCF ∠=°,求ABC ∠;(2)求证:BE 是ABC ∠的平分线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.(8 分)某中学八年级(1)班数学课外兴趣小组在探究:“n 边形共有多少条
对角线”这一问题时,设计了如下表格:
多边形的
4
5
6
7
8
…
第5页(共8页)
边数
从多边形
…
一个顶
点出发
可引起
的对角
线条数
多边形对
…
角线的
总条数
(1)探究:假若你是该小组的成员,请把你研究的结果填入上表;
(2)猜想:随着边数的增加,多边形对角线的条数会越来越多,从 n 边形的一
E 在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠
1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设:
;结论:
.(均填写序号)
证明:
23.(8 分)如图,在△ABC 中,已知∠A=90°,AB=BD,ED⊥BC 于 D. 求证:DE+CE=AC.
第2页(共8页)
A.4
B.3
C.6
D.5
11.(3 分)如图,正方形 ABCD 的边长为 8,E 在 CD 上,DE=6,过点 B 作 EB⊥
FB,交 DA 的延长线于点 F,则 FD 的长为( )
A.6
B.8
C.9
D.10
12.(3 分)如图,等腰三角形 ABC 中,AB=AC,D、E 都在 BC 上,要使△ABD≌
为
.
14.(3 分)若一个八边形的七个内角的和为 1000°,则第八个内角的度数
为
.
15.(3 分)一个等腰三角形的边长分别是 4cm 和 7cm,则它的周长是
.
16.(3 分)如图,在△ABC 中,∠ACB=90°,∠ABC=60°,BD 平分∠ABC,P 点是
第3页(共8页)
BD 的中点,若 AD=8,则 CP 的长为
3.(3 分)下列四根木棒中,能与 5cm,8cm 长的两根木棒钉成一个三角形的是
()
A.3cm
B.8cm
C.13cm
D.15cm
4.(3 分)如图,已知 AB∥CD,∠B=60°,∠E=25°,则∠D 的度数为( )
A.25°
B.35°
C.45°
D.55°
5.(3 分)如图,△ABC 中,点 D 在 BC 上,△ACD 和△ABD 面积相等,线段 AD
△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方
案:
①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
A.1 种
B.2 种
C.3 种
D.4 种
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
13.(3 分)如果等腰三角形顶角为 70°,那么它一腰上的高与底边的夹角
.
17.(3 分)已知△ABC 的顶点坐标分别为:A(﹣2,3),B(﹣5,0),C(﹣1,
0).若△DBC 与△ABC 全等,则 D 的坐标为
.
18.(3 分)如图,把△ABC 放置在平面直角坐标系中,已知 AB=BC,∠ABC=90°,
A(3,0),B(0,﹣1),点 C 在第四象限,则点 C 的坐标是
P,Q 两点分别在线段 AC 和 AC 的垂线 AX 上移动,若△ABC 和△APQ 全等,
则 AP 的值为( )
A.6cm
B.12cm
C.12cm 或 6cm
D.以上答案都不对
10.(3 分)如图,AD 是△ABC 中∠BAC 的平分线,DE⊥AB 于点 E,DF⊥AC 交
AC 于点 F.S△ABC=7,DE=2,AB=4,则 AC 长是( )
.
三、解答题(本大题共 8 小题,共 66 分) 19.(6 分)如图,在△ABC 中,∠B=40°,∠C=70°,AD 是△ABC 的角平分线,
求∠ADC 的度数.
20.(8 分)如图,直线 l 是一条河,A,B 是两个村庄.欲在 L 上的某处修建一 个水泵站 M,向 A,B 两地供水.
(1)在图 1 中标出水泵站的位置 P 点,使它到 A、B 两地的距离相等. (2)在图 2 中标出水泵站的位置 M 点,使所需管道 MA+MB 的长度最短.(本
是三角形的( )
A.高
B.角平分线
C.中线
D.无法确定
6.(3 分)在正方形网格中,∠AOB 的位置如图所示,到∠AOB 两边距离相等的
第1页(共8页)
点应是( A.M 点
) B.N 点
C.P 点
D.Q 点
7.(3 分)如图所示,线段 AC 的垂直平分线交线段 AB 于点 D,∠A=50°,则∠
BDC=( )
题不写作法,不要求证明,保留做题痕迹)
第4页(共8页)
21.(8 分)已知:如图,△ABC 中,BO,CO 分别是∠ABC 和∠ACB 的平分线, 过 O 点的直线分别交 AB、AC 于点 D、E,且 DE∥BC,若 AB=6cm,AC=8cm, 求△ADE 的周长.
22.(8 分)在数学课上,林老师在黑板上画出如图所示的图形(其中点 B、F、C、
A.50°
B.100°
C.120°
D.130°
8.(3 分)根据下列已知条件,能唯一画出△ABC 的是( )
A.AB=3,BC=4,AC=8
B.∠C=90°,AB=6
C.∠A=60°,∠B=45°,AB=4
D.AB=3,BC=3,∠A=30°
9.(3 分)如图,在 Rt△ABC 中,∠C=90°,AC=12cm,BC=6cm,一条线段 PQ=AB,
个顶点出发可引的对角线条数为
,n 边形对角线的总条数为
.
(3)应用:10 个人聚会,每不相邻的人都握一次手,共握多少次手?
25.(10 分)已知:如图,在 Rt△ABC 中,∠BAC=90°,AC=2AB,点 D 是 AC 的
中点,以 AD 为斜边在△ABC 外作等腰直角三角形 AED,连接 BE、EC.
河北省保定市定州市八年级(上)期中数学试卷
一、选择题(本大题共 12 小题,每小题 3 分,共 42 分) 1.(3 分)下列图案中,是轴对称图形的有( )
A.
B.
C.
D.
2.(3 分)点 P(2,﹣3)关于 x 轴对称的点是( )
A.(﹣2,3) B.(2,3)
C.(﹣2,﹣3) D.(2,﹣3)
Hale Waihona Puke 求证:BE=CE,BE⊥CE.26.(10 分)以点 A 为顶点作等腰 Rt△ABC,等腰 Rt△ADE,其中∠BAC=∠DAE=90°, 如图 1 所示放置,使得一直角边重合,连接 BD、CE.
(1)试判断 BD、CE 的数量关系,并说明理由; (2)延长 BD 交 CE 于点 F 试求∠BFC 的度数; (3)把两个等腰直角三角形按如图 2 放置,(1)、(2)中的结论是否仍成立?请
