塑性材料应力应变图(精)
塑性理论课件-塑性变形时的应力应变关系

3、如果從初始狀態先加純剪應力通過 屈服點B到達D點,這時的應力和應變見表 5.1的第3行。
4、如同樣經後繼屈服軌跡裏面的任意 路線變載到F點,則應力應變見表5.1第4行。
5、如果從初始狀態沿真線OF`F到達F 點,則應力和應變見表5.1第5行,這時主軸 重合。
下一頁 返回
上述的第1、3、5種加載路線就是簡單加載。 由表中可看出,同樣的一種應力狀態σf、τf,由於 加載路線不同,就有好幾種應變狀態(如C、D點 應變);同樣,一種應變狀態(如εc),也可有 幾種應力狀態(如C、F點應力),而且應力應變 主軸不一定重合。從上述簡單的例子中,我們可 以看到,離開加載路線來建立應力與全量塑性應 變之間的普遍關係是不可能的。因此,一般情況 下只能建立起應力和應變增量之間的關係爭然後 根據具體的加載路線,具休分析。另一方面,我 們從上述例子中也看到,在簡單加載的條件下, 應力和應變的主軸重合,而且它們之間有對應關 係,因此可以建立全量理論。
下一頁 返回
另一方面,從工程角度來看,對於一 些繁雜的問題,那怕是能給出定性結果也 很可貴,具體的定量問題可以從實驗中進 一步探索(由於如摩擦條件等數學模型還 未給出,要精確計算也很難辦到)。鑒於 壓力加工理論中關於成形規律闡述上存在 的一些問題,吸取了增量理論及全量理論 的共同點,提出了應力應變順序對應規律, 並使該規律的闡述逐漸簡明和便於應用。 現簡述如下:
返回
5.2增量理論(流動理論) 一、列維-密席斯方程 二、普朗特-勞斯方程
返回
一、列維-密席斯方程
列維-密席斯方程適用條件:
(1)材料是理想剛塑性材料,即彈性應變增 量為零,塑性應變增量就是總應變增量;
(2)材料符合密席斯屈服準則,即 s
应力-应变曲线
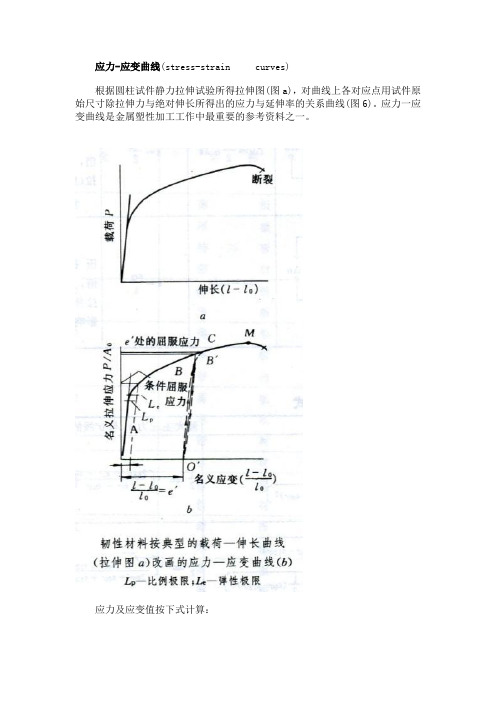
应力-应变曲线(stress-strain curves)根据圆柱试件静力拉伸试验所得拉伸图(图a),对曲线上各对应点用试件原始尺寸除拉伸力与绝对伸长所得出的应力与延伸率的关系曲线(图6)。
应力一应变曲线是金属塑性加工工作中最重要的参考资料之一。
应力及应变值按下式计算:式中σi 表示拉伸图上任意点的应力值,δi为i点的延伸率,Pi及Δli为该点的拉力与绝对伸长值,F0及l为试件的断面积和计算长度。
试件受拉伸时,先产生弹性变形,这时应力应变成比例,当出现二者不能保持线性关系的点时,表示材料已屈服而将发生塑性变形,这时的应力定义为屈服应力或流变应力,用σs表示,其求法见屈服点。
拉伸时当试件计算长度上的均匀变形阶段结束而产生细颈时,变形将集中在细颈部分。
出现细颈前材料所能承受的应力名为强度极限或抗拉强度,用σb表示σb =Pmax/F式中Pmax为拉伸图上所记录的最大载荷值。
试件出现细颈后很快即断裂,断裂应力σfσf =Pf/Tf式中Pf 是断裂时的拉力,Ff是断口面积。
试件拉断时的延伸率δf(%)或断面收缩率ψ(%)是表示材料可承受最大塑性变形能力的指标:矾一牮×100(4)£fPf=盐≯×100(5)』’0式中厶和Ff是将断开的试件对合后测定的试件长度和断口处的面积。
抗拉强度靠及延伸率d或断面收缩率妒是材料性能的两个基本指标,在工程上有着广泛的应用。
屈服应力民(或乱:)是金属塑性加工时变形体开始产生塑性变形所必需的最小应力,它是计算变形力的一个重要参数。
应力-应变曲线表征材料受外力作用时的行为。
材料受力后即发生弹性变形,这时应力应变呈简单的线性关系,继续增加作用力至一定大小后材料将出现塑性变形,以后变形与应力的关系复杂,当塑性变形至一定程度以后,试件破断则变形过程终结。
所以任何变形过程均包括弹性变形、塑性变形及破断3个典型阶段。
金属的塑性加工过程处于弹性变形与破断二者之间。
首先要创造一定的应力状态条件使金属能发生塑性变形,其次是安排一个使塑性变形尽可能大又不致发生破坏的热力学条件。
低碳钢应力-应变曲线

、 值越大,其塑性越好。一般把 ≥5%的材 料称为塑性材料,如钢材、铜、铝等;把 <5%的
材料称为脆性材料,如铸铁、混凝土、石料等。
.
11
工程应用:冷作硬化
e
d
b
b
e P
a c s
即材料在卸载过程中 应力和应变是线形关系,
f 这就是卸载定律。
材料的比例极限增高, 延伸率降低,称之为冷作硬 化或加工硬化。
10
4.塑性指标 试件拉断后,弹性变形消失,但塑性变形仍保 留下来。工程上用试件拉断后遗留下来的变形
表示材料的塑性指标。常用的塑性指标有两个:
伸长率: L1 L 100 % 断面收缩率 : LA A1 100 %
A L1 —试件拉断后的标距
L —是原标距 A1 —试件断口处的最小横截面面积 A —原横截面面积。
2.标用标于距准测:试试件的:等截面部分长度;
圆截面试件标距:L0=10d0或5d0
.
3
2、试验机
.
4
.
5
3、低碳钢拉伸曲线
.
6
e
b
b
e P
a c s
o
f
2、屈服阶段bc(失去抵 抗变形的能力)
s — 屈服极限
3、强化阶段ce(恢复抵抗 变形的能力)
b — 强度极限
4、局部径缩阶段ef
弹性极限与比例极限非常接近,工程实际中通常对二者不
作严格区分,而近似地用比例极限代替弹性极限。
.
8
(2)屈服阶段 屈服点
s
曲线超过b点后,出现了一段锯齿形曲线,
这—阶段应力没有增加,而应变依然在增加,材
料好像失去了抵抗变形的能力,把这种应力不增
塑性理论 第五章 应变分析

u y x
dx
u y y
dy
u y z
dz
x
uz
'
uz
(x
dx,
y
dy,
z
dz)
uz (x,
y, z)
uz x
dx
uz y
dy
uz z
dz
z
ui
M
' 1
ui ui
M1
uz
M(xi)
uy
ux
0
u
' z
u'
M (x dxi )
y
u
' x
y
变形体内无限接近两点的位移分量
——M’点位移到M’1点
z
第五章 应变分析
radius 3/8 in.
diameter, 0.5 in.
diameter, 0.75 in.
gauge length, 2 in.
reduced section, 2.25 in.
主要内容
5.1 应变的基本概念 5.2 几何方程 5.3 一点附近的应变分析 5.4 主应变、应变张量不变量 5.5 主剪应变,最大剪应变 5.6 应变速率 5.7 变形表示法 5.8 应力一应变曲线 5·9 变形体模型 5.10 变形协调方程 5.11 平面变形问题和轴对称问题
crack propagation
(in shear)
单元体均匀变形:直线—→直线,平行—→平行
小变形:
大变形:
103 ~ 102
102 ~ 101
例:将矩形六面体在千锤下进行撤粗,其塑性变形前后物体的形状:
图 矩形件塑性变形前后形状
第一类变形:诸棱边的相对变化,其下标表示伸长的方向或与棱边平行的轴向。
应力应变曲线材料力学讲解

坏的标志,所以屈服点 s是衡量材料强度的一
个重要指标。
(3)强化阶段 抗拉强度 b
经过屈服阶段后,曲线从c点又开始逐渐上
升,说明要使应变增加,必须增加应力,材料 又恢复了抵抗变形的能力,这种现象称作强化, ce段称为强化阶段。曲线最高点所对应的应力
明显的四个阶段 1、弹性阶段ob P — 比例极限 e — 弹性极限
E E tan
(1)弹性阶段 比例极限σ p
oa段是直线,应力与应变在此段成正比关系,材
料符合虎克定律,直线oa的斜率 tan E 就是材
料的弹性模量,直线部分最高点所对应的应力值 记作σ p,称为材料的比例极限。曲线超过a点,图 上ab段已不再是直线,说明材料已不符合虎克定 律。但在ab段内卸载,变形也随之消失,说明ab 段也发生弹性变形,所以ab段称为弹性阶段。b点 所对应的应力值记作σ e ,称为材料的弹性极限。
、 值越大,其塑性越好。一般把 ≥5%的材
料称为塑性材料,如钢材、铜、铝等;把 <5%的
材料称为脆性材料,如铸铁、混凝土、石料等。
工程应用:冷作硬化
e
d
b
b
e P
a c s
即材料在卸载过程中 应力和应变是线形关系,
f 这就是卸载定律。
材料的比例极限增高, 延伸率降低,称之为冷作硬 化或加工硬化。
塑性材料和脆性材料力学性能比较
塑性材料
脆性材料
延伸率 δ > 5%
延伸率 δ < 5%
断裂前有很大塑性变形
塑性应力学---第五章 真实应力-应变曲线

准静态塑性变形:塑性变形速率小于 2 103 妙 时 变形过程称 为准静态塑性变形。
拉伸图:简单拉伸实验中记录下来的拉伸力和试件所发生的绝 对伸长量之间的关系曲线称为拉伸图。
条件应力:单拉实验中拉伸力除以试件原始横截面积。
工程应变:单拉实验中伸长量除以试件的原始长度(标距部 分)。
真实应力:单拉实验中某一时刻的载荷除以此刻试件的横截面 积。 沈阳航空工业学院 主讲人:韩志仁
塑性成形力学基础
p
强度极限
弹性变形阶段oe(线性和非线性);
屈服应力 屈服平台 弹性极限 比例极限
均匀塑性变形阶段eb;
集中变形阶段bk;
e
沈阳航空工业学院
主讲人:韩志仁
塑性成形力学基础
5.2拉伸时真实应力-应变曲线
真实应力与条件应力(工程应力)的关系:
0(1 )
真实应变(对数应变)的特性:
塑性成形力学基础
第五章 真实应力-应变曲线
沈阳航空工业学院
主讲人:韩志仁
塑性成形力学基础
本章主要内容
• • • • 拉伸图和条件应力-应变曲线 拉伸时真实应力-应变曲线 拉伸真实应力-应变曲线塑性失稳点的特点 真实应力-应变曲线的简化模型
沈阳航空工业学院
主讲人:韩志仁
塑性成形力学基础
5.1拉伸图和条件应力-应变曲线
σ
b
1Leabharlann 沈阳航空工业学院主讲人:韩志仁
塑性成形力学基础
5.4真实应力-应变曲线的简化模型
1.理想全弹性材料
沈阳航空工业学院
主讲人:韩志仁
塑性成形力学基础 2.理想刚塑性材料
沈阳航空工业学院
主讲人:韩志仁
塑性成形力学基础
应力-应变曲线

应力-应变曲线
四、强度
1.强度是指金属材料抵抗塑性变形和断裂的能力。 2.强度特性指标主要是指屈服强度和抗拉强度。 (1)屈服强度:当材料受外力作用产生0.2%残余变形的应力,作为 该材料的屈服强度。
式中:
——材料屈服时的最小载荷, ;
——试件的原始横截面面积,;—源自屈服强度, 。应力-应变曲线
(4)强化:材料经过屈服点后,其变形抗力增大,这种现象称为强化。
应力-应变曲线
五、塑性
1.塑性:金属材料受力后在断裂之前产生塑性变形的能力。
2.塑性指标
(1)断后伸长率:
式中: ——试件拉断后的长度, ;
——试件的原始长度,
。
(2)断面收缩率:
式中: ——试件的原始横截面面积, mm2 ; ——试件拉断处的横截面面积,mm2 。
图1-6 卸荷曲线
应力-应变曲线
三、弹性
1.弹性的定义:具有弹性变形特性的材料能够发生弹性变形而不发生永久 变形的能力,称为弹性。
2.弹性模量 (1)表示引起单位应变所需的应力的大小。 (2)工程上常用弹性模量作为衡量材料刚度的指标,E越大,刚度越好。 (3)刚度是材料抵抗弹性变形的能力。 (4)材料在一定外力作用下,弹性变形越大,刚度越小,反之,其刚度 越大。 (5)弹性极限是试件在最大弹性变形时材料所承受的应力。
四、强度
(2)屈服:应力没有增加,但试件变形仍自动增长的现象称为屈服。 (3)抗拉强度:材料在断裂前所能承受的最大应力称为抗拉强度。 当应力达到抗拉强度时,试件某一部分的横截面积显著缩小。试件的变形 主要集中在该处,故抗拉强度通常被作为零件因断裂失效的设计依据。
式中: ——材料在屈服阶段后所能抵抗的最大力, ; ——试件的原始横截面面积, ; ——抗拉强度, 。
塑性变形-变化

第 六 章
第二节 单晶体的塑性变形
5. 多滑移和交滑移 (1)滑移的分类 单滑移:只有一组滑移系处于最有利的位置,进行的单 系滑移 多滑移:在多个(>2)滑移系上同时或交替进行的滑移。
第 二 节 单 晶 体 的 塑 性 变 形
单滑移
多滑移
第 六 章
第二节 单晶体的塑性变形
对于面心立方,滑移系为 {111}<110>。4个{111}面构成一 个四面体。 对所有的{111}面,φ相同, 对所有的<110>晶向,λ角都相等
e3
A E
e1 e2
C
B
(a)Tc>T>Tb A
L+A L L+C C A
(b)Te3>T>Te1 L+A+C L+A L L+B
L+C
C
B
B
(c)Te2>T>TE A L+A+C L+A L L+A+B L+B L+C L+B+C C A
(d) T=TE L+A+C L+A+B+C L+A+B L+B+C C
0
流变曲线:
S ke
n
n: 形变强化指数,n 越 大,强 化效果越大。
第 六 章
第一节 金属的变形概述
真应力-真应变曲线与标称应力-应变曲线的比较
Y ,
第 一 节 金 属 变 形 概 述
均匀变形
存在颈缩
o
—— 真实应力-对数应变曲线 —— 标称应力-对数应变曲线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/
水利水电建筑工程
工程力学
d
(2)屈服阶段 (bc段)
当应力超过弹性极限后到达某一数值时,
应变 而应力 显著增加; 先是下降, 然后作微小波动,
σ
b a
e c
ε O
在曲线上出现接近水平线的小锯齿形线段。 屈服或流动: 应力基本保持不变,
而应变显著增加
σ
b a
e c
该段内变形在外力撤销后会完全消失; O 发生的变形均称为弹性变形。 而撤去外力后仍不会消失的变形成为残余变形或塑性变形。 弹性极限 e
ε
b点所对应的应力是弹性阶段的最高值,
是材料只出现弹性变形的极限值; σe
工程力学
/
水利水电建筑工程
工程力学
工程力学
/
水利水电建筑工程
工程力学
低碳钢拉伸破坏的四个阶段
d σ b a c e
ε O
1、弹性比例阶段ob
3、强化阶段cd
工程力学
2、屈服阶段bc
4、局部颈缩阶段de
/
水利水电建筑工程
工程力学
d
(1)弹性比例阶段 (oab段)
5%
为脆性材料;
/
平均值约为20%-30%;
水利水电建筑工程
工程力学
②截面收缩率ψ:
A A1 100% A
拉断后颈缩处最小横截面面积与试件原始截面面积的比值×100%。 Q235钢:≈60%
工程力学
/
工程力学
塑性材料应力应变图
主 讲 人: 管 欣
黄河水利职业技术学院
2014.09
工程力学
/
工程力学
低碳钢拉伸时的力学性能
低碳钢是指含碳量在0.30%以下的碳素钢。
由于F—ΔL曲线与 试样的尺寸有关, 为了消除试件尺寸 的影响,可采用应 力应变曲线,即σ -ε曲线来代替F— ΔL曲线。
屈服阶段所发生的变形
工程力学
主要是塑性变形;
/
水利水电建筑工程
工程力学
屈服极限
S
d σ b a e c
上屈服极限、下屈服极限: 屈服阶段的最高应力,最低应力; 上屈服极限的数值: 与试件的形状、加载速度等因素有关, 一般是不稳定的。 下屈服极限较稳定,
水利水电建筑工程
工程力学
工程力学
/
水利水电建筑工程
d σ b a e c
σ
O
b
ε
大部分为塑性变形,
强度极限
b
是衡量材料强度的另一个重要指标;
强化阶段中最高点d点所对应的应力, 材料在拉伸破坏之前所能承受的最大应力;
工程力学
/
水利水电建筑工程
工程力学
(局部变形阶段) (4)颈缩阶段
试件内的应力超过强度极限后, 在试件的某局部范围内, 横向尺寸急剧缩小, 形成颈缩现象。
工程力学
/
水利水电建筑工程
工程力学
注意
①只有工作应力
F P A
时,
E σ 、ε之间才服从胡克定律 P e 时, ② ab段内
、
胡克定律不再成立,但仍为弹性变形;
p 相差不大, ③ 由于 e 工程中并不严格区分。
σs
O
ε
能够反映材料的力学性能,
工程力学
定义为材料的屈服极限
/
水利水电建筑工程
工程力学
45°滑移线:
表面磨光的试件会看到 出现与轴线大约成45°角的斜线,称为滑移线; 这是由于晶粒之间发生相对错动而形成的, 由最大切应力引起。 45
注意: 当试件内的应力接近材料的屈服极限时,
弹性阶段 在弹性阶段内有一段特殊的直线段 在该段内σ、ε之间呈线性关系,
称为比例阶段,也称为线弹性阶段; 在线弹性阶段内应力-应变之间满足
d
Oa段,
σ
b a
e c
ε O
E
(胡克定律)
E称为材料的弹性模量; E = tg σP 一般钢材 : E=200GPa 。 比例极限 p a点对应比例阶段的最高应力; 比例极限是应力-应变之间服从胡克定律的应力的最大值。
试件开始出现塑性变形。 屈服极限 S 塑性材料的一个重要的强度指标
工程力学
/
水利水电建筑工程
工程力学
(3)强化阶段 (cd段) 材料的强化:
过屈服强度以后, 材料又恢复了抵抗变形的能力; 要使它继续变形, 必须增大拉力。 强化阶段所发生的变形: 也有一小部分的弹性变形。
形状为杯锥状。
断面
工程力学
位于横截面,
由最大正应力引起破坏
/
水利水电建筑工程
工程力学
(5)材料的塑形指标
①延伸率δ: 试件的变形量与原长的比值×100%;
l1 l 100 0 0 l
工程中 5% 称为塑性材料; 低碳钢的伸长率
工程力学
工程力学
/
水利水电建筑工程
工程力学
颈缩阶段 (局部变形阶段)
由于横截面面积减小,
(de段)
σ b a cBiblioteka d e拉力也相应减小,
O
ε
曲线呈下降趋势;
到达e点试件被拉断。
工程力学
/
水利水电建筑工程
工程力学
拉断试件
