高中数学学案回归分析

合集下载

高中数学 3.2 回归分析学案新人教B版选修2-3(2021年整理)

2016-2017学年高中数学3.2 回归分析学案新人教B版选修2-3 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2016-2017学年高中数学3.2 回归分析学案新人教B版选修2-3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2016-2017学年高中数学3.2 回归分析学案新人教B版选修2-3的全部内容。

3.2 回归分析1。

通过对典型案例的探究，了解回归分析的基本思想、方法及其初步应用。

2。

会求回归直线方程，并用回归直线方程进行预报。

（重点难点）［基础·初探］教材整理1 回归直线方程阅读教材P83~P84探究与研究以上部分,完成下列问题。

1。

回归直线方程其中错误!的计算公式还可以写成错误!＝错误!.2.线性回归模型：y＝bx＋a＋εi,其中εi称为随机误差项，a和b是模型的未知参数，自变量x称为解释变量，因变量y称为预报变量。

设某大学的女生体重y(单位：kg）与身高x(单位：cm)具有线性相关关系.根据一组样本数据（x i，y i)（i＝1,2,…,n)，用最小二乘法建立的回归方程为错误!＝0。

85x－85.71，则下列结论中正确的是________（填序号)。

(1）y与x具有正的线性相关关系；（2）回归直线过样本点的中心(x，错误!）;(3)若该大学某女生身高增加1 cm,则其体重约增加0.85 kg；(4）若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg.【解析】回归方程中x的系数为0。

85〉0，因此y与x具有正的线性相关关系，A正确；由回归方程系数的意义可知回归直线过样本点的中心(错误!，错误!）,B正确；依据回归方程中错误!的含义可知，x每变化1个单位,错误!相应变化约0.85个单位,C正确；用回归方程对总体进行估计不能得到肯定结论，故D不正确.【答案】（1）（2)(3)教材整理2 相关性检验阅读教材P87~P89例3以上部分，完成下列问题。

高中数学必修3回归直线最新学案

回归分析一、定义1、两个变量x,y, x 变，y 也变，随x 的变化而变化，y 与x 的关系可以用一个式子来表达，我们称，x 与y 具有函数关系。

2、两个变量x,y, x 变，y 也变，随x 的变化而变化，y 与x 的关系不可以用一个式子来表达，我们称x 与y 具有相关关系。

3、相关关系是一种不确定的关系。

二、1、对于相关关系的两个变量进行分析，称之为回归分析2、两个变量的相关性可以分为正相关、负相关。

如3、上图中将两个变量的关系用一个图形表示出来，称为作散点图。

4、如果散点途中两个变量对应的点都大致分布在一条直线周围，称该相关为线性相关。

5、高中只研究线性相关。

6、具有相关关系的两个变量x,y ，一般先画散点图，再利用公式求回归直线yˆ=b ˆx+a 7、bˆ=∑∑==--i in i i ix n xy x n y x 1221，a=x b y -。

8、n x x x x n +++=...21，ny y y y n +++= (21)9、∑=+++=ni nn ii y x y x y x yx 12211...10、例题：已知产品销售量与广告投放有关，先收集近5年产品销量y 与广告费x 数据如下：（1）画出散点图（1）求回归方程yˆ=b ˆx+a （3）根据回归方程预计投放广告费x=100时，销售量Y11、相关系数r 是用来衡量相关性强弱的，|r |≤1，r=±1表示完全相关，也就是我们所说的函数关系。

12、所有的回归直线都要经过样本中心点（y x ,）。

由于样本点不可能共线，而只是散布在一条直线的周围，所以回归直线也可以用直线y=bx+a+e 来表示。

e 称随机误差。

13、因为y 可以预计下一步销售量，称之为预报变量，x 叫解释变量。

14、随机误差越小，相关性越强，当e=0,完全相关。

15、残差：已知两个变量线性相关，回归直线为 y=x+2 所对应的数据表如下求残差16、残差分布图如下：残差比较均匀的分布在一带状区域，说明回归分析拟合好，带状区域越窄，精度越高16、相关指数=2R 1-偏差平方和残差平方和，2R 越接近1,残差越小，回归拟合越好，2R =0.64，说明x 对整体的贡献为0.64，另外的0.36来自于随机误差。

高中数学回归讲解教案

高中数学回归讲解教案
教案主题：回归分析
教学目标：
1. 了解回归分析的基本概念和原理
2. 掌握简单线性回归分析和多元线性回归分析的计算方法
3. 能够应用回归分析方法解决实际问题
4. 培养学生的数理统计思维和分析能力
教学内容：
1. 回归分析的概念和基本原理
2. 简单线性回归分析
3. 多元线性回归分析
4. 实际问题的回归分析方法应用
教学步骤：
第一步：导入（5分钟）
介绍回归分析的基本概念和作用，引起学生对回归分析的兴趣和重要性。

第二步：简单线性回归分析（20分钟）
1. 讲解简单线性回归的定义和公式
2. 演示简单线性回归的计算方法
3. 给出一个简单线性回归的实例，让学生自行计算
第三步：多元线性回归分析（20分钟）
1. 讲解多元线性回归的定义和公式
2. 演示多元线性回归的计算方法
3. 给出一个多元线性回归的实例，让学生自行计算
第四步：实际问题应用（15分钟）
1. 给出一个实际问题，让学生利用回归分析方法进行分析
2. 引导学生思考回归分析在实际问题中的应用价值
第五步：总结（10分钟）
1. 总结回归分析的基本原理和方法
2. 强调回归分析在实际问题中的重要性和应用价值
3. 解答学生的问题并进行互动交流
教学反思：
通过本节课的教学，学生了解了回归分析的基本概念和原理，掌握了简单线性回归和多元线性回归的计算方法，并通过实际问题的应用进行了综合训练。

同时，也培养了学生的数理统计思维和分析能力，提高了他们解决实际问题的能力。

希望学生能够在今后的学习和工作中，充分运用回归分析方法，发挥其应用价值。

人教新课标版数学高一-学案 1.2 回归分析

1.2 回归分析1.会建立线性回归模型分析两个变量间的相关关系.2.能通过相关系数判断两个变量间的线性相关程度.1.什么叫回归分析？答回归分析是对具有相关关系的两个变量进行统计分析的一种方法. 2.回归分析中，利用回归直线方程求出的函数值一定是真实值吗？答不一定是真实值，利用线性回归方程求的值，在很多时候是个预报值，例如，人的体重与身高存在一定的线性关系，但体重除了受身高的影响外，还受其他因素的影响，如饮食、是否喜欢运动等.1.回归直线方程在回归直线方程y ^＝a ^＋b ^x 中，b ^＝i ＝1n (x i －x )(y i －y )i ＝1n (x i －x )2＝∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n x2，a ^＝y －b ^x .其中x ＝1n ∑i ＝1n x i ，y ＝1n ∑i ＝1ny i ，(x ，y )称为样本点的中心，回归直线过样本点的中心. 2.相关系数对于变量x 与y 随机抽到的n 对数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，检测统计量是样本相关系数r ＝i ＝1n (x i －x )(y i －y )i ＝1n (x i －x )2i ＝1n (y i －y )2＝∑i ＝1nx i y i －n x y(∑i ＝1nx 2i －n x 2)(∑i ＝1ny2i －n y 2)相关系数r 的取值范围是[－1,1]，|r |越接近1，变量之间的线性相关程度越高，|r |越接近0，线性相关程度越弱，当|r |>r 0.05时，有95%的把握认为两个变量之间有线性相关关系. 3.非线性回归分析回归曲线方程也可以线性化(1)将幂函数型函数y ＝ax n (a 为常数，a ，x ，y 均取正值)化为线性函数：将y ＝ax n 两边取常用对数，则有lg y ＝n lg x ＋lg a ，令μ＝lg y ，v ＝lg x ，b ＝lg a ，代入上式得μ＝n v ＋b (其中n 、b 是常数)，其图象是一条直线.(2)将指数型函数y ＝ca x (a ＞0，c ＞0，a ，c 为常数)化为线性函数；将y ＝ca x 两边取常用对数，则有lg y ＝x lg a ＋lg c ，令μ＝lg y ，b ＝lg c ，d ＝lg a ，代入上式得μ＝dx ＋b (d ，b 是常数)，它的图象是一条直线.要点一求回归直线方程例1 某班5名学生的数学和物理成绩如下表：(1)画出散点图；(2)求物理成绩y 对数学成绩x 的回归直线方程； (3)一名学生的数学成绩是96，试预测他的物理成绩. 解 (1)散点图如图.(2)x ＝15×(88＋76＋73＋66＋63)＝73.2，y ＝15×(78＋65＋71＋64＋61)＝67.8.∑i ＝15x i y i ＝88×78＋76×65＋73×71＋66×64＋63×61＝25054.∑i ＝15x 2i ＝882＋762＋732＋662＋632＝27174.所以b ^＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x2＝25054－5×73.2×67.827174－5×73.22≈0.625.a ^＝y －b ^x ≈67.8－0.625×73.2＝22.05. 所以y 对x 的回归直线方程是y ^＝0.625x ＋22.05. (3)x ＝96，则y ^＝0.625×96＋22.05≈82，即可以预测他的物理成绩是82.规律方法 (1)散点图是定义在具有相关关系的两个变量基础上的，对于性质不明确的两组数据，可先作散点图，在图上看它们有无关系，关系的密切程度，然后再进行相关回归分析. (2)求回归直线方程，首先应注意到，只有在散点图大致呈线性时，求出的回归直线方程才有实际意义，否则，求出的回归直线方程毫无意义.跟踪演练1 某研究机构对高三学生的记忆力x 和判断力y 进行统计分析，得下表数据：(1)请画出上表数据的散点图((2)请根据上表提供的数据，用最小二乘法求出y 关于x 的回归直线方程y ^＝b ^x ＋a ^； (3)试根据求出的回归直线方程，预测记忆力为9的同学的判断力.解 (1)如图：(2)∑ni ＝1x i y i ＝6×2＋8×3＋10×5＋12×6＝158， x ＝6＋8＋10＋124＝9，y ＝2＋3＋5＋64＝4，∑ni ＝1x 2i ＝62＋82＋102＋122＝344， b ^＝158－4×9×4344－4×92＝1420＝0.7，a ^＝y －b ^x ＝4－0.7×9＝－2.3，故回归直线方程为y ^＝0.7x －2.3.(3)由②中回归直线方程当x ＝9时，y ^＝0.7×9－2.3＝4，预测记忆力为9的同学的判断力约为4.要点二相关性检验例2 下面的数据是从年龄在40到60岁的男子中随机抽出的6个样本，分别测定了心脏的功能水平y (满分100)以及每天花在看电视上的平均时间x (小时).(1)(2)求心脏的功能水平y 与每天花在看电视上的平均时间x 的回归直线方程，并讨论方程是否有意义；(3)估计平均每天看电视3小时的男子的心脏的功能水平. 解 n ＝6，x ＝16(4.4＋4.6＋…＋4.6)≈3.7167，y ＝16(52＋53＋…＋65)≈64.1667，∑i ＝16x 2i －6(x )2＝(4.42＋4.62＋…＋4.62)－6×3.71672≈19.7668，∑i ＝16y 2i －6(y )2＝(522＋532＋…＋652)－6×64.16672≈964.8077，∑i ＝16x i y i －6x y ＝(4.4×52＋4.6×53＋…＋4.6×65)－6×3.7167×64.1667≈－124.6302.(1)心脏的功能水平y 与每天花在看电视上的平均时间x 之间的相关系数r ＝∑i ＝16x i y i －6x y(∑i ＝16x 2i －6(x )2)(∑i ＝16y 2i －6(y )2)≈－124.630219.7668×964.8077≈－0.9025.(2)b ^＝∑i ＝16x i y i －6x y∑i ＝16x 2i －6(x )2≈－124.630219.7668≈－6.3050，a ^＝y －b ^x ≈64.1667＋6.3050×3.7167≈87.6005，所以心脏的功能水平y 与每天花在看电视上的平均时间x 的回归直线方程为y ^＝－6.3050x ＋87.6005.查表n －2＝4，r 0.05＝0.811，因为|r |≈0.9025>0.811，所以有95%以上的把握认为y 与x 之间有线性关系，这个方程是有意义的.(3)将x ＝3代入回归直线方程y ^＝－6.3050x ＋87.6005可得y ^≈69(分).因此估计平均每天看电视3小时的男子的心脏的功能水平为69分.规律方法解决这一类问题时，首先应对问题进行必要的相关性检验，如果不作相关性检验，我们仍然可以求出x 与y 的回归直线方程，但不知道这时的回归直线方程是否有意义，也就不知道能否反映变量x 与y 之间的变化规律，只有在x 与y 之间具有相关关系时，求得的回归直线方程才有意义.跟踪演练2 维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y 来衡量，这个指标越高，耐热水性能也越好，而甲醛浓度是影响缩醛化度的重要因素，在生产中常用甲醛浓度x (g/L)去控制这一指标，为此必须找出它们之间的关系，现安排一批实验，获得如下数据.(2)求回归直线方程；(3)求相关系数r ，并进行相关性检验. 解 (1)(2)列表：x ＝1687＝24，y ＝202.947，b ^＝∑i ＝17x i y i －7x y∑i ＝17x 2i －7(x )2＝4900.16－7×24×202.9474144－7×242＝0.2643，a ^＝y －b ^x ＝202.947－0.2643×24≈22.648，∴回归直线方程为y ^＝22.648＋0.2643x . (3)∑i ＝17y 2i ＝5892，r ＝∑i ＝17x i y i －7x y(∑i ＝17x 2i －7(x )2)(∑i ＝17y 2i －7(y )2)＝4900.16－7×24×202.947(4144－7×242)×(5892－7×(202.947)2)＝0.96.计算得r ＝0.96>r 0.05＝0.754.说明甲醛浓度与缩醛化度两个变量之间有较强的线性相关关系. 要点三非线性回归模型例3 某地区不同身高的未成年男性的体重平均值如下表：解根据上表中数据画出散点图如图所示.由图看出，样本点分布在某条指数型函数曲线y ＝c 12e c x的周围，于是令z ＝ln y .由计算器计算可得下表，由表中数据可得z 与x 之间的回归直线方程： z ^＝0.693＋0.020x ，则有y ^＝e 0.693＋0.020x .规律方法根据已有的函数知识，可以发现样本分布在某一条指数型函数曲线y ＝c 12e c x的周围，其中c 1和c 2是待定参数；可以通过对x 进行对数变换，转化为线性相关关系. 跟踪演练3 某种书每册的成本费Y (元)与印刷册数x (千册)有关，经统计得到数据如下：检验每册书的成本费Y 与印刷册数的倒数1x之间是否具有线性相关关系？若有，求出Y 对x的回归方程；若无，说明理由.解设μ＝1x ，则Y 与μ的数据关系如下表所示：0.05＝0.632.从而有95%的把握认为这两个变量具有线性相关关系，从而求Y 与μ的回归直线方程有意义.又b ^＝Σ10i ＝1μi y i －10μy Σ10i ＝1μ2i －10μ2＝15.20878－10×0.2248×3.141.413014－10×0.22482≈8.98， a ^＝y －b ^μ＝3.14－8.98×0.2248＝1.12，所以y 关于μ的回归直线方程为y ^＝1.12＋8.98μ，Y 与x 的回归方程为y ^＝1.12＋8.98x.1.下列各组变量之间具有线性相关关系的是( ) A.出租车费与行驶的里程 B.学习成绩与学生身高 C.身高与体重 D.铁的体积与质量答案 C2.若劳动生产率x (千元)与月工资y (元)之间的回归直线方程为y ^＝50＋80x ，则下列判断正确的是( )A.劳动生产率为1000元时，月工资为130元B.劳动生产率提高1000元时，月工资平均提高80元C.劳动生产率提高1000元时，月工资平均提高130元D.月工资为210元时，劳动生产率为2000元答案 B3.某商品销售量y (件)与销售价格x (元/件)负相关，则其回归直线方程可能是( ) A.y ^＝－10x ＋200 B.y ^＝10x ＋200 C.y ^＝－10x －200D.y ^＝10x －200答案 A解析由于销售量y 与销售价格x 成负相关，故排除B.D.又当x ＝10时，A 中y ＝100，而C 中y ＝－300，C 不符合实际情况，故选A.4.某电脑公司有6名产品推销员，其工作年限与年推销金额数据如下表：(1)求年推销金额y (2)若第6名推销员的工作年限为11年，试估计他的年推销金额. 解 (1)设所求的回归直线方程为y ^＝b ^x ＋a ^，则b ^＝i ＝15(x i －x )(y i －y )i ＝15(x i －x )2＝1020＝0.5， a ^＝y －b ^x ＝0.4.所以年推销金额y 关于工作年限x 的回归直线方程为y ^＝0.5x ＋0.4. (2)当x ＝11时，y ^＝0.5x ＋0.4＝0.5×11＋0.4＝5.9(万元). 所以可以估计第6名推销员的年推销金额为5.9万元.回归分析的基本思路：(1)确定研究对象，明确哪个变量是解释变量，哪个变量是预报变量；(2)画出确定好的解释变量和预报变量的散点图，观察它们之间的关系(如是否存在线性关系等)；(3)由经验确定回归方程的类型(如果呈线性关系，则选用回归直线方程y ^＝b ^x ＋a ^)； (4)按一定规则估计回归方程中的参数.。

高中数学 3.2 回归分析教案2 苏教版选修23

3.2回归分析（2）教学目标（1）通过实例了解相关系数的概念和性质，感受相关性检验的作用；（2）能对相关系数进行显著性检验，并解决简单的回归分析问题；（3）进一步了解回归的基本思想、方法及初步应用．教学重点，难点相关系数的性质及其显著性检验的基本思想、操作步骤．教学过程一．问题情境1．情境：下面是一组数据的散点图，若求出相应的线性回归方程，求出的线性回归方程可以用作预测和估计吗？2．问题：思考、讨论：求得的线性回归方程是否有实际意义．二．学生活动对任意给定的样本数据，由计算公式都可以求出相应的线性回归方程，但求得的线性回归方程未必有实际意义．左图中的散点明显不在一条直线附近，不能进行线性拟合，求得的线性回归方程是没有实际意义的；右图中的散点基本上在一条直线附近，我们可以粗略地估计两个变量间有线性相关关系，但它们线性相关的程度如何，如何较为精确地刻画线性相关关系呢？这就是上节课提到的问题①，即模型的合理性问题．为了回答这个问题，我们需要对变量x 与y 的线性相关性进行检验（简称相关性检验）．三．建构数学1．相关系数的计算公式：对于x ，y 随机取到的n 对数据(,)i i x y (1,2,3,,)i n =L ，样本相关系数r 的计算公式为112222221111()()()()(())(())nniii ii i n nn niii i i i i i x x y y x y nx yr x x y y x n x y n y ======---==-⋅-⋅--∑∑∑∑∑∑．()22．相关系数r 的性质：246810051015系0246810051015（1）||1r ≤；（2）||r 越接近与1，x ，y 的线性相关程度越强；（3）||r 越接近与0，x ，y 的线性相关程度越弱．可见，一条回归直线有多大的预测功能，和变量间的相关系数密切相关． 3．对相关系数r 进行显著性检验的步骤：相关系数r 的绝对值与1接近到什么程度才表明利用线性回归模型比较合理呢？这需要对相关系数r 进行显著性检验．对此，在统计上有明确的检验方法，基本步骤是：（1）提出统计假设0H ：变量x ，y 不具有线性相关关系；（2）如果以95%的把握作出推断，那么可以根据10.950.05-=与2n -（n 是样本容量）在附录2（教材P111）中查出一个r 的临界值0.05r （其中10.950.05-=称为检验水平）；（3）计算样本相关系数r ；（4）作出统计推断：若0.05||r r >，则否定0H ，表明有95%的把握认为变量y 与x 之间具有线性相关关系；若0.05||r r ≤，则没有理由拒绝0H ，即就目前数据而言，没有充分理由认为变量y 与x 之间具有线性相关关系．说明：1．对相关系数r 进行显著性检验，一般取检验水平0.05α=，即可靠程度为95%． 2．这里的r 指的是线性相关系数，r 的绝对值很小，只是说明线性相关程度低，不一定不相关，可能是非线性相关的某种关系．3．这里的r 是对抽样数据而言的．有时即使||1r =，两者也不一定是线性相关的．故在统计分析时，不能就数据论数据，要结合实际情况进行合理解释． 4．对于上节课的例1,可按下面的过程进行检验：（1）作统计假设0H ：x 与y 不具有线性相关关系；（2）由检验水平0.05与29n -=在附录2中查得0.050.602r =；（3）根据公式()2得相关系数0.998r =；（4）因为0.9980.602r =>，即0.05r r >，所以有95﹪的把握认为x 与y 之间具有线性相关关系,线性回归方程为$527.59114.453y x =+是有意义的．四．数学运用 1．例题：例1．下表是随机抽取的8对母女的身高数据,试根据这些数据探讨y与x之间的关系．母亲身高/x cm154157158159160161162163女儿身高/y cm155156159162161164165166解：所给数据的散点图如图所示：由图可以看出，这些点在一条直线附近，因为()1541571638159.25x=+++÷=L，()1551561668161y=+++÷=L，()82222218()1541638159.2559.5iix x=-=++-⨯=∑L，()82222218()1551668161116iiy y=-=++-⨯=∑L，()8181541551631668159.2516180i iix y x y=-⨯++⨯-⨯⨯=∑L，所以963.01165.5980≈⨯=r，由检验水平0.05及26n-=，在附录2中查得707.005.0=r，因为0.9630.707>,所以可以认为x与y之间具有较强的线性相关关系．线性回归模型y a bxε=++中,a b 的估计值$,a b$分别为()81822181.345,8i iiiix y x ybx x==-=≈-∑∑$53.191a y bx=-≈-$，故y对x的线性回归方程为xy345.1191.53+-=)．例2．要分析学生高中入学的数学成绩对高一年级数学学习的影响，在高一年级学生中学生编号1 2 3 4 5 6 7 8 9 10入学成绩x 63 67 45 88 81 71 52 99 58 76 高一期末成绩y65 78 52 82 92 89 73 98 56 75 x y （2）如果x 与y 之间具有线性相关关系，求线性回归方程；（3）若某学生入学数学成绩为80分，试估计他高一期末数学考试成绩．解：(1)因为()16367767010x =⨯+++=L ，()16578757610y =⨯+++=L ，101()()1894xy i i i L x x y y ==--=∑，2101()2474xx i i L x x ==-=∑，1021()2056yy i i L y y ==-=∑．因此求得相关系数为10110102211()()0.840()()iii xx yyi i i i x x y y L r L L x x y y ===--===--∑∑∑．结果说明这两组数据的相关程度是比较高的；小结解决这类问题的解题步骤：（1）作出散点图，直观判断散点是否在一条直线附近；（2）求相关系数r ；（3）由检验水平和2n -的值在附录中查出临界值，判断y 与x 是否具有较强的线性相关关系；（4）计算$a，b $，写出线性回归方程． 2．练习：104P 练习第1题．五．回顾小结：1．相关系数的计算公式与回归系数b$计算公式的比较； 2．相关系数的性质；3．探讨相关关系的基本步骤．六．课外作业：106P 习题3.2第1题．。

人教版高中数学全套教案导学案3.2 回归分析(1)

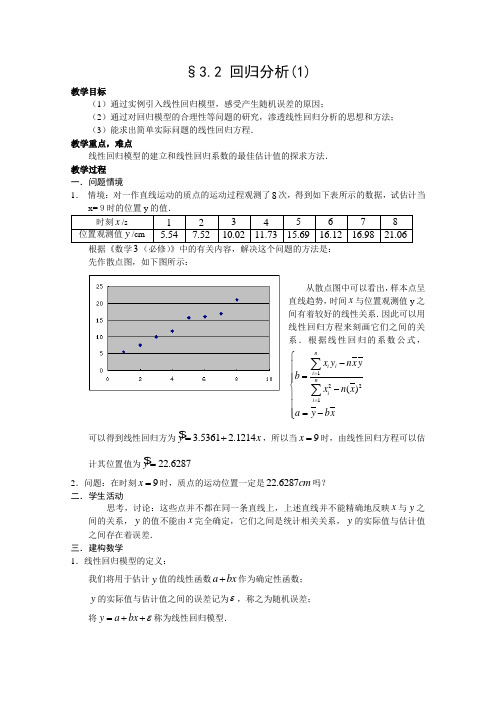
§3.2 回归分析(1)教学目标（1）通过实例引入线性回归模型，感受产生随机误差的原因；（2）通过对回归模型的合理性等问题的研究，渗透线性回归分析的思想和方法；（3）能求出简单实际问题的线性回归方程．教学重点，难点线性回归模型的建立和线性回归系数的最佳估计值的探求方法．教学过程一．问题情境1．情境：对一作直线运动的质点的运动过程观测了8次，得到如下表所示的数据，试估计当根据《数学（必修）》中的有关内容，解决这个问题的方法是：先作散点图，如下图所示：从散点图中可以看出，样本点呈直线趋势，时间x 与位置观测值y 之间有着较好的线性关系．因此可以用线性回归方程来刻画它们之间的关系．根据线性回归的系数公式，1221()ni i i n i i x y nx y b x n x a y bx==⎧-⎪⎪=⎪⎨-⎪⎪=-⎪⎩∑∑ 可以得到线性回归方为 3.5361 2.1214y x =+，所以当9x =时，由线性回归方程可以估计其位置值为22.6287y =2．问题：在时刻9x =时，质点的运动位置一定是22.6287cm 吗？二．学生活动思考，讨论：这些点并不都在同一条直线上，上述直线并不能精确地反映x 与y 之间的关系，y 的值不能由x 完全确定，它们之间是统计相关关系，y 的实际值与估计值之间存在着误差．三．建构数学1．线性回归模型的定义：我们将用于估计y 值的线性函数a bx +作为确定性函数；y 的实际值与估计值之间的误差记为ε，称之为随机误差；将y a bx ε=++称为线性回归模型．说明：（1）产生随机误差的主要原因有：①所用的确定性函数不恰当引起的误差； ②忽略了某些因素的影响； ③存在观测误差．（2）对于线性回归模型，我们应该考虑下面两个问题： ①模型是否合理（这个问题在下一节课解决）； ②在模型合理的情况下，如何估计a ，b ？ 2．探求线性回归系数的最佳估计值：对于问题②，设有n 对观测数据(,)i i x y (1,2,3,,)i n =，根据线性回归模型，对于每一个i x ，对应的随机误差项()i i i y a bx ε=-+，我们希望总误差越小越好，即要使21nii ε=∑越小越好．所以，只要求出使21(,)()niii Q y x αββα==--∑取得最小值时的α，β值作为a ，b 的估计值，记为a ，b ．注：这里的i ε就是拟合直线上的点(),i i x a bx +到点(),i i i P x y 的距离．用什么方法求a ，b ？回忆《数学3（必修）》“2．4线性回归方程”P71“热茶问题”中求a ，b 的方法：最小二乘法．利用最小二乘法可以得到a ，b 的计算公式为1122211()()()()nni i i ii i n ni ii i x x y y x y nx yb x x xn x a y bx====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑，其中11n i i x x n ==∑，11ni i y y n ==∑由此得到的直线y a bx =+就称为这n 对数据的回归直线，此直线方程即为线性回归方程．其中a ，b 分别为a ，b 的估计值，a 称为回归截距，b 称为回归系数，y 称为回归值．在前面质点运动的线性回归方程 3.5361 2.1214y x =+中， 3.5361a =， 2.1214b =． 3．线性回归方程y a bx =+中a ，b 的意义是：以a 为基数，x 每增加1个单位，y 相应地平均增加b 个单位；4．化归思想（转化思想）在实际问题中，有时两个变量之间的关系并不是线性关系，这就需要我们根据专业知识或散点图，对某些特殊的非线性关系，选择适当的变量代换，把非线性方程转化为线性回归方程，从而确定未知参数．下面列举出一些常见的曲线方程，并给出相应的化为线性回归方程的换元公式．（1）b y a x =+，令'y y =，1'x x=，则有''y a bx =+．（2）by ax =，令'ln y y =，'ln x x =，'ln a a =，则有'''y a bx =+．（3）bxy ae =，令'ln y y =，'x x =，'ln a a =，则有'''y a bx =+．（4）b x y ae =，令'ln y y =，1'x x=，'ln a a =，则有'''y a bx =+．（5）ln y a b x =+，令'y y =，'ln x x =，则有''y a bx =+．四．数学运用 1．例题：例1．下表给出了我国从1949年至1999年人口数据资料，试根据表中数据估计我国2004年的人口数．解：为了简化数据，先将年份减去1949，并将所得值用x 表示，对应人口数用y 表示，作出11个点(),x y 构成的散点图，由图可知，这些点在一条直线附近，可以用线性回归模型y a bx ε=++来表示它们之间的关系．根据公式（1）可得14.453,527.591.b a ⎧≈⎪⎨≈⎪⎩ 这里的,a b 分别为,a b 的估计值，因此线性回归方程为527.59114.453y x =+由于2004年对应的55x =,代入线性回归方程527.59114.453y x =+可得1322.50y =（百万），即2004年的人口总数估计为13.23亿. 例2．某地区对本地的企业进行了一次抽样调查，下表是这次抽查中所得到的各企业的人均资本x （万元）与人均产出y （万元）的数据：（1）设y 与x 之间具有近似关系by ax ≈（,a b 为常数），试根据表中数据估计a 和b 的值；（2）估计企业人均资本为16万元时的人均产出（精确到0.01）．分析：根据x ，y 所具有的关系可知，此问题不是线性回归问题，不能直接用线性回归方程处理．但由对数运算的性质可知，只要对by ax ≈的两边取对数，就能将其转化为线性关系．解（1）在by ax ≈的两边取常用对数，可得lg lg lg y a b x ≈+，设lg y z =，lg a A =，lg x X =，则z A bX ≈+．相关数据计算如图327--所示．仿照问题情境可得A ，b 的估计值A ，b 分别为0.2155,1.5677,A b ⎧=-⎪⎨=⎪⎩由lg 0.2155a =-可得0.6088a ≈，即a ，b 的估计值分别为0.6088和1.5677．（2）由（1）知1.56770.6088y x =．样本数据及回归曲线的图形如图328--（见书本102P页）当16x =时， 1.56770.60881647.01y =⨯≈（万元），故当企业人均资本为16万元时，人均产值约为47.01万元．2．练习：104P 练习第1题．五．回顾小结：1．线性回归模型y a bx ε=++与确定性函数y a bx =+相比，它表示y 与x 之间是统计相关关系（非确定性关系）其中的随机误差ε提供了选择模型的准则以及在模型合理的情况下探求最佳估计值a ，b 的工具；2．线性回归方程y a bx =+中a ，b 的意义是：以a 为基数，x 每增加1个单位，y 相应地平均增加b 个单位； 3．求线性回归方程的基本步骤．六．课外作业：106P 第2题．。

北师大版高中数学导学案《回归分析》

§1.1回归分析一、学习目标1、理解两个变量间的函数关系与相关关系的区别；（重点）2、通过对案例的探究，会对两个随机变量进行线性回归分析；（重点）3、理解相关系数的含义，户计算两个随机变量的线性相关系数，会通过线性相关系数判断它们之间的线性相关程度；（重点）4、通过对数据之间的散点图的观察，能够对两个随机变量进行可线性化的回归分析。

（难点）二、自主学习（预习教材，找出疑惑之处）复习：1.相关关系概念： . 2.回归分析的相关概念：回归分析是处理两个变量之间的一种统计方法．若两个变量之间具有线性相关关系，则称相应的回归分析为．3. 回归直线方程其中=∧b，=∧a，恒过定点新课：4.平均值的符号表示：假设样本点为()(),,,,2211y x y x …()n n y x , ，在统计上，用x 表示一组数据,,21x x …n x 的平均值，即x = = ，用y 表示一组数据,,21y y …n y 的平均值，即y = = 。

5. 参数a ，b 的求法：==xxxy l l b =。

=a 。

6.相关系数的计算：假设两个随机变量的数据分别为()(),,,,2211y x y x …()n n y x , ，则变量间线性相关系数==yyxx xy l l l r= 。

7.相关系数的性质：① r 的取值范围：；② |r|值越大，误差Q 越小，变量之间的线性相关程度越； ③ |r|值越接近0，误差Q 越大，变量之间的线性相关程度越； ④ 相关性的分类：，，。

8.可线性化的回归分析：Ⅰ 幂函数曲线如何做变化？变换公式？变换后的线性函数为什么？ Ⅱ 指数曲线，倒指数曲线，对数曲线呢？三、典例分析例1 从某大学中随机选取8名女大学生，其身高和体重数据如下表所示：生的体重.提示：第一步：作散点图第二步：求回归方程第三步：代值计算探究一如何理解回归直线方程中的系数b ∧，a ∧？探究二身高为172cm 的女大学生的体重一定是60.316kg 吗？例2 为分析学生初中升高中的数学成绩对高一数学学习的成绩，在高一年级随机抽取10（1）画出散点图；（2）对变量x 与y 进行相关性检验，如果x 与y 之间具有线性相关关系求出回归直线方程；（3）若某学生入学的数学成绩为80分，试估计他在高一期末考试中的数学成绩。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

§3.2 回归分析(1)
教学目标
（1）通过实例引入线性回归模型，感受产生随机误差的原因；
（2）通过对回归模型的合理性等问题的研究，渗透线性回归分析的思想和方法；（3）能求出简单实际问题的线性回归方程．教学重点，难点
线性回归模型的建立和线性回归系数的最佳估计值的探求方法．教学过程
一．问题情境
1．情境：对一作直线运动的质点的运动过程观测了8次，得到如下表所示的数据，试估计当
根据《数学（必修）》中的有关内容，解决这个问题的方法是：先作散点图，如下图所示：
从散点图中可以看出，样本点呈直线趋势，时间x 与位置观测值y 之间有着较好的线性关系．因此可以用线性回归方程来刻画它们之间的关系．根据
线性回归的系数公式，
1
221()n
i i i n i i x y nx y b x n x a y bx
==⎧
-⎪
⎪=⎪⎨-⎪⎪=-⎪⎩∑∑ 可以得到线性回归方为 3.5361 2.1214y x =+，所以当9x =时，由线性回归方程可以估计其位置值为22.6287y =
2．问题：在时刻9x =时，质点的运动位置一定是22.6287cm 吗？
二．学生活动
思考，讨论：这些点并不都在同一条直线上，上述直线并不能精确地反映x 与y 之间的关系，y 的值不能由x 完全确定，它们之间是统计相关关系，y 的实际值与估计值之间存在着误差．三．建构数学
1．线性回归模型的定义：
我们将用于估计y 值的线性函数a bx +作为确定性函数；
y 的实际值与估计值之间的误差记为ε，称之为随机误差；
将y a bx ε=++称为线性回归模型．
说明：（1）产生随机误差的主要原因有：
①所用的确定性函数不恰当引起的误差； ②忽略了某些因素的影响； ③存在观测误差．
（2）对于线性回归模型，我们应该考虑下面两个问题： ①模型是否合理（这个问题在下一节课解决）； ②在模型合理的情况下，如何估计a ，b ？ 2．探求线性回归系数的最佳估计值：
对于问题②，设有n 对观测数据(,)i i x y (1,2,3,
,)i n =，根据线性回归模型，对于
每一个i x ，对应的随机误差项()i i i y a bx ε=-+，我们希望总误差越小越好，即要使
2
1
n
i
i ε
=∑越小越好．所以，只要求出使2
1
(,)()
n
i
i
i Q y x αββα==
--∑取得最小值时的α，β值作
为a ，b 的估计值，记为a ，b ．
注：这里的i ε就是拟合直线上的点(),i i x a bx +到点(),i i i P x y 的距离．用什么方法求a ，b ？
回忆《数学3（必修）》“2．4线性回归方程”P71“热茶问题”中求a ，b 的方法：最小二乘法．
利用最小二乘法可以得到a ，b 的计算公式为
1
1
22211
()()()()n
n
i i i i
i i n n
i i
i i x x y y x y nx y
b x x x
n x a y bx
====⎧
---⎪
⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑，
其中11n i i x x n ==∑，1
1n
i i y y n ==∑
由此得到的直线y a bx =+就称为这n 对数据的回归直线，此直线方程即为线性回归方程．其中a ，b 分别为a ，b 的估计值，a 称为回归截距，b 称为回归系数，y 称为回归值．
在前面质点运动的线性回归方程 3.5361 2.1214y x =+中， 3.5361a =， 2.1214b =． 3．线性回归方程y a bx =+中a ，b 的意义是：以a 为基数，x 每增加1个单位，y 相应地
平均增加b 个单位；
4．化归思想（转化思想）
在实际问题中，有时两个变量之间的关系并不是线性关系，这就需要我们根据专业知识或散点图，对某些特殊的非线性关系，选择适当的变量代换，把非线性方程转化为线性回归方程，从而确定未知参数．下面列举出一些常见的曲线方程，并给出相应的化为线性回归方程的换元公式．（1）b y a x =+
，令'y y =，1
'x x
=，则有''y a bx =+．（2）b
y ax =，令'ln y y =，'ln x x =，'ln a a =，则有'''y a bx =+．（3）bx
y ae =，令'ln y y =，'x x =，'ln a a =，则有'''y a bx =+．（4）b x y ae =，令'ln y y =，1
'x x
=
，'ln a a =，则有'''y a bx =+．（5）ln y a b x =+，令'y y =，'ln x x =，则有''y a bx =+．
四．数学运用 1．例题：
例1．下表给出了我国从1949年至1999年人口数据资料，试根据表中数据估计我国2004年的人口数．
解：为了简化数据，先将年份减去1949，并将所得值用x 表示，对应人口数用
y 表示，
作出11个点(),x y 构成的散点图，
由图可知，这些点在一条直线附近，可以用线性回归模型y a bx ε=++来表示它们之间的关系．
根据公式（1）可得
14.453,
527.591.
b a ⎧≈⎪⎨
≈⎪⎩ 这里的,a b 分别为,a b 的估计值，因此线性回归方程为527.59114.453y x =+
由于2004年对应的55x =,代入线性回归方程527.59114.453y x =+可得1322.50
y =（百万），即2004年的人口总数估计为13.23亿. 例2．某地区对本地的企业进行了一次抽样调查，下表是这次抽查中所得到的各企业的
人均资本x （万元）与人均产出y （万元）的数据：
（1）设y 与x 之间具有近似关系b
y ax ≈（,a b 为常数），试根据表中数据估计a 和b 的值；（2）估计企业人均资本为16万元时的人均产出（精确到0.01）．
分析：根据x ，y 所具有的关系可知，此问题不是线性回归问题，不能直接用线性回归方
程处理．但由对数运算的性质可知，只要对b
y ax ≈的两边取对数，就能将其转化为线性关系．
解（1）在b
y ax ≈的两边取常用对数，可得lg lg lg y a b x ≈+，设lg y z =，lg a A =，
lg x X =，则z A bX ≈+．相关数据计算如图327--所示．
仿照问题情境可得A ，b 的估计值A ，b 分别为0.2155,
1.5677,
A b ⎧=-⎪⎨=⎪⎩由lg 0.2155a =-可得
0.6088a ≈，即a ，b 的估计值分别为0.6088和1.5677．
（2）由（1）知1.56770.6088y x =．样本数据及回归曲线的图形如图328--（见书本102P
页）
当16x =时， 1.56770.60881647.01y =⨯≈（万元），故当企业人均资本为16万元时，人均产值约为47.01万元．
2．练习：104P 练习第1题．五．回顾小结：
1．线性回归模型y a bx ε=++与确定性函数y a bx =+相比，它表示y 与x 之间是统计相
关关系（非确定性关系）其中的随机误差ε提供了选择模型的准则以及在模型合理的情况下探求最佳估计值a ，b 的工具；
2．线性回归方程y a bx =+中a ，b 的意义是：以a 为基数，x 每增加1个单位，y 相应地
平均增加b 个单位； 3．求线性回归方程的基本步骤．六．课外作业：106P 第2题．。