立体几何练习题精
立体几何经典大题(各个类型的典型题目)

1.如图,已知△ABC 是正三角形,EA ,CD 都垂直于平面ABC ,且EA =AB =2a ,DC =a ,F 是BE 的中点.(1)FD ∥平面ABC ;(2)AF ⊥平面EDB .2.已知线段PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点。
(1)求证:MN //平面PAD ; (2)当∠PDA =45°时,求证:MN ⊥平面PCD ;F CBAEDA B C D EF 3.如图,在四面体ABCD 中,CB=CD,BD AD ⊥,点E ,F 分别是AB,BD 的中点.求证: (1)直线EF// 面ACD ; (2)平面⊥EFC 面BCD .4.在斜三棱柱A 1B 1C 1—ABC 中,底面是等腰三角形,AB =AC ,侧面BB 1C 1C ⊥底面ABC (1)若D 是BC 的中点,求证 AD ⊥CC 1;(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1, 求证 截面MBC 1⊥侧面BB 1C 1C ;(3)AM =MA 1是截面MBC 1⊥平面BB 1C 1C 的充要条件吗?请你叙述判断理由]立体几何大题训练(3)C15. 如图,在正方体ABCD —A 1B 1C 1D 1中,M 、N 、G 分别是A 1A ,D 1C ,AD 的中点. 求证:(1)MN//平面ABCD ; (2)MN ⊥平面B 1BG .6. 如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点. (1)求证:EF ∥平面CB 1D 1;(2)求证:平面CAA 1C 1⊥平面CB 1D 1.立体几何大题训练(4)7、如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,AB=4,BC=CD=2,AA 1=2,_ G_ M _ D_1_ C_1_ B_1_ A_1_ N_ D _ C_ B _ ABA 1FE、E1分别是棱AD、AA1的中点(1)设F是棱AB的中点,证明:直线EE1∥面FCC1;(2)证明:平面D1AC⊥面BB1C1C。
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
高中数学必修二第八章立体几何初步考点精题训练(带答案)

高中数学必修二第八章立体几何初步考点精题训练单选题1、南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5m时,相应水面的面积为140.0km2;水位为海拔157.5m时,相应水面的面积为180.0km2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m上升到157.5m时,增加的水量约为(√7≈2.65)()A.1.0×109m3B.1.2×109m3C.1.4×109m3D.1.6×109m3答案:C分析:根据题意只要求出棱台的高,即可利用棱台的体积公式求出.依题意可知棱台的高为MN=157.5−148.5=9(m),所以增加的水量即为棱台的体积V.棱台上底面积S=140.0km2=140×106m2,下底面积S′=180.0km2=180×106m2,∴V=13ℎ(S+S′+√SS′)=13×9×(140×106+180×106+√140×180×1012)=3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3).故选:C.2、如图已知正方体ABCD−A1B1C1D1,M,N分别是A1D,D1B的中点,则()A.直线A1D与直线D1B垂直,直线MN//平面ABCDB.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1C.直线A1D与直线D1B相交,直线MN//平面ABCDD.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1答案:A分析:由正方体间的垂直、平行关系,可证MN//AB,A1D⊥平面ABD1,即可得出结论.连AD1,在正方体ABCD−A1B1C1D1中,M是A1D的中点,所以M为AD1中点,又N是D1B的中点,所以MN//AB,MN⊄平面ABCD,AB⊂平面ABCD,所以MN//平面ABCD.因为AB不垂直BD,所以MN不垂直BD则MN不垂直平面BDD1B1,所以选项B,D不正确;在正方体ABCD−A1B1C1D1中,AD1⊥A1D,AB⊥平面AA1D1D,所以AB⊥A1D,AD1∩AB=A,所以A1D⊥平面ABD1,D1B⊂平面ABD1,所以A1D⊥D1B,且直线A1D,D1B是异面直线,所以选项C错误,选项A正确.故选:A.小提示:关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.3、在正方体ABCD −A 1B 1C 1D 1中,三棱锥A −B 1CD 1的表面积为4√3,则正方体外接球的体积为( )A .4√3πB .√6πC .32√3πD .8√6π答案:B解析:根据三棱锥的表面积进一步求出正方体的棱长,最后求出正方体的外接球的半径,进一步求出结果. 解:设正方体的棱长为a ,则B 1D 1=AC =AB 1=AD 1=B 1C =D 1C =√2a ,由于三棱锥A −B 1CD 1的表面积为4√3,所以S =4S △AB 1C =4×12×√32(√2a)2=4√3所以a =√2所以正方体的外接球的半径为√(√2)2+(√2)2+(√2)22=√62, 所以正方体的外接球的体积为43π·(√62)3=√6π故选:B .小提示:与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.4、已知三棱锥P −ABC ,其中PA ⊥平面ABC ,∠BAC =120°,PA =AB =AC =2,则该三棱锥外接球的表面积为( )A .12πB .16πC .20πD .24π答案:C分析:根据余弦定理、正弦定理,结合球的性质、球的表面积公式进行求解即可.根据题意设底面△ABC 的外心为G ,O 为球心,所以OG ⊥平面ABC ,因为PA ⊥平面ABC ,所以OG//PA ,设D 是PA 中点,因为OP =OA ,所以DO ⊥PA ,因为PA ⊥平面ABC ,AG ⊂平面ABC ,所以AG ⊥PA ,因此OD//AG ,因此四边形ODAG 是平行四边形,故OG =AD =12PA =1,由余弦定理,得BC =√AB 2+AC 2−2AB ⋅AC ⋅cos120°=√4+4−2×2×2×(−12)=2√3,由正弦定理,得2AG =√3√32⇒AG =2,所以该外接球的半径R 满足R 2=(OG )2+(AG )2=5⇒S =4πR 2=20π,故选:C .小提示:关键点睛:运用正弦定理、余弦定理是解题的关键.5、牟合方盖是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法,该方法不直接给出球体的体积,而是先计算牟合方盖的体积.刘徽通过计算,“牟合方盖”的体积与球的体积关系为V 牟V 球=4π,并且推理出了“牟合方盖”的八分之一的体积计算公式,即V 牟8=r 3−V 方盖差,从而计算出V 球=43πr 3.如果记所有棱长都为r 的正四棱锥的体积为V ,则V 方差盖:V =( )A.√22B.1C.√2D.2√2答案:C分析:计算出V方盖差,V,即可得出结论.由题意,V方盖差=r3−18V牟=r3−18×4π×43×π×r3=13r3,所有棱长都为r的正四棱锥的体积为V正=13×r×r×r2−(√2r2)2=√26r3,∴V方盖差V正=13r3√2r36=√2,故选:C.6、如图,已知正方体的棱长为a,沿图1中对角面将它分割成两个部分,拼成如图2的四棱柱,则该四棱柱的全面积为()A.(8+2√2)a2B.(2+4√2)a2C.(4+2√2)a2D.(6−4√2)a2答案:C分析:拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面,据此变化,进行求解. 由题意,拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面,由于截面为矩形,长为√2a,宽为a,所以面积为√2a2,所以拼成的几何体的表面积为4a2+2√2a2=(4+2√2)a2.故选:C.7、如图所示的正方形SG1G2G3中,E , F分别是G1G2,G2G3的中点,现沿SE,SF,EF把这个正方形折成一个四面体,使G1,G2,G3重合为点G,则有()A.SG⊥平面EFG B.EG⊥平面SEFC.GF⊥平面SEF D.SG⊥平面SEF答案:A解析:根据正方形的特点,可得SG⊥FG,SG⊥EG,然后根据线面垂直的判定定理,可得结果. 由题意:SG⊥FG,SG⊥EG,FG∩EG=G,FG,EG⊂平面EFG所以SG⊥平面EFG正确,D不正确;.又若EG⊥平面SEF,则EG⊥EF,由平面图形可知显然不成立;同理GF⊥平面SEF不正确;故选:A小提示:本题主要考查线面垂直的判定定理,属基础题.8、如图,PA垂直于矩形ABCD所在的平面,则图中与平面PCD垂直的平面是()A.平面ABCD B.平面PBCC.平面PAD D.平面PCD答案:C分析:由线面垂直得到线线垂直,进而证明出线面垂直,面面垂直.因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD,由四边形ABCD为矩形得CD⊥AD,因为PA∩AD=A,所以CD⊥平面PAD.又CD⊂平面PCD,所以平面PCD⊥平面PAD.故选:C多选题9、沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上(细管长度忽略不下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的23计).假设该沙漏每秒钟漏下0.02cm3的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是()A.沙漏中的细沙体积为1024πcm381B.沙漏的体积是128πcm3C.细沙全部漏入下部后此锥形沙堆的高度约为2.4cmD.该沙漏的一个沙时大约是1565秒(π≈3.14)答案:AC解析:A.根据圆锥的体积公式直接计算出细沙的体积;B.根据圆锥的体积公式直接计算出沙漏的体积;C.根据等体积法计算出沙堆的高度;D.根据细沙体积以及沙时定义计算出沙时.A.根据圆锥的截面图可知:细沙在上部时,细沙的底面半径与圆锥的底面半径之比等于细沙的高与圆锥的高之比,所以细沙的底面半径r=23×4=83cm,所以体积V=13⋅πr2⋅2ℎ3=13⋅64π9⋅163=1024π81cm3B.沙漏的体积V=2×13×π×(ℎ2)2×ℎ=2×13×π×42×8=2563πcm3;C.设细沙流入下部后的高度为ℎ1,根据细沙体积不变可知:1024π81=13×(π(ℎ2)2)×ℎ1,所以1024π81=16π3ℎ1,所以ℎ1≈2.4cm;D.因为细沙的体积为1024π81cm3,沙漏每秒钟漏下0.02cm3的沙,所以一个沙时为:1024π810.02=1024×3.1481×50≈1985秒.故选:AC.小提示:该题考查圆锥体积有关的计算,涉及到新定义的问题,难度一般.解题的关键是对于圆锥这个几何体要有清晰的认识,同时要熟练掌握圆锥体积有关的计算公式.10、(多选题)在四棱锥A-BCDE中,底面四边形BCDE为梯形,BC∥DE.设CD,BE,AE,AD的中点分别为M,N,P,Q,则()A.PQ=1MN B.PQ∥MN2C.M,N,P,Q四点共面D.四边形MNPQ是梯形答案:BCD分析:根据中位线的性质,结合平行的性质逐个判定即可DE,且DE≠MN,由题意知PQ=12所以PQ≠1MN,故A不正确;又PQ∥DE,DE∥MN,2所以PQ∥MN,又PQ≠MN,所以B,C,D正确.故选:BCD11、给出以下关于斜二测直观图的结论,其中正确的是()A.水平放置的角的直观图一定是角B.相等的角在直观图中仍然相等C.相等的线段在直观图中仍然相等D.两条平行线段在直观图中仍是平行线段答案:AD分析:根据直观图和斜二测画法的规则,判断选项.水平放置的角的直观图一定是角,故A正确;角的大小在直观图中都会发生改变,有的线段在直观图中也会改变,比如正方形的直方图中,故BC错误;由斜二测画法规则可知,直观图保持线段的平行性,所以D正确.故选:AD填空题12、如图所示,P为平行四边形ABCD所在平面外一点,E为AD的中点,F为PC上一点,若PA//平面EBF,则PF=_______FC答案:12##0.5 分析:连接AC 交BE 于点M ,连接FM ,由线面平行的性质得线线平行,由平行线性得结论. 连接AC 交BE 于点M ,连接FM ,∵PA//平面EBF ,PA ⊂平面PAC ,平面PAC ∩平面EBF =EM ,∴PA//EM ,又AE//BC ,∴PF FC =AM MC =AE BC =12. 所以答案是:12. 13、已知一个圆锥的底面半径为6,其体积为30π则该圆锥的侧面积为________.答案:39π分析:利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案. ∵V =13π62⋅ℎ=30π∴ℎ=52∴l =√ℎ2+r 2=√(52)2+62=132 ∴S 侧=πrl =π×6×132=39π. 所以答案是:39π.14、如图,拿一张矩形纸片对折后略微展开,竖立在桌面上,折痕与桌面的关系是______.答案:垂直分析:根据给定条件,利用线面垂直的判定推理作答.令桌面所在的平面为α,折痕所在直线为l,纸片与桌面公共部分所在直线为a,b,如图,依题意有a∩b=A,因l⊥a,l⊥b,a,b⊂α,所以l⊥α,所以折痕与桌面垂直.所以答案是:垂直解答题15、如图,四棱锥P−ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1)证明:平面PAM⊥平面PBD;(2)若PD=DC=1,求四棱锥P−ABCD的体积.答案:(1)证明见解析;(2)√23.分析:(1)由PD⊥底面ABCD可得PD⊥AM,又PB⊥AM,由线面垂直的判定定理可得AM⊥平面PBD,再根据面面垂直的判定定理即可证出平面PAM⊥平面PBD;(2)由(1)可知,AM⊥BD,由平面知识可知,△DAB~△ABM,由相似比可求出AD,再根据四棱锥P−ABCD的体积公式即可求出.(1)因为PD⊥底面ABCD,AM⊂平面ABCD,所以PD⊥AM,又PB⊥AM,PB∩PD=P,所以AM⊥平面PBD,而AM⊂平面PAM,所以平面PAM⊥平面PBD.(2)[方法一]:相似三角形法由(1)可知AM⊥BD.于是△ABD∽△BMA,故ADAB =ABBM.因为BM=12BC,AD=BC,AB=1,所以12BC2=1,即BC=√2.故四棱锥P−ABCD的体积V=13AB⋅BC⋅PD=√23.[方法二]:平面直角坐标系垂直垂直法由(2)知AM⊥DB,所以k AM⋅k BD=−1.建立如图所示的平面直角坐标系,设BC =2a(a >0).因为DC =1,所以A(0,0),B(1,0),D(0,2a),M(1,a).从而k AM ⋅k BD =a−01−0×2a−00−1=a ×(−2a)=−2a 2=−1. 所以a =√22,即DA =√2.下同方法一.[方法三]【最优解】:空间直角坐标系法建立如图所示的空间直角坐标系D −xyz ,设|DA|=t ,所以D(0,0,0),C(0,1,0),P(0,0,1),A(t,0,0),B(t,1,0).所以M (t 2,1,0),PB ⃑⃑⃑⃑⃑ =(t,1,−1),AM ⃑⃑⃑⃑⃑⃑ =(−t 2,1,0).所以PB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =t ⋅(−t 2)+1×1+0×(−1)=−t 22+1=0. 所以t =√2,即|DA|=√2.下同方法一.[方法四]:空间向量法由PB ⊥AM ,得PB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0.所以(PD⃑⃑⃑⃑⃑ +DA ⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ )⋅AM ⃑⃑⃑⃑⃑⃑ =0. 即PD ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +DA ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0.又PD ⊥底面ABCD ,AM 在平面ABCD 内,因此PD ⊥AM ,所以PD ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0.所以DA ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0,由于四边形ABCD 是矩形,根据数量积的几何意义,得−12|DA ⃑⃑⃑⃑⃑ |2+|AB ⃑⃑⃑⃑⃑ |2=0,即−12|BC ⃑⃑⃑⃑⃑ |2+1=0. 所以|BC⃑⃑⃑⃑⃑ |=√2,即BC =√2.下同方法一. 【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长,从而求得该四棱锥的体积;方法二构建平面直角坐标系,利用直线垂直的条件得到矩形的另一个边长,从而求得该四棱锥的体积;方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法,为最优解;方法四利用空间向量转化求得矩形的另一边长.。
高中空间立体几何经典例题精选全文完整版

可编辑修改精选全文完整版立体几何一、选择题1.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D2 2.(20XX 年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C 【答案】A3 3.(20XX 年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A4 4.(20XX 年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B .2C .2-12D .2+12【答案】C5.(20XX 年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,底面是边长为3.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A.512πB .3πC.4πD.6π【答案】B6.(20XX年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为()A.5603B.5803C.200D.240【答案】C7.(20XX年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为,m n,那么m n+=()A.8 B.9 C.10 D.11【答案】A二、填空题8.(20XX年高考北京卷(理))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________.1D1BPD1CCEBA1A【答案】2559.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2410.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-11.(20XX 年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π12.(20XX 年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______AB C1A D EF1B 1C【答案】3π三、解答题13.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值D 1 C 1 B 1A 1D C AB14.(20XX 年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,113tan 6233BC CC BC C =⋅∠==从而2333ABC S BC ∆==因此该三棱柱的体积为1336183ABC V S AA ∆=⋅==15.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))B 1 A 1C 1ACB如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF ∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF ∥平面ABC 同理:FG ∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC ∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SAB AF ⊥SB∴AF ⊥平面SBC 又∵BC ⊆平面SBC ∴AF ⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC ⊥平面SAB 又∵SA ⊆平面SAB ∴BC ⊥SA16.(20XX 年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯=而1AD C ∆中,11AC DC AD ==故132AD C S ∆= AB CSGFE所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.17.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE,在OCD ∆中,由余弦定理可得OD=由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O =,所以A O '⊥平面BCDE . (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos OH A HO A H '∠=='所以二面角ACD B '--向量法:以O 点为原点,建立空间直角坐标系O -.CO BDEA CDOBE'A图1图2C DO BE'AH则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,1,n =- 由(Ⅰ)知,(OA '=为平面CDB 的一个法向量,所以3cos ,3n OA n OA n OA'⋅'===',即二面角A CD B '--的平面角的余弦值为5.18.(20XX年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为2, 求线段AM的长.6【答案】19.(20XX年高考陕西卷(理))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,12AB AA==(Ⅰ) 证明: A1C⊥平面BB1D1D;(Ⅱ) 求平面OCB1与平面BB1D1D的夹角θ的大小.1A【答案】解:(Ⅰ) BDOAABCDBDABCDOA⊥∴⊂⊥11,,面且面;又因为,在正方形AB CD 中,BDCAACACAACABDAACOABDAC⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD中,AO = 1 . .111=∆OAOAART中,在OECAOCEAEDB1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又OOBDDDBBODDBBBD=⋂⊂⊂111111E.E,DDBBCA111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O为原点,以OC为X轴正方向,以OB为Y轴正方向.则)1,0,1()1,1,1(),10(),1(,0,1,0111-=⇒CABACB,,,,)(.由(Ⅰ)知, 平面BB1D1D的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OCOBCAn设平面OCB1的法向量为,则0,0,2122=⋅=⋅OCnOBnn).1-,1,0(法向量2=n为解得其中一个21221||||||,cos|cos212111=⋅=⋅=><=nnnnnnθ.所以,平面OCB1与平面BB1D1D的夹角θ为3π1A。
立体几何基础题题库(360道附详细答案)

S P
S
SS
S
PP
P
R
RR
Pபைடு நூலகம்
Q
R Q
QR
R
P
QR P PQ
Q
R
P
R
Q
QS
R
SS
Q
R
S
SQ R
Q
Q
RP
Q
P
R
S SQ R
P S
R Q
(A)
(B)
(C)
(D)
D
解析: A 项: PS 底面对应的中线,中线平行 QS,PQRS 是个梯形
D'
P
A'
S
C'
B'
R
D
A
B 项: 如图
Q
C B
C 项:是个平行四边形
EG2 FH 2 =2 (EF 2 FG2 ) = 1 ( AC2 BD2 ) 1 (a2 2b)
2
2
27. 如图,在三角形⊿ABC 中,∠ACB=90º, AC=b,BC=a,P 是⊿ABC 所在平面外一点,PB⊥AB, 点,AB⊥MC,求异面直 MC 与 PB 间的距离.
M 是 PA 的中
四边形矛盾。∴EF 和 AD 为异面直线.
26. 在空间四边形 ABCD 中,E,H 分别是 AB,AD 的中点,F,G 分别是 CB,CD 的中点,若 AC + BD
= a ,AC BD =b,求 EG2 FH 2 . A
解析:四边形 EFGH 是平行四边形,…………(4 分)
E H
B F
D
G C
得 OX2+OY2+OZ2=37,OP= 37 .
高考必刷小题 立体几何

11.如图所示,在正方体ABCD-A1B1C1D1中,E是平面ADD1A1的中心,M, N,F分别是B1C1,CC1,AB的中点,则下列说法正确的是 A.MN=12EF
√B.MN≠12EF √C.MN与EF异面
D.MN与EF平行
1 A.4
dm2
C.
3 4
dm2
√B.
2 4
dm2
D.34 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
根据题意,在平面VAC内,过点P作EF∥AC分别交VA,VC于点F,E, 在平面VBC内,过点E作EQ∥VB交BC于点Q, 在平面VAB内,过点F作FD∥VB交AB于点D,连接DQ,如图所示, 因为EF∥AC, 所以△VEF∽△VCA,设其相似比为k, 则VVAF=VVCE=AECF=k,0<k<1, 因为 VA=VB=VC=1,且两两垂直,所以 AC= 2,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
因为EF⊂平面VAC, 所以FD⊥EF, 所以四边形 FEQD 是矩形,即 S 矩形 FEQD=
FD·EF=(1-k)· 2k=- 2k-122+ 42,
所以当
k=12时,S
矩形 FEQD
有最大值
2 4.
故该截面面积的最大值是
对于A,如图(1),α∩β=l,m⊥l,n∥l,则满足m∥α,n∥β,m⊥n, 平面α与β不一定垂直,故A错误; 对于B,如图(2),α∩β=l,n∥l,m⊥α,则满足n∥β,m⊥n,平面 α与β不一定垂直,故B错误;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
高三精选立体几何大题30题(含详细解答)
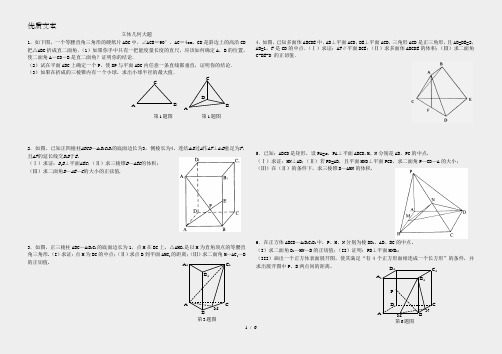
A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
立体几何经典习题集(含答案)

立体几何基础A 组题一、选择题:1.下列命题中正确命题的个数是 ( ) ⑴ 三点确定一个平面⑵ 若点P 不在平面α内,A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案:A2.已知异面直线a 和b 所成的角为︒50,P 为空间一定点,则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 ( ) A.1条 B.2条 C.3条 D.4条答案:B 3.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是 ( ) (1) 若βα//,则m l ⊥ (2) 若βα⊥,则m l // (3) 若m l //,则βα⊥ (4) 若 m l ⊥,则βα//A.(3)与(4)B.(1)与(3)C.(2)与(4)D.(1)与(2)答案:B4.已知m 、n 为异面直线,⊂m 平面α,⊂n 平面β,l =βα ,则l ( ) A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案:B5.设集合A={直线},B={平面},B A C =,若A a ∈,B b ∈,C c ∈,则下列命题中的真命题是 ( )A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案:A6.已知a 、b 为异面直线,点A 、B 在直线a 上,点C 、D 在直线b 上,且AC=AD ,BC=BD ,则直线a 、b 所成的角为 ( ) A. ︒90 B. ︒60 C. ︒45 D. ︒30答案:A7.下列四个命题中正确命题的个数是 ( ) 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案:D8.设M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},则这些集合之间关系是 ( ) A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案:B9.正四棱锥P —ABCD 中,高PO 的长是底面长的21,且它的体积等于334cm ,则棱AB 与侧面PCD 之间的距离是 ( ) A.cm 2 B. cm 2 C. cm 1 D.cm 22答案:A10.纬度为α的纬圈上有A 、B 两点,弧在纬圈上,弧AB 的长为απcos R (R 为球半径),则A 、B 两点间的球面距离为 ( )A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案:D11.长方体三边的和为14,对角线长为8,那么 ( ) A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案:D12.正四棱锥P —ABCD 的所有棱长都相等,E 为PC 的中点,那么异面直线BE 与PA 所成角的余弦值等于( )A.21B. 22C. 32D. 33答案:D13.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是 ( )A.正方形B.矩形C.菱形D.一般平行四边形答案:B二、填空题:14.正方体1111D C B A ABCD -中,E 、F 、G 分别为AB 、BC 、CC 1的重点,则EF 与BG 所成角的余弦值为________________________答案:510 15.二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4,到棱a 的距离为24,则这个二面角的大小为__________________答案:︒︒16575或16.四边形ABCD 是边长为a 的菱形,︒=∠60BAD ,沿对角线BD 折成︒120的二面角A —BD —C 后,AC 与BD 的距离为_________________________答案:a 43 17.P 为︒120的二面角βα--a 内一点,P 到α、β的距离为10,则P 到棱a 的距离是_________________答案:3320 18.如图:正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角,则异面直线AD 与BF 所成角的余弦值是______________________答案:4219.已知三棱锥P —ABC 中,三侧棱PA 、PB 、PC 两两互相垂直,三侧面与底面所成二面角的大小分别为γβα,,,则=++γβα222cos cos cos _______________答案:1 20.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练 体 何 题几 习 2CBDCA2^2 n CBD335B D ■/iEFAED. 4A. 1B. 2C. 3A. 81.设a 、休丫为两两不重合的平面,I 、m 、n 为两两不重合的直线,给岀下列四个命题: m? a, n? a, m // B, n // p,贝Uall B ;若a 丄Y, B 丄Y 贝U all B ;②其中真命题的个数是() 若AG 与 所成角为30,则二面角EF 为③若all B l?a,则I // B ④若 aQp ,=l B^Y =m 丫门% 亍nl ll 丫,贝U的体积为4•三个平面两两垂直,它们的三条交线交于点 则OP 长为() A. 5 .「; B . 2 口5•如图,四棱锥 S- ABCD 的底面为正方形,A. ACL SB B . AB//平面 SCD6•如图,四棱锥 P- ABCD 的底面为正方形,PD 丄底面ABCD, PD=AD=1,A. 1 v d i v d 2 C. d 1 v 1 v 7•在锐角的二面8•给出下列四个命(1)若平面 上有不共线的三点到平面的距离相等,则〃0,空间一点P 到三个平面的距离分别为 3、4、5,C. 3 仃D. 5. ■:SD 丄底面ABCD,则下列结论中不正确的是()C. SA 与平面SBD 所成的角等于 SC 与平面SBD 所成的角D. AB 与SC 所成的角等于DC 与 SA 所成的角设点CG 到平面PAB 的距离为d 1,点B 到平面PAC 的距离为d 2,则有(2•正方体A.- ABCD- A 1B 1C 1D 1 中, 3BD 1与平面ABCD 所成角的余弦值为() 3•三棱ABC- A 1B 1C 1 中,AA 1=2 且 AA 1 丄平面 ABC, △ ABC 是边长为二的正三角形,该三棱柱的六个顶点都在一个球面上, 则这个球d 1 v d 2v d 2< d 1 vA EF , AG , GAE45 ,(2) 两条异面直线在同一平面内的射影可能是两条平行直线; (3) 两条异面直线中的一条平行于平面,则另一条必定不平行于平面;(4) a,b 为异面直线,则过 a 且与b 平行的平面有且仅有一个.其中正确命题的序号是 _________________________9•已知正方体 ABCD AB i C i D i 中,点E 是棱 AR 的中点,则直线 AE 与平而 BDD iB 所成角 的正弦值是 . 10•已知直三棱柱 ABC A 1B 1C 1 中,ABC 90° , AC AA , 2.2 , AB 2 , M 为 BB i 的中其余恰好拼接成该正四棱锥的4个侧面,则-的取值范围是a12•已知矩形 ABCD 的长AB 4,宽AD 3,将 其沿对角线BD 折起,得到四面体 A BCD ,如 图所示, 给出下列结论:① 四面体A BCD 体积的最大值为72;5② 四面体A BCD 外接球的表面积恒为定值; ③ 若E 、F 分别为棱AC 、BD 的中点,则恒有EF ④ 当二面角A BD C 为直二面角时,直线⑤当二面角A BD C 的大小为60时,棱AC 的长为14.5其中正确的结论有 _____________________ (请写出所有正确结论的序号 ).13.如图,在直三棱柱 ABC- A1BG 中,/ BAC=90°, AB=BB ,直线 BQ 与平面 ABC 成 30° 角.(I )求证:平面 B 1ACL 平面 ABBA ;(II )求直线AC 与平面BAC 所成角的正弦值.14.如图,在三棱锥 P -ABC 中,D, E , F 分别为棱PC, AC AB 的中点.已知 PAL AC PA=AB=6 BC=8 DF=5.(1)若PB 丄BC 证明平面 BDEL 平面 ABC点,贝V B ,与平面ACM 的距离为 ___________11•边长分别为a 、b 的矩形, 按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,AC 且 EF BD ;16.-AB 、CD 所成角的余弦值为(2)求直线BD与平面ABC所成角的正切值.15.如图,长方体ABCD- A i BQDi中,AB=AD=1 AA=2,点P为DD的中点.(1)求证:直线BD//平面PAC(2)求证:平面PACL平面BDDB;(3)求CP与平面BDDB i所成的角大小.16.如图,四棱锥P-ABCD勺底面是正方形,PD丄底面ABCD点E在棱PB上(1)求证:ACL平面PDB(2)当PD= 'AB且E为PB的中点时,求AE与平面PDB所成的角的大小.17.在四棱锥P- ABCD中,底面ABCD为平行四边形,/ ADC=45°,D=AC=1 O为AC中点,P0丄平面ABCD P0=2, M为PD中点.(I)求证:PB//平面ACM(H)求证:ADL平面PAC(川)求二面角M- AC- D的正切值.18.如图所示,在四棱锥P- ABCD中,底面ABCE为矩形,PA丄平面ABCD点E在线段PC上,PC丄平面BDE(1)证明:BD L平面PAC(2)若PA=1, AD=2,求二面角B- PC- A的正切值.19.如图,直三棱柱ABC- A1B1C1 中,CA L CB AA1=AC=CB=2 D是AB的中点.(1)求证:BC//平面ACD(2)求证:AC丄AB;(3)若点E在线段BB上,且二面角E- CD- B的正切值是•儿,求此时2|三棱锥C- ADE的体积.20.如图,四棱锥S- ABCD的底面是正方形,每条侧棱的长都是底面边长的..倍,P为侧棱SD上的点.(1)求证:ACL SD(2)若SDL平面PAC求二面角P- AC- D的大小;(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE//平面PAC若存在,求SE EC的值; 若不存在,试说明理由.试卷答案: 解:若a丄丫,B丄丫,则a与B可能平行也可能相交,故①-错误; 由于m n不一定相交,故a//B不一定成立,故②错误;由面面平行的性质定理,易得③正确;由线面平行的性质定理,我们易得④正确;故选B考点:棱柱的结构特征.专题:空间角.分析:找出BD与平面ABCD所成的角,计算余弦值.•/ DD丄平面ABCD:BD是BD在平面ABCD勺射影,•••/ DBD是BD与平面ABCD所成的角;设AB=1,则BD= :':, BD=二• cos / DBD^^-=^=空;故选:D.点评:本题以正方体为载体考查了直线与平面所成的角,是基础题.考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:根据题意,正三棱柱的底面中心的连线的中点就是外接球的球心,求出球的半径即可求出球的体积.解答:解:由题意可知:正三棱柱的底面中心的连线的中点就是外接球的球心,因为△ ABC是边长为.】的正三角形,所以底面中心到顶点的距离为:因为AA=2且AA丄平面ABC所以外接球的半径为:「=府了=应.解答: 解:连接V冷"晋…近)呼H.所以外接球的体积为:故选:C.点评:本题给出正三棱柱有一个外接球,在已知底面边长的情况下求球的体积.着重考查了正三棱柱的性质、正三角形的计算和球的体积公式等知识,属于中档题.考点:平面与平面垂直的性质.专题:计算题;空间位置关系与距离.分析:构造棱长分别为a, b, c的长方体,P到三个平面的距离即为长方体的共顶点的三条棱的长,0P为长方体的对角线,求出0P即可.解答:构造棱长分别为a, b, c的长方体,P到三个平面的距离即为长方体的共顶点的三条棱的长,则a2+b2+c2=32+42+52=50因为0P为长方体的对角线.所以0P=5.':.故选:D.点评:本题考查点、线、面间的距离计算,考查计算能力,是基础题.考点:直线与平面垂直的性质.专题:综合题;探究型.分析:根据SDL底面ABCD底面ABCD为正方形,以及三垂线定理,易证ACL SB根据线面平行的判定定理易证AB//平面SCD根据直线与平面所成角的定义,可以找出/ ASO是SA与平面SBD所成的角,/ CSO是SC与平面SBD所成的角,根据三角形全等,证得这两个角相等;异面直线所成的角,利用线线平行即可求得结果.解答:解:•••SDL底面ABCD底面ABCD为正方形,•••连接BD,则BD L AC根据三垂线定理,可得AC L SB故A正确;•/ AB// CD AB?平面SCD CD?平面SCD• AB//平面SCD故B正确;• SDL底面ABCD/ ASO是SA与平面SBD所成的角,/ DSO是SC与平面SBD所成的,而厶SAO^A CSO•••/ ASO M CSO即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;••• AB// CD •- AB与SC所成的角是/ SCD DC与SA所成的角是/ SAB而这两个角显然不相等,故D不正确;故选D.点评:此题是个中档题•考查线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角等问题,综合性强.考点:点、线、面间的距离计算.专题:综合题;空间位置关系与距离;空间角.分析:过C做平面PAB的垂线,垂足为E,连接BE则三角形CEB为直角三角形,根据斜边大于直角边,再根据面PAC和面PAB与底面所成的二面角,能够推导出d2V d i v 1 •解答:解:过C做平面PAB的垂线,垂足为E,连接BE,则三角形CEB为直角三角形,其中/ CEB=90 ,根据斜边大于直角边,得CE v CB即d2V 1 •同理,d i v 1 •再根据面PAC和面PAB与底面所成的二面角可知,前者大于后者,所以d2v d i.所以d2v d i v 1.故选D.点评:本题考查空间距离的求法,解题时要认真审题,仔细解答,注意空间角的灵活运用.7 —48.(2)(4)9.10112.②③④ 13.考点:平面与平面垂直的判定;直线与平面所成的角.专题:证明题.分析:(I )欲证平面BACL平面ABBA,关键是寻找线面垂直,而AC!平面ABBA i,又AC?平面BAC,满足面面垂直的判定定理;(II )过A i做A i M LBi A i,垂足为M,连接CM, /AQ M为直线A i C与平面B i AC所成的角,然后在三角形A i CM中求出此角的正弦值即可.解答:解:(I )证明:由直三棱柱性质,B i B丄平面ABC•••Bi B丄AC 又BAL AC B B A BA=B••• AC丄平面ABBA ,又AC?平面B i AC,•平面B i AC L平面ABBA i.(II )解:过A i做A i M LB A ,垂足为Ml,连接CM•••平面B i AC L平面ABBA ,且平面B i AC A平面ABBA i=B A,••AM!平面B AC.• /A i CM为直线AC与平面B i AC所成的角,•••直线B i C与平面ABC成30° 角,「./B i CB=30 .设AB=BB=a ,可得B i C=2a, BC=「- 丄-一 :-i ,•直线A i C与平面B AC所成角的正弦值为JE6 '点评:本题主要考查了平面与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力.i 4.考点:直线与平面所成的角;平面与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(i )由已知得DE L AC DE+EF=DF ,从而DE L平面ABC由此能证明平面BDE L平面ABC(2)由DE L平面ABC得/ DBE是直线BD与平面ABC所成的角,由此能求出直线BD与平面ABC所成角的正切值.解答: (i )证明:•••在三棱锥P- ABC中,D, E , F分别为棱PC AC AB的中点.PA^ AC PA=AB=6 BC=8 DF=5,••• DE I AC DE=3 EF=4, DF=5,••• D W+E R D F,• DELEF,又EF A AC=F • DEL平面ABC又DE?平面BDE •平面BDEL平面ABC(2)v DEL平面ABC •- PAL平面ABC •- PA L AB•/ PB丄BC • AB丄BC•-AC=J%W4=1O,•BE#\C=5,由DEL平面ABC得/ DBE是直线BD与平面ABC所成的角,tan / DBE^~:=—I.BE!•直线BD与平面ABC所成角的正切值为半.5点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.15.考点:直线与平面平行的判定;平面与平面垂直的判定;直线与平面所成的角.专题:证明题.分析:(1 )设AC和BD交于点0,由三角形的中位线的性质可得P0// BD i ,从而证明直线BD//平面PAC(2)证明AC L BD DD L AC,可证AC L面BDDB ,进而证得平面PAC L平面BDDB i .(3)CP在平面BDDBi内的射影为0P故/ CP0是CP与平面BDDB所成的角,在Rt△ CP0中,利用边角关系求得/ CP0的大小.解答:(1 )证明:设AC和BD交于点0,连PQ由P, 0分别是DD , BD的中点,故P0// BD ,•/ P0平面PAC BD?平面PAC 所以,直线BD //平面PAC(2)长方体ABCD- A i B C D 中,AB=AD=1 底面ABCD是正方形,贝U AC L BD 又DD L 面ABCD 贝U DD L AC •/ BD?平面BDDB , D D?平面BDDB1 , BD AD 1D=D •- AC L面BDDB1.V AC?平面PAC ••平面PACL平面BDDBi .(3)由(2)已证:AC L面BDDB1 , • CP在平面BDDB内的射影为0P CP0是CP与平面BDDB 所成的角.依题意得丨-「- - —,在Rt△ CPO中, •••/ CPO=30• CP与平面BDDB所成的角为30°.点评:本题考查证明线面平行、面面垂直的方法,求直线和平面所称的角的大小,找出直线和平面所成的角是解题的难点,属于中档题.16.考点:直线与平面所成的角;直线与平面垂直的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)根据题意证明ACL BD PDLAC可得ACL平面PDB(2)设ACH BD=O连接OE根据线面所成角的定义可知/ AEO为AE与平面PDB所的角,在Rt△ AOE 中求出此角即可.解答:(1)证明:•••四边形ABCD是正方形,• AC L BD■/ PD L底面ABCD•PD L AC又BD H PD=D. AC L平面PDB (3 分)(2)设ACH BD=O 连接OE 由(1)知AC L平面PDB于O,•••/ AEO为AE与平面PDB所的角,(5 分)又O, E分别为DB PB的中点,•OE/ PD OE丄PD,1在Rt△ AOE中,OE~PD=ilAB=AO2 2•/ AEO=45 , (7 分)即AE与平面PDB所成的角的大小为45°. (8分)点评:本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于中档题.17.考点:与二面角有关的立体几何综合题;直线与平面平行的判定;直线与平面垂直的判定.专题:计算题.分析:(I)连接OM BD,由M O分别为PD和AC中点,知OM/ PB由此能够证明PB//平面ACM(H)由PQL平面ABCD 知PQL AD,由/ADC=45 , AD=AC=1 知ACL AD,由此能够证明ADL平面PAC (川)取DQ中点N,连接MN)由MN/ PQ知MN L平面ABCD过点N作NE L AC于E,由E为AQ中点,连接ME由三垂线定理知/ MEN即为所求,由此能求出二面角M- AC- D的正切值.解答:(I)证明:连接QM BD•/ M Q分别为PD和AC中点,•••QM/ PB•••QM平面ACM PB?AC呼面,•PB//平面ACIM-. (4 分)(H)证明:由已知得PQL平面ABCD•PQL AD,•••/ ADC=45 , AD=AC=1•AC L AC,•/ AS PQ=Q AC, PQ平面PAC•ADL平面PAC…..(8分)(川)解:取DQ中点N,连接MN贝U MIN/ PQ•MN L平面ABCD过点N作NEL AC于E,贝U E为AQ中点,连接ME由三垂线定理可知/ MEN即为二面角M- AC- D的平面角,•/ MN=1 NE=•tan / MEN=-2-.. (13 分)点评:本题考查直线与平面平行、直线现平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,仔细解答,注意三垂直线定理的合理运用.18.考点:二面角的平面角及求法;直线与平面垂直的判定.专题:空间位置关系与距离;空间角;立体几何.分析:(1)由题设条件及图知,可先由线面垂直的性质证出PA!BD与PCLBD再由线面垂直的判定定理证明线面垂直即可;(2)由图可令AC与BD的交点为0,连接0E证明出/ BEO为二面角B- PC- A的平面角,然后在其所在的三角形中解三角形即可求出二面角的正切值.解答:(1)•.• PA!平面ABCD••• PA! BD•/ PCL平面BDE•PCL BD 又PA P PC=P•BD L平面PAC(2)设AC与BD交点为0,连0E•/ PC L平面BDE•PC L平面B0E•PC L BE•/ BE0为二面角B- PC- A的平面角•/ BD L平面PAC•BD L AC•四边形ABCD为正方形,又PA=1, AD=2,可得BD=AC=2 : , PC=3•0C='- =-..■:■在厶PA3A 0EC中,更县—芈二唾OC PC V2 3 3又BD L 0E•tanZbEQ=-|j=3•二面角B- PC- A的平面角的正切值为3点评:本题考查二面角的平面角的求法及线面垂直的判定定理与性质定理,属于立体几何中的基本题型,二面角的平面角的求法过程,作,证,求三步是求二面角的通用步骤,要熟练掌握19.考点:棱柱、棱锥、棱台的体积;空间中直线与直线之间的位置关系;直线与平面平行的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)连接AG交AQ于点F,由三角形中位线定理得BG // DF,由此能证明BG//平面AQD(2)利用线面垂直的判定定理证明AC丄平面ABC i ,即可证明AQ丄AB;(3)证明/ BDE为二面角E- CD- B的平面角,点E为BB的中点,确定DEL A i D,再求三棱锥C-ADE的体积.解答:(1)证明:连结AG,交A i C于点F,则F为AG中点,又D是AB中点,连结DF,贝U BC// DF,因为DF?平面A i CD BC?平面A i CD所以BG//平面A i CD •••(3分)(2)证明:直三棱柱ABC- A B i C i中,因为AA=AC 所以AG丄AQ・・(4分)因为CALCB BG // BC所以B i C L平面ACCA,所以B i C丄6分)因为B i C P AC=C i,所以A i C丄平面ABC i所以A i C L AB •••(8 分)(3)在直三棱柱ABC- A i B C i中,AA丄CD因为AC=CB D为AB的中点,所以CDLAB CDL平面ABBA i.所以CD L DE CDL DB所以/ BDE为二面角E- CD- B的平面角.在Rt△ DEB中,tan/BD匸誓.由AA=AC=CB=2 CAL CB所以丄•二,-L ._.所以——一,得BE=i .所以点E为BB的中点.…(i i分)DB 2又因为CM,处g抚,DE=V3, A E=3,故A^D^DE^AjE2,故有 DELA i D所以比“吕冥S △町DE X* %后x衍x运二1 •••(i 4分厂点评:本题主要考查直线与平面平行、垂直等位置关系,考查线面平行、二面角的概念、求法、三棱锥C- A i DE的体积等知识,考查空间想象能力和逻辑推理能力,是中档题.20.考点:直线与平面平行的判定;直线与平面垂直的判定;与二面角有关的立体几何综合题.专题:计算题;证明题;压轴题.分析: (1)连BD 设AC 交于BD 于0,由题意知SQL 平面ABCD 以0为坐标原点,|「「.厂 -[ 分别为x 轴、y 轴、z 轴正方向,建立坐标系 0- xyz ,设底面边长为 a ,求出高SQ 从而得到点 S与点C 和D 的坐标,求出向量丨「与:才,计算它们的数量积,从而证明出(2) 根据题意先求出平面 PAC 的一个法向量| :和平面DAC 的一个法向量 :,设所求二面角为 0, 则亡朋日二 兰•巴 护,从而求出二面角的大小;|0S||ES| 2(3) 在棱SC 上存在一点E 使BE//平面PAC 根据(H )知:是平面PAC 的一个法向量,设二—::,内,故BE//平面PAC解答: 证明:(1 )连BD 设AC 交于BD 于Q 由题意知 SQL 平面ABCD以°为坐标原点,:: 分别为x 轴、y 轴、z 轴正方向,建立坐标系 0- xyz 如图.设底面边长为a ,则高于是:•: i. i. _ ,.故 OC L SD设所求二面角为 0,则所求二面角的大小为 30°.(3)在棱SC 上存在一点 E 使BE//平面PAC由(n )知厂是平面PAC 的一个法向量,OC L SD 贝U AC L SD求出「,根据二.F- I :- I 可求出t 的值,从而即当 SE: EC=2 1时,西丄瓦,而BE 不在平面PAC-半宜),foc-SD^O 从而 AC L SD(2) 由题设知,平面 09平面 DAC 的一个法向量厉二(-,0, PAC 的一个法向量’下^BE=BC+(i=ECHCS=(-冷& 净(1 - t)f ■ • ..而上丄.即当 SE EC=2: 1 时,「 而BE 不在平面 PAC 内,故 BE//平面 PAC点评: 本题主要考查了直线与平面平行的判定,以及空间两直线的位置关系的判定和 法,涉及到的知识点比较多,知识性技巧性都很强..面角的求。
