绕极轴旋转体侧面积公式
旋转体的侧面积ppt课件

s b 1 f 2 (x)dx. a
3、极坐标方程 r f ( ),
b
s
f 2(q ) f 2(q )dq.
a
9
三、立体体积
b
1、空间立体 v a p( x)dx
2、旋转体:y f ( x), a x b绕x轴旋转
v b f 2( x)dx a
,
]严格减少,A
|
(t
)
| (t
)dt
3、极坐标方程 r f ( ),
A 1 r2d
2
8
二、平面曲线的弧长
1、参数方程 x (t), y (t), t
s
(t)2 (t)2dt.
2、直角坐标系 y f ( x),a x b
(t)
2(t) 2(t)dt.
6
若曲线由极坐标方程r f 给出,则绕x轴旋转
一周所得旋转体的侧面积
A 2
f
sin
f 2 f 2 d
因为这时可看作参数方程:
x f ( )cos y f ( )sin
7
小结
ay b2
y2
)2
b2(b2 y2 ) a2 y2 b2(b2 y2 )
A 2
b
x
1 x2 dy
b
2 a b
b b
b2 y2
b2(b2 y2 ) a2 y2 b2 (b2 y2 ) dy
4
2 a
b2
b b
b4 b2 y2 a2 (t), t [, ] 给出, 且 (t) 0, 则曲线 C 绕 x 轴旋转所得旋转
侧面积公式推导

定积分在几何上的应用3——求旋转体的侧面积
设旋转体是曲线y=f(x)(≥0,a≤x≤b),直线x=a,x=b绕x轴旋转而生成.任取一微区间[x,x+dx],如图1.有P(x,y),Q(x+dx,y+Δy),由弧微分中的讨论知:
弧长=Δs=ds+o(dx) ①
线段=+o(dx)=ds+o(dx) ②
因为绕x轴旋转生成的旋转体的侧面积是侧面积量A的增量ΔA,线段PQ绕x轴旋转生成的面积恰好是上、下底面半径为y和y+Δy,侧高为的圆台的侧面积Δ∑.由圆台侧面积公式可知后者等于
Δ∑=π(y+y+Δy)
=π[2y+dy+o(dx)][ds+o(dx)]
=2πyds+o(dx),
显然ΔA=Δ∑+o(dx),故有
从而旋转体的侧面积为
相应地也可写出曲线在参数坐标和极坐标下的侧面积公式,这里不列出了.例18 求抛物线y2=2px(0≤x≤a)绕x轴旋转生成的旋转体的侧面积.
由⑤式得侧面积为
例19 求由圆x2+(y-a)2=r2(r<a)绕x轴旋转而成的环体的表面积.
故对哪个半圆周都有
代入公式⑤即得所求表面积为
解采用参数坐标较为方便.令x=acost,y=bsint 0≤t≤2π弧长微分
故表面积为
我们说过椭圆的周长不能准确计算,但椭圆的旋转面积却能准确算出来.当e
习题
29.求抛物线y2=4x,直线x=8所围成图形绕x轴旋转所得旋转体的侧面积.求旋转下列曲线所成曲面的面积
33.x=a(t-sint),y=a(1-cost)(0≤t≤2π)分别绕x轴和y轴.
答案
如有侵权请联系告知删除,感谢你们的配合!。
旋转体的侧面积公式证明过程

旋转体的侧面积公式证明过程摘要:一、旋转体的概念及分类二、旋转体侧面积公式的推导三、旋转体侧面积公式的应用举例四、总结正文:一、旋转体的概念及分类旋转体是由一个平面图形围绕一条定直线旋转所形成的几何体。
根据底面的不同,旋转体可以分为圆柱体、圆锥体、椭圆柱体、椭圆锥体等。
其中,圆柱体和圆锥体是常见的旋转体。
二、旋转体侧面积公式的推导为了更好地理解旋转体侧面积公式的推导过程,我们先来了解一下旋转面的概念。
旋转面是由一个平面图形围绕着其中的一条定直线旋转所形成的曲面。
在这个过程中,旋转面的侧面积公式是一个重要的公式。
假设我们有一个长方形,以一边为轴顺时针或逆时针旋转一周,所经过的空间形成一个圆柱体。
我们可以将这个圆柱体展开成一个扇形,其弧长等于圆柱体的底面周长,半径等于圆柱体的高。
根据扇形的面积公式,我们可以计算出扇形的面积为:s = 1/2 * l * r,其中l 为弧长,r 为半径。
由于旋转体是由无数个这样的扇形组成的,所以我们需要将扇形的面积公式积分,以得到旋转体的侧面积公式。
设旋转体的高为h,底面半径为r,母线长为L,则有:s 侧= ∫[0, 2π] ∫[0, h] 1/2 * l * r dx dy通过积分计算,我们可以得到旋转体的侧面积公式为:s 侧= πrL。
三、旋转体侧面积公式的应用举例假设我们有一个圆柱体,底面半径为r,高为h,则根据旋转体侧面积公式,我们可以计算出其侧面积为:s 侧= πr * h。
同样地,对于一个圆锥体,底面半径为r,高为h,其侧面积公式为:s 侧= πr * √(r^2 + h^2)。
四、总结通过以上的推导和举例,我们可以看出旋转体的侧面积公式在计算旋转体侧面积时起到了关键作用。
旋转体的侧面积

设平面光滑曲线
求
它绕 x 轴旋转一周所得到的旋转曲面的侧面积 .
取侧面积元素:位于
上的圆台的侧面积
d S 2 y ds
y f (x)
yy
积分后得旋转体的侧面积
oo aa x
S 2
b
f (x)
1 f 2 (x) dx
a
bb xx
注意: 侧面积元素
y
y f (x)
上绕
y
应用公式得
S 2 x2 x1
R2 x2
1
R2
x Leabharlann 2x2dx
2
x2 x1
R
dx
2
R(x2
x1)
当球台高 h=2R 时, 得球的表面积公式
S 4 R2
x1 o
x R x2
y
o x
z
求由星形线
绕 x 轴旋转
一周所得的旋转体的表面积 S .
解: 利用对称性
S 2 2 2 a sin3 t 0
3a cos2 t sin t 2 3a sin2 t cost 2 dt
12 a2 2 sin4 t cos t dt
0
12
a2
1 5
sin5
t
2 0
12 a2
5
d S 2 y ds 2 y dx
2 y dx 不是薄片侧面积△S 的 o a x b x
的线性主部 .
ds
若光滑曲线由参数方程
dx
给出, 则它绕 x 轴旋转一周所得旋转体的
8.5 旋转体的侧面积
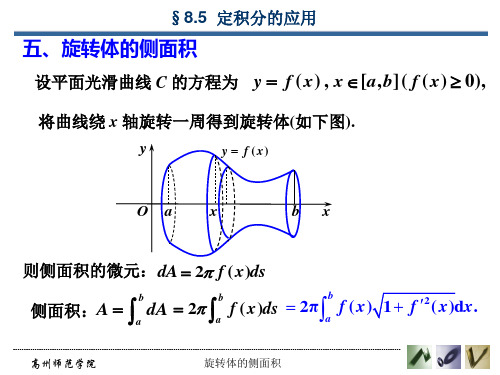
b
a
dA 2 a
b
2π f ( x ) 1 f 2 ( x )dx . f ( x )ds a
b
旋转体的侧面积
§8.5 定积分的应用
设平面光滑曲线 C 的方程为
x ( y ) , y [c, d ] ( ( y ) 0),
将曲线绕 y 轴旋转一周得到旋转体. 则侧面积:
y x r 2 x2
r
x
x
r x r
r2 1 y 2 1 ( )2 2 2 2 r x2 r x
r
A 2 y 1 y2 dx 2 - r r 2 x 2
r
r2 dx 4 r 2 . r 2 x2
高州师范学院
旋转体的侧面积
2 d f f
2
因为这时可看作参数方程:
x f ( )cos
y f ( )sin
高州师范学院
旋转体的侧面积
§8.5 定积分的应用
一、( x ), a x b
2、参数方程
x (t ), y (t ), t
§8.5 定积分的应用
x2 y2 例2、求椭圆 2 2 1(0 b a )绕y轴旋转所成旋转体的表面积. a b y 解:右半椭圆的方程为:
y2 a 2 x a 1 2 b y2 . b b
b y b
x
x
ay b b2 y 2
ay
b 2 (b 2 y 2 ) a 2 y 2 1 x 2 1 ( )2 2 2 b 2 (b 2 y 2 ) b b y
A | f ( x ) | dx
高等数学旋转体表面积公式

高等数学旋转体表面积公式
1. 绕x轴旋转体的表面积公式。
- 设y = f(x)在[a,b]上具有连续导数,那么由曲线y = f(x),a≤slant x≤slant b绕x轴旋转一周所得到的旋转体的表面积S为:
- S = 2π∫_a^bf(x)√(1 + [f^′(x)]^2)dx。
- 推导过程(简单理解):
- 我们把曲线y = f(x)分成很多小段弧,对于一小段弧Δ s,当它绕x轴旋转时,近似得到一个圆台的侧面。
- 圆台侧面积公式为S=π(r_1 + r_2)l,这里r_1=f(x),r_2 = f(x+Δ x),l近似为√((Δ x)^2)+(Δ y)^{2},当Δ xto0时,l=√(1+(y^′)^2)Δ x。
- 对每一小段弧旋转得到的侧面积求和取极限就得到上述积分公式。
2. 绕y轴旋转体的表面积公式。
- 若x = g(y)在[c,d]上具有连续导数,由曲线x = g(y),c≤slant y≤slant d绕y轴旋转一周所得到的旋转体的表面积S为:
- S = 2π∫_c^dg(y)√(1+[g^′(y)]^2)dy。
- 推导过程与绕x轴旋转类似,也是将曲线分割成小段弧,考虑小段弧绕y轴旋转得到近似的旋转体侧面积,然后求和取极限得到积分公式。
定积分侧面积绕x轴和y轴公式

一、概述在数学领域中,积分是一种非常重要的概念,它广泛应用于物理学、工程学和经济学等多个领域。
而定积分侧面积绕x轴和y轴的公式则是定积分的一个重要应用,它在求解旋转体的体积和表面积等问题中发挥着重要作用。
本文将围绕定积分侧面积绕x轴和y轴公式展开详细的阐述,希望能够帮助读者更好地理解和应用这一概念。
二、定积分侧面积绕x轴的公式1.1 定积分侧面积的定义在介绍定积分侧面积绕x轴的公式之前,首先需要明确定积分侧面积的概念。
当我们需要计算曲线围成的封闭图形绕x轴旋转一周所形成的立体的侧面积时,就需要用到定积分侧面积的概念。
这个侧面积可以通过定积分的方法来求解,得到的结果就是旋转体的侧面积。
1.2 定积分侧面积绕x轴的公式设函数y=f(x)在区间[a,b]上连续且非负(f(x)≥0),曲线y=f(x)与x轴所围成的平面图形绕x轴旋转一周所得的旋转体侧面积S可表示为:S = ∫[a,b] 2πy√(1+(f'(x))^2) dx其中f'(x)表示f(x)的导函数。
三、定积分侧面积绕y轴的公式除了绕x轴旋转的情况之外,我们还会遇到绕y轴旋转的情况。
与绕x 轴类似,当曲线y=f(x)在区间[a,b]上连续且非负(f(x)≥0)时,曲线y=f(x)与y轴所围成的平面图形绕y轴旋转一周所得的旋转体侧面积也可以通过定积分的方法来求解。
2.2 定积分侧面积绕y轴的公式曲线y=f(x)与y轴所围成的平面图形绕y轴旋转一周所得的旋转体侧面积S可表示为:S = ∫[a,b] 2πx√(1+(f'(y))^2) dy其中f'(y)表示f(y)的导函数。
四、定积分侧面积绕轴的实例分析3.1 求解绕x轴旋转的示例现以具体函数y=x^2在区间[0,1]上绕x轴旋转一周为例,来计算其旋转体的侧面积。
根据上述给出的公式,可以得到:S = ∫[0,1] 2πx√(1+(2x)^2) dx= π∫[0,1] 2x√(1+4x^2) dx= π∫[0,1] 2x√(4x^2+1) dx3.2 求解绕y轴旋转的示例再以具体函数y=x^2在区间[0,1]上绕y轴旋转一周为例,来计算其旋转体的侧面积。
10.04旋转曲面的面积

o x
当球台高 h=2R 时, 得球的表面积公式
S 4 R
数学分析
2
z
目录 上页 下页 返回 结束
3
求由星形线 一周所得的旋转体的表面积 S . 解: 利用对称性
S 2 2
例2.
绕 x 轴旋转
0
2
2
a sin t
2
2
3
12 a
12 a
3a cos t sin t 3a sin t cos t d t
2 2 0
目录 上页 下页 返回 结束
2
o
x
例1. 计算圆 x 轴旋转一周所得的球台的侧面积 S . 解: 对曲线弧 应用公式得
S 2 2
y
x1 o
2 2 dx R x 1 2 2 R x
x2 R x
x1 x1
x2
x
2
y
x2
R dx 2 R( x2 x1 )
数学分析
2
2
0
cos t sin t dt
4
32 5
a
2
目录 上页 下页 返回 结束
5
作业 P255 1.(1),(2),(4); 3.(1)
数学分析
目录 上页 下页 返回 结束
6
第四节
第十章
旋转曲面的面积
设平面光滑曲线 它绕 x 轴旋转一周所得到的旋转曲面的面积 . 取侧面积元素:
d S 2 y d s y f (x)
求
y
积分后得旋转体的侧面积
S 2数Βιβλιοθήκη 分析oa ax
b b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绕极轴旋转体侧面积公式
绕极轴旋转体侧面积公式是指计算绕极轴旋转体侧面积的一种公式,它可以帮助我们更清楚地了解物体的形状和尺寸。
绕极轴旋转体侧面积公式的组成部分有两部分:一部分是外径,另一部分是内径。
外径指的是以极轴为轴心的外层旋转体的半径,内径指的是以极轴为轴心的内层旋转体的半径。
绕极轴旋转体侧面积公式的计算方法是:首先,将外径和内径分别记为r1和r2,则侧面积S=2πr1π(r1-r2)。
其中,2π表示旋转体的周长,r1表示外径,r2表示内径,(r1-r2)表示旋转体的厚度。
绕极轴旋转体侧面积公式是一个十分简单明了的公式,只需要知道外层旋转体和内层旋转体的半径,就可以很容易地计算出旋转体的侧面积。
它可以帮助我们更准确地测量物体的体积和尺寸,同时也可以更好地掌握物体的形状。
因此,绕极轴旋转体侧面积公式在物理测量中发挥着重要作用,它可以帮助我们更准确地了解物体的形状和尺寸,从而更好地掌握物体的形状。
