人教版数学八年级下册第十八章平行四边形性质与判定专题复习辅导讲义
人教版八年级数学下册第十八章-平行四边形- 小结与复习-课件PPT

解:(1)证明:∵M、N、E分别是PD、PC、CD的
中点,
∴ME∥PC,EN∥PD. ∴四边形PMEN是平行四边形.
(2)解:当点P运动到AB的中点时,四边形PMEN是菱形.
理由如下:
∵P是AB中点,∴PA=PB.
∵四边形ABCD是矩形, ∴∠A=∠B=90°,AD=BC. ∴△PAD≌△PBC(SAS).∴PD=PC.
1.两条平行线之间的距离: 两条平行线中,一条直线上任意一点到另一条直线的距离 叫做两条平行线之间的距离.
2.三角形的中位线定理: 三角形的中位线平行于第三边,并且等于第三边的一半.
3.直角三角形斜边上的中线: 直角三角形斜边上的中线等于斜边的一半.
考点讲练
考点一 平行四边形的性质与判定
例1 如图,在直角梯形ABCD中,AD∥BC,∠B=90°, AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
D.8cm
2.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个
条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选
两个条件,能使四边形ABCD为平行四边形的选法有( B )
A.3种
B.4种
C.5种
D.6种
3.如图是某公交汽车挡风玻璃的雨刮器,其工作原理如图
.雨刷EF⊥AD,垂足为A,AB=CD,且AD=BC,这样能使雨 刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结
∵CF= 12BC, 2
2
∴DE∥FC,DE=FC,
∴四边形DEFC是平行四边形,
∴DC=EF, ∴EF= 1 AB=6.
2
针对训练
4.如图,等边三角形ABC中,点D,E分别为AB,AC 的中点,则∠DEC的度数为( B )
【最新】人教版八年级数学下册第十八章《平行四边形的性质》精品课件.ppt

18.1.1 平行四边形的性质(1)
课件说明
• 本课是在复习小学关于平行四边形学习经验的基础 上,进一步用观察实验的方法得到平行四边形边和 角的性质的猜想,并用演绎推理证明猜想,发展理 性思维,获得平行四边形的新知识. zxxk
课件说明
• 学习目标: 1.理解平行四边形的概念; 2.探索并掌握平行四边形对边相等、对角相等的性 质; 3.初步体会几何研究的一般思路与方法.
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
• 学习重点: 平行四边形边角性质的证明和应用.
观察抽象 形成概念
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗? 两组对边分别平行的四边形叫做平行四边形.
观察抽象 形成概念
我们用符号“△”与三个顶点字母表示三角形;对 于平行四边形,我们也有类似的表示方法吗?学科网
D
C
A
B
ABCD
∵ 四边形ABCD是平行四边形(已知), ∴ AB∥CD,AD∥BC(平行四边形的定义). 反过来 ∵ AB∥CD,AD∥BC(已知), ∴ 四边形ABCD是平行四边形(平行四边形的定义).
数学八年级下册第十八章平行四边形小结与复习教学课件 新人教版

7、 如图,平行四边形ABCD中,AC、BD为对角线,其交点为O, 若BC=6,BC边上的高为4,试求阴影部分的面积.
4、如图,ABCD为平行四边形,E、F分别为AB、CD的中点,①求 证:AECF也是平行四边形;②连接BD,分别交CE、AF于G、H, 求证:BG=DH;③连接CH、AG,则AGCH也是平行四边形吗?
解: ❶:根据已知可知:
AE∥FC且AE=FC AD=BC DF=EB ∠ABC=∠ADC ∴△ADF≌△CBE (SAS) ∴AF=CE ∠DAF=∠ECB ∴四边形AECF是平行四边形
(3)在(2)的条件下,△ABC应该满足什么条件时, 四边形AECF为正方形.
解:当点O运动到AC的中点时, 且满足∠ACB为直角时,四边形AECF是正方形. ∵由(2)知当点O运动到AC的中点时,四边形AECF 是矩形, 已知MN∥BC, 当∠ACB=90°, 则∠AOF=∠COE=∠COF=∠AOE=90°, 即AC⊥EF, ∴四边形AECF是正方形.
轴对称图形 轴对称图形 轴对称图形
二、几种特殊四边形的常用判定方法:
四边形
平行 四边形
矩形
菱形 正方形
条件
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等
4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形 2.对角线相等的平行四边形 3.有三个角是直角的四边形
8、 如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥BC, 设MN交∠BCA的平分线于点E,交∠BCA的外角∠ACG的平分线于点F, 连接AE、AF.
人教版八年级数学下册-第18章-平行四边形-章节知识点和常考易错点归纳

平行四边形章节知识梳理一.知识点:1、定义两组对边分别平行的四边形是平行四边形.定义中的“两组对边平行”是它的特征,抓住了这一特征,记忆理解也就不困难了.平行四边形的定义揭示了图形的最本质的属性,它既是平行四边形的一条性质,又是一个判定方法.同学们要在理解的基础上熟记定义.2、性质平行四边形的有关性质和判定都是从边、角、对角对称性四个方面的特征进行简述的.(1)角:平行四边形的邻角互补,对角相等;(2)边:平行四边形两组对边分别平行且相等;(3)对角线:平行四边形的对角线互相平分;(4)对称性:平行四边形是中心对称图形,对角线的交点是对称中心;(5)面积:①=底×高=ah;②平行四边形的对角线将四边形分成4个面积相等的三角形.3.平行四边形的判别方法①定义:两组对边分别平行的四边形是平行四边形②方法1:两组对角分别相等的四边形是平行四边形③方法2:两组对边分别相等的四边形是平行四边形④方法3:对角线互相平分的四边形是平行四边形⑤方法4:一组平行且相等的四边形是平行四边形4、.几种特殊四边形的有关概念(1)矩形:有一个角是直角的平行四边形是矩形,它是研究矩形的基础,它既可以看作是矩形的性质,也可以看作是矩形的判定方法,对于这个定义,要注意把握:1.平行四边形;2.一个角是直角,两者缺一不可.(2)菱形:有一组邻边相等的平行四边形是菱形,它是研究菱形的基础,它既可以看作是菱形的性质,也可以看作是菱形的判定方法,对于这个定义,要注意把握:1.平行四边形;2.一组邻边相等,两者缺一不可.(3)正方形:一组邻边相等的矩形叫做正方形,它是最特殊的平行四边形,它既是平行四边形,还是菱形,也是矩形,它兼有这三者的特征,是一种非常完美的图形.(4)梯形:一组对边平行而另一组对边不平行的四边形叫做梯形,对于这个定义,要注意把握:1.一组对边平行;2.一组对边不平行,同时要注意和平行四边形定义的区别,还要注意腰、底、高等概念以及梯形的分类等问题.5.几种特殊四边形的有关性质(1)矩形:1.边:对边平行且相等;2.角:对角相等、邻角互补;3.对角线:对角线互相平分且相等;4.对称性:既是轴对称图形又是中心对称图形.(2)菱形:1.边:四条边都相等;2.角:对角相等、邻角互补;3.对角线:对角线互相垂直平分且每条对角线平分每组对角;4.对称性:既是轴对称图形又是中心对称图形.(3)正方形:1.边:四条边都相等;2.角:四角相等;3.对角线:对角线互相垂直平分且相等,对角线与边的夹角为450;4.对称性:既是轴对称图形又是中心对称图形.6、几种特殊四边形的判定方法(1)矩形的判定:满足下列条件之一的四边形是矩形①有一个角是直角的平行四边形;②对角线相等的平行四边形;③四个角都相等(2)菱形的判定:满足下列条件之一的四边形是矩形①有一组邻边相等的平行四边形;②对角线互相垂直的平行四边形;③四条边都相等.(3)正方形的判定:满足下列条件之一的四边形是正方形.①有一个角是直角的菱形;②有一组邻边相等的矩形;③对角线相等的菱形;④对角线互相垂直的矩形.7、几种特殊四边形的常用说理方法与解题思路分析(1)识别矩形的常用方法①先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的任意一个角为直角.②先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的对角线相等.③说明四边形ABCD的三个角是直角.(2)识别菱形的常用方法①先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的任一组邻边相等.②先说明四边形ABCD 为平行四边形,再说明对角线互相垂直. ③说明四边形ABCD 的四条边相等.(3)识别正方形的常用方法①先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的一个角为直角且有一组邻边相等.②先说明四边形ABCD 为平行四边形,再说明对角线互相垂直且相等. ③先说明四边形ABCD 为矩形,再说明矩形的一组邻边相等.④先说明四边形ABCD 为菱形,再说明菱形ABCD 的一个角为直角.二、几种特殊四边形的面积问题(1)设矩形ABCD 的两邻边长分别为a,b ,则 S 矩形=ab .(2)设菱形ABCD 的一边长为a ,高为h ,则 S 菱形=ah ;若菱形的两对角线的长分别为a,b ,则 S 菱形=2ab。
人教版八年级下册数学《正方形》平行四边形研讨复习说课教学课件

A
B
O
D
C
阶段归纳
正方形判定的常用方法:
+
一个角是直角 或对角线相等
先判定菱形
矩形条件(二选一)
先判定矩形
+
一组邻边相等, 或对角线垂直
菱形条件(二选一)
正方形 正方形
阶段归纳
平行四边形、矩形、菱形、正方形的判定总结
矩形
5种判定方法 四边形
平行四边形
一个角是直角且一组邻边相等
正方形
菱形
当堂练习
6.对角线互相平分,垂直,相等的四边形是正方形
几何语言表示 ∵AC⊥BD,AC平分BD,BD平分AC,AC=BD, ∴四边形ABCD是正方形
知识点四:正方形,菱形矩形平行四边形之间的关系
归纳总结:正方形是特殊的平行四边形,还是特殊的矩
形、特殊的菱形,因此正方形具有这些图形的所有性质. 判定正方形有两个思路:(1)先判定四边形是矩形,再判定
这个矩形是菱形;(2)先判定四边形是菱形,再判定这个菱形 是矩形.
例1 求证:正方形的两条对角线把这个正方形分成四个全等的 等腰直角三角形.
已知:如图,正方形ABCD中,对角线AC、BD相交于O。 求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形。
证明:∵四边形ABCD是正方形。
知识点二:正方形的性质(从边,角,对角线,对称性四个方面研究)
1.角:正方形的四个角都是直角; 几何语言表示:在正方形ABCD中,∠ABC=∠BCD=∠CDA=∠DAB=90° 2.边:正方形的四条边都相等;对边平行。
几何语言表示:在正方形ABCD中,AB=BC=CD=DA,AB∥CD,AD∥BC
证一证
对角线互相垂直的矩形是正方形.
八年级数学下册 第18章 平行四边形复习课件 (新版)新人教版.pptx

(平行四边形)与三角形的联系;从性质定理的 逆命题的讨论中研究判定定理;类比、一般到特 殊.
这是研究图形的基本思路.
7
7
整理知识 优化知识结构
你能说一下平行四边形、矩形、菱形和正方形的性 质和判定吗?
你能把本章知识整理成知识结构图吗?试一试!
四边形 平行四边形
矩形
正方形 菱形
8
8
整理知识 优化知识结构
你能说一下平行四边形、矩形、菱形和正方形的性 质和判定吗?
你能把本章知识整理成知识结构图吗?试一试!
两组对边 四边形 分别平行
平行四 边形
矩形 菱形
正方形
9
9
基础练习
练习1 在图中的标号下面写出所有的判定定理: ___________________________________________; ___________________________________________; ___________________________________________.
正方形
边、角、对 角线的特征
下定义→探性 质→研判定
研究方法
观察、猜想、证明;把四边形问 题转化为三角形问题;从性质定 理的逆命题讨论中研究判定定理
一般到特殊的方法, 类比平行四边形
一般到特殊的方法,类 比平行四边形和矩形
一般到特殊的方法, 类比矩形和菱形
6
6
创设情境 回顾知识
(1)本章研究内容:各种平行四边形的边、角、对角 线的特征;
第18章
1
1
• 学习目标: 1.进一步理解平行四边形、矩形、菱形、正方形的 概念及其相互联系; 2.掌握平行四边形、矩形、菱形、正方形的性质和 判定; 3.会把各种平行四边形的相关知识进行结构化整理.
人教版初二下册数学第18章《平行四边形》讲义第12讲平行四边形-复习训练(有答案)
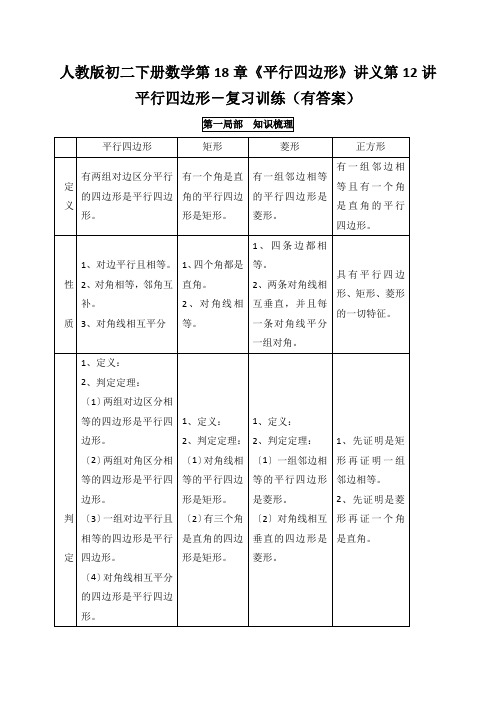
人教版初二下册数学第18章《平行四边形》讲义第12讲平行四边形-复习训练(有答案)对称 中心对称 中心对称轴对称图形 中心对称 轴对称图形 中心对称 轴对称图形第二局部 考点精讲精练考点一、平行四边形的性质及判定【知识要点】〔1〕、平行四边形的边、角、对角线性质, 对称性〔2〕、平行四边形判定方法〔3〕、三角形中位线【典型例题】例1、以下图形中是中心对称图形,但不是轴对称图形的是〔 〕A 、菱形B 、矩形C 、正方形D 、平行四边形例2、如图,□ABCD 与□DCFE 的周长相等,且∠BAD=60°,∠F=110°,那么∠DAE 的度数为 例3、如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延伸线交于点E,与DC 交于点F,且点F 为边DC 的中点,DG ⊥AE,垂足为G,假定DG=1,那么AE 的长为〔 〕 A 、2 B 、4 C 、4 D 、8例4、平面直角坐标系中,□ABCD 的顶点,A ,B ,D 的坐标区分是〔0,0〕〔5,0〕,〔2,3〕,那么顶点C 的坐标是〔 〕A 、〔3,7〕B 、(5,3)C 、(7,3)D 、 (8,2)〔例2〕 〔例3〕 〔例4〕例5、如图,E 是平行四边形内任一点, 假定S平行四边形ABCD =8,那么图中阴影局部的面积是〔 〕A 、3B 、4C 、5D 、6 例6、如图,将平行四边形ABCD 纸片沿EF 折叠,使点C 与点A 重合,点D 落在点G A yB CD处。
〔1〕求证:AE =AF〔2〕求证:△ABE ≌△AGF例7、如下图:四边形ABCD 是平行四边形,DE 平分BF ADC ,∠平分ABC ∠.试证明四边形BFDE 是平行四边形.例8、如图,在△ABC 中,AB =4,AC =3,BC =5,以三边为边,在BC 的同侧区分作三个等边三角形即△ABD 、△BCE 、△ACF 。
〔1〕求证:四边形EFAD 是平行四边形;〔2〕求四边形EFAD 的面积。
最新人教版初中数学八年级下册-第18章《平行四边形》复习课件-

第 1 题图
第 2 题图
2.(4分)如图,在四边形ABCD中,E是BC边的中点,
连接DE并延长,交AB的延长线于F点,AB=BF.添
加一个条件,使四边形ABCD是平行四边形.你认为
下面四个条件中可选择的是( D )
A.AD=BC;
B.CD=BF;
C.∠A=∠C;
D.∠F=∠CDE。
3.(8分)(2013·镇江)如图,AB∥CD,AB=CD,点
6.(5分)小玲的爸爸在钉制平行四边形框架时,采用了
一种方法:如图所示,将两根木条AC,BD的中点
重叠,并用钉子固定,则四边形ABCD就是平行四
边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形 7.(8分)如图,在▱ABCD中,点E,F是对角线AC上两
四边形的个数为( ) A.4个; B.3个; C.2个; D.1个
9.已知三条线段的长分别为10 cm, 14 cm和8 cm, 如 果以其中的两条为对角线, 另一条为边, 那么可以 画出所有不同形状的平行四边形的个数为( ) A. 1个; B. 2个; C. 3个; D. 4个.
10.如图, 在▱ABCD中, 对角线AC, BD相交于点O, E,
∠CFD+∠DFE=180°,∴∠AEF=∠DFE.∴AE∥DF.∴四边形 AFDE 为平行四边形
4.(4分)如图,在▱ABCD中,点E,F分别在AD,BC
上,且BE∥DF,若∠EBF=45°,则∠EDF的度数
为 45 。
5.(A41第B分8C2.)1D如课.2为图时平,平行四行平四边边四行形形边四A,B形边C则D形的可中的判添,性定加AB的质∥条与C件D判,是定要的使四综边合形应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辅导讲义学员编号:年级:课时数:学员姓名:辅导科目:学科老师:授课类型T 平行四边形的概念、性质T 平行四边形的断定C中位线定理授课日期时段教学内容一、同步学问梳理学问点1:平行四边形的定义:两组对边分别平行的四边形是平行四边形.表示:平行四边形用符号“”来表示.如图,在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD,记作ABCD”,读作“平行四边形ABCD”.留意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.学问点2:平行四边形的性质:(1)边:平行四边形的对边平行且相等.(2)角:平行四边形的对角相等.邻角互补(3)对角线:平行四边形的对角线相互平分对称性:平行四边形是中心对称图形,两条对角线的交点是对称中心;二、同步题型分析题型1:平行四边形的边、角例1:已知,如图1,四边形ABCD为平行四边形,∠A+∠C=80°,平行四边形ABCD的周长为46 cm,且AB-BC=3 cm,求平行四边形ABCD的各边长和各内角的度数.分析:由平行四边形的对角相等,邻角互补可求得各内角的度数;由平行四边形的对边相等,得AB+BC=23 cm,解方程组即可求出各边的长.解:由平行四边形的对角相等,∠A+∠C=80°,得∠A=∠C=40°又DC∥AB,∠D及∠A为同旁内角互补,∴∠D=180°-∠A=180°-40°=140°.∴∠B=140°.由平行四边形对边相等,得AB=CD,AD=BC.因周长为46 am,因此AB+BC=23 cm,而AB-BC=3 cm,得AB=13 cm,BC=10 cm,∴CD=13 am.AD=10 cm.题后反思:留意充分利用性质解题.例2:如图2,在平行四边形ABCD中,E、F是直线BD上的两点,且DE=BF,你认为AE=CF吗?试说明理由.分析:本题主要考察平行四边形的性质.要证明AE=CF,可以把两线段分别放在两个三角形里,然后证明两三角形全等.解:AE=CF.理由:在平行四边形ABCD中,∵AB=CD且AB∥CD.∴∠ABE=∠CDF.∵DE=BF,∴ DE+BD=BF+BD,即BE=DF:∴△ABE≌△CDF ∴ AE=CF题后反思:利用平行四边形的性质解题时,一般要用到三角形全等学问,此题还可以证明其他三角形全等来证明两线段相等.题型2:平行四边形的周长例1:如图3,在平行四边形ABCD中,AC、BD相交于点O,作OE⊥BD于O,交CD于E,连接BE,若△BCE的周长为6,则平行四边形ABCD的周长为( B )图3A. 6B. 12C. 18D. 不确定分析:本题主要考察平行四边形的性质:对角线相互平分。
再由OE⊥BD,依据垂直平分线的性质得DE=BE,△BCE的周长=BE+BC+EC=CD+BC=6,平行四边形ABCD的周长就为12.例2:在平行四边形ABCD中,已知对角线AC、BD相交于点O,且AC+BD=20,△AOB的周长为15,则CD=______.解:因为:三角形ABO的周长为15,AB=6,所以:AO+BO=15--6=9,因为:四边形ABCD是平行四边形,所以:AC=2AO,BD=2BO,所以:AC+BD=2AO+2BO =2(AO+BO ) =2×9 =18题型3:平行四边形的面积例1:如图4,AB ∥CD ,AC 、BD 交于点O ,且OB =OD .已知S △OBC =1,求四边形ABCD 的面积.图4分析:要求四边形ABCD 的面积,就要找到其及 OBC 的关系,考虑四边形ABCD 是否为特别四边形,即平行四边形,而从题中条件,利用“等底等高的两三角形面积相等”,问题得解.解:因为AB ∥CD ,且OB =OD ,据“等底等高的两三角形面积相等”可得:四边形ABCD 为平行四边形.利用平行四边形的性质,可得四边形ABCD 的面积=4S △OBC =4.题后反思:“等底等高的两三角形面积相等”在平行四边形中也有许多不经意的好用途.例2:在□ABCD 中,点A 1、A 2、A 3、A 4和C 1、C 2、C 3、C 4分别是AB 和CD 的五等分点,点B 1、B 2、和D 1、D 2分别是BC 和DA 的三等分点,已知四边形A 4B 2C 4D 2的面积为1,则□ABCD 的面积为( )A .2B .53 C .35 D .15图5分析:可以设平行四边形ABCD 的面积是S ,依据等分点的定义利用平行四边形ABCD 的面积减去四个角上的三角形的面积,就可表示出四边形A 4B 2C 4D 2的面积,从而得到两个四边形面积的关系,即可求解.解:设平行四边形ABCD 的面积是S ,设AB=5a ,BC=3b .AB 边上的高是3x ,BC 边上的高是5y .则S=5a•3x=3b•5y.即ax=by=15s △AA 4D 2及△B 2CC 4全等,B 2C= 13BC=b ,B 2C 边上的高是45•5y=4y. 则△AA 4D 2和△B 2CC 4的面积是2by= 215s . 同理△D 2C 4D 及△A 4BB 2的面积是15s.解得S= 53. 故选C .题后反思:考察平行四边形的性质和三角形面积计算,正确利用等分点的定义,得到两个四边形的面积的关系是解决本题的关键. 例3:已知:如图6,在ABCD 中,点E 在AC 上,AE =2EC ,点F 在AB 上,BF=2AF ,若△AEF 的面积为2cm 2,求ABCD 的面积.图6解:由△AEF 的面积为2,先以AB 为底看,设Q 为BF 中点,则△FQE 的面积=△AEF 的面积(底相等,高也相等),同理,△QBE 的面积=△AEF 的面积=2,则△AEB 的面积为6;再以AC 为底看△ABC ,EC=13AC ,AE=23AC ,则△EBC 的面积=△ABE 的面积的一半=3,则△ABC 的面积=9,平行四边形ABCD 的面积=18三、课堂达标检测1.如图,ABCD中,CE⊥AB,垂足为E,假如∠A=115°,则∠BCE=______.2.如图,在□ABCD中,DB=DC、∠A=65°,CE⊥BD于E,则∠BCE=______.3.如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.4.如图,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.5.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.6.已知:如图,ABCD的对角线AC、BD相交于点O,EF过点O及AB、CD分别相交于点E、F.求证:OE=OF,AE=CF,BE=DF.7.如图,ABCD中,∠B=60°,AB=6,则BC边上的高等于________.(第7题) (第8题)8.如图,在ABCD中,∠A的平分线交BC于点E.若AB=3,AD=8,则EC=_______.9.如图,已知的周长为60 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求这个四边形各边长.10.如图,假如△AOB及△AOD的周长之差为8,而AB∶AD=3∶2,那么的周长为多少?11.公园有一片绿地,它的形态是平行四边形,绿地上要修几条笔直的小路,如图,AB=15cm,AD=12cm,AC⊥BC,求小路BC,CD,OC的长,并算出绿地的面积.12.已知:如图,在□ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,已知□ABCD的周长为8.6cm,△ABD的周长为6cm,求AB、BC的长.13.已知:如图,在平行四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=CG,BF=DH。
求证:△AEH≌△CGF。
【实力提升】1.如图,在ABCD中EF分别是AD、 CD 边上的点,连接BE 、AF,他们相交于G,延长BE交CD的延长线于点H,则图中的全等三角形有()A、2对B、3对C、4对D、5对2.在□ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=()A.1:2 B.1:3 C.2:3 D.2:53.如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,及DC的延长线相交于点H,则△DEF的面积是 .4.一题多变,培育应变实力已知:如图1,□ABCD 的对角线AC 、BD 交于点O , EF 过点O 及AB 、CD 分别交于点E 、F . 求证:OE=OF .(图1)(图2) (图3) (图4)变式1.在图1中,连结哪些线段可以构成新的平行四边形?为什么?(图2、图3)变式2.在图1中,假如过点O 再作GH ,分别交AD 、BC 于G 、H (如图4),AB C DOEFABC DOEFA BCD OEF GHA B CD OEF GH你又能得到哪些新的平行四边形?为什么?5. 如图12-57,在△ABC中,点M,N在AB上,AM=BN,ME∥BC交AC于E,MG∥AC交BC于G,NH∥AC交BC于H,求证:AC=NH+MG。
6.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD=BF,以AD•为边作等边△ADE。
(1)求证:△ACD≌△CBF;(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且∠DEF=30°?证明你的结论。
一、同步学问梳理学问点3:平行四边的断定:(1)⎧⎪⎨⎪⎩两组对边分别平行的四边形是平行四边形(定义)边两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形(2)角:两组对角分别相等的四边形是平行四边形(3)对角线:对角形相互平行的四边形是平行四边形二、同步题型分析题型1:平行四边形的断定例1:如图7所示,在平行四边形ABCD中,EF∥AB,HG∥AD,EF及GH相交于点O,则该图中平行四边形的个数共有()图7A. 7个B. 8个C. 9个D. 11个解析:本题主要考察平行四边形的定义.两条平行线把平行四边形ABCD分成8个(不含原来)四边形,看这些四边形是否都符合平行四边形的定义,∵ EF ∥AB,HG∥AD,它们的各边都平行.即有□ABCD,□DEOH,□HOFC,□AGOE,□GOFB,□AGHD,□GBCH,□ABFE,□EFCD.答案C题后反思:先分清图中共有哪些四边形,然后依据定义去推断.例2:如图8,已知六边形ABCDEF的每一个内角都是120°且AB=l,DE=2,BC+CD=8,求这个六边形的周长.图8分析:要求其周长,只要求出AF及EF的和即可.如何求?考虑到特别角,结合三角形学问,可将六边形化归为平行四边形来解.解:如图5,延长FA、CB相交于点G,延长CD、FE相交于点H,由已知,△ABG和△DEH都是等边三角形.所以∠G=∠H=60°.因为∠C=∠F=120°,则四边形CGFH为平行四边形,GF+FH=CH+CG=CD+DH+CB+BG =CD+BC+DE+AB=8+1+2=11.所以AF+FE=11-1-2=8.则该六边形的周长为:8+8+1+2=19.题后反思:解题关键是作协助线,将不规则的六边形变成平行四边形.题型2:平行四边形的性质、断定例1:已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.图9证明:因为ABCD是平行四边形,所以 AD//BC,AD=BC,因为 E,F分别是AD,BC的中点,所以 ED=AD/2,BF=BC/2,因为 AD=BC,所以 ED=BF,因为 AD//BC,ED=BF,所以四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)所以 BE=DF,且BE//DF。
