信息论基础试卷及详细答案
信息论基础试卷及详细答案

W log(1 +
P ) N 0W
(169 面)
8 在 BSC(二元对称信道)中,错误率为 p,则其信道容量 C= 1-H(p) 9 差熵为 h(X)的连续随机变量集合 X 的熵功率为 σ = 10.一个最小距离为 d 的二元分组码能纠错能力为 [
⎛1 ⎜ 8.一信道的转移概率矩阵为 ⎜ 3 ⎜1 ⎜ ⎝6 1 3 1 3 1 6 1 6 1⎞ ⎟ 6⎟, 求信道容量和达到容量时的输出概率(112 面) 1⎟ ⎟ 3⎠
解:设输出概率分别为 q1 , q2 , q3 , q4 。该信道为准对称信道,当输入等概率时达到信道容量 可计算输出概率为
1 1 1 1 1 1 1 1 1 1 1 1 q1 = ( + ) = , q2 = ( + ) = , q3 = ( + ) , q4 = 2 6 3 4 2 3 3 3 2 6 6 4
PE =1/2,信道疑义度上界为:H(1/2)+(1/2) × log2=1.5bit
3
(2)对于规则 B,由于 1 − PE =
∑ P(ai )P(bi | ai ) =
i =1
1 1 1 1 1 3 P(bi | ai ) = × ( + + ) =1/3, ∑ 3 2 6 3 3 i =1
所以 PE =2/3,信道疑义度上界为:H(2/3)+2/3 × log2= log 2 3 (bit) 5.设 X 和 Y 时分别具有均值 mx , m y ,方差 σ x , σ y 的两个独立的高斯随机变量集合,且 U= ( X + Y ) / 2 ,V= ( X − Y ) / 2 ,试求 h(UV)。 (70 面) 解:依据题意有
信息论基础各章参考答案

各章参考答案2.1. (1)4.17比特 ;(2)5.17比特 ; (3)1.17比特 ;(4)3.17比特2.2. 1.42比特2.3. (1)225.6比特 ;(2)13.2比特2.4. (1)24.07比特; (2)31.02比特2.5. (1)根据熵的可加性,一个复合事件的平均不确定性可以通过多次实验逐步解除。
如果我们使每次实验所获得的信息量最大。
那么所需要的总实验次数就最少。
用无砝码天平的一次称重实验结果所得到的信息量为log3,k 次称重所得的信息量为klog3。
从12个硬币中鉴别其中的一个重量不同(不知是否轻或重)所需信息量为log24。
因为3log3=log27>log24。
所以在理论上用3次称重能够鉴别硬币并判断其轻或重。
每次实验应使结果具有最大的熵。
其中的一个方法如下:第一次称重:将天平左右两盘各放4枚硬币,观察其结果:①平衡 ②左倾 ③右倾。
ⅰ)若结果为①,则假币在未放入的4枚币,第二次称重:将未放入的4枚中的3枚和已称过的3枚分别放到左右两盘,根据结果可判断出盘中没有假币;若有,还能判断出轻和重,第三次称重:将判断出含有假币的三枚硬币中的两枚放到左右两盘中,便可判断出假币。
ⅱ)若结果为②或③即将左盘中的3枚取下,将右盘中的3枚放到左盘中,未称的3枚放到右盘中,观察称重砝码,若平衡,说明取下的3枚中含假币,只能判出轻重,若倾斜方向不变,说明在左、右盘中未动的两枚中其中有一枚为假币,若倾斜方向变反,说明从右盘取过的3枚中有假币,便可判出轻重。
(2)第三次称重 类似ⅰ)的情况,但当两个硬币知其中一个为假,不知为哪个时,第三步用一个真币与其中一个称重比较即可。
对13个外形相同的硬币情况.第一次按4,4,5分别称重,如果假币在五个硬币的组里,则鉴别所需信息量为log10>log9=2log3,所以剩下的2次称重不能获得所需的信息.2.6. (1)215log =15比特; (2) 1比特;(3)15个问题2. 7. 证明: (略) 2.8. 证明: (略)2.9.31)(11=b a p ,121)(21=b a p ,121)(31=b a p ,61)()(1312==b a b a p p ,241)()()()(33233222====b a b a b a b a p p p p。
信息论试卷含答案资料讲解

《信息论基础》参考答案一、填空题(共15分,每空1分)1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为32log bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H r (S))。
5、当R=C 或(信道剩余度为0)时,信源与信道达到匹配。
6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。
7、根据是否允许失真,信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是高斯分布或正态分布或()222x f x σ-=时,信源具有最大熵,其值为值21log 22e πσ。
9、在下面空格中选择填入数学符号“,,,=≥≤〉”或“〈”(1)当X 和Y 相互独立时,H (XY )=H(X)+H(X/Y)=H(Y)+H(X)。
(2)()()1222H X X H X =≥()()12333H X X X H X = (3)假设信道输入用X 表示,信道输出用Y 表示。
在无噪有损信道中,H(X/Y)> 0, H(Y/X)=0,I(X;Y)<H(X)。
二、(6分)若连续信源输出的幅度被限定在【2,6】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
()1,2640,x f x ⎧≤≤⎪=⎨⎪⎩Q 其它()()()62log f x f x dx ∴=-⎰相对熵h x=2bit/自由度该信源的绝对熵为无穷大。
三、(16分)已知信源1234560.20.20.20.20.10.1S s s s s s s P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用霍夫曼编码法编成二进制变长码;(6分) (2)计算平均码长L ;(4分)(3)计算编码信息率R ';(2分)(4)计算编码后信息传输率R ;(2分) (5)计算编码效率η。
信息论基础B卷及答案
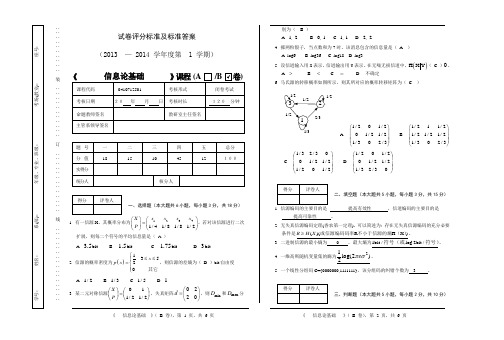
∶∶∶∶∶∶∶∶∶∶装∶∶∶∶∶∶∶∶∶∶∶订∶∶∶∶∶∶∶∶∶∶∶∶∶线∶∶∶∶∶∶∶∶∶∶∶∶∶∶∶∶试卷评分标准及标准答案(2013 — 2014 学年度第 1 学期)《课程(A 卷)一、选择题(本大题共6小题,每小题3分,共18分)1. 有一信源X,其概率分布为12341/41/81/81/2X x x x xP⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,若对该信源进行二次扩展,则每二个符号的平均信息量是(A )A. 3.5bitB. 1.5bitC. 1.75bitD. 3bit2. 信源的概率密度为()1352xp x⎧≤≤⎪=⎨⎪⎩其它,则信源的差熵为(D )bit/自由度.A.1/2B.1/3C.1/5D.13. 某二元对称信源011/21/2XP⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,失真矩阵0220d⎛⎫⎪⎝⎭=,则minD和maxD分别为( B )A. 1, 2B. 0, 1C. 1, 1D. 2, 24. 掷两粒骰子,当点数和为7时,该消息包含的信息量是(A )A. log6B. log36C. log18D. log35. 设信道输入用X表示,信道输出用Y表示。
在无噪无损信道中,()H X Y(C )0。
A. >B. <C. =D. 不确定6. 马氏源的转移概率如图所示,则其所对应的概率转移矩阵为(C )1/2A.1/201/201/21/21/302/3⎛⎫⎪⎪⎪⎝⎭B.1/211/21/21/21/21/302/3⎛⎫⎪⎪⎪⎝⎭C.1/32/3001/21/21/201/2⎛⎫⎪⎪⎪⎝⎭D.1/201/201/21/21/32/30⎛⎫⎪⎪⎪⎝⎭二、填空题(本大题共5小题,每小题3分,共15分)1. 信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2. 无失真信源编码定理(香农第一定理),可以简述为:存在无失真信源编码的充分必要条件是R H X()()R H X≥或信源编码码率不小于信源的熵()。
信息论基础智慧树知到课后章节答案2023年下潍坊学院

信息论基础智慧树知到课后章节答案2023年下潍坊学院潍坊学院第一章测试1.信息论的奠基人是()。
A:香农 B:阿姆斯特朗 C:哈特利 D:奈奎斯特答案:香农2.下列不属于信息论的研究内容的是()。
A:纠错编码 B:信息的产生 C:信道传输能力 D:信源、信道模型答案:信息的产生3.下列不属于消息的是()A:文字 B:图像 C:信号 D:语音答案:信号4.信息就是消息. ()A:错 B:对答案:错5.信息是不可以度量的,是一个主观的认识。
()A:错 B:对答案:错6.任何已经确定的事物都不含有信息。
()A:对 B:错答案:对7.1948年香农的文章《通信的数学理论》奠定了香农信息理论的基础。
()A:错 B:对答案:对8.信息论研究的目的就是要找到信息传输过程的共同规律,以提高信息传输的(),使信息传输系统达到最优化。
A:有效性 B:认证性 C:可靠性 D:保密性答案:有效性;认证性;可靠性;保密性9.下列属于香农信息论的主要研究理论的是()。
A:压缩理论 B:调制理论 C:保密理论 D:传输理论答案:压缩理论;保密理论;传输理论10.信源编码的作用包含()。
A:检错纠错 B:对信源的输出进行符号变换 C:数据压缩 D:提升信息传输的安全性答案:对信源的输出进行符号变换;数据压缩第二章测试1.信息传输系统模型中,用来提升信息传输的有效性的部分为()A:信源 B:信道编码器、信道译码器 C:信道 D:信源编码器、信源译码器答案:信源编码器、信源译码器2.对于自信息,以下描述正确的是()A:以2为底时,单位是奈特。
B:以2为底时,单位是比特。
C:以10为底时,单位是奈特。
D:以e为底时,单位是比特答案:以2为底时,单位是比特。
3.信息熵的单位是()A:比特 B:比特每符号 C:无法确定答案:比特每符号4.必然事件和不可能事件的自信息量都是0 。
()A:错 B:对答案:错5.概率大的事件自信息量大。
信息基础试题及答案

信息基础试题及答案一、单选题(每题2分,共10分)1. 计算机中数据的最小单位是什么?A. 字节B. 位C. 字D. 兆答案:B2. 下列哪个选项不是计算机硬件?A. 中央处理器B. 操作系统C. 内存D. 硬盘答案:B3. 以下哪种网络协议用于网页传输?A. FTPB. HTTPC. SMTPD. POP3答案:B4. 以下哪种存储设备不是永久存储设备?A. 固态硬盘B. 机械硬盘C. 光盘D. 随机存取存储器(RAM)答案:D5. 以下哪个选项是计算机病毒的特点?A. 可自我复制B. 只能通过用户手动传播C. 总是立即显现症状D. 不能通过电子邮件传播答案:A二、多选题(每题3分,共15分)6. 以下哪些属于计算机软件的分类?A. 系统软件B. 应用软件C. 硬件D. 网络软件答案:A、B、D7. 以下哪些是计算机操作系统的功能?A. 进程管理B. 设备管理C. 文件管理D. 网络管理答案:A、B、C、D8. 以下哪些是计算机病毒的传播途径?A. 通过电子邮件B. 通过U盘C. 通过社交软件D. 通过正规软件下载答案:A、B、C9. 以下哪些属于计算机硬件的组成部分?A. 中央处理器B. 显卡C. 键盘D. 鼠标答案:A、B、C、D10. 以下哪些是计算机安全防护措施?A. 安装防病毒软件B. 定期更新操作系统C. 从不下载不明来源的软件D. 忽略安全警告答案:A、B、C三、判断题(每题1分,共10分)11. 计算机的存储设备包括硬盘、固态硬盘和内存。
(对)12. 计算机病毒只能通过电子邮件传播。
(错)13. 计算机的中央处理器(CPU)是计算机的核心部件,负责执行程序指令。
(对)14. 计算机的内存(RAM)是永久存储设备。
(错)15. 计算机操作系统的主要功能是管理计算机硬件资源。
(对)16. 计算机的显卡负责处理和输出图形和视频信号。
(对)17. 计算机的网络协议决定了数据在网络中的传输方式。
信息论基础1答案

信息论基础1答案LT计算信息量:1.当点数和为3时,该消息包含的信息量是多少?2.当点数和为7是,该消息包含的信息量是多少?3.两个点数中没有一个是1的自信息是多少?解:1.P(“点数和为3”)=P(1,2)+ P(1,2)=1/36+1/36=1/18则该消息包含的信息量是:I=-logP(“点数和为3”)=log18=4.17bit2.P(“点数和为7”)=P(1,6)+ P(6,1)+ P(5,2)+ P(2,5)+ P(3,4)+ P(4,3)=1/36 6=1/6则该消息包含的信息量是:I=-logP(“点数和为7”)=log6=2.585bit3.P(“两个点数没有一个是1”)=1-P (“两个点数中至少有一个是1”)=1-P(1,1or1,jori,1)=1-(1/36+5/36+5/36)=25/36则该消息包含的信息量是:I=-logP (“两个点数中没有一个是1”)=log25/36=0.53bit三、设X 、Y 是两个相互统计独立的二元随机变量,其取-1或1的概率相等。
定义另一个二元随机变量Z ,取Z=YX (一般乘积)。
试计算: 1.H (Y )、H (Z ); 2.H (XY )、H (YZ ); 3.I (X;Y )、I (Y;Z ); 解: 1.2i 11111H Y P y logP y log log 2222i i =⎡⎤=-+⎢⎥⎣⎦∑()=-()()=1bit/符号Z=YX 而且X 和Y 相互独立∴1(1)(1)(1)P P X P Y P X ⋅=+=-⋅=-(Z =1)=P(Y=1)= 11122222⨯+⨯=2(1)(1)(1)P P X P Y P X ⋅=-+=-⋅=(Z =-1)=P(Y=1)=11122222⨯+⨯=故H(Z)= i2i1(z )log (z )i P P =-∑=1bit/符号2.从上式可以看出:Y 与X 的联合概率分布为:H(YZ)=H(X)+H(Y)=1+1=2bit/符号 3.X与Y相互独立,故H(X|Y)=H(X)=1bit/符号∴I (X;Y )=H(X)-H(X|Y)=1-1=0bit/符号I(Y;Z)=H(Y)-H(Y|Z)=H(Y)-[H(YZ)-H(Z)]=0 bit/符号四、如图所示为一个三状态马尔科夫信源的转移概率矩阵P=1102211022111424⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭1. 绘制状态转移图;P(Y,Z) Y=1 Y=-1Z=1 0.25 0.25 Z=-1 0.25 0.252. 求该马尔科夫信源的稳态分布;3. 求极限熵;解:1.状态转移图如右图 2.由公式31()()(|)jiji i p E P E P EE ==∑,可得其三个状态的稳态概率为:1123223313123111()()()()22411()()()2211()()()24()()()1P E P E P E P E P E P E P E P E P E P E P E P E P E ⎧=++⎪⎪⎪=+⎪⎨⎪=+⎪⎪⎪++=⎩1233()72()72()7P E P E P E ⎧=⎪⎪⎪⇒=⎨⎪⎪=⎪⎩3.其极限熵:3i i 13112112111H = -|E =0+0+72272274243228=1+1+ 1.5=bit/7777i P H H H H ∞=⨯⨯⨯⨯⨯⨯∑(E )(X )(,,)(,,)(,,)符号五、在干扰离散对称信道上传输符号1和0,已知P (0)=1/4,P(1)=3/4,试求:1. 该信道的转移概率矩阵P2. 信道疑义度H (X|Y )3. 该信道的信道容量以及其输入概率分布 解:1.该转移概率矩阵为P=0.90.10.10.9⎡⎤⎢⎥⎣⎦2.根据P (XY )=P (Y|X )⋅P (X ),可得联合概率P (XY ) Y Y X=0 9/40 1/40 X=13/4027/401 0.0.0.0.1P(Y=i) 12/40 28/40 由P (X|Y )=P(X|Y)/P(Y)可得P(X|Y) Y=0 Y=1 X=0 3/4 1/28 X=1 1/427/28H(X|Y)=-i jiji j(x y )log x |y =0.09+0.12+0.15+0.035=0.4bit/P P∑,()符号 3.该信道是对称信道,其容量为: C=logs-H=log2-H(0.9,0.1)=1-0.469=0.531bit/符号这时,输入符号服从等概率分布,即0111()22X P X ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦六、某信道的转移矩阵⎥⎦⎤⎢⎣⎡=1.006.03.001.03.06.0P试求:该信道的信道容量及其最佳输入概率分布。
信息论基础—— 期末试卷 A 答案

○?○?大学 2008-2009 学年第一学期2006级 信息与计算科学专业 本 科 卷 A 参考答案与评分标准课程名称 信息论基础课程号(???) 考试形式(闭卷笔试) 时间(120分钟))一、判断题:本题共10小题,每题2分,满分20分。
1、√;2、√;3、×;4、×;5、√;6、×;7、×;8、√;9、√;10、×。
二、填空题:本题共7小题,每空2分,满分20分。
1、码字的最小距离(min d );2、(减少)冗余,提高编码效率; 提高信息传递的可靠性;3、系统码;4、无失真信源编码定理,信道编码定理,限失真信源编码定理;5、信道和信源都是无记忆;6、香农编码;7、2a。
三、计算题:本题共4小题,满分50分。
(15分)解:1/21/201/21/41/4P ⎡⎤=⎢⎥⎣⎦联合概率(,)i p x y则Y(2分)(1)11+414()log 2log log 24141a a H Y a a -=+++- ------------------(2分) 211161log 2log log 24141a aa a -=++-+ 211111log 2log16log log 244141a aa a -=+++-+23111log 2log log 24141a aa a-=++-+;取2为底2223111()(log log )24141a aH Y bit a a-=++-+; ------------------(1分) (2)11111111(|)log log log log log 2222224444aa a a a H Y X ---⎡⎤=-++++⎢⎥⎣⎦3(1)log 2log 22a a -=-+3log 22a-=; 取2为底,3(|)2aH Y X bit -=; ------------------(2分) (3)[]2()()()111max (;)max ()(|)max log 2log log 24411i i i p x p x p x aa a C I X Y H Y H Y X a a -⎛⎫==-=++ ⎪+-⎝⎭。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R(D)=
1 2 1 4 1 2 2 log + log = log 4 D 4 D 2 D
如果仅使用 X 2 ,有 B=2D-2 和 2<B ≤ 4,得 2<D ≤ 3
R(D)=
1 4 1 2 = log log 4 2D − 2 2 D −1
由 2 Dmax =2+4,得 Dmax =3 所求 R(D)函数:
信息论基础模拟试题
命题者:08 级命题委员会小组 高级顾问:韩海清 一.填空题 1.某随机变量集合有 n 个符号,其最大熵为 logn (26 面) 2.一个线性分组码 C={000000,111111},该分组码的纠错个数为 2 (提示:观察两个字符串不同数字的个数,设为 n,则纠错个数为[
(136 面)
总能量改为 E=15 时有: ⎨ C=
1 1 3 1 169 log(1 + 12) + log(1 + ) = log 2 2 10 2 10
7.写出错误率为 p 的二元对称信道的转移概率矩阵, 并计算其二次扩展信道的转移概率矩阵 和容量。 (121 面) 解:该信道的转移概率矩阵为 ⎜ ⎜
p ⎞ ⎛1 − p ⎟ ⎟ ⎝ p 1− p ⎠
π ] = log 2 2 =0.5 比特/符号 (3 + 1)
3.一个二维独立高斯信源( X 1 X 2 ) ,其中 X 1 , X 2 均值都为零,方差分别为 2 和 4,采用均 方失真测度,求该信源的 R(D)函数。 (201 面) 解:如果 X 1 , X 2 都使用,有 B=2D/2 和 B ≤ 2,得 D ≤ 2
四.解答题 1.一个二阶马氏链, 符号集 A={0, 1}, 转移概率为 p(0|00)=p(1|11)=0.8,p(1|00)=p(0|11)=0.2, p(0|01)=p(0|10)=p(1|01)=p(1|10)=0.5 (1)确定所对应的马氏源的状态,写出状态转移矩阵; (2)若信源初始状态分布为平稳分布,求 8 次扩展源的熵; (3)求信源的符号熵; (4)求信源效率; (5)求信源剩余度。 (49,52,54 面) 解:(1)马氏源状态为 A2 ={ w0 = 00, w1 = 01, w2 = 10, w3 = 11 } 状态a1 ⎟ ⎟ =⎜ ⎟ ⎜ ⎟ ,求其二次扩展源的熵 ⎝ P ⎠ ⎝1 / 2 1 / 4 1 / 4 ⎠
H ( X 2 ) 。 (40 面)
解: H ( X 2 ) =2H(X)=2[ −
1 1 1 1 log − ( log ) × 2 ]=3 比特/扩展符号 2 2 4 4
⎧ (1 / 2) log 2 2 D,0 < D ≤ 2 ⎪ R( D) = ⎨(1 / 2) log 2 /( D − 1) ,2 < D ≤ 3 ⎪ 0, D ≥ 3 ⎩ ⎛1 / 2 1 / 3 1 / 6 ⎞ ⎜ ⎟ 4.已知信道的转移概率矩阵为 ⎜1 / 6 1 / 2 1 / 3 ⎟ ,现有两种判决规则: ⎜1 / 3 1 / 6 1 / 2 ⎟ ⎝ ⎠ ⎧ g ( y = b1 ) = a1 ⎪ 规则 A: ⎨ g ( y = b2 ) = a2 ⎪g( y = b ) = a 3 3 ⎩ ⎧ g ( y = b1 ) = a1 ⎪ ,规则 B: ⎨ g ( y = b2 ) = a3 ⎪g( y = b ) = a 3 2 ⎩
设输入等概率,求信道的疑义度和两种译码规则下信道疑义度的上界。 (139 面) 解:由于信道为强对称信道,所以当信道输入等概率时,输出也等概率,H(X)=H(Y)。又因为 H(X)-H(X|Y)=H(Y)-H(Y|X),所以信道疑义度: H(X|Y)=H(Y|X)=H(1/2,1/3,1/6)= −
二次扩展信道的转移概率矩阵为
p ⎞ ⎛1 − p p ⎞ ⎛1 − p ∏=⎜ ⎜ p 1− p ⎟ ⎟⊗⎜ ⎜ p 1− p ⎟ ⎟ ⎝ ⎠ ⎝ ⎠
⎛ (1 − p) 2 ⎜ ⎜ p (1 − p) =⎜ ⎜ p (1 − p) ⎜ p2 ⎝
p (1 − p) (1 − p) 2 p2 p (1 − p)
q
置码存在的充要条件是:
∑r
i =1
− li
≤1
(课本 88 面,Kraft 定理) db (课本 173 面)
5.加性高斯白噪声 (AWGN) 信道实现可靠通信的信噪比的下界为 -1.59 6.一维高斯随机变量集的熵为
1 log(2πeσ 2 ) (注意 σ 是平均方差,而 σ 2 是方差,69 面) 2 N 7.一个加性高斯白噪声(AWGN)信道的噪声的功率谱密度为 0 ,输入信号平均功率限制 2
⎛1 ⎜ 8.一信道的转移概率矩阵为 ⎜ 3 ⎜1 ⎜ ⎝6 1 3 1 3 1 6 1 6 1⎞ ⎟ 6⎟, 求信道容量和达到容量时的输出概率(112 面) 1⎟ ⎟ 3⎠
解:设输出概率分别为 q1 , q2 , q3 , q4 。该信道为准对称信道,当输入等概率时达到信道容量 可计算输出概率为
1 1 1 1 1 1 1 1 1 1 1 1 q1 = ( + ) = , q2 = ( + ) = , q3 = ( + ) , q4 = 2 6 3 4 2 3 3 3 2 6 6 4
2 2
⎛ ⎜ 所以 h(UV)=h(XY)+log det ⎜ ⎜ ⎜ ⎝
6.设有一个二维独立并联高斯信道,两个子信道的噪声的方差分别为 σ 1 = 1, σ 2 = 10 ,输 入信号的总能量为 E=6,求信道容量 C 和达到容量时的能量分配 E1 , E2 ;若其他条件不变, 将输入信号的总能量改为 E=15,结果又是多少呢?(165 面) 解:依题意得:
PE =1/2,信道疑义度上界为:H(1/2)+(1/2) × log2=1.5bit
3
(2)对于规则 B,由于 1 − PE =
∑ P(ai )P(bi | ai ) =
i =1
1 1 1 1 1 3 P(bi | ai ) = × ( + + ) =1/3, ∑ 3 2 6 3 3 i =1
所以 PE =2/3,信道疑义度上界为:H(2/3)+2/3 × log2= log 2 3 (bit) 5.设 X 和 Y 时分别具有均值 mx , m y ,方差 σ x , σ y 的两个独立的高斯随机变量集合,且 U= ( X + Y ) / 2 ,V= ( X − Y ) / 2 ,试求 h(UV)。 (70 面) 解:依据题意有
1 1 1 1 1 1 2 1 log − log − log = + log 2 3 (bit) 2 2 3 3 6 6 3 2 1 1 1 3 P(ai )P(bi | ai ) = ∑ P(bi | ai ) = × 3 × =1/2,所以 ∑ 3 2 3 i =1 i =1
3
(1)对于规则 A,由于 1 − PE =
为 P,信道的带宽为 W,那么信道每单位时间的容量为 C=
W log(1 +
P ) N 0W
(169 面)
8 在 BSC(二元对称信道)中,错误率为 p,则其信道容量 C= 1-H(p) 9 差熵为 h(X)的连续随机变量集合 X 的熵功率为 σ = 10.一个最小距离为 d 的二元分组码能纠错能力为 [
则
Dmin = 1, Dmax = 5 / 3 。 (√) (186 面)
3.若(X,Y,Z)为马氏链,则(Z,Y,X)也是马氏链。 (√) (60 面) 4.分组码的最小距离就是其最小重量的非零码字的重量。 (×) (135 面, 应该是线性分组码) 5.为有效抵抗加性高斯噪声干扰,信道输入应该是高斯分布。 (√) (164 面) 6.信道疑义度始终为正。 (×) (138 面,应该是非负,可以为 0) 7.信道输入和输出之间的平均互信息是下凸函数。 (×) (29 面,应该是上凸函数) 8.信息处理过程中熵是不会增加的。 (√) (26 面) 9.典型序列信源符号出现的概率近似等于其频率。 (√) (86 面) 10.若 信 道 的 输 入 与 输 出 分 别 为 X,Y , 输 入 符 号 的 数 目 为 r , 那 么 信 道 疑 义 度 满 足 H(X|Y) ≤ H ( p E ) + p E log r 。 (×) (138 面,应该是 r-1) 11.一个离散平稳无记忆信道的极限熵等于最小平均熵。 (√) (119 面) 12.对于离散无记忆信道,达到容量时输入概率分布是唯一的。 (×) (123 面,不唯一) 13.噪声功率相同的加性信道中以高斯噪声信道容量最大。 (×) (应该是最小) 14.R(D)函数是平均失真函数的下凸函数。 (√) (187 面) 15.MAP 准则是使译码平均错误率最小的准则。 (√) (132 面) 16.任意两个典型序列的联合序列是典型序列。 (×) 17.与离散信源一样,连续信源的平均互信息也具有对称性和非负性。 (√) (73 面) 18.通过一一变换后,连续信源的差熵一定会变化。 (×) (67 面,应该是可能会变化) 19.转移概率矩阵不随时间变化的马氏链是平稳马氏链。 (×) (47 面,那是齐次马氏链) 20.R ≥ H ⇔ 存在无失真信源编码。 (√) (7 面,还有几个类似的,如 R ≤ C ⇔ 存在译码差错 任意小的信道编码;R ≥ R ( D ) ⇔ 存在平均失真) 三.计算题 1.给定离散无记忆信源的数学模型为 ⎜ ⎜
2
(121 面) (72 面)
1 2h( X ) e 2πe
d −1 ] (参考第二题) 2
二.判断题 1.对称信道达到容量时,输入概率和输出概率唯一。
(√) (123 面)
⎛ 1 2 3⎞ ⎜ ⎟ 2.设试验信道输入符号{ a1 , a2 , a3 },概率分别为 1/3,1/3,1/3,失真矩阵为 ⎜ 2 1 3 ⎟ , ⎜ 3 2 1⎟ ⎝ ⎠
