高等数学(同济版)第一章习题
高等数学(本科少学时类型)同济第三版课后习题答案选解1

高等数学(本科少学时类型)同济第三、四版课后习题答案选解1第一章函数与极限1.1函数P.17习题1.11..005.0:01.0;05.0:1.0,222,1),,1(<=<=<<-<-∈δεδεεδδδx x U x 1..3.下列函数是否为同一函数?为什么?(1)2()2ln ()ln f x x x x j ==与;(2)()f x =()x x j =;(2)(3)()f x =与()g x x =;(4)()f x =与()sin g x x =;解:(1)否;因为定义域不同;(2)否;因为对应关系不同;(2)否;因为函数的定义域不同;(3)是;因为定义域和对应关系及值域都相同;(4)否;因为对应关系及值域都相同;4.求下列函数的定义域:(1)1y x =(2)2232x y x x =-+;(3)arcsin(3)y x =-;(4)1arctan y x =;(5)ln(1)y x =+;(6)1x y e =;解:(1)要使1y x=有意义,需使20,10x x ¹-³故函数的定义域为[-1,0)[(0,1].(2)要使2232x y x x =-+有意义,需使2320x x -+¹故函数的定义域为(-,-2)(-2,1)[1,+.) (3)要使arcsin(3)y x =-有意义,需使31x -£故函数的定义域为[2,4].(4)要使1arctan y x=有意义,需使30,0x x ->¹故函数的定义域为(-,0)(0,3].¥(5)要使ln(1)y x =+有意义,需使10x +>故函数的定义域为+).(1,-¥(6)要使1xy e =有意义,需使0x ≠故定义域为(,0)(0,)-∞+∞ .5.6.7.8.9.10.下列函数中哪些是偶函数,哪些是奇函数,哪些是非奇函数又非偶函数?(1)22(1)y x x =-;(2)233y x x =-;(3)(1)(1)y x x x =-+;(4)2x xa a y -+=;(5)2x xa a y --=;(6)sin cos 1y x x =-+;解:(1)按运算:偶函数与偶函数的和差积仍是偶函数;也可以按定义判定;(2)定义域对称,但()();()()f x f x f x f x -¹-¹-所以是非奇非偶函数;(3)按运算:奇函数与奇函数的积是偶函数;奇函数与偶函数的积是奇函数;所以是奇函数;也可以按定义判定;(4)定义域对称,()()f x f x -=所以函数是偶函数;(5)定义域对称,()()f x f x -=-所以函数是奇函数;(6)定义域对称,但()();()()f x f x f x f x -¹-¹-所以是非奇非偶函数;11.设下面所考虑的函数都是定义在对称区间(,)l l -内的,证明:(1)两个偶函数的和是偶函数;两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数。
高等数学(同济第五版)课后答案第1章

习题1−11. 设A=(−∞, −5)∪(5, +∞), B=[−10, 3), 写出A∪B, A∩B, A\B及A\(A\B)的表达式.解A∪B=(−∞, 3)∪(5, +∞),A∩B=[−10, −5),A\B=(−∞, −10)∪(5, +∞),A\(A\B)=[−10, −5).2. 设A、B是任意两个集合, 证明对偶律: (A∩B)C=AC ∪B C.证明因为x∈(A∩B)C⇔x∉A∩B⇔ x∉A或x∉B⇔ x∈AC或x∈B C ⇔ x∈AC ∪B C,所以(A∩B)C=AC ∪B C .3. 设映射f : X →Y, A⊂X, B⊂X . 证明(1)f(A∪B)=f(A)∪f(B);(2)f(A∩B)⊂f(A)∩f(B).证明因为y∈f(A∪B)⇔∃x∈A∪B, 使f(x)=y⇔(因为x∈A或x∈B) y∈f(A)或y∈f(B)⇔ y∈f(A)∪f(B),所以f(A∪B)=f(A)∪f(B).(2)因为y∈f(A∩B)⇒∃x∈A∩B, 使f(x)=y⇔(因为x∈A且x∈B) y∈f(A)且y∈f(B)⇒ y∈f(A)∩f(B),所以f(A∩B)⊂f(A)∩f(B).4. 设映射f : X→Y, 若存在一个映射g: Y→X, 使, , 其中IXIfg=YIgf=X、IY 分别是X、Y上的恒等映射, 即对于每一个x∈X, 有IX x=x; 对于每一个y∈Y, 有IY y=y. 证明: f是双射, 且g是f的逆映射: g=f −1.证明因为对于任意的y∈Y, 有x=g(y)∈X, 且f(x)=f[g(y)]=I y y=y, 即Y中任意元素都是X中某元素的像, 所以f为X到Y的满射.又因为对于任意的x1≠x2, 必有f(x1)≠f(x2), 否则若f(x1)=f(x2) ⇒g[ f(x1)]=g[f(x2)] ⇒ x1=x2.因此f既是单射, 又是满射, 即f是双射.对于映射g: Y→X, 因为对每个y∈Y, 有g(y)=x∈X, 且满足f(x)=f[g(y)]=I y y=y, 按逆映射的定义, g是f的逆映射.5. 设映射f : X→Y, A⊂X . 证明:(1)f −1(f(A))⊃A;(2)当f是单射时, 有f −1(f(A))=A .证明(1)因为x∈A ⇒ f(x)=y∈f(A) ⇒ f −1(y)=x∈f −1(f(A)),所以f −1(f(A))⊃A.(2)由(1)知f −1(f(A))⊃A.另一方面, 对于任意的x∈f −1(f(A))⇒存在y∈f(A), 使f −1(y)=x⇒f(x)=y . 因为y∈f(A)且f是单射, 所以x∈A. 这就证明了f −1(f(A))⊂A. 因此f −1(f(A))=A .6. 求下列函数的自然定义域:(1)23+=xy;解由3x+2≥0得32−>x. 函数的定义域为) ,32[∞+−.(2)211xy−=;解由1−x2≠0得x≠±1. 函数的定义域为(−∞, −1)∪(−1, 1)∪(1, +∞).(3)211xxy−−=;解由x≠0且1−x2≥0得函数的定义域D=[−1, 0)∪(0, 1].(4)241xy−=;解由4−x2>0得|x|<2. 函数的定义域为(−2, 2).(5)xysin=;解由x≥0得函数的定义D=[0, +∞).(6) y=tan(x+1);解由21π≠+x(k=0, ±1, ±2, ⋅⋅⋅)得函数的定义域为12−+≠ππkx(k=0, ±1, ±2, ⋅⋅⋅). (7) y=arcsin(x−3);解由|x−3|≤1得函数的定义域D=[2, 4].(8)xxy1arctan3+−=;解由3−x≥0且x≠0得函数的定义域D=(−∞, 0)∪(0, 3).(9) y=ln(x+1);解由x+1>0得函数的定义域D=(−1, +∞).(10)xey1=.解由x≠0得函数的定义域D=(−∞, 0)∪(0, +∞).7. 下列各题中, 函数f(x)和g(x)是否相同?为什么?(1)f(x)=lg x2, g(x)=2lg x;(2) f(x)=x, g(x)=2x;(3)334)(xxxf−=,31)(−=xxxg.(4)f(x)=1, g(x)=sec2x−tan2x .解(1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x<0时, g(x)=−x.(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin|)(ππϕxxxx, 求)6(πϕ, )4(πϕ, )4(πϕ−, ϕ(−2), 并作出函数y=ϕ(x)的图形.解21|6sin|)6(==ππϕ, 22|4sin|)4(==ππϕ, 22|)4sin(|)4(=−=−ππϕ, 0)2(=−ϕ.9. 试证下列函数在指定区间内的单调性:(1)xxy−=1, (−∞, 1);(2)y=x+ln x, (0, +∞).证明(1)对于任意的x1, x2∈(−∞, 1), 有1−x 1>0, 1−x 2>0. 因为当x1<x2时,0)1)(1(112121221121<−−−=−−−=−xxxxxxxxyy,所以函数xxy−=1在区间(−∞, 1)内是单调增加的.(2)对于任意的x1, x2∈(0, +∞), 当x1<x2时, 有0ln)()ln()ln(2121221121<+−=+−+=−xxxxxxxxyy,所以函数y=x+ln x在区间(0, +∞)内是单调增加的.10. 设f(x)为定义在(−l, l)内的奇函数, 若f(x)在(0, l)内单调增加, 证明f(x)在(−l, 0)内也单调增加.证明对于∀x1, x2∈(−l, 0)且x1<x2, 有−x1, −x2∈(0, l)且−x1>−x2.因为f(x)在(0, l)内单调增加且为奇函数, 所以f(−x2)<f(−x1), − f(x2)<−f(x1), f(x2)>f(x1),这就证明了对于∀x1, x2∈(−l, 0), 有f(x1)< f(x2), 所以f(x)在(−l, 0)内也单调增加.11. 设下面所考虑的函数都是定义在对称区间(−l, l)上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明(1)设F(x)=f(x)+g(x). 如果f(x)和g(x)都是偶函数, 则F(−x)=f(−x)+g(−x)=f(x)+g(x)=F(x),所以F(x)为偶函数, 即两个偶函数的和是偶函数.如果f(x)和g(x)都是奇函数, 则F(−x)=f(−x)+g(−x)=−f(x)−g(x)=−F(x),所以F(x)为奇函数, 即两个奇函数的和是奇函数.(2)设F(x)=f(x)⋅g(x). 如果f(x)和g(x)都是偶函数, 则F(−x)=f(−x)⋅g(−x)=f(x)⋅g(x)=F(x),所以F(x)为偶函数, 即两个偶函数的积是偶函数.如果f(x)和g(x)都是奇函数, 则F(−x)=f(−x)⋅g(−x)=[−f(x)][−g(x)]=f(x)⋅g(x)=F(x),所以F(x)为偶函数, 即两个奇函数的积是偶函数.如果f(x)是偶函数, 而g(x)是奇函数, 则F(−x)=f(−x)⋅g(−x)=f(x)[−g(x)]=−f(x)⋅g(x)=−F(x),所以F(x)为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y=x2(1−x2);(2)y=3x2−x3;(3)2211xxy+−=;(4)y=x(x−1)(x+1);(5)y=sin x−cos x+1;(6)2xxaay−+=.解(1)因为f(−x)=(−x)2[1−(−x)2]=x2(1−x2)=f(x), 所以f(x)是偶函数.(2)由f(−x)=3(−x)2−(−x)3=3x2+x3可见f(x)既非奇函数又非偶函数.(3)因为())(111)(1)(2222xfxxxxxf=+−=−+−−=−, 所以f(x)是偶函数.(4)因为f(−x)=(−x)(−x−1)(−x+1)=−x(x+1)(x−1)=−f(x), 所以f(x)是奇函数.(5)由f(−x)=sin(−x)−cos(−x)+1=−sin x−cos x+1可见f(x)既非奇函数又非偶函数.(6)因为)(22)()()(xfaaaaxfxxxx=+=+=−−−−−, 所以f(x)是偶函数.13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y=cos(x−2);(2)y=cos 4x;(3)y=1+sin πx;(4)y=x cos x;(5)y=sin2 x.解(1)是周期函数, 周期为l=2π.(2)是周期函数, 周期为2π=l.(3)是周期函数, 周期为l=2.(4)不是周期函数.(5)是周期函数, 周期为l=π.14. 求下列函数的反函数:(1)31+=xy;(2)xxy+−=11;(3)dcxbaxy++=(ad−bc≠0);(4) y=2sin3x;(5) y=1+ln(x+2);(6)122+=xxy.解(1)由31+=xy得x=y3−1, 所以31+=xy的反函数为y=x3−1.(2)由xxy+−=11得yyx+−=11, 所以xxy+−=11的反函数为xxy+−=11.(3)由dcxbaxy++=得acybdyx−+−=, 所以dcxbaxy++=的反函数为acxbdxy−+−=.(4)由y=2sin 3x得2arcsin31yx=, 所以y=2sin 3x的反函数为2arcsin31xy=.(5)由y=1+ln(x+2)得x=e y−1−2, 所以y=1+ln(x+2)的反函数为y=e x−1−2.(6)由122+=xxy得yyx−=1log2, 所以122+=xxy的反函数为xxy−=1log2.15. 设函数f(x)在数集X上有定义, 试证: 函数f(x)在X上有界的充分必要条件是它在X上既有上界又有下界.证明先证必要性. 设函数f(x)在X上有界, 则存在正数M, 使|f(x)|≤M, 即−M≤f(x)≤M. 这这就证明了f(x)在X上有下界−M和上界M.再证充分性. 设函数f(x)在X上有下界K1和上界K2, 即K1≤f(x)≤ K2 .取M=max{|K1|, |K2|}, 则−M≤ K1≤f(x)≤ K2≤M ,即|f(x)|≤M.这就证明了f(x)在X上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x1和x2的函数值:(1) y=u2, u=sin x, 61π=x, 32π=x;(2) y=sin u, u=2x, ,81π=x,42π=x;(3)uy=, u=1+x2, x1=1, x2= 2;(4) y=eu, u=x2, x1 =0, x2=1;(5) y=u2 , u=ex , x1=1, x2=−1.解(1)y=sin2x, 41)21(6sin221===πy,43)23(3sin222===πy.(2)y=sin2x, 224sin)82sin(1==⋅=ππy,12sin)42sin(2==⋅=ππy.(3)21xy+=, 21121=+=y, 52122=+=y.(4), , . 2xey=1201==eyeey==212(5)y=e2x, y1=e2⋅1=e2, y2=e2⋅(−1)=e−2.17. 设f(x)的定义域D=[0, 1], 求下列各函数的定义域:(1) f(x2);(2) f(sinx);(3) f(x+a)(a>0);(4)f(x+a)+f(x−a)(a>0).解(1)由0≤x2≤1得|x|≤1, 所以函数f(x2)的定义域为[−1, 1].(2)由0≤sin x≤1得2nπ≤x≤(2n+1)π (n=0, ±1, ±2⋅⋅⋅), 所以函数f(sin x)的定义域为[2nπ, (2n+1)π] (n=0, ±1, ±2⋅⋅⋅) .(3)由0≤x+a≤1得−a≤x≤1−a, 所以函数f(x+a)的定义域为[−a, 1−a].(4)由0≤x+a≤1且0≤x−a≤1得: 当210≤<a时, a≤x≤1−a; 当21>a时, 无解. 因此当210≤<a时函数的定义域为[a, 1−a], 当21>a时函数无意义.18. 设⎪⎩⎪⎨⎧>−=<=1|| 11|| 01|| 1)(xxxxf, g(x)=ex , 求f[g(x)]和g[f(x)], 并作出这两个函数的图形.解⎪⎩⎪⎨⎧>−=<=1|| 11|| 01|| 1)]([xxxeeexgf, 即⎪⎩⎪⎨⎧>−=<=0 10 00 1)]([xxxxgf. , 即()⎪⎩⎪⎨⎧>=<==−1|| 1|| e1|| ][101)(xexxeexfgxf()⎪⎩⎪⎨⎧>=<=−1|| 1|| 11|| ][1xexxexfg.19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40°(图1−37). 当过水断面ABCD的面积为定值S0时, 求湿周L(L=AC+CD+DB)与水深h之间的函数关系式, 并说明定义域.图1−37解40sinhDCAb==, 又从0)]40cot2([21ShBCBCh=⋅++得hhSBC⋅−=40cot0, 所以hhSL40sin40cos20−+=.自变量h的取值范围应由不等式组h>0, 040cot0>⋅−hhS确定, 定义域为40cot00Sh<<.20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p表示为订购量x的函数;(2)将厂方所获的利润P表示成订购量x的函数;(3)某一商行订购了1000台, 厂方可获利润多少?解(1)当0≤x≤100时, p=90.令0. 01(x0−100)=90−75, 得x0=1600. 因此当x≥1600时, p=75.当100<x<1600时,p=90−(x−100)×0. 01=91−0. 01x.综合上述结果得到. ⎪⎩⎪⎨⎧≥<<−≤≤=1600 751600100 01.0911000 90xxxxp(2). ⎪⎩⎪⎨⎧≥<<−≤≤=−=1600 151600100 01.0311000 30)60(2xx xxxxxxpP(3) P=31×1000−0. 01×10002=21000(元).习题1−21. 观察一般项xn如下的数列{xn}的变化趋势, 写出它们的极限:(1)nnx21=;(2)nxnn1)1(−=;(3)212nxn+=;(4)11+−=nnxn;(5) xn=n(−1)n.解(1)当n→∞时, nnx21=→0, 021lim=∞→nn.(2)当n→∞时, nxnn1)1(−=→0, 01)1(lim=−∞→nnn.(3)当n→∞时, 212nx n+=→2, 2)12(lim2=+∞→nn.(4)当n→∞时, 12111+−=+−=nnnxn→0, 111lim=+−∞→nnn.(5)当n→∞时, xn=n(−1)n没有极限.2. 设数列{xn}的一般项nnxn2cosπ=. 问=? 求出N, 使当n>N时, xnnx∞→limn与其极限之差的绝对值小于正数ε, 当ε=0.001时, 求出数N.解. 0lim=∞→nnxnnnxn1|2cos||0|≤=−π. ∀ε >0, 要使|x n−0|<ε , 只要ε<n1, 也就是ε1>n. 取]1[ε=N, 则∀n>N, 有|xn−0|<ε .当ε=0.001时, ]1[ε=N=1000.3. 根据数列极限的定义证明:(1)01lim2=∞→nn;(2)231213lim=++∞→nnn;(3)1lim22=+∞→nann(4). 19 999.0lim=⋅⋅⋅∞→个nn(1)分析要使ε<=−221|01|nn, 只须ε12>n, 即ε1>n.证明因为∀ε>0, ∃]1[ε=N, 当n>N时, 有ε<−|01|2n, 所以01lim2=∞→nn. (2)分析要使ε<<+=−++nnnn41)12(21|231213|, 只须ε<n41, 即ε41>n.证明因为∀ε>0, ∃]41[ε=N, 当n>N时, 有ε<−++|231213|nn, 所以231213lim=++∞→nnn.(3)分析要使ε<<++=−+=−+nanannannannan22222222)(|1|, 只须ε2an>.证明因为∀ε>0, ∃][2εaN=, 当∀n>N时, 有ε<−+|1|22nan, 所以1lim22=+∞→nan n.(4)分析要使|0.99 ⋅⋅⋅9−1|ε<=−1101n, 只须1101−n<ε , 即ε1lg1+>n.证明因为∀ε>0, ∃]1lg1[ε+=N, 当∀n>N时, 有|0.99 ⋅⋅⋅9−1|<ε , 所以. 19 999.0lim=⋅⋅⋅∞→n4. , 证明. 并举例说明: 如果数列{|xaunn=∞→lim||||limaunn=∞→n|}有极限, 但数列{xn}未必有极限.证明因为, 所以∀ε>0, ∃N∈N, 当n>N时, 有, 从而aunn=∞→limε<−||aun||un|−|a||≤|un−a|<ε .这就证明了|. |||limaunn=∞→数列{|xn|}有极限, 但数列{xn}未必有极限. 例如, 但不存在. 1|)1(|lim=−∞→nnnn)1(lim−∞→5. 设数列{xn}有界, 又, 证明: . 0lim=∞→nny0lim=∞→nnnyx证明因为数列{xn}有界, 所以存在M, 使∀n∈Z, 有|xn|≤M.又, 所以∀ε>0, ∃N∈N, 当n>N时, 有0lim=∞→nnyMynε<||. 从而当n>N时, 有εε=⋅<≤=−MMyMyxyxnnnnn|||||0|,所以. 0lim=∞→nnnyx6. 对于数列{xn}若x2k→a (k →∞), x2k+1→a (k →∞), 证明: xn→a (n →∞).证明因为x2k→a (k →∞), x2k+1→a (k →∞), 所以∀ε>0,∃K1, 当2k>2K1时, 有| x2k−a |<ε ;∃K2, 当2k+1>2K2+1时, 有| x2k+1−a |<ε..取N=max{2K1, 2K2+1}, 只要n>N, 就有|xn−a |<ε . 因此xn→a (n →∞).习题1−31. 根据函数极限的定义证明:(1); 8)13(lim3=−→xx(2); 12)25(lim2=+→xx(3)424lim22−=+−−→xxx;(4)21241lim321=+−−→xxx.证明(1)分析|(3x−1)−8|=|3x−9|=3|x−3|, 要使|(3x−1)−8|<ε , 只须ε31|3|<−x.证明因为∀ε>0, ∃εδ31=, 当0<|x−3|<δ时, 有|(3x−1)−8|<ε , 所以.8)13(lim3=−→xx(2)分析|(5x+2)−12|=|5x−10|=5|x−2|, 要使|(5x+2)−12|<ε , 只须ε51|2|<−x.证明因为∀ε>0, ∃εδ51=, 当0<|x−2|<δ时, 有|(5x+2)−12|<ε , 所以.12)25(lim2=+→xx(3)分析|)2(||2|244)4(2422−−=+=+++=−−+−xxxxxxx, 要使ε<−−+−)4(242xx, 只须ε<−−|)2(|x.证明因为∀ε>0, ∃εδ=, 当0<|x−(−2)|<δ时, 有ε<−−+−)4(242xx, 所以424lim22−=+−−→xxx.(4)分析|)21(|2|221|212413−−=−−=−+−xxxx, 要使ε<−+−212413xx, 只须ε21|)21(|<−−x.证明因为∀ε>0, ∃εδ21=, 当δ<−−<|)21(|0x时, 有ε<−+−212413xx, 所以21241lim321=+−−→xxx.2. 根据函数极限的定义证明:(1)2121lim33=+∞→xxx;(2)0sin lim=+∞→xxx.证明(1)分析333333||21212121xxxxxx=−+=−+, 要使ε<−+212133xx, 只须ε<3||21x, 即321||ε>x.证明因为∀ε>0, ∃321ε=X, 当|x|>X时, 有ε<−+212133xx, 所以2121lim33=+∞→xxx.(2)分析xxxxx1|sin|0sin≤=−, 要使ε<−0sinxx, 只须ε<x1, 即21ε>x.证明因为∀ε>0, ∃21ε=X, 当x>X时, 有ε<−0sinxx, 所以0sinli m=+∞→xxx.3. 当x→2时, y=x2→4. 问δ等于多少, 使当|x−2|<δ时, |y−4|<0. 001?解由于x→2, |x−2|→0, 不妨设|x−2|<1, 即1<x<3. 要使|x2−4|=|x+2||x−2|<5|x−2|<0. 001, 只要0002.05001.0|2|=<−x, 取δ=0. 0002, 则当0<|x−2|<δ时, 就有|x2−4|<0. 001.4. 当x→∞时, 13122→+−=xxy, 问X等于多少, 使当|x|>X时, |y−1|<0.01?解要使01.034131222<+=−+−xxx, 只397301.04||=−>x, 397=X.5. 证明函数f(x)=|x| 当x→0时极限为零.6. 求,)(xxxf= xxx||)(=ϕ当x→0时的左﹑右极限, 并说明它们在x→0时的极限是否存在.证明因为11limlim)(lim000===−−−→→→xxxxxxf,11limlim)(lim000===+++→→→xxxxxxf,, )(lim)(lim00xfxfxx+→→=−所以极限存在. )(lim0xfx→因为1lim||lim)(lim000−=−==−−−→→→xxxxxxxxϕ,1lim||lim)(lim000===+++→→→xxxxxxxxϕ,, )(lim)(lim00xxxxϕϕ+→→≠−所以极限不存在. )(lim0xxϕ→7. 证明: 若x→+∞及x→−∞时, 函数f(x)的极限都存在且都等于A, 则. Axfx=∞→)(lim证明因为, , 所以∀ε>0, Axfx=−∞→)(limAxfx=+∞→)(lim∃X1>0, 使当x<−X1时, 有|f(x)−A|<ε ;∃X2>0, 使当x>X2时, 有|f(x)−A|<ε .取X=max{X1, X2}, 则当|x|>X时, 有|f(x)−A|<ε , 即. Axfx=∞→)(lim8. 根据极限的定义证明: 函数f(x)当x→x0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明先证明必要性. 设f(x)→A(x→x0), 则∀ε>0, ∃δ>0, 使当0<|x−x0|<δ 时, 有|f(x)−A|<ε .因此当x0−δ<x<x0和x0<x<x0+δ 时都有|f(x)−A|<ε .这说明f(x)当x→x0时左右极限都存在并且都等于A .再证明充分性. 设f(x0−0)=f(x0+0)=A, 则∀ε>0,∃δ1>0, 使当x0−δ1<x<x0时, 有| f(x)−A<ε ;∃δ2>0, 使当x0<x<x0+δ2时, 有| f(x)−A|<ε .取δ=min{δ1, δ2}, 则当0<|x−x0|<δ 时, 有x0−δ1<x<x0及x0<x<x0+δ2 , 从而有| f(x)−A|<ε ,即f(x)→A(x→x0).9. 试给出x→∞时函数极限的局部有界性的定理, 并加以证明.解x→∞时函数极限的局部有界性的定理: 如果f(x)当x→∞时的极限存在, 则存在X>0及M>0, 使当|x|>X时, |f(x)|<M.证明设f(x)→A(x→∞), 则对于ε=1, ∃X>0, 当|x|>X时, 有|f(x)−A|<ε =1. 所以|f(x)|=|f(x)−A+A|≤|f(x)−A|+|A|<1+|A|.这就是说存在X>0及M>0, 使当|x|>X时, |f(x)|<M, 其中M=1+|A|.习题1−41. 两个无穷小的商是否一定是无穷小?举例说明之.解不一定.例如, 当x→0时, α(x)=2x, β(x)=3x都是无穷小, 但32)()(lim0=→xxxβα, )()(xxβα不是无穷小.2. 根据定义证明:(1)392+−=xxy当x→3时为无穷小;(2)xxy1sin=当x→0时为无穷小.证明(1)当x≠3时|3|39||2−=+−=xxxy. 因为∀ε>0, ∃δ=ε , 当0<|x−3|<δ时, 有εδ=<−=+−=|3|39||2xxxy,所以当x→3时392+−=xxy为无穷小.(2)当x≠0时|0||1sin|||||−≤=xxxy. 因为∀ε>0, ∃δ=ε , 当0<|x−0|<δ时, 有εδ=<−≤=|0||1sin|||||xxxy,所以当x→0时xxy1sin=为无穷小.3. 根据定义证明: 函数xxy21+=为当x→0时的无穷大. 问x应满足什么条件, 能使|y|>104?证明分析2||11221||−≥+=+=xxxxy, 要使|y|>M, 只须Mx>−2||1, 即21||+<Mx.证明因为∀M>0, ∃21+=Mδ, 使当0<|x−0|<δ时, 有Mxx>+21,所以当x→0时, 函数xxy21+=是无穷大.取M=104, 则21014+=δ. 当2101|0|04+<−<x时, |y|>104.4. 求下列极限并说明理由:(1)xxn12lim+∞→;(2)xxx−−→11lim20.解(1)因为xxx1212+=+, 而当x→∞ 时x1是无穷小, 所以212lim=+∞→xxn. (2)因为xxx+=−−1112(x≠1), 而当x→0时x为无穷小, 所以111lim20=−−→xxx.5. 根据函数极限或无穷大定义, 填写下表:6. 函数y=xcos x在(−∞, +∞)内是否有界?这个函数是否为当x→+∞ 时的无穷大?为什么?解函数y=xcos x在(−∞, +∞)内无界.这是因为∀M>0, 在(−∞, +∞)内总能找到这样的x, 使得|y(x)|>M. 例如y(2kπ)=2kπ cos2kπ=2kπ (k=0, 1, 2, ⋅⋅⋅),当k充分大时, 就有| y(2kπ)|>M.当x→+∞ 时, 函数y=xcos x不是无穷大.这是因为∀M>0, 找不到这样一个时刻N, 使对一切大于N的x, 都有|y(x)|>M. 例如0)22cos()22()22(=++=+ππππππkkky(k=0, 1, 2, ⋅⋅⋅),对任何大的N, 当k充分大时, 总有Nkx>+=22ππ, 但|y(x)|=0<M.7. 证明: 函数xxy1sin1=在区间(0, 1]上无界, 但这函数不是当x→0+时的无穷大. 证明函数xxy1sin1=在区间(0, 1]上无界. 这是因为∀M>0, 在(0, 1]中总可以找到点xk, 使y(xk)>M. 例如当221ππ+=kxk(k=0, 1, 2, ⋅⋅⋅)时, 有22)(ππ+=kxyk,当k充分大时, y(xk)>M.当x→0+ 时, 函数xxy1sin1=不是无穷大. 这是因为∀M>0, 对所有的δ>0, 总可以找到这样的点xk, 使0<xk<δ, 但y(xk)<M. 例如可取πkxk21=(k=0, 1, 2, ⋅⋅⋅),当k充分大时, xk<δ, 但y(xk)=2kπsin2kπ=0<M.习题1−51. 计算下列极限:(1)35lim22−+→xxx;解9325235lim222−=−+=−+→xxx.(2)13lim223+−→xxx;解01)3(3)3(13lim22223=+−=+−→xxx.(3)112lim221−+−→xxxx;解02011lim)1)(1()1(lim112lim121221==+−=+−−=−+−→→→xxxxxxxxxxx.(4)xxxxxx2324lim2230++−→;解2123124lim2324lim202230=++−=++−→→xxxxxxxxxx.(5)hxhxh220)(lim−+→;解xhx hxhhxxhxhxhhh2)2(lim2lim)(lim02220220=+=−++=−+→→→.(6))112(lim2xxx+−∞→;解21lim1lim2)112(lim22=+−=+−∞→∞→∞→xxxxxxx.(7)121lim22−−−∞→xxxx;解2111211lim121lim2222=−−−=−−−∞→∞→xxxxxxxx.(8)13lim242−−+∞→xxxxx;解013lim242=−−+∞→xxxxx(分子次数低于分母次数, 极限为零)或012111lim13lim4232242=−−+=−−+∞→∞→xxxxxxxxxx.(9)4586lim224+−+−→xxxxx;解32142412lim)4)(1()4)(2(lim4586lim44224=−−=−−=−−−−=+−+−→→→xxxxxxxxxx xxx.(10))12)(11(lim2xxx−+∞→;解221)12(lim)11(lim)12)(11(lim22=×=−⋅+=−+∞→∞→∞→xxxxxxx.(11))21 41211(limnn+⋅⋅⋅+++∞→;解2211)21(1lim)21 41211(lim1=−−=+⋅⋅⋅++++∞→∞→nnnn.(12)2)1( 321limnnn−+⋅⋅⋅+++∞→;解211lim212)1(lim)1( 321lim22=−=−=−+⋅⋅⋅+++∞→∞→∞→nnnnnnnnnn.(13)35)3)(2)(1(limnnnnn+++∞→;解515)3)(2)(1(lim3=+++∞→nnnnn (分子与分母的次数相同, 极限为最高次项系数之比).或51)31)(21)(11(lim515)3)(2)(1(lim3=+++=+++∞→∞→nnnnnnnnn.(14))1311(lim31xxx−−−→;解112lim)1)(1()2)(1(lim)1)(1(31lim)1311(lim212122131−=+++−=++−+−−=++−−++=−−−→→→→xxxxxxxxxxxxxxxxxxx.2. 计算下列极限:(1)2232)2(2lim−+→xxxx;解因为01602)2(lim2322==+−→xxxx, 所以∞=−+→2232)2(2limxxxx.(2)12lim2+∞→xxx;解∞=+∞→12lim2xxx (因为分子次数高于分母次数).(3). )12(lim3+−∞→xxx解(因为分子次数高于分母次数). ∞=+−∞→)12(lim3xxx3. 计算下列极限:(1)xxx1sinlim20→;解01sinlim20=→xxx(当x→0时, x2是无穷小, 而x1sin是有界变量).(2)xxxarctanlim∞→.解0arctan1limarctanlim=⋅=∞→∞→xxxxxx(当x→∞时, x1是无穷小, 而arctan x是有界变量).4. 证明本节定理3中的(2).习题1−61. 计算下列极限:(1)xxxωsinlim0→;解ωωωωω==→→xxxxxxsinlimsinlim00.(2)xxx3tanlim0→;解33cos133sinlim33tanlim00=⋅=→→xxxxxxx.(3)xxx5sin2sinlim0→;解52525sin522sinlim5sin2sinlim00=⋅⋅=→→xxxxxxxx.(4); xxxcotlim0→解1coslimsinlimcossinlimcotlim0000=⋅=⋅=→→→→xxxxxxxxxxxx.(5)xxxxsin2cos1lim0−→;解法一()2sinlim2sin2lim2cos1limsin2cos1lim20220200===−=−→→→→xxxxxxxxxxxxx. 解法二2sinlim2sinsin2limsin2cos1lim0200===−→→→xxxxxxxxxxx.(6)nnnx2sin2lim∞→(x为不等于零的常数).解xxxxxnnnnnn=⋅=∞→∞→22sinlim2sin2lim.2. 计算下列极限:(1)xxx10)1(lim−→;解{}11)(10)1()(1010)](1[lim)](1[lim)1(lim−−−→−−→→=−+=−+=−exxxxxxxxx. (2)xxx10)21(lim+→;解[]22210221010)21(lim)21(lim)21(limexxxxxxxxx=+=+=+→⋅→→.(3)xxxx2)1(lim+∞→;解[]222)11(lim)1(limexxxxxxx=+=+∞→∞→.(4)kxxx)11(lim−∞→(k为正整数).解kkxxkxxexx−−−∞→∞→=−+=−))(()11(lim)11(lim.3. 根据函数极限的定义, 证明极限存在的准则I′.解4. 利用极限存在准则证明:(1)111lim=+∞→nn;证明因为nn11111+<+<,而且11lim=∞→n1)11(lim=+∞→nn,由极限存在准则I, 111lim=+∞→nn.(2)()11 211lim222=++⋅⋅⋅++++∞→πππnnnnnn;证明因为()πππππ+<++⋅⋅⋅++++<+22222221 211nnnnnnnnnn,而1lim22=+∞→πnnnn, 1lim22=+∞→πnnn,所以()11 211lim222=++⋅⋅⋅++++∞→πππnnnnnn.(3)数列2, 22+, 222++, ⋅⋅⋅的极限存在;证明21=x, nnxx+=+21(n=1, 2, 3, ⋅⋅⋅).先证明数列{xn}有界. 当n=1时221<=x, 假定n=k时xk<2, 当n=k+1时, 22221=+<+=+kkxx,所以xn<2(n=1, 2, 3, ⋅⋅⋅), 即数列{xn}有界.再证明数列单调增.nnnnnnnnnnnnxxxxxxxxxxxx+++−−=++−+=−+=−+2)1)(2(22221,而xn−2<0, xn+1>0, 所以xn+1−xn>0, 即数列{xn}单调增.因为数列{xn}单调增加有上界, 所以此数列是有极限的.(4)11lim0=+→nxx;证明当|x|≤1时, 则有1+x≤1+|x|≤(1+|x|)n ,1+x≥1−|x|≥(1−|x|)n,从而有||11||1xxxn+≤+≤−.因为, 1|)|1(lim|)|1(lim00=+=−→→xxxx根据夹逼准则, 有11lim0=+→nxx.(5)[]11lim0=+→xxx.证明因为[]xxx1111≤<−, 所以[]111≤<−xxx.又因为, 根据夹逼准则, 有11lim)1(lim00==−++→→xxx[]11lim0=+→xxx.习题1−71. 当x→0时, 2x−x2 与x2−x3相比, 哪一个是高阶无穷小?解因为02lim2lim202320=−−=−−→→xxxxxxxxx,所以当x→0时, x2−x3是高阶无穷小, 即x2−x3=o(2x−x2).2. 当x→1时, 无穷小1−x和(1)1−x3, (2))1(212x−是否同阶?是否等价?解(1)因为3)1(lim1)1)(1(lim11lim212131=++=−++−=−−→→→xxxxxxxxxxx,所以当x→1时, 1−x和1−x3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim211)1(21lim121=+=−−→→xxxxx,所以当x→1时, 1−x和)1(212x−是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x→0时, 有:(1) arctanx~x;(2)2~1sec2xx−.证明(1)因为1tanlimarctanlim00==→→yyxxyx(提示: 令y=arctan x, 则当x→0时, y →0),所以当x→0时, arctanx~x.(2)因为()122sin2lim22sin2limcoscos1lim2211seclim202202020===−=−→→→→xxxxxxxx xxxxx,所以当x→0时, 2~1sec2xx−.4. 利用等价无穷小的性质, 求下列极限:(1)xxx23tanlim0→;(2)mnxxx)(sin)sin(lim0→(n, m为正整数);(3)xxxx30sinsintanlim−→;(4))1sin1)(11(tansinlim320−+−+−→xxxxx.解(1)2323lim23tanlim00==→→xxxxxx.(2) ⎪⎩⎪⎨⎧<∞>===→→mnmnmnxxxxmnxmnx 0 1lim)(sin)si n(lim00.(3)21cos21limsincoscos1limsin)1cos1(sinlimsinsintanlim220203030==−=−=−→→→→xxxxxxxxxxxxxxxx.(4)因为32221)2(2~2sintan2)1(costantansinxxxxxxxxx−=⋅−−=−=−(x→0),23232223231~11)1(11xxxxx++++=−+(x→0),xxxxx~sin~1sin1sin1sin1++=−+(x→0),所以33121lim)1sin1)(11(tansinlim230320−=⋅−=−+−+−→→xxxxxxxxx.5. 证明无穷小的等价关系具有下列性质:(1) α ~α (自反性);(2) 若α~β, 则β~α(对称性);(3)若α~β, β~γ, 则α~γ(传递性).证明(1)1lim=αα, 所以α~α ;(2) 若α~β, 则1lim=βα, 从而1lim=αβ. 因此β~α ;(3) 若α~β, β~γ, 1limlimlim=⋅=βαγβγα. 因此α~γ.习题1−81. 研究下列函数的连续性, 并画出函数的图形:(1); ⎩⎨⎧≤<−≤≤=21 210 )(2xxxxxf(2). ⎩⎨⎧>≤≤−=1|| 111 )(xxxxf解(1)已知多项式函数是连续函数, 所以函数f(x)在[0, 1)和(1, 2]内是连续的.在x=1处, 因为f(1)=1, ,1lim)(lim211==−−→→xxfxx1)2(lim)(lim11=−=++→→xxfxx所以, 从而函数f(x)在x=1处是连续的. 1)(lim1=→xfx综上所述,函数f(x)在[0, 2]上是连续函数.(2)只需考察函数在x=−1和x=1处的连续性.在x=−1处, 因为f(−1)=−1, , , 所以函数在x=−1处间断, 但右连续. )1(11lim)(lim11−≠==−−−→−→fxfxx)1(1lim)(lim11−=−==++−→−→fxxfxx在x=1处, 因为f(1)=1, =f(1), =f(1), 所以函数在x=1处连续. 1lim)(lim11==−−→→xxfxx11lim)(lim11==++→→xxxf综合上述讨论, 函数在(−∞, −1)和(−1, +∞)内连续, 在x=−1处间断, 但右连续. 2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+−−=xxxy, x=1, x=2;(2)xxytan=, x=k, 2ππ+=kx (k=0, ±1, ±2, ⋅⋅⋅);(3),1cos2xy= x=0;(4), x =1. ⎩⎨⎧>−≤−=1 31 1xxxxy解(1))1)(2()1)(1(23122−−−+=+−−=xxxxx xxy. 因为函数在x=2和x=1处无定义, 所以x=2和x=1是函数的间断点.因为∞=+−−=→→231limlim2222xxxyxx, 所以x=2是函数的第二类间断点;因为2)2()1(limlim11−=−+=→→xxyxx, 所以x=1是函数的第一类间断点, 并且是可去间断点. 在x=1处, 令y=−2, 则函数在x=1处成为连续的.(2)函数在点x=kπ(k∈Z)和2 ππ+=kx(k∈Z)处无定义, 因而这些点都是函数的间断点.因∞=→xxkxtanlimπ(k≠0), 故x=kπ(k≠0)是第二类间断点;因为1tanlim0=→xxx, 0tanlim2=+→xxkxππ(k∈Z), 所以x=0和2 ππ+=kx(k∈Z) 是第一类间断点且是可去间断点.令y|x=0=1, 则函数在x=0处成为连续的;令2 ππ+=kx时, y=0, 则函数在2 ππ+=kx处成为连续的.(3)因为函数xy1cos2=在x=0处无定义, 所以x=0是函数xy1cos2=的间断点. 又因为xx1coslim20→不存在, 所以x=0是函数的第二类间断点.(4)因为,所以x=1是函数的第一类不可去间断点.0)1(lim)(lim11=−=−−→→xxfxx2)3(lim)(lim11=−=++→→xxfxx3. 讨论函数xxxxfnnn2211lim)(+−=∞→的连续性, 若有间断点, 判别其类型.解⎪⎩⎪⎨⎧<=>−=+−=∞→1|| 1|| 01|| 11lim)(22xxxxxxxxxfnnn.在分段点x=−1处, 因为, , 所以x=−1为函数的第一类不可去间断点.1)(lim)(lim11=−=−−−→−→xxfxx1lim)(lim11−==++−→−→xxfxx在分段点x=1处, 因为, , 所以x=1为函数的第一类不可去间断点. 1lim)(lim11==−−→→xxfxx1)(lim)(lim11−=−=++→→xxfxx4. 证明: 若函数f(x)在点x0连续且f(x0)≠0, 则存在x0的某一邻域U(x0), 当x ∈U(x0)时, f(x)≠0.证明不妨设f(x0)>0. 因为f(x)在x0连续, 所以, 由极限的局部保号性定理, 存在x0)()(lim00>=→xfxfxx0的某一去心邻域, 使当x∈时f(x)>0, 从而当x∈U(x)(0xU)(0xU0)时, f(x)>0. 这就是说, 则存在x0的某一邻域U(x0), 当x∈U(x0)时, f(x)≠0.5. 试分别举出具有以下性质的函数f(x)的例子:(1)x=0, ±1, ±2, 21±, ⋅⋅⋅, ±n, n1±, ⋅⋅⋅是f(x)的所有间断点, 且它们都是无穷间断点;(2)f(x)在R上处处不连续, 但|f(x)|在R上处处连续;(3)f(x)在R上处处有定义, 但仅在一点连续.解函数xxxfππcsc)csc()(+=在点x=0, ±1, ±2, 21±, ⋅⋅⋅, ±n, n1±, ⋅⋅⋅处是间断的, 且这些点是函数的无穷间断点.解(2)函数在R上处处不连续, 但|f(x)|=1在R上处处连续. ⎩⎨⎧∉∈−=QQxxxf 1 1)( 解(3)函数在R上处处有定义, 它只在x=0处连续. ⎩⎨⎧∉−∈=QQxxxxxf )(习题1−91. 求函数633)(223−+−−+=xxxxxxf的连续区间, 并求极限, 及. )(lim0xfx→)(lim3xfx−→)(lim2xfx→解)2)(3()1)(1)(3(633)(223−++−+=−+−−+=xxxxxxxxxxxf, 函数在(−∞, +∞)内除点x=2和x=−3外是连续的, 所以函数f(x)的连续区间为(−∞, −3)、(−3, 2)、(2, +∞). 在函数的连续点x=0处, 21)0()(lim0==→fxfx.在函数的间断点x=2和x=−3处,∞=−++−+=→→)2)(3()1)(1)(3(lim)(lim22xxxxxxfxx,582)1)(1(lim)(lim33−=−+−=−→−→xxxxfxx.2. 设函数f(x)与g(x)在点x0连续, 证明函数ϕ(x)=max{f(x), g(x)}, ψ(x)=min{f(x), g(x)}在点x0也连续.证明已知, . )()(lim00xfxfxx=→)()(lim00xgxgxx=→可以验证] |)()(|)()([21)(xgxfxgxfx−++=ϕ,] |)()(|)()([21)(xgxfxgxfx−−+=ψ.因此] |)()(|)()([21)(00000xgxfxgxfx−++=ϕ,] |)()(|)()([21)(00000xgxfxgxfx−−+=ψ.因为] |)()(|)()([21lim)(lim00xgxfxgxfxxxxx−++=→→ϕ] |)(lim)(lim|)(lim)(lim[210000xgxfxgxfxxxxxxxx→→→→−++=] |)()(|)()([210000xgxfxgxf−++==ϕ(x0),所以ϕ(x)在点x0也连续.同理可证明ψ(x)在点x0也连续.3. 求下列极限:(1)52lim20+−→xxx;(2)34)2(sinlimxxπ→;(3))2cos2ln(lim6xxπ→(4)xxx11lim0−+→;(5)145lim1−−−→xxxx;(6)axaxax−−→sinsinlim;(7))(lim22xxxxx−−++∞→.解(1)因为函数52)(2+−=xxxf是初等函数, f(x)在点x=0有定义, 所以55020)0(52lim220=+⋅−==+−→fxxx.(2)因为函数f(x)=(sin 2x)3是初等函数, f(x)在点x=4π有定义, 所以1)42(sin)4()2(sinlim334=⋅==→πππfxx.(3)因为函数f(x)=ln(2cos2x)是初等函数, f(x)在点x=6π有定义, 所以0)62cos2ln()6()2cos2ln(lim6=⋅==→πππfxx.(4)211101111lim)11(lim)11()11)(11(lim11lim0000=++=++=++=++++−+=−+→→→→xxxxxxxxxxxxxx.(5))45)(1(44lim)45)(1()45)(45(lim145lim111xxxxxxxxxxxxxxxxx+−−−=+−−+−−−=−−−→→→214154454lim1=+−⋅=+−=→xxx.(6)axaxaxaxaxaxax−−+=−−→→2sin2cos2limsinsinlimaaaaxaxaxaxaxcos12cos22sinlim2coslim=⋅+=−−⋅+=→→.(7))())((lim)(lim22222222xxxxxxxxxxxxxxxxxx−++−++−−+=−−++∞→+∞→1)1111(2lim)(2lim22=−++=−++=+∞→+∞→xxxxxxxxx.4. 求下列极限:(1)xxe1lim∞→;(2)xxxsinlnlim0→;(3)2)11(limxxx+∞→;(4); xxx2cot20)tan31(lim+→(5)21)63(lim−∞→++xxxx;(6)xxxxxx−++−+→20sin1sin1tan1lim.解(1) 1lim01lim1===∞→∞→eeexxxx.(2) 01ln)sinlimln(sinlnlim00===→→xxxxxx.(3) []eexxxxxx==+=+∞→∞→21212)11(lim)11(lim.(4) []33tan3120cot2022)tan31(lim)tan31(limexxxxxx=+=+→→.(5)21633621)631()63(−+−⋅−+−+−+=++xxxxxxx. 因为exxx=+−+−+∞→36)631(lim, 232163lim−=−⋅+−∞→xxx,所以2321)63(lim−−∞→=++exxxx.(6))sin1tan1)(1sin1()1sin1)(sin1tan1(limsin1sin1tan1lim22020xxxxxxxx xxxxxx+++−++++−+=−++−+→→21)2(2limsin2sin2tanlim)sin1tan1(sin)1sin1)(sin(tanlim320220220=⋅=⋅=+++++−=→→→xxxxxxxxxxxxxxxxx.5. 设函数应当如何选择数a, 使得f(x)成为在(−∞, +∞)内的连续函数?⎩⎨⎧≥+<=0 0 )(xxaxexfx解要使函数f(x)在(−∞, +∞)内连续, 只须f(x)在x=0处连续, 即只须. afxfxfxx===+→−→)0()(lim)(lim00因为, , 所以只须取a=1. 1lim)(lim00==−→−→xxxexfaxaxfxx=+=+→+→)(lim)(lim00习题1−101. 证明方程x5−3x=1至少有一个根介于1和2之间.证明设f(x)=x5−3x−1, 则f(x)是闭区间[1, 2]上的连续函数.因为f(1)=−3, f(2)=25, f(1)f(2)<0, 所以由零点定理, 在(1, 2)内至少有一点ξ(1<ξ<2), 使f(ξ)=0, 即x=ξ 是方程x5−3x=1的介于1和2之间的根.因此方程x5−3x=1至少有一个根介于1和2之间.2. 证明方程x=asinx+b, 其中a>0, b>0, 至少有一个正根, 并且它不超过a+b.证明设f(x)=asin x+b−x, 则f(x)是[0, a+b]上的连续函数.f(0)=b, f(a+b)=a sin (a+b)+b−(a+b)=a[sin(a+b)−1]≤0.若f(a+b)=0, 则说明x=a+b就是方程x=asinx+b的一个不超过a+b的根;若f(a+b)<0, 则f(0)f(a+b)<0, 由零点定理, 至少存在一点ξ∈(0, a+b), 使f(ξ)=0, 这说明x=ξ 也是方程x=asinx+b的一个不超过a+b的根.总之, 方程x=asinx+b至少有一个正根, 并且它不超过a+b.3. 设函数f(x)对于闭区间[a, b]上的任意两点x、y, 恒有|f(x)−f(y)|≤L|x−y|, 其中L 为正常数, 且f(a)⋅f(b)<0. 证明: 至少有一点ξ∈(a, b), 使得f(ξ)=0.证明设x0为(a, b)内任意一点. 因为, 0||lim|)()(|lim00000=−≤−≤→→xxLxfxfxxxx所以, 0|)()(|lim00=−→xfxfxx即. )()(lim00xfxfxx=→因此f(x)在(a, b)内连续.同理可证f(x)在点a处左连续, 在点b处右连续, 所以f(x)在[a, b]上连续.因为f(x)在[a, b]上连续, 且f(a)⋅f(b)<0, 由零点定理, 至少有一点ξ∈(a, b), 使得f(ξ)=0.4. 若f(x)在[a, b]上连续, a<x1<x2< ⋅⋅⋅ <xn<b, 则在[x1, xn]上至少有一点ξ, 使nxfxfxffn)( )()()(21+⋅⋅⋅++=ξ.证明显然f(x)在[x1, xn]上也连续. 设M和m分别是f(x)在[x1, xn]上的最大值和最小值.因为xi∈[x1, xn](1≤ i≤n), 所以有m≤f(xi)≤M, 从而有, Mnxfxfxfmnn⋅≤+⋅⋅⋅++≤⋅)( )()(21Mnxfxfxfmn≤+⋅⋅⋅++≤)( )()(21.由介值定理推论, 在[x1, xn]上至少有一点ξ使nxfxfxffn)( )()()(21+⋅⋅⋅++=ξ.5. 证明: 若f(x)在(−∞, +∞)内连续, 且存在, 则f(x)必在(−∞, +∞)内有界. )(limxfx∞→证明令, 则对于给定的ε>0, 存在X>0, 只要|x|>X, 就有Axfx=∞→)(lim|f(x)−A|<ε , 即A−ε<f(x)<A+ε .又由于f(x)在闭区间[−X, X]上连续, 根据有界性定理, 存在M>0, 使|f(x)|≤M, x∈[−X, X].取N=max{M, |A−ε|, |A+ε|}, 则|f(x)|≤N, x∈(−∞, +∞), 即f(x)在(−∞, +∞)内有界. 6. 在什么条件下, (a, b)内的连续函数f(x)为一致连续?总习题一1. 在“充分”、“必要”和“充分必要”三者中选择一个正确的填入下列空格内: (1)数列{xn}有界是数列{xn}收敛的________条件. 数列{xn}收敛是数列{xn}有界的________的条件.(2)f(x)在x0的某一去心邻域内有界是存在的________条件. 存在是f(x)在x)(lim0xfxx→)(lim0xfxx→0的某一去心邻域内有界的________条件.(3) f(x)在x0的某一去心邻域内无界是∞=→)(lim0xfxx的________条件. 是f(x)在x∞=→)(lim0xfxx0的某一去心邻域内无界的________条件.(4)f(x)当x→x0时的右极限f(x0+)及左极限f(x0−)都存在且相等是存在的________条件. )(lim0xfxx→解(1) 必要, 充分.(2) 必要, 充分.(3) 必要, 充分.(4) 充分必要.2. 选择以下题中给出的四个结论中一个正确的结论:设f(x)=2x+3x−2. 则当x→0时, 有( ).(A)f(x)与x是等价无穷小; (B)f(x)与x同阶但非等价无穷小;(C)f(x)是比x高阶的无穷小; (D)f(x)是比x低阶的无穷小.解因为xxxxxfxxxxxxxx13lim12lim232lim)(lim0000−+−=−+=→→→→3ln2ln)1ln(lim3ln)1ln(lim2ln00+=+++=→→uuttut(令2x−1=t, 3x−1=u) .所以f(x)与x同阶但非等价无穷小. 故应选B.3. 设f(x)的定义域是[0, 1], 求下列函数的定义域:(1) f(ex);(2) f(ln x);(3) f(arctan x);(4) f(cos x).解(1)由0≤ex≤1得x≤0, 即函数f(ex)的定义域为(−∞, 0].(2) 由0≤ ln x≤1得1≤x≤e , 即函数f(ln x)的定义域为[1, e].(3) 由0≤ arctan x ≤1得0≤x≤tan 1, 即函数f(arctan x)的定义域为[0, tan 1].(4) 由0≤ cos x≤1得2222ππππ+≤≤−nxn(n=0, ±1, ±2, ⋅⋅⋅),即函数f(cos x)的定义域为[2 ,22ππππ+−nn], (n=0, ±1, ±2, ⋅⋅⋅).4. 设, , ⎩⎨⎧>≤=0 0 0)(xxxxf⎩⎨⎧>−≤=0 0 0)(2xxxxg求f[f(x)], g[g(x)], f[g(x)], g[f(x)].解因为f(x)≥0, 所以f[f(x)]=f(x); ⎩⎨⎧>≤=0 0 0xxx因为g(x)≤0, 所以g[g(x)]=0;因为g(x)≤0, 所以f[g(x)]=0;因为f(x)≥0, 所以g[f(x)]=−f 2(x) . ⎩⎨⎧>−≤=0 0 02xxx5. 利用y=sin x的图形作出下列函数的图形:(1)y=|sin x|;(2)y=sin|x|;(3)2sin2xy=.6. 把半径为R的一圆形铁片, 自中心处剪去中心角为α的一扇形后围成一无底圆锥. 试将这圆锥的体积表为α的函数.解设围成的圆锥的底半径为r, 高为h, 依题意有R(2π−α)=2πr , παπ2)2(−=Rr,παπαπαπ244)2(2222222−=−−=−=R RRrRh.圆锥的体积为παπαπαππ244)2(312222−⋅−⋅=RRV22234)2(24aR−⋅−=πααππ (0<α<2π).7. 根据函数极限的定义证明536lim23=−−−→xxxx.证明对于任意给定的ε>0, 要使ε<−−−−|536|2xxx, 只需|x−3|<ε , 取δ=ε,当0<|x−3|<δ时, 就有|x−3|<ε , 即ε<−−−−|536|2xxx, 所以536lim23=−−−→xxxx.8. 求下列极限:(1)221)1(1lim−+−→xxxx;(2))1(lim2xxxx−++∞→;(3)1)1232(lim+∞→++xxxx;(4)30sintanlimxxxx−→;(5)xxxxxcba10)3(lim++→(a>0, b>0, c>0);(6)xxxtan2)(sinlimπ→.解(1)因为01)1(lim221=+−−→xxxx, 所以∞=−+−→221)1(1limxxxx.(2))1()1)(1(lim)1(lim2222xxxxxxxxxxxx++++−+=−++∞→+∞→211111lim1lim22=++=++=+∞→+∞→xxxxxx.(3) 2121211)1221(lim)1221(lim)1232(lim++∞→+∞→+∞→++=++=++xxxxxxxxxx 21212)1221()1221(lim++++=+∞→xxxxexxxxx=++⋅++=∞→+∞→21212)1221(lim)1 221(lim.(4)xxxxxxxxxxxxxcos)cos1(sinlim)1cos1(sinlimsintanlim303030−=−=−→→→21)2(2limcos2sin2sinlim320320=⋅=⋅=→→xxxxxxxxx (提示: 用等价无穷小换) . (5)xcbacbaxxxxxxxxxxxxxxxcbacba3333010)331(lim)3(lim−++⋅−++→→−+++=++ , 因为ecbaxxxcbaxxxx=−+++−++→330)331(lim,)111(lim3133lim00xcxbxaxcbaxxxxxxxx−+−+−=−++→→])1ln(1limln)1ln(1limln)1ln(1lim[ln31000vcub tavut+++++=→→→3ln)lnln(ln31abccba=++=,所以3ln103)3(limabcecbaabcxxxxx==++→.提示: 求极限过程中作了变换ax−1=t, bx−1=u, cx−1=v.(6)xxxxxxxxtan)1(sin1sin12tan2)]1(sin1[lim)(sinlim−⋅−→→−+=ππ, 因为exxx=−+−→1sin12)]1(sin1[limπ,xxxxxxxcos)1(sinsinlimtan)1(sinlim22−=−→→ππ01sincossinlim)1(sincos)1(sinsinlim222=+−=+−=→→xxxxxxxxxππ,所以1)(sinlim0tan2==→exxxπ.9. 设⎪⎩⎪⎨⎧≤+>=0 0 1sin)(2xxaxxxxf, 要使f(x)在(−∞, +∞)内连续, 应怎样选择数a ?解要使函数连续, 必须使函数在x=0处连续.因为f(0)=a, axaxfxx=+=−−→→)(lim)(lim200, 01sinlim)(lim00==++→→xxxfxx,所以当a=0时, f(x)在x=0处连续. 因此选取a=0时, f(x)在(−∞, +∞)内连续.10. 设⎪⎩⎪⎨⎧≤<−+>=−01 )1ln(0 )(11xxxexfx, 求f(x)的间断点, 并说明间断点所属类形.解因为函数f(x)在x=1处无定义, 所以x=1是函数的一个间断点.因为0lim)(lim1111==−→→−−xxxexf(提示−∞=−−→11lim1xx),∞==−→→++1111lim)(limxxxexf(提示+∞=−+→11lim1xx),所以x=1是函数的第二类间断点.又因为0)1ln(lim)(lim00=+=−−→→xxfxx, eexfxxx1lim)(lim1100==−→→++,所以x=0也是函数的间断点, 且为第一类间断点.11. 证明()11 2111lim222=++⋅⋅⋅++++∞→nnnnn.证明因为()11 211122222+≤++⋅⋅⋅++++≤+nnnnnnnnn, 且。
同济大学版高等数学课后习题答案第1章

习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式.解 A ⋃B =(-∞, 3)⋃(5, +∞),A ⋂B =[-10, -5),A \B =(-∞, -10)⋃(5, +∞),A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C .证明 因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f (A ⋃B )=f (A )⋃f (B );(2)f (A ⋂B )⊂f (A )⋂f (B ).证明 因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B )⇔ y ∈f (A )⋃f (B ),所以 f (A ⋃B )=f (A )⋃f (B ).(2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )),所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A . 6. 求下列函数的自然定义域:(1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞).(3)211x xy --=; 解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1].(4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2).(5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞).(10)x e y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数xx y -=1在区间(-∞, 1)内是单调增加的. (2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0l n )()l n ()l n (2121221121<+-=+-+=-x x x x x x x x y y ,所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加. 11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211x x y +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);解 是周期函数, 周期为l =2π.(2)y =cos 4x ;解 是周期函数, 周期为2π=l . (3)y =1+sin πx ;解 是周期函数, 周期为l =2.(4)y =x cos x ;解 不是周期函数.(5)y =sin 2x .解 是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y 错误!未指定书签。
高等数学(同济第七版)课后答案解析

(3)相同、因为定义域、对应法则均相同.
(4)不同、因为定义域不同.
际3.设
求。(寻)“仔)・9(-骨)顽-2).并作出函数L)的囲形.
TT
S,,,T i
1(、)的,形如图丨・1所示.
S4.试让F列陥数在指定区间内的单Wi性:
第一章函故与扱限
(2)j = x+In n(0, *8).证(I) y=/(^)=rL-=-丨+宀(-8』).
F(-T)=/|(-X)+/2(F=/|(对+人(x) =F(x),
枚,(大)为偶函数.
设幻(T),&2(愛)均为奇函数.则幻(-工)=-们(*),幻(-X)=-g2(■*)•令。(])=g]())+&《]),于是
G(-X)=X|(-X)+评2(-X)=■•幻(x) -&2(1)=f),
故c(x)为奇函数.
解因为AC= 20= 15,所以,Ali= /^后IF=25.
Ih20 <2-15 <20・25可知,点P、Q在斜边AH上相讷.
令a + 2% = 15+20 + 25J!;x = 20.即当x= 2()时•点七。相遇.因此•所求函數的定义域为(0.20).
(I )当Ov — vIO时,点P在CR上•点Q在CA上(图1-5).
洎6.&卜血所考虑的函救都是定义在区间U)上的.i止明:
(1)两个偶函数的和是偶函数.两个奇函数的和是奇函数;
(2)两个偶函数的乘枳是偶函数,两个奇函数的乘枳是偶函数,偶函数与奇丽数的乗积是奇函数.
证(1)设J|(X)./2(X)均为偶函数,则乂(-X)”('),(-X)=6(x).今/⑴=/|(^)+/i(x),于是
高等数学 同济二版上册课后答案

第一章1-4节 1、计算下列极限7)2382lim 222+--+→x x x x x分析:本题分子分母同时趋近于0,根据表达式的形式,考虑利用约分将趋于0的项约去。
解:原式6)1(lim )4(lim 14lim )2)(1()2)(4(lim2222=-+=-+=---+=→→→→x x x x x x x x x x x x 9))sin(sin sin lima x ax a x --→分析:本题分子分母同时趋于0,但不能约分,利用复合函数求极限,通过变量替换进行求解 解一:令0,,,→→+=-=u a x u a x a x u 时则。
a uua a u u u a a u u a a uau a u a u a u a u u u u u cos )2cos42sinsin (cos lim ]2cos2sin 2)2sin 21(sin [cos lim ]sin )1(cos sin [cos lim sin sin sin cos cos sin limsin sin )sin(lim020000=-=-+=-+=-+=-+=→→→→→原式 解二:利用三角函数的和差化积,以及等价替换a ax ax a x a x a x a x a x ax cos 22cos 2lim )sin(2sin 2cos2lim=--⋅+⋅=--+=→→原式11)6)1(lim )4(lim 14lim 4lim 020202230=++-=++-=++-→→→→t t t t t t t t t t t t t t t (应该为4) 13)31)312(lim 2lim )312)(4()4(2lim )312)(4(9)12(lim 4312lim44444=++=++--=++--+=--+→→→→→x x x x x x x x x x x x x x本题利用了分子有理化 2、计算下列极限 1)nnn arctan lim∞→解:因为2arctan 01π<→∞→n ,n,n 而时,无穷小与有界函数之积仍然为无穷小,所以原式n nn arctan 1lim∞→==0 2)0sin 1lim 1sin lim=+=+∞→∞→n n nn n n n n 3)1arctan 11arctan 11lim arctan arctan lim =+-=+-∞→∞→xxxx x x x x x x 第一章1-5节 1、计算下列极限 2)βαβαββααβα==→→x x x x x x x x sin sin lim sin sin lim00解法2:原式βαβα==→x x x 0lim5)212cos122sin 21lim 2cos 2sin 22sin 2lim sin cos 1lim 0200=⋅⋅=⋅=-→→→x x x x x x xx x x x x x 解法2:原式2121lim 20=⋅=→x x x x7)πππππ-=-=-=-=-→→→→uu u u u u x x u u u x 0001lim tan lim )1(tan lim 1tan lim分析:本题利用了变量替换和等价替换 9)2)2(21lim )12(coslim 222-=⎥⎦⎤⎢⎣⎡-=-∞→∞→x x x x x x分析:∞→x 时,02→x 。
第六版同济大学高等数学上下课后答案详解

|sin x | | x | 3 求 ( ) ( ) ( ) (2) 并作出函数 y(x) 8 设 ( x) 4 6 4 | x | 0 3
的图形 解 ( ) |sin | 1 ( ) |sin | 2 ( ) |sin( )| 2 (2) 0 6 6 2 4 4 2 4 4 2 9 试证下列函数在指定区间内的单调性 (1) y x ( 1) 1 x (2)yxln x (0 ) 证明 (1)对于任意的 x1 x2( 1) 有 1x10 1x20 因为当 x1x2 时
对于映射 g YX 因为对每个 yY 有 g(y)xX 且满足 f(x)f[g(y)]Iy yy 按逆映射的定义 g 是 f 的逆映射 5 设映射 f XY AX 证明 (1)f 1(f(A))A (2)当 f 是单射时 有 f 1(f(A))A 证明 (1)因为 xA f(x)yf(A) f 1(y)xf 1(f(A)) f 1(f(A))A 所以 (2)由(1)知 f 1(f(A))A 另一方面 对于任意的 xf 1(f(A))存在 yf(A) 使 f 1(y)xf(x)y 因为 yf(A)且 f 是单射 所以 xA 这就证明了 f 1(f(A))A 因此 f 1(f(A))A 6 求下列函数的自然定义域 (1) y 3x 2 解 由 3x20 得 x 2 函数的定义域为 [ 2 , ) 3 3 (2) y 1 2 1 x 解 由 1x20 得 x1 函数的定义域为( 1)(1 1)(1 ) (3) y 1 1 x 2 x 解 由 x0 且 1x20 得函数的定义域 D[1 0)(0 1] (4) y
y1 y2
x1 x x1 x2 2 0 1 x1 1 x2 (1 x1)(1 x2 )
【同济第六版高数】第01章函数与极限教案与习题讲解(2)

第一章 函数与极限§1. 2 数列的极限一个实际问题:如可用渐近的方程法求圆的面积?设有一圆, 首先作内接正四边形, 它的面积记为A 1;再作内接正八边形, 它的面积记为A 2;再作内接正十六边形, 它的面积记为A 3;如此下去, 每次边数加倍, 一般把内接正8×2n -1边形的面积记为A n . 这样就得到一系列内接正多边形的面积:A 1, A 2, A 3, ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ , A n , ⋅ ⋅ ⋅设想n 无限增大(记为n →∞, 读作n 趋于穷大), 即内接正多边形的边数无限增加, 在这个过程中, 内接正多边形无限接近于圆, 同时A n 也无限接近于某一确定的数值, 这个确定的数值就理解为圆的面积. 这个确定的数值在数学上称为上面有次序的数(数列) A 1, A 2, A 3, ⋅ ⋅ ⋅ , A n , ⋅ ⋅ ⋅当n →∞时的极限.数列的概念:如果按照某一法则, 使得对任何一个正整数n 有一个确定的数x n , 则得到一列有次序的数x 1, x 2, x 3, ⋅ ⋅ ⋅ , x n , ⋅ ⋅ ⋅这一列有次序的数就叫做数列, 记为{x n }, 其中第n 项x n 叫做数列的一般项. 数列的例子:{1+n n }: 21, 32, 43, ⋅ ⋅ ⋅ , 1+n n ⋅ ⋅ ⋅; {2n }: 2, 4, 8, ⋅ ⋅ ⋅ , 2n , ⋅ ⋅ ⋅;{n 21}: 21, 41, 81, ⋅ ⋅ ⋅ , n 21, ⋅ ⋅ ⋅ ; {(-1)n +1}: 1, -1, 1, ⋅ ⋅ ⋅ , (-1)n +1, ⋅ ⋅ ⋅ ;{n n n 1)1(--+}: 2, 21, 34, ⋅ ⋅ ⋅ , n n n 1)1(--+, ⋅ ⋅ ⋅ . 它们的一般项依次为1+n n , 2n , n 21, (-1)n +1, n n n 1)1(--+. 数列的几何意义:数列{x n }可以看作数轴上的一个动点, 它依次取数轴上的点x 1, x 2, x 3, ⋅ ⋅ ⋅ , x n , ⋅ ⋅ ⋅.数列与函数:数列{x n }可以看作自变量为正整数n 的函数:x n =f (n ),它的定义域是全体正整数.数列的极限:数列的极限的通俗定义:对于数列{x n }, 如果当n 无限增大时, 数列的一般项x n 无限地接近于某一确定的数值a , 则称常数a 是数列{x n }的极限, 或称数列{x n }收敛a . 记为a x n n =∞→lim . 如果数列没有极限, 就说数列是发散的.例如11lim =+∞→n n n ,021lim =∞→n n , 1)1(lim 1=-+-∞→nn n n ; 而{2n}, { (-1)n +1}, 是发散的.对无限接近的刻划:x n 无限接近于a 等价于|x n -a |无限接近于0,极限的精确定义:定义 如果数列{x n }与常a 有下列关系:对于任意给定的正数ε (不论它多么小), 总存在正整数N , 使得对于n >N 时的一切x n , 不等式|x n -a |<ε都成立, 则称常数a 是数列{x n }的极限, 或者称数列{x n }收敛于a , 记为a x n n =∞→lim 或x n →a (n →∞). 如果数列没有极限, 就说数列是发散的.数列极限的几何解释: 例题:例1. 证明1)1(lim 1=-+-∞→nn n n . 分析: |x n -1|=nn n n 1|1)1(|1=--+-. 对于∀ε >0, 要使|x n -1|<ε , 只要ε<n 1, 即ε1>n . 证明: 因为∀ε >0, ∃]1[ε=N ∈N +, 当n >N 时, 有 |x n -1|=ε<=--+-n n n n 1|1)1(|1, 所以1)1(lim 1=-+-∞→nn n n . 例2. 证明0)1()1(lim2=+-∞→n n n . 分析: |x n -0||0)1()1(|2-+-=n n 11)1(12+<+=n n . 对于∀ε >0, 要使|x n -0|<ε , 只要ε<+11n , 即11->εn . 证明: 因为∀ε >0, ∃]11[-=εN ∈N +, 当n >N 时, 有 |x n -0|=ε<+<+=-+-11)1(1|0)1()1(|22n n n n , 所以0)1()1(lim 2=+-∞→n n n . 例3. 设|q |<1, 证明等比数列1, q , q 2, ⋅ ⋅ ⋅ , q n -1, ⋅ ⋅ ⋅的极限是0.分析: 对于任意给定的ε >0, 要使|x n -0|=| q n -1-0|=|q | n -1<ε ,只要n >log |q |ε +1就可以了, 故可取N =[log |q |ε +1]。
同济第七版高等数学第1章习题解答
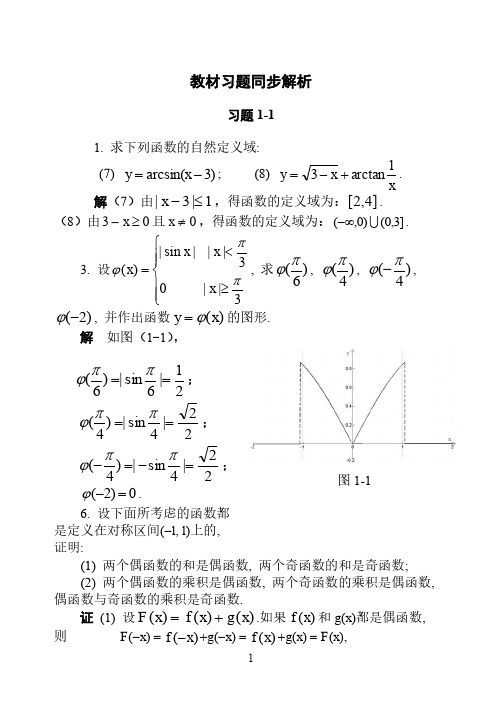
1教材习题同步解析习题1-11. 求下列函数的自然定义域:(7) )3arcsin(-=x y ; (8) xx y 1arctan 3+-=. 解(7)由1|3|≤-x ,得函数的定义域为:]4,2[.(8)由03≥-x 且0≠x ,得函数的定义域为:]3,0()0,( -∞.3. 设⎪⎪⎩⎪⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, )2(-ϕ, 并作出函数)(x y ϕ=的图形.解 如图(1-1),21|6sin |)6(==ππϕ; 22|4sin |)4(==ππϕ; 22|4sin |)4(=-=-ππϕ; 0)2(=-ϕ. 6. 设下面所考虑的函数都是定义在对称区间(-l , l )上的,证明:(1) 两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2) 两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证 (1) 设)()()(x g x f x F +=.如果)(x f 和g (x )都是偶函数, 则 F (-x ) =)(x f -+g (-x ) =)(x f +g (x ) = F (x ),图1-12所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果)(x f 和g (x )都是奇函数, 则F (-x ) = f (-x ) + g (-x ) = -)(x f -g (x ) = -F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2) 设F (x ) =)(x f ⋅g (x ). 如果)(x f 和g (x )都是偶函数, 则F (-x ) = f (-x )⋅g (-x ) =)(x f ⋅g (x ) = F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果)(x f 和g (x )都是奇函数,则F (-x ) = f (-x )⋅g (-x ) = [-f (x )][-g (x )] =)(x f ⋅g (x ) = F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果)(x f 是偶函数, 而g (x )是奇函数,则F (-x ) = f (-x )⋅g (-x ) = f (x )[-g (x )] = -)(x f ⋅g (x ) = -F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.9. 求下列函数的反函数:(3)dcx b ax y ++= (ad -bc ≠0); (6)122+=x x y . 解 (3) 由dcx b ax y ++=,得a cy b dy x -+-=, 所以d cx b ax y ++=的反函数为:acx b dx y -+-=. (6)由122+=x x y ,得y y x -=1log 2, 所以122+=x x y 的反函数为:xx y -=1log 2. 10. 设函数)(x f 在数集X 上有定义, 试证: 函数)(x f 在X 上有界的充分必要条件是它在X 上既有上界又有下界.证 先证必要性.设函数)(x f 在X 上有界, 则存在正数M , 使|)(|x f ≤ M ,即 -M ≤)(x f ≤ M . 这就证明了)(x f 在X 上既有下界-M 又有上界M .再证充分性.3 设函数)(x f 在X 上有下界K 1和上界K 2, 即K 1 ≤)(x f ≤ K 2 . 取M = max{|K 1|, |K 2|}, 则-M ≤ K 1≤)(x f ≤ K 2≤M , 即|)(|x f ≤ M . 这就证明了)(x f 在X 上有界.12. 设)(x f 的定义域为]1,0[=D ,求下列函数的定义域: ⑴)(2x f ; ⑵)(sin x f ;⑶)0()(>+a a x f ;⑷)()(a x f a x f -++ )0(>a .解(1)由,11,102≤≤≤≤x x -所以)(2x f 的定义域为;]1,1[-(2) 由,1sin 0≤≤x ),()12(2Z k k x k ∈+≤≤ππ故)(sin x f 的定义域为:])12(,2[ππ+k k )(Z k ∈;(3)由,10≤+≤a x ,1a x a -≤≤-故函数)(a x f +的定义域为:]1,[a a --. (4) 由⎩⎨⎧≤-≤≤+≤1010a x a x 知,11⎩⎨⎧+≤≤-≤≤a x a a x a -从而当210≤<a 时, 定义域为:]1,[a a -;当21>a 时, 定义域为空集. 13. 设⎪⎩⎪⎨⎧>-=<=1|| 11|| 01|| 1)(x x x x f , x x g e )(=, 求)]([x g f ,)]([x f g , 并作出这两个函数的图形.解 1 |e |[()]0 |e |11 |e |1x x x f g x ⎧<⎪==⎨⎪->⎩, 即⎪⎩⎪⎨⎧>-=<=0 10 00 1)]([x x x x g f . 如图(1-2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tan x 2
x 2
2 lim ( 1 cos x) x 2
sin x cos x 2 cos2 x 1
1
lim [(1 cos x )
2 x 2
cos2 x
显然f ( x)在(,1),(1,1),(1,)内连续.
机动 目录 上页 下页 返回 结束
当x 1时,
15/13
x lim f ( x ) lim cos 0. x 1 x 1 2
x 1
lim f ( x ) lim (1 x ) 2. lim f ( x ) lim f ( x )
机动 目录 上页 下页 返回 结束
2e
1 x
10/13
8. lim (sinx )
x 2
tan x
tan xln sin x 0 lim e e 1. x 2
sin x 1 2 lim ln ( 1 cos x) lim tan x lnsinx x 2 cos x 2 x 2 sin x 1 2 lim ( cos x ) 0, x 2 cos x 2
1 使 f ( ) f ( ) 成立. 2
机动 目录 上页 下页 返回 结束
n 2 )n (1 ) ( 3 3
n
3 e 3.
0
机动 目录 上页 下页 返回 结束
二、关于函数的连续性
13/13
1 e x 1 , x 0 , 求f ( x )的间断点并说明类型 . 例2 设 f ( x ) ln(1 x ), 1 x 0
1 12 2. lim ( 3 ) x 2 x 2 x 8
x 2 2 x 4 12 lim x 2 ( x 2)( x 2 2 x 4)
x4 1 lim 2 . x 2 x 2 x 4 2
机动 目录 上页 下页 返回 结束
6/13
且f (0) b 0, f (a b) a[1 sin( a b)] 0.
16/13
若f (a b) 0, 则a b即为方程的根; 若f (a b) 0,
则由零点定理,至少存 在一点 (0, a b), 使f ( ) 0,
即为方程的根.
机动 目录 上页 下页 返回 结束
18/13
1 若F (0) 0, F ( ) 0, 则 2
1 1 F (0) F ( ) [ f ( ) f (0)]2 0. 2 2 1 由零点定理知, (0, ), 使F ( ) 0. 2 1 即 f ( ) f ( )成立. 2 1 综上, 必有一点 (0, ] (0,1), 2
lim
x 0
2e
1 x
1 x
e ( 2e
4 x
4 x
4 x
e )
4 x
3 x
e (1 e )
1 1,
1 x
sin x 2 e sinx lim ( ) lim ( ) 4 4 x x0 1 e x x 0 x 1 e x
21 1
6、利用极限存在准则 f ( x ) A lim 7、利用 xlim x x x
0
0
f ( x ) lim f ( x) A
x x0
8、利用 lim f ( x) a 0, limg( x) b lim f 下页 返回 结束
a b c 9. lim ( ) x 0 3
x x x
1 x
10. lim(1 2 n 3 )
n
1 n n
机动 目录 上页 下页 返回 结束
5/13
解
1 2x 3 ( x 2)2( x 4) 4 1. lim lim . x 4 x 4 ( x 4)( 1 2 x 3) 3 x 2
1 x 1 x
x 0
机动 目录 上页 下页 返回 结束
9/13
sin x 7. lim( ) 1. 4 x 0 x 1 ex
2 e
1 x
sin x 2 e sinx lim ( ) lim( ) 4 4 x 0 1 e x x x 0 1 e x x
综上所述,方程x a sin x b至少有一个正根, 且不超过a b.
机动 目录 上页 下页 返回 结束
17/13
例5 设f ( x )在闭区间 [0,1]上连续, 且f (0) f (1),
1 证明 令 F ( x ) f ( x ) f ( x ), 2
1 证明必有一点 (0,1), 使得f ( ) f ( ). 2
x 1 x 1 x 1
故f ( x)在x 1间断.
lim f ( x ) lim f ( x)
x 1 x 1
当x 1时,
x lim f ( x ) lim cos 0. x 1 x 1 2
f (1) cos
2
0
lim f ( x ) lim ( x 1) 0.
sin 2 x lim 2 x 0 x sin x
1 . 2
机动 目录 上页 下页 返回 结束
7/13
5. lim
x 1
ln(1 3 x 1) arcsin( 23 x 2 1)
3
lim
x 1
x 1
23 x 2 1
1 lim 3 x 1 2 x 1
1 1 2 x sin x sin x x lim 3. l im x x ( x ) 2 x 2 2x2 1
2
lim(
x
1 2 x
2
sin 1 x
1 x
1 ) . 2
1 sin2 x 1 4. lim x x 0 ( e 1) ln( 1 sin x )
机动 目录 上页 下页 返回 结束
10. lim(1 2 3 )
n n
1 n n
12/13
解法1
1 n 2 3 (1 2 3 ) 3[1 ( ) ( ) ] 3 n 3 , 3 3 1 1 又 limn 3 l i m 3 x 1,由夹逼准则 l im(1 2 n 3 n ) n 3 n x
3/13
例1
求下列极限
1 12 2. lim ( 3 ) x 2 x 2 x 8
1 sin2 x 1 4. lim x x 0 ( e 1) ln( 1 sin x )
1 2x 3 1. lim x 4 x 2
1 x sin x 3. l im x 2x2 1
x 0
x 0是f ( x)的第一类(跳跃)间断 点.
机动 目录 上页 下页 返回 结束
14/13
x 1, x 1 例3 讨论f ( x ) 的连续性. x cos , x 1 2
解
将f ( x )改写成
1 x , x 1 x f ( x ) cos , 1 x 1 2 x 1, x 1
1/13
第一章 函数、极限、连续
习题课
机动 目录 上页 下页 返回 结束
一、
关于极限的计算
2/13
1、利用极限的运算法则和函数的连续性 (不满足运算条件的可通过:分解因式、有理化、 分离无穷小、通分等方法恒等变形) 2、利用无穷小的性质(无穷小与有界量乘积 是无穷小;无穷小与无穷大互为倒数) 3、 利用等价无穷小代换(注意:一定是因子) 4、利用变量代换 5、利用两个重要极限
n
n 1 n n 1 ln( 1 2 n 3 n ) n n n
1 2 ( )n ( )n 3 lim 3 n n
1 n n
1 n n
解法2 l im (1 2 n 3 ) lime
lime
n
1 1 2 ln 3 n [1 ( ) n ( ) n ] n 3 3
x 1 x 1
故f ( x )在x 1连续.
f ( x )在( ,1) ( 1,)连续.
机动 目录 上页 下页 返回 结束
例4 证明方程x a sin x b (a , b 0)至少有一个正根, 且不超过a b.
证 令 f ( x ) x a sinx b, 则f ( x )在[0, a b]上连续,
]
sin x cos x 2
e 0 1.
机动 目录 上页 下页 返回 结束
11/13
a b c 9. lim ( ) x 0 3
x x x
1 x
lime
x 0
1 a x b x c x ln x 3
3 abc.
1 a x bx c x lim ln x 0 x 3 1 a x 1 bx 1 c x 1 lim ln( 1 ) x 0 x 3 1 a x 1 bx 1 c x 1 1 lim ( ) ln (abc), 3 x 0 x x x 3
3e
3.
1
1 n 2 n n n (1 2 3 ) 3 lim [1 ( ) ( ) ] 解法3 lim n n 3 3
n 2 )n 1 n 2 n (1 ) ( 3 lim {[1 ( ) ( ) ] 3 3 } n 3 3
1 n n
1
解
