§1_6_3 热力学第一定律在相变化中的应用
合集下载
5热力学第一定律的应用
指定产物 C H N CO2(g) ) H2O(l) () N2(g) )
其他单质, 其他单质,另有说明
c H m (C2H5OH,l,298K) ,, C2H5OH(l,298K,p )+ 3O2 (g,298K ,p ) , , , =2CO2(g,298K, p )+ 3H2O(l,298K ,p ) , , , r H m (298K) = c H m (C2H5OH,l,298K)
CO 2 (g ) + 4H 2 (g ) = CH 4 (g ) + 2H 2 O(g )
r H m (T ) = f H m (CH 4 ) + 2 × f H m (H 2 O) - f H m (CO 2 ) - 4 × f H m (H 2 )
思路: 公式推导 思路:
CO 2 + 4H 2 = CH 4 + 2H 2 O(g )
H2(g, 298.15K, p )+ )+1/2O2(g, 298.15K, p ) = H2O(g, 298.15K, p ) rHm = fHm (H2O, g, 298.15K)
rHm = fHm 参考状态的单质 (T,标准态) ,标准态) 1mol B (T,标准态) ,标准态)
反应的特点: 反应的特点: 定温变化 始态和终态都处于标准态 终态的物质为B,物质的量为1mol 终态的物质为 ,物质的量为
U , H Q,W
H2O(g) n = 2mol t2 = 100℃ ℃ p2 = 101325Pa
=2 × 40.67 kJ = 81.34 kJ W=- β-Vα)=- =-p(V =-nRT =- =- U = Qp+ W
物理化学知识点(全)
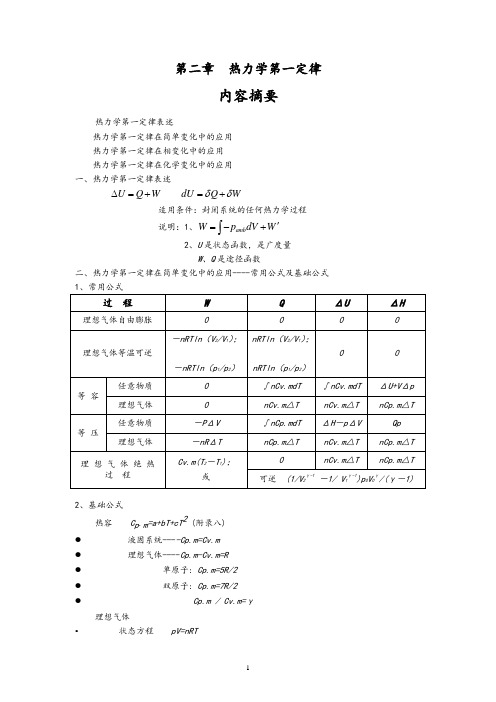
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件：封闭系统的任何热力学过程 说明：1、amb W p dV W '=-+⎰2、U 是状态函数，是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 过 程WQΔUΔH理想气体自由膨胀理想气体等温可逆－nRTln （V 2/V 1）； －nRTln （p 1/p 2） nRTln （V 2/V 1）；nRTln （p 1/p 2）0 0等 容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等 压任意物质－P ΔV ∫nCp.mdT ΔH －p ΔV Qp 理想气体－nR ΔT nCp.m △TnCv.m △T nCp.m △T 理 想 气 体 绝 热过 程 Cv.m(T 2－T 1)；或nCv.m △TnCp.m △T可逆 (1/V 2γ-1－1/ V 1γ-1)p 0V 0γ/(γ－1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、 可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m － p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = －Δ蒸发H m (T)Δ凝固H m (T) = －Δ熔化H m (T) Δ凝华H m (T) = －Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点： 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
热力学基本定律及其应用
16
①流体流经换热器、反应器、管道等设备 物系与环境之间没有轴功的交换，WS=0 进出口之间动能的变化和位能的变化可以忽略
1 2 u 0，gz 0 2 H Q
17
②流体流经泵、压缩机、透平等设备 体系在设备进出之间动能的变化、位能的变化 与焓变相比可以忽略不计
1 2 u 0，gz 0 2 H Q WS H WS
如热力学能、焓和以热量形式传递的能量
③完全不能转化为功的能量称为僵态能量 如大气、大地和海洋等具有的热力学能
38
3 由高级能量变为低级能量称为能量品位的降低，意味着
能量做功能力的损耗。化工过程中由于过程进行需要推动
力，因此能量品位的降低是必然的，合理选择推动力，尽 可能减少能量品位的降低，避免不必要的做功能力的损耗
18
③流体流经喷管和扩压管
流体流经设备如果足够快、可以假设为绝热，Q=0
设备没有轴传动结构，WS=0 流体进出口高度变化不大，重力势能的改变可以忽略，g△z=0
1 2 H u 2
19
④流体经过节流膨胀、绝热反应和绝热混合等过程 体系与环境没有热量交换、也不做轴功， 进出口动能、位能的变化可以忽略不计
W pdV W pdV WS W f WS ( p 2V2 p1V1 ) d ( pV ) pdV Vdp
p 2 ,V2
p1 ,V1
d ( pV ) p 2V2 p1V1 pdV Vdp
V1 p1 p2 p1
V2
p2
WS Vdp
6
②可逆轴功 流体流动过程中通过机械设备的旋转轴在体系和环境之间
交换的功称为轴功，用WS表示。在化工设备中，常用的
热力学第一定律的应用
TV
pV T nR
nRT V p
1
常数
……①
代入上式，得 代入，得
PV 常数
……②
Tp1γ / γ 常数 ……③
式①、 ②、 ③称为理想气体绝热可逆过程方程式 应用条件：封闭系统，W′＝0，理想气体，绝热， 可逆过程
(3) 理想气体绝热可逆过程的体积功
W U nCV ,m T2 T1
W pdV
V1 V2
将 pV =常数 代入，积分后得
p1V1 V1 W 1 V2
1
1
练习7 1mol 单 原 子 理 想 气 体 ， 从 273.15K 、 1013.25kPa的始态，经绝热可逆膨胀至终态 压力为101.325kPa ，求 (1) 终态温度； (2) ΔU, ΔH，Q 和W
H1 nCp,m (T )dT
T1 T2
2 75.31 (100 25)J
H 2 n vap H m
H 3 nCp,m (T )dT
T1 T2
2 33.6 (25 100)J
1.7 热力学第一定律的应用之三 —— 在化学变化中的应用 1. 几个术语 反应进度
H＝f ( T )
dU CV dT nCV ,mdT
U nCV ,m (T )dT
T1 T2
dH C p dT nCp,mdT
H nCp,m (T )dT
T1
T2
U nCV ,m (T )dT
T1
T2
应用条件：封闭系统，W′＝0，真实气体、液体、固 体单纯 p、V、T变化的定容过程；理想气体任意 p、 V、T变化过程
热力学第一定律应用
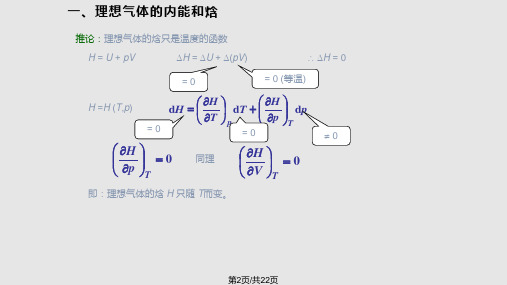
单原子分子
双原子分子 非线性多原子分子 (3) 实际气体 (4) 凝聚系统
CV ,m
3 2
R
5 CV ,m 2 R
CV，m = 3R
Cp, m-CV, m R
Cp, m CV, m
如He
如H2 ，O2 ，N2 如H2O (g)
第4页/共22页
三、理想气体非绝热过程Q,W,U,H计算
1 恒温过程
H = n Cp，m ( T2 -T1 ) = …… = -9005 J
第16页/共22页
五、热力学第一定律对实际气体应用
理想气体U、H只是T的函数，与p、V无关， 因为分子间无作用力，无位能。
实际气体分子间有作用力，p、V的变化影响U、H
1. 焦耳－汤姆逊实验
节流膨胀实验
恒定压力的气体， 经多孔塞膨胀， 使其为压力恒定的低压气体
(1) 恒温可逆
273 K 200 kPa
(2) 向真空 (3) 恒温恒外压
(4) 恒容降温
100 kPa
解 (1) 恒温可逆
U = H = 0
Q = -W (2) 向真空
nRT ln p2 8.314 273 ln 100 = 1573 J
p1
200
U = H = 0
Q =-W=0
第6页/共22页
U = 0 H = 0 Q =-W
按不同过程计算W
2 非恒温过程 先求出终态温度 T2 H = nCp，m (T2－T1 ) U = nCV，m (T2－T1 ) Q = U-W
按不同过程计算W及Q
第5页/共22页
三、理想气体非绝热过程Q,W,U,H计算
例 计算1mol单原子理想气体以下过程的Q、W、U、H
物理化学第一章热力学第一定律
→→确定系统的状态，其他的性质。 独立变量：被选来确定系统状态的独立变化
的性质。
11
若对于一定量的纯物质单相系统，已知系统的独 立性质为 x 与 y ，则系统任一其它性质 X 是这两个 变量的函数，即：
X = f (x, y)
例对物质的量为n的某纯物质、单相系统，其状 态可由T，p来确定，其它性质，如V，即是T，p的 函数。V=f (T, p)
14
还需掌握的一个数学公式（以后推导其他公 式要用到）
z = f(x ,y )
dz
=
( ∂z ∂x
)y dx
+
(
∂z ∂y
)x dy
如理想气体： V = nRT 即：V = f ( p,T) p
15
4.过程与途径 定义
系统从一个状态变到另一个状态，称为过程。 前一个状态称为始态，后一个状态称为末态。 实现这一过程的具体步骤称为途径。 过程与途径这两个概念常常不严格区别。
循环过程 (始态=末态， ∮dZ=0)
17
5.热力学平衡态(自学） 定义
在一定条件下，系统中各个相的宏观性质不随时间 变化;且如系统已与环境达到平衡,则将系统与环境 隔离，系统性质仍不改变的状态。
系统若处于平衡态,则系统满足：
①内部有单一的温度，即热平衡； ②内部有单一的压力，即力平衡； ③内部各相组成不变，即相间扩散平衡； ④内部各组分的物质的量不变，即化学平衡。
21
特点： （1）热力学能的绝对值无法确定 （2）热力学能是状态函数 （3）热力学能是广度性质
22
热力学第一定律的文字表述（自学）
在化学热力学中，研究的体系大多为宏观上静 止且无特殊外电场存在，故EK=EP=0,E=U
的性质。
11
若对于一定量的纯物质单相系统，已知系统的独 立性质为 x 与 y ，则系统任一其它性质 X 是这两个 变量的函数，即：
X = f (x, y)
例对物质的量为n的某纯物质、单相系统，其状 态可由T，p来确定，其它性质，如V，即是T，p的 函数。V=f (T, p)
14
还需掌握的一个数学公式（以后推导其他公 式要用到）
z = f(x ,y )
dz
=
( ∂z ∂x
)y dx
+
(
∂z ∂y
)x dy
如理想气体： V = nRT 即：V = f ( p,T) p
15
4.过程与途径 定义
系统从一个状态变到另一个状态，称为过程。 前一个状态称为始态，后一个状态称为末态。 实现这一过程的具体步骤称为途径。 过程与途径这两个概念常常不严格区别。
循环过程 (始态=末态， ∮dZ=0)
17
5.热力学平衡态(自学） 定义
在一定条件下，系统中各个相的宏观性质不随时间 变化;且如系统已与环境达到平衡,则将系统与环境 隔离，系统性质仍不改变的状态。
系统若处于平衡态,则系统满足：
①内部有单一的温度，即热平衡； ②内部有单一的压力，即力平衡； ③内部各相组成不变，即相间扩散平衡； ④内部各组分的物质的量不变，即化学平衡。
21
特点： （1）热力学能的绝对值无法确定 （2）热力学能是状态函数 （3）热力学能是广度性质
22
热力学第一定律的文字表述（自学）
在化学热力学中，研究的体系大多为宏观上静 止且无特殊外电场存在，故EK=EP=0,E=U
物理化学-第二章-热力学第一定律及其应用精选全文
上一内容 下一内容 回主目录
返回
2024/8/13
状态与状态函数
状态函数的特性： 异途同归，值变相等；周而复始，数值还原。
状态函数的性质：
(1) 状态函数的值取决于状态，状态改变则状态函数必定改 变（但不一定每个状态函数都改变）；任何一个状态函数 改变，系统的状态就会改变。
上一内容 下一内容 回主目录
即
ΔU=Q+W （封闭系统）
对于无限小过程，则有
dU=δQ+δW （封闭系统）
上一内容 下一内容 回主目录
返回
2024/8/13
3. 焦耳实验 盖.吕萨克—焦尔实验
实验结果：水温未变 dT=0 dV≠0
表明：Q =0
自由膨胀 W=0
上一内容 下一内容 回主目录
返回
2024/8/13
dU= Q+ W =0
1. 热(heat)
a) 定义：体系与环境之间因温差而传递的能量称为热，用 符号Q 表示。单位：KJ 或 J。 b) Q的取号：体系吸热，Q>0；体系放热，Q<0 。
c) 性质：热不是状态函数，是一个过程量；热的大小和具 体的途径有关。
上一内容 下一内容 回主目录
返回
2024/8/13
功和热
不能说在某个状态时系统有多少热量，只能说 在某个具体过程中体系和环境交换的热是多少。
热力学能是状态函数，用符号U表示，单位为J。它 的绝对值无法测定，只能求出它的变化值。
U= U2 –U1
上一内容 下一内容 回主目录
返回
2024/8/13
热力学能
纯物质单相系统
若n确定
U=U ( n,T,V ) U=U (T,V )
第3课热力学第一定律在化学反应中的应用
R
m
T
一般燃烧反应分子数变化不大
Q p Qv
理想气体定压热效应和定容热效应举例
例
1 CO O2 CO2 2 n R 1 .5 np 1
Q p 2 8 2 7 6 1k J /k m o lC O
Q v 2 8 1 5 1 3 k J /k m o lC O Q p Qv Qp 0 .4 %
mA
bH
mB
) in d h
,p T 2 5 ,1 a tm T ,p 2 5 ,1 a tm m 0 f C 0 f
C
m
,p T 2 5 ,1 a tm ,p T 2 5 ,1 a tm
Standard reference state
标准定压热效应 Q
0 p
或 H 查手册
0
四、标准摩尔反应焓
1. 摩尔反应焓变: ξ =1mol时化学反应的焓变 以 r H m 表示。 说明:1) r H m 的数值与反应式的写法有关，单位J·mol−1
指按所给计量方程式进行ξ为1 mol的反应时的焓变。
赫斯定律举例
1.盖斯定律内容：
一确定的化学反应的恒容热或恒压热只取决于 过程的始态与末态， 而与中间变化的途径无关。
2.意义：
有些化学反应慢，量热器容易因辐射或散热使量度不准确， 有些化学反应的热效应难以直接测量(如有机反应常伴随有副反应) 等，则可用此定律设计过程求算过程的热效应。
3.盖斯定律适用:
又因H为状态函数，其变化量只与体系状态有关， 以CO(g)+O 2(g) 为初始状态， 以CO2(g)为终了状态设计途径， 将三个化学反应联系起来
热效应与反应热Heat of reaction
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
小结：理想气体在各种过程中Q, W, ΔU, ΔH 的计算
（前提：封闭系统，W ′=0，无化学变化） 定温过程 WV=－psuΔV WV=－∫pdV
Q=W QV=ΔU Qp=ΔH Q=0
ΔU=0
ΔH=0
定容过程 定压过程 绝热过程
可逆相变化
End
WV=0 WV=－psuΔV WV=ΔU WV=－psuΔV
Hale Waihona Puke ①定压升温101.3 kPa, 25℃
H2O(g)
③定压降温
2mol H2O(l) ΔH1 =
101.3 kPa, 100℃
②可逆相变
H2O(g)
则 Qp=ΔH =ΔH1＋ΔH2＋ΔH3
∫
T2 T1
nC
p ,m
( l ) d T = nC
p ,m
(l ) Δ T
ΔH2 = n ·ΔvapHm ΔH3 = ∫ T nC
升华焓: ΔsubHm, 晶型转变焓: ΔtrsHm(α→β)
纯物质 B(α)
2、相变化过程的体积功和ΔU
定温、定压 WV =－p(Vβ－Vα)
B(β) Qp＝ΔαβH
由热一律, W′＝0 时 ΔU＝Qp＋WV 或 ΔU＝ΔH －p(Vβ－Vα) 1)对熔化和晶型转变 ΔV≈0，WV≈0， ΔU≈ΔH （s→l ， s1→s2） 2)若β为气相，α为凝聚相 (蒸发和升华) WV =－pVβ Vβ >>Vα，所以 ΔU =ΔH －pVβ 若气相视为理想气体 WV =－pVβ=－nRT 则 ΔU ＝ ΔH－nRT
（1-53）
典型例题
水的正常沸点
例1：2mol 水在101.3 kPa，100℃时蒸发，变成同温 同压下的水蒸气（设水蒸气为理想气体），求此过程 的Q、W、ΔU和ΔH。已知水在100℃及标准压力下的摩尔
汽化热ΔvapHm为40.67 kJ·mol-1。
101.3 kPa, 100℃
解：定温定压下可逆相变 2mol H2O(l) Qp ＝ ΔH ≈ n ·ΔvapHm W＝－pVg＝－nRT 则
101.3 kPa, 25℃
解：定温定压相变化 2mol H2O(l)
①定压升温
ΔH
H2O(g)
③定压降温
非该温度下的 平衡压力，需 设计可逆途径!
2mol H2O(l)
101.3 kPa, 100℃
可逆相变
H2O(g)
非该温度下平衡压力，设计可逆途径!
解：定温定压相变化 2mol H2O(l) ΔH
§1.6.3 热力学第一定律在相变化中的应用
相变化过程——包括气化、冷凝、熔化、 凝固、升华、凝华以及晶型转化等。
1、相变热Q 及相变焓 ΔH
定温、定压，W′=0 时，纯物质 B(α) 相变热
β Q p = Δ αH
B(β)
Vapour Fusion Sublimation Transform
◇ 摩尔相变焓(基础热数据) 蒸发焓: ΔvapHm，熔化焓: ΔfusHm,
H2O(g)
ΔU = Qp + W = ΔH－nRT
例2： 25℃、101.3 kPa下, 2 mol 液态水蒸发，变成 同温同压下的水蒸气(设水蒸气为理想气体), 求此过 程的Q、W、ΔU 和 ΔH。已知水和水蒸气的平均定压摩
尔热容分别为75.31和33.47 J·K-1·mol-1;水在100℃及101.3 kPa 下的摩尔汽化热ΔvapHm为40.67 kJ·mol-1。
WV=－psuΔV
ΔU=nCv,mΔT ΔH=nCp,mΔT
Qp=ΔαβH ΔU=ΔH -pΔV
2
难 点
T1
p ,m
( g ) d T = nC
p ,m
( g )ΔT
W = －pVg =－nRT （仅考虑实际过程） ΔU = ΔH－p· Δ V = ΔH－nRT （=Q+W）
小结：
理想气体在各种过程中 Q、W、ΔU、ΔH 的计算 （前提：封闭系统，W ′ =0，无化学变化） 定温过程 定容过程 定压过程 绝热过程 可逆相变化