§7.5强电解质溶液理论简介
第5节 强电解质溶液理论简介
二、德拜-休克尔极限定律的常用表示式
lg A | z z | I
这个公式只适用于强电解质的稀溶液、 离子可以作为点电荷处理的体系。式中γ±为离 子平均活度系数，从这个公式得到的γ±为理论 计算值。用电动势法可以测定γ±的实验值，用 来检验理论计算值的适用范围。
应用德拜-休克尔极限公式计算25 ℃ 时0.002 mol·kg-1 CaCl2溶液中γ(Ca2+)、 γ(Cl-)和γ± 。
§7.5 强电解质溶液理论简介
一、离子氛模型及德拜-尤格尔极限公式 1、离子氛（ionic atmosphere）
这是德拜-休克尔理论中的一个重要概 念。他们认为在溶液中，每一个离子都被反 号离子所包围，由于正、负离子相互作用， 使离子的分布不均匀。
若中心离子取正离子，周围有较多的负离 子，部分电荷相互抵消，但余下的电荷在 距中心离子 r 处形成一个球形的负离子氛； 反之亦然。一个离子既可为中心离子，又 是另一离子氛中的一员。
解：该溶液中的离子强度为：
I 1 (0.002 22 0.002 212 ) 2
0.006 mol kg1 根据德拜-休克尔定律：
பைடு நூலகம்
lg r Az z I 0.509 21 0.006 0.0789
r 0.8340
lg r(Ca2 ) Az2 I 0.509 22 0.006 0.1577 r(Ca 2 ) 0.6955 lg r(Cl ) Az2 I 0.50912 0.006 0.0394 r(Ca 2 ) 0.9132
2、德拜-休克尔极限定律
德拜-休克尔根据离子氛的概念，并引入若 干假定，推导出强电解质稀溶液中离子活度系数 γi的计算公式，称为德拜-休克尔极限定律。
基础化学 电解质溶液
例 计算0.100 mol· L-1HAc溶液的解离度α及[H3O+]。
解 HAc的Ka=1.75×10-5
HAc(aq) + H2O(l) c(1-α)≈c Ka= (cα)2/c = cα 2 H3O+(aq) + Ac-(aq) cα cα
K / c 1.75105 / 0.100 1.32102 1.32%
lg A z z I 0.509kg1/2 mol1/ 2 (1) (1) 0.010mol kg1 0.051
c(NaCl) ≈ 0.0089 mol·L-1 根据П=icBRT , i=2 П=2×0.0089 mol· L-1×8.314 J· mol-1· K-1×298.15 K ×1 KPa· L/1J = 44 kPa
[H3O ][OH ] K [H2O][H2O]
[H2O]看成常数，与K合并，得
Kw= [H3O+][OH-]
Kw称质子自递平衡常数，又称水的离子积
0℃时 Kw= 1.15×10-15
25℃时
100℃时
Kw= 1.01×10-14
Kw= 5.44×10-13
水的离子积不仅适用于纯水，也适用于所 有稀水溶液。
a bB /bθ 0.89 0.010mol kg-1 /(1mol kg1 ) 0.0089
0.89
(2) 0.020 mol· kg-1KBr+0.030 mol· kg-1ZnSO4溶液的离子强度 。 解：I = [b(K+)z2(K+) + b(Br-)z2(Br-) + b(Zn2+)z2(Zn2+) + b(SO42-)z2(SO42-)] = [(0.020mol· kg-1)(+1)2 + (0.020mol· kg-1)(-1)2 + (0.030mol· kg-1)(+2)2 + (0.030 mol· kg-1)(-2)2] = 0.14 mol· kg-1 对于1-1价型及2-2价型的强电解质，I=bZ2。故上述可简化计 算： I = I(KBr) + I(ZnSO4) = 0.020 mol· kg-1×12+0.030 mol· kg-1×22=0.14 mol· kg-1
电解质溶液理论
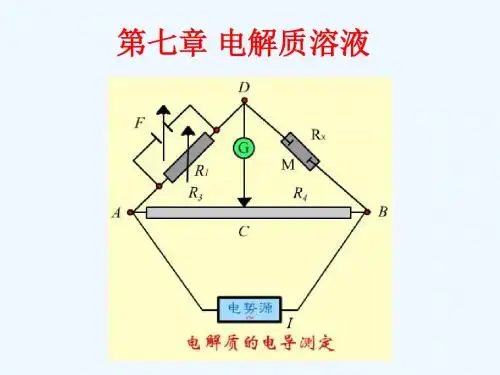
通电结束，阳极部正、负离子各少了3mol，阴极 部只各少了1mol，而中部溶液浓度仍保持不变。
1.离子的电迁移现象
2.离子电迁移的规律
1.向阴、阳两极迁移的正、负离子物质的量总和恰好等 于通入溶液的总电量。
正 离 子 所 传 导 的 电 量 ( Q ) 阳 极 部 电 解 质 物 质 的 量 的 减 少 2 . 阴 极 部 电 解 质 物 质 的 量 的 减 少 负 离 子 所 传 导 的 电 量 ( Q ) 正 离 子 的 迁 移 速 率 ( r ) = 负 离 子 的 迁 移 速 率 ( r )
如果溶液中有多种电解质，共有 i 种离子，则：
t t t 1
i +
4.离子迁移数
设相距为l、面积为A的两个平行惰性电极，左方
接外电源负极，右方接正极，外加电压为E。在电极
间充以电解质 M x N y 的溶液，它的浓度为c （单位为
mol m-3 ），解离度为 。
4.离子迁移数
如果正、负离子荷电量不等，如果电极本身也发 生反应，情况就要复杂一些。
3.离子的电迁移率
离子在电场中运动的速率用公式表示为：
r U (dE / dl ) r U (dE / dl )
式中 d E d l 为电位梯度，比例系数 U 和 U 分别称为正、 负离子的电迁移率，又称为离子淌度（ionic mobility）， 即相当于单位电位梯度时离子迁移的速率。它的单位是 2 1 。 m s 1V
I ( c xA r ) zF
同理
I ( c yA r ) zF
4.离子迁移数
因为溶液是电中性的，所以 xz yz
I I I cx z A(r r ) F cy z A(r r ) F
强电解质溶液理论简介
当溶液很稀，可看作是理想溶液，B,m1,则：
aB,m
mB mo
强电解质溶液的活度和活度系数
对强电解质：
（1）强电解质几乎完全电离成离子，整体电解质 不复存在，其浓度与活度的简单关系不再适用；
（2）与极稀的非电解质溶液可视作理想(稀)溶液， 活度系数近似等于1不同，对极稀的强电解质溶液， 由于离子间的相互作用，使它比非电解质溶液的 情况复杂得多，此时的活度与理想(稀)溶液的活度 仍有一定的偏差。
• 离子氛：每一离子周围被相反电荷离子包围，由于 离子间的相互作用，使得离子在溶液中不是均匀分 布，而是形成了球形对称的离子氛。
离 子 氛 示 意 图
负离子
正离子
中心正离子 中心负离子
Debye-Hückel 离子互吸理论要点：
ⅰ.离子氛的离子分布遵守Boltzmann分布律，电荷密 度与电位的关系遵守Poisson公式。
8kTa
kT 2e2Lsln
1
I
化简得：
ln j
Azj2 1 Ba
I I
其中：
B
2e2 Ls ln
e2 A
2e2Lsln
kT
8kT kT
采用平均活度系数时
ln
Az z 1 Ba
I I
对于水溶液： A0.509 mol1kg1/2 B0.3291010 mol1kg1/2m1
当溶液极稀时，Ba I 1 可得Debye－Hückel极限公式
B (o RTlna)(o RTlna) (o RTlna)(o RTlna)
类似的，定义
离子平均活度系数（mean activity coefficient of ions）
def
物理化学中的电解质溶液理论
物理化学中的电解质溶液理论电解质溶液理论是物理化学中的一个重要分支，在化学和生物化学领域中有着广泛的应用。
它主要研究电解质溶液中的离子、溶剂和溶液中的现象及其相互关系。
电解质溶液理论包括电离平衡、电导率、溶解热、渗透压、溶解度、活度系数等多个方面，涉及数学、化学和物理等多个学科知识。
1.电离平衡在电解质溶液理论中，电离平衡是非常重要的概念。
电离平衡指的是电解质在水中溶解时，电离成离子的平衡状态，通俗地说，就是离子和未离子的相对浓度保持不变的状态。
其中，离子浓度与本身浓度和电离程度有关，未电离部分的浓度则由溶解度决定。
电离平衡的两个特征是平衡常数和解离度。
平衡常数指的是在电解质溶液中，电离反应的反应速率相等时，浓度比例的平衡常数。
解离度是指溶液中一个电解质所能释放的带电粒子的数量。
2.电导率电导率是电解质溶液中电流通过的能力的物理性质。
在电解质溶液中，离子作为带电粒子，能够与电场发生作用，使电流通过。
电导率是指单位距离内所包含的电解质中离子数与电流比例的倒数。
电导率随着温度的变化而变化，一般来说，温度越高电导率越高。
3.溶解热和焓在电解质溶液中，溶解热是一个重要的物理化学概念。
溶解热是指让一个电解质固体溶解在水中所需的热量。
在溶解过程中，离子与离子之间相互作用会发生变化，当离子中的分子与溶剂中的分子之间相互作用能量足够大时，这种相互作用便会破坏把固体形态的离子转化为水溶液形态。
4.渗透压电解质溶液中的渗透压是指浓度梯度下流体的渗透行为，其大小取决于溶液中的溶质浓度和温度。
人体内的细胞，需要维持一定的细胞内环境平衡，而渗透压是影响细胞的一大因素。
如果渗透压梯度过大，代谢的正常运转就会受到影响。
5.溶解度和活度系数溶解度是指在一定温度下，溶液中能溶解的物质的最大量。
在电解质溶液中，溶解度是根据离解平衡的比例来计算的。
活度系数指的是在溶液中，一定浓度的溶质实际浓度与理论预期浓度的比值，它的大小是对离子化程度的度量。
强电解质溶液理论简介
的能量，也即 zie×y = kT ，（这一点对于稀溶液，可以成
立 ），于是对上式进行级数展开，即有：
(r)= i
Ci,0zie1ziek T(r)i
Ci,0zie
i
Ci,0Lzi2e2(r)
kT
= Ci,0Lzi2e2(r)
i
kT
(1)
静电场泊松方程
8kTa
kT 2e2Lsln
1
I
化简得：
ln j
Azj2 1 Ba
I I
其中：
B
2e2 Ls ln
e2 A
2e2Lsln
kT
8kT kT
采用平均活度系数时
ln
Az z 1 Ba
I I
对于水溶液： A0.509 mol1kg1/2 B0.3291010 mol1kg1/2m1
当溶液极稀时，Ba I 1 可得Debye－Hückel极限公式
Ci Ci,0expziekT(r)
这里，Ci,0 即为当r ，因而0 处的离子数密度，显
然， Ci,0 即为 i 离子的本体数密度，也即平均数密度。
因此，距离为 r 的体积元 dV 内电荷密度 是各离子电荷密
度的总和，即 ci zie
= i C iz ie i C i,0 z ie e x p z ie k T (r )
zie
4 r
exp(Ka) 1 Ka
exp(Kr)
1
当 r = a 时:
(a)4ziea1K1
与
zje
4(a 1)
比较，显然：
K 2e2Lsln I kT
于是离子氛的厚度－1即可确定，它与溶液离子强度，溶 液介电常数、温度等均有关。将上式代入活度系数表达 式中，即可得活度系数方程：
化学反应机理的电解质溶液理论
化学反应机理的电解质溶液理论化学反应机理是研究化学反应过程中分子间相互作用以及反应物转变为产物的步骤和路径。
在溶液中进行化学反应时，电解质溶液理论被广泛应用。
本文将探讨电解质溶液理论在化学反应机理研究中的重要性，以及其原理和应用。
一、电解质溶液理论的概念电解质溶液理论是描述电解质在溶液中行为的理论。
电解质是指能够在水溶液中产生离子的物质，包括阳离子和阴离子。
在溶液中，电解质会发生电离，即分解为离子。
电解质溶液理论描述了电解质在溶液中的电离过程和溶液中离子间的相互作用。
二、电解质溶液理论的原理电解质溶液理论基于电离动力学和离子间相互作用力的研究。
电离动力学研究了电解质在溶液中的电离过程。
根据电离动力学的理论，溶液中电解质的电离程度与浓度有关。
高浓度下，电离程度较低，反之亦然。
离子间相互作用力研究了溶液中离子间的相互作用。
这些相互作用力包括离子间的库仑作用力、水合作用力等。
三、电解质溶液理论的应用1. 酸碱中和反应机理电解质溶液理论在酸碱中和反应机理研究中起着重要作用。
酸碱反应是指酸和碱之间的中和反应。
根据电解质溶液理论，酸和碱在溶液中电离生成离子，然后发生中和反应。
酸的电离产生H+离子，碱的电离产生OH-离子，H+和OH-离子结合形成水，完成中和反应。
2. 氧化还原反应机理电解质溶液理论也广泛应用于氧化还原反应机理研究。
氧化还原反应是指反应物中的电子从一种物质转移到另一种物质的过程。
电解质溶液理论中的电离过程能够帮助解释氧化还原反应中的电子转移过程。
在氧化还原反应中，电解质以及溶液中的离子起到了重要的催化作用。
3. 反应速率的影响电解质溶液理论还可以解释溶液中反应速率的影响。
由于电解质溶液中的离子浓度较高，因此它们能够增加反应物的有效碰撞机会，从而提高反应速率。
在一些反应中，电解质的添加可以作为催化剂，促进反应的进行。
四、总结电解质溶液理论在化学反应机理研究中具有重要的作用。
它能够帮助我们理解溶液中电解质的电离行为，解释酸碱中和反应和氧化还原反应的机理，并能够影响反应速率。
强电解质溶液理论
=θ(T)+RT ln a
(2) 完全解离性 溶液中实际是以正负离子形成存在（不是分 溶液中实际是以正负离子形成存在（ 子状态存在）， ），因此化学势 子状态存在），因此化学势
+=θ+(T)+RT ln a＋
对于任意强电解质 Mν Aν
+
–=θ–(T)+RT ln a–
a = aν + aν +
路易斯根据实验事实， 进一步总结出稀溶液范围内活 路易斯根据实验事实 ， 度系数和离子强度之间的经验关系式
ln γ ± = 常数 I
上面两式仅适用于离子强度小于0.01mol Kg-1的稀溶液。 的稀溶液。 上面两式仅适用于离子强度小于
三、德拜-休克尔极限定律 德拜 休克尔极限定律
德拜-休克尔根据电解质溶液中离子之间相互静电作用 德拜 休克尔根据电解质溶液中离子之间相互静电作用 的理论模型，并引入若干假定， 的理论模型，并引入若干假定，稀溶液中离子活度系数 的 计算公式，称为德拜 休克尔极限定律 计算公式，称为德拜-休克尔极限定律
+
+
+
+ +
+
+
-
+
第四节 溶液中电解质的活度和活度系数
一、强电解质的平均活度和平均活度系数
强电解质溶液与非电解质溶液比较，有两点显著不同： 强电解质溶液与非电解质溶液比较，有两点显著不同： (1) 非理想性 由于质点相互作用，使其性质大大偏离理想溶 由于质点相互作用， 液性质，必须以活度a代替浓度 其化学势： 代替浓度， 液性质，必须以活度 代替浓度，其化学势：
因此， 因此，对于任意强电解质 Mν Aν
电解质溶液理论和实验研究
电解质溶液理论和实验研究
电解质溶液是指含有游离离子的溶液，它们能够通过溶剂分子之间的电磁相互
作用和游离离子之间的静电作用而形成。
电解质溶液的研究涉及多种领域，包括物理学、化学、生物学等，对于电解质的电导率、浓度、温度等重要参数的测量和理解，具有重要的理论和实践应用价值。
电解质溶液理论方面，最基本的是电解质离子的动力学反应，包括离子散射、
化学反应、跟踪分子技术等。
其中离子散射研究是用来测定离子大小及其运动性质的一种方法。
光散射、中性子散射等技术可以得到离子动力学反应的基本信息。
简单来说，它可以从数据中推断出离子粒子的体积，形状和运动速率。
另外，也有很多电化学理论模型，如德拜广域离子流体动力学模型、线性响应近似、稀溶液中离子间相互作用的理论等。
电解质溶液的实验研究直接关注离子的浓度、溶液温度和电导率等性质的测量。
首先需要确定离子的组成和浓度，这可以用光谱分析、质谱分析、原子吸收光谱等方法。
其次，该溶液的电导率也可通过计算机模拟离子在水溶液中的运动来获得。
适当的电化学电导率理论模型可以帮助我们理解离子溶液的物理化学性质并预测其电导率。
除了基本理论和实验分析，电解质溶液也影响到了我们的日常生活。
例如，软
饮料制备中的矿泉水就是含有电解质的水溶液，并且作为传递电信号的体液中的离子也是电解质溶液的本质成分。
此外，电解质溶液也是重要的工业生产和科学研究领域。
总之，电解质溶液理论和实验研究对我们的生活和科技发展都发挥着重要的作用。
我们需要继续深入探索电解质溶液的各种理论和实验方法来加深我们对这些化学基础知识的理解和应用。
强电解质溶液理论简介
o
)
RT
ln(a
a
)
Bo
RT
ln(a
a
)
比较电解质化学势的表示式，有 aB a a
平均活度和平均活度系数
正负离子总是成对出现，单个离子的a+(-),不易直接测出。 定义离子平均活度（mean activity of ions）
a def (a a )1
=+
在电解质化学势的表示式中，用离子平均活度分
德拜-休克尔以强电解质稀溶液中离子间的相互作 用所形成的离子氛为出发点，并运用“离子强度”的 概念，从理论上导出强电解质稀溶液的热力学平均活 度系数与离子强度的关系，成功解释了Lewis经验公 式。极限定律的常用表示式为：
lg A | z z | I (I 0.01 mol kg1)
德拜-休克尔极限定律的修正式
别替代正、负离子的活度系数，则可用离子平均活度 求出电解质的化学势：
B
(
o
RT
ln a ) (o
RT
ln a )
(
o
RT
ln
a
)
(
o
RT
ln a )
类似的，定义
离子平均活度系数（mean activity coefficient of ions）
def ( )1
m
m
m
1/
m
+ 2
Na2SO4 : mNa 2m, mSO42 m, + 2, 1, + 3
m
m
m
1/
2m
2
m
1/
3
41/3 m
Al2 SO4 3 :
理论电化学电解质溶液理论
❖ 导电体根据导电载流子不同，分为两类： 第一类导体：导电载流子为电子或空穴的导体 第二类导体：导电载流子为正负离子的导体
❖ 电解质就是以离子作为载流子的导电体系，属于第二类导体。 ❖ 当电化学体系中，正是由于第一类导体和第二类导体的接触面上发生
电荷传递时伴随有化学反应，从而产生电化学现象。 ❖ 电解质是构成电化学体系、实现电化学反应必不可少的物质。电解质
偶极子间的相互作用的势能
1.1分子间的力
4.色散力：中性分子或离子具有瞬间的周期变化的偶极距，伴随 这种周期性变化的偶极距有一同步的电场，它使邻近的分子极 化，两者异极相邻，产生净的吸引力，色散力就是在这样的反 变作用力下产生的。特点：近程且有加和性。
5.静电作用力形成的氢键。形成氢键的物质只限于电负性很强的 原子，如O、F、N。氢键的存在不形成新的物质，但是会明显 影响物质的性质。
❖ 因此从发现电化学现象一开始，人们就致力于电解质溶液的研究和理 论的建立。
❖ 对电解质溶液的研究包括两个方面： 一.为什么电解质可以导电？为什么离解，怎样离解？ 二.描述电解质性质有哪些参数？什么因素可以影响到电解质的性质？
第一章 电解质溶液理论
第一章 电解质溶液理论
❖ 静态性质： 没有外加电场情况下电解质的性质。包括：活度、电离度、凝固点、
第一章 电解质溶液理论
1.1分子间的力
❖ 我们可以把溶液中的各种粒子归纳为一个广义的分子； ❖ 如果这个粒子的正电荷负电荷数大少相等，电荷中心重合，那么就是
电中性的，这就一个中性且没有极性的分子。
❖ 如果粒子的正负电荷相等，但中心不重合，那么这个粒子就是带有极 性的分子即一个偶极子；
＋－
❖ 如果这个粒子的正负电荷不相等，就是一个离子。
电解质溶液理论
徐亮 20910026 化学工程
电解质溶液 主要理论
离子互吸 电离理论 理论
水化作用 理论
瑞典化学家阿累尼乌斯电离学说
1887年阿累尼乌斯 1887年阿累尼乌斯(Arrhenius)提出了部分 年阿累尼乌斯(Arrhenius)提出了部分 电离学说： 电离学说： 1、在水溶液中，溶质分为电解质和非电解质 在水溶液中， 2、电解质分子在水中可程度不同的离解，成 电解质分子在水中可程度不同的离解， 为电荷不同的离子 3、根据解离程度不同，可把电解质分为强电 根据解离程度不同， 解质和弱电解质
从微观结构看，溶液中的所有离子都处于不停的热运动之 从微观结构看， 在热运动作用下，离子趋向于均匀分布。而阳、 中。在热运动作用下，离子趋向于均匀分布。而阳、阴离子间 的异性相吸、同性相斥的静电作用则使它们按一定的规则排列。 若在体系中选择任意一个离子为参考离子( 的异性相吸、同性相斥的静电作用则使它们按一定的规则排列。 若在体系中选择任意一个离子为参考离子(称为中 心离子) 心离子) 假设中心离子是阳离子，静电作用使阴离子靠近中心离子， ，假设中心离子是阳离子，静电作用使阴离子靠近中心离子， 其它阳离子将远离中心离子，而离子的热运动又促使离子在溶 其它阳离子将远离中心离子， 液中均匀分布。 液中均匀分布。 只有溶液很稀时，离子间的距离很远， 只有溶液很稀时，离子间的距离很远，静电力才小于热运 动作用力。由于中心离子对阳离子的排斥和对阴离子的吸引， 动作用力。由于中心离子对阳离子的排斥和对阴离子的吸引， 平均统计地看，距中心离子越近，阳离子出现的概率越小， 平均统计地看，距中心离子越近，阳离子出现的概率越小，阴 离子出现的概率越大，中心离子周围总的效果好象是被一层符 离子出现的概率越大， 号相反，大小相等的电荷包围着。 号相反，大小相等的电荷包围着。这层电荷所构成的球壳称为 离子氛或离子云， 离子氛或离子云，
基础化学第三章 电解质溶液
第二节 酸碱的质子理论
局限性： 把酸碱限制在水溶液中， 局限性：1, 把酸碱限制在水溶液中， 无法解释： 无法解释： 如 非水溶剂中的酸碱反应 NH3 + HCl = NH4Cl 无法解释： 无法解释：
2,把碱限制为氢氧化物 把碱限制为氢氧化物. 把碱限制为氢氧化物
NaHCO3、Na3PO4等水溶液呈碱性
第一节 强电解质溶液理论
三、强电解质溶液理论 1923年, Debye P和 年 和 Hückel E 提出电解质 1. 离子相互作用理论 (ion interaction theory) 强电解质在水中全部解离 离子间静电力相互作用（同性相斥，异性相吸） 离子间静电力相互作用（同性相斥，异性相吸） 形成离子氛
HPO42-+H2O
3−
PO43-+H3O+
K a3
[ PO 4 ][ H 3 O + ] = = 4 . 79 × 10 − 13 2− [ HPO 4 ]
第三章 电解质溶液 (Electrolytic Solution)
第一节
强电解质溶液理论
一、电解质溶液的定义及分类: 电解质溶液的定义及分类
电解质 (electrolyte) 熔融或溶液状态 下能导电的化合 物 强电解质 强酸 在水溶液中几乎 强碱 完全解离成离子 盐 弱电解质 在水溶液中只 弱酸 一元 能部分解离成 二元 弱碱 离子 三元
3.水溶液的 值 水溶液的pH值 水溶液的 定义： 定义： pH = - lg aH+ ( 稀溶液中 pH= -lg［H+］) ［ 关系： 关系：pH+pOH=14 酸性pH<7 碱性 碱性pH >7 酸性
写出下列物质的共轭酸或共轭碱， 例1 写出下列物质的共轭酸或共轭碱，并指出 其酸碱性。 其酸碱性。 HCO3- SO32 - H2PO4H2O NH2解： H2CO3 CO32- HSO3 - H3PO4 HPO42H3O+ OHNH3 同温度的HCl、 NH3 · H2O、HAc溶液 例2 同温度的 、 、 溶液 间 (pH + pOH) 相等。这句话对吗? 相等。这句话对吗 ture
无机化学-强电解质溶液
稀溶液中，f < 1； 极稀溶液中， f 接近1，活度近似等于浓度
实际粒子数是N的倍数 1.92 1.94 1.97 1.98 1.99
怎么解离？ 解离的是否彻底？
（二）活度和活度系数 电解质溶液中离子实际发挥作用的浓度称为有效浓度或活度。 浓度（c）与活度的关系为：
=fc
f 为活度系数，离子自身电荷越高，溶液的离子强度越 高，f 越小；
用 f 修正后, 得到活度 a , 它能更真实地体现溶液的行为
§1 电解质溶液理论和酸碱理论
一、强电解质溶液理论
❖ 在 1dm3 浓度为 0.1mol•dm-3 的蔗糖溶液中，能独立 发挥作用的溶质的粒子数目是 0.1mol 个。
❖ 强电解质 KCl
[KCl]/ mol•dm-3 0.10 0.05 0.01 0.005 0.001
N (KCl个数)
0.10 0.05 0.01 0.005 0.001
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
*§7.5 强电解质溶液理论简介
通过对强电解质溶液的系统研究，人们得出了两个重要的经验公式：科尔劳什经验公式和路易斯经验公式。
如何来解释这两个经验公式所展现的关系呢？因为路易斯经验公式是热力学的和静态的，理论处理相对容易，而科尔劳什经验公式是动力学的和动态的，其处理也相对复杂，因此，我们可以首先讨论路易斯经验公式并建立相关的理论，而后再处理科尔劳什经验公式。
1．德拜－休克尔离子活度理论
因为理想溶液的化学势可以表示为ln B B B RT m μμ=+，而非理想溶液的化学势可以表示为ln ln B B B B RT m RT μμγ=++，因此，当将1 mol 的电解质从理想溶液转入非理想溶液中时，需要做的功可以表示为：
Δ(,)ln 'B G T p RT W γ==- 因此，'ln B W RT
γ=-（7.11） 式（7.11）建立了活度系数与溶质转移过程中所做的有效功之间的联系。
所以，描述离子活度系数变化的关键是求算有效功。
对电解质溶液而言，显然这种有效功来源于离子由于静电吸引而导致的势能。
但由于电解质溶液的复杂性，给求解离子间的势能带领困难。
1918～1920年，高什(Ghosh)曾假设电解质溶液具有离子晶体的结构而试图求算该势能，但不成功。
直至1923年，德拜(Debye)和休克尔(Hückel)建立了“离子氛（ionic atmosphere ）”模型，才较好地解决了电解质溶液中阴阳离子间的势能问题。
如图7.9所示，由于阴阳离子间的静电吸引，如果在一个阳离子周围选取一个小的立方体空间，则在此小立方体内由于阴离子出现的几率要比正离子大，导致该小体积带部分负电荷。
从统计力学观点看，在阳离子周围存在一个球形对称的负电荷氛围，称为“离子氛”。
离子氛的总电量与中心离子电量相等。
同理，在一个阴离子周围也存在一个正电的离子氛。
也就是说，在强电解质溶液中，每一个离子都作为“中心离子”而被带有相反电荷的离子氛包围；同时，每—个离子又对构成另一个或若干个其他中心离子的离子氛作出贡献。
图7.9 离子氛示意图
德拜—休克尔借助离子氛模型，成功地把电解质溶液中众多离子之间原本纷繁复杂、难以理出头绪的相互作用简化为各中心离子与其周围离子氛的静电引力，而后通过假设1）离子为点电荷；2）离子间仅存在静电作用；3）溶液中水的介电常数不变；和4）离子氛中的电荷分布符合玻尔兹曼分布和泊松公式的前提下，德拜—休克尔导出了离子活度系数的公式
2B B ln Az I γ=- (7.20)
该式称为德拜—休克尔极限公式(limiting law)。
由于处理过程中引入一系列假设，导致该公式只能在接近无限稀释时方严格成立，因此被称为“极限”公式。
式中z B 是离子价数，I 是离子强度，A 是与温度T 及溶剂介电常数D 有关的常数。
显然，该式比式(7.19)所示的经验公式更进一步，说明了式（7.19）中的常数A ’与哪些因素有关，而且凸现了离子电荷的影响，使人们对相关实验事实有了更深刻的理解，这就是理论研究的意义所在。
式（7.20）提供了一种计算单个离子活度系数的方法。
但由于单独离子的活度系数无法直接测定，因此要验证(7.20)式是否正确，必须将其转换成离子平均活度系数的表达式。
根据γ±与γ+、γ-的关系，并考虑到电中性条件ν+z +＝ν-z -，有
22ln ln ln ()v v v Av z I Av z I
v v A z z I γγγ±++--++--+-+-=+=--=-+
即 ln A z z I γ±+-=- (7.21)
与路易斯经验公式一致。
这表明德拜－休克尔提出和离子氛模型能够反映强电解质稀溶液的客观情况，是正确，而其处理过程中引入的一些假设也都是比较合理的。
但由于点电荷等假设的不合理性，该极限公式只能适用于离子强度0.01 mol·kg -1以下的稀溶液，但对其进行修正后，可用于0.1 mol·kg -1，甚至1 mol·kg -1的溶液。
【习题18】 应用德拜—尤格尔极限公式，(1)计算25℃时0.002 mol ⋅kg -1CaCl 2和0.002 mol ⋅kg -1 ZnSO 4混合液中Zn 2+的活度系数；(2)计算25℃时0.001 mol ⋅kg -1 K 3Fe(CN)6的离子平均活度系数。
[答案：(1) 0.574，
(2)0.762]
【习题19】 25℃时，AgBrO 3的活度积为5.77⨯10-5，试用极限公式计算AgBrO 3在 (1)纯水中；(2) 0.01 mol ⋅kg -1 KBr 中的溶解度。
[答案：(1) 8.41×10-3 mol ⋅dm -3；(2)5.06⨯10-3 mol ⋅dm -3]
【习题20】 25℃时AgCl 的溶度积K sp =1.71⨯10-10，试求在饱和水溶液中，AgCl 的离子平均活度及离子平均活度系数各为多少? [答案：1.31⨯10-5，0.996]
2．德拜—休克尔尤格尔—盎萨格电导理论
受德拜－休克尔理论的启发，1927年，盎萨格(Onsager)将离子氛模型引入到有外加电场作用下的电解质溶液，试图从理论上解释科尔劳什经验公式。
盎萨格认为，首先在无限稀释时，离子间相距甚远，离子间的静电作用可以忽略，此时不存在离子氛，电解质的摩尔电导率最大，即∞
m Λ。
当电解质溶液浓度增加时，中心离子因受离子氛的影响而致使导电能力下降为Λm 。
离子氛影响中心离子迁移速率，进而影响电解质导Λm 的因素主要体现在如下两个方面：
1．弛豫力。
图7.11显示，当中心阳离子在外
加电场作用下向阴极迁移时，由于其离子氛中的
阴离子同时向相反的方向迁移从而离开离子氛的
范围内，而前方的离子又不断进入其离子氛的范
围，导致旧的离子氛不断被破坏，而新的离子氛
不断生成，这一过程称为弛豫(relaxation)过程，并
引发离子氛不对称性。
不对称离子氛对中心阳离
子产生的作用力被称为弛豫力，会阻碍中心阳离子的迁移，导致其摩尔电导率的下降。
2．电泳力。
图7.11显示，在电场作用下，当
阳离子带着水合层一起向阴极迁移时，其前方和离子氛中的阴离子也带着水合层向相反的方向迁移，因此，中心阳离子只能在阴离子形成的“水流”中逆流泳进，导致其迁移受到溶液黏滞阻力的作用，由此所产生的阻滞力被称为电泳力。
图7.11 不对称离子氛示意图
根据以上分析，昂萨格从理论上推导出，对1—1价型的电解质溶液，其摩尔电导率与浓度之间存在下述关系：
c q Λp ΛΛ][m m m ∞∞--= (7.22)
式中，p 是与溶剂介电常数、黏度以及温度有关的因子，对应于电泳力的作用；而q 是与溶剂介电常数及温度有关的因子，对应于松弛力的影响。
该公式即德拜—休克尔—盎萨格电导公式，与科尔劳什总结的式(7.7)一致，表明盎萨格引入离子氛概念处理电导率是成功的。
由于在推导公式时同样将离子作为点电荷看待，因此德拜—休克尔—盎萨格电导公式只能适用于浓度小于10-3 mol·kg -1的稀溶液，但经过校正后，其适用浓度可提高到0.1 mol·kg -1以上。
之后的理论发展，可以使电导公式适用的浓度范围提高到几个mol·kg -1。
【思考题】从独立运动的离子到离子氛，再到离子对，请说明浓度变化对离子间作用力的大小和离子导电能力的影响。
【思考题】通过建立理论模型，对研究对象进行简化处理对理论研究是十分重要，试比较高什的电解质溶液“晶体结构模型”和德拜－休克尔的“离子氛模型”两个模型，说明这两个模型的合理性及其意义。