第五章_开环伯德图
合集下载
自控 邹伯敏第05章1

0 ≤ ξ ≤ 0.707
图5-16 Mr与ζ 的关系曲线
2010-12-27 第五章 频率响应 14
自动控制理论 5. 滞后因子
e −τjω
G ( jω ) = e −τjω = 1
ϕ (ω ) = −τω
图5-17 滞后因子的相频特性
2010-12-27 第五章 频率响应 15
自动控制理论
二、开环系统的伯德图
例5-2 G ( s ) H ( s ) =
10 (1 + 0.1s ) 绘制Bode图。 s (1 + 0.5 s )
解: (1)幅频特性
G ( jω ) =
10 (1 + j
ω
10 2
) )
16
jω (1 + j
ω
2010-12-27
第五章 频率响应
自动控制理论
L (ω ) = 20 lg 10 − 20 lg ω − 20 lg 1 − ( ) 2 + 20 lg 1 + ( ) 2 2 10
图5-9
2010-12-27
1 (1 + jωT ) −的对数幅频曲线、渐近线和相角曲线
第五章 频率响应
9
自动控制理论
由于(1 + jωT )与(1 + jωT ) −1 互为倒数,则有
20 lg 1 + jωT = −20 lg arg(1 + jωT ) = − arg( 1 1 + jω T
试绘制系统的幅频和相频特性曲线。 解:令
S , jq =
10( j 2 + 1) ( j 2 + 2 + j 3)( j 2 + 2 − j 3)
BODE图的讲解

§5.6 利用开环频率特性分析系统的性能
§5.7 利用闭环频率特性分析系统的性能
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode )
Bode图介绍
(jièshào)
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode)(2)
Bode图介绍(jièshào)
横轴 按 lg 刻度,dec “十倍频程”
绘制开环系统(xìtǒng)Bode图的 步骤
⑴ 化G(j)为尾1标准型
⑵ 顺序列出转折频率
例1
G(s)
s(
40(s 0.5) 0.2)( s2 s 1)
100( s 1)
G(s)
0.5
s( s 1)(s2 s 1)
0.2
0.2 惯性环节
0.5 一阶复合微分
1 振荡环节
⑶ 确定低频特性
例1 根据(gēnjù)Bode图确定系统传递函数。
解. 依图有 G(s) K
Ts 1
30
20lg K 30 K 1020 31.6
转折频率 2 1 T T 0.5
G(s)
3.16 s 1
2
• Bode图与Nyquist图之间的对应(duìyìng)
关系: • 截止频率c:G( jc ) 1
最小转折频率之左 的特性或其延长线
基准点 ( 1, L(1) 20lg K ) 斜率 20 v dB dec
⑷ 叠加作图
一阶
二阶
惯性环节 -20dB/dec
复合微分 +20dB/dec
振荡环节 -40dB/dec
复合微分 +40dB/dec
共二十三页
0.2 惯性环节 -20
§5.7 利用闭环频率特性分析系统的性能
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode )
Bode图介绍
(jièshào)
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode)(2)
Bode图介绍(jièshào)
横轴 按 lg 刻度,dec “十倍频程”
绘制开环系统(xìtǒng)Bode图的 步骤
⑴ 化G(j)为尾1标准型
⑵ 顺序列出转折频率
例1
G(s)
s(
40(s 0.5) 0.2)( s2 s 1)
100( s 1)
G(s)
0.5
s( s 1)(s2 s 1)
0.2
0.2 惯性环节
0.5 一阶复合微分
1 振荡环节
⑶ 确定低频特性
例1 根据(gēnjù)Bode图确定系统传递函数。
解. 依图有 G(s) K
Ts 1
30
20lg K 30 K 1020 31.6
转折频率 2 1 T T 0.5
G(s)
3.16 s 1
2
• Bode图与Nyquist图之间的对应(duìyìng)
关系: • 截止频率c:G( jc ) 1
最小转折频率之左 的特性或其延长线
基准点 ( 1, L(1) 20lg K ) 斜率 20 v dB dec
⑷ 叠加作图
一阶
二阶
惯性环节 -20dB/dec
复合微分 +20dB/dec
振荡环节 -40dB/dec
复合微分 +40dB/dec
共二十三页
0.2 惯性环节 -20
自动控制原理—第五章(3)
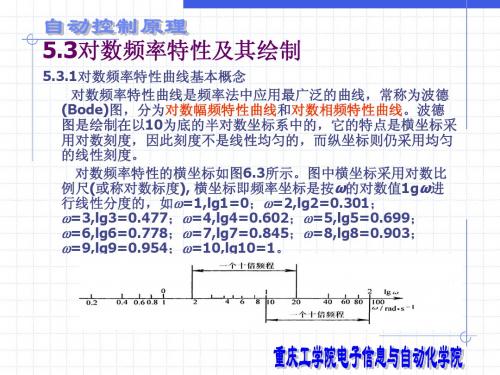
对数幅频特性曲线的纵坐标是将 A(ω)取常用对数,并乘上20倍,变成对数幅值 L() 2 0 lg G ( j ) 2 0 lg A ( ) ,单位为dB(分贝)。 由于直接标注 L()的数值,纵坐标是均匀的普通比例尺。 A()每变大十倍,L() 增加20dB。 至于对数相频特性,其横坐标与幅频特性的横坐标相同,不是均匀的线性刻度;其纵 坐标直接表示相角位移,单位为“度”(),采用普通比例尺。 对数频率特性曲线坐标系如图所示,在绘制函数关系时,相当于lgω为自变量。
2 2
幅频特性为
A ( ) 1 (1 T ) ( 2 T )
2 2 2 2
对数幅频特性为
L ( ) 20 lg A ( ) 20 lg (1 T ) ( 2 T )
2 2 2 2
1.低频段
T<<1(或<<1/T)时, L()20lg1=0dB,低频渐近线与0dB线重合。
一、比例环节 比例环节的频率特性表达式为 G(j)=K 幅频特性A(ω)= K,则比例环节的对数 幅频特性为 L() = 20lg|G(j)| = 20lgK
在对数频率特性上表现为平行于横轴的一条直线。若K=100,则 L()=20lg100=40分贝,如图6.5所示。当K>1时,该平行线位于 0dB线之上;当0<K<1时,该平行线位于0dB线之下;当K=1时, 该平行线与0dB线重合。 比例环节的相频特性仍为()=0,与无关,为相频特性图的横轴,如 图5-29所示。
在 T=1/T 附近,用渐近线得到 的对数 幅 频 特 性 存 在 较 大 误差,近似值为
L(T)=20lg1=0
而准确值为
L(T)=20lg[1/(2)]
只在=0.5时,二者相等。在 不同时,精确曲线如图5-36所 示。 当ζ<0.707时,可以明显地看 出振荡环节出现了谐振。而且 ζ越小,谐振峰值Mr越大,谐 振角频率ωr越接近于转折频率 T(无阻尼自然振荡频率三、微Βιβλιοθήκη 环节理想微分环节的频率特性为
bode图 nyquist图

系统开环Nyquist图的绘制
例1 已知系统的开环传递函数如下,试绘制系统的 开环Nyquist图。
举例说明
系统开环Nyquist图的绘制
举例说明
例2 已知系统的开环传递函数如下,试绘制系统的 开环Nyquist图,并求与实轴的交点。
Nyquist图与实轴相交时
系统开环Nyquist图的绘制
延迟环节 是不是 最小相位环节 ?
系统开环Bode图的绘制
Bode图的绘制举例
系统开环Bode图的绘制
单回路开环系统Bode图的绘制
系统开环Nyquist图的绘制
概述
K ( n s 1) ( k s 2 k k s 1)
2 2
G( s) s
v
n 1
k 1
举例说明
例3 已知系统的开环传递函数如下,试绘制系统的 开环Nyquist图。
系统开环Nyquist图的绘制
总结
0型系统(v = 0)
G ( j ) K (1 j 1 )(1 j 2 )...(1 j m ) ( j ) (1 jT1 )(1 jT2 )...(1 jTn )
n m
0
A(0) K
只包含惯性环节的0型系统Nyquist图
( 0) 0
A( ) 0
( ) ( n m ) 90
系统开环Nyquist图的绘制
总结
I型系统(v = 1)
G ( j ) K (1 j 1 )(1 j 2 )...(1 j m ) ( j ) (1 jT1 )(1 jT2 )...(1 jTn )
自动控制原理第五章

•表5-1 RC网络的幅频特性和相频特性数据
A( )
( )
0 1 0
1 0.707
45
2 0.45
5 0.196
0
63.4 78.69 90
图5-2 RC网络的幅频和相频特性
图5-3 RC网络频率特性的幅相曲线
对数频率特性图又称伯德图(Bode图),包 括对数幅频特性和对数相频特性两条曲线, 其中,幅频特性曲线可以表示一个线性系 统或环节对不同频率正弦输入信号的稳态 增益;而相频特性曲线则可以表示一个线 性系统或环节对不同频率正弦输入信号的 相位差。对数频率特性图通常绘制在半对 数坐标纸上,也称单对数坐标纸。
图5-20控制系统结构图
将系统的开环频率特性函数按典型环节划分, 可以分解为: ( j 1) ( ( j ) 2 ( j ) 1) k
m1 m2
G ( j ) H ( j )
k
2 l
2
l l
( j )
0
k 1 n1
( i s 1) ( 2 ( j ) 2 2 j j ( j ) 1) j
图5-19 Ⅱ型三阶系统幅相频率特性图
讨论更一般的情况,对于如图5-20所示的闭 环控制系统结构图,其开环传递函数为 G( s) H ( s) ,可以把系统的开环频率特性写作如 下的极坐标形式或直角坐标形式:
G( j)H ( j) G( j)H ( j) e j () P() jQ()
•图5-6积分环节频率特性的极坐标图
在伯德图上,积分环节的对数频率特性为
L( ) lg A( ) lg G( j ) lg ( ) 2
图5-7积分环节的伯德图
自动控制原理第五章第二部分
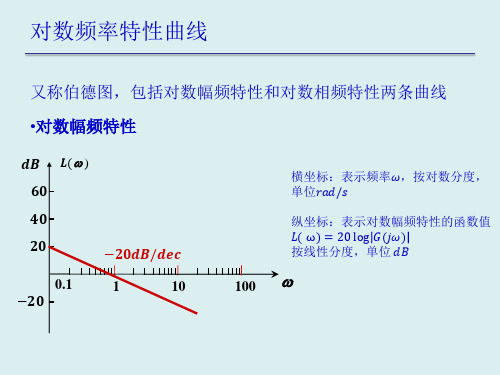
当L(w=0时:
L(w
)
20
lg
K
w
0K
wv
I型系统
斜率为-20db/dec的低频段渐近线或其延长线与横轴的 交点的频率值与开环放大系数K相等。
II型系统
斜率为-40db/dec的低频段渐近线或其延长线与横轴的 交点的频率值的平方与开环放大系数K相等。
例1:已知某最小相位系统由频率响应实验获得的对数幅 频曲线如图所示,试确定其传递函数。
3.开环对数幅频特性:
L(w)
60
40dB / dec
40
转折频率 w1 1
w2 2
w3 20
环节 惯性 一阶微分
振荡
20
60dB / dec
0
0.1
12
10 20
100 w
20
40dB / dec
40
80dB / dec
传递函数的频域实验确定
1.频率响应实验
Asinwt
L(w )
20dB / dec
0dB / dec
20
20dB / dec
0
0.1
1
20
w
40dB / dec
解: (1)确定系统积分环节的个数
低频段的渐近线为-20dB/dec 1
(2)确定系统传递函数
K ( 1 s 1)
G(s)
0.1 s(s 1)( 1
s 1)
20
L(w )
一阶微分环节 二阶微分环节
一点+一斜率确定初始段渐近线
(4)从低频渐近线开始,沿w 增大的方向,每遇到一个
转折频率改变一次渐近线斜率,直到绘出转折频率最高 的环节为止;
自动控制原理—第五章(6)

3
2 2
4 4 1
arctan
2
2 2 4 4 1
ts c
6
tan
上式表示二阶系统tsc与γ之间的关系,绘成曲线如图5—71所示。 由以上分析可知,对二阶系统,tsc与γ成反比;当γ给定后,ts与c成反比;当要求 系统具有相当的灵敏度时,c应该较大。从物理意义上解释,c越大,说明系统能 够响应的输入信号的频率越高,也就是跟踪输入信号的速度越快,系统的惯性较小, 即快速性好。由于在控制系统的实际运行中,输入的控制信号一般为低频信号,而干 扰信号(如调速系统中电网电压的波动等)一般为高频信号,c越大,说明系统对高 频干扰信号的抑制能力就越差。因此,c的取值要同时根据系统的快速性与抗高频干 扰信号的要求确定。
2.中频段的穿越频率c的选择,决定于系统瞬态响应速 度与抗干扰能力的要求,c较大可保证足够的快速性。
5.6.3开环对数幅频特性L()高频段与系统抗干扰性能的
关系
一、高频段与系统动态性能的关系
从图中可以看出,三个系统的低频段与中频段完全相同,仅高频段的衰减速度有所差别。 由于系统1在高频段的衰减速度最快,说明系统对高频信号有较强的抑制能力,对于输 入信号中的高频分量不能很好地复现,因此,其单位阶跃响应在起始阶段的上升速度相 对较慢。系统开环频率特性的高频段主要影响单位阶跃过程的起始阶段。
由以上对二阶系统与高阶系统的分析可知,如果两个同阶的系统,其γ相同, 那么它们的超调量大致是相同的,而幅值穿越频率c越大的系统,调节时 间ts越短。
根据以上分析可知,一个设计合理的系统,要以动态 性能的要求来确定中频段的形状。为保证系统具有较
好的动态性能,L()中频段应该满足以下要求:
第5章4——Bode图
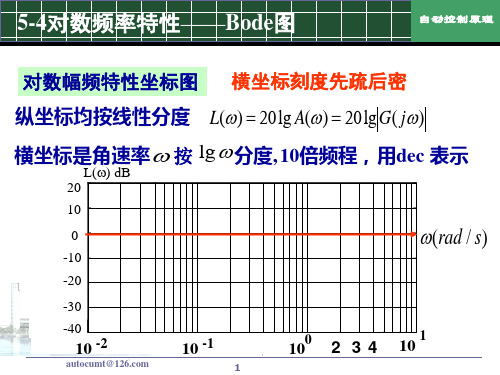
2
1 2 n
2
n
2 arc tg n 2 1 2 n
0 0 ( ) 90 n 180
autocumt@ 22
振荡环节L()
L()dB 40 20 0dB -20
(rad / s)
10 -2
10 -1
1
10
0
2 3 4
10
1
autocumt@
自动控制原理
对数分度:
lg 2 0.301
lg 3 0.4771 lg 4 2lg 2 0.602 lg 5 0.699 lg 6 lg 3 lg 2 0.778
lg 7 0.845 lg 8 3 lg 2 0.903 lg 9 2 lg 3 0.954
()º
(rad / s)
10 -2
autocumt@
10 -1
3
100
10
1
20 10 0
自动控制原理
L() dB -10
-20 -30 -40 900 450
( )
00 0 -450 -900
-1350
完 整 图 二 合 一
-1800
10 -2
autocumt@
[-20] 0.1 0.2
1
2
10 20
[-20]
100
16
5-4 对数频率特性——Bode图
(5)一次微分环节
传递函数: G(S) TS+ 1 频率特性: G ( j ) Tj 1
0 0 1 相频特性 ( ) arctanT 45 T 90
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22
10 G( j ) j (0.1 j 1)
L ( ) 40 ① ④
20
1
20
②
10
100
③
( )
0
①
③
45
②
90
④ 180
23
三、最小相位系统
1. 定义: 在系统的开环传递函数中,没有位于S右半平 面的 零点和极点,且没有纯时间延迟环节的系统为 最小相位系统,反之为非最小相位系统。 七种典型环节组成的系统必为最小相位系统。 2. 最小相位系统特征: a.在n≥m且幅频特性相同的情况下,最小相位 系统的相角变化范围最小。 这里n和m分别表示传递函数分母和分子多项式 的阶次。
2 2 2
dω
dω
ωr
1 1 2ζ 2 ωn 1 2ζ 2 T
1 0 ζ 2
式中
ωn
1 T
17
将 ωr ωn 1 2ζ 2 代入 ,不难求得 。 因此,在ω=ωr处 gω 具有最小值,亦即 G jω 此刻具 有最大值。将 ωr ωn 1 2ζ 2 代入幅频特性 G jω r 中, 得谐振峰值Mr为
0.3 0.2
( )
180 90 0
1 10T 1 T 10 T
0.7
0.3 0.2
20
8.延迟环节
幅频特性 相频特性
( )
0 100 200 300 400
1 10T
e jω T
Lω 20lgG jω 20lg1 0 dB
20
0.1 -20 -40 1 2 3 4 5 6 7 8 10
0
90
180
-60
2
6-3 典型环节的伯德图
1. 放大环节
L ( )
G(jω)=K
20
10
20 lg K
0
( )
10 0
10
100
10 100
放大环节的对数幅频特性是一条幅值为20lgK分 贝,且平行于横轴的直线,相频特性是一条和横轴重 合的直线。K>1时,20lgK>0dB;K<1时,20lgK<0dB。
即高频渐近线是一条斜率为-40dB/dec的直线。 当 ωω 1 时
n
T
L( ) 40 lg T 40 lg 1 0(dB )
1 T
说明
ω ωn
为二阶系统(振荡环节)的转折频率。
14
。10
0
0.1
0.2 0. 3
L ( )
dB
0 .7 1
10
0
0.1
1 T 1 20
2
1 T2
( )
0
G1
90
G2
180
显然,两个系统的幅频特性一样,但相频特性不同。由 图可见, 2 ω 的变化范围要比 1 ω 大得多。 G1 ( s) ——最小相位系统 G 2 ( s ) ——非最小相位系统
26
b、当ω=∞时,其相角等于-90°(n-m),对 数幅频特性曲线的斜率为–20(n–m)dB/dec。有时 用这一特性来判别该系统是否为最小相位系统。 c、对数幅频特性与相频特性之间存在确定的对 应关系。对于一个最小相位系统,我们若知道了 其幅频特性,它的相频特性也就唯一地确定了。 也就是说:只要知道其幅频特性,就能写出此最 小相位系统所对应的传递函数,而无需再画出相 频特性。 非最小相位系统高频时相角迟后大,起动性能 差,响应缓慢。对响应要求快的系统,不宜采用 非最小相位元件。
12
6. 振荡环节 对数幅频特性 对数相频特性
G jω
1 2 T 2 jω 2ζ T jω 1
Lω 20lg 1 T 2ω2 2ζ Tω
2
ຫໍສະໝຸດ 2 ω t g1
2ζ Tω 1 T 2ω2
低频段,即ωT<<1时
Lω 20lg1 0 dB =
1 T
时,是一条斜率为-20dB/dec的直线。
8
两条渐近线相交处的频率 或交接频率。
L ( )
ω
1 T
称为转折频率
dB
0
1 T
精确曲线 20
10
( )
0 45 90
9
惯性环节的相频特性 ω tg1ω T
1 当ω=0时, ω 0o,当 ω T 时, ω -45 ;当 ω趋于 无穷时, ω 趋于-90°。 采用渐近线在幅频曲线上产生的误差是可以计算 1 的。幅值的最大误差发生在转折频率 ω T 处,近似等 于3dB。 20lg 1 1 10lg2 3.01dB
o
分析表明:惯性环节具有低通特性,对低频输入能 精确地复现,而对高频输入要衰减,且产生相位迟后。 因此,它只能复现定常或缓慢变化的信号。
10
5. 一阶微分环节
G jω 1 jω T
一阶微分环节的频率特性(1+jωT) 与惯性环节的频率特性互为倒数关系,此 其对数幅频曲线和相频曲线仅差一负号。 即
4
相频与ω无关,值为-90°且平行于横轴的直线。
L ( )
20 0 0.1
( )
20
1
10
0 90
0.1
1
10
5
3. 微分环节
G jω jω
微分环节是积分环节的倒数,它们的曲 线斜率和相位移也正好相差一个负号。
L ( )
20
0
20
0.1 20
1
10
( )
L 2 ω 20lg 1 ω T2
L ( ) dB
2
20lg 1 ω T1
2
2 ω tg1ω T1 tg1ω T2
1 T2
1
0
1 T 1 20
2
( )
0
G 1
90
G2
180
25
L ( ) dB
1
0
27
M r G jωr 1 2ζ 1 ζ 2
d 2 g ω dω 2
d 2 gω 0 dω2
谐振频率ωr及谐振峰值Mr都与ζ有关。ζ越小, ωr越接近 ωn, Mr将越大。当>0.707时,r为虚数,说明不存在 谐振峰值,幅频特性单调衰减。当=0.707时,r=0, Mr=1。<0.707时,r>0,Mr>1。 0时,r n, Mr∞。谐振时,G(jω)的相角为
——低频渐近线为一条0dB的水平直线。
13
Lω 20lg 1 T 2ω2 2ζ Tω
2
2
高频段,即ωT>>1时
L ( ) 20 lg( 2T 2 ) 40 lg( T )
当ω增加10倍
L( ) 40lg10T ω 40 40lgT ω
3
2. 积分环节
1 G jω jω
1 Lω 20lgG jω 20lg 20lg dB ω jω
当ω=1时 当ω=10时
L 20lg1 0 dB ω
Lω 20lg10 20 dB
ω每增加10倍,L(ω)则衰减20dB,记为: -20dB/十倍频程,或-20dB/dec。或直接写成-20。 说明积分环节的对数幅频曲线是一条经过横轴 上ω=1这一点,且斜率为-20的直线。
20lg 1 jω T 20lg 1 ω 2 T 2
ω tg1ω T
11
L ( )
dB
20
20 0
( )
90
1 10T
1 T
10 T
45 0
1 10T
1 T
10 T
一阶微分环节高频渐近线的斜率是+20dB/dec,其 相位变化范围由0°(ω=0)经+45°至90°(ω=∞)
G jωr tg 1
ζ 1 2ζ 2 900 sin1 1 2ζ ζ
2
18
7. 二阶微分环节 G jω 1 2ζ T jω T 2 jω2 频率特性 2 2 Lω 20lg 1 T 2ω2 2ζ Tω 对数幅频特性 相频特性 2ζ Tω ω tg 1
24
例:两个系统的开环传递函数分别为(T1>T2)
G1 S 1 T2S 1 T1S G 2 S 1 T2S 1 T1S
它们的对数幅频和相频特性为
L1 ω 20lg 1 ω T2
2
20lg 1 ω T1
2
1 ω tg1ω T1 tg1ω T2
o
o
n
r
16
振荡环节的幅频 特性为
G jω
1 T ω 2ζ
2 2 2
1
Tω
1 gω
2
其中 :
gω 1 T ω
2
2 2
2ζ Tω
2
2
当出现揩振峰值时,G jω 有最大值,即 gω 有最小值。 dg ω d 得到 1 T ω 2ζ Tω 0
90
0
0.1
1
10
6
4. 惯性环节
惯性环节的幅频特性为
G jω 1 1 jω T
惯性环节的幅频特性
20 lg 1 1 20 lg 20 lg 1 2T 2 1 jT 1 2T 2
