影响我国粮食产量的因素分析
中国粮食产量影响因素分析

中国粮食产量影响因素分析摘要:粮食是人类最基本的生活消费品,粮食问题是关系到国家的国计民生的头等问题。
众所周知,农业是国民经济发展的基础,粮食是基础的基础,因此粮食生产是关系到一个国家发展与生产的一个关键的主题。
建国以来我国的粮食产量出现了多次的变动,给消费者和生产者带来了很大的影响,所以了解影响粮食生产因素很重要。
通过计量经济学方法创建我国粮食生产函数,我们会发现粮食播种、化肥施用量、受灾面积是影响粮食生产的三大因素,其中粮食播种面积的影响最大。
【关键词】粮食产量;影响因素;回归分析一、引言众所周知,粮食是我们人类生命得以延续的最基础的物质条件,没有粮食这个重要基础,人类将无法继续生存。
回顾我国粮食的生产情况,我们会发现,随着技术水平的提高,社会的发展,从整体来讲我国粮食产量呈上升的趋势。
二、中国粮食生产现状分析在改革开放(1978年)之前我国粮食产量非常缓慢增长,一直都在30000万吨以下。
改革开放后,我国粮食产量从30000万吨一路疯狂走高,粮食生产得到飞速发展,但波动也更频繁复杂。
在1997年总产量首次跨上50000万吨的大难关,达到了50453万吨,增长率为8.13%。
但在2004年开始出现了几年的连续减产的现象,曾一路降到43069万吨的局面,一下子退回到十几年前的水平,让人更加担忧。
从2004年以来的5年里,我国粮食产量连续10年增产。
在2013年粮食产量达到60193.8万吨。
改革开放以来粮食产量一直是我国最关心的问题,我国逐步改革统购统销的体制,减少定购数量,提高粮食收购价格,使粮食生产实现高速增长。
我国粮食产量从30000万吨开始一路走高。
1980—2010年这30年,我国粮食生产得到快速发展。
1978年我国农村实行改革和粮食价格提高,极大地调动了农民的积极性。
1978年中国粮食产量首次突破30000万吨,增长了7.8%。
1979年粮食产量继续增长8.9%,主要是由于国家大幅度提高粮食收购价格,粮食统购价提高20%,超购部分加价50%,从而促进粮食产量飞速增长。
我国粮食产量的影响因素分析计量经济学模型
我国粮食产量的影响因素分析一.研究背景:改革开放以来,中国经济迅速发展,人口增长迅猛,对粮食的需求日益增加。
粮食产量无疑成了影响中国经济发展的重大因素。
同时,粮食的产量直接关系到农业劳动力的生活水平,因此,“三农”问题成为中国经济研究的热点问题,提高粮食产量,关注农村居民收入迫在眉睫。
为此,本文将就粮食产量影响因素进行分析,希望从中发现一些对粮食产量关键作用的因素。
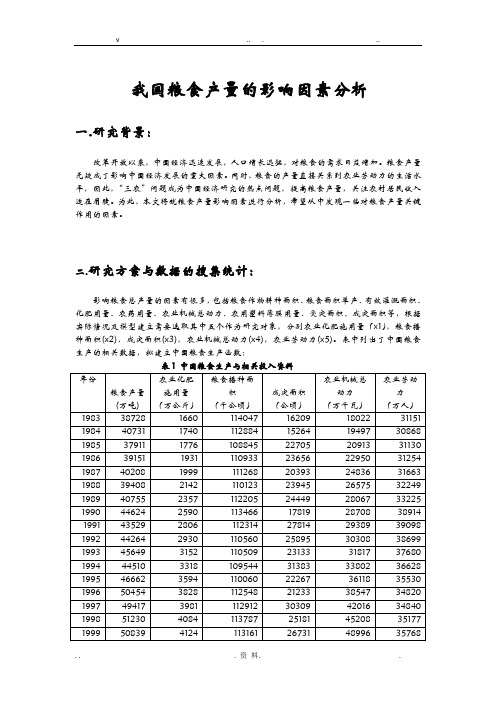
二.研究方案与数据的搜集统计:影响粮食总产量的因素有很多,包括粮食作物耕种面积、粮食面积单产、有效灌溉面积、化肥用量、农药用量、农业机械总动力、农用塑料薄膜用量、受灾面积、成灾面积等,根据实际情况及模型建立需要选取其中五个作为研究对象,分别农业化肥施用量(x1),粮食播种面积(x2),成灾面积(x3),农业机械总动力(x4),农业劳动力(x5)。
表中列出了中国粮食生产的相关数据,拟建立中国粮食生产函数:表1 中国粮食生产与相关投入资料2000 46218 4146 108463 34374 52574 36043 2001 45264 4254 106080 31793 55172 36513 2002 45706 4339 103891 27319 57930 36870 2003 43070 4412 99410 32516 60387 36546 2004 46947 4637 101606 16297 64028 35269 2005 48402 4766 104278 19966 68398 33970 2006 49804 4928 104958 24632 72522 32561 2007 50160 5108 105638 25064 76590 31444资料来源:《中国统计年鉴》(1995,2008)。
研究假设:农业化肥施用量(x1)与粮食产量正相关粮食播种面积(x2) 与粮食产量正相关成灾面积(x3) 与粮食产量负相关农业机械总动力(x4) 与粮食产量正相关农业劳动力(x5) 与粮食产量正相关三、模型的估计、检验、确认1.画散点图由于点较分散,将他们取对数,使其更集中。
中国粮食生产的综合影响因素分析

中国粮食生产的综合影响因素分析一、本文概述《中国粮食生产的综合影响因素分析》这篇文章旨在全面深入地探讨影响中国粮食生产的主要因素,以期为相关政策制定和农业可持续发展提供科学依据。
粮食生产作为国家安全和社会稳定的重要基石,其影响因素众多且复杂,包括自然资源、政策导向、科技进步、市场需求、农业生产组织方式等。
本文将从多个维度出发,系统地分析这些因素对中国粮食生产的影响机制和效果,以期揭示其内在规律和潜在问题。
在文章的结构上,本文将首先对中国粮食生产的现状进行概述,包括粮食产量、种植结构、区域布局等方面的情况。
然后,将逐一分析各影响因素对粮食生产的具体作用,包括自然资源条件、农业政策调整、科技进步与创新、市场需求变化、农业生产组织方式变革等。
在此基础上,本文将运用定性和定量相结合的研究方法,对影响因素进行综合评价,以明确各因素的作用大小和方向。
文章将提出相应的政策建议和研究展望,以期为提升中国粮食生产能力和保障国家粮食安全提供有益参考。
通过本文的研究,我们期望能够更全面地了解中国粮食生产的发展现状和面临的挑战,为制定更加科学、合理的农业政策和技术推广策略提供支撑。
本文也希望能够引起社会各界对粮食生产问题的关注和重视,共同推动中国农业的可持续发展。
二、中国粮食生产的总体状况中国,作为世界上人口最多的国家,粮食生产一直是国家安全和社会稳定的重要基石。
多年来,中国粮食生产在政策的引导、科技的推动以及农民的努力下,取得了显著的成绩。
总体上,中国粮食生产的状况呈现出稳定增长的态势,为保障国家粮食安全奠定了坚实的基础。
从产量上看,中国粮食总产量连续多年保持在较高水平,稳居世界前列。
粮食作物的播种面积和单位面积产量均有所增长,特别是科技含量较高的粮食作物,如杂交水稻、优质小麦等,其产量和品质都得到了显著提升。
同时,粮食生产的结构也在不断优化,逐步由传统的以口粮为主向多元化、优质化转变。
在粮食生产的布局上,中国形成了多个粮食主产区和优势产区,如东北平原、黄淮海平原、长江中下游平原等,这些地区的粮食生产能力强,对全国粮食总产的贡献率逐年提高。
粮食产量影响因素回归分析

粮食产量影响因素回归分析粮食产量是一个复杂的系统工程,受到多个因素的影响,包括自然因素和人为因素。
为了深入了解这些影响因素,可以运用回归分析方法对其进行量化分析。
下面将详细介绍粮食产量影响因素回归分析的步骤和应用。
回归分析是一种统计学方法,用于确定自变量与因变量之间的关系。
在粮食产量影响因素回归分析中,因变量是粮食产量,自变量则包括多个可能的因素,如天气、土壤条件、农业技术等。
首先,需要收集相关的数据,包括粮食产量的历史数据和可能的影响因素的数据。
对于年度产量数据,可以从农业统计年鉴等公开渠道获取,而对于自变量数据,可以通过相关研究或者实地调查获得。
接下来,对数据进行预处理,包括缺失值填充、异常值处理、数据标准化等。
这些步骤可以提高回归模型的准确性和可靠性。
然后,选择适当的回归模型进行分析。
根据问题的具体情况,可以选择线性回归模型、多项式回归模型、逻辑回归模型等。
线性回归模型是一种常用的回归模型,假设因变量与自变量之间存在线性关系。
而多项式回归模型可以描述因变量和自变量之间的非线性关系。
逻辑回归模型则用于因变量为分类变量的情况。
在建立回归模型后,需要对模型进行拟合和评估。
拟合是指找到最佳的回归系数,使得模型对数据的误差最小化。
评估包括解释模型的统计显著性、对模型的拟合优度进行检验等。
常用的评估指标包括R平方、调整R平方、F统计量等。
最后,根据回归模型得到的结果,可以分析各个自变量对粮食产量的影响程度和方向。
通过回归系数的正负来判断自变量对因变量的增益或减益作用。
此外,还可以进行模型的预测和验证,对未来的粮食产量进行预测,并与实际数据进行比较以验证模型的准确性。
总之,粮食产量影响因素回归分析是一种有效的量化分析方法,可以深入了解粮食产量背后的驱动因素,为农业生产提供科学指导。
这一方法在农业经济学、农业科学等领域具有广泛应用前景。
粮食产量提升的关键因素与策略分析

粮食产量提升的关键因素与策略分析随着全球人口的不断增加和经济的快速发展,粮食产量的提升成为我国农业发展的重要任务之一。
然而,在实现粮食产量提升的过程中,我们面临着许多挑战和困难。
本文将探讨粮食产量提升的关键因素,并提出相应的策略分析。
一、科技进步与创新科技进步是粮食产量大幅提升的重要因素。
在现代农业中,农业机械化、生物技术、信息技术等科技手段的应用,可以大幅度提高粮食生产效率。
例如,在种植领域,先进的农业机械可以提高耕作效率和作业质量;而在育种领域,通过遗传改良和基因工程等手段,可以培育出高产、抗病虫害的新品种。
此外,信息技术的发展也能够提供农业生产管理决策的科学依据,进一步提高粮食产量。
为了促进科技创新,在政府的引导和支持下,可以加大科研投入,培育一批具有创新能力的科技人才。
同时,建立科技成果转化机制,将科研成果快速应用到农业生产中,加快科技进步与创新在粮食产量提升中的应用。
二、农业基础设施建设农业基础设施的建设是保障粮食产量提升的另一个重要因素。
对于种植业来说,建设灌溉系统、排水系统和道路网络等基础设施,可以提高农田的水分供应和排水排涝能力,减少自然灾害对农田的影响。
对于养殖业来说,修建标准化养殖场和畜禽粪污处理设施,可以提高养殖效益和环境保护水平。
在农村基础设施建设中,政府应提供必要的资金支持,并加强规划与管理。
同时,鼓励农民参与基础设施建设,落实农民自建自管的原则,提高基础设施的建设和使用效益。
三、农业投入品供给农业投入品的供给是提高粮食产量的关键环节。
农业投入品包括种子、化肥、农药、饲料等。
其中,种子是农业生产的基础,正确选择种子品种可以提高产量和质量。
化肥和农药的合理使用能够有效地控制害虫和病害,保障农田的健康生长。
饲料的供给与养殖业发展息息相关,科学配方和高质量的饲料可以提高畜禽的生长速度和产量。
为了保障农业投入品的供给,政府可以引导农资企业加大研发投入,开发节水、高效、环保的农业投入品。
基于计量经济学分析我国粮食产量的影响因素

基于计量经济学分析我国粮食产量的影响因素粮食是人类的基本生活物资之一,粮食产量的增加直接影响着国家的粮食供应和粮食安全。
了解和研究影响我国粮食产量的因素对于保障国家粮食供应具有重要意义。
种植面积是影响粮食产量的关键因素之一。
种植面积的增加可以提高粮食产量,而减少则会导致粮食产量下降。
影响种植面积的因素包括耕地面积、农业政策和制度等。
耕地面积的扩大有助于增加种植面积,而耕地面积的减少则会限制种植面积的增长。
农业政策和制度也对种植面积有着重要的影响,例如对农民耕地保护政策的支持与限制等。
农业投入是影响粮食产量的重要因素。
农业投入包括劳动力、资本、农药、化肥等。
劳动力的增加可以提高农业生产效率,从而增加粮食产量。
资本的投入可以提高农民的种植技术和设备水平,从而提高粮食产量。
农药和化肥的使用可以防治病虫害,提高农作物的产量和质量。
气候条件是影响粮食产量的重要因素。
充足的阳光、适宜的温度和降水量都对粮食产量的增长起着至关重要的作用。
不同的粮食作物对气候条件的要求不同,不同的气候条件对各地粮食产量的影响也存在差异。
第四,技术进步是提高粮食产量的关键因素。
种植技术、农业机械和农业科技的进步可以提高粮食生产效率,从而增加粮食产量。
新品种的引进和适宜的耕作措施可以提高作物的产量和抗病虫能力。
市场需求也是影响我国粮食产量的重要因素。
市场需求对粮食价格的影响可以影响农民的粮食种植决策。
当市场需求较高时,农民倾向于增加粮食种植面积以满足市场需求,从而增加粮食产量。
我国粮食产量的影响因素与农业政策、经济发展、气候条件、农业投入、技术进步和市场需求等因素紧密相关。
深入研究和分析这些因素的作用,有助于制定合理的粮食生产政策,提高粮食产量,保障国家粮食供应和粮食安全。
基于计量经济学分析我国粮食产量的影响因素

基于计量经济学分析我国粮食产量的影响因素一、概述粮食产量作为国家经济安全和社会稳定的重要基础,历来受到广泛关注。
中国作为世界上人口最多的国家,粮食产量的稳定与增长对于保障国家粮食安全、促进经济社会持续健康发展具有重大意义。
随着全球气候变化、土地资源紧张、农业生产技术革新等多重因素的影响,我国粮食产量面临着诸多不确定性。
深入分析影响我国粮食产量的因素,对于制定科学合理的农业政策、提高粮食生产效率和保障国家粮食安全具有重要的理论价值和现实意义。
本文旨在运用计量经济学的方法,系统分析我国粮食产量的影响因素。
通过对国内外相关文献的梳理和评价,明确粮食产量影响因素的研究现状和不足。
结合我国粮食生产的实际情况,选取适当的计量经济学模型,如多元线性回归模型、面板数据模型等,对影响粮食产量的因素进行定量分析和检验。
在此基础上,深入探讨各因素对粮食产量的具体影响程度和方向,揭示各因素之间的内在联系和作用机制。
根据分析结果,提出针对性的政策建议,为我国粮食生产的可持续发展和国家粮食安全的保障提供科学依据。
通过本文的研究,期望能够为我国粮食生产领域的决策提供有益参考,同时也为计量经济学在农业经济领域的应用拓展新的思路和方法。
简述粮食产量对国家经济和社会发展的重要性粮食产量对一个国家经济和社会发展的重要性不言而喻。
粮食是人类生存的基础,是满足人民基本生活需求的必需品。
粮食产量的稳定增长是保障国家粮食安全、维护社会稳定的重要前提。
只有粮食供应充足,人民才能安居乐业,社会才能和谐稳定。
粮食产业是国民经济的重要组成部分。
粮食的种植、加工、储运、销售等环节涉及众多行业和领域,对经济增长和就业有着直接的拉动作用。
粮食产量的增加不仅意味着农业生产水平的提升,也为工业和服务业的发展提供了有力支撑。
粮食产量还是国家宏观调控的重要工具。
政府通过调整粮食生产政策、价格等手段,可以影响市场供求关系,进而调控经济运行。
在面临经济危机或通货膨胀等复杂经济环境时,粮食产量的稳定对于稳定物价、保障民生、维护国家经济安全具有重要意义。
我国粮食产量的影响因素分析
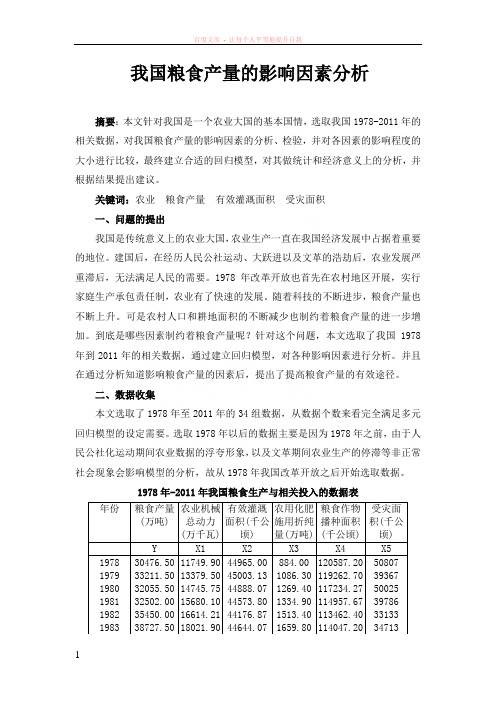
我国粮食产量的影响因素分析摘要:本文针对我国是一个农业大国的基本国情,选取我国1978-2011年的相关数据,对我国粮食产量的影响因素的分析、检验,并对各因素的影响程度的大小进行比较,最终建立合适的回归模型,对其做统计和经济意义上的分析,并根据结果提出建议。
关键词:农业粮食产量有效灌溉面积受灾面积一、问题的提出我国是传统意义上的农业大国,农业生产一直在我国经济发展中占据着重要的地位。
建国后,在经历人民公社运动、大跃进以及文革的浩劫后,农业发展严重滞后,无法满足人民的需要。
1978年改革开放也首先在农村地区开展,实行家庭生产承包责任制,农业有了快速的发展。
随着科技的不断进步,粮食产量也不断上升。
可是农村人口和耕地面积的不断减少也制约着粮食产量的进一步增加。
到底是哪些因素制约着粮食产量呢?针对这个问题,本文选取了我国1978年到2011年的相关数据,通过建立回归模型,对各种影响因素进行分析。
并且在通过分析知道影响粮食产量的因素后,提出了提高粮食产量的有效途径。
二、数据收集本文选取了1978年至2011年的34组数据,从数据个数来看完全满足多元回归模型的设定需要。
选取1978年以后的数据主要是因为1978年之前,由于人民公社化运动期间农业数据的浮夸形象,以及文革期间农业生产的停滞等非正常社会现象会影响模型的分析,故从1978年我国改革开放之后开始选取数据。
1978年-2011年我国粮食生产与相关投入的数据表年份粮食产量(万吨) 农业机械总动力(万千瓦)有效灌溉面积(千公顷)农用化肥施用折纯量(万吨)粮食作物播种面积(千公顷)受灾面积(千公顷)Y X1 X2 X3 X4 X5 1978 30476.50 11749.90 44965.00 884.00 120587.20 50807 1979 33211.50 13379.50 45003.13 1086.30 119262.70 39367 1980 32055.50 14745.75 44888.07 1269.40 117234.27 50025 1981 32502.00 15680.10 44573.80 1334.90 114957.67 39786 1982 35450.00 16614.21 44176.87 1513.40 113462.40 33133 1983 38727.50 18021.90 44644.07 1659.80 114047.20 347131984 40730.50 19497.22 44453.00 1739.80 112883.93 31887 1985 37910.80 20912.55 44035.93 1775.80 108845.13 44365 1986 39151.20 22950.00 44225.80 1930.60 110932.60 471351987 40297.70 24836.0044403.00 1999.30 111267.77420861988 39408.10 26575.00 44375.91 2141.50 110122.60 50874 1989 40754.90 28067.00 44917.20 2357.10 112204.67 46991 1990 44624.30 28707.70 47403.07 2590.30 113465.87 38474 1991 43529.30 29388.60 47822.07 2805.10 112313.60 55472 1992 44265.80 30308.40 48590.10 2930.20 110559.70 51332 1993 45648.80 31816.60 48727.90 3151.80 110508.70 48827 1994 44510.10 33802.50 48759.10 3317.90 109543.70 55046 1995 46661.80 36118.05 49281.60 3593.70 110060.40 45824 1996 50453.50 38546.90 50381.60 3827.90 112547.92 46991 1997 49417.10 42015.60 51238.50 3980.70 112912.10 53427 1998 51229.53 45207.71 52295.60 4083.69 113787.40 50145 1999 50838.58 48996.12 53158.41 4124.32 113160.98 49980 2000 46217.52 52573.61 53820.33 4146.41 108462.54 54688 2001 45263.67 55172.10 54249.39 4253.76 106080.03 52215 2002 45705.75 57929.85 54354.85 4339.39 103890.83 46946 2003 43069.53 60386.54 54014.23 4411.56 99410.37 54506 2004 46946.95 64027.91 54478.42 4636.58 101606.03 37106 2005 48402.19 68397.85 55029.34 4766.22 104278.38 38818 2006 49804.23 72522.12 55750.50 4927.69 104957.70 41091 2007 50160.28 76589.56 56518.34 5107.83 105638.36 48992 2008 52870.92 82190.41 58471.68 5239.02 106792.65 39990 2009 53082.08 87496.10 59261.45 5404.35 108985.75 47214 2010 54647.71 92780.48 60347.70 5561.68 109876.09 37426 2011 57120.85 97734.66 61681.56 5704.24 110573.02 32471三、模型设定1、分别做被解释变量(Y)与解释变量(X1、X2、X3、X4、X5)的散点图,结果如下:由散点图可知,解释变量与别解释变量间的线性关系并不明确,故对原方程两边同时取对数,建立新的回归方程3、为了方便计算,对变量进行重新定义,在eviews对话框中输入genr y=log(y)genr x1=log(x1)genr x2=log(x2)genr x3=log(x3)genr x4=log(x4)genr x5=log(x5)建立新的回归模型,结果如下图由上图可知新的多元回归模型为54321128441.0461565.1401626.0603457.0078124.0408078.2X X X X X Y -++-+-=四、模型的检验与调整(一)经济意义检验由经济分析可知,粮食产量(Y )与农业机械总动力(X1)、有效灌溉面积(X2)、农用化肥施用折纯量(X3)、粮食作物播种面积(X4)应成正相关关系,与受灾面积(X5)应成负相关关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
影响我国粮食产量的因素分析摘要:通过时1990一2012年间我国粮食产量的分析,在影响我国粮食产量的诸多原因中选出了3个主要影响因素,建立了多元线性回归模型,利用模型对粮食产量情况进行多元线性回归分析,研究了这些影响因素对粮食产量的影响与作用,最后,在此基础上提出了提高我国粮食产量的对策建议.关键词:粮食产量;影响因素;回归分析;建议一、研究意义粮食安全问题是一个关系到国计民生的重要战略问题! 它影响到经济的发展" 人民生活质量的提高和社会的稳定#尽管我国粮食总体上虽然保持了较高的自给率! 但大豆进口量近年来持续快速增长! 目前我国超过70%的大豆依赖进口! 而其中30%以上进口自美国$当前的形势提醒我们! 必须进一步加强对粮食安全问题的重视$ 而对我国这样一个人口众多的农业大国来说! 粮食供给必须首先立足于国生产$ 随着我国粮食需求日益增长! 以及城市化和工业化的加速推进! 大量资源不断流向城市! 农业可耕地面积日益萎缩! 使得粮食生产面临较为严峻的形势$ 粮食生产问题如果解决不好! 就会给我国的经济发展和社会稳定带来制约和冲击粮食是人民生存之本、经济发展之柱,对稳定社会、经济具有重要的作用。
粮食问题是一个关系到国计民生的重要战略问题,它更影响到经济的发展和社会的稳定。
中国是世界上的农业大国,同时又是一个农业相对落后的国家。
近几年世界粮食价格的大围浮动,应该引起我们的注意,大起大落更使我们重新审视起粮食生产的重要性。
同时只有抓住了影响粮食产量的主要因素,改府才能正确的做出举措来将粮食生产引向健康合理的发展路线并且实现农业的现代化。
二、文献回顾影响粮食产量的因素很多,我国学者从不同角度研究了粮食生产问题.于法稳选择有效灌溉面积、化肥施用量、农业机械总动力、粮食播种面积和受灾面积等5个指标作为影响粮食生产的因素,并采用灰色关联分析的方法对这5个因素进行了分析,指出有效灌溉面积、农机总动力和粮食播种面积是影响粮食生产的3个最主要因素;肖海峰将影响粮食综合生产能力的影响因素选择为粮食播种面积、其他物质费用、成灾面积、劳动力和化肥费用,通过柯布一道格拉斯生产函数证实了粮食播种面积是影响粮食产量最重要的因素;熊华等人应用灰色关联分析和C一D生产函数相结合的分析方法证实了化肥施用量、粮食作物播种面积和有效灌溉面积均对粮食生产具有重要影响[’〕;此外,xinagL采用粗糙集理论,建平、Yunzhang和WuY 等人运用灰色关联分析与BP神经网络相结合的方法,在对影响粮食产量的因素中又加人了农村用电量、地膜覆盖面积、水电建设投资和支农支出等因素,从多种角度验证了这些影响因素对粮食产量的重要性。
应该说前人在关于影响粮食产量的因素这个问题上做得研究已经很多而且很深,每一位学者对于影响粮食产量的因素都有自己独到的见解。
本文将各位学者认为的影响因素综合起来,采用最小二乘法进行分析,试图在综合了各位学者的研究成果后,找出更具有代表性的,更准确的影响因素。
三、理论的框架我国以往的关于粮食产量的不同计量模型,虽然结论有所差异,但细究起来,影响和制约粮食产量的主要因素为:化肥施用量(万吨);有效灌溉面积(千公顷);农村用电量(亿千瓦时);粮食作物播种面积;农用机械总动力(万千瓦);成灾面积(千公顷);水电建设投资额(万元)等。
目前我国粮食生产的影响因素日益明朗化,随着科技的发展,化肥的施用量,以及农业机械总动力的普及使用必然会对粮食的产量产生积极影响;有效灌溉面积和建设投资的增加也会使粮食产量增加;同时不能忽略自然和认为因素造成的灾情。
所以综合了前人的研究成果,选取的因变量分别为化肥施用量(万吨);有效灌溉面积(千公顷);农村用电量(亿千瓦时);粮食作物播种面积;农用机械总动力(万千瓦);成灾面积(千公顷);水电建设投资额(万元)。
通过查阅2013年的中国统计年鉴,最终搜集整理了从1990年到2012年的粮食总产量、化肥施用量(万吨);有效灌溉面积(千公顷);农村用电量(亿千瓦时);粮食作物播种面积;农用机械总动力(万千瓦);成灾面积(千公顷);水电建设投资额(万元)的数据。
数据资料其中y代表全国粮食产量(万吨),x1代表化肥施用量(万吨),x2代表有效灌溉面积(千公顷),x3代表农村用电量(亿千瓦时) ,x4代表粮食作物播种面积(千公顷),x5代表农用机械总动力(万千瓦) ,x6代表成灾面积(千公顷),x7代表水电建设投资额(万元),u代表随机误差项。
四、数据分析统计描述1.用最小二乘法对数据进行回归用OLS法估计模型,利用Stata软件回归,结果如表二所示表二Stata软件回归结果Source | SS df MS Number of obs = 22-------------+------------------------------ F( 7, 14) = 180.07 Model | 310989892 7 44427127.4 Prob> F = 0.0000 Residual | 3454029.8 14 246716.414 R-squared = 0.9890-------------+------------------------------ Adj R-squared = 0.9835 Total | 314443921 21 14973520.1 Root MSE = 496.71------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x1 | 4.390838 .8990985 4.88 0.000 2.462464 6.319213x2 | 1.096818 .5223734 2.10 0.054 -.0235615 2.217197x3 | 2.132321 .8610323 2.48 0.027 .2855907 3.979052x4 | .5264878 .0471756 11.16 0.000 .4253061 .6276695x5 | -.4503675 .1596835 -2.82 0.014 -.7928545 -.1078804x6 | -.1472115 .027 -5.45 0.000 -.2051207 -.0893024x7 | .0004409 .0004026 1.09 0.292 -.0004227 .0013044 _cons | -65129.16 17722.32 -3.67 0.002 -103139.8 -27118.56------------------------------------------------------------------------------利用Stata最小二乘估计结果如下:Y=-65129.16+4.390838x1……2.模型检验(1)经济意义检验根据结果分析,除X5外其他解释变量前的参数均通过了经济意义检验;模型中X 5代表农用机械总动力,从经济行为上来看,农用机械总动力越高,粮食产量应该越高。
显然此处存在经济意义上的矛盾,由此可以推出解释变量间存在多重共线性。
(2)统计意义检验模型的判定系数R2=0.9890,调整过的判定系数=0.9835,表明模型的整体拟合优度非常高,解释变量对被解释变量的解释程度很高,因此,可以推测模型总体线性关系成立。
但在5%的显著性水平,X2(有效灌溉面积)前参数估计值没有通过t检验,即结解释变量X2对被解释变量没有显著影响,其他6个解释变量均对被解释变量有显著影响。
(3)计量经济学检验1>多重共线性检验①检验简单相关系数X1X2X3X4X5X6X7的相关系数如下表. pwcorr x1 x2 x3 x4 x5 x6 x7| x1 x2 x3 x4 x5 x6x7-------------+---------------------------------------------------------------x1 | 1.0000x2 | 0.9765 1.0000x3 | 0.9604 0.9708 1.0000x4 | -0.3488 -0.2757 -0.3012 1.0000x5 | 0.9749 0.9902 0.9927 -0.3241 1.0000x6 | -0.3297 -0.3518 -0.4644 -0.1062 -0.4088 1.0000x7 | 0.9217 0.8681 0.9129 -0.5352 0.9096 -0.3530 1.0000由表中数据发现,X1 X2 X3 X5 X7存在高度相关性另外,也可以利用方差扩大因子法检验多重共线性. estatvifVariable | VIF 1/VIF-------------+----------------------x5 | 1030.90 0.000970x2 | 402.33 0.002486x3 | 249.84 0.004003x1 | 56.26 0.017776x7 | 35.62 0.028075x4 | 3.08 0.324680x6 | 1.97 0.506396-------------+----------------------Mean VIF | 254.29由此可以看出解释变量x5与其他解释变量存在高度的线性相关性②找出最简单的回归形式分别作Y与X1 X2 X3 X4 X5 X6 X7之间的回归:1>. regress y x1Source | SS df MS Number of obs = 23 -------------+------------------------------ F( 1, 21) = 36.92Model | 268589257 1 268589257 Prob> F = 0.0000 Residual | 152782257 21 7275345.59 R-squared = 0.6374-------------+------------------------------ Adj R-squared = 0.6202 Total | 421371515 22 19153250.7 Root MSE = 2697.3------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x1 | 3.695517 .6082159 6.08 0.000 2.430663 4.960372 _cons | 32979.17 2671.068 12.35 0.000 27424.38 38533.96------------------------------------------------------------------------------2>. regress y x2Source | SS df MS Number of obs = 23-------------+------------------------------ F( 1, 21) = 42 Model | 280904599 1 280904599 Prob> F = 0.0000 Residual | 140466916 21 6688900.75 R-squared = 0.6666-------------+------------------------------ Adj R-squared = 0.6508 Total | 421371515 22 19153250.7 Root MSE = 2586.3------------------------------------------------------------------------------y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x2 | .7884354 .1216646 6.48 0.000 .5354201 1.041451 _cons | 6383.302 6574.434 0.97 0.343 -7288.982 20055.59------------------------------------------------------------------------------3.>regress y x3Source | SS df MS Number of obs = 23-------------+------------------------------ F( 1, 21) = 38.31 Model | 272173219 1 272173219 Prob> F = 0.0000 Residual | 149198296 21 7104680.74 R-squared = 0.6459-------------+------------------------------ Adj R-squared = 0.6291 Total | 421371515 22 19153250.7 Root MSE = 2665.5------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x3 | 1.644425 .265683 6.19 0.000 1.091907 2.196943 _cons | 43227.34 1064.234 40.62 0.000 41014.14 45440.53------------------------------------------------------------------------------4.>regress y x4Source | SS df MS Number of obs = 23-------------+------------------------------ F( 1, 21) = 1.44 Model | 27116041.4 1 27116041.4 Prob> F = 0.2428 Residual | 394255473 21 18774070.2 R-squared = 0.0644-------------+------------------------------ Adj R-squared = 0.0198 Total | 421371515 22 19153250.7 Root MSE = 4332.9------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x4 | .2791902 .2323091 1.20 0.243 -.203923 .7623033 _cons | 18490.46 25273.38 0.73 0.472 -34068.42 71049.33------------------------------------------------------------------------------5.>. regress y x5Source | SS df MS Number of obs = 23-------------+------------------------------ F( 1, 21) = 35.61 Model | 265055325 1 265055325 Prob> F = 0.0000 Residual | 156316190 21 7443628.11 R-squared = 0.6290-------------+------------------------------ Adj R-squared = 0.6114 Total | 421371515 22 19153250.7 Root MSE = 2728.3------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x5 | .1483408 .0248591 5.97 0.000 .0966435 .200038 _cons | 40232.77 1551.274 25.94 0.000 37006.72 43458.82------------------------------------------------------------------------------6.>. regress y x6Source | SS df MS Number of obs = 22-------------+------------------------------ F( 1, 20) = 9.28 Model | 99672847.4 1 99672847.4 Prob> F = 0.0064 Residual | 214771074 20 10738553.7 R-squared = 0.3170-------------+------------------------------ Adj R-squared = 0.2828 Total | 314443921 21 14973520.1 Root MSE = 3277------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+----------------------------------------------------------------x6 | -.386187 .12676 -3.05 0.006 -.6506037 -.1217704 _cons | 57830.17 3177.974 18.20 0.000 51201.03 64459.31------------------------------------------------------------------------------7.>. regress y x7Source | SS df MS Number of obs = 23-------------+------------------------------ F( 1, 21) = 12.47 Model | 157018165 1 157018165 Prob> F = 0.0020 Residual | 264353349 21 12588254.7 R-squared = 0.3726-------------+------------------------------ Adj R-squared = 0.3428 Total | 421371515 22 19153250.7 Root MSE = 3548------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+---------------------------------------------------------------- x7 | .0016835 .0004767 3.53 0.002 .0006922 .0026748 _cons | 44460.4 1445.12 30.77 0.000 41455.11 47465.69------------------------------------------------------------------------------可见,粮食生产受有效灌溉面积的影响最大,因此,选1为初始的回归模型。
