第三章 刚体力学2【原子物理精品讲义】
合集下载
大学物理课件第3章-刚体
究力的平衡和静力问题。
刚体的分类总结
根据是否可以发生平动或转动， 可以将刚体分为可动刚体和固定 刚体两类。不同类型的刚体在研 究力和运动关系时具有不同的应
用场景和特点。
02
刚体的运动
平动
01
02
03
平动定义
刚体在运动过程中，其上 任意两点都保持相对位置 不变的运动。
平动特点
刚体上任意两点在运动过 程中保持相对位置不变， 刚体整体做平行移动，没 有发生旋转。
刚体的稳定性
总结词
刚体的稳定性是指刚体在外力作用下保 持原有平衡状态的能力。
VS
详细描述
刚体的稳定性是指刚体在外力作用下保持 原有平衡状态的能力。如果外力较小，刚 体能够恢复到原来的平衡状态，则称该平 衡状态是稳定的。反之，如果外力较小， 刚体不能恢复到原来的平衡状态，则称该 平衡状态是不稳定的。刚体的稳定性可以 通过对平衡状态的稳定性进行分析来确定 。
刚体的性质总结
刚体的性质包括不发生形变、具有无限大的弹性和重心位 置不变。这些性质使得刚体成为研究力和运动关系的理想 化模型。
刚体的分类
可动刚体
可动刚体是指可以发生平动或转 动的刚体。这类刚体通常用于研 究物体的运动状态和力的作用效
果。
固定刚体
固定刚体是指形状和大小始终不 变的刚体。这类刚体通常用于研
06
刚体的应用
刚体在日常生活中的应用
钟表
钟表内部的齿轮、指针等都是刚 体，其运动规律符合刚体的运动
定理。
ቤተ መጻሕፍቲ ባይዱ
交通工具
自行车、汽车、火车等交通工具中 的轮子、轴承等都是刚体，其运动 规律符合刚体的运动定理。
家居用品
家具如椅子、桌子等，其结构大多 由刚体组成，符合刚体的运动定理 。
刚体的分类总结
根据是否可以发生平动或转动， 可以将刚体分为可动刚体和固定 刚体两类。不同类型的刚体在研 究力和运动关系时具有不同的应
用场景和特点。
02
刚体的运动
平动
01
02
03
平动定义
刚体在运动过程中，其上 任意两点都保持相对位置 不变的运动。
平动特点
刚体上任意两点在运动过 程中保持相对位置不变， 刚体整体做平行移动，没 有发生旋转。
刚体的稳定性
总结词
刚体的稳定性是指刚体在外力作用下保 持原有平衡状态的能力。
VS
详细描述
刚体的稳定性是指刚体在外力作用下保持 原有平衡状态的能力。如果外力较小，刚 体能够恢复到原来的平衡状态，则称该平 衡状态是稳定的。反之，如果外力较小， 刚体不能恢复到原来的平衡状态，则称该 平衡状态是不稳定的。刚体的稳定性可以 通过对平衡状态的稳定性进行分析来确定 。
刚体的性质总结
刚体的性质包括不发生形变、具有无限大的弹性和重心位 置不变。这些性质使得刚体成为研究力和运动关系的理想 化模型。
刚体的分类
可动刚体
可动刚体是指可以发生平动或转 动的刚体。这类刚体通常用于研 究物体的运动状态和力的作用效
果。
固定刚体
固定刚体是指形状和大小始终不 变的刚体。这类刚体通常用于研
06
刚体的应用
刚体在日常生活中的应用
钟表
钟表内部的齿轮、指针等都是刚 体，其运动规律符合刚体的运动
定理。
ቤተ መጻሕፍቲ ባይዱ
交通工具
自行车、汽车、火车等交通工具中 的轮子、轴承等都是刚体，其运动 规律符合刚体的运动定理。
家居用品
家具如椅子、桌子等，其结构大多 由刚体组成，符合刚体的运动定理 。
第三章 刚体力学精品PPT课件
定 进动 角
自转 角
节线ON
0 0 2 0 2
2.欧勒运动学方程
在直角坐标系
xiyjzk
x sin sin cos
y sin cos sin
z cos
§3.4 刚体运动方程与平衡方程
1.力系的简化
力的可传性原理
力的作用线不能随意移动
共点力系的简化 平行四边形法则 共面非平行力系的简化 力的可传性原理+平行四边形法则
第三章 刚体力学
刚体也是一个理想模型，它可以看作是一 种特殊的质点组，这个质点组中任何两个质点 之间的距离不变，这使得问题大为简化，使我 们能更详细地研究它的运动性质，得到的结果 对实际问题很有用。
我们先研究刚体运动的描述，在建立动力 学方程后，着重研究平面平行运动和定点运动。
第三章 刚体力学
§3.1 刚体运动的分析 §3.2 角速度矢量 §3.3 欧勒角 §3.4 刚体运动方程与平衡方程 §3.5 转动惯量 §3.6 刚体的平动与绕固定轴的转动
ri
1 2
n
rim ivi
i 1
T1J1I
M z
0
对共面力系，有 F x0 ,F y0 ,M z0
例 p171，如图，求A处的摩擦系数。 解 是共面力系的平衡问题
Fx 0: N1 cos 900 0 f 0
Fy 0: N1 sin 900 0 N2 P 0
Mz
0:
Pl
cos0
N1
h
sin0
0
解出
f
N2
l sin 2 0 cos 0 h l sin 0 cos 2 0
1. 刚体的动量矩
§3.5 转动惯量
刚体对O点的动量矩
自转 角
节线ON
0 0 2 0 2
2.欧勒运动学方程
在直角坐标系
xiyjzk
x sin sin cos
y sin cos sin
z cos
§3.4 刚体运动方程与平衡方程
1.力系的简化
力的可传性原理
力的作用线不能随意移动
共点力系的简化 平行四边形法则 共面非平行力系的简化 力的可传性原理+平行四边形法则
第三章 刚体力学
刚体也是一个理想模型，它可以看作是一 种特殊的质点组，这个质点组中任何两个质点 之间的距离不变，这使得问题大为简化，使我 们能更详细地研究它的运动性质，得到的结果 对实际问题很有用。
我们先研究刚体运动的描述，在建立动力 学方程后，着重研究平面平行运动和定点运动。
第三章 刚体力学
§3.1 刚体运动的分析 §3.2 角速度矢量 §3.3 欧勒角 §3.4 刚体运动方程与平衡方程 §3.5 转动惯量 §3.6 刚体的平动与绕固定轴的转动
ri
1 2
n
rim ivi
i 1
T1J1I
M z
0
对共面力系，有 F x0 ,F y0 ,M z0
例 p171，如图，求A处的摩擦系数。 解 是共面力系的平衡问题
Fx 0: N1 cos 900 0 f 0
Fy 0: N1 sin 900 0 N2 P 0
Mz
0:
Pl
cos0
N1
h
sin0
0
解出
f
N2
l sin 2 0 cos 0 h l sin 0 cos 2 0
1. 刚体的动量矩
§3.5 转动惯量
刚体对O点的动量矩
第三章 刚体力学3【原子物理精品讲义】
vx vAx ( y y0 )=0 v y vAy ( x x0 )=0
xc
xo
v Ay
yc
yo
v Ax
在刚体系中：
vx vAx y=0 v y vAy x=0
xc
v Ay
yc
v Ax
上页 下页
2 ) 几何法：
根据v vA r，可以选取转动顺心 C 为基点， vA 0，v r，各点绕 C 作纯转动：v CP
约束方程
(1) (2) (3)
能量守恒可以代替上方程其中之一（可以避免约束力)
上页 下页
例P149:已知半径a、质量m的圆柱，沿倾角的斜面无滑动的滚下，
求质心沿斜面运动的加速度及约束反力的法向分量N和切向分量f
方法一、机械能守恒定律
1 2
mxC2
1 2
mk 2
2
mgxC
sin
E
mxC xC mk 2 mgxC sin 0
§3.7 刚体的平面平行运动
一、平面平行运动的运动学
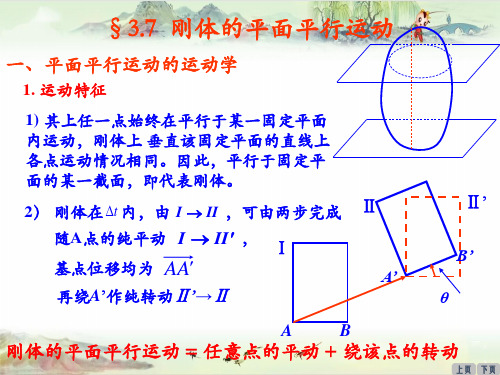
1. 运动特征
1) 其上任一点始终在平行于某一固定平面 内运动，刚体上 垂直该固定平面的直线上 各点运动情况相同。因此，平行于固定平 面的某一截面，即代表刚体。
2） 刚体在 t 内，由 I II ，可由两步完成 随A点的纯平动 I II ， Ⅰ
1 3
ml 2
fθ
x
O
A mg
约束关系：
xC yC
l cos l sin
xC yC
l sin l cos
xC yC
=l
l sin cos
l cos l sin 2
2
(4)
1 ml 2
3
大学物理课件第3章刚体力学
d dt
3
二. 刚体的定轴转动 1.力矩
力F 对o点的力矩定义为：
M=r×F 力矩的大小: M=Frsin =Fd 方向: r F 右手螺旋 注意: 对定轴转动, (1)只有 在垂直于转轴平面内的力才会 产生力矩; 平行于转轴的力是 不会产生力矩的。 (2)力矩的方向沿转轴。
2
T2
m: mg-T2= ma
a=R1= r2 , 2=2ah
求解联立方程，代入数据，可得
m mg
=2m/s, T1=50N, T2=60N。
17
例题1.6 均匀细棒(m、长l)AB可绕o轴转 动，Ao= l/3。求棒从水平位置静止开始转过 角 时的角加速度和角速度。 解 重力集中在质心，其力矩为
即一对内力的力矩的矢量和为零。 也可以从力矩大小对应于平行四边形面积的角 度来看。 两个平行四边形底和高都相等，故而面积相同； 两力矩大小相等，方向相反，于是矢量和为零。 任意质点系的合内力矩都为零。
6
三. 转动惯量
1.转动惯量的物理意义
M I F ma
质量m—物体平动惯性大小的量度。
2
1
2
t1
26
例题2.1 一质点的质量为m，位矢为： r =acos t i+bsin t j (式中a、b、 均为常量); 求质点的角动量及它所受的力矩。 z dr k 解 asinti bcostj j o dt
i x L r ( m ) mr m(acosti bsintj ) ( asinti bcostj ) 2 2 mabsin tk mabcos tk
25
第3章 刚体力学.PPT
Q ∑ Fit ri = M 外 合外力矩） （合外力矩）
∑
i
Fit ri + ∑ f it ri = β ∑ ∆ m i ri 2
i i
J = ∑∆ mi ri 2 定义：转动惯量—— 定义：转动惯量
i
注意： 是质元至转轴的垂直距离） （注意：ri 是质元至转轴的垂直距离）
则可得刚体定轴转动的 转动定律为： M 外 = Jβ
难点：角动量定理、角动量守恒及其应用 难点：角动量定理、
刚体是一种特殊 的质点系统，无论在 的质点系统， 多大外力作用下， 多大外力作用下，系 统内任意两质点间的 距离始终保持不变。 距离始终保持不变。 物体的形状、大小都 物体的形状、 不变的固体称为刚体。 不变的固体称为刚体。 刚体是可以忽略由于受力而引起的形状和 刚体是可以忽略由于受力而引起的形状和 体积的改变的理想模型 体积的改变的理想模型 演示动画 刚体的平动
演示实验 角速度矢量合成
转动物体的线速度和加速度 （1）线速度
r r r r r v =ω × R =ω ×r
v = ωR sin α = ω r
在与转轴垂直的平面上 （2）加速度 v2 an = = ω 2r r dω aτ = r = rβ dt o
α
练习：在高速旋转的微型电动机里，有一圆柱形转子 练习：在高速旋转的微型电动机里，
0
ri
∆ mi r et
v fi
上式两边同乘 ri 得： Fit ri + f it ri = ∆ m i ri 2 β
应用于所有的质元有：
r Fi
∆ mi
o
2
ri
∑F r +∑
it i i i
f it ri = β ∑ ∆ m i ri
∑
i
Fit ri + ∑ f it ri = β ∑ ∆ m i ri 2
i i
J = ∑∆ mi ri 2 定义：转动惯量—— 定义：转动惯量
i
注意： 是质元至转轴的垂直距离） （注意：ri 是质元至转轴的垂直距离）
则可得刚体定轴转动的 转动定律为： M 外 = Jβ
难点：角动量定理、角动量守恒及其应用 难点：角动量定理、
刚体是一种特殊 的质点系统，无论在 的质点系统， 多大外力作用下， 多大外力作用下，系 统内任意两质点间的 距离始终保持不变。 距离始终保持不变。 物体的形状、大小都 物体的形状、 不变的固体称为刚体。 不变的固体称为刚体。 刚体是可以忽略由于受力而引起的形状和 刚体是可以忽略由于受力而引起的形状和 体积的改变的理想模型 体积的改变的理想模型 演示动画 刚体的平动
演示实验 角速度矢量合成
转动物体的线速度和加速度 （1）线速度
r r r r r v =ω × R =ω ×r
v = ωR sin α = ω r
在与转轴垂直的平面上 （2）加速度 v2 an = = ω 2r r dω aτ = r = rβ dt o
α
练习：在高速旋转的微型电动机里，有一圆柱形转子 练习：在高速旋转的微型电动机里，
0
ri
∆ mi r et
v fi
上式两边同乘 ri 得： Fit ri + f it ri = ∆ m i ri 2 β
应用于所有的质元有：
r Fi
∆ mi
o
2
ri
∑F r +∑
it i i i
f it ri = β ∑ ∆ m i ri
第3章-刚体 大学物理课件
2020/10/29
例4. 质量为M =16 kg的实心滑轮，半径为R = 0.15 m。 一根细绳绕在滑轮上，一端挂一质量为m的物体。
求（1）由静止开始1秒钟后，物体下降的距离。（2）
绳子的张力。
解: (1) T
M
M
m
mg
m
2020/10/29
TR1MR2 a 2R
T
mgTma
T 1 Ma 2
m
NT
2
2
m2g
m2 g
a
T2
Ny
rom
Nx
mg T 1
T1
m1 a
列方程如下：
m 1g T1 m 1a
T2 m 2g m 2a
T1r
T2r
1 2
mr
2
a r
m1 g
可求解
解：在地面参考系中，选取m1 、 m2和滑轮m为研 究对象，分别运用牛顿定律和刚体定轴转动定律得。
2020/10/29
2020/10/29
（2） 由刚体的机械能守恒得：
mgl 1 J2
22
1 ml22
6
3g l
A
c
o
B
0
零势点
2020/10/29
例11. 长为 l 的均质细直杆OA，一端悬于O点铅直下
垂，如图所示。一单摆也悬于O点，摆线长也为l，摆
球质量为m。现将单摆拉到水平位置后由静止释放，
摆球在 A 处与直杆作完全弹性碰撞后恰好静止。试
转轴固定不动的转动。
2020/10/29
定轴转动的特点：
• 各质点都作圆周运动； • 各质点圆周运动的平面垂直于轴线，圆心
在轴线上； • 各质点的矢径在相同的时间内转过的角度
物理第三章刚体力学
原则上，由以上基本方程，就可以求解刚体动力 学问题，还可用动能定理或机械能守恒定律代替其 中任一个方程。
n
F (i) i
dri
0
i 1
n
动能定理：
dT
F (e) i
dri
③
i 1
对保守力系，刚体机械能守恒
T V E
④
三、刚体的平衡方程
1、平衡条件：刚体的平衡条件是受的主矢和主矩同时为
零, 若主矢 F 0 ,而主矩 M 0 则刚体有转动；若主
1、力的可传性原理 力可沿它的作用线向前或向后移动，刚体运动不因力 沿力的作用前后移动而改变。即：作用在刚体上的力 是滑移矢量，而不是自由矢量。
F F
作用于刚体的力的三要素：大小、方向和作用线
2、力系的简化 ⑴ 共点力系：采用平行四边形法则简化为一个单 力—合力 ⑵ 共面非平行力的简化： 利用力的可传性原理，将两力沿力的作用线滑 移汇集于一点，再用平行四边形法则简化为一个单 力—合力。
第三章 刚体力学
§3.1 刚体运动的分析
一、什么是刚体 特殊的质点组
Jz ri mii miri2 I
i
i
ri
i
mi
形状和大小都不发生变化(任意
两质点间的距离不发生变化) 二、研究刚体运动的方法
M
e
z
dJ z dt
Izz
d
dt
Izz
运用质点组的基本定理及守恒定律， 再考虑到刚体的特殊性加以修正。
矢 F 0，而主矩 M 0 , 则刚体有平动, 故刚体的平衡
条件为：F 0, M 0。
2、平衡方程
空间力系
F
0
Fx Fy
0 0
Fz 0
n
F (i) i
dri
0
i 1
n
动能定理：
dT
F (e) i
dri
③
i 1
对保守力系，刚体机械能守恒
T V E
④
三、刚体的平衡方程
1、平衡条件：刚体的平衡条件是受的主矢和主矩同时为
零, 若主矢 F 0 ,而主矩 M 0 则刚体有转动；若主
1、力的可传性原理 力可沿它的作用线向前或向后移动，刚体运动不因力 沿力的作用前后移动而改变。即：作用在刚体上的力 是滑移矢量，而不是自由矢量。
F F
作用于刚体的力的三要素：大小、方向和作用线
2、力系的简化 ⑴ 共点力系：采用平行四边形法则简化为一个单 力—合力 ⑵ 共面非平行力的简化： 利用力的可传性原理，将两力沿力的作用线滑 移汇集于一点，再用平行四边形法则简化为一个单 力—合力。
第三章 刚体力学
§3.1 刚体运动的分析
一、什么是刚体 特殊的质点组
Jz ri mii miri2 I
i
i
ri
i
mi
形状和大小都不发生变化(任意
两质点间的距离不发生变化) 二、研究刚体运动的方法
M
e
z
dJ z dt
Izz
d
dt
Izz
运用质点组的基本定理及守恒定律， 再考虑到刚体的特殊性加以修正。
矢 F 0，而主矩 M 0 , 则刚体有平动, 故刚体的平衡
条件为：F 0, M 0。
2、平衡方程
空间力系
F
0
Fx Fy
0 0
Fz 0
理论力学第三章 刚体力学-2
y Ay ( x xA ) 0
Ay x xC xA y y y Ax C A
x Ax y 0 ( S系中) y Ay x 0 Ay x xC ( S 系中) y y Ax C
n J o ri mii i 1
ri mi ( ri )
i 1 n
n
mi [ri ( ri )]
i 1
n J o mi [ri ( ri )] i 1
mi [ri ( ri )ri ]
②瞬心的速度为零
③瞬心可以在刚体上、也可以在刚体外。 ④对瞬心而言，刚体上任一点P的速度都垂直 于瞬心c与该点p的连线CP。
P
p
C
瞬心的求法
方法一：由刚体上任一点速度公式求。
x Ax ( y y A ) 0 A r
第三章 刚体力学
• 刚体运动方程与平衡方程 • 刚体的定轴转动 • 刚体的平面平行运动
• 刚体的定点转动
§3.3 刚体的平动与绕固定轴的转动
一、 刚体的平动 运动分析：各点运动情况相同，自由度为3。 平动
z
转动
o y
z
x
z
o x
z
y
xo y
xo y
结论可用一点（常用质心）的运动代表刚体的整 体运动，由质心运动定理(固定坐标系中)
y
r xi yj
z
S
y P S r r x
A rA
x Ax ( y y A ) y Ay ( x x A )
Ay x xC xA y y y Ax C A
x Ax y 0 ( S系中) y Ay x 0 Ay x xC ( S 系中) y y Ax C
n J o ri mii i 1
ri mi ( ri )
i 1 n
n
mi [ri ( ri )]
i 1
n J o mi [ri ( ri )] i 1
mi [ri ( ri )ri ]
②瞬心的速度为零
③瞬心可以在刚体上、也可以在刚体外。 ④对瞬心而言，刚体上任一点P的速度都垂直 于瞬心c与该点p的连线CP。
P
p
C
瞬心的求法
方法一：由刚体上任一点速度公式求。
x Ax ( y y A ) 0 A r
第三章 刚体力学
• 刚体运动方程与平衡方程 • 刚体的定轴转动 • 刚体的平面平行运动
• 刚体的定点转动
§3.3 刚体的平动与绕固定轴的转动
一、 刚体的平动 运动分析：各点运动情况相同，自由度为3。 平动
z
转动
o y
z
x
z
o x
z
y
xo y
xo y
结论可用一点（常用质心）的运动代表刚体的整 体运动，由质心运动定理(固定坐标系中)
y
r xi yj
z
S
y P S r r x
A rA
x Ax ( y y A ) y Ay ( x x A )
大学物理第三章刚体力学
第三节 定轴转动的动能定理
1. 力矩的功
dA F dl F cos dl F cos rd Frsin d Md
A Md
1 2
d
dl
r
F
dA d M M 功率为： P dt dt
2.转动动能
刚体中任一质元 mi 动能：
1 1 2 2 2 mi vi mi ri 2 2
因此，刚体的转动动能：
ri
vi
1 1 2 2 2 2 Ek mi ri mi ri 2 2
1 2 Ek J 2
3.刚体做定轴转动时的动能定理
d dA Md J d J d d t 2 1 1 2 2 A dA J d J 2 J 1 1 2 2 1 2 1 2 A J 2 J 1 2 2
刚体各质元的角量相同，线量一般不同。 对刚体的运动描述，要注意角量、线量的特点。 对于定轴转动任意一点线速度与角速度、线加速度与角加 速度的关系：
v r
at r an r 2
刚体作匀变速转动时， 0 t 有以下的运动方程： 1 2 0 0t t 2 2 2 0 2 0
定轴转动角动量定理：作定轴转动的刚体所受的对轴的的 冲量矩等于系统角动量的增量。
对于绕固定点的转动，可以做如下变化
dL M dt
t2 dL Mdt L2 L1 M t1 dt t2 是力矩在t1 到t2时间内的冲量矩。 M d t
t1
3.角动量守恒定律 ������ = 0 , ������������ = 0 , ������ = const. ������������ ������2 = ������1 ������2 ������ 2 = ������1 ������ 1 若系统合外力矩为零，则系统的角 动量守恒。 ——自然界重要的普遍规律
大学物理讲稿(第3章刚体力学)第二节
第3章 刚体力学§3.2刚体动力学一、刚体的转动动能刚体绕定轴转动时,构成刚体的所有质点的动能和,称为刚体的转动动能.设某时刻刚体绕 轴转动的角速度为,刚体中任一质元的质量为,离 轴的垂直距离为 ,则其线速率为 .该质元的动能为2222121ω∆=υ∆=∆i i i i i r m m E 将此式对所有质元求和即得整个刚体的动能2221ω∆=∆=∑∑)(ii i i k r m E E (3.9a) 轴的转动惯量为刚体对定义Z r m J i i i z ∑∆=2221ω=z k J E 则 (3.9b) 二、刚体的转动惯量转动惯量 由前面讨论可知,刚体的转动惯量∑∆=ii i z r m J 2 (3.10)也就是说,转动惯量等于刚体中每个质元的质量与这一质元到转轴的垂直距离的平方的乘积的和,而与质元的运动速度无关.与平动动能比较可知,转动惯量相当于平动时的质量.是物体在转动中惯性大小的量度.如果刚体的质量是连续分布的,需将(3.10)式的求和变为积分⎰⎰ρ−−→−=VdV r dm r J 22体积分 (3.11) 转动惯量的单位在国际单位中为千克⋅米2（kg ⋅m 2）.由转动惯量的定义式可知,刚体的转动惯量与刚体的质量、质量分布、转轴的位置有关.因此,在谈及转动惯量时,必须明确哪一刚体对哪一转轴的转动惯量. 平行轴定理 刚体对任意轴的转动惯量J,等于它对通过刚体质心且与该轴平行的轴的转动惯量J c ,加上刚体的质量与两轴距离d 的平方的乘积.即 2md J J c += (3.12) 这一关系称为平行轴定理.正交轴定理 薄板状刚体的质量均匀分布时,它对于板面内的两条正交轴的转动惯量之和,等于过这两轴的交点且垂直于板面的轴的转动惯量.现对正交轴定理简单给出证明.取板平面为坐标面,坐标轴即为三条正交轴,如图3.3所示.∑∑+==)(222i i i i i z y x m r m Jx y i i i i J J y m x m +=+=∑∑22 (3.13)例3.2试求质量为m 、长为l 的匀质细棒对通过中心且与棒垂直的轴的转动惯量.解： 22222121ml dx x dm x J l l =λ==⎰⎰-// 若将轴移到左端,利用平行轴定理则得222231411212ml ml ml l m J J =+=+=)/(' 例3.3 试求质量为m 、半径为R 的匀质圆盘对过它边缘上一点且垂直于盘面的轴的转动惯量.解该圆盘对过中心且垂直于盘面的轴的转动惯量为22040202122mR R m r rdr r J R R =ππ=σπ=⎰| 根据平行轴定理有 2222321mR mR mR J =+= 三、刚体的重力势能构成刚体的所有质点与地球组成的物体组的重力势能之和,称为刚体的重力势能.设第i 个质元的质量为i m ∆，其z 坐标为z i ,设XOY 平面为参照水平面,则z i 即该质元的高度,它和地球组成的物体组的重力势能为i i gz m ∆,刚体的重力势能为g mZ g z m gz m E c m z m Z i i i i P i i c −−−−→−∆=∆=∑∆=∑∑/)( (3.14)上式表明:在计算刚体的重力势能时,刚体的质量可看作集中于刚体的质心.因此,只要确定了刚体的质心位置,其重力势能就确定了,而与刚体的方位无关.四、力矩与转动定律力矩 与上章讨论质点角动量中力矩一样，刚体的力矩F r M ϖϖϖ⨯= (3.15)前已介绍在外力矩的作用下，刚体获得加速度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
I zz
mga
sin
（3）
上页 下页
上页 下页
J Ixzi I yz j Izzk
由 dJ M（对固定点o的动量距定理） dt
取Z分量：
dJ z dt
Mz
Mz Izz Izz =Izz
（见书139页例题1）
若已知
Mz ,
I
，可解得
zz
(t )
3. 转动动能
T
1 2
(
I
xx
2 x
I
yy
2 y
I
zz
2 z
2 I yz yz
xC yC 0
2
0,
2
必有
I yz I xz 0
即刚体重心在转轴上，且转轴为惯量主轴， 此时称刚体达到动平衡，该转轴为自由转轴， 即使消去约束，刚体还会绕它继续转动。
上页 下页
3.14 试求复摆悬点上的反作用力在水平方向的投影Rx，与竖直方向的投影Ry 。设 此摆重量mg，对转动轴的回转半径为k，转轴到摆重心距离为a，且摆无初速地自
Izx 2 I yz AB N Bx M y
Izz M z
3. 讨论：
1)上式中最后一式可解得运动规律，其余五式可解得
NAx ， NAy ，NAz， NBx ， NBy
2 ) 0 , 0时，方程组化为通常的平衡方程；
求得的N A , N B为静力反力；
上页 下页
mxc 2 myc N Ax N Bx Fix myc 2 mxc N Ay N By Fiy
0 N Az Fiz
I yz 2 Izx AB N By M x Izx 2 I yz AB N Bx M y
Izz M z
3 ) 0 , 0时，求得的N A , N B为动力反力，
与静力反力相差很大，即对轴承有附加压力， 附加压力由刚体转动时产生的惯性离心力决定；
离平衡位置为一动量距定理求解
Ry
Rx
mxC
Rx
O
x
a
myC mg Ry
I zz
mga
sin
C
mg
其中Izz mk 2 ,
y
xC a sin , yC a cos
mxC myC
2 2
myC mxC
Rx mg
Ry
（1） （2）
ai vi Ri Ri
ain
vi 2 Ri
Ri 2
2. 定轴转动微分方程
k
J Ixzi I yz j Izzk
J
x
I xx
J y I yx
I xy I yy
I I
xz yz
0 0
I I
xz yz
Jz
Izx
I yz
Izz
I zz
i
§3.6 刚体的平动与定轴转动
一、平动：
1. 运动学特征：刚体上各点的速度，加速度均相同，通常以 质心的运动来代表刚体的整体运动。
2. 运动微分方程
1) 自由刚体：取质心为代表（力系向质心简化）。 由三个独立变数可以描述
mrC
Fi
mxC myC
Fix Fiy
mzC Fiz
xC xC ( t )
2 Izxzx
2 I xyx y
)
1 2
I
zz
2 z
1 2
Izz 2
若外力是保守力 F V
则
1 2
Izz 2
V
E
机械能守恒
上页 下页
三、轴上的附加压力
1. 约束反力：轴是一种约束，轴 对刚体的作用力为约束反力；刚 体绕轴转动等价于A、B保持不动 时刚体的运动
2. 约束反力求解方程
仅有Izz Mz，不能求出约束反力
动力反力=静力反力 静力反力满足 ：
N Ax N Bx Fix 0， N Ay Niy Fiy 0
AB N By M x 0， AB N Bx M y 0
上页 下页
故
xC xC
2 yC yC 2
0 0
I yz 2 Izx 0
I yz
Izx 2
0
由于
2 0 , 必有 2
上页 下页
mxc 2 myc N Ax N Bx Fix myc 2 mxc N Ay N By Fiy
0 N Az Fiz
I yz 2 Izx AB N By M x Izx 2 I yz AB N Bx M y
Izz M z
4 ) 0, 0时不产生附加压力的充要条件：
d
由 dt
d
mi ri
= dt
mrc
Fi N A N B
dJ A
dt
AB N B
ri Fi
上页 下页
写成分量形式并简化，有:
mxc 2 myc N Ax N Bx Fix
myc 2 mxc N Ay N By Fiy
0 N Az Fiz
I yz 2 Izx AB N By M x
已知Fi ,可以解出 yC yC ( t )
zC
zC ( t
)
J 0, dJ M 不需用,可见自由刚体的平动和质心运动无区别。
dt
上页 下页
2）实际刚体作平动都受约束，则有刚体运动微分方程：
mrC Fi
M
i
0
其次还需要考虑约束方程，才能解出约束反力及运动规律。
例：汽车沿轴x平动，静止时N1=N2，刹车时加速度为xc a
求地面对汽车的作用力。
y
mxc ma f
myc
0
N1
N2
mg
N
2
l
N1l
fhc
0
z
N1 C N2
f
mg
x
上页 下页
二、定轴转动
1. 运动学特征：
1、刚体上各点均在垂直于转轴的平面内作圆周运动，平行 于z轴的直线上的各点的运动情况相同，故可用垂直于z轴的 任一截面代表刚体，仅有一变量θ。
2、 vi ri ,vi ri sini Ri