电路分析第十一章
电路分析第11章 胡翔骏

这一章不准备完全按照书上来讲!
§11-1 单个元件的功率 R、L、C单个元件所吸收的功率 → 单口的功率
一.基本概念
在关联参考方向下:
二. 电阻的功率
R
1.瞬时功率
2.平均功率
三. 电感、电容的平均功率与平均储能
1.电感元件
1.瞬时功率
A) p按正弦规律变化,变化的角频率为电压或电流角频率的两倍。 B) p可能大于零,也可能小于零, p>0 吸收功率; p <0 放出功率
堂 板
书
根据所给的条件的不同,将有以下几种解题方法。
下
页
1. u(t)和i(t)的三角函数形式
的
例
2. u(t)和i(t)的相量形式(有幅角)
子
3. u(t)和i(t)的相量形式(复数形式)
转换为2
..
复功率P =Re(U·I*)
4.只给出u(t)和i(t)中的一个,并给出单口输入阻抗(分为2种情况)
解: (2)求UOC
利用分流公式
代公式
例:
j20
10A +
•
U1
•
1 _ 4U1
a
2 ZL
b
+
+
_
_
Байду номын сангаас
+ _
省略
小结
(见黑板)
第十一章结束
2.平均功率
3. 电感的平均储能 平均储能:
4. 电容元件
对比
§11-2 单口网络的功率
1.瞬时功率 2.平均功率
令:
有: 3.复功率
为了便于用相量来进行计算,引入复功率的概念。
电路分析基础ppt第11章 耦合电感

j ( L1 L2 2 M ) I Z I jLI L
+
U
I
. . jL jL
1
jM
2
等效电感
L L1 L2 2 M
等效感抗 Z L jL
通过测量顺接串联和反接串联时的电流I ,可判别同名端。 .
第十一章 耦合电感和理想变压器
§11-1 §11-2 基本概念 耦合电感的VCR 耦合系数
电路分析基础
§11-3
§11-4
空心变压器的电路分析 反映阻抗
耦合电感的去耦等效电路
§11-5
§11-6 §11-7 §11-8
理想变压器的VCR
理想变压器的阻抗变换性质 理想变压器的实现 铁心变压器的模型
§11-2耦合电感的VCR 耦合系数 …. 电路分析基础
第十一章 耦合电感和理想变压器
§11-2耦合电感的VCR 耦合系数 …. 电路分析基础
3. 耦合系数
1 2 w L (t ) Li L (t ) 0 2 L1 L2 M 2 L 0 L1 L2 M 2 0 L1 L2 2 M
M L1 L2
M L1 L2 1
1
第十一章
耦合电感和理想变压器
电路分析基础 §11-3 空心变压器电路的分析 反映阻抗…..
二、反映阻抗法
若令
则
.. 初级自阻抗 次级自阻抗 ①
Z 11 R1 jL1 Z 22 R2 jL2 Z L jMI U Z I
11 1 2 S
+
i1
M
u1
. . L L
1
chap11 电路分析

Lb M
Lc
L2
M
耦合电感
u1
L1
di1 dt
M
di2 dt
u2
M
di1 dt
L2
di2 dt
u1
( La
Lb )
di1 dt
Lb
di2 dt
u2
Lb
di1 dt
( Lb
Lc )
di2 dt
L1 La Lb
Lab
L1
M
M (L2 M ) M L2 M
L1
M2 L2
也可将耦合电感 a、c两端相连,进行求解。
5H 6H 耦合电感
例 用去耦等效电路求图示电路的电阻两端的电压。
j12
j0
+
j16
_ 100
j4
US 1
+ _U
+ _ 100
-j8
j4
+
-j8
1 _U
解:可以利用耦合电感的附加电压源等效电路求解。 这里利用去耦等效电路求解,做出去耦等效电路
耦合电感
例 写出图示耦合电感电路的VCR
耦合电感
例 求:
1)
I1 U2
Us Us 2)求M的极限值
3)k=0.707,求i1(t)
L1 4H ,L2 4H , R 10,us (t) 26 cos(10t)
利用耦合电感相量形式的VCR进行求解 画出附加源等效后的相量模型,利用网孔法求解
电路分析基础-第11章拉普拉斯变换课件

+ am + bn
m
F(s)=H0
i=1
(s–zi)
n
j=1
(s–pj)
H0 实数常数。
zi F(s)的零点。 pj F(s)的极点。
把F(s)分解成若干简单项之和,而这些简单项可
以在拉氏变换表中找到,这种方法称为部分分式
展开法,或称为分解定理。
2. nm F(s)为假分式,用长除法,得:
(1) n=m:F (s) = A +
2 k et cos(t ) (t 0)
cosx 1 (ejx ejx ) 2
应用举例
例:11-8 求F (s) =
s2
s+3 + 2s + 5
பைடு நூலகம்
的原函数f (t)。
解:F (s)
=
s2
s+3 + 2s + 5
=
s
k1 - p1
+
s
k2 - p2
极点为 p1,2 1 j2
k1
N(s) D(s)
?
解: ℒ [t] ℒ [ t ( )d ] 0
ℒ [ (t)]
s
1 s2
4. 延迟性质
ℒ ℒ 例:11-5 求下图所示矩形脉冲的象函数。
f (t) 1
0T
t
解: f (t) (t) (t T )
F (s) 1 1 esT ss
5. 位移性质 ℒ
ℒ 例:11-6 应用位移性质求下列函数的象函数。
简 表
te-at sin(t)
1
(s a)2
F (s)
s2 2
e-atsin(t)
11.第十一章(电路的复频域)

−2sT
+e
−3sT
1 F (s) +⋅⋅⋅] = −sT 1 1− e
返 回
上 页
下 页
1 L[ f (t)] = F (s) −sT 1 1− e
T 对于本题脉冲序列 f1(t) = ε (t) −ε (t − ) 2 1 1 −sT / 2 F (s) = ( − e ) 1 s s 1 1 1 −sT / 2 1 1 ) ( − e )= ( L[ f (t)] = −sT / 2 −sT s 1+ e 1− e s s
−st
= − f (0 ) + sF(s)
若σ足够大 足够大
返 回 上 页 下 页
例 利用导数性质求下列函数的象函数
(1) f (t) = cos(ω t)的象函数
解
dsin( ωt) = ωcos(ωt) dt 1 d(sinωt) cos(ωt) = ω dt
1 d L[cosωt] = L (sin( ωt) ω dt s 1 ω = = s 2 − 0 2 2 2 ω s +ω s +ω
1 f (ξ)dξ] = F(s) s
应用微分性质
F(s) = sφ(s) − ∫ f (t)dt t =0−
0−
d t L[ f (t)] = L ∫ − f (t)dt dt 0 0
t
F(s) φ(s) = s
返 回 上 页 下 页
例 求: f (t) = tε ( t)和 (t) = t ε (t)的象函数 f
1 c+ j∞ st (1)利用公式 f (t) = 利用公式 ∫c− j∞ F(s)e ds 2πj
(2)对简单形式的 对简单形式的F(s)可以查拉氏变换表得原函数 可以查拉氏变换表得原函数 对简单形式的 可以 (3)把F(s)分解为简单项的组合 把 分解为简单项的组合
电路分析第十一章习题解答
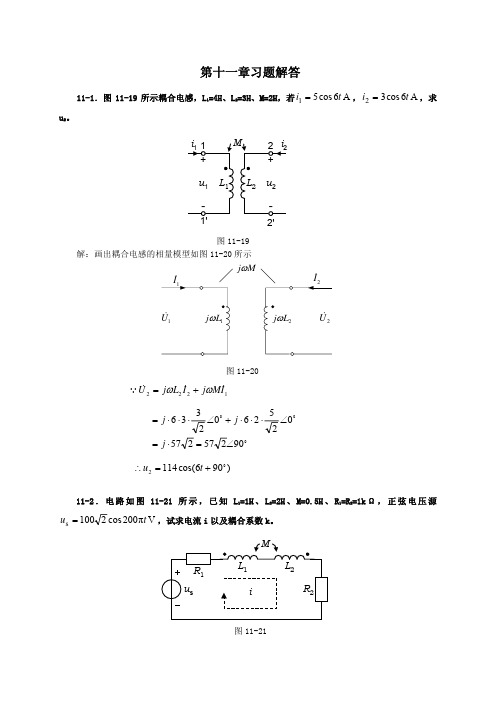
Lab = ( L + M ) + ( L + M ) //[ L + ( L − M ) //( L − M )]
= Z + M − (3 + 1) //[3 + 2 // 2] = 3 + 1 + 4 // 4 = 3 +1+ 2 = 6H
& 和输出电压 U & ,各阻抗值的单位为Ω。 11-7.求图 11-30 电路中的输入电流 I 1 2
R1
+
L1 M L2 C
& U
图 11-24 解法一:
+
& U
−
& I 1
R1 Z1
jωL1 − jωM
Z2
jωM
Z3
Z4
& I m1
jωL2 − jωM
& I 2
& I m2
Z5
−j
& I 3
1 ωC
图 11-25 由于耦合电感线圈是同侧相连,将其去耦后,等效相量模型如图 11-25 所示,列出网孔方程为
& = − jω MI & + j 0.1I & = [− j 0.05(− j10.5) + j 0.1⋅ (− j )]V QU ab 2 1
= (−0.525 + 0.1)V = −0.425V ∴ uab = −0.425cos tV
(6)左侧电感电流即 is = sin tA
& +U & = (−0.425 + 1)V = 0.575V (7)Q 电流源电压相量 = U ab s ∴ 电流源电压 = 0.575cos tV & −I & = [− j10.5 − (− j )] = − j 9.5 = 9.5∠ − 90 A (8)Q 电压源电流相量 = I 2 1
第十一章 拉谱拉斯变换20151030

∞
11.2 拉普拉斯变换的基本性质
11.2 拉普拉斯变换的基本性质
4.积分性质 f(t)
t
F(s)
L[
d dt
∫
t
0−
f (ξ ) d ξ ] = L [ f ( t )] = F ( s )
5. 延迟性质 证明:
L[ f (t − t0 )ε (t − t0 )] = F(s)e−st0
L[ ∫ f (ξ )dξ ] =
F (s) = 5s + 12 5s + 12 k k k = = 1+ 2 + 3 s ( s 2 + 5s + 6) s ( s + 2)( s + 3) s s + 2 s + 3
f (t ) = L−1 [ F ( s )] = k 1e p1t + k 2 e p 2t + L + k n e p nt = ∑ k i e pit
0−
F ( s) s
L[
对上式左边部分运用微分性质,
d dt
∫
t
0− t
f (ξ )d ξ ] = sL [ ∫ f (ξ )d ξ ] − [ ∫ f (ξ )d ξ ] t = 0 −
0− 0−
t
t
证明:
L[ f (t − t0 )ε (t − t0 )] = ∫
∞
d 由于 ∫ f (ξ ) dξ = f (t ) dt 0 − 对上式两边进行拉普拉斯变换:
11.3 拉氏反变换的部分分式展开法
11.3 拉氏反变换的部分分式展开法
方法二
F (s) =
5s + 12 N ( s) = s ( s 2 + 5s + 6) D( s)
电路分析第十一章习题参考答案
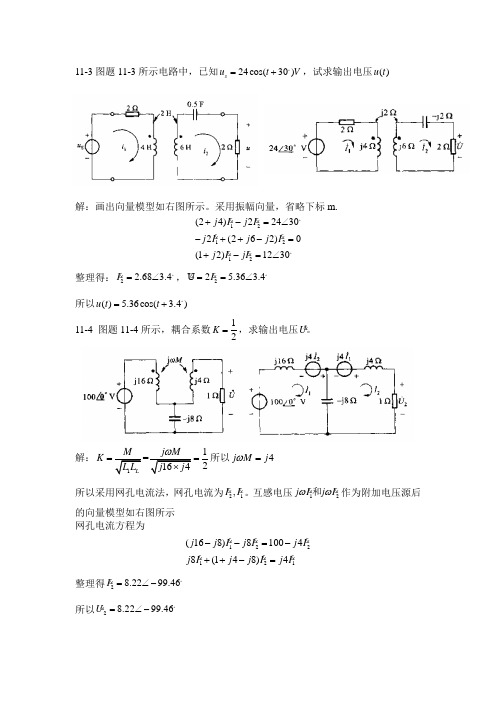
11-3图题11-3所示电路中,已知24cos(30)s u t V =+。
,试求输出电压()u t解:画出向量模型如右图所示。
采用振幅向量,省略下标m.121212(24)224302(262)0(12)1230j I j I j I j j I j I jI +-=∠-++-=+-=∠ 。
整理得:2 2.68 3.4I =∠ 。
,2U 2 5.36 3.4I ==∠ 。
所以() 5.36cos( 3.4)u t t =+。
11-4 图题11-4所示,耦合系数12K =,求输出电压U 。
解:12K ==所以4j M j ω= 所以采用网孔电流法,网孔电流为21,I I 。
互感电压12j I j I ωω 和作为附加电压源后的向量模型如右图所示网孔电流方程为122121(168)810048(148)4j j I j I j I j I j j I j I --=-++-= 整理得28.2299.46I =∠- 。
所以28.2299.46U =∠- 。
11-8电路图题11-8所示,试求对电源端的输入阻抗、电流12I I 和。
解:列网孔方程1212(24)21202(22)0j I j I j I j I +-=∠-++= 。
整理得12(22),2I j A I A =-= 所以12Z (33)22i j j =Ω=+Ω- 11-9 已知空心变压器的参数:1122L =9H,R =200,L =4H,R =1000.5.k ΩΩ=及所接负载为800Ω电阻和1F μ电容串联,所接正弦电压源频率为400rad/s, 电压有效值为300V ,内阻为500,Ω内电感为0.25H .试求传送给负载的功率P 和空心变压器的功率传输效率。
解:(1)可以画出电路如上图所示。
M=3H =做出向量模型后可以列出网孔方程为1212(500200100300)12003001200(10080016002500)0j j I j I j I j j I +++-=-+++-=整理得1271.56A 0.0596116.6A 50I I -==∠- 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
QL ω0 LI02 ,
QC
1
ω0C
I 02
0
LI
2 0
Q UI sin QL QC 0
电源不向电路输送无功。电
LC
感中的无功与电容中的无功 +
Q
大小相等,互相补偿,彼此 _ 进行能量交换。
R P
(4) 谐振时的能量关系
设 u Um cos 0t
阻抗幅频特性
阻抗相频特性
2. 电流谐振曲线
幅值关系:
I(ω)
U
| Y (ω) | U
R2
(ωL
1 ωC
)2
I( )与 |Y( )|相似。
I( )
U/R
电流谐振曲线
I( )
|Y( )|
O
0
选择性 (selectivity)
从电流谐振曲线看到,谐振时电流达到最大,当 偏 离0时,电流从最大值U/R降下来。即,串联谐振电路对
电流I达到最大值 I0=U/R (U一定)。
•
IR
+
•
U
+
•
UR
_+ • U_L
•+
_
UC_
j L
1 jω C
Z ( )
R O
|Z( )|
XL( ) X( )
0
XC( )
(2) LC上的电压大小相等,相位相反,串联总电压为零,
也称电压谐振,即
•
•
•
UL UC
0,
LC相当于短路。
UL
电源电压全部加在电阻上,UR U
不同频率的信号有不同的响应,对谐振信号最突出(表现为 电流最大),而对远离谐振频率的信号加以抑制(电流小)。 这种对不同输入信号的选择能力称为“选择性”。
通用谐振曲线 为了不同谐振回路之间进行比较,把电流谐振曲线的
横、纵坐标分别除以0和I(0),即
ω ω η , I(ω) I(ω) I(η )
性的能量交换,而不与电源进行能量交换。
(2)总能量是常量,不随时间变化,正好等于最大值。
W总
WL
WC
1 2
LIm2
1 2
CU C2m
LI02
电感、电容储能的总值与品质因数的关系:
Q
0 L R
0
LI02 RI02
2π
LI
2 0
RI02T0
2π
谐振时电路中电磁场的总储能 谐振时一周期内电路消耗的能量
串联电路实现谐振的方式:
(1) L C 不变,改变 。
0由电路本身的参数决定,一个 R L C 串联电路只 能有一个对应的0 , 当外加频率等于谐振频率时,电路
发生谐振。
(2) 电源频率不变,改变 L 或 C ( 常改变C )。
3. RLC串联电路谐振时的特点
(1).
•
U
与
I•同
相
.
入端阻抗Z为纯电阻,即Z=R。电路中阻抗值|Z|最小。
信号,求(1)调谐电容C值;(2)如输入电压为1.5V 求谐振电流和此时的电容电压。
解
ω0
1 LC
+ u
_
(1)
C
(2
1 f
)2
L
269
pF
(2)
I0
U R
1.5 10
0.15
A
UC
I0 XC
I0 C
158.5 V
1.5 V
or
UC
QU
0L
R
U
R L
C
(3) 谐振时的功率
P=UIcos=UI=RI02=U2/R,
第十一章 电路的谐振
谐振(resonance)是正弦电路在特定条件下所产生的一
种特殊物理现象,谐振现象在无线电和电工技术中得到广泛 应用,对电路中谐振现象的研究有重要的实际意义。
1. 谐振的定义
含有R、L、C的一端口电路,在特定条件下出现端口
电压、电流同相位的现象时,称电路发生了谐振。
I
R,L,C
U
Q是反映谐振回路中电磁振荡程度的量,品质因数越大, 总的能量就越大,维持一定量的振荡所消耗的能量愈小, 振荡程度就越剧烈。则振荡电路的“品质”愈好。一般讲在 要求发生谐振的回路中总希望尽可能提高Q值。
4. RLC串联谐振电路的谐振曲线和选择性
谐振曲线
物理量与频率关系的图形称谐振曲线, 研究谐振曲线可以加深对谐振现象的认识。
ω0
I (ω0 ) I0
I(ω) U / | Z |
I(ω0 ) U / R
R
R2 (ω L 1 )2
ωC
1 1 (ωL 1 )2
R ωRC
1
1
1 (ω0 L ω 1 ω0 )2 R ω0 ω0 RC ω
1 (Q ω Q ω0 )2
ω0
ω
I (η )
I0
1
1
Q2
(η
1
η
)2
(1) 阻抗的频率特性
幅频
Z
R
j(ωL
1 ωC
)
|
Z
(ω)
|
φ
(ω)
特性
| Z(ω) |
R2
(L
1
C
)2
R2 (X L XC )2
R2 X 2
(ω
)
tg
1
ωL
1
ωC
tg 1
XL XC
tg 1
X
R
R
R
相频
特性
Z ( )
|Z( )|
XL( )
( )
X( ) /2
R
O
0
XC( ) O
0
–/2
I(η ) I0
0.707
I (η )
I0
1
1
Q2
(η
1
η
)2
0
通用谐振曲线
Q=0.5
1 1 '2
Q=1 Q=10
Q越大,谐振曲线越尖。当稍微偏离谐振点时,曲线就 急剧下降,电路对非谐振频率下的电流具有较强的抑制能力, 所以选择性好。因此, Q是反映谐振电路性质的一个重要指 标。
根据声学研究,如信号功率不低于原有最大值一半, 人的听觉辨别不出,这是定义通频带的实践依据。
电路
UI Z R
发生 谐振
2. 串联谐振的条件
•
IR
+
Z
R
j(ωL
1
ωC
)
R
j( X L
XC
)
•
U
_
j L
1
R jX
jω C
当 X 0
ω0
1 LC
ω
0
L
1
0C
时,电路发生谐振。
谐振条件
谐振角频率 (resonant angular frequency)
仅与电路参数有关
f0
2π
1 LC
谐振频率 (resonant frequency)
在I / I0 1/ 2 0.707处作一水平线,与每一谐振曲线 交于两点, 对应横坐标分别为 1和2 .
ω ω2 ω1 称为通频带BW (Band Width)
则
i
Um R
cos0
t
Im cos
0t
uC
Im 0C
cos(0
t
90o )
L C
Im
sin
0t
WC
1 2
CuC2
1 2
LIm2
sin
2
0
t
电场能量
WL
1 2
Li
2
1 2
LIm2
cos2
0
t
磁场能量
表明
(1)电感和电容能量按正弦规律变化,最大值相等
WLm=WCm。L、C的电场能量和磁场能量作周期振荡
•
•
UR I
•
UC
•
UL
j
LI
j
L U R
jQU
•
UC
I j
C
j
L U R
jQU
UL UC QU
品质因数 (quality factor)
Q 0L 1 L
R RC R
特性阻抗 characteristic
impedence
当 =0L=1/(0C )>>R 时,
UL= UC >>U
例 某收音机 L=0.3mH,R=10,为收到中央电台560kHz
