习题二
计算机word考试习题2(附答案)

计算机考试word习题二(附答案)一、判断题(每小题2分,共16分,用A表示正确,B表示错误,下同)1.Word的"页面设置"中能够设置页边距、纸张类型。
(A)2.Word打印预览时,只能预览一页,不能多页同时预览。
(B) 3.在Word中可设置自动保存编辑文档时间。
(A)4.在Word中,能够利用公式计算表格中的数据。
(A)5.可用快捷键来执行打印预览。
(A)6.Word的工具栏中的按钮不可改变。
(B)7.Word中可以把文字转换成表格,但不能把表格转换成文字。
(B)8.在Word保存新文件时默认路径是MyDocuments。
(A)二、选择填空题(每小题2分,共16分)9.在工具栏中(按钮的功能是__A____。
(A)撤销上次操作(B)加粗(C)设置下划线(D)改变所选择内容的字体颜色10.在WORD的编辑状态,按先后顺序依次打开了d1.doC、d2.doC、d3.doC、d4.doc四个文档,当前的活动窗口是___D___。
(A)d1.doc的窗口(B)d2.doc的窗口(C)d3.doc的窗口(D)d4.doc的窗口11.对所编辑文档进行全部选中的快捷键是___A___。
(A)Ctrl+A(B)Ctrl+V(C)Alt+A(D)Ctrl+C12.在下列说法中,正确的是_____D______。
(A)在word编辑中不能变更文档显示的比例(B)用户只能用鼠标对Word进行操作(C)Word没有英文拼写错误的检查功能(D)Word中的表格可以平均分布行和列13.对"文本框"描述正确的是____C_______。
(A)文本框的文字排列不分横竖(B)文本框的大小不能改变(C)文本框的边框可以根据需要进行设置(D)文本框内的文字大小不能改变14.在Word主窗口的右上角、可以同时显示的按钮是____C_______。
(A)最小化、还原和最大化(B)还原、最大化和关闭(C)最小化、还原和关闭(D)还原和最大化15.在"格式"菜单下的"分栏"中,下列说法正确的是_______A____。
习题二解答
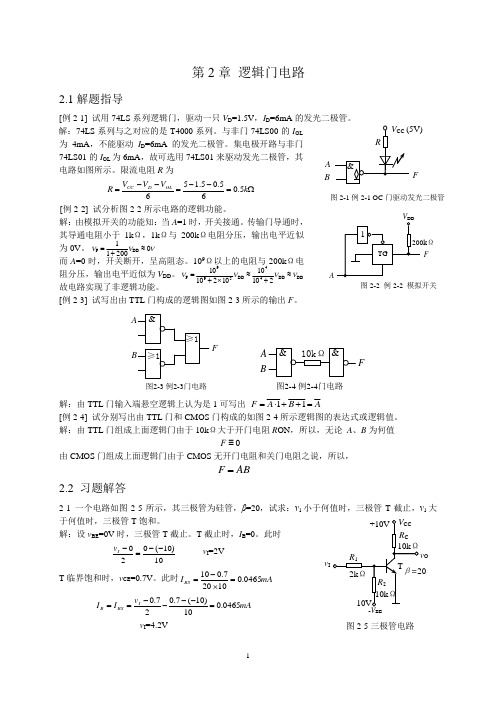
第2章 逻辑门电路2.1解题指导[例2-1] 试用74LS 系列逻辑门,驱动一只V D =1.5V ,I D =6mA 的发光二极管。
解:74LS 系列与之对应的是T4000系列。
与非门74LS00的I OL为4mA ,不能驱动I D =6mA 的发光二极管。
集电极开路与非门74LS01的I OL 为6mA ,故可选用74LS01来驱动发光二极管,其电路如图所示。
限流电阻R 为Ω=--=--=k V V V R OL D CC 5.065.05.156[例2-2] 试分析图2-2所示电路的逻辑功能。
解:由模拟开关的功能知:当A =1时,开关接通。
传输门导通时,其导通电阻小于1k Ω,1k Ω与200k Ω电阻分压,输出电平近似为0V 。
而A =0时,开关断开,呈高阻态。
109Ω以上的电阻与200k Ω电阻分压,输出电平近似为V DD 。
故电路实现了非逻辑功能。
[例2-3] 试写出由TTL 门构成的逻辑图如图2-3所示的输出F 。
&≥1F≥1A B图2-3 例2-3门电路A BF图2-4 例2-4门电路解:由TTL 门输入端悬空逻辑上认为是1可写出 [例2-4] 试分别写出由TTL 门和CMOS 门构成的如图2-4所示逻辑图的表达式或逻辑值。
解:由TTL 门组成上面逻辑门由于10k Ω大于开门电阻R ON ,所以,无论 A 、B 为何值由CMOS 门组成上面逻辑门由于CMOS 无开门电阻和关门电阻之说,所以,2.2 习题解答2-1 一个电路如图2-5所示,其三极管为硅管,β=20,试求:ν1小于何值时,三极管T 截止,ν1大于何值时,三极管T 饱和。
解:设v BE =0V 时,三极管T 截止。
T 截止时,I B =0。
此时 10)10(020--=-I v v I =2VT 临界饱和时,v CE =0.7V 。
此时mA I BS 0465.010207.010=⨯-= mA v I I I BS B 0465.010)10(7.027.0=----==v I=4.2Vv I v O BB 图2-5三极管电路A BF 图2-1例2-1 OC 门驱动发光二极管FA 图2-2 例2-2 模拟开关ΩV V 020011DD F ≈+=DD DD 44DD599F 210101021010V V V V ≈+≈⨯+=AB A F =++⋅=110≡F AB F =上述计算说明v I <2V 时,T 截止;v I >4.2V 时,T 饱和。
《随机过程及其在金融领域中的应用》习题二答案

0
sin
ux
f
xdx
0
sin
ux
f
xdx
0
0
sin
u
x
f
xdx
sin ux 0
f
x dx
0
令其中一式中的 x t
0
sin
ut
f
t
d
t
0
sin
ux
f
xdx
0
sin ut 0
证明:
X u
eiux f xdx
cos ux i sin ux f xdx
cos ux
f
xdx
i
sin
ux
f
xdx
(a)充分性:
当f
x
f
x时,sin ux
f
x
为奇函数
,
则i
c o vY Y, E Y 2 E Y 2 3 80
故(X,Y)的协方差矩阵为
cov X , X cov Y , X
1
cov X ,Y cov Y ,Y
18 0
0
3 80
4、已知二维随机变量(X,Y)服从联合正态分布,且
dFX
x
e tx f xdx
etxexdx etxdx
数学习题2

相似形71、如图,梯形ABCD两腰DA、CB的延长线交于O,已知三角形AOB的面积=4,三角形AOC的面积=9,则梯形ABCD的面积=?∴△QAD的面积也为6,故答案为:45.2、如图,直角三角形ABC中,角BAC=90度,M、N是BC边上一点,BM=MN=NC,如果AM=4,AN=3,则MN=?答:作MM1垂直AB交AB于M1,作NN1垂直BC交BC于N1,设AM1=NN1=x,MM1=CN1=y,由题可得,x^2+(2y)^2=9,y^2+(2x)^2=16,两式联立可得x^2+y^2=5,所以MN=根号53、如图,梯形ABCD被对角线分为四个小三角形,已知三角形AOB和三角形BOC的面积分别为25CM^2和35CM^2,那么,梯形的面积是=CM^2?答:=解:设AB = a 梯形的高为h,△AOB边AB上的高为h1,△DOC边CD上的高为h2,h1 = 2S(AOB)÷ AB = 50/a;h = 2S(ABC)÷ AB = 120/ah2 = h – h1 = 120/a-50/a = 70/a;S(DOC) :S(AOB) = h2²:h1²S(DOC) = 25 × (h2/h1)² = 25×49/25 = 49而S(AOD)=S(BOC)=35∴S(ABCD)=S(AOB)+S(BOC)+S(DOC)+S(AOD)=25+35+49+35 = 1444、点D、E分别在三角形ABC的边AC和BC上,角C为直角,DE平行AB,且3.DE=2.AB,AE=13,BD=9,那么,AB的长等于?DE平行于AB,且3DE=2AB;所以有:CD/CA=CE/CB=DE/AB=2/3;所以CD=2/3AC,CE=2/3BC;设AC=3X,BC=3Y;那么CD=2X,CE=2Y再由角C=90度且AE=13,BD=9有:AE^2=169=CE^2+AC^2=4Y^2+9X^2;BD^2=81=BC^2+CD^2=9Y^2+4X^2 相加得到:13(X^2+Y^2)=250;AB^2=AC^2+BC^2=9(X^2+Y^2)=9*250/13所以AB=15根号(10/13)5、在直角梯形ABCD中,上底AD=根号3,下底BC=3*根号3,与两底垂直的腰AB=6,在AB上选取一点P,使三角形PAD与三角形PBC相似,这样的点P有几个?相似形(8)1、已知,如图,在三角形ABC中,BD和CE分别是两边上的中线,并且BD=4,CE=6,则三角形ABC的面积为:答:做AG⊥BD交BD延长线于G;AG⊥BD;CE⊥BD;∴AG//CE;∵AD=CD;∴△AGD≌△CFD;∴GD=FD;AG=CF;∵AG//CE;AE=BE;∴EF是△BAG的中位线;∴BF=FG=GD+FD=2GD;; AG=2EF;BF=BD-DF=BD-GD=4-GD=;∴2GD=4-GD;GD=4/3;∵CF=AG=2EF;CE=CF+EF=3EF;∴EF=1/3CE=1/3*6=2;∴AG=2EF=4;∴S△ABC=2S△ABD=2*1/2BD*AG=2*1/2*4*4=162、如图,三角形ABC内有一点O,过O作各边的平行线,把三角形ABC分成三个三角形和三个平行四边形,若三个三角形的面积分别是1,1,2,则三角形ABC的面积是:答:分析:由题中条件易知三个三角形与△ABC均相似,又有三个三角形的面积,则再由三角形的面积比等于对应边的平方比,进而即可得出结论.解:如图,易知三个三角形与△ABC均相似,记△ABC的面积为S,则√S1/√S +√S2 /√S +√S3/√S =OR /BC +OT/ BC +PQ /BC =(OR+OT+PQ )/BC =1,故S=( √S1 + √S2 +√S3 )^2=(1+1+ √2 )^2=6+4√ 2 .故答案为:6+4√2 .3、如图,在梯形ABCD中,AB//CD且AB=2CD,O是对角线AC的中点,过点O作EF//BD 交AB、AD于点E、F,若BD=a,则EF=?答:延长EF交CD延长线于G,已知AB//CD,EF//BD,所以易知DG=BE (1)已知O是AC的中点,所以三角形OAE与OCG相似,CG:AE=OC:OA=1,即CG=AE,即CD+DG=AE ……(2),已知AB=2CD,即AE+EB=2CD……(3),由(1)、(2)、(3)得到AE:EB=3:1,推出AE:AB=3:4,又因为EF:BD=AE:AB,且BD=24,所以EF=18。
最新侵权责任法习题(二)

侵权责任法习题二1、甲将数箱蜜蜂放在自家院中槐树下采蜜。
在乙家帮忙筹办婚宴的丙在帮乙喂猪时忘记按照乙的嘱咐关猪圈,猪冲入甲家院内,撞翻蜂箱,使来甲家串门的丁被蛰伤,经住院治疗后痊愈。
下列说法正确的是()A.丁可请求甲进行侵权损害赔偿B.丁可请求乙进行侵权损害赔偿C. 丁可请求丙进行侵权损害赔偿D. 丁可请求乙、丙共同进行侵权损害赔偿【答案】ABCD【解析】《人身损害赔偿解释》第13条规定:“为他人无偿提供劳务的帮工人,在从事帮工活动中致人损害的,被帮工人应当承担赔偿责任。
被帮工人明确拒绝帮工的,不承担赔偿责任。
帮工人存在故意或者重大过失,赔偿权利人请求帮工人和被帮工人承担连带责任的,人民法院应予支持。
”《侵权责任法》第83条规定:“因第三人的过错致使动物造成他人损害的,被侵权人可以向动物饲养人或者管理人请求赔偿,也可以向第三人请求赔偿。
动物饲养人或者管理人赔偿后,有权向第三人追偿。
”基于《侵权责任法》的规定,本题中丁也有权向甲请求赔偿。
2、某电视演员因一儿童电视剧而出名,某公司未经该演员许可将印有其表演形象的宣传海报大量用于玩具、书包、文具等儿童产品的包装和装潢上。
对该公司的行为应如何定性?A.侵犯了制片者的发表权B.侵犯了该演员的表演者权C.侵犯了该演员的肖像权D.侵犯了该演员的复制权【答案】C【解析】《著作权法》第15条第1款规定:“电影作品和以类似摄制电影的方法创作的作品的著作权由制片者享有,但编剧、导演、摄影、作词、作曲等作者享有署名权,并有权按照与制片者签订的合同获得报酬。
”本题中该演员的表演形象除署名权属于该演员外,发表权、复制权等著作权属于制片者。
该演员由于电视剧出名,意味着电视剧已经发表,因此不存在侵害发表权的问题,A错误。
复制权属于制片者,而不是该演员,所以D错误。
该演员对于自己的表演形象享有肖像权,不经其同意,不能为营利目的使用,该公司擅自使用该演员表演形象的行为侵害了该演员的肖像权,所以C正确。
概率论与数理统计习题解答 (2)

x<0 0 ≤ x <1 x ≥1
1/ 2
P{ X < 1 / 2} = P{X > 3 / 2} =
−∞ ∞
∫ f ( x)dx = ∫ 2 xdx =1/ 4 或 P{X < 1/ 2} = F (1/ 2) = 1/ 4
0
1/ 2
3/ 2
∫
∞
f ( x)dx =
3/ 2
∫ 0dx = 0
或
P{X > 3 / 2} = 1 − P{X ≤ 3 / 2} = 1 − F (3 / 2) = 1 − 1 = 0
x<0 0 ≤ x <1 x ≥1
求
(1)常数 A
(2)概率密度函数
(3) P{X < 1 / 2} ; P{X > 3 / 2} ;
P{0 ≤ X ≤ 2} 。
解法一:由于连续型随机变量 X 的分布函数是连续的
⎧0 ⎪ ∴ 1 = F( 1 ) = lim F ( x) = lim Ax = A f ( x) = F ' ( X ) = ⎨ 2 x x⎯ ⎯→ 1 x⎯ ⎯→ 1 ⎪0 ⎩
+∞
所以一年中该地区受台风袭击次数为 3~5 的概率为 0.547027 11、有 10 台机床,每台发生故障的概率为 0.08, 而 10 台机床工作独立,每台 故障只需一个维修工人排除。问至少要配备几个维修工人,才能保证有故障而 不能及时排除的概率不大于 5%。 解:随机变量 X 示发生故障的机床的台数则 设配备 n 个维修工人 (0 ≤ n < 10) 则“有故障而不能及时排除”事件为
−1 r k −r (2) P{X = k } = Ckr − , k = r , r + 1,...... 1 p (1 − p )
习题二及答案
习 题 二2-1 何为等效变换?两电路等效需要满足什么条件?答:用一个较为简单的电路替代原电路,从而使分析的问题得以简化,这就是电路的等效变换。
两电路等效需要满足的条件是:电路对外的伏安特性不变。
2-2 设计一个电阻衰减器,如图2-62所示,衰减器的输入电压为10V ,而输出电压分别为10V 、5V 及1V ,电阻中流过的电流为2mA ,试求R 1、R 2及R 3的值。
10V5V1V图2-62解:R 1=(10-5)/2=2.5K Ω;R 2=(5-1)/2=2K Ω;R 3=1/2=0.5K Ω; 2-3 求图2-63电路中等效电阻Rab 。
b习题2-63解:Rab =4//(2+4//4)=2Ω2-4 求图2-64电路中等效电阻R ab 。
3Ω3Ωba解:R ab =(6//3+6//3)//4=2Ω 2-5 求图2-65电路中等效电阻R ab 。
ba图2-65解:R ab =3//3//3=1Ω2-6 求图2-66电路中①S 打开;②S 闭合时等效电阻R ab 。
36Ω24ΩbaS图2-66解:S 打开:R ab =0.5*(36+24)=30Ω S 闭合:R ab =36/2+24/2=30Ω2-7 图2-67中,试求:①R=0时的电流I ;②I=0时的电阻R ;③R =∞时的电流I 。
3Ω4Ω图2-67解:① I 总=6/((3*6)/(3+6))=3A ,∴I =(6/(3+6))* I 总=2A; ② 3/6=4/R ,∴R=8Ω③ I 总=6/(4+3*6/(3+6))=1A ,I=-(3/(3+6))* I 总=-1/3A 2-8 电路如图2-68所示,已知30Ω电阻中电流为0.2A ,试求此电路的总电压U 和总电流I 。
60Ω图2-68解:I=(0.2+30*0.2/60)+ (0.2+30*0.2/60)*(10+60*30/(60+30))/15=0.9AU=0.9*10+(0.2+30*0.2/60)*(10+60*30/(60+30))=18V2-9 将图2-69所示电路中星形与三角形网络进行等效变换。
习题2_软件测试基本技术(静态分析)练习-讲解版
习题二软件测试基本技术(静态分析)1.在代码检查过程中,发现大部分错误的人通常是()。
A.程序员B.测试员C.审查者D.架构师2.桌面检查(Desk Checking)是一种()的检查方法。
A.程序员自己检查自己编写的程序B.有同行帮忙检查自己编写的程序C.几个同行自行组成小组,以小组为单位检查编写的程序D.程序员在桌子上检查编写程序的活动3.下列选项中,不属于桌上检查的检查项目是()。
A.等价性检查B.检查子程序、宏、函数C.功能检查D.风格检查4.下列选项中,不属于静态错误分析的是()。
A.类型和单位分析B.功能分析C.引用分析D.表达式分析5.在代码检查的准备阶段和检查会议阶段都据有发现产品错误责任的是()。
A.检查人员B.开发人员C.协调人员D.讲解员6.下列检查项目中不属于风格检查的是()。
A.编程标准B.变量命名C.结构化程序设计D.命名规则7.下列叙述中,说法正确的是()。
A.桌上检查的文档是最后要公开的文档B.桌上检查是一个完全没有约束的过程,所以通常效率会比较低。
C.代码检查是程序员自己检查自己的程序D.桌上检查最好由程序的编写人员来完成8.在对程序代码进行静态分析时,要生成各种引用表,这些引用表按功能可分为()。
A.为用户提供辅助信息的B.直接从表中查出说明/使用错误C.用来做错误预测和程序复杂性计算D.以上全部9.下列引用表是为用户提供辅助信息的是()。
A.函数引用表B.变量交叉引用表C.循环层次表D.操作符统计表10.在代码检查中,负责提供关于检查项目的资料并回答检查人员问题的角色是()。
A.协调员B.开发人员C.检查人员D.讲解员11.走查的主要目标有()。
○1发现缺陷、遗漏和矛盾的地方○2改进产品○3考虑可替换的实现方法A.○1和○2B.○1和○3C.○2和○3D.○1、○2和○312.通常走查小组中,程序编写者占()个。
A.0 B.1C. 2 D.不确定13.走查程序中的静态分析技术用到调用图,通过调用图我们不可以做的是()。
习题二
1. 静止点电荷所带电量为-6Q ,它在空间激发电场,其场强可表示为 。
解:r r Q E ˆ2320πε-=2. 在XOY 平面上有两个点电荷,分别带电量4q 、q ,位于原点及点(a ,0)处,如图所示,则场强为零的点是 。
解:)0,32(a3. 如图,一质量为6101-⨯千克的小球,带电量为11102-⨯库仑,悬于一细线的下端。
线与一块垂直放置的很大的带电平面成30°角。
则此带电平面的电荷面密度为 。
解:5×10-6库/米24.场强迭加原理是指:。
解:空间某点的场强,等于各点电荷单独存在时在该点场强的矢量和。
5. 一根细玻璃棒弯成半径R 为的41圆周,均匀地带有正电荷+q,则中心O 处场强的大小是,方向是 。
解:022R q επ;沿与X 轴成45°方向。
6.真空中有两平行平板AB ,电荷均匀分布,电量分别为±8.89×10-4C ,每板面积为5.02m ,相距4.0mm ,则每板单位面积受的静电力为 。
解:1.78×103N7.离点电荷0.6米处的场强是1牛顿/库仑,则这电荷的电量是 库仑。
解:4×10-118. 两块均匀带电的无限大薄板互相垂直,面电荷密度分别为+σ和-σ,则空间的电场强度大小为 。
解:022εσ9. 能够作为试探电荷的是: ( )(A)电量很小的电荷; (B)体积很小的电荷;(C)点电荷; (D)带电量和线度都足够小的带电体。
解:D10. 一个带正电的质点,在电场中从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点的速率是递减的,下图中关于C 点场强方向正确的画法是: ( )解:B11. 半径为R 、电荷线密度为λ的半圆弧,在其圆心处产生的场强大小为: ( )(A );40R πελ (B );20R πελ (C );420R πελ (D );20R ελ 解:B12. 在电场强度定义式E = F q中,q 必须是: ( )(A)正电荷; (B)微量点电荷,正负均可;(C)微量的正电荷; (D)点电荷,正负均可。
习题二
• 18.生理年龄对心理行为活动的影响是 ( 18、D)。 • (A)不同年龄对同一事件的心理反应是相同 的 • (B)儿童的心理障碍少数是以行为障碍为主 的 • (C)儿童的心理问题不容易转化为心理障碍 • (D)复杂的人际关系对儿童构不成直接的威 胁
• 19.寻找社会性原因时,应该确定( 19、 C)。 • (A)求助者对生活事件和人际关系有无误解 • (B)求助者的临床表现与错误观念有无关系 • (C)社会文化因素与心理障碍的发生有无关 系 • (D)求助者对生活事件和人际关系有无偏见
• 5.疑病性神经症的主要临床特点是(5、D )。 • (A)对健康状况存在一些忧虑 (B)对身体 状况的注意程度减退 • (C)感觉过敏不属于躯体障碍 (D)觉得患 病,但无妄想的特点
• 6.抑郁性神经症的主要临床特点是(6、D )。 • (A)对前途悲观,偶有失望 (B)感到生 活还有意义 • (C)兴趣减退,但不丧3、ABCD)。 • (A)对什么都不感兴趣 (B)对事情感 到无法挽回 • (C)对自己的痛苦感到无能为力 (D)认为 自己一无是处
• 4.抑郁性神经症与抑郁症的鉴别要点包括 ( 4、BC)。 • (A)缺乏自信、自我评价低 • (B)其沮丧和无力感是长期心理冲突的结果 • (C)病程至少持续两年 • (D)情绪低落在两周以上
• 15.发病前从未接受过检测的AIDS患者的特 点是(15、ACD)。 • (A)一经确诊常会受到巨大的心理冲击 (B)少 数患者会出现心理或情绪的危机 • (C)病情重者迅速进入抑郁和接受期 (D)在 心理危机期后,会逐渐地恢复常态
• 16.对心理问题的社会性原因分析时,应注 意的是( 16、ACD)。 • (A)负性社会生活事件会成为应激源 (B)正 性社会生活事件不会成为应激源 • (C)生活事件的发生频度起重要的作用 (D)道 德、风俗习惯等因素起重要的作用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A BA BA ,
所求概率为
P( B | A)
P( B) P( A | B) P( B) P( A | B) P( B ) P( A | B )
m 1 mn 2
r r
m 1 n mn 2 mn
m . m n 2r
15.甲、乙两人独立地对同一目标各射击一次,命中率分别为 0.6 和 0.5,现已知目标被
1 1 3 2 ( ) . 2 5 5 5
P( A1 A2 ) P( A1 A2 B1 A1 A2 B2 ) P( A1 ) P( A1 ) P( B1 ) P( A1 A2 | B1 ) P( B2 ) P( A1 A2 | B2 ) P( A1 )
2 2 1 C10 C18 2 2 2 C C30 9 51 50 4 0.4856 . 2 49 29 5
7.一个盒子中装有 15 个乒乓球,其中 9 个新球,在第一次比赛时任意抽取 3 只,比赛 后仍放回原盒中; 在第二次比赛时同样地任取 3 只球,求第二次取出的 3 个球均为新球的概 率。 , 解 设 A ‘第二次取出的均为新球’
பைடு நூலகம்
Bi ‘第一次取出的 3 个球恰有 i 个新球’ i 0, 1, 2, 3.
1 [ P( AB | C1 ) P( AB | C2 ) P( AB | C3 )] 3 P( B) 1 3 7 7 8 5 20 3 10 9 15 14 25 24 20 . 61 61 90 14.一袋中装有 m 枚正品硬币, n 枚次品硬币(次品硬币的两面均印有国徽)从袋中 任取一枚,已知将它投掷 r 次,每次都得到国徽,问这枚硬币是正品的概率是多少? 解 设 A ‘任取一枚硬币掷 r 次得 r 个国徽’ , B ‘任取一枚硬币是正品’ ,
解 2 事件如上所设,则
4 2 3 3 P ( A) 1 P ( A) 1 P ( B1 B2 B3 ) 1 0.6 . 5 3 4 5
17.甲、乙、丙三人向一架飞机进行射击,他们的命中率分别为 0.4,0.5,0.7。设飞机 中一弹而被击落的概率为 0.2,中两弹而被击落的概率为 0.6,中三弹必然被击落,今三人各 射击一次,求飞机被击落的概率. 解 则 , Bi ‘飞机中 i 弹’ 设 A ‘飞机被击落’
B ‘后取到的是男生表’ , , i 1, 2,3. Ci ‘取到第 i 个地区的表’
(1) p P (C1 ) P ( A | C1 ) P (C2 ) P ( A | C2 ) P (C3 ) P ( A | C3 )
1 3 7 5 29 ; 3 10 15 25 90
1 1 1 ,求他们将此密码译 5 3 4
16.三人独立地破译一个密码,他们能译出的概率分别是 , , 出的概率. 解 1 设 A ‘将密码译出’ , Bi ‘第 i 个人译出’ 则
i 1, 2,3.
P( A) P( B1 B2 B3 ) P( B1 ) P( B2 ) P( B3 ) P( B1 B2 ) P( B1 B3 ) 1 1 1 1 1 1 1 1 1 P ( B2 B3 ) P ( B1 B2 B3 ) 5 3 4 5 3 5 4 3 4 1 1 1 3 0.6 . 5 3 4 5
(2) P( B0 | A)
P( AB0 ) 0.8 0.85 . P( A) 0.94
13.设有来自三个地区的各 10 名,15 名和 25 名考生的报名表,其中女生报名表分别为 3 份、7 份和 5 份,随机地取一个地区的报名表,从中先后取出两份 (1)求先取到的一份为女生表的概率 p ; (2)已知后取到的一份是男生表,求先抽到的一份是女生表的概率 q . 解 设 A ‘先取到的是女生表’ ,
12.玻璃杯成箱出售,每箱 20 只,假设各箱含 0,1,2 只残次品的概率分别为 0.8,0.1, 0.1,一顾客欲购一箱玻璃杯,售货员随意取一箱,顾客开箱随意地察看四只,若无残次品, 则买下该箱,否则退回。试求: (1)顾客买下该箱的概率 ; (2)在顾客买下的一箱中,确无残次品的概率 . 解 设 A ‘顾客买下该箱’ ,
击中,求甲击中的概率. 解 设 A ‘目标被击中’ , Bi ‘第 i 个人击中’ 所求概率为
i 1, 2,
P( B1 | A)
P( B1 A) P( B1 ) P( B1 ) P( A) P( B1 B2 ) 1 P( B1 B2 ) 0.6 0.75 . 1 0.4 0.5
29 61 ,所以先取出的是男生表的概率为 ,按抓 90 90 61 阄问题的道理,后取的是男生表的概率 P ( B ) . 90
(2)因为先取出的是女生表的概率为 于是 (2) q P( A | B)
P( AB) P( ABC1 ABC2 ABC3 ) P( B) P( B)
1 1 2 C4 C6 C4 P( A) P( B1 ) P( B2 ) 2 2 , C10 C10
所求概率为
P( B2 | A)
P( B2 ) C2 1 1 14 2 . P( A) C4C6 C4 5
3.袋中有 5 只白球 6 只黑球,从袋中一次取出 3 个球,发现都是同一颜色,求这颜色 是黑色的概率. 解 设 A ‘发现是同一颜色’ , B ‘全是白色’ , C ‘全是黑色’ ,则
9.在第 6 题中,已知从乙袋中取得的球是白球,求从甲袋中取出的球是一白一黑的概 率. 解 事件如第 6 题所设,所求概率为
1 1 1 2 P( B1 ) P( A | B1 ) C3C2 / C5 2 15 P( B1 | A) 13 P( A) 26 25
10.已知一批产品中 96%是合格品,检查产品时,一个合格品被误认为是次品的概率是
B ‘箱中恰有 i 件残次品’ , i 0,1, 2 ,
(1) P ( A) P ( B0 ) P ( A | B0 ) P ( B1 ) P ( A | B1 ) P ( B2 ) P ( A | B2 )
4 4 C19 C18 0.8 0.1 4 0.1 4 0.94 ; C20 C20
A BC ,
所求概率为
3 3 P( AC ) P (C ) C6 / C11 2 P(C | A) 3 3 3 3 P( A) P( B C ) C6 / C11 C5 / C11 3
4.从 52 张朴克牌中任意抽取 5 张,求在至少有 3 张黑桃的条件下,5 张都是黑桃的概 率. 解 设 A ‘至少有 3 张黑桃’ , Bi ‘5 张中恰有 i 张黑桃’ , i 3, 4,5 , 则
0.02,一个次品被误认为是合格品的概率是 0.05,求在检查后认为是合格品的产品确是合格 品的概率。 , 解 设 A ‘任取一产品,经检查是合格品’
B ‘任取一产品确是合格品’ ,
则
A BA BA P( A) P( B) P( A | B) P( B ) P( A | B )
故
P ( A1 | A3 )
6 2 . 9 3
2. 设 10 件产品中有 4 件不合格品, 从中任取两件, 已知所取两件中有一件是不合格品, 求另一件也是不合格品的概率. 解 设 A ‘所取两件中有一件是不合格品’
Bi ‘所取两件中恰有 i 件不合格’ i 1, 2.
则
A B1 B2
习 题 二
1.假设一批产品中一、二、三等品各占 60%,30%,10%,从中任取一件,发现它不是 三等品,求它是一等品的概率. 解 设 Ai ‘任取一件是 i 等品’ 所求概率为
i 1, 2, 3 ,
P( A1 | A3 )
因为 所以
P( A1 A3 ) , P( A3 )
A3 A1 A2 P ( A3 ) P ( A1 ) P( A2 ) 0.6 0.3 0.9 P ( A1 A3 ) P ( A1 ) 0.6
A B3 B4 B5 ,
所求概率为
5 P( AB5 ) P( B5 ) C13 9 . P( B5 | A) 3 2 4 1 5 P( A) P( B3 B4 B5 ) C13C39 C13C39 C13 1686
5.设 P ( A) 0.5, P ( B ) 0.6, P ( B | A) 0.8 求 P ( A B ) 与 P ( B A) . 解
P( A B) P( A) P( B) P( AB) 1.1 P( A) P( B | A) 1.1 0.4 0.7 P ( B A) P( B ) P ( AB ) 0.6 0.4 0.2 .
6.甲袋中有 3 个白球 2 个黑球,乙袋中有 4 个白球 4 个黑球,今从甲袋中任取 2 球放 入乙袋,再从乙袋中任取一球,求该球是白球的概率。 解 , Bi ‘从甲袋中取出的两球恰有 i 个白球’ 设 A ‘从乙袋中取出的是白球’
由全概公式
P( A) P( B0 ) P( A | B0 ) P(B1 ) P( A | B1 ) P( B2 ) P( A | B2 ) P( B3 )P( A | B3 )
3 3 1 2 3 1 3 3 3 C6 C9 C9 C6 C8 C92C6 C7 C9 C6 3 3 3 3 3 3 3 3 C15 C15 C15 C15 C15 C15 C15 C15 528 0.089 . 5915
0.96 0.98 0.04 0.05 0.9428 ,
所求概率为
P( B | A)
