tsk模糊逻辑系统的基本框架
第三章、模糊控制系统
当ki 取µv (vi )时
重心法
模糊化计算的其它方法:左取大、右取大等。
第二节:模糊控制系统的设计 一、模糊控制器的结构设计 模糊控制器的结构设计包括:输入输出变量选择、模糊化 算法、模糊推理规则和精确化计算方法。 一维模糊控制器 被控对象 输入输出 (按模糊控制器输入变量个数) 变量 多输入多输出 单输入单输出 二维模糊控制器 多维模糊控制器
-50 -150 -64 -4 1 0 0 0 0 -3 0.5 0.5 0 0 0
…… …… …… -2 0 1 0 0 0 -1 0 0.5 0.5 0 0 0 0 0 1 0 0 1 0 0 0.5 0.5 0 2 0 0 0 1 0 3 0 0 0 0.5 0.5 相关的隶属度函数
50 150 64 4 0 0 0 0 1
50
量化
语言变量值(整数论域)
de:[-150,150]
k2 = 4 150
u:[-64,64]
k3 = ?
k3 = 64 = 16 4
量化为:{-4, -3, -2, -1, 0, 1, 2, 3, 4}
语言值分档:( NB、NS、ZE、PS、PB)
模糊集的隶属度函数(表格表示法)
e de u 量化等级 语言变量值 NB NS ZE PS PB
v0 =
∑ω v
i =1 N
N
i i
∑ω
i =1
i
其中:权系数 ω i :第i条模糊推理规则的可信度
0 ω i = µ A ( x10 ) ∧ µ A ( x2 ) ∧ K ∧ µ A ( x 0 ) p 其计算公式为:
i 1 i 2 i p
即:p个输入变量隶属于第i个对应的模糊集函数中最小的隶属 度值。
《TS模糊模型》PPT课件讲义

T-S 模糊系统模型模糊化
设非线性系统为:
其中x是状态变量,u是输入变量, F,f,g 是光滑的非线性函数。 T-S 模糊模型是由一组“IF-THEN”模糊规则来描述非线性系统,每 一个规则代表一个子系统,整个模糊系统即为各个子系统的线性组合 。
式 中 M i j是 模 糊 集 合 , ( A I, B I) 是 第 i个 系 统 相 应 的 系 数 矩 阵 , z i( t) 是 前 件 变 量 。
TS模糊模型
(Suitable for teaching courseware and reports)
传统模糊系统的基本思想 一种基于规则的控制,通过语言表达的模糊性控制规则来实现 对难以精确描述系统的控制,在设计中不需要建立被控对象的 精确数学模型.
T-S 模糊模型的基本思想 T-S 模糊模型是将正常的模糊规则及其推理转换成一种数学表达 形式。本质是将全局非线性系统通过模糊划分建立多个简单的 线性关系,对多个模型的输出再进行模糊推理和判决,可以表示复 杂的非线性关系.
Thank you.
演讲结速,谢谢观赏!
PPT常用编辑图使用方法
1.取消组合
2.填充颜色
3.调整大小
选择您要用到的图标单击右键选择“ 取消组 合”
右键单击您要使用的图标选择“填充 ”,选 择任意 颜色
拖动控制框调整大小
商务
图标元素
商务
图标元素商务图标元素 Nhomakorabea商务
图标元素
4.5
5
x
MF Degree of input 2
1 0.8 little
0.6
0.4
0.2
0
0
1
2
3
4
基于PSOFS和TSK模糊系统的不平衡心电数据分类算法

基于PSOFS和TSK模糊系统的不平衡心电数据分类算法
李鑫辉;申情;张雄涛
【期刊名称】《大数据》
【年(卷),期】2022(8)5
【摘要】提出基于粒子群优化特征选择(PSOFS)算法和TSK(Takagi-Sugeno-Kang)模糊系统的心电信号分类模型,即基于PSOFS和TSK的并行集成模糊神经网络(PE-PT-FN),用于心电图预测。
首先对训练集中的各类样本进行随机放回抽样,然后将抽样得到的样本合并在一起,再独立且并行地通过PSOFS算法进行特征选择。
PSOFS算法中不同的位置表示不同的特征子集,初始位置随机的粒子经过多次迭代收敛至最佳位置。
每个子集得到一个特征子集用于并行训练多组独立的小型TSK
模糊神经网络(TSK-FNN)。
模糊系统的可解释性和PSOFS算法挑选出来的特征子集能有效地帮助医学研究者找出心电信号数据与不同类型病例之间的关联。
实验证明,PE-PT-FN在保留可解释性的前提下,能将预测结果的宏召回率提升至92.35%。
【总页数】14页(P139-152)
【作者】李鑫辉;申情;张雄涛
【作者单位】湖州师范学院信息工程学院;浙江省现代农业资源智慧管理与应用研
究重点实验室;湖州学院理工学院
【正文语种】中文
【中图分类】TP301
【相关文献】
1.基于模糊子空间聚类的〇阶L2型TSK模糊系统
2.基于中心型TSK模糊模型的分层模糊系统
3.基于一型模糊规则自主构建二型TSK神经模糊系统方法设计
4.用于不平衡数据分类的0阶TSK型模糊系统
5.基于迭代模糊聚类算法与K近邻和数据字典的集成TSK模糊分类器
因版权原因,仅展示原文概要,查看原文内容请购买。
MATLAB中的模糊逻辑与模糊系统应用

MATLAB中的模糊逻辑与模糊系统应用引言:模糊逻辑是一种处理含糊和不确定性的推理方法,而模糊系统是基于模糊逻辑的一种工程应用。
在实际问题中,很多情况下无法准确界定事物的属性或关系,这就需要使用模糊逻辑和模糊系统进行描述和分析。
MATLAB作为一种强大的数学软件工具,提供了丰富的函数库和模块,可以非常方便地进行模糊逻辑和模糊系统的建模与分析。
本文将探讨MATLAB中的模糊逻辑与模糊系统应用,并介绍一些实际案例。
一、模糊逻辑的基本概念:1.1 模糊集合与隶属度函数在传统的逻辑中,事物的属性通常只有真和假两种取值,而在模糊逻辑中,属性被描述为一个介于[0,1]之间的隶属度。
模糊集合是指由一组对象组成的集合,每个对象在集合中的隶属度不是二进制的,而是介于0和1之间的实数。
隶属度函数是用来描述某个对象对于某个属性的隶属程度,通常使用三角形、梯形等形状的函数来表示。
1.2 模糊逻辑运算模糊逻辑中的运算方式与传统逻辑不同,引入了模糊的概念。
模糊逻辑运算包括交集、并集和补集等操作,用于描述模糊集合之间的关系。
这些运算可以通过模糊控制器、模糊推理等方式进行实现。
MATLAB提供了丰富的函数和工具箱来进行模糊逻辑运算和推理。
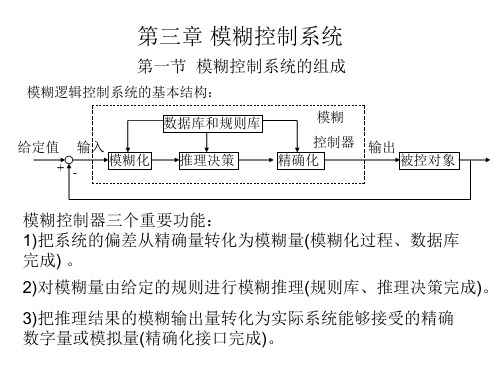
二、模糊系统的框架与建模过程:2.1 模糊系统的框架模糊系统通常由模糊化、模糊推理和去模糊化三个主要部分组成。
模糊化是将输入的实际值映射到模糊集合中,模糊推理是根据规则和隶属度函数进行推理,得出输出的模糊结果,去模糊化则是将模糊结果转化为实际值。
2.2 模糊系统的建模过程模糊系统的建模过程包括变量的模糊化、规则的定义、隶属度函数的设定以及模糊推理等步骤。
MATLAB提供了一系列的函数和工具箱用于模糊系统的建模和分析。
利用MATLAB的模糊工具箱,可以方便地进行隶属度函数的设定、规则的定义以及模糊推理的实现。
三、模糊逻辑与模糊系统在实际问题中的应用:3.1 模糊控制器模糊控制器是模糊逻辑和模糊系统的一种应用,它利用模糊推理和模糊系统来实现对控制系统的控制。
第3章 模糊控制

期望值
+ - y
e
ec
ke d/dt kec
E
EC
ห้องสมุดไป่ตู้
模糊
控制器
U
u
ku
图中ke、kec为量化因子,ku为比例因子
量化: 将一个论域离散成确定数目的几小段(量化 级)。每一段用某一个特定术语作为标记,这 样就形成一个离散域。
假设在实际中,误差的连续取值范围是 e=[eL,eH],eL表示低限值,eH表示高限值。 将离散语言变量E的论域定义为{-m,„,-1, 0,1, „,m}。则有量化因子: 2m ke eH eL 量化因子实际上类似于增益的概念,在这 个意义上称量化因子为量化增益更为合适。
i Ri : IF x1 IS A1i AND x2 IS A2 AND xp IS Aip
i i THEN vi a0 a1 x aip x p i 1 , , N
(3 1)
vi 是模糊语言值; xi是一个输入变量;是输 i 出变量;系数集{a j }是待辨识的参数。模型的辨 i i ( N , p ) { A , a 识分两步。即结构参数 的辨识和系数 j j } 的确定。
1、最大隶属度函数法 简单地取所有规则推理结果的模糊集合中隶属 度最大的那个元素作为输出值。即: 当论域 V 中,其最大隶属度函数对应的输出 值多于一个时,简单取最大隶属度输出的平均即 可: U 0 max v (v) v V 为具有相同最大隶属度输出的总数。 此方法计算简单,但丢失信息,控制性能不高。
式中,<>代表取整运算。 模糊控制器的输出U可以通过下式转换为 实际的输出值u:
uH uL u ku U 2
问题的提出 变量量化会导致一定的量化误差。 解决方法 在量化级之间,加入插值运算。对于任意一 个连续的测量值可以通过相邻两个离散值的加 权运算得到模糊度的值。
模糊系统

3. 修正型最大平均法 (modified mean of maxima defuzzifier)
y* = 其中 µC ( y j ) = height (C )
max{ y j } + min{ y j }
j j
2
4. 中心平均法 (modified center average defuzzifier)
■
■
将经过模糊推理之后产生的结论,转换为一明确数值的过程,我们称之 为 “去模糊化 。 去模糊化” 去模糊化 由于不同的模糊规则所采用的后件会有所不同,因此,经过模糊推理后 所得到的结论,有的是以模糊集合 模糊集合来表示(如语言式模糊规则),而有的是 模糊集合 以明确数值 明确数值来表示。 明确数值
3.1.3 模糊推理引擎
■
模糊推理引擎是模糊系统的核心,它可以藉由近似推理 模糊推理 近似推理或模糊推理 模糊推理引擎 近似推理 模糊推理的进行,来仿真 人类的思考决策模式,以达到解决问题的目地。 前提一(premise) 1:x is A´ 前提二(premise) 2:If x is A, Then y is B -----------------------------------------------------------结论:y is B´
■
■ ■
■
推理引擎将藉由这些模糊规则来进行推理,以决定下一步骤所要 推理引擎 采取的决定。 三种规则的主要差别只在于模糊规则的后件有所不同而已 后件有所不同而已。 后件有所不同而已 至于模糊规则从何而来呢?一般说来,有两种取得模糊规则的方 式:第一种方式也是最直接的方式,就是由专家来提供所须的模 专家来提供所须的模 糊规则;第二种方式是先收集一些量测数据后,再经由特定的训 糊规则 练算法则来从量测数据中抽取出模糊规则 量测数据中抽取出模糊规则。 量测数据中抽取出模糊规则 模糊规则中前件与后件的模糊集合,其隶属函数的设定 隶属函数的设定从何而来 隶属函数的设定 呢?假若模糊规则是由人类专家所给定的,则隶属函数就必须由 人类专家一起给定。若模糊规则是由特定的训练算法则从量测数 据中抽取出来的,选定合适的隶属函数型式之后,则以收集之量 测数据来细调隶属函数的参数,以便提高系统的有效性。
模糊控制的基本原理和方法
NM
NM
NS
NS
NB
PS
PL
PM
NS
NS
NS
NS
NM
NB
de Z
PL
PM
PS
Z
Z
NS
NM
NB
NS
PL
PM
PS
PS
PS
PS
NM
NB
NM
NM
NB
NB
PL
PL
PL
PM
PM
PM
NM
NB
4. 隐含和推理方法的制定
• 隐含采用 ‘mamdani’方法: ‘max-min‘ • 推理方法, 即 ‘min‘ 方法 • 去模糊方法:面积中心法。 • 选择隶属函数的形式:三角型
c
8
NS ZE NM
g
9
ZE ZE NS
k
10
ZE PB PB
d
11
ZE PM PM
h
12
ZE PS PS
i
13
ZE
ZE
ZE 设置点
关于语言相平面方法调整规则
Ri : if误差e是Ai和误差导数e是Bi ,then控制规则为Ci可以写成: K3[u(k)] F[K1e(k), K2e(k)]
xi 和y的 论域 分别 为U i 和V, 用 模糊 隐含 表 示:
Ri ˆ Aij Ci 或Ri ˆ Ai (xi ) Bi ( y)
j
j
● 模糊控制系统的设计
1. 模糊化的策略 ▲ 采用单点模糊化
▲ 选择合适的模糊函数 ☆ 考虑噪声的概率密度函数。使W f 5 n
yr +
模糊逻辑系统介绍课件
02
模糊分类器设计:利用模糊逻辑对数据进行分类和识别
03
模糊聚类分析:通过模糊逻辑对数据进行聚类分析
04
模糊决策分析:利用模糊逻辑进行决策分析和优化
模糊逻辑系统的 应用案例
模糊逻辑系统在控制领域的应用
01
模糊逻辑控制 器:用于控制 复杂系统的输 出,提高系统 的稳定性和准
确性
02
03
模糊逻辑自适 应控制:根据 系统状态和输 入信号的变化, 自动调整控制 参数,实现最
04
并、交、补等。
模糊关系
01
模糊关系是一种 描述事物之间关 系的概念,它允 许事物之间存在 一定程度的不确 定性和模糊性。
02
模糊关系可以用 一个模糊集合来 表示,其中包含 了事物之间关系 的各种可能性。
03
模糊关系的程度可 以通过隶属度函数 来衡量,隶属度函 数是一个定义在模 糊集合上的函数, 它表示一个元素属 于该集合的程度。
模糊逻辑系统的应用领域
控制领域:模糊逻辑系统 可以用于控制系统的设计 和优化,提高系统的稳定 性和准确性。
医疗领域:模糊逻辑系统 可以用于医疗诊断和治疗, 帮助医生做出更准确的诊 断和治疗方案。
交通领域:模糊逻辑系统 可以用于交通控制系统的 设计和优化,提高交通系 统的效率和安全性。
工业领域:模糊逻辑系统 可以用于工业控制系统的 设计和优化,提高工业生 产的效率和稳定性。
模糊推理的应用广 泛,包括控制、决 策、模式识别等领 域。
模糊逻辑系统的 设计方法
模糊逻辑系统的设计步骤
确定模糊逻辑系 统的目标:明确 系统的功能、性 能和需求
建立模糊逻辑模 型:根据目标, 建立模糊逻辑模 型,包括输入、 输出和模糊规则
人工智能第五章模糊逻辑系统85
10
二、模糊集合的定义及表示方法、名词术语
定义:设论域为U,称映射
A~ :U [0,1] u A~ (u)
确定U的一个模糊集合 A~ 。A~ (u) 称为 A~ 的隶属函数。 A~ (u) A~(u),表示u隶属于 A~ 的程度,简称隶属度。
论域U指的是所讨论的事物的全体。
模糊幂集:论域U上的全体模糊子集构成的集合,记为F(U), F (U ) P(U )
∧ 取小运算
C~ 0.1 0.1 0.6 0.5 0.7 0.9 0.9 1
u1
u2
u3
u4
0.1 0.5 0.7 0.9 u1 u2 u3 u4
2019/11/29
19
5、 余
A~c (u) 1 A~ (u)
A~c (u) 1 A~(u)
3、有界和
A~
B~
A~
B~
(u)
min{1,
A~
(u)
B~
(u)}
4、有界差
A~ B~ A~ B~ (u) max{0, A~ (u) B~ (u)}
2019/11/29
24
5、有界积
A~ B~ A~ B~ (u) max{0, A~ (u) B~ (u) 1}
改善后的Fuzzy算子尽管在某种意义上更加接近人类思维,然 而由于其变化复杂且失去了许多好的运算性质而很少使用。
2019/11/29
23
1、代数和 A~ ˆ B~ A~ˆ B~ (u) A~ (u) B~ (u) A~ (u)B~ (u)
2、代数积 A~ B~ A~B~ (u) A~ (u)B~ (u)
基于TSK型递归模糊神经网络的永磁直线同步电机位置控制研究
基于TSK型递归模糊神经网络的永磁直线同步电机位置控制研究熊渊琳;方宝英【摘要】针对基于磁场定向控制的永磁直线同步电机(PMLSM)伺服系统的位置精准控制问题,提出了一种TSK型递归模糊神经网络(TSKRFNN)控制方法.在考虑了系统易受参数变化、外部扰动和摩擦力等不确定性因素影响的基础上,建立了含有不确定性因素在内的PMLSM动态数学模型;利用TSKFRNN对系统同时进行了实时在线的结构学习和参数学习,提高了系统抑制不确定性因素的鲁棒性,保证了系统的动态跟踪性能.实验及研究结果表明:与模糊神经网络PID控制方法相比,TSKFRNN可以有效辨识电机参数,抑制系统的不确定性对系统伺服性能的影响,提高了系统的鲁棒性和跟踪性能.【期刊名称】《机电工程》【年(卷),期】2019(036)004【总页数】5页(P413-417)【关键词】永磁直线同步电动机;不确定性因素;TSK型递归模糊神经网络;鲁棒性;跟踪性【作者】熊渊琳;方宝英【作者单位】江苏海事职业技术学院电气学院,江苏南京211170;上海理工大学光电信息与计算机工程学院,上海200093【正文语种】中文【中图分类】TM301.2;TP2730 引言随着科技的发展,伺服系统对于高速高轮廓精度的要求越来越高。
由于以永磁直线同步电动机(PMLSM)为直接驱动的系统具有无背隙、摩擦小、机械构造简单、高可靠性、高传动刚度和大推力等优点,使PMLSM直驱设计适用于许多高性能要求的场合[1-2]。
然而,PMLSM结构上的简化使控制难度增加,导致参数变化、外部扰动、摩擦力等不确定性因素直接作用在电机上,严重影响电机的伺服性能。
因此,抑制不确定性因素对系统的影响,提高系统控制性能是PMLSM伺服驱动的关键问题[3-4]。
近年来,针对PMLSM中存在不确定性因素而降低系统伺服性能的问题,国内外学者进行了深入地研究,包括经典PID控制、滑模控制、反推控制等。
由于PMLSM是一种多变量、强耦合的非线性系统,传统PID控制无法满足一些高精密应用场合控制要求,且PID控制算法需根据专家经验,采用试凑法,经调试才能得到最优参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TSK模糊逻辑系统的基本框架
引言
随着人工智能的快速发展,模糊逻辑系统作为一种处理模糊信息的方法变得越来越重要。
TSK(Takagi-Sugeno-Kang)模糊逻辑系统是一种常用的模糊逻辑系统,在控制系统、决策系统等领域有着广泛的应用。
本文将详细探讨TSK模糊逻辑系统的基本框架。
二级标题1:模糊逻辑系统概述
模糊逻辑系统是一种能够处理模糊信息的推理系统。
与传统的二值逻辑系统不同,模糊逻辑系统可以处理不确定性、模糊性和不完备性等问题。
模糊逻辑系统的基本原理是基于模糊集合理论,通过定义模糊集合的隶属度函数来描述模糊性。
TSK模糊逻辑系统是一种特殊的模糊逻辑系统,它基于Takagi-Sugeno-Kang模型,具有较强的表达能力和计算效率。
二级标题2:TSK模糊逻辑系统的基本结构
TSK模糊逻辑系统由模糊化、规则库、推理机制和解模糊化四个部分组成。
三级标题1:模糊化
模糊化是将输入的实际值映射到模糊集合的隶属度函数上。
常用的模糊化方法有高斯函数、三角函数等。
模糊化的结果是一组隶属度值,表示了输入值在各个模糊集合中的隶属度。
三级标题2:规则库
规则库是TSK模糊逻辑系统的核心部分,定义了输入和输出之间的关系。
规则库由一系列模糊规则组成,每条模糊规则包含若干个前提和一个结论。
前提是输入变量与模糊集合的隶属度之间的逻辑关系,结论是输出变量的模糊集合隶属度的组合方式。
三级标题3:推理机制
推理机制是TSK模糊逻辑系统的推理引擎,用于根据输入的前提和规则库进行推理,生成输出结果。
常用的推理方法有最大隶属度法、加权平均法等。
推理机制的输出是一组模糊集合的隶属度,表示了输出变量在不同模糊集合中的隶属度。
三级标题4:解模糊化
解模糊化是将模糊化的隶属度结果转换为具体的实际值。
常用的解模糊化方法有质心法、加权平均法等。
解模糊化的结果是模糊逻辑系统的最终输出。
二级标题3:TSK模糊逻辑系统的应用
TSK模糊逻辑系统在控制系统、决策系统等领域有着广泛的应用。
以下是一些常见
的应用案例:
三级标题1:智能控制系统
TSK模糊逻辑系统可以用于智能控制系统中的控制器设计。
通过建立适当的规则库,根据输入的传感器数据进行推理,生成控制信号,实现对控制系统的自动调节和优化。
三级标题2:风险评估与决策支持系统
TSK模糊逻辑系统可以用于风险评估与决策支持系统中的决策模型构建。
通过建立
适当的规则库,根据输入的风险指标数据进行推理,生成决策结果,为决策者提供决策支持。
三级标题3:模式识别与数据挖掘
TSK模糊逻辑系统可以用于模式识别与数据挖掘中的模型构建。
通过建立适当的规
则库,根据输入的数据特征进行推理,生成分类或回归结果,实现对数据的分析和预测。
三级标题4:人工智能与机器学习
TSK模糊逻辑系统可以用于人工智能与机器学习中的模型构建。
通过建立适当的规
则库,根据输入的特征进行推理,生成预测结果,实现对复杂问题的智能求解。
二级标题4:总结
TSK模糊逻辑系统是一种常用的模糊逻辑系统,具有较强的表达能力和计算效率。
本文从模糊逻辑系统的概述、基本结构、应用等方面对TSK模糊逻辑系统进行了深入的探讨。
TSK模糊逻辑系统在控制系统、决策系统等领域有着广泛的应用前景,将为人工智能的发展提供有力的支持。
