海淀区初三期末数学试题及答案
2023北京海淀初三(上)期末数学及答案

2023北京海淀初三(上)期末数 学2022.12第一部分选择题一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.刺绣是中国民间传统手工艺之一.下列刺绣图案中,是中心对称图形的为2.点A (1, 2)关于原点对称的点的坐标为(A)(-1, -2) (B) ( -1,2) (C) (1, -2) (D)(2,1)3.二次函数22y x =+的图象向左平移1个单位长度,得到的二次函数解析式为(A) 23y x =+ (B) 2(1)2y x =-+(C) 21y x =+ (D) 2(1)2y x =++4.如图,已知正方形ABCD ,以点A 为圆心,AB 长为半径作⊙A , 点C 与⊙A 的位置关系为 (A)点C 在⊙A 外(B)点C 在⊙A 内 (C)点C 在⊙A 上(D)无法确定5.若点M(0,5), N(2,5)在抛物线22()3y x m =-+上,则m 的值为 (A)2 (B) 1(C)0 (D) -16.勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由 三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心O 旋转一定角 度 a 后能与自身重合,则该角度a 可以为 (A) 30°(B ) 60°(C) 120° (D) 150°7.如图,过点A 作⊙O 的切线AB , AC ,切点分别是B , C ,连接BC.过BC 上 一点D 作⊙O 的切线,交AB , AC 于煎E ,F.若∠A =90°,△AEF 的周长 为 4,则BC 的长为 (A)2 (B) 22(C)4 (D) 428.遥控电动跑车竞速是青少年喜欢的活动.如图是某赛道的部分通行路线示意图,某赛车从入口 4驶入,行至每个岔路口选择前方两条线路的可能性相同,则该赛车从F 口驶出的概率是(A)13 (B) 14 (C) 15 (D) 16第二部分非选择题二、填空题(共16分,每题2分)9.二次函数243y x x =-+的图象与y 轴的交点坐标为 . 10.半径为3,圆心角为120°的扇形的面积为 . 11.下表记录了一名球员在罚球线上投篮的结果.根据以上数据,估计这名球员在罚球线上投篮一次,投中的概率为 .12.若关于x 的一元二次方程230x x m -+=有两个不相等的实数根,则m 的取值范围是 13.二次函数2y ax bx =+的图象如图所示,则ab 0(填“>”“<”或“=”)14.如图,△ABC 是⊙O 的内接三角形,OD ⊥AB 于点E ,若⊙O 2,∠ACB =45°,则OE= .15.对于二次函数2y ax bx c =++, y 与x 的部分对应值如表所示. x 在某一范围内,y 随x 的增大而减小,写出一个符合条件的x 的取值范围 .16.如图,AB , AC ,AD 分别是某圆内接正六边形、正方形、等边三角形的一边.若AB= 2,下 面四个结论中,①该圆的半径为2 ; ②AC 的长为2π; ③AC 平分心∠BAD ;④连接BC , CD ,则△ABC 与的面积比为13 所有正确结论的序号是 .三、解答题(共68分,第17-20题,每题5分,第21题6分,第22-23题,每题5分,第 24-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程. 17.解方程:226x x -=.18.已知抛物线22y x bx c =++过点(1, 3)和(0, 4),求该抛物线的解析式.19.已知a 为方程22310x x --=的一个根,求代数式(1)(1)3(2)a a a a +-+-的值.20.如图,四边形ABCD 内接于⊙O ,AB 为直径,BC =CD .若∠A=50°,求∠B 的度数.21.为了发展学生的兴趣爱好,学校利用课后服务时间开展了丰富的社团活动.小明和小天参加 的篮球社共有甲、乙、丙三个训练场.活动时,每个学生用抽签的方式从三个训练场中随机 抽取一个场地进行训练. (1)小明抽到甲训练场的概率为 ;(2)用列表或画树状图的方法,求小明和小天在某次活动中抽到同一场地训练的概率.22.已知:如图,AB 是⊙O 的切线,A 为切点. 求作:⊙O 的另一条切线PB , B 为切点.作法:以P 为圆心,PA 长为半径画弧,交⊙O 于点B ; 作直线PB. 直线PB 即为所求.(1)根据上面的作法,补全图形(保留作图痕迹); (2)完成下面证明过程. 证明:连接OA ,OB , OP. ∵PA 是⊙O 的切线,A 为切点, ∴OA ⊥PA. ∴∠ PAO = 90°. 在△PAO 与△PBO 中,______PA PB OP OP =⎧⎪=⎨⎪⎩∴△PAO ≌△PBO ∴∠PAO=∠PBO = 90°. ∴OB ⊥PB 于点 B. ∵是⊙O 的半径,∴PB 是⊙O的切线( )(填推理的依据). 23.紫砂壶是我国特有的手工制造陶土工艺品,其制作过程需要几十种不同的工具,其中有一种工具名为“带刻度嘴巴架”,其形状及, 使用方法如图1.当制壶艺人把“带刻度嘴巴架”上圆弧部分恰好 贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上.图2是正确使用该工具时的示意图.如图3, ⊙O 为某紫砂壶的壶口,已知A ,B 两点在⊙O 上,直线l 过点O ,且l ⊥AB 于点D ,交⊙O 于点C.若AB=30mm , CD =5mm ,求这个紫砂壶的壶口半径r 的长.24.如图,AB 是⊙O 的直径,点C 在⊙O 上.过点C 作⊙O 的切线l ,过点B 作 BD ⊥l 于点D 。
海淀区2024届初三二模数学试题及答案

海淀区九年级第二学期末练习数 学2024.05学校_____________ 姓名______________ 准考证号______________第一部分 选择题一、选择题(共16分,每题2分)第1 - 8题均有四个选项,符合题意的选项只有一个.1.截至2023年底,我国人工智能核心产业规模接近5800亿元,形成了京津冀、长三角、珠三角三大集聚发展区.将580000000000 用科学记数法表示应为 (A )105810⨯(B )115.810⨯(C )125.810⨯(D )120.5810⨯2.右图是一张长方形纸片,用其围成一个几何体的侧面,这个几何体可能是 (A )圆柱 (B )圆锥 (C )球(D )三棱锥3.五边形的内角和为 (A )900︒(B )720︒(C )540︒(D )360︒4.若a b >,则下列结论正确的是 (A )0a b +>(B )0a b −>(C )0ab >(D )0ab> 5.如图,实数5在数轴上对应的点可能是(A )点A(B )点B(C )点C(D )点D6.如图,12l l ,点A 在1l 上,以点A 为圆心,适当长度为半径画弧,分别交1l ,2l 于点B ,C ,连接AC ,BC .若140∠=︒,则ABC ∠的大小为 (A )80︒ (B )75︒ (C )70︒(D )65︒考生须知1.本试卷共7页,共两部分,28道题,满分100分。
考试时间120分钟。
2.在试卷和答题纸上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,请将本试卷、答题纸和草稿纸一并交回。
ABC1l 1l 20 1 2 3–1 A B CD7.九年级(1)班羽毛球小组共有4名队员,其中两名男生,两名女生.从中随机选取两人,恰好能组成一组混双搭档的概率是 (A)14(B )13(C )12(D )238.某种型号的纸杯如图1所示,若将n 个这种型号的杯子按图2中的方式叠放在一起,叠在一起的杯子的总高度为H .则H 与n 满足的函数关系可能是 (A )0.3H n = (B )100.3H n=(C )100.3H n =−(D )100.3H n =+第二部分 非选择题二、填空题(共16分,每题2分) 9. 若代数式12x −有意义,则实数x 的取值范围是 . 10.若1x =是方程230x x m −+=的一个根,则实数m 的值为 . 11.如图,在△ABC 中,D ,E 分别在边AB ,BC 上,DEAC .若2AD =,4BD =,则DEAC的值为 .12.在平面直角坐标系xOy 中,点1(1)A y ,,2(2)B y ,在反比例函数ky x=(0k ≠) 的图象上. 若12y y <,则满足条件的k 的值可以是 (写出一个即可).13.如图所示的网格是正方形网格,A ,B ,C 是网格线的交点,C 在以AB 为直径的半圆上.若点D 在BC 上,则BDC ∠= ︒.14.一组数据3,2,4,2,6,5,6的平均数为4,方差为20s .再添加一个数据4,得到一组新数据.若记这组新数据的方差为21s ,则21s 20s (填“>”“=”或“<”).A DBE C图1图2D CBA15.下表是n 与2n (其中n 为自然数)的部分对应值表:n5 10 15 20 25 30 35 2n321 02432 7681 048 57633 554 4321 073 741 82434 359 738 368根据表格提供的信息,计算102432768⨯的结果为 . 16.在ABC 中,D 为边AB 的中点,E 为边AC 上一点,连接DE .给出下面三个命题:①若AE EC =,则12DE BC =; ②若12DE BC =,则DE BC ∥; ③若DE BC ∥,则AE EC =.上述命题中,所有真命题的序号是 .三、解答题(共68分,第17-19题,每题5分,第20-21题,每题6分,第22-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分) 解答写出文字说明、演算步骤或证明过程.17.计算:020242sin 45|3|8−︒+−+.18.解不等式组:532342(1).x x x x +⎧<⎪⎨⎪−>+⎩,19.已知2230m n −−=,求代数式2()2()m n n m n +−+的值.20.如图,点A ,B ,C ,D 在一条直线上,AB BC CD ==,AE EC =,四边形ECDF 是平行四边形. (1)求证:四边形EBCF 是矩形; (2)若12AD =,4cos 5A =,求BF 的长.21.我国古代著作《管子·地员篇》中介绍了一种用数学运算获得“宫商角徵羽”五音的方法.研究发现,当琴弦的长度比满足一定关系时,就可以弹奏出不同的乐音.例如,三根弦按长度从长到短排列分别奏出乐音“do ,mi ,so ”,需满足相邻弦长的倒数差相等.若最长弦为15个单位长,最短弦为10个单位长,求中间弦的长度.ODACBFE22.在平面直角坐标系xOy 中,一次函数0y kx b k =+≠()的图象由函数12y x =的图象平移得到,且经过点(24),.(1)求这个一次函数的解析式;(2)当2x >时,对于x 的每一个值,函数y x n =+的值与一次函数0y kx b k =+≠()的值的差大于1,直接写出n 的取值范围.23.一本图鉴中的照片由1开始连续编号,由于装订线脱落,照片散落一地.小云想利用统计学知识估计照片总数,于是从中随机抽取20张照片,将其编号作为样本,数据整理如下: a .20张照片的编号:4,8,15,25,34,39,41,48,68,79,85,86,89,91,102,104,110,121,144,147 b .20张照片编号的最小值、最大值、平均数和中位数:最小值 最大值 平均数 中位数 414772m(1)写出表中m 的值;(2)设照片总数为n ,所有照片编号分别为1,2,…,n ,这n 个数的平均数和中位数均为12n +. ①利用样本平均数估计全体平均数,可估算出照片的总数1n 为_________, ②利用样本中位数估计全体中位数,可估算出照片的总数2n 为_________,小云发现,有一个估算结果不合理,这个不合理的结果是_________(填“1n ”或“2n ”); (3)小云想到还可使用样本数据的“平均间隔长度”进行估计.在下面的示意图中,用1220x x x ,,…,表示随机抽取的20张照片编号从小到大排序,则从0到20x 的平均间隔长度为2020x ,从0到n 的平均间隔长度为21n,直接写出此时估算出照片的总数3n (结果取整数).24.如图,P 是⊙O 外一点,P A ,PB 分别切⊙O 于点A ,B ,PO 与⊙O 交于点H ,AH OH =. (1)求证:△ABP 是等边三角形;(2)过点A 作PO 的平行线,与⊙O 的另一个交点为C ,连接CP .若6AB =,求⊙O 的半径和tan CPB ∠的值.HBAOPnx 20x 19 …x3 x 2x 125.生活垃圾水解法是一种科学处理生活垃圾的技术.有研究表明,在生活垃圾水解过程中添加一些微生物菌剂能够加快原料的水解.某小组为研究微生物菌剂添加量对某类生活垃圾水解率的影响,设置了六组不同的菌剂添加量,分别为0%,2%,4%,6%,8%,10%,每隔12h 测定一次水解率,部分实验结果如下:a .不同菌剂添加量的生活垃圾,在水解48 h 时,测得的实验数据如下图所示:为提高这类生活垃圾在水解48 h 时的水解率,在这六组不同的菌剂添加量中,最佳添加量 为 %;b .当菌剂添加量为p %时,生活垃圾水解率随时间变化的部分实验数据记录如下:时间t (h )1224364860728496108120水解率y (%)0 28.0 35.1 39.4 42.5 44.9 46.8 48.5 50.0 51.2 52.3通过分析表格中的数据,发现当菌剂添加量为p %时,可以用函数刻画生活垃圾水解率y 和时间t 之间的关系,在平面直角坐标系中画出此函数的图象.结合实验数据,利用所画的函数图象可以推断,当水解132 h 时,生活垃圾水解率超过54%(填“能”或“不能”).根据以上实验数据和结果,解决下列问题: (1)直接写出p 的值;(2)当菌剂添加量为6%时,生活垃圾水解率达到50%所需的时间为0t 小时,当菌剂添加量为p %时,生活垃圾水解0(48)t +小时的水解率 50%(填“大于”“小于”或“等于”).t (h)1224364860728496108120132O菌剂添加量 (%)水解率 (%)25 30 35 40 4550 55 46810220 O26.在平面直角坐标系xOy 中,抛物线2y ax bx c =++(0a >)的对称轴为x t =,点1()2A t m ,,(2)B t n ,,00()C x y ,在抛物线上.(1)当2t =时,直接写出m 与n 的大小关系;(2)若对于067x <<,都有0m y n <<,求t 的取值范围.27.在ABC △中,AB AC =,60A ∠<︒,点D 在边AC 上(不与点A ,C 重合),连接BD ,平移线段BD ,使点B 移到点C ,得到线段CE ,连接DE .(1)在图1中补全图形,若2BAC E ∠=∠,求证:CBD ∠与CDE ∠互余;(2)连接AE ,若AC 平分BAE ∠,用等式表示CBD ∠与BAE ∠之间的数量关系,并证明.图1 备用图28.在平面直角坐标系xOy 中,⊙O 的半径为1,AB 是⊙O 的一条弦,以AB 为边作平行四边形ABCD .对于平行四边形ABCD 和弦AB ,给出如下定义:若边CD 所在直线是⊙O 的切线,则称四边形ABCD 是弦AB 的“弦切四边形”.(1)若点(01)A −,,(10)C ,,四边形ABCD 是弦AB 的“弦切四边形”,在图中画出“弦切四边形”ABCD ,并直接写出点D 的坐标;(2)若弦AB 的“弦切四边形”为正方形,求AB 的长;(3)已知图形M 和图形N 是弦AB 的两个全等的“弦切四边形”,且均为菱形,图形M 与N 不重合.P ,Q 分别为两个“弦切四边形”对角线的交点,记PQ 的长为t ,直接写出t 的取值范围.海淀区九年级第二学期期末练习数学试卷参考答案第一部分选择题一、选择题(共16分,每题2分)第二部分非选择题二、填空题(共16分,每题2分)9.2x≠10.211.2312.答案不唯一,0k<即可13.135 14.<15.33 554 432 16.①③三、解答题(共68分,第17-19题,每题5分,第20-21题,每题6分,第22-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 解:原式1232=−⨯++………………………………………………………………..4分13=+4=+…………………………………………………………………5分18. 解:原不等式组为56342 2.x xx x+<⎧⎨−>+⎩,①②解不等式①,得1x>. ………………………………………………………………….2分解不等式②,得6x>. …………………………………………………………………..4分∴原不等式组的解集为6x>. ……………………………………………………………..5分19. 解:原式222222m mn n mn n=++−−22m n=−. ……………………………………………………………………….3分∵2230m n −−=,∴223m n −=. …………………………………………………………………………4分∴原式3=. ………………………………………………………………………… 5分 20.(1)证明:∵四边形ECDF 为平行四边形,∴EF // CD ,EF CD =. …………………………………………………………1分 ∵B ,C ,D 在一条直线上,BC CD =, ∴EF // BC ,EF =BC .∴四边形EBCF 为平行四边形. ……………………………………………………2分 ∵AE EC =,AB BC =, ∴EB AC ⊥.∴90EBC ∠=.∴四边形EBCF 为矩形. …………………………………………………………3分(2)解:∵A ,B ,C ,D 在一条直线上,AB BC CD ==,12AD =,∴4AB =. …………………………………………………………………….4分 ∵EB AC ⊥. ∴90EBA ∠=. ∵4cos 5A =. ∴5cos ABAE A==. …………………………………………………………………….5分 ∵AE EC =, ∴5EC =.∵四边形EBCF 为矩形, ∴5BF EC ==.∴BF 的长为5. ………………………………………………………………….6分21. 解:设中间弦的长度为x 个单位长. …………………………. ………………. ………………..1分由题意可得11111510x x−=−. …………………………………………………………….3分 解得 12x =. ……………………………………………………………………………. 4分 经检验,12x =是原方程的解且符合题意. ………………………………………………. 5分 答:中间弦的长度为12个单位长. ……………………………………………………….6分22.解:(1)∵一次函数(0)y kx b k =+≠的图象由函数12y x =的图象平移得到, ∴12k =. .…..…..……………………………………………………………………..1分 ∵一次函数(0)y kx b k =+≠的图象经过点(24),,∴1242b ⨯+=. ∴3b =. .…..…..……………………………………………………………………..2分 ∴该一次函数的解析式为132y x =+. …………………...………………………..3分 (2)3n ≥. ….….….….…………………………………………………………………..5分23.解:(1)82; ….…….……………………………………..…………………………………..1分(2)143,163,1n ; ………………………………………………………………………... 4分 (3)154. ………………………………………………………………………….…..5分24.(1)证明:连接OA ,如图.∵OA OH =,AH OH =, ∴OA OH AH ==. ∴△AOH 为等边三角形.∴60AOH ∠=︒. …………………………………………………………………..….1分 ∵P A 切O 于点A , ∴PA AO ⊥. ∴90PAO ∠=︒.∴30APO ∠=︒. ………………………………………………………………..….2分 ∵P A ,PB 分别切O 于点A ,B , ∴PA PB =,30APO BPO ∠=∠=︒. ∴60APB ∠=︒.∴△ABP 为等边三角形. …………………………………………………………….3分(2)解:如图,连接BC .∵△ABP 为等边三角形,6AB =, ∴6PA PB AB ===.由(1)得,在Rt △P AO 中,90PAO ∠=︒,30APO ∠=︒.P∴tan 3063OA PA =︒=⨯= ∴O的半径为. ……………………………..…………………………4分 ∵△AOH 为等边三角形. ∴60HAO HOA ∠=∠=︒.由(1)得PA PB =,APO BPO ∠=∠, ∴PO AB ⊥. ∵AC // PO , ∴AC AB ⊥. ∴90BAC ∠=︒.∴BC 是O 的直径. ………………………..…………………………5分∴BC = ∵PB 切O 于点B , ∴PB BC ⊥. ∴90PBC ∠=︒.∴tan BC CPB PB ∠===………………………..…………………………6分 25.解:a . 6; ………………………………………………………..……………………………..1分b . 图象如下图.………………………………………..…………………………………....2分 不能. ……………………………………………………..……………………………..3分y(h )P(1) 4; …………………………………………………………..……………………………..4分 (2) 小于. ……………………………………………..……………………………..……..5分 26.解:(1) <; ………………………………………………………………………………………2分(2)∵0a >, 抛物线的对称轴为x t =,∴ 当x t ≥时,y 随x 的增大而增大;当x t ≤时,y 随x 的增大而减小. ① 当7t ≥时,122t t t <<.点(2)B t n ,关于抛物线对称轴x t =的对称点为'(0)B n ,, 此时点,',A B C 均在抛物线对称轴左侧. ∵对于067x <<,都有0m y n <<,∴06,17.2t ≤⎧⎪⎨≥⎪⎩解得 14t ≥. ② 当67t <<时,取0x t =,此时0y 为最小值,与0m y <矛盾,不符合题意. ③ 当06t <≤时,122t t t <<.点1()2A t m ,关于抛物线对称轴x t =的对称点为3'()2A t m ,, 此时点',,ABC 均在抛物线对称轴右侧. ∵对于067x <<,都有0m y n <<, ∴36,227.t t ⎧≤⎪⎨⎪≥⎩解得742t ≤≤. ④ 当0t =时,122t t t ==,m n =,不符合题意. ⑤ 当0t <时,122t t t <<.点(2)B t n ,关于抛物线对称轴x t =的对称点为'(0)B n ,, 此时点',B C 在抛物线对称轴右侧. ∵'06B x x <<, ∴0n y <,不符合题意.综上所述,t 的取值范围是742t ≤≤或14t ≥. …………………………………………6分 27.(1)补全图形如图1:图1…………………………………………………………………………………………1分 证明:设E α∠=,则22BAC E α∠=∠=.∵AB AC =, ∴180902BACABC ACB α︒−∠∠=∠==︒−.由平移可知,BC // DE ,BC DE =.∴四边形BCED 为平行四边形. ……………………………………………………2分 ∴CBD E α∠=∠=. ∵BC // DE ,∴90CDE ACB α∠=∠=︒−. ∴90CBD CDE ∠+∠=︒.∴CBD ∠与CDE ∠互余. ………………………………………………………3分(2)CBD ∠与BAE ∠之间的数量关系为12CBD BAE ∠=∠. …………………4分解:如图2,连接BE ,交AC 于点O ,延长AC 至F ,使OF OA =,连接EF .图2BB由(1)可得,四边形BCED 为平行四边形.∴OB OE =.∵OA OF =,BOA EOF ∠=∠,∴△BOA ≌△EOF .∴AB FE =,BAO EFO ∠=∠. ∵AC 平分BAE ∠,∴12BAO EAO BAE ∠=∠=∠.∴EFO EAO ∠=∠. ∴AE FE =.∴AB AE =. ………………………………………………………………………5分 ∵OB OE =, ∴AC BE ⊥.∴四边形BCED 为菱形.∴BD BC =. ……………………………………………………………………………6分 ∴BDC BCD ∠=∠.∴在△BCD 中,2180CBD BCD ∠+∠=︒. ∵在△ABC 中,2180BAC BCD ∠+∠=︒. ∴BAC CBD ∠=∠.∴12CBD BAE ∠=∠. ………………………………………………………………7分28.(1)如图,四边形ABCD 即为所求.……………………………………………………………………………………………….1分x点D 的坐标为(1,2)D −. …………………………………………………………………..2分 (2)如图,弦AB 的弦切四边形为正方形ABCD ,设正方形ABCD 的边长为a ,CD 与O 的切点为E ,连接EO 并延长交AB 于点F . ∵CD 与O 的切点为E ,EF 经过圆心O , ∴EF CD ⊥.∵四边形ABCD 为正方形, ∴AB // CD ,AB BC a ==. ∴EF AB ⊥. ∴1122AF AB a ==,EF BC a ==. ∵1OE =, ∴1OF a =−.在Rt △OAF 中,由勾股定理得,222OA OF AF =+.∴22211(1)()2a a =−+.解得 85a =. ∴AB 的长为85. ………………………………………………………………………..5分(3)05t <≤或2t =. ………………………………………………………………………..2分。
北京海淀区北京市十一学校2022-2023学年九年级上学期期末数学试题及解析

北京海淀区北京市十一学校2022-2023学年九年级上学期期末数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.若)(250y x xy =≠,则下列比例式正确的是( ) A .52x y=B .25x y= C .25x y = D .25y x = 2.在Rt ABC △中,90C ∠=︒,4AB =,3BC =,则sin A 的值是( )A B .34C .35D .453.在平面直角坐标系xOy 中,抛物线2y x =向上平移2个单位长度得到的抛物线为( ) A .)(22y x =+B .)(22y x =-C .22y x =-D .22y x =+4.在平面直角坐标系xOy 中,抛物线)(20y ax bx c a =++≠的示意图如图所示,下列说法中正确的是( )A .a<0B .0b <C .0c >D .0∆>5.在平面直角坐标系xOy 中,若函数)(0ky x x=<的函数值y 随着自变量x 的增大而增大,则函数)(0ky x x=<的图象所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限6.如图,四边形ABCD 内接于O ,若四边形ABCO 是菱形,则D ∠的度数为( )A .45°B .60°C .90°D .120°7.正方形的面积y 与它的周长x 满足的函数关系是( ) A .正比例函数B .一次函数C .二次函数D .反比例函数8.在平面直角坐标系xOy 中,点123(1)(2)(4)y y y -,,,,,在抛物线22y ax ax c =-+上,当0a >时,下列说法一定正确的是( ) A .若120y y <,则30y > B .若230y y >,则10y < C .若130y y <,则20y >D .若1230y y y =,则20y =二、填空题 9.如图,ABCD ,AD ,BC 交于点O ,12AO OD =.若3BO =,则OC 的长为______.10.在半径为3的圆中,60°的圆心角所对的劣弧长等于_____. 11.如图,在平面直角坐标系xOy 中,P 为函数)(0my x x=>图象上一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为M ,N .若矩形PMON 的面积为3,则m 的值为______.12.如图,ABC 的高AD ,BE 相交于点O ,写出一个与AOE △相似的三角形,这个三角形可以是______.13.如图,PA ,PB 是O 的切线,切点分别为A ,B .若30OBA ∠=︒,3PA =,则AB 的长为________.14.有一块三角形的草坪,其中一边的长为10m .在这块草坪的图纸上,这条边的长为5cm .已知图纸上的三角形的周长为15cm ,则这块草坪的周长为______m . 15.北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如图,赛道剖面图的一部分可抽象为线段AB .已知坡AB 的长为30m ,坡角ABH∠约为37°,则坡AB 的铅直高度AH 约为______m .(参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈.)16.如图,在平面直角坐标系xOy 中,P 为x 轴正半轴上一点.已知点)(0,2A ,)(0,8B ,M 为ABP 的外接圆.(1)点M 的纵坐标为______;(2)当APB ∠最大时,点P 的坐标为______.三、解答题17)(0604cos 451π︒-︒--18.如图,AE 平分BAC ∠,D 为AE 上一点,B C ∠=∠.(1)求证:ABEACD ;(2)若D 为AE 中点,4BE =,求CD 的长.19.在平面直角坐标系xOy 中,已知抛物线243y x x =-+. (1)求它的顶点坐标; (2)求它与x 轴的交点坐标.20.下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程. 已知:如图,ABC .求作:直线BD ,使得BD AC ∥. 作法:如图,①分别作线段AC ,BC 的垂直平分线1l ,2l ,两直线交于点O ; ①以点O 为圆心,OA 长为半径作圆;①以点A 为圆心,BC 长为半径作弧,交AB 于点D ; ①作直线BD .所以直线BD 就是所求作的直线. 根据小石设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹) (2)完成下面的证明. 证明:连接AD ,①点A ,B ,C ,D 在O 上,AD BC =, ①AD =______.①DBA CAB ∠=∠(______)(填推理的依据). ①BD AC ∥.21.如图,在ABC 中,45B ∠=︒,2tan 3C =,AC =BC 的长.22.在平面直角坐标系xOy 中,二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:(1)求这个二次函数的表达式; (2)画出这个二次函数的图象;(3)若3y <-,结合函数图象,直接写出x 的取值范围.23.如图,AB 为O 的直径,点C 在O 上,连接AC ,BC ,过点O 作OD BC ⊥于点D ,过点C 作O 的切线交OD 的延长线于点E .(1)求证:E B ∠=∠;(2)连接AD .若CE =8BC =,求AD 的长.24.如图,排球运动场的场地长18m ,球网高度2.24m ,球网在场地中央,距离球场左、右边界均为9m .一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.某次发球,排球从左边界的正上方发出,击球点的高度为2m ,当排球飞行到距离球网3m 时达到最大高度2.5m .小石建立了平面直角坐标系xOy (1个单位长度表示1m ),求得该抛物线的表达式为215722y x =-+.根据以上信息,回答下列问题:(1)画出小石建立的平面直角坐标系; (2)判断排球能否过球网,并说明理由.25.在平面直角坐标系xOy 中,反比例函数)(0ky k x=≠的图象过点)(2,3A . (1)求k 的值;(2)过点)()(,00P m m ≠作x 轴的垂线,分别交反比例函数)(0ky k x =≠,4y x=-的图象于点M ,N .①当2m =-时,求MN 的长;①若5MN ≥,直接写出m 的取值范围.26.在平面直角坐标系xOy 中,()11,A m y -,()23,B y 是抛物线2224y x mx m =-+-上两点.(1)将2224y x mx m =-+-写成()2y a x h k =-+的形式; (2)若1m =,比较1y ,2y 的大小,并说明理由; (3)若12y y <,直接写出m 的取值范围.27.如图,AD 是ABC 的高,点B 关于直线AC 的对称点为E ,连接CE ,F 为线段CE 上—点(不与点E 重合),AF AB =.(1)比较AFE ∠与ABC ∠的大小;(2)用等式表示线段BD ,EF 的数量关系,并证明.(3)连接BF ,取BF 的中点M ,连接DM .判断DM 与AC 的位置关系,并证明.28.在平面直角坐标系xOy 中,O 的半径为2.点P ,Q 为O 外两点,给出如下定义:若O 上存在点M ,N ,使得P ,Q ,M ,N 为顶点的四边形为矩形,则称点P ,Q 是O 的“成对关联点”.(1)如图,点A ,B ,C ,D 横、纵坐标都是整数.在点B ,C ,D 中,与点A 组成O 的“成对关联点”的点是______;(2)点)(,E t t 在第一象限,点F 与点E 关于x 轴对称.若点E ,F 是O 的“成对关联点”,直接写出t 的取值范围;(3)点G 在y 轴上.若直线4y =上存在点H ,使得点G ,H 是O 的“成对关联点”,直接写出点G 的纵坐标G y 的取值范围.参考答案:1.C【分析】根据“内项之积等于外项之积”对四个选项进行计算,然后与条件进行对比即可判断. 【详解】解:A 、52xy =,得25x y =,故选项A 不符合题意; B 、 25x y=,得10xy =,故选项B 不符合题意; C 、25x y =,得52x y =,故选项C 符合题意; D 、25y x =,得52y x =,故选项D 不符合题意; 故选:C .【点睛】此题主要考查了比例的性质,正确将已知变形是解题关键. 2.B【分析】根据锐角的正弦为对边比斜边求出sin A 的值即可. 【详解】解:在Rt ABC △中,90C ∠=︒,4AB =,3BC =, ①3sin 4BC A AB ==. 故选:B .【点睛】本题考查锐角三角函数的定义及运用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边. 3.D【分析】抛物线的平移规律:左加右减,上加下减,利用平移规律直接可得答案. 【详解】解:抛物线2y x =向上平移2个单位长度得到的抛物线为22,y x故选D【点睛】本题考查的是抛物线的平移,掌握“抛物线的上下平移规律”是解本题的关键. 4.A【分析】根据抛物线开口方向可得a<0,可对A 进行判断;根据对称轴位置可得b >0,可对B 进行判断;根据抛物线与y 轴交点位置可得c <0,可对C 进行判断;根据抛物线与x 轴无交点可得①<0,可对D 进行判断;综上即可得答案. 【详解】①抛物线开口向下, ①a<0,故A 选项正确, ①对称轴在y 轴右侧,①2ba->0, ①b >0,故B 选项错误, ①抛物线与y 轴交于y 轴负半轴, ①c <0,故C 选项错误, ①抛物线与x 轴无交点, ①①<0,故D 选项错误, 故选:A .【点睛】本题考查二次函数图象与系数的关系,当a =0时,抛物线开口向上,当a <0时,开口向下;当对称轴在y 轴左侧时,a 、b 同号,当对称轴在y 轴右侧时,a 、b 异号;c 的符号由图象与y 轴的交点位置决定;当①>0时,图象与x 轴有2个交点,当①=0时,图象与x 轴有1个交点;①<0时,图象与x 轴没有交点;熟练掌握相关知识是解题关键. 5.B【分析】根据反比例函数的性质求解. 【详解】解:反比例函数)(0ky x x=<的函数值y 随着自变量x 的增大而增大, 所以双曲线的两支分别位于第二、第四象限,而x <0,则分支在第二象限. 故选:B .【点睛】本题考查了反比例函数的性质:反比例函数ky x=(k ≠0)的图象是双曲线;当k >0,双曲线的两支分别位于第一、第三象限,在每一象限内y 随x 的增大而减小;当k <0,双曲线的两支分别位于第二、第四象限,在每一象限内y 随x 的增大而增大. 6.B【分析】设①ADC =α,①ABC =β,由菱形的性质与圆周角定理可得18012,求出β即可解决问题.【详解】解:设①ADC =α,①ABC =β; ①四边形ABCO 是菱形, ①①ABC =①AOC β=; ∴ ①ADC =12β;四边形ABCD 为圆的内接四边形,∴α+β=180°,①18012,解得:β=120°,α=60°,则①ADC =60°, 故选:B .【点睛】该题主要考查了圆周角定理及其应用,圆的内接四边形的性质,菱形的性质;掌握“同圆或等圆中,一条弧所对的圆周角是它所对的圆心角的一半”是解本题的关键. 7.C【分析】由周长,先求出正方形的边长,然后结合面积公式,即可得到答案. 【详解】解:①正方形的周长为x ,①正方形的边长为4x,①正方形的面积221()416x y x ==; 故选:C .【点睛】本题考查了函数表达式,解题的关键是掌握正方形的面积和周长公式. 8.A【分析】根据二次函数解析式可得抛物线对称轴及开口方向,根据各点横坐标可判断312y y y >>,进而求解.【详解】解:①22y ax ax c =-+中0a >, ①抛物线开口向上,对称轴为直线212ax a-=-=, ①411(1)21->-->-, ①312y y y >>,当120y y <时,12y y ,异号, ①1200y y ><,,①310y y >>,选项A 正确. 当3120y y y >>>时,230y y >, ①选项B 错误,当130y y <时,3100y y ><,, ①210y y <<,选项C 错误.当1230y y y =时,123y y y ,,中有1个值为0即可, ①选项D 错误. 故选:A .【点睛】本题考查二次函数图象上点的坐标特征,解题关键是掌握二次函数的性质,掌握二次函数图象与系数的关系. 9.6【分析】根据ABCD 可以证明ODC OAB △∽△,进而得出比例式,再根据12AO OD =和3BO =即可求出OC 的长度. 【详解】解:①ABCD ,AD ,BC 交于点O ,①D A ∠=∠,C B ∠=∠. ①ODC OAB △∽△. ①OD OCOA OB=. ①12AO OD =, ①2ODOA=. ①2OCOB=. ①3BO =, ①6OC =. 故答案为:6.【点睛】本题考查相似三角形的判定定理和性质,综合应用这些知识点是解题关键. 10.π【分析】弧长公式为l =n 180rπ,把半径和圆心角代入公式计算就可以求出弧长. 【详解】解:半径为3的圆中,60°的圆心角所对的劣弧长=603180π⨯=π, 故答案为:π.【点睛】本题主要考查了弧长计算,关键是掌握弧长计算公式.11.3【分析】根据反比例函数的解析式是m y x=,设点(,)P a b ,根据已知得出3ab =,即3xy =,求出即可.【详解】解:设反比例函数的解析式是my x=, 设点(,)P a b 是反比例函数图象上一点, 矩形PMON 的面积为3,3ab ∴=,即3m xy ==, 故答案为:3.【点睛】本题考查了矩形的面积和反比例函数的有关内容的应用,解题的关键是主要考查学生的理解能力和运用知识点解题的能力. 12.ACD ∆(答案不唯一)【分析】根据已知条件得到90AEO BDO ∠=∠=︒,AOE BOD ∠=∠,推出AOE BOD ∆∆∽;同理AOE ACD ∆∆∽,根据相似三角形的性质得到AFE C ∠=∠,又90AEO BEC ∠=∠=︒,于是得到AOE BCE ∆∆∽.【详解】解:本题答案不唯一;与AOE ∆相似的三角形有:BOD ∆,ACD ∆,BCE ∆, 选择求证:ACD AOE ∆∆∽.证明:ABC ∆的高AD ,BE 交于点O ,90ADC AEO ∴∠=∠=︒. CAD OAE ∠=∠, ACD AOE ∴∆∆∽,故答案是:ACD ∆.【点睛】本题考查了相似三角形的判定,三角形的高的定义,解题的关键是掌握有两角对应的两个三角形相似. 13.3【分析】根据切线长定理和切线的性质,得出PA PB =,90PBO ∠=︒,再根据等腰三角形的判定定理,得出PAB 为等腰三角形,再根据角之间的数量关系,得出60PBA ∠=︒,再根据等边三角形的判定定理,得出PAB 为等边三角形,再根据等边三角形的性质,得出AB PA =,进而即可得出答案.【详解】解:①PA ,PB 分别为O 的切线, ①PA PB =,90PBO ∠=︒, ①PAB 为等腰三角形, ①30OBA ∠=︒,①60PBA PBO OBA ∠=∠-∠=︒, ①PAB 为等边三角形, ①AB PA =, ①3PA =, ①3AB =. 故答案为:3【点睛】本题考查了切线长定理、切线的性质、等腰三角形的判定定理、等边三角形的判定与性质,解本题的关键在熟练掌握相关的性质定理. 14.30【分析】设这块草坪的周长为x m ,由实际的三角形草坪与图纸上的三角形草坪是相似三角形,再利用相似三角形的性质列方程即可. 【详解】解:设这块草坪的周长为x m ,由题意可得:实际的三角形草坪与图纸上的三角形草坪是相似三角形,10,155x解得:30x =,所以这块草坪的周长为30m. 故答案为:30【点睛】本题考查的是相似三角形的性质,掌握“相似三角形的周长之比等于相似比”是解本题的关键. 15.18【分析】由30,37,90,AB ABHAHB 结合sin 37,AHAB再解方程即可. 【详解】解:由题意得:30,37,90,AB ABH AHBsin 37,AHAB300.6018AHm ,故答案为:18【点睛】本题考查的是解直角三角形的实际应用,掌握“由锐角的正弦求解直角三角形的边长”是解本题的关键. 16. 5 (4,0)【分析】(1)根据点M 在线段AB 的垂直平分线上求解即可;(2)点P 在①M 切点处时,APB ∠最大,而四边形OPMD 是矩形,由勾股定理求解即可. 【详解】解:(1)①①M 为△ABP 的外接圆, ①点M 在线段AB 的垂直平分线上, ①A (0,2),B (0,8), ①点M 的纵坐标为:8252+=, 故答案为:5;(2)过点)(0,2A ,)(0,8B ,作①M 与x 轴相切,则点M 在切点处时,APB ∠最大, 理由:若点P '是x 轴正半轴上异于切点P 的任意一点, 设AP '交①M 于点E ,连接AE ,则①AEB =①APB , ①①AEB 是ΔA P 'E 的外角, ①①AEB>①A P 'B ,①①APB >①A P 'B ,即点P 在切点处时,①APB 最大, ①①M 经过点A (0,2)、B (0,8),①点M 在线段AB 的垂直平分线上,即点M 在直线y =5上,①①M 与x 轴相切于点P ,MP ①x 轴,从而MP =5,即①M 的半径为5,设AB 的中点为D ,连接MD 、AM ,如上图,则MD ①AB ,AD =BD =12AB =3,BM =MP =5,而①POD =90°,①四边形OPMD 是矩形,从而OP =MD , 由勾股定理,得MD 4=, ①OP =MD =4,①点P 的坐标为(4,0),故答案为:(4,0).【点睛】本题考查了切线的性质,线段垂直平分线的性质,矩形的判定及勾股定理,正确作出图形是解题的关键. 17.2【分析】将特殊角的三角函数值代入,然后利用二次根式的运算法则计算即可得.()0604cos 451π︒-︒--41-+31=-+2=.【点睛】题目主要考查特殊角的三角函数值的计算,二次根式的混合运算,0次幂的运算,熟记特殊角的三角函数值是解题关键. 18.(1)证明见详解;(2)CD 的长为2.【分析】(1)由角平分线的定义可得BAE EAC ∠=∠,根据相似三角形的判定定理即可证明; (2)由中点的定义可得12AD AE =,再由(1)中结论相似三角形的性质即可得. 【详解】解:(1)证明∵AE 平分BAC ∠, ∴BAE EAC ∠=∠, 在ABE ∆与ACD ∆中, ∵BAE EAC ∠=∠,B C ∠=∠,∴~ABE ACD ∆∆;(2)∵D 为AE 中点, ∴12AD AE =, ∵~ABE ACD ∆∆, ∴12AD CD AE BE ==, ∴122CD BE ==, ∴CD 的长为2.【点睛】题目主要考查相似三角形的判定和性质,角平分线和线段中点的性质,熟练掌握相似三角形的判定和性质是解题关键. 19.(1)()2,1-;(2)1,0,3,0. 【分析】(1)把抛物线化为顶点式即可;(2)令0,y = 则2430,x x -+=再利用因式分解法解一元二次方程即可. 【详解】解:(1)224321,yx x x所以抛物线的顶点坐标为:2,1. (2)令0,y = 则2430,x x -+=()()130,x x ∴--=10x ∴-=或30,x -=解得:121,3,x x ==所以抛物线与x 轴的交点坐标为:1,0,3,0.【点睛】本题考查的是求解抛物线的顶点坐标,抛物线与x 轴的交点坐标,掌握“把抛物线化为顶点式以及把0y =代入抛物线求解与x 轴的交点坐标”是解本题的关键. 20.(1)作图见解析;(2),BC 在同圆中,等弧所对的圆周角相等 【分析】(1)根据题干的作图步骤依次作图即可;(2)由作图可得AD BC =,证明AD BC =,利用圆周角定理可得DBA CAB ∠=∠,从而可得答案.【详解】解:(1)如图,直线BD 就是所求作的直线(2)证明:连接AD ,①点A ,B ,C ,D 在O 上,AD BC =, ①AD BC =.①DBA CAB ∠=∠(在同圆中,等弧所对的圆周角相等). ①BD AC ∥.故答案为:,BC 在同圆中,等弧所对的圆周角相等【点睛】本题考查的是作线段的垂直平分线,三角形的外接圆,平行线的作图,圆周角定理的应用,掌握“圆周角定理”是理解作图的关键. 21.10【分析】过点A 作AD ①BC ,结合三角函数值,分别求出BD 、CD 的长度,即可得到答案. 【详解】解:根据题意,过点A 作AD ①BC ,如图:①①ABD ,①ACD 都是直角三角形, ①2tan 3AD C CD ==, 设2AD x =,3CD x =,①AC == 解得:2x =(负值已舍去), ①4=AD ,6CD =, ①45B ∠=︒, ①4BD AD ==, ①4610BC =+=;【点睛】本题考查了三角函数,勾股定理,等腰直角三角形的性质,解题的关键是正确的求出BD 、CD 的长度.22.(1)22y x x =-+;(2)图象见解析;(3)1x <-或x >3【分析】(1)设二次函数的表达式为2y ax bx c =++,根据三组横坐标x 和纵坐标y 的值列出方程组求出a ,b ,c 的值即可得到二次函数的表达式;(2)计算并补充出一些横坐标x 和纵坐标y 的对应值,然后在平面直角坐标系中描点,并用平滑曲线连接即可;(3)根据二次函数的图象应用数形结合思想即可得到x 的取值范围. 【详解】解:(1)设二次函数的表达式为2y ax bx c =++. 将三组横坐标x ,纵坐标y 的值代入可得222000,111,022a b c a b c a b c ⎧=⨯++⎪=⨯++⎨⎪=⨯++⎩.解得1,2,0a b c =-⎧⎪=⎨⎪=⎩.所以二次函数的表达式为22y x x =-+. (2)横坐标x 与纵坐标y 的对应值如下表:建立平面直角坐标系,描点并用平滑曲线连接即可得到该二次函数的图象.(3)3y <-,即223x x -+<-.根据(2)中二次函数图象可以看出当1x <-或x >3时,3y <-. 所以x 的取值范围是1x <-或x >3.【点睛】本题考查二次函数的解析式,二次函数的图象和性质,熟练掌握这些知识点是解题关键.23.(1)证明见解析;(2)AD 【分析】(1)连接OC 通过垂径定理和等腰三角形性质证明①E =①B(2)连接AD 通过计算发现BC =EC ,再通过证明①CED ①①ABC 得到AC =DC =4. 【详解】(1)证明:连接OC 如图:OD ①CB①OB =OC ,①B =OCD又CE 为圆O 的切线①OC ①CE①①ECD +①DCO =①ECD +①E =90°①①E =①DCO =①B①①E =①B(2)连接AD 如图①①EDC 为R t①①DE由(1)得①E =①B又AB 为直径①①BCA =90°在①CED 和①ABC 中 ①B E EDC BCA ED BC ∠=∠⎧⎪∠=∠⎨⎪=⎩①①CED ①①ABC (AAS )①AC =DC =12BC =4①AD ==【点睛】本题考查垂径定理和全等三角形的判定与性质,掌握这些是本题解题关键.24.(1)见解析;(2)排球能过球网,理由见解析【分析】(1)根据该抛物线的表达式为215722y x =-+,可得抛物线的顶点坐标为50,2⎛⎫⎪⎝⎭,从而得到小石建立的平面直角坐标系是以O 为坐标原点,OB 所在的直线为x 轴,OA 所在的直线为y 轴,即可求解;(2)根据题意得:当3x = 时,2153 2.375 2.24722y =-⨯+=> ,即可求解. 【详解】解:(1)如图,①该抛物线的表达式为215722y x =-+, ①抛物线的顶点坐标为50,2⎛⎫ ⎪⎝⎭ ,①当排球飞行到距离球网3m 时达到最大高度2.5m .根据题意得:点A 的坐标为50,2⎛⎫ ⎪⎝⎭,①小石建立的平面直角坐标系是以O 为坐标原点,OB 所在的直线为x 轴,OA 所在的直线为y 轴,如下图:(2)排球能过球网,理由如下:根据题意得:点B 的横坐标为3,①当3x = 时,2153 2.375 2.24722y =-⨯+=> , ①排球能过球网.【点睛】本题主要考查了建立二次函数的图象和性质,建立适当的平面直角坐标系,熟练掌握二次函数的图象和性质是解题的关键.25.(1)6;(2)①5;①20m -<<或02m <<【分析】(1)把(2,3)A 代入k y x =中即可得出k 的值; (2)①令2x =-代入6y x =和4y x =-中,求出点M 、N 的坐标,即可得出MN 的长; ①令x m =代入6y x =和4y x=-中,求出点M 、N 的坐标,即可得出MN 含m 的表达式,由5MN >即可求出m 的取值范围.【详解】(1))把(2,3)A 代入k y x=中得:32k =, ①6k =;(2)①令2x =-代入6y x =中得:632y ,①(2,3)M --, 令2x =-代入4y x =-中得:422y =-=-, ①(2,2)N -,①235MN =+=;①令x m =代入6y x =中得:6y m =, ①6(2,)M m-, 令x m =代入4y x=-中得:4y m =-, ①4(2,)N m --,①6410+MN m m m==, 当0m >时,105MN m=>, 解得:2m <,①02m <<, 当0m <时,105MN m=->, 解得:2m >-,①20m -<<, 综上述所,m 的取值范围为20m -<<或02m <<.【点睛】本题考查反比例函数的综合应用,掌握待定系数法求解析式以及两点长度的表示是解题的关键.26.(1)()24y x m =-- (2)12y y <(3)2m <或4m >【分析】(1)利用完全平方公式即可求解;(2)当1m =时,确定函数解析式,根据点A ,点B 到对称轴的距离即可判断1y ,2y 的大小; (3)先求出抛物线的对称轴,根据12y y <可知点A 到对称轴的距离小于点B 到对称轴的距离,解不等式即可.【详解】(1)解:2224y x mx m =-+-()24x m =--;(2)解:12y y <,理由如下:若1m =,则抛物线的解析式为()214y x =--,()10,A y ,()23,B y , ∴对称轴为1x =,0131-<-,∴点()23,B y 到对称轴的距离大于点()10,A y 到对称轴的距离,0a >,∴12y y <;(3)解:()24y x m =--的图象开口向上,对称轴为x m =, ∴点()11,A m y -到对称轴的距离为11m m --=,点()23,B y 到对称轴的距离为3m -,12y y <, ∴31m ->,∴31m ->或31m -<-,∴2m <或4m >.【点睛】本题考查二次函数的顶点式,利用函数图象判断函数值的大小,解一元一次不等式等,熟练掌握二次函数的图象和性质是解题的关键.27.(1)AFE ABC ∠=∠,理由见详解;(2)2EF BD =,理由见详解;(3)DH①AC .【分析】(1)过点A 作AG ①CE ,然后利用HL 证明Rt ①ABD ①Rt ①AFG ,即可得到结论成立; (2)连接AE ,则AE =AF ,则AG 垂直平分EF ,则BD FG EG ==,即可得到答案;(3)连接BF ,取BF 的中点M ,连接AM ,DM 并延长交AC 于H ,由等腰三角形的性质知①BAM+①ABM=90°,再利用四边形内角和定理说明①ACB+①BAM=90°,则①ACD=①ABM ,由①AMB=①ADB=90°,由四点A 、B 、D 、M 共圆解决问题.【详解】解:(1)AFE ABC ∠=∠;理由如下:过点A 作AG ①CE ,如图:根据题意,点B 关于直线AC 的对称点为E ,①AC 平分①BCE ,①AD ①BC ,AG ①CE ,①AD =AG ,①AF =AB ,①Rt①ABD①Rt①AFG(HL),∠=∠;①AFE ABC(2)2=;EF BD理由如下:连接AE,如图:①Rt①ABD①Rt①AFG,=,①BD FG①点B关于直线AC的对称点为E,①AB=AE,①AE=AF,①AG垂直平分EF,=,①FG EG==,①BD FG EG①2=;EF BD(3)DM①AC,理由如下:连接BF,取BF的中点M,连接AM,DM并延长交AC于H,①AB=AF,点M为BF的中点,①AM①BF,①①BAM+①ABM=90°,①点B 关于直线AC 的对称点为E ,①①ACB=①ACF ,①①ABC=①AFE ,①①ABC+①AFC=180°,①①BAF+①BCF=180°,①①ACB+①BAM=90°,①①ACD=①ABM ,①①AMB=①ADB=90°,①四点A 、B 、D 、M 共圆,①①ABM=①ADM ,①①ADM+①HDC=90°,①①ACD+①HDC=90°,①DH①AC .【点睛】本题考查了轴对称的性质,全等三角形的判定和性质,垂直平分线的性质,角平分线的性质定理,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行解题.28.(1)B 和C ;(22t ≤;(3)42G y <≤+【分析】(1)根据图形可确定与点A 组成O 的“成对关联点”的点;(2)如图,点E 在直线y x =上,点F 在直线y x =-上,当点E 在线段01E E 上,点F 在线段01F F 上时,有O 的“成对关联点”,求出即可得出t 的取值范围;(3)分类讨论:点G 在4y =上,点G 在4y =的下方和点G 在4y =的上方,构造O 的“成对关联点”,即可求出G y 的取值范围.【详解】(1)如图所示:在点B ,C ,D 中,与点A 组成O 的“成对关联点”的点是B 和C ,故答案为:B 和C ;(2)①(,)E t t①(,)E t t 在直线y x =上,①点F 与点E 关于x 轴对称,①(,)F t t -在直线y x =-,如下图所示:直线y x =和y x =-与O 分别交于点0E ,0F ,与直线2x =分别交于1E ,1F ,由题可得:0E ,当点E 在线段01E E 上时,有O 的“成对关联点”2t ≤;(3)如图,当点G 在4y =上时,GH x ∥轴,在O 上不存在这样的矩形;如图,当点G 在4y =下方时,也不存在这样的矩形;如图,当点G 在4y =上方时,存在这样的矩形GMNH ,当恰好只能构成一个矩形时,设(0,)G m ,直线4y =与y 轴相交于点K ,则GHK OGM ∠=∠,2OM =,OG m =,4GH MN ==,4GK m =-,①sin sin GHK OGM ∠=∠,即GK OM GH OG =, ①424m m-=,解得:2m =+2m =-,综上:当42G y <≤+G ,H 是O 的“成对关联点”.【点睛】本题考查几何图形综合问题,属于中考压轴题,掌握“成对关联点”的定义是解题的关键.。
2025届北京市海淀区名校九年级数学第一学期期末监测试题含解析

2025届北京市海淀区名校九年级数学第一学期期末监测试题请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)1.如图,点E 是△ABC 的内心,AE 的延长线和△ABC 的外接圆相交于点D ,连接BD ,CE ,若∠CBD =32°,则∠BEC 的大小为( )A .64°B .120°C .122°D .128°2.我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总 人口为4400000000人,这个数用科学记数法表示为( )A .4.4×108B .4.40×108C .4.4×109D .4.4×10103.如图,已知在△ABC 纸板中,AC =4,BC =8,AB =11,P 是BC 上一点,沿过点P 的直线剪下一个与△ABC 相似的小三角形纸板,如果有4种不同的剪法,那么CP 长的取值范围是( )A .0<CP ≤1B .0<CP ≤2C .1≤CP <8D .2≤CP <84.下列选项中,y 是x 的反比例函数的是( )A .23y x =B .45x y =C .1y 2x -=-D .k y x= 5.抛掷一个质地均匀且六个面上依次刻有1-6的点数的正方体型骰子,如图.观察向上的一面的点数,下列情况属必然事件的是( ).A .出现的点数是7B .出现的点数不会是0C .出现的点数是2D .出现的点数为奇数6.成语“水中捞月”所描述的事件是( ).A .必然事件B .随机事件C .不可能事件D .无法确定 7.若反比例函数(0)k y k x=≠的图象经过点(1,2)-,则这个函数的图象一定还经过点( ) A .(2,1)- B .(,)122- C .(2,1)-- D .1(,2)2 8.如图,点D 是△ABC 的边BC 上一点,∠BAD =∠C ,AC =2AD ,如果△ACD 的面积为15,那么△ABD 的面积为( )A .15B .10C .7.5D .59.在△ABC 中,若三边BC ,CA ,AB 满足BC :CA :AB =3:4:5,则cos A 的值为( )A .34B .43C .35D .45 10.二次函数2y ax bx c =++(,,a b c 是常数,0a ≠)的自变量x 与函数值y 的部分对应值如下表: x … 2- 1- 01 2 … 2y ax bx c =++ … t m 2- 2- n …且当12x =-时,与其对应的函数值0y >.有下列结论:①0abc >;②2-和3是关于x 的方程2ax bx c t ++=的两个根;③0m <203n +<.其中,正确结论的个数是( ) A .0 B .1 C .2 D .3二、填空题(每小题3分,共24分)11.如图,以等边△ABC 的一边AB 为直径的半圆O 交AC 于点D ,交BC 于点E ,若AB =4,则阴影部分的面积是______.12.已知:a ,b 在数轴上的位置如图所示,化简代数式:22(1)()|1|a a b b --++-=_____.13.如图,AB 是O 的直径,点C 在O 上,且CD AB ⊥,垂足为D ,4CD =,3OD =,则BD =__________.14.如图,在四边形ABCD 中,AD BC =,E 、F 、G 分别是AB 、CD 、AC 的中点,若15DAC ∠=︒,87ACB ∠=︒,则FEG ∠等于______________.15.若二次函数y =mx 2+2x +1的图象与x 轴有公共点,则m 的取值范围是 _____.16.如图,在平面直角坐标系中,直线l 的函数表达式为y =x ,点O 1的坐标为(1,0),以O 1为圆心,O 1O 为半径画圆,交直线l 于点P 1,交x 轴正半轴于点O 2,以O 2为圆心,O 2O 为半径画圆,交直线l 于点P 2,交x 轴正半轴于点O 3,以O 3为圆心,O 3O 为半径画圆,交直线l 于点P 3,交x 轴正半轴于点O 4;…按此做法进行下去,其中20172018P O 的长为_____.17.若a 、b 、c 、d 满足,则=_____.18.写出一个对称轴是直线1x =,且经过原点的抛物线的表达式______.三、解答题(共66分)19.(10分)某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处回合,如图所示,以水平方向为x 轴,喷水池中心为原点建立平面直角坐标系.(1)求水柱所在抛物线(第一象限部分)的函数表达式;(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?20.(6分)如图,在□ABCD 中,AD 是⊙O 的弦,BC 是⊙O 的切线,切点为B .(1)求证:=AB BD ;(2)若AB =5,AD =8,求⊙O 的半径.21.(6分)东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.(1)求第一批悠悠球每套的进价是多少元;(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?22.(8分)如图,Rt ABO ∆的顶点A 是双曲线k y x=与直线()1y x k =--+在第二象限的交点.AB x ⊥轴于B ,且32ABO S ∆=.(1)求反比例函数的解析式;(2)直线与双曲线交点为A 、C ,记AOC ∆的面积为1S ,AOB ∆的面积为2S ,求12:S S23.(8分)用配方法解方程:22480x x --=24.(8分)解方程:x+3=x (x+3)25.(10分)(1)计算:2sin 60tan 452cos60︒︒︒-+;(2)解方程:2450x x -=+.26.(10分)体育文化公司为某学校捐赠甲、乙两种品牌的体育器材,甲品牌有A 、B 、C 三种型号,乙品牌有D 、E 两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.(1)下列事件是不可能事件的是 .A .选购乙品牌的D 型号B .既选购甲品牌也选购乙品牌C .选购甲品牌的A 型号和乙品牌的D 型号 D .只选购甲品牌的A 型号(2)写出所有的选购方案(用列表法或树状图);(3)如果在上述选购方案中,每种方案被选中的可能性相同,那么A 型器材被选中的概率是多少?参考答案一、选择题(每小题3分,共30分)1、C【分析】根据圆周角定理可求∠CAD=32°,再根据三角形内心的定义可求∠BAC ,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB ,再根据三角形内角和定理可求∠BEC 的度数.【详解】在⊙O 中,∵∠CBD=32°,∴∠CAD=32°,∵点E是△ABC的内心,∴∠BAC=64°,∴∠EBC+∠ECB=(180°-64°)÷2=58°,∴∠BEC=180°-58°=122°.故选:C.【点睛】本题考查了三角形的内心,圆周角定理,三角形内角和定理,关键是得到∠EBC+∠ECB的度数.2、C【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:4 400 000 000=4.4×109,故选C.3、B【分析】分四种情况讨论,依据相似三角形的对应边成比例,即可得到AP的长的取值范围.【详解】如图所示,过P作PD∥AB交AC于D或PE∥AC交AB于E,则△PCD∽△BCA或△BPE∽△BCA,此时0<PC<8;如图所示,过P作∠BPF=∠A交AB于F,则△BPF∽△BAC,此时0<PC<8;如图所示,过P作∠CPG=∠B交AC于G,则△CPG∽△CAB,此时,△CPG∽△CBA,当点G与点A重合时,CA1=CP×CB,即41=CP×8,∴CP=1,∴此时,0<CP≤1;综上所述,CP 长的取值范围是0<CP ≤1.故选B .【点睛】本题主要考查了相似三角形的性质,解决本题的关键是要熟练掌握相似三角形的性质.4、C【解析】根据反比例函数的定义“一般的,如果两个变量x ,y 之间的关系可以表示成k y x=,其中k 为常数,0,0k x ≠≠,我们就叫y 是x 的反比例函数”判定即可.【详解】A 、x 的指数是2-,不符定义B 、x 的指数是1,y 与x 是成正比例的,不符定义C 、1y 2x -=-可改写成2y x =-,符合定义 D 、k y x=当0k =是,函数为0y =,是常数函数,不符定义 故选:C.【点睛】本题考查了反比例函数的定义,熟记定义是解题关键.5、B【解析】分析:必然事件就是一定发生的事件,根据定义即可作出判断.解答:解:A 、不可能发生,是不可能事件,故本选项错误,B 、是必然事件,故正确,C 、不一定发生,是随机事件,故本选项错误,D 、不一定发生,是随机事件,故本选项错误.故选B .6、C【分析】根据必然事件、不可能事件、随机事件的概念进行解答即可.【详解】水中捞月是不可能事件.故选C .【点睛】本题考查了必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件. 7、A【分析】根据反比例函数的定义,得122k xy ==-⨯=-,分别判断各点的乘积是否等于2-,即可得到答案. 【详解】解:∵反比例函数(0)k y k x =≠的图象经过点(1,2)-, ∴122k xy ==-⨯=-;∵2(1)2⨯-=-,故A 符合题意; ∵1()212-⨯=-,2(1)2-⨯-=,1212⨯=,故B 、C 、D 不符合题意; 故选:A.【点睛】本题考查了反比例函数的定义,解题的关键是熟记定义,熟练掌握=k xy .8、D【分析】首先证明△BAD ∽△BCA ,由相似三角形的性质可得:△BAD 的面积:△BCA 的面积为1:4,得出△BAD 的面积:△ACD 的面积=1:3,即可求出△ABD 的面积.【详解】解:∵∠BAD =∠C ,∠B =∠B ,∴△BAD ∽△BCA ,∵AC =2AD , ∴214BAD BCA S AD S AC ∆∆⎛⎫== ⎪⎝⎭, ∴13BAD ACD S S ∆∆=, ∵△ACD 的面积为15,∴△ABD 的面积=13×15=5, 故选:D .【点睛】本题主要考查了相似三角形的判定与性质,掌握相似三角形的判定与性质是解题的关键.9、D【分析】根据已知条件,运用勾股定理的逆定理可得该三角形为直角三角形,再根据余弦的定义解答即可.【详解】解:设,,BA CA AB 分别为3,4,5k k k ,()()()222345k k k +=,∴ABC ∆为直角三角形, ∴4cos 5AC A AB ==. 【点睛】 本题主要考查了勾股定理的逆定理和余弦,熟练掌握对应知识点是解答关键.10、C【分析】首先确定对称轴,然后根据二次函数的图像和性质逐一进行分析即可求解.【详解】∵由表格可知当x=0和x=1时的函数值相等都为-2∴抛物线的对称轴是:x=-2b a =12; ∴a 、b 异号,且b=-a ;∵当x=0时y=c=-2∴c 0<∴abc >0,故①正确;∵根据抛物线的对称性可得当x=-2和x=3时的函数值相等都为t∴2-和3是关于x 的方程2ax bx c t ++=的两个根;故②正确;∵b=-a ,c=-2∴二次函数解析式:2-a -2=y ax x ∵当12x =-时,与其对应的函数值0y >. ∴3204a ->,∴a 83>; ∵当x=-1和x=2时的函数值分别为m 和n ,∴m=n=2a-2,∴m+n=4a-4203>;故③错误 故选C .【点睛】本题考查了二次函数的综合题型,主要利用了二次函数图象与系数的关系,二次函数的对称性,二次函数与一元二次方程等知识点,要会利用数形结合的思想,根据给定自变量x 与函数值y 的值结合二次函数的性质逐条分析给定的结论是关键.二、填空题(每小题3分,共24分)11、3 【分析】作辅助线证明△AOD ≌△DOE ≌△EOB ≌△CDE,且都为等边三角形,利用等边三角形面积公式S=23a 4即可解题.【详解】解:连接DE,OD,OE,在圆中,OA=OD=OE=OB,∵△ABC 是等边三角形,∴∠A=60°,∴△AOD ≌△DOE ≌△EOB ≌△CDE,且都为等边三角形,∵AB =4,即OA=OD=OE=OB=2,易证阴影部分面积=S △CDE =1232⨯⨯=3.【点睛】本题考查了圆的性质,等边三角形的判定和面积公式,属于简单题,作辅助线证明等边三角形是解题关键.12、1.2a |a|开平方,再结合数轴确定a ﹣1,a+b ,1﹣b 的正负性,然后去绝对值,最后合并同类项即可.【详解】原式=|a ﹣1|﹣|a+b|+|1﹣b|=1﹣a ﹣(﹣a ﹣b )+(1﹣b )=1﹣a+a+b+1﹣b =1,故答案为:1.【点睛】此题主要考查了二次根式的化简和性质,正确把握绝对值的性质是解答此题的关键.13、2【分析】先连接OC ,在Rt △ODC 中,根据勾股定理得出OC 的长,即可求得答案.【详解】连接OC ,如图,∵CD=4,OD=3,CD AB ⊥,在Rt △ODC 中, ∴2222345OC OD CD =+=+=,∵OC OB =,∴532BD OB OD =-=-=.故答案为:2.【点睛】此题考查了圆的认识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.14、36°【分析】根据三角形中位线定理得到FG ∥AD ,FG=12AD ,GE ∥BC ,GE=12BC ,根据等腰三角形的性质、三角形内角和定理计算即可.【详解】解:∵F 、G 分别是CD 、AC 的中点,∴FG ∥AD ,FG=12AD , ∴∠FGC=∠DAC=15°,∵E 、G 分别是AB 、AC 的中点,∴GE ∥BC ,GE=12BC , ∴∠EGC=180°-∠ACB=93°,∴∠EGF=108°,∵AD=BC ,∴GF=GE ,∴∠FEG=12×(180°-108°)=36°; 故答案为:36°.【点睛】本题考查的是三角形中位线定理、等腰三角形的性质,三角形的中位线平行于第三边,且等于第三边的一半.15、m ≤1且m ≠1.【分析】由抛物线与x 轴有公共点可知△≥1,再由二次项系数不等于1,建立不等式即可求出m 的取值范围.【详解】解:y =mx 2+2x+1是二次函数,∴m≠1,由题意可知:△≥1,∴4﹣4m≥1,∴m≤1∴m≤1且m≠1故答案为m≤1且m≠1.【点睛】本题考查二次函数图像与x 轴的交点问题,熟练掌握交点个数与△的关系是解题的关键.16、22015π【分析】连接P 1O 1,P 2O 2,P 3O 3,易求得P n O n 垂直于x 轴,可知1n n P O 为14圆的周长,再找出圆半径的规律即可解题.【详解】解:连接P 1O 1,P 2O 2,P 3O 3…,∵P 1 是⊙O 1上的点,∴P 1O 1=OO 1,∵直线l 解析式为y =x ,∴∠P 1OO 1=45°,∴△P 1OO 1为等腰直角三角形,即P 1O 1⊥x 轴,同理,P n O n 垂直于x 轴,∴1n n P O 为14圆的周长, ∵以O 1为圆心,O 1O 为半径画圆,交x 轴正半轴于点O 2,以O 2为圆心,O 2O 为半径画圆,交x 轴正半轴于点O 3,以此类推,∴OO 1=1=20,OO 2=2=21,OO 3=4=22,OO 4=8=23,…,∴OO n =12n -, ∴12112224n n n n P O ,∴201520172018P 2O π=,故答案为:22015π.【点睛】 本题考查了图形类规律探索、一次函数的性质、等腰直角三角形的性质以及弧长的计算,本题中准确找到圆半径的规律是解题的关键.17、【解析】根据等比性质求解即可.【详解】∵,∴=. 故答案为:.【点睛】本题考查了比例的性质,主要利用了等比性质.等比性质:在一个比例等式中,两前项之和与两后项之和的比例与原比例相等. 对于实数a ,b ,c ,d ,且有b ≠0,d ≠0,如果,则有. 18、答案不唯一(如22y x x =-)【分析】抛物线的对称轴即为顶点横坐标的值,根据顶点式写出对称轴是直线1x =的抛物线表达式,再化为一般式,再由经过原点即为常数项c 为0,即可得到答案.【详解】解:∵对称轴是直线1x =的抛物线可为:22(1)21y x x x =-=-+又∵抛物线经过原点,即C=0,∴对称轴是直线1x =,且经过原点的抛物线的表达式可以为:22y x x =-,故本题答案为:22y x x =-(答案不唯一).【点睛】 本题考查了抛物线的对称轴与抛物线解析式的关系.关键是明确对称轴的值与顶点横坐标相同.三、解答题(共66分)19、(1)()2161608555y x x x =-++≤≤;(2)王师傅必须在7米以内. 【分析】(1)由抛物线的顶点坐标为(3,5),设抛物线解析式为y=a(x-3)+5,把(8,0)单人宽求出a 的值,即可得抛物线解析式;(2)把y=1.8代入解析式求出x 的值,根据函数图像的对称性求出负半轴的坐标即可.【详解】(1)设()235y a x =-+,过点()80, ∴代入,解得15a =- ∴抛物线(第一象限部分)的函数表达式为()2161608555y x x x =-++≤≤ (2)091.85y ==∴200916165555x x =-++ 07x ∴=或-108x ≤≤,图象对称∴负半轴为-7答:王师傅必须在7米以内.【点睛】本题考查了待定系数法求二次函数解析式以及二次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数表达式;(2)利用二次函数图象上点的坐标特征求出当y=1.8时x 的值.20、(1)证明见解析;(2)⊙O 的半径为256【分析】(1) 连接OB ,根据题意求证OB⊥AD,利用垂径定理求证;(2) 根据垂径定理和勾股定理求解.【详解】解:(1)连接OB,交AD 于点E.∵BC 是⊙O 的切线,切点为B ,∴OB ⊥BC .∴∠OBC =90°∵ 四边形ABCD 是平行四边形∴AD // BC∴∠OED =∠OBC =90°∴ OE ⊥AD又 ∵ OE 过圆心O∴ =AB BD(2)∵ OE ⊥AD ,OE 过圆心O∴ AE=12AD=4 在Rt △ABE 中,∠AEB =90°,BE =3,设⊙O 的半径为r ,则OE=r -3在Rt △ABE 中,∠OEA =90°,OE 2+AE 2 = OA 2即(r -3)2+42= r 2 ∴r=256 ∴⊙O 的半径为256【点睛】掌握垂径定理和勾股定理是本题的解题关键.21、(1)第一批悠悠球每套的进价是25元;(2)每套悠悠球的售价至少是1元.【解析】分析:(1)设第一批悠悠球每套的进价是x 元,则第二批悠悠球每套的进价是(x+5)元,根据数量=总价÷单价结合第二批购进数量是第一批数量的1.5倍,即可得出关于x 的分式方程,解之经检验后即可得出结论; (2)设每套悠悠球的售价为y 元,根据销售收入-成本=利润结合全部售完后总利润不低于25%,即可得出关于y 的一元一次不等式,解之取其中的最小值即可得出结论.详解:(1)设第一批悠悠球每套的进价是x 元,则第二批悠悠球每套的进价是(x+5)元,根据题意得: 9005001.55x x=⨯+, 解得:x=25,经检验,x=25是原分式方程的解.答:第一批悠悠球每套的进价是25元.(2)设每套悠悠球的售价为y 元,根据题意得:500÷25×(1+1.5)y-500-900≥(500+900)×25%, 解得:y≥1.答:每套悠悠球的售价至少是1元.点睛:本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程是解题的关键;(2)根据各数量之间的关系,正确列出一元一次不等式.22、(1)3y x=-;(2)12S :S 8:3= 【分析】(1)由13222∆=⨯⨯==ABO k S OB AB 可得3k =,再根据函数图像可得3k =-,即可得到函数解析式. (2)先求得一次函数解析式,再联立方程组求得点A 和点C 的坐标,记直线AC 与x 轴的交点为D ,求得D 点坐标为()2,0,111422C S OD AB OD y =⋅+⋅=,即可求得12:S S . 【详解】解:(1)∵13222∆=⨯⨯==ABOk S OB AB , ∴3k =双曲线在二、四象限 3k ∴=-∴反比例函数的解析式为3y x=- (2)由(1)可得3k =-,代入可得一次函数的解析式为2y x =-+, 联立方程组23y x y x =-+⎧⎪⎨=-⎪⎩, 得11x =-,23x =易求得点A 为()1,3-,点C 为()3,1-记直线AC 与x 轴的交点为D ,在2y x =-+中,当y=0,则x=2,∴D 点坐标为()2,0111422C S OD AB OD y =⋅+⋅=,23S 2=, 12S :S 8:3∴=.【点睛】此题首先利用待定系数法确定函数解析式,然后利用解方程组来确定图象的交点坐标,及利用坐标求出线段和图形的面积.23、x 1,x 2=【分析】先把方程进行整理,然后利用配方法进行解方程,即可得到答案.【详解】解:∵22480x x --=,∴2240x x --=,∴2(1)5x -=,∴1x -=,∴x 1,x 2=【点睛】本题考查了解一元二次方程,解题的关键是熟练掌握配方法进行解一元二次方程.24、x 1=1,x 2=﹣1【分析】先利用乘法分配律将括号外面的分配到括号里面,再通过移项化成一元二次方程的标准形式,利用提取公因式即可得出结果.【详解】解:方程移项得:(x+1)﹣x (x+1)=0,分解因式得:(x+1)(1﹣x )=0,解得:x 1=1,x 2=﹣1.【点睛】本题主要考查的是一元二次方程的解法,一元二次方程的解法主要包括:提取公因式,公式法,十字相乘等.25、(1)34;(2)11x =,25x =- 【分析】(1)利用特殊角的三角函数值计算即可;(2)利用因式分解法解一元二次方程即可.【详解】(1)原式=2133(12112244-+⨯=-+= (2)原方程可变形为(5)(1)0x x +-=50x +=或10x -=125,1x x ∴=-=【点睛】本题主要考查特殊角的三角函数值及解一元二次方程,掌握特殊角的三角函数值及因式分解法是解题的关键.26、(1)D;(2)见解析;(3)13.【分析】(1)根据不可能事件和随机随机的定义进行判断;(2)画树状图展示所有6种等可能的结果数;(3)找出A型器材被选中的结果数,然后根据概率公式求解.【详解】(1)只选购甲品牌的A型号为不可能事件.故答案为D;(2)画树状图为:共有6种等可能的结果数;(3)A型器材被选中的结果数为2,所以A型器材被选中的概率=2163 .【点睛】此题考查列表法与树状图法,解题关键在于利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A 或B的结果数目m,然后利用概率公式求事件A或B的概率.。
海淀区初三期末数学试题及答案
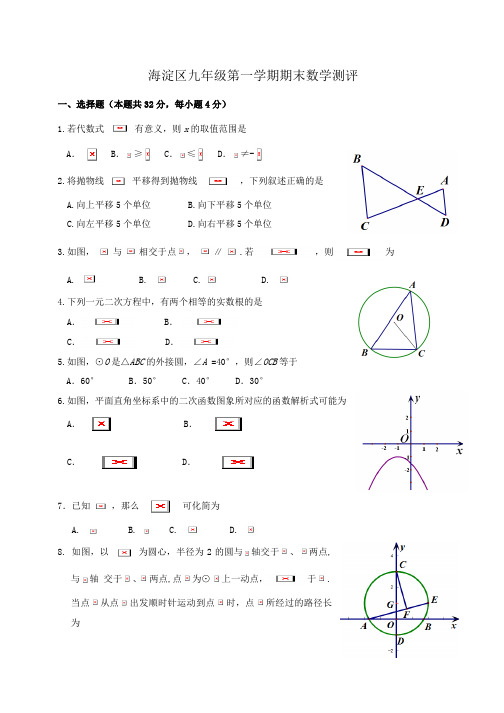
海淀区九年级第一学期期末数学测评一、选择题(本题共32分,每小题4分)1.若代数式有意义,则x的取值范围是A.B.≥C.≤D.≠-2.将抛物线平移得到抛物线,下列叙述正确的是A.向上平移5个单位B.向下平移5个单位C.向左平移5个单位D.向右平移5个单位3.如图,与相交于点,∥.若,则为A. B. C. D.4.下列一元二次方程中,有两个相等的实数根的是A.B.C. D.5.如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于A.60°B.50° C.40°D.30°6.如图,平面直角坐标系中的二次函数图象所对应的函数解析式可能为A. B.C. D.7.已知,那么可化简为A. B. C. D.8. 如图,以为圆心,半径为2的圆与轴交于、两点,与轴交于、两点,点为⊙上一动点,于.当点从点出发顺时针运动到点时,点所经过的路径长为A. B. C. D.二、填空题(本题共16分,每小题4分)9.计算= .10. 若二次函数的图象上有两个点、,则(填“<”或“=”或“>”).11.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 _________cm.12.小聪用描点法画出了函数的图象F,如图所示.结合旋转的知识,他尝试着将图象F绕原点逆时针旋转得到图象,再将图象绕原点逆时针旋转得到图象,如此继续下去,得到图象.在尝试的过程中,他发现点P在图象上(写出一个正确的即可);若点P(a,b)在图象上,则= (用含的代数式表示) .三、解答题(本题共30分,每小题5分)13. 计算:.14. 解方程: .15.已知,求代数式的值.16.如图,正方形网格中,△ABC的顶点及点O在格点上.(1)画出与△ABC关于点O对称的△;(2)画出一个以点O为位似中心的△,使得△与△的相似比为2.17.如图,在△与△中,,,=6,求的长.18.如图,二次函数的图象与x轴交于A、B两点,与y轴交于点C,顶点为D, 求△BCD的面积.四、解答题(本题共20分,每小题5分)19.已知关于的方程有两个不相等的实数根.(1)求m的取值范围;(2)若m为符合条件的最大整数,求此时方程的根.20. 已知:二次函数中的和满足下表:…0 1 2 3 4 5 …… 3 0 0 8 …(1) 可求得的值为;(2) 求出这个二次函数的解析式;(3) 当时,则y的取值范围为 .21.图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?22.如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:(1)DE为⊙O的切线;(2)延长ED交BA的延长线于F,若DF=4,AF=2,求BC的长.五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23. 小明利用等距平行线解决了二等分线段的问题.作法:(1)在e上任取一点C,以点C为圆心,AB长为半径画弧交c于点D,交d于点E;(2)以点A为圆心,CE长为半径画弧交AB于点M;∴点M为线段AB的二等分点.图1解决下列问题:(尺规作图,保留作图痕迹)(1)仿照小明的作法,在图2中作出线段AB的三等分点;图2(2)点P是∠AOB内部一点,过点P作PM⊥OA于M,PN⊥OB于N,请找出一个满足下列条件的点P. (可以利用图1中的等距平行线)①在图3中作出点P,使得;②在图4中作出点P,使得.图3 图424.抛物线与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC.(1)求这条抛物线的解析式;(2)若点P与点Q在(1)中的抛物线上,且,PQ=n.①求的值;②将抛物线在PQ下方的部分沿PQ翻折,抛物线的其它部分保持不变,得到一个新图象.当这个新图象与x轴恰好只有两个公共点时,b的取值范围是 .25.如图1,两个等腰直角三角板和有一条边在同一条直线上,,.将直线绕点逆时针旋转,交直线于点.将图1中的三角板沿直线向右平移,设、两点间的距离为.图1 图2 图3 解答问题:(1)①当点与点重合时,如图2所示,可得的值为;②在平移过程中,的值为(用含的代数式表示);(2)将图2中的三角板绕点逆时针旋转,原题中的其他条件保持不变.当点落在线段上时,如图3所示,请补全图形,计算的值;(3)将图1中的三角板ABC绕点C逆时针旋转度,≤,原题中的其他条件保持不变.计算的值(用含k的代数式表示).海淀区九年级第一学期期末练习数学试卷答案及评分参考一、选择题(本题共32分,每小题4分)题号 1 2 3 4 5 6 7 8 答案 B A D A B D C B 二、填空题(本题共16分,每小题4分)题号9101112答案(答案不唯一)、13. 计算:.解:原式=…………………………………………4分=. …………………………………………5分14. 解方程: .解法一:. …………………………………………3分或.∴ . …………………………………………5分解法二:, …………………………………1分. ……………………………………2分∴ . …………………………………………3分∴ . …………………………………………5分15.解法一:∵,∴=………………………2分=………………………3分=………………………4分==. ………………………5分解法二:∵,∴. .…………………………1分原式= .…………………………2分=.…………………………3分=.…………………………4分=. ………………………5分16.例如:∴△、△为所求.(注:第(1)问2分;第(2)问3分,画出一个正确的即可.)17. 解:∵,∴. ………………………1分∵,∴△∽△. ………………………3分∴. ………………………4分∵=6,∴.∴.∴. ………………………5分18. 解法一:依题意,可得=.∴顶点. ……………1分令,可得或.∴、. ……………2分令,可得.∴. ……………3分∴直线的解析式为.设直线交轴于.∴.∴. …….………….…………4分∴.∴△BCD的面积为3. …….………….…………5分解法二:同解法一,可得、、、. ……………3分∴直线的解析式为.过点作∥交轴于,连接.∴设过、两点的直线的解析式为.∵,∴直线的解析式为.∴.∴. ….…………4分∵∥,∴.∴△的面积为3. . .………….………………5分四、解答题(本题共20分,每小题5分)19.解:(1)∵关于的方程有两个不相等的实数根,∴. …………………………1分∴. .…………………………2分(2)∵m为符合条件的最大整数,∴. .…………………………3分∴...,.∴方程的根为,. .…………………………5分20.解:(1)的值为3;.…………………………1分(2) ∵二次函数的图象经过点(1,0),(3,0),∴设二次函数的解析式为. .…………………………2分∵图象经过点,∴. .…………………………3分∴这个二次函数的解析式为. .…………………………4分(3) 当时,则y的取值范围为≤. .…………………5分21.解:如图所示,建立平面直角坐标系.设二次函数的解析式为. .…………………1分∵图象经过点,.…………………2分∴,.∴. .…………………3分当时,. .…………………4分答:当水面高度下降1米时,水面宽度为米. .…………………5分22.(1)如图,连接. ………………1分∵在⊙O中,,∴∠1=∠2.∵是⊙O的直径,∴.∵E为BC中点,∴.∴∠3=∠4.∵BC切⊙O于点B,∴.∴,即.∴⊥.∵点在⊙O上,∴是⊙O的切线. ……………2分(2)∵⊥,∴.设.∵, DF=4,AF=2,∴.解得. ……………………………………3分∴.∵,∴△∽△. ……………………………………4分∴.∴∵E为BC中点,∴……………………………………5分五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23. 解:(1)……………………2分(注:直接等分不给分,在等距平行线上有正确痕迹的给分,作出一个给1分.) (2)①②……………………4分……………………7分24.解:(1)解法一:∵抛物线与y轴交于点C,∴. ……………………1分∵抛物线与x轴交于A、B两点,OB=OC,∴(3,0)或(-3,0).∵点A在点B的左侧,,∴抛物线经过点(3,0). ……………………2分∴.∴.∴抛物线的解析式为.……………………3分解法二:令,∴.∴.∴.,点A在点B的左侧,∴. ……………………1分令,可得.∴.∴. ……………………2分,∴.∴.∴.……………………3分(2)①由抛物线可知对称轴为. ……………4分∵点P与点Q在这条抛物线上,且,,∴. ……………………5分∴.∴原式=. ……………………6分②或. ……………………8分(注:答对一部分给1分.)25.解:(1)①1;……………………1分②;……………………2分(2)解:连接AE.∵,∴∴∴∴点为的中点. ……………………3分∴∴,∵∴.∴∴∽.∴……………………4分∴.∴.∴. ……………………5分(3)过作的垂线交直线于点,连接、.∴.∵,∴.∴.∵△为等腰直角三角形,∴∴.∴△≌△. ……………………6分∴.∵,∴.∴∥.∴△∽△.∴……………………7分(注:本卷中许多问题解法不唯一,请老师根据评分标准酌情给分.)。
海淀区2022-2023学年第一学期期末九年级数学试题及答案

海淀区九年级练习数 学 答 案第一部分 选择题一、选择题(本题共16分,每小题2分)第二部分 非选择题二、填空题(本题共16分,每小题2分)9.(0,3);10.3π; 11.0.51(答案不唯一); 12.49<m ; 13.<; 14.1;15.2x >(答案不唯一,满足32x ≥即可); 16.①③④. 三、解答题(共68分,第17-20题,每题5分,第21题6分,第22-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)17. 解:22161x x , …………………………………………………………………………………1分2(1)7.x ……………………………………………………………………………………… 3分∴ 17x . ∴ 117x ,217x . …………………………………………………………………… 5分18. 解:∵抛物线22y x bx c =++过点(1,3)和(0,4),∴ 324.b c c , ……………………………………………………………………………………… 2分 解方程组,得 34.b c , …………………………………………………………………… 4分∴抛物线的解析式是2234y x x =−+. …………………………………………………………. 5分19. 解:∵ a 为方程22310x x −−=的一个根,∴ 22310a a −−=. ………………………………………………………………………1分∴ 223 1.a a −=原式=22136a a a −+− ……………………………………………………………………3分=2461a a −− ………………………………………………………………………4分=22(23)1a a −−=211⨯−=1 . …………………………………………………………………5分20. 解:如图,连接AC. ……………………………………………………………………1分∵ BC CD =,∴ ∠DAC=∠BAC. ………………………………………… 2分∵ 50DAB ∠=, ∴ 1252BAC DAB ∠=∠=. ……………………………… 3分 ∵ AB 为直径,∴ 90ACB ∠=. ………………………………………………………………… 4分 ∴ 9065B BAC ∠=−∠=. …………………………………………………………………5分21. 解:(1)13; …………………………………………………………………… 2分 (2)根据题意,可以画出如下树状图:…………………………………… 4分由树状图可以看出,所有可能出现的结果有9种,并且这些结果出现的可能性相等.小明和小天抽到同一场地训练(记为事件A )的结果有3种,所以,P (A )31==93. …………………………………………………………………………………6分 22. (1)补全图形,如图所示:…………………………………………………………………2分(2)OA=OB , ……………………………………………………………………3分经过半径外端并且垂直于这条半径的直线是圆的切线. …………………………………………5分23. 解:如图,连接OB . ……………………………………………………………………1分∵ l 过圆心O ,l ⊥AB ,30AB =,∴ 1152BD AB ==. ……………………………………… 3分 ∵ 5CD =,∴ 5DO r =−.∵ 222BO BD DO =+,∴ 22215(5)r r =+−. ……………………………………………………………………4分解得 25r =.∴ 这个紫砂壶的壶口半径r 的长为25mm . ……………………………………………………………5分24. 证明:(1) 如图,连接OC .∵ 直线l 与⊙O 相切于点C ,∴ OC ⊥l 于点C . ………………………………………1分∴ 90OCD ∠=︒.∵ BD l ⊥于点D ,∴ 90BDC ∠=︒.∴ 180OCD BDC ∠+∠=︒.∴ OC // BD . ………………………………………2分∴ OCB CBD ∠=∠.∵ OC OB =,∴ OBC OCB ∠=∠.∴ OBC CBD ∠=∠.∴ BC 平分ABD ∠. ………………………………………………………………………………3分(2)连接AC .∵ AB 是⊙O 的直径,∴ 90ACB ∠=︒. …………………………………………………………………………………4分∵ 60ABD ∠=︒,∴ OBC CBD ∠=∠=1302ABD ∠=︒. 在Rt △BDC 中,C∵30CBD ∠=︒,CD =3,∴ 26BC CD ==. …………………………………………………………………………………5分 在Rt △ACB 中,∵30ABC ∠=︒,∴ 2AB AC =.∵ 222AC BC AB +=,∴AB =∴12OC AB == 在Rt △OCD 中,∵222OC CD OD +=,∴OD = …………………………………………………………………………………6分25. 解:(1)答案不唯一.如图,以抛物线顶点为原点,以抛物线对称轴为y 轴,建立平面直角坐标系. ……………1分 设这条抛物线表示的二次函数为y =ax 2. ………………………………………………2分∵ 抛物线过点()5 6.25−,, ∴ 25 6.25a =−. ………………………………………………………………………………3分 ∴ 0.25a =−.∴ 这条抛物线表示的二次函数为20.25y x =−. ………………………………………………4分(2)能实现; ………………………………………………………………………………………5分a ………………………………………………………………………………………6分26. 解:(1)抛物线21y ax bx =++过点(2,1),∴22211a b ⋅+⋅+=. ………………………………………………………………………………1分∴2b a =−. ………………………………………………………………………………………2分 (2)① <; …………………………………………………………………………………………3分② 由(1)知2b a =−,∴221y ax ax =−+. ∴抛物线对称轴为1x =.抛物线过点M (﹣2,m ),N (1,n ),P (3,p ),∴81m a =+,1n a =−+,31p a =+. …………………………………………………4分 当0a >时,抛物线开口向上,对称轴为1x =,∴抛物线在1x =时,取得最小值n . M ,N ,P 恰有两点在x 轴上方,∴M ,P 在x 轴上方,N 在x 轴上或x 轴下方.∴ 81031010a a a +>⎧⎪+>⎨⎪−+≤⎩,解得1a ≥. ………………………………………………………5分当0a <时,抛物线开口向下,对称轴为1x =,∴抛物线在1x =时,取得最大值n ,且m p <. M ,N ,P 恰有两点在x 轴上方,∴N ,P 在x 轴上方,M 在x 轴上或x 轴下方. ∴ 10310810a a a −+>⎧⎪+>⎨⎪+≤⎩,解得1138a −<≤−.综上,a 的取值范围是1138a −<≤−或1a ≥. …………………………………………………6分27.(1)线段AD 与AE 的数量关系:AD =2AE . …………………………………………………………1分证明:∵ DE ⊥AC ,∴ ∠DEA =90°. ∵ ∠BAC =120°,∴ ∠ADE =∠BAC -∠DEA =30°.∴ AD =2AE . …………………………………………………………2分(2)① 补全图形,如图. …………………………………………………………3分② 结论:△DCF 是等边三角形. …………………………………………………………4分 证明:延长BA 至点H 使AH =AB ,连接CH ,FH ,如图.∵ AB =AC , ∴ AH =AC .∵ ∠HAC =180°-∠BAC =60°, ∴ △ACH 是等边三角形.∴ HC =AC ,∠AHC =∠ACH =60°. ∵ AH =AB ,EF =BE ,∴ HF =2AE ,HF ∥AE . …………………………5分 ∴ ∠FHA =∠HAC =60°.∴ ∠FHC =∠FHA +∠AHC =120°. ∴ ∠FHC =∠DAC . ∵ AD =2AE , ∴ HF =AD . ∵ HC =AC ,∴ △FHC ≌△DAC . …………………………………………………………6分 ∴ FC =DC ,∠HCF =∠ACD . ∴ ∠FCD =∠ACH =60°.∴ △DCF 是等边三角形. ………………………………………………………7分28.(1)① P 1 ,P 3; ………………………………………………………2分②线段AB 融合点的轨迹为分别以点A ,B 为圆心,AB 长为半径的圆及两圆内区域. ……3分 当直线y =t 与两圆相切时,记为l 1,l 2.H∵A (3,0),B (5,0),∴t =2或t =-2. ………………………………………………………4分 ∴当-2≤ t ≤2时,直线y =t 上存在线段AB 的融合点. ……………………………………………5分 (21a ≤≤1a ≤≤ ……………………………………………………7分。
2022-2023学年北京海淀区初三第一学期数学期末试卷及答案

2022-2023学年北京海淀区初三第一学期数学期末试卷及答案第一部分 选择题一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1. 刺绣是中国民间传统手工艺之一.下列刺绣图案中,是中心对称图形的为( )A. B.C. D.【答案】B 【解析】【分析】如果一个图形绕某一点旋转180度后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.依据中心对称图形的概念即可解答. 【详解】解:A 、是轴对称图形不是中心对称图形,故此选项不符合题意; B 、是中心对称图形,故此选项符合题意; C 、不是中心对称图形,故此选项不符合题意; D 、不是中心对称图形,故此选项不符合题意; 故选:B .【点睛】本题考查中心对称图形,熟练掌握中心对称图形的概念是解题的关键. 2. 点关于原点对称的点的坐标是( ) ()1,2A A. B.C. D.()1,2-()1,2-()1,2--()2,1【答案】C 【解析】【分析】根据关于原点对称点的坐标特点:横、纵坐标均取相反数可直接得到答案. 【详解】解:点A (1,2)关于原点对称的点的坐标是(-1,-2), 故选:C .【点睛】此题主要考查了关于原点对称点的坐标特点,关键是掌握点的坐标的变化规律. 3. 二次函数的图象向左平移1个单位长度,得到的二次函数解析式为( ) 22y x =+A.B.23y x =+()212y x =-+C. D.21y x =+()212y x =++【答案】D 【解析】【分析】根据函数平移规律:左加右减,上加下减即可得到答案. 【详解】解:由题意可得,的图象向左平移1个单位长度可得,22y x =+, 2(1)2y x =++故选D .【点睛】本题考查函数图像平移规律,解题关键是熟练掌握规律:左加右减,上加下减. 4. 如图,已知正方形,以点为圆心,长为半径作,点与的位置关ABCD A AB A C A 系为( )A. 点在外B. 点在内C. 点在上D. 无法确C A C A C A 定 【答案】A 【解析】【分析】设正方形的边长为,用勾股定理求得点到的圆心之间的距离,为a C A AC AB 的半径,通过比较二者的大小,即可得到结论.A 【详解】解:设正方形的边长为, a则,,AB a =AC ==,AB AC < 点在外,∴C A 故选:A .【点睛】本题考查了点与圆的位置关系,解题的关键是确定圆的半径和点到圆心之间的距离的大小关系.5. 若点,在抛物线上,则的值为( )()0,5M ()2,5N ()223y x m =-+m A. 2 B. 1 C. 0 D.1-【答案】B 【解析】【分析】由函数的解析式可知函数对称轴为,从而得出的值. 022x m +==m 【详解】由函数可知对称轴是直线, ()223y x m =-+x m =由,可知,M ,N 两点关于对称轴对称,即 ()0,5M ()2,5N 0212x +==,,1m ∴=故选B .【点睛】本题考查二次函数图象上点的坐标特征,注意掌握二次函数图像上点的对称性是解题的关键.6. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该O α角度可以为( )αA. B. C. D.30︒60︒120︒150︒【答案】C 【解析】【分析】连接,可得,从而得到,即可,OA OB AB AC BC==13601203AOC ∠=⨯︒=︒求解.【详解】解:如图,连接,,OA OC∵是等边三角形, ABC ∴,AB AC BC ==即, AB AC BC==∴. 13601203AOC ∠=⨯︒=︒∴该角度可以为.α120︒故选:C【点睛】本题主要考查了弧,弦,圆心角的关系,图形的旋转,等边三角形的性质,熟练掌握弧,弦,圆心角的关系是解题的关键.7. 如图,过点作的切线,,切点分别是,,连接.过上一点A O AB AC B C BC BC作的切线,交,于点,.若,的周长为4,则的D O AB ACEF 90A ∠=︒AEF △BC 长为( )A. 2B.C. 4D. 【答案】B 【解析】【分析】利用切线长定理得出,,,再根据三角形周长等于AB AC =DF FC =DE EB =4,可求得,从而利用勾股定理可求解.2AB AC ==【详解】解:∵,是的切线,切点分别是,, AB AC O B C ∴,AB AC =∵、是的切线,切点是D ,交,于点,, DF DE O AB AC E F ∴,,DF FC =DE EB =∵的周长为4,即, AEF △4AF EF AE AF DF DE AE AC AB ++=+++=+=∴, 2AB AC ==∵, 90A ∠=︒∴BC ===故选:B .【点睛】本题考查切线长定理,勾股定理,熟练掌握切线长定理是解题的关键. 8. 遥控电动跑车竞速是青少年喜欢的活动.如图是某赛道的部分通行路线示意图,某赛车从人口A 驶入,行至每个岔路口选择前方两条线路的可能性相同,则该赛车从口驶出的F 概率是( )A.B.C.D.13141516【答案】B 【解析】【分析】根据“在每个岔路口都有向左或向右两种可能,且可能性相等”可知在点H 、G 、E 、F 处都是等可能情况,从而得到在四个出口H 、G 、E 、F 也都是等可能情况,然后根据概率的意义列式即可得解.【详解】解:由图可知,在每个岔路口都有向左或向右两种可能,且可能性相等, 赛车最终驶出的点共有H 、G 、E 、F 四个, 所以,最终从点F 驶出的概率为, 14故选:B .【点睛】本题考查了概率,读懂题目信息,得出所给的图形的对称性以及可能性相等是解题的关键,用到的知识点为:概率=所求情况数与总情况数之比.第二部分 非选择题二、填空题(共16分,每题2分) 9. 二次函数的图象与轴的交点坐标为______.243y x x =-+y 【答案】 ()0,3【解析】【分析】令,求得的值即可. 0x =y 【详解】令,得, 0x =2433y x x =-+=∴二次函数的图象与轴的交点坐标为, y ()0,3故答案为:.()0,3【点睛】本题考查的是二次函数与轴的交点,正确计算是解答此题的关键. y 10. 半径为3且圆心角为的扇形的面积为________. 120︒【答案】3π. 【解析】【分析】直接利用扇形的面积公式S=,进而求出即可.2360n r π【详解】解:∵半径为3,圆心角为120°的扇形,∴S 扇形===3π.2360n r π21203360π⨯⨯故答案为3π.【点睛】此题主要考查了扇形面积公式应用,熟练记忆扇形面积公式是解题关键. 11. 下表记录了一名球员在罚球线上投篮的结果. 投篮次数 n 50 100 150 200 300 400 500 投中次数 m 284978102153208255投中频率m n0.56 0.49 0.52 0.51 0.51 0.52 0.51根据以上数据,估计这名球员在罚球线上投篮一次,投中的概率为______. 【答案】0.51(答案不唯一) 【解析】【分析】根据频率估计概率的方法结合表格数据可得答案.【详解】解:由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数0.51附近,∴这名球员在罚球线上投篮一次,投中的概率为0.51, 故答案为:0.51(答案不唯一).【点睛】此题考查了利用频率估计概率的知识,注意这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.12. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是x 230x x m -+=m ______. 【答案】 94m <【解析】【分析】根据一元二次方程根的判别式列出关于m 的不等式,即可解得答案. 【详解】解:∵的一元二次方程有两个不相等的实数根, 230x x m -+=∴,即, 0∆>()2340m -->解得:, 94m <故答案为:. 94m <【点睛】本题考查一元二次方程根的判别式,解题的关键是掌握时,一元二次方程有0∆>两个不相等的实数根.13. 二次函数的图象如图所示,则______0(填“”,“”或“”).2y ax bx =+ab ><=【答案】 <【解析】【分析】根据抛物线的开口方向,判断的符号,根据对称轴的位置,判断的符号,进而a b 得到的符号.ab 【详解】解:由图象,可知:抛物线的开口向上:, 0a >对称轴在的右侧:,即:, y bx 02a=->0b <∴; 0ab <故答案为:.<【点睛】本题考查二次函数的图象与二次函数的系数之间的关系.熟练掌握二次函数的图象和性质,是解题的关键.14. 如图,是的内接三角形,于点,若,ABC O OD AB ⊥E O ,则______.45ACB ∠=︒OE =【答案】1 【解析】【分析】连接,,由圆周角定理求得,再由等腰三角OA OB 224590AOB ACB ∠=∠=⨯︒=︒形三线合一性质求得,从而求得,1452AOE BOE AOB ∠=∠=∠=︒45AOE OAE ∠=∠=︒得到,然后在中,,由勾股定理求解即可. OE AE =Rt AOE △90AEO ∠=︒【详解】解:连接,,OA OB∴, 224590AOB ACB ∠=∠=⨯︒=︒∵于点, OD AB ⊥E OA OB =∴, 1452AOE BOE AOB ∠=∠=∠=︒∴, 45AOE OAE ∠=∠=︒∴,OE AE =在中,,由勾股定理,得Rt AOE △90AEO ∠=︒,222OE AE OA +=∴,2222OE OA ==∴, 1OE =故答案为:1.【点睛】本题考查圆周角定理,等腰三角形的性质,勾股定理,熟练掌握圆周角定理,等腰三角形三线合一性质是解题的关键.15. 对于二次函数,与的部分对应值如表所示.在某一范围内,2y ax bx c =++y x x y 随的增大而减小,写出一个符合条件的的取值范围______.x xx …1-0 1 2 3 …y …3- 1331…【答案】(答案不唯一,满足即可) 2x >32x ≥【解析】【分析】根据表格,用待定系数法求出二次函数解析式,再根据二次函数的性质求解即可.【详解】解:把,;,;,分别代入=1x -=3y -0x =1y =1x =3y =,得2y ax bx c =++,解得:, 313a b c c a b c -+=-⎧⎪=⎨⎪++=⎩131a b c =-⎧⎪=⎨⎪=⎩∴,22373124y x x x ⎛⎫=-++=--+ ⎪⎝⎭∵, 10a =-<∴当时,随的增大而减小, 32x >y x ∴当时,随的增大而减小, 2x >y x 故答案为:(答案不唯一,满足即可). 2x >32x ≥【点睛】本题考查待定系数法求二次函数解析式,二次函数的性质,熟练掌握二次函数的性质是解题的关键.16. 如图,,,分别是某圆内接正六边形、正方形、等边三角形的一边.若AB AC AD ,下面四个结论中,2AB =①该圆的半径为2; ②的长为; AC π2③平分; ④连接,,则与的面积比为AC BAD ∠BC CD ABC ACD .所有正确结论的序号是______.【答案】①③④ 【解析】【分析】根据圆内接正六边形、内接正方形的性质、弧长公式,勾股定理逐一判断可选项即可.【详解】解:根据题干补全图形,连接,BC CD OA OB OC OD OE ,,,,,,根据内接正六边形的性质可知:, 60AOB ∠=︒OA OB =∴是等边三角形,AOB ,圆的半径为2,所以①正确;2OA OB AB ===根据内接正方形的性质可知:,=90AOC ︒∠的长为:,所以②错误; AC90π2π180⨯=∵,, OA OD =120AOD ∠=︒∴,30OAD ∠=︒∵,, OA OC ==90AOC ︒∠∴, 45OAC ∠=︒∵,60OAB ∠=︒∴, 604515BAC =︒-︒=︒∠∴,BAC DAC ∠=∠∴平分, 所以③正确;AC BAD ∠过点A 作交延长线于点H ,交延长线于点G , AH BC ⊥CB AG CD ⊥DC ∵, 1302ACB AOB ∠=∠=︒∴, 12AH AC =∵AC==∴AH =, 1245ADC AOC ∠=∠=︒∴, AG AD =设交于点M ,OB AD ∵,60AOM ∠=︒∴,,OM AD ⊥2AD AM =∵,30OAM ∠=︒∴, 112MD OA ==∴,AM==∴,2AD AM ==∴AG =∵,=BAC CAD ∠∠∴,CD BC =∴,所以④正确;1212ABCACD BC AH S AH S AG DC AG ∙====∙ 因此正确的结论:①③④故答案为:①③④【点睛】本题考查圆内接正六边形、内接正方形的性质、弧长公式,勾股定理,得出圆形的半径是解题的关键.三、解答题(共68分,第17-20题,每题5分,第21题6分,第22-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 解方程:.226x x -=【答案】,11x =+21x =-【解析】【分析】用配方法求解即可.【详解】解:,22161x x -+=+,()217x -=∴1x -=∴,.11x =+21x =-【点睛】本题考查解一元二次方程,熟练掌握用配方法求解一元二次方程是解题的关键.18. 已知抛物线过点和,求该抛物线的解析式.22y x bx c =++()1,3()0,4【答案】2234y x x =-+【解析】【分析】把和代入,解方程组求出b 、c 的值即可得答案.()1,3()0,422y x bx c =++【详解】解:∵抛物线过点和,∴ 22y x bx c =++()1,3()0,432,4.b c c =++⎧⎨=⎩解方程组,得 3,4.b c =-⎧⎨=⎩∴抛物线的解析式是.2234y x x =-+【点睛】本题考查待定系数法求二次函数解析式,把抛物线上的点的坐标代入解析式确定字母的值是解题关键.19. 已知为方程的一个根,求代数式的值.a 22310x x --=()()()1132a a a a +-+-【答案】1【解析】【分析】将a 代入方程中得,将所求代数式化简整理后,把整体2231a a -=2231a a -=代入即可.【详解】解:∵为方程的一个根,a 22310x x --=∴.22310a a --=∴.2231a a -=∴原式=.()222213646122312111a a a a a a a -+-=--=--=⨯-=【点睛】本题主要考查了一元二次方程的解的概念,以及用整体代入法求代数式的值.解题的关键是掌握整体代入法. 20. 如图,四边形内接于,为直径,.若,求的ABCD O AB BCCD =50A ∠=︒B ∠度数.【答案】65B ∠=︒【解析】【分析】连接.利用等弧所对圆周角相等,得出,从而得出AC DAC BAC ∠=∠,再利用直径所对圆周角是直角,最后由直角 三角形两锐角互1252BAC DAB ∠=∠=︒余求解即可.【详解】解:如图,连接. AC∵, BCCD =∴.DAC BAC ∠=∠∵,50DAB ∠=︒∴. 1252BAC DAB ∠=∠=︒∵为直径,AB ∴.90ACB ∠=︒∴.9065B BAC ∠=︒-∠=︒【点睛】本题考查圆周角定理的推论,直角三角形的性质,熟练掌握圆周角定理的推论是解题的关键.21. 为了发展学生的兴趣爱好,学校利用课后服务时间开展了丰富的社团活动.小明和小天参加的篮球社共有甲、乙、丙三个训练场.活动时,每个学生用抽签的方式从三个训练场中随机抽取一个场地进行训练.(1)小明抽到甲训练场的概率为______;(2)用列表或画树状图的方法,求小明和小天在某次活动中抽到同一场地训练的概率.【答案】(1) 13(2) 13【解析】【分析】(1)直接根据概率公式求解即可;(2)画树状图得出所有等可能结果,从中找到符合条件的结果,再根据概率公式求解即可.【小问1详解】 解:小明抽到甲训练场的概率为, 13故答案为:; 13【小问2详解】根据题意,可以画出如下树状图:由树状图可以看出,所有可能出现的结果有9种,并且这些结果出现的可能性相等. 小明和小天抽到同一场地训练(记为事件)的结果有3种,A 所以,. ()3193P A ==【点睛】此题考查了树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.22. 已知:如图,是的切线,为切点.PA O A 求作:的另一条切线,为切点.O PB B 作法:以为圆心,长为半径画弧,交于点;P PA O B 作直线. PB 直线即为所求.PB(1)根据上面的作法,补全图形(保留作图痕迹);(2)完成下面证明过程.证明:连接,,.OA OB OP ∵是的切线,为切点,PA O A ∴.OA PA ⊥∴.90PAO ∠=︒在与中,PAO PBO ,,______,PA PB OP OP =⎧⎪=⎨⎪⎩∴.∴.PAO PBO ≌△△90∠=∠=︒PAO PBO ∴于点.∵是的半径,OB PB ⊥B OB O ∴是的切线(____________________)(填推理的依据).PB O 【答案】(1)见解析 (2),经过半径外端并且垂直于这条半径的直线是圆的OA OB =切线【解析】【分析】(1)按照作法作出图形即可;(2)连接,,,证明即可证明是的切线.OA OB OP PAO PBO ≌△△PB O 【小问1详解】补全图形,如图所示:【小问2详解】连接,,.OA OBOP∵是的切线,A 为切点,PA O ∴.OA PA ⊥∴.90PAO ∠=︒在与中,PAO PBO ,,,PA PB OP OP OA OB =⎧⎪=⎨⎪=⎩∴.∴.PAO PBO ≌△△90∠=∠=︒PAO PBO ∴于点.∵是的半径,OB PB ⊥B OB O ∴是的切线(经过半径外端并且垂直于这条半径的直线是圆的切线).PB O 故答案为:,经过半径外端并且垂直于这条半径的直线是圆的切线.OA OB =【点睛】本题考查了尺柜作图,切线的性质和判定,以及全等三角形的判定与性质,熟练掌握切线的判定与性质是解答本题的关键.23. 紫砂壶是我国特有的手工制造陶土工艺品,其制作过程需要几十种不同的工具,其中有一种工具名为“带刻度嘴巴架”,其形状及使用方法如图1.当制显艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上.图2是正确使用该工具时的示意图.如图3,为某紫砂壶的壶口,已知,两点O A B 在上,直线过点,且于点,交于点.若,O l O l AB ⊥D O C 30mm AB =,求这个紫砂壶的壶口半径的长.5mm CD =r【答案】25mm 【解析】【分析】连接,根据垂径定理求得,又由,即可由勾股定OB 1152BD AB ==5DO r =-理求解.【详解】解:如图,连接.OB∵过圆心,,,l O l AB ⊥30AB =∴. 1152BD AB ==∵,5CD =∴.5DO r =-∵,222BO BD DO =+∴.()222155r r =+-解得.25r =∴这个紫砂壶的壶口半径的长为.r 25mm 【点睛】本题考查垂径定理,勾股定理,熟练掌握垂径定理是解题的关键.24. 如图,是的直径,点在上.过点作的切线,过点作AB O C O C O l B BD l ⊥于点. D(1)求证:平分;BC ABD ∠(2)连接,若,,求的长.OD 60ABD ∠=︒3CD =OD【答案】(1)见解析 (2)OD =【解析】【分析】(1)连接,求得,得到,即可求得平分.OC OC BD ∥OBC CBD ∠=∠BC ABD ∠(2)连接,求得,在中,求得;在中,AC 90ACB ∠=︒Rt BDC 6BC =Rt ACB △,;在中,利用勾股定理可求得.2AB AC =OC =Rt OCD △OD =【小问1详解】证明:如图,连接. OC∵直线与相切于点,l O C ∴于点.OC l ⊥C ∴.90OCD ∠=︒∵于点,BD l ⊥D ∴.=90BDC ∠︒∴.180OCD BDC ︒∠+∠=∴.OC BD ∥∴.OCB CBD ∠=∠∵,OC OB =∴.OBC OCB ∠=∠∴.OBC CBD ∠=∠∴平分.BC ABD ∠【小问2详解】解:连接. AC∵是的直径,AB O ∴.90ACB ∠=︒∵,60ABD ∠=︒∴. 1302OBC CBD ABD ︒∠=∠=∠=在中,Rt BDC ∵,,30CBD ∠=︒3CD =∴.26BC CD ==在中,Rt ACB △∵,30ABC ∠=︒∴.2AB AC =∵,222AC BC AB +=∴ AB =∴. 12OC AB ==在中,Rt OCD △∵,222OC CD OD +=∴OD =【点睛】本题是圆与三角形综合题,考查了切线的性质、角平分线的判定和和勾股定理,作出恰当的辅助线是解决问题的关键25. 学校举办“科技之星”颁奖典礼,颁奖现场人口为一个拱门.小明要在拱门上顺次粘贴“科”“技”“之”“星”四个大字(如图1),其中,“科”与“星”距地面的高度相同,“技”与“之”距地面的高度相同,他发现拱门可以看作是抛物线的一部分,四个字和五角星可以看作抛物线上的点.通过测量得到拱门的最大跨度是10米,最高点的五角星距地面6.25米.(1)请在图2中建立平面直角坐标系,并求出该抛物线的解析式;xOy (2)“技”与“之”的水平距离为米.小明想同时达到如下两个设计效果: 2a ① “科”与“星”的水平距离是“技”与“之”的水平距离的2倍;②“技”与“科”距地面的高度差为1.5米.小明的设计能否实现?若能实现,直接写出的值;若不能实现,请说明理由.a 【答案】(1)(答案不唯一)20.25y x =-(2)能实现;a =【解析】【分析】(1)建立平面直角坐标系,写出点的坐标,代入求解析式即可; (2)设“技”的坐标,表示“科”,列出方程解方程即可. ()20.25a a --,()22a a --,【小问1详解】 解:如图,以抛物线顶点为原点,以抛物线对称轴为轴,建立平面直角坐标系. y设这条抛物线表示的二次函数为.2y ax =∵抛物线过点,()5, 6.25-∴25 6.25a =-∴0.25a =-∴这条抛物线表示的二次函数为.20.25y x =-【小问2详解】能实现;.a =由“技”与“之”的水平距离为米,设“技”,“之”, 2a ()20.25a a --,()20.25a a -,则 “科”,()22a a --,“技”与“科”距地面的高度差为1.5米,,()220.25 1.5a a ∴---=解得:舍去)a =a =【点睛】本题考查运用二次函数解决实际问题,建立适当的平面直角坐标系,求出函数解析式是解题的关键.26. 在平面直角坐标系中,抛物线过点.xOy 21y ax bx =++()2,1(1)求(用含的式子表示); b a(2)抛物线过点,,.()2,M m -()1,N n ()3,P p ①判断:______0(填“>”“<”或“=”);()()11m n --②若,,恰有两个点在轴上方,求的取值范围.M N P x a 【答案】(1)2b a =-(2)①<②的取值范围是或 a 1138a -<≤-1a ≥【解析】【分析】(1)把代入,计算即可;()2,121y ax bx =++(2)①把代入,得,把代入()2,M m -21y ax bx =++18m a -=()1,N n ,得,当时,,,得21y ax bx =++1n a -=-0a >180m a -=>10n a -=-<;当时,,,得;()()110m n --<a<0180m a -=<10n a -=->()()110m n --<即可得出结论;②把,,代入,得,,()2,M m -()1,N n ()3,P p 21y ax bx =++81m a =+1n a =-+.当时,抛物线开口向上,对称轴为,则抛物线在时,取得最31p a =+0a >1x =1x =小值.所以,在轴上方,在轴上或轴下方,则,解得.当n M P x N x x 81031010a a a +>⎧⎪+>⎨⎪-+≤⎩1a ≥时,抛物线开口向下,对称轴为,所以抛物线在时,取得最大值,且0a <1x =1x =n .所以,在轴上方,在轴上或轴下方.则,解得<m p N P x M x x 10310810a a a -+>⎧⎪+>⎨⎪+≤⎩. 1138a -<≤-【小问1详解】解:把代入,得()2,121y ax bx =++,4211a b ++=∴;2b a =-【小问2详解】解:①把代入,得()2,M m -21y ax bx =++,421m a b =-+由(1)知:,2b a =-∴,18m a -=把代入,得()1,N n 21y ax bx =++,1n a b =++,1n a -=-当时,,,0a >180m a -=>10n a -=-<∴,()()110m n --<当时,,,a<0180m a -=<10n a -=->∴,()()110m n --<绽上,;()()110m n --<②由(1)知,2b a =-∴221y ax ax =-+∴抛物线对称轴为.1x =∵抛物线过点,,,()2,M m -()1,N n ()3,P p ∴,,.81m a =+1n a =-+31p a =+当时,抛物线开口向上,对称轴为,0a >1x =∴抛物线在时,取得最小值.1x =n ∵,,恰有两点在轴上方,M N P x ∴,在轴上方,在轴上或轴下方.M P x N x x ∴,解得.81031010a a a +>⎧⎪+>⎨⎪-+≤⎩1a ≥当时,抛物线开口向下,对称轴为,0a <1x =∴抛物线在时,取得最大值,且.1x =n <m p ∵,,恰有两点在轴上方,M N P x ∴,在轴上方,在轴上或轴下方.N P x M x x ∴,解得. 10310810a a a -+>⎧⎪+>⎨⎪+≤⎩1138a -<≤-综上,的取值范围是或. a 1138a -<≤-1a ≥【点睛】本题考查二次函数图象上点的坐标特征,二次函数的性质,熟练掌握二次函数的图象性质是解题的关键.27. 如图,在中,,.是边上一点,交ABC AB AC =120BAC ∠=︒D AB DE AC ⊥的延长线于点.CA E(1)用等式表示与的数量关系,并证明;AD AE (2)连接,延长至,使.连接,,.BE BE F EF BE =DC CF DF ①依题意补全图形;②判断的形状,并证明.DCF 【答案】(1),理由见解析;2AD AE =(2)①如图;②结论:是等边三角形,理由见解析.DCF 【解析】【分析】(1)根据,可知,DE AC ⊥120BAC ∠=︒90DEA ∠=︒,利用含角的直角三角形性质:角所对直角边等30ADE BAC DEA ∠=∠-∠=︒30︒30︒于斜边的一半,可得.2AD AE =(2)①根据题意补全图形即可;②延长至点使,连接,,根据可知,由BA H AH AB =CH FH AB AC =AH AC =,得是等边三角形,,18060HAC BAC ∠=︒-∠=︒ACH HC AC =, 根据,,可知,,60AHC ACH ∠=∠=︒AH AB =EF BE =2HF AE =HF AE ∥得,,,由60FHA HAC ∠=∠=︒120FHC FHA AHC ∠=∠+∠=︒FHC DAC ∠=∠,得,由,可证明,可得,2AD AE =HF AD =HA AC =FHC DAC ≌△△FC DC =,,从而可证明是等边三角形.HCF ACD ∠=∠60FCD ACH ∠=∠=︒DCF 【小问1详解】解:线段与的数量关系:.AD AE 2AD AE =证明: ,DE AC ⊥ .90DEA ∴∠=︒,120BAC ∠=︒30ADE BAC DEA ∴∠=∠-∠=︒;2AD AE ∴=【小问2详解】解:①补全图形,如图.②结论:是等边三角形.DCF 证明:延长至点使,连接,,如图.BA H AH AB =CH FH,AB AC =. ∴AH AC =,18060HAC BAC ∠=︒-∠=︒是等边三角形.∴ACH ,.∴HC AC =60AHC ACH ∠=∠=︒,,AH AB =EF BE =,.∴2HF AE =HF AE ∥.∴60FHA HAC ∠=∠=︒.∴120FHC FHA AHC ∠=∠+∠=︒,∴FHC DAC ∠=∠,2AD AE =.∴HF AD =,HC AC =()∴FHC DAC ≌△△SAS ,.∴FC DC =HCF ACD ∠=∠.∴60FCD ACH ∠=∠=︒是等边三角形.∴DCF【点睛】此题考查了含角的直角三角形性质,等边三角形的判定和性质,全等三角形的30︒判定和性质,综合掌握相关知识点是解题关键.28. 在平面直角坐标系中,对于点和线段,若线段或的垂直平分线与线xOy P AB PA PB 段有公共点,则称点为线段的融合点.AB P AB(1)已知,, ()30A ,()50B ,①在点,,中,线段的融合点是______; ()160P ,()212P -,()332P ,AB ②若直线上存在线段的融合点,求的取值范围;y t =AB t (2)已知的半径为4,,,直线过点,记线段关于O (),0A a ()1,0B a +l ()0,1T -AB 的对称线段为.若对于实数,存在直线,使得上有的融合点,直接写出l A B ''a l O A B ''a 的取值范围.【答案】(1)①,;②当时,直线上存在线段的融合点 1P 3P 22t -≤≤y t =AB(2或1a -≤≤1a -≤≤【解析】【分析】(1)①画出对应线段的垂直平分线,再根据融合点的定义进行判断即可;②先确定线段融合点的轨迹为分别以点,为圆心,长为半径的圆及两圆内区域,则当直AB A B AB 线与两圆相切时是临界点,据此求解即可;y t =(2)先推理出的融合点的轨迹即为以T 为圆心,的长为半径的圆和以T 为圆A B ''()1TA -心,以的长为半径的圆的组成的圆环上(包括两个圆上),再求出两个圆分别与()1TB +O 内切,外切时a 的值即可得到答案. 【小问1详解】解:①如图所示,根据题意可知,是线段的融合点,1P 3P AB故答案为;,;1P 3P②如图1所示,设的垂直平分线与线段的交点为Q ,PA AB ∵点Q 在线段的垂直平分线上,PA ∴,PQ AQ =∴当点Q 固定时,则点P 在以Q 为圆心,的长为半径的圆上,AQ ∴当点Q 在上移动时,此时点P 的轨迹即线段的融合点的轨迹为分别以点,为AB AB A B 圆心,长为半径的圆及两圆内区域. AB当直线与两圆相切时,记为,,如图2所示.y t =1l 2l∵,, ()30A ,()50B ,∴,2AB =∴或.2t =2t =-∴当时,直线上存在线段的融合点.22t -≤≤y t =AB 【小问2详解】解:如图3-1所示,假设线段位置确定,AB 由轴对称的性质可知,TA TA TB TB ''==,∴点在以T 为圆心,的长为半径的圆上运动,点在以T 为圆心,以的长为半径A 'TA B 'TB 的圆上运动,∴的融合点的轨迹即为以T 为圆心,的长为半径的圆和以T 为圆心,以A B ''()1TA -的长为半径的圆的组成的圆环上(包括两个圆上);()1TB +当时,TA TB <如图3-2所示,当以T 为圆心,为半径的圆与外切时,()1TA -O ∴,141TA -=+, 6=∴,2136a +=∴(负值舍去); a =如图3-3所示,当以为圆心,为半径的圆与内切时,T ()1TB +O ∴,13TB +=, 2=∴,22114a a +++=∴(负值舍去);1a -时,存在直线,使得上有的融合点;1a ≤≤l O A B ''同理当时,TA TB >当以T 为圆心,为半径的圆与外切时,()1TB -O ∴,141TB -=+, 6=∴,221136a a +++=∴(正值舍去);1a =-当以为圆心,为半径的圆与内切时,T ()1TA +O ∴,13TA +=, 2=∴,214a +=∴;a =∴时,存在直线,使得上有的融合点;1a ≤≤l O A B ''或时存在直线,使得上有1a -≤≤1a -≤≤l O A B ''的融合点.【点睛】本题主要考查了坐标与图形,轴对称的性质,线段垂直平分线的性质,勾股定理,圆与圆的位置关系等等,正确推理出对应线段的融合点的轨迹是解题的关键.。
2022北京海淀区初三(上)期末数学试卷及答案

2022北京海淀初三(上)期末数学一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个. 1.在平面直角坐标系xOy中,下列函数的图象经过点(0,0)的是()A.1y x=+B.2y x=C.2(4)y x=−D.1 yx =2.下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的,其中是中心对称图形的是() A.B.C.D.3.抛物线2(2)1y x=−+的顶点坐标为()A.(2,1)B.(2,1)−C.(2,1)−−D.(2,1)−4.在ABC∆中,CA CB=,点O为AB中点.以点C为圆心,CO长为半径作C,则C与AB的位置关系是()A.相交B.相切C.相离D.不确定5.小明将图案绕某点连续旋转若干次,每次旋转相同角度α,设计出一个外轮廓为正六边形的图案(如图),则α可以为()A.30︒B.60︒C.90︒D.120︒6.把长为2m的绳子分成两段,使较长一段的长的平方等于较短一段的长与原绳长的积.设较长一段的长为x m,依题意,可列方程为( ) A .22(2)x x =−B .22(2)x x =+C .2(2)2x x −=D .22x x =−7.如图,A ,B ,C 是某社区的三栋楼,若在AC 中点D 处建一个5G 基站,其覆盖半径为300m ,则这三栋楼中在该5G 基站覆盖范围内的是( )A .A ,B ,C 都不在B .只有BC .只有A ,CD .A ,B ,C8.做随机抛掷一枚纪念币的试验,得到的结果如下表所示:①当抛掷次数是1000时,“正面向上”的频率是0.512,所以“正面向上”的概率是0.512;②随着试验次数的增加,“正面向上”的频率总在0.520附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.520;③若再次做随机抛掷该纪念币的试验,则当抛掷次数为3000时,出现“正面向上”的次数不一定是1558次. 其中所有合理推断的序号是( ) A .②B .①③C .②③D .①②③二、填空题(共16分,每题2分)9.已知y 是x 的函数,且当0x >时,y 随x 的增大而减小.则这个函数的表达式可以是 .(写出一个符合题意的答案即可)10.在一个不透明袋子中有3个红球和2个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则取出红球的概率是 .11.若点1(1,)A y −,2(2,)B y 在二次函数22y x =的图象上,则1y ,2y 的大小关系为:1y 2y (填“> ”,“ = ”或“<” ).12.如图,在平面直角坐标系xOy 中,点(2,0)A −,点(0,1)B .将线段BA 绕点B 旋转180︒得到线段BC ,则点C 的坐标为 .13.若关于x 的方程220x x k −+=有两个不相等的实数根,则k 的取值范围为 .14.如图,PA ,PB 分别切O 于点A ,B ,Q 是优弧AB 上一点,若40P ∠=︒,则Q ∠的度数是 .15.小明烘焙了几款不同口味的饼干,分别装在同款的圆柱形盒子中,为区别口味,他打算制作“**饼干”字样的矩形标签粘贴在盒子侧面.为了获得较好的视觉效果,粘贴后标签上边缘所在弧所对的圆心角为90︒(如图).已知该款圆柱形盒子底面半径为6cm ,则标签长度l 应为 cm .(π取3.1)16.给定二元数对(,)p q ,其中0p =或1,0q =或1.三种转换器A ,B ,C 对(,)p q 的转换规则如下:;(2)在图2所示的“①C −−②”组合转换器中,若当输入(1,1)和(0,0)时,输出结果均为0,则该组合转换器为“ C −− ”.(写出一种组合即可).三、解答题(共68分,第17-21题,每题5分,第22题6分,第23题5分,第24-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17.(5分)解方程:2680−+=.x x18.(5分)已知a是方程2−−=的一个根,求代数式(27)5x x2710a a−+的值.19.(5分)在平面直角坐标系xOy中,抛物线2=−−经过点(2,1).y a x(3)1(1)求该抛物线的表达式;(2)将该抛物线向上平移个单位后,所得抛物线与x轴只有一个公共点.20.(5分)如图,在Rt ABCBAC∠=︒,30∠=︒,将线段CA绕点C逆时针旋转60︒,得到线段CD,ACB∆中,90连接AD,BD.(1)依题意补全图形;(2)若1BC=,求线段BD的长.21.(5分)“化圆为方”是古希腊尺规作图难题之一.即:求作一个方形,使其面积等于给定圆的面积.这个问题困扰了人类上千年,直到19世纪,该问题被证明仅用直尺和圆规是无法完成的,如果借用一个圆形纸片,我们就可以化圆为方,方法如下:已知:O(纸片),其半径为r.求作:一个正方形,使其面积等于O的面积.作法:①如图1,取O的直径AB,作射线BA,过点A作AB的垂线l;②如图2,以点A为圆心,AO长为半径画弧交直线l于点C;③将纸片O沿着直线l向右无滑动地滚动半周,使点A,B分别落在对应的A',B'处;④取CB'的中点M,以点M为圆心,MC长为半径画半圆,交射线BA于点E;⑤以AE为边作正方形AEFG.正方形AEFG即为所求.根据上述作图步骤,完成下列填空:(1)由①可知,直线l为O的切线,其依据是.(2)由②③可知,AC r =,AB r π'=,则MC = ,MA = (用含r 的代数式表示).(3)连接ME ,在Rt AME ∆中,根据222AM AE EM +=,可计算得2AE = (用含r 的代数式表示). 由此可得OAEFG S S=正方形.22.(6分)已知关于x 的一元二次方程2(2)10x m x m +−+−=. (1)求证:该方程总有两个实数根;(2)若0m <,且该方程的两个实数根的差为3,求m 的值. 23.(5分)如图,ABC ∆内接于O ,高AD 经过圆心O . (1)求证:AB AC =;(2)若8BC =,O 的半径为5,求ABC ∆的面积.24.(6分)邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传北京2022年冬奥会,中国邮政发行了若干套冬奥会纪念邮票,其中有一套展现雪上运动的邮票,如图所示:某班级举行冬奥会有奖问答活动,答对的同学可以随机抽取邮票作为奖品.(1)在抢答环节中,若答对一题,可从4枚邮票中任意抽取1枚作为奖品,则恰好抽到“冬季两项”的概率是 ; (2)在抢答环节中,若答对两题,可从4枚邮票中任意抽取2枚作为奖品,请用列表或画树状图的方法,求恰好抽到“高山滑雪”和“自由式滑雪”的概率.25.(6分)如图,AB 为O 的直径,弦CD AB ⊥于E ,连接AC ,过A 作AF AC ⊥,交O 于点F ,连接DF ,过B 作BG DF ⊥,交DF 的延长线于点G . (1)求证:BG 是O 的切线;(2)若30DFA ∠=︒,4DF =,求FG 的长.26.(6分)在平面直角坐标系xOy 中,点(4,3)在抛物线23(0)y ax bx a =++>上. (1)求该抛物线的对称轴;(2)已知0m >,当222m x m −+时,y 的取值范围是13y −.求a ,m 的值;(3)在(2)的条件下,是否存在实数n ,使得当2n x n −<<时,y 的取值范围是3335n y n −<<+.若存在,直接写出n 的值;若不存在,请说明理由.27.(7分)如图,在ABC ∆中,90BAC ∠=︒,1AB AC ==,延长CB ,并将射线CB 绕点C 逆时针旋转90︒得到射线l ,D 为射线l 上一动点,点E 在线段CB 的延长线上,且BE CD =,连接DE ,过点A 作AM DE ⊥于M . (1)依题意补全图,用等式表示线段DM 与ME 之间的数量关系,并证明; (2)取BE 的中点N ,连接AN ,添加一个条件:CD 的长为 ,使得12AN DE =成立,并证明.28.(7分)在平面直角坐标系xOy 中,图形W 上任意两点间的距离有最大值,将这个最大值记为d .对点P 及图形W 给出如下定义:点Q 为图形W 上任意一点,若P ,Q 两点间的距离有最大值,且最大值恰好为2d .则称点P 为图形W 的“倍点”.(1)如图1,图形W 是半径为1的O .①图形W 上任意两点间的距离的最大值d 为 ;②在点1(0,2)P ,2(3,3)P ,3(3,0)P −中,O 的“倍点”是 ; (2)如图2,图形W 是中心在原点的正方形ABCD ,点(1,1)A −.若点(,3)E t 是正方形ABCD 的“倍点”,求t 的值; (3)图形W 是长为2的线段MN ,T 为MN 的中点,若在半径为6的O 上存在线段MN 的“倍点”,直接写出所有满足条件的点T 组成的图形的面积.参考答案一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.【分析】根据反比例函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数函数图象上点的坐标特征判断即可.【解答】解:A 、直线1y x =+不经过点(0,0),故不符合题意;B 、抛物线2y x =经过点(0,0),故符合题意;C 、抛物线2(4)y x =−不经过点(0,0),故不符合题意;D 、双曲线1y x=不经过点(0,0),故不符合题意; 故选:B .【点评】本题考查了反比例函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数函数图象上点的坐标特征,熟练掌握各函数图象上点的坐标特征是解题的关键.2.【分析】根据中心对称图形的概念求解.在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.这个旋转点,就叫做中心对称点.【解答】解:选项A 、B 、D 均不能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以不是中心对称图形,选项C 能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以是中心对称图形, 故选:C .【点评】此题主要考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后与原图重合. 3.【分析】抛物线的顶点式为:2()y a x h k =−+,其顶点坐标是(,)h k ,可以确定抛物线的顶点坐标. 【解答】解:抛物线2(2)1y x =−+是以抛物线的顶点式给出的, 其顶点坐标为:(2,1). 故选:A .【点评】本题考查的是抛物线的性质,根据抛物线的顶点式确定抛物线的顶点坐标.4.【分析】连接CO ,根据等腰三角形的性质得到OC AB ⊥,于是得到点C 到AB 的距离等于C 的半径,根据切线的判定定理即可得到结论. 【解答】解:连接CO , CA CB =,点O 为AB 中点, OC AB ∴⊥,以点C 为圆心,CO 长为半径作C , ∴点C 到AB 的距离等于C 的半径, C ∴与AB 的位置关系是相切,故选:B .【点评】本题考查了直线与圆的位置关系,等腰三角形的性质,熟练掌握切线的判定方法是解题的关键. 5.【分析】根据旋转的定义确定两个对应点的位置,求得其与O 点连线的夹角即可求得旋转角. 【解答】解:如图,当经过一次旋转后点C 旋转至点B 的位置上,此时360660COB ∠=︒÷=︒, 故选:B .【点评】本题考查了利用旋转设计图案,解题的关键是能够找到一对对应点确定旋转角,从而确定旋转角的度数,难度不大.6.【分析】由较长一段的长为x m 可得出较短一段的长为(2)x m −,根据较长一段的长的平方等于较短一段的长与原绳长的积,即可得出关于x 的一元二次方程,此题得解. 【解答】解:较长一段的长为x m , ∴较短一段的长为(2)x m −.依题意得:22(2)x x =−. 故选:A .【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键. 7.【分析】根据勾股定理的逆定理证得ABC ∆是直角三角形,可以根据直角三角形斜边中线的性质求得BD 的长,然后与300m 比较大小,即可解答本题.【解答】解:300AB cm =,400BC cm =,500AC cm =,222AB BC AC ∴+=, ABC ∴∆是直角三角形, 90ABC ∴∠=︒,点D 是斜边AC 的中点, 250AD CD cm ∴==,12502BD AC cm ==, 250300<,∴点A 、B 、C 都在圆内,∴这三栋楼中在该5G 基站覆盖范围内的是A ,B ,C .故选:D .【点评】本题考查点和圆的位置关系,勾股定理的逆定理,解题的关键是求出三角形三个顶点到D 点的距离.8.【分析】根据用频率估计概率以及频率和概率的概念判断.【解答】解:①当抛掷次数是1000时,“正面向上”的频率是0.512,但“正面向上”的概率不一定是0.512,本小题推断不合理;②随着试验次数的增加,“正面向上”的频率总在0.520附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.520,本小题推断合理;③若再次做随机抛掷该纪念币的试验,则当抛掷次数为3000时,出现“正面向上”的次数不一定是1558次,本小题推断合理; 故选:C .【点评】本题考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.二、填空题(共16分,每题2分)9.【分析】反比例函数的图象在每个象限内,函数值y 随自变量x 的增大而增大,则反比例函数的反比例系数0k <;反之,只要0k <,则反比例函数在每个象限内,函数值y 随自变量x 的增大而增大. 【解答】解:只要使反比例系数大于0即可.如1(0)y x x =>,答案不唯一.故答案为:1(0)y x x=>,答案不唯一.【点评】本题主要考查了反比例函数(0)ky k x=≠的性质:①0k >时,函数图象在第一,三象限.在每个象限内y 随x 的增大而减小;②0k <时,函数图象在第二,四象限.在每个象限内y 随x 的增大而增大.10.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:在一个不透明袋子中有3个红球和2个黑球,共5个球, ∴取出红球的概率是35.故答案为:35.【点评】本题考查概率的求法:如果一个事件有n 种可能,而且这些事件的可能性相同,其中事件A 出现m 种结果,那么事件A 的概率P (A )m n=. 11.【分析】由抛物线开口向上可得距离对称轴越远的点y 值越大,从而求解. 【解答】解:由22y x =可得抛物线开口向上,对称轴为y 轴, |1||2|−<, 12y y ∴<,故答案为:<.【点评】本题考查二次函数的性质,解题关键是掌握二次函数的性质,掌握比较函数值大小的方法. 12.【分析】设(,)C m n .利用中点坐标公式构建方程组求解即可.【解答】解:设(,)C m n .线段BA 绕点B 旋转180︒得到线段BC ,AB BC ∴=,点(2,0)A −,点(0,1)B , ∴202m −+=,012n +=, 2m ∴=,2n =,(2,2)C ∴.【点评】本题考查坐标与图形变化−旋转,中点坐标公式等知识,解题的关键是学会利用参数解决问题即可.13.【分析】利用根的判别式进行计算,令△0>即可得到关于k 的不等式,解答即可. 【解答】解:关于x 的方程220x x k −+=有两个不相等的实数根,∴△0>,即440k −>,1k <.故答案为:1k <.【点评】本题考查了根的判别式,要知道一元二次方程根的情况与判别式△的关系:(1)△0>⇔方程有两个不相等的实数根;(2)△0=⇔方程有两个相等的实数根;(3)△0<⇔方程没有实数根.14.【分析】连接OA 、OB ,根据切线的性质得到OA PA ⊥,OB PB ⊥,根据四边形内角和等于360︒求出AOB ∠,根据圆周角定理计算即可.【解答】解:连接OA 、OB , PA ,PB 分别切O 于点A ,B ,OA PA ∴⊥,OB PB ⊥,360909040140AOB ∴∠=︒−︒−︒−︒=︒,111407022Q AOB ∴∠=∠=⨯︒=︒, 故答案为:70︒.【点评】本题考查的是切线的性质、圆周角定理,掌握圆的切线垂直于经过切点的半径是解题的关键.15.【分析】利用弧长公式求解即可. 【解答】解:标签长度90639.3()180l cm ππ⋅⋅===,故答案为:9.3. 【点评】本题考查弧长的计算,解题的关键是记住弧长公式180n r l π=. 16.【分析】(1)根据题中的转换规则计算即可得到结果;(2)根据输入的二元数,由A 确定出第一个数,由C 确定出第二个数,再由B 确定出结果即可.【解答】解:(1)在图1所示的“A B C −−”组合转换器中,若输入(1,0),则输出结果为1;故答案为:1;(2)若当输入(1,1)和(0,0)时,输出结果均为0,则该组合转换器为“B C A −−”.(写出一种组合即可). 故答案为:B ,A .【点评】此题考查了代数式求值,以及有理数的混合运算,弄清转换器中的规则是解本题的关键.三、解答题(共68分,第17-21题,每题5分,第22题6分,第23题5分,第24-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17.【分析】把方程左边分解得到(2)(4)0x x −−=,则原方程可化为20x −=或40x −=,然后解两个一次方程即可.【解答】解:2680x x −+=(2)(4)0x x −−=,20x ∴−=或40x −=, 12x ∴= 24x =.【点评】本题考查了解一元二次方程−因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).18.【分析】根据一元二次方程的解的定义得到22710a a −−=,则2271a a −=,再把(27)5a a −+变形为2275a a −+,然后利用整体代入的方法计算.【解答】解:a 是方程22710x x −−=的一个根,22710a a ∴−−=,2271a a ∴−=,2(27)5275156a a a a ∴−+=−+=+=.【点评】本题考查一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.19.【分析】(1)把点(2,1)代入抛物线的解析式即可得出答案;(2)求出抛物线的顶点坐标,根据纵坐标即可得出答案.【解答】解:(1)把点(2,1)代入2(3)1y a x =−−中,得:21(23)1a =−−,解得2a =,22(3)1y x ∴=−−;(2)由(1)知抛物线的顶点坐标为(3,1)−,∴把该抛物线向上平移1个单位后,与x 轴的交点个数位1,故答案为:1.【点评】本题主要考查二次函数的图象与性质,关键是要或用待定系数法求函数的解析式.20.【分析】(1)根据题意,利用旋转的性质即可补全图形;(2)根据含30度角的直角三角形和旋转的性质可得AD AC ==90DAB ∠=︒,再利用勾股定理即可解决问题.【解答】解:(1)如图,即为补全的图形;(2)在Rt ABC ∆中,90ACB ∠=︒,30BAC ∠=︒,1BC =,22AB BC ∴==,AC ∴由旋转可知:60DAC ∠=︒,AD AC ==90DAB DAC AC ∴∠=∠+∠∠=︒,BD ∴===.【点评】本题考查了作图−旋转变换,含30度角的直角三角形的性质,勾股定理,掌握旋转的性质是解决本题的关键.21.【分析】(1)利用已知条件结合切线的判定定理解答即可;(2)利用中点的定义和线段和差的意义解答即可;(3)利用勾股定理将(2)中的数据代入即可得出结论.【解答】解:(1)l OA ⊥于点A ,OA 为O 的半径,∴直线l 为O 的切线(经过半径的外端并且垂直于这条半径的直线是圆的切线). 故答案为:经过半径的外端并且垂直于这条半径的直线是圆的切线;(2)以点A 为圆心,AO 长为半径画弧交直线l 于点C ,AC r ∴=.纸片O 沿着直线l 向右无滑动地滚动半周,使点A ,B 分别落在对应的A ',B '处,22r AB r ππ'∴==, (1)CB CA AB r r r ππ∴'=+'=+=+. M 为CB '的中点,1(1)22r MC CB π+∴='=. (1)(1)22r r MA MC AC r ππ+−∴=−=−=. 故答案为:(1)2r π+;(1)2r π−; (3)连接ME ,如图,则(1)2r ME MC π+==. 在Rt AME ∆中,222AM AE EM +=,222AE EM AM ∴=−22(1)(1)[][]22r r ππ+−=− (1)(1)(1)(1)[][]2222r r r r ππππ+−+−=+− r r π=⨯2r π=.O AEFG S S ∴=正方形.故答案为:2r π.【点评】本题主要考查了圆的切线的判定,圆的周长与面积,正方形的面积,勾股定理,本题是操作型题目,根据题干中的作图步骤转化成几何语言是解题的关键.22.【分析】(1)利用根的判别式进行求解即可;(2)设方程的较大的实数根为1x ,较小的实数根为2x ,则有123x x −=,122x x m +=−,121x x m =−,从而可进行求解.【解答】(1)证明:△22(2)41(1)0m m m =−−⨯⨯−=,∴原方程有两个相等的实数根或两个不等的实数根,即该方程总有两个实数根;(2)设方程的较大的实数根为1x ,较小的实数根为2x ,依题意得:123x x −=,122x x m +=−,121x x m =−,2212()3x x ∴−=,22112229x x x x −+=,2212129292(1)112x x x x m m +=+=+−=−,2212()(2)x x m +=−,2221122244x x x x m m ∴++=−+,21122(1)44m m m m ∴−+−=−+,整理得:29m =,解得:3m =或3m =−,0m <,3m ∴=−.【点评】本题主要考查根与系数的关系,解答的关键是对根与系数的关系的掌握并灵活运用.23.【分析】(1)根据垂径定理得到AB AC =,根据圆心角、弧、弦之间的关系定理证明结论;(2)连接OB ,根据垂径定理求出BD ,根据勾股定理求出OD ,根据三角形 的面积公式计算,得到答案.【解答】(1)证明:OD BC ⊥,∴AB AC =,AB AC ∴=;(2)解:连接OB ,OD BC ⊥,8BC =,118422BD DC BC ∴===⨯=,在Rt ODB ∆中,3OD ===,538AD ∴=+=,188322ABC S ∆∴=⨯⨯=.【点评】本题考查的是三角形的外接圆与外心,掌握垂径定理、圆心角、弧、弦之间的关系定理是解题的关键.24.【分析】(1)直接由概率公式求解即可;(2)画树状图,共有12种等可能结果,其中恰好抽到“高山滑雪”和“自由式滑雪”的有2种结果,再由概率公式求解即可.【解答】解:(1)恰好抽到“冬季两项”的概率是14,故答案为:14; (2)“越野滑雪”、“高山滑雪”、“冬季两项”、“自由式滑雪”分别记为甲、乙、丙、丁,画树状图如下:共有12种等可能结果,其中恰好抽到“高山滑雪”和“自由式滑雪”的有2种结果,∴恰好抽到“高山滑雪”和“自由式滑雪”的概率为:21126=. 【点评】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.25.【分析】(1)由题意根据切线的判定证明半径OB BG ⊥,即可证明BG 是O 的切线;(2)根据题意连接CF ,根据圆周角定理和中位线性质得出12EO DF =,进而依据等边三角形和四边形BEDG 是矩形,由矩形的性质可得出FG 的长.【解答】(1)证明:C ,A ,D ,F 在O 上,90CAF ∠=︒,90D CAF ∴∠=∠=︒. AB CE ⊥,BG DF ⊥,90BED G ∴∠=∠=︒.∴四边形BEDG 中,90ABG ∠=︒.∴半径OB BG ⊥.BG ∴是O 的切线.(2)解:连接CF ,90CAF ∠=︒,CF ∴是O 的直径.OC OF ∴=.直径AB CD ⊥于E ,CE DE ∴=.OE ∴是CDF ∆的中位线.122OE DF ∴==. AD AD =,30AFD ∠=︒,30ACD AFD ∴∠=∠=︒.9060CAE ACE ∴∠=︒−∠=︒.OA OC =,AOC ∴∆是等边三角形.CE AB ⊥,E ∴为AO 的中点,24OA OE ∴==,4OB =.6BE OB OE ∴=+=.90BED D G ∠=∠=∠=︒,∴四边形BEDG 是矩形.6DG BE ∴==.2FG DG DF ∴=−=.【点评】本题考查了切线的判定、圆周角定理、等边三角形的判定和性质、等腰三角形的性质、矩形的判定与性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.26.【分析】(1)利用对称点与对称轴的关系:对称点的横坐标之和等于对称轴的2倍,即可求出该抛物线的对称轴.(2)分别讨论222m x m −+的取值范围与对称轴的位置,分别求出不同情况下y 取最大值与最小值时,对应的x 的取值,进而求出a ,m 的值.(3)由于y 的取值范围是3335n y n −<<+,取不到最大值和最小值,故不包含对称轴,分别讨论2n x n −<<在对称轴的左右两侧即可.【解答】解:(1)抛物线23y ax bx =++,0x ∴=时,3y =,∴抛物线23y ax bx =++过点(0,3),抛物线23y ax bx =++过点(4,3),∴该抛物线的对称轴为直线2x =.(2)抛物线23y ax bx =++的对称轴为直线2x =,22b a∴−=,即4b a =−①. 0m >,2222m m ∴−<<+.0a >,抛物线开口向上,∴当2x =时,函数值在222m x m −<<+上取得最小值1−.即4231a b ++=−②.联立①②,解得1a =,4b =−.∴抛物线的表达式为243y x x =−+,即2(2)1y x =−−.0m >,∴当22m x −时,y 随x 的增大而减小,当2x m =−时取得最大值,当222x m +时,y 随x 的增大而增大,当22x m =+时取得最大值,对称轴为2x =,2x m ∴=−与2x m =+时的函数值相等.2222m m <+<+,∴当22x m =+时的函数值大于当2x m =+时的函数值,即2x m =−时的函数值.∴当22x m =+时,函数值在2222m m −<<+上取得最大值3.代入有2413m −=,舍去负解,得1m =.(3)存在,1n =.当2n x n −<<时,y 的取值范围是3335n y n −<<+,y 无法取到最大值与最小值,∴关于x 的取值范围一定不包含对称轴,①当2n 时,2n x n −<<在对称轴的左侧,二次函数开口向上,2x n ∴=−时,y 有最大值,x n =时,y 有最小值,由题意可知:22(2)4(2)3354333n n n n n n ⎧−−−+=+⎨−+=−⎩,解得:1n =, 故1n =,②当22n −时,2n x n −<<在对称轴的右侧,二次函数开口向上,2x n ∴=−时,y 有最小值,x n =时,y 有最大值,由题意可知:22(2)4(2)3334335n n n n n n ⎧−−−+=−⎨−+=+⎩,此时n 无解, 故不符合题意,1n ∴=.【点评】本题是二次函数综合题,考查了二次函数的性质,二次函数的最值,解方程组,待定系数法,正确进行分类讨论是解题的关键.27.【分析】(1)根据要求作出图形即可.结论:DM EM =.证明()ABE ACD SAS ∆≅∆,推出AE AD =,可得结论;(2)当CD =时,12AN DE =成立.过点A 作AT BC ⊥于点T ,AH DC ⊥交DC 的延长线于点H 则四边形ATCH 是正方形.分别求出AN ,DE ,即可判断.【解答】解:(1)图形如图所示,结论:DM EM =.理由:连接AE ,AD .AB AC =,90BAC ∠=︒,45ABC ACB ∴∠=∠=︒,CD CB ⊥,90DCB ∴∠=︒,135ABE ACD ∴∠=∠=︒,BA CA =,BE CD =,()ABE ACD SAS ∴∆≅∆,AE AD ∴=,AM DE ⊥,DM ME ∴=.(2)当CD =12AN DE =成立. 理由:过点A 作AT BC ⊥于点T ,AH DC ⊥交DC 的延长线于点H 则四边形ATCH 是正方形. 1AB AC ==,90BAC ∠=︒,BC ∴==AT CB ⊥,AT TB TC ∴===,CD BE ==EN BN =,BN ∴,2AN ∴===,AH CH AT ==DH ∴==AD ∴==, ABE ACD ∆≅∆, EAB CAD ∴∠=∠,90EAD BAC ∴∠=∠=︒,AE AD ∴==DE ∴=12AN DE ∴=. 【点评】本题考查作图−旋转变换,全等三角形的判定和性质,等腰三角形的判定和性质等知识,解题的关键是理解题意,正确寻找全等三角形解决问题,属于中考常考题型.28.【分析】(1)①根据定义解答可;②分别找出1PQ 、2P Q 、3P Q 的最大值,再根据定义判断即可;(2)正方形ABCD 上的任意两点间的距离最大值为E 是正方形ABCD 的“倍点”,则点E 到ABCD 上点的最大距离好为(3)分线段MN 在O 内部和在O 外两种情况讨论即可求解.【解答】解:(1)①图形W 是半径为1的O ,图形W 上任意两点间的距离的最大值d 为2.故答案为:2;②如图1,连接2P O 并延长交O 于点E ,23P O ==212P E d ∴=+≠,2P ∴不是O 的“倍点”;1P 到O 上各点连线中最大距离为2132d +=≠, 1P ∴不是O 的“倍点”; 3P 到O 上各点连线中最大距离为3142d +==,3P ∴是O 的“倍点”.故答案为:3P .(2)如图2,在正方形ABCD 中,正方形ABCD 上任意两点之间距离的最大距离d =,∴2d =由图可知当点E 在如图所示的位置时,E 是正方形ABCD 的“倍点“,∴OE =,t ∴的值为:3或3−.(3)MN 上2d =,24d =,当线段MN 在O 外部时,4EM =,1TM =,21 / 21ET ∴==∴大O的半径为6+同理,小O的半径为6,点T所构成的图形是圆环,它的面积22(6(6ππ⋅+−⋅=.故答案为:.【点评】此题考查了圆的性质和新定义等知识,解题的关键是理解题意,学会寻找特殊位置解决数学问题,属于中考压轴题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区九年级第一学期期末数学测评一、选择题(本题共32分,每小题4 分) 1•若代数式.2x-1有意义,则x 的取值围是 A . x - B . x > -C . x < -D . x 工--2 2 2 22.将抛物线y x 2平移得到抛物线y x 2 5,下列叙述正 确的是A.向上平移5个单位B.向下平移5个单位3.如图,AC 与BD 相交于点E , AD // BC .若AE :EC A. 1: 2 B. 1:2C. 1:3D.1: 44•下列一元二次方程中,有两个相等的实数根的是A . 60 °B . 50 °C . 40 °D . 306.如图,平面直角坐标系中的二次函数图象所对应的函 数解读式可能为 11A . y-x 2 B. y (x 1)222C . y 1(x 1)2 1D . y1(x 1)2 12 27 .已知a 0,那么-v a 2 2a 可化简为C.向左平移5个单位D.向右平移5个单位 A . 2 x 2x 1B .x 2 2x 4 0 C . x 22x 5 0 D . x 2 2x 4A =40 °,则/ 等CB1:2,贝"S A ED :S CEB5.如图,00 是厶ABC 的外接圆,/A. aB.aC. 3aD. 3a8.如图,以G(0,1)为圆心,半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,点E 为。
G 上一 动点,CF AE 于F .当点E 从点B 出发顺时针运动 到点D 时,点F 所经过的路径长为矚慫润厲钐瘗 睞枥庑赖賃軔朧碍鳝绢。
二、填空题(本题共16分,每小题4 分) 9 .计算,3(1 . 6)=.10.若二次函数y 2x 2 3的图象上有两个点A(3,m)、B(2, n),则 m n (填“ <”或“二”或“ >”).11.如图,将半径为2cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,贝浙痕AB 的长为 ____________ c m.聞創沟燴鐺險爱氇谴净祸測樅 锯鳗鲮。
12.小聪用描点法画出了函数y , x 的图象F ,如图 所示.结合旋转的知识,他尝试着将图象 F 绕原点逆 时针旋转90得到图象F 1,再将图象F 1绕原点逆时针 旋转90得到图象F 2,如此继续下去,得到图象F n . 在尝试的过程中,他发现点 P ( 4, 2)在图象上(写出一个正确的即可);若点 P (a , b )在图象F 127上,则a =(用含b 的代数式 表示).残骛楼諍锩瀨濟溆塹籟婭骤東戇鳖納。
三、解答题(本题共30分,每小题5 分)八FD£13. 计算:i ^2 (-)2(3)0屈.314. 解方程:x2 + 2x- 8= 0 .15 .已知a b 3,求代数式a2 b2 2a 8b 5的值.16.如图,形网格中,△AB顶点及点0在格点上.(1)画出与△ AB(关于点0对称的△ ABG ;⑵画出一个以点0为位似中心的△ A2B2C2,使得△ A2B2C2与厶ABG的相似比为2.17 .如图,在△ ABC与厶ADE中,C E ,1 2, AC AD 2AB=6,求AE 的长.18.如图,二次函数y x2 2x 3的图象与x轴交于A、B两点,与y轴交于点C ,顶点为D,求厶BCD的面积.四、解答题(本题共20分,每小题5分)19 .已知关于x的方程X2 3x 3m 0有两个不相等4的实数根.五、解答题(本题共22分,第23题7分,第24题8分,第25题7 分) 23. 小明利用等距平行线解决了二等分线段的问题作法:(1 )求m 的取值围;(2) 若m 为符合条件的最大整数,求此时方程的根 x・・・ 0 123 45 ・・・ y・・・31m8・・・(2)求出这个二次函数的解读式;⑶当o x 3时,则y 的取值围为.21. 图中是抛物线形拱桥,当水面宽为 高度下降1M 时,水面宽度为多少 M ? 額閉镇桧猪訣锥顧荭钯詢鳕驄。
22. 如图,AB 为OO 的直径,BC 切OO B , AC 交OO 于点D , E 为BC 中点. 求证:(1) DE 为OO 的切线;(2)延长ED 交BA 的延长线于F ,若DF=4 , AF=2,求BC 的长.20.已知:二次函数y ax 2 bx c (a 0)中的x 和y 满足下表:(1)可求得m 的值为;(1)在e上任取一点C,以点C为圆心,AB长为半径画弧交c于点D, 交d于点E;(2)以点A为圆心,CE长为半径画弧交AB于点M ;•••点M为线段AB的二等分点.A M~Kfi图1解决下列问题:(尺规作图,保留作图痕迹)(1)仿照小明的作法,在图2中作出线段AB的三等分点;A--------------- B图2(2 )点P是/ AOB部一点,过点P作PM丄OA于M , PN丄OB于N , 请找出一个满足下列条件的点P.(可以利用图1中的等距平行线) 彈贸摄尔霁毙攬砖卤庑诒尔肤亿鳔简。
①在图3中作出点P,使得PM PN ;②在图4中作出点P,使得24 .抛物线y mx2 (m 3)x 3(m 0)与x轴交于A、B两点,且点A在点B 的左侧,与y 轴交于点C , OB=OC .(1)求这条抛物线的解读式;(2)若点P(x,,b)与点Q(x2,b)在(1)中的抛物线上,且x, x2,PQ二n.①求4x i2 2x2n 6n 3的值;②将抛物线在PQ下方的部分沿PQ翻折,抛物线的其它部分保持不变,得到一个新图象•当这个新图象与x轴恰好只有两个公共点时,b的取值围是•謀养抟箧飆鐸怼类蒋薔點鉍杂篓鳐驱。
25 .如图1,两个等腰直角三角板ABC和DEF有一条边在同一条直线I上,DE 2 , AB 1 .将直线EB绕点E逆时针旋转45,交直线AD于点M .将图1中的三角板ABC沿直线I向右平移,设C、E两点间的距离为k .厦礴恳蹒骈時盡继價骚卺癩龔长鳏檷f(O图3解答问题:("①当点C与点F重合时'如图2所示'可得誥的值为;②在平移过程中,处的值为(用含k的代数式表示);DM(2)将图2中的三角板ABC绕点C逆时针旋转,原题中的其他条件保持不变.当点A落在线段DF上时,如图3所示,请补全图形,计算如的DM 值;茕桢广鳓鯡选块网羈泪镀齐鈞摟鳎饗。
(3)将图1中的三角板ABC绕点C逆时针旋转度,0 < 90,原题中的其他条件保持不变.计算如的值(用含k的代数式表示).鹅娅尽DM損鹌惨歷茏鴛賴縈诘聾諦鳍皑。
海淀区九年级第一学期期末练习数学试卷答案及评分参考一、选择题(本题共32分,每小题4 分)二、填空题(本题共16分,每小题4 分)三、解答题(本题共30分,每小题5 分)13.计算:1 (-) 2(3)0庞.解:原式=、、2 1 9 1 2.2=7 J2.14.解方程:x2 + 2x- 8= 0.解法一:(x 4)(x 2) 0 . ....................................................................... 3分x 4 0或x 2 0.x(4, x2 2 . ........................................................................... 5 分解法二:a 1,b 2,c 8, ........................................................ 1 分22 4 1 ( 8) 36 0 . ................................................................. 2分二 * 4, X2 2 .15 .解法一:T a b 3,・ 2 2二 a b 2a 8b 5=(a b)(a b) 2a 8b 5 ....................................................... 2 分= 3(a b) 2a 8b 5 ................................................. 3 分= 5(a b) 5= 5 3 5= 20. ................................... 5 分解法二:T a b 3,二 b 3 a.. ................................. 分原式二a2 (3 a)2 2a 8(3 a) 5. .............................................................. 2 分=a2(9 6a a2) 2a 24 8a 5. ............................................. 3 分=a29 6a a2 2a 24 8a 5. ............................................. 4 分= 20.16.例如::,△ ABQ、△ A2B2C2为所求.(注:第(1)问2分;第(2)问3分,画出一个正确的即可.)17.解:T 1 2,CAB EAD .二△ CAB EAD .AB ACAD AET AC AD 2AB =6 ,AB=3..3_ 6..——6 AE '二AE 12. ................ 5 分18.解法一:依题意,可得y x2 2x 3 —(x 1)2 4.二顶点D(1,4). ........ 分令y o,可得x 3或x 1 .A( 1,0)、B (3,0). ......分 (2)令x 0,可得y 3.「• C(0,3).二直线CD 的解读式为y x 3. 设直线CD 交x 轴于E . 二 E( 3,0). 二 BE 6.分 (3)分 (4)• • S VBCDS V BED S V BCE3.3.解法二:同解法一,可得 A ( 1,0)、 B (3,0) > C(0,3)、 D(1,4).二直线BC 的解读式为yx 3.过点D 作DE // BC 交x 轴于E ,连接CE . •••设过D 、E 两点的直线的解读式为T D(1,4),二直线DE 的解读式为y x 5. 二 E(5,0). …BE 2.分 (4)•/ DE // BC ,. 1…S VBC D S vBCE — BE OC 3 .2BCD 的面积为3.四、解答题(本题共20分,每小题5 分)19 .解:(1 )T 关于x 的方程x 2 3x 弓40有两个不相等的实数根,9 3m 0.(2)•- mTm2..为符合条件的最大整数,........... 分2 3 c• x3x0.22,3 233x2 x3x(二) F).2223、23(x-)2433 3 3X12x2 2 '方程的根为X1宁,X2十. ............. .................... 5分20 .解:(1) m的值为3; . .................................. 1分(2) •••二次函数的图象经过点(1, 0),( 3, 0),• ••设二次函数的解读式为y a(x 1)(x 3).. ................................ 分T图象经过点(0,3),•- a 1 . . ........................ 分 (3)•这个二次函数的解读式为y x2 4x 3.. ................................................ 4分(3)当0 x 3时,贝S y的取值围为K y 3.. ................................. 5分21.解:如图所示,建立平面直角坐标系.设二次函数的解读式为y ax2(a 0)..…T图象经过点(2, 2) , . ...................................... 2分• 2 4a,1 a .2. 1 2 …y x ..2ADB CDB 90 .TE 为BC 中点,• ED 〔BC EB .2T BC 切OO 于点B,EBA 90 . 1324 90 ,即 ODE 90 . 二 OD 丄 DE . •••点D 在OO 上, • DE 是OO 的切线.(2) V OD 丄 DE , FDO 90 .设 OA OD r .V OF 2 FD 2 OD 2, DF=4 , AF=2 ,2 2 2…(r 2) 4 r .>IZ当y 3时,x .6答:当水面高度下降1M 时,水面宽度为2 6 M.. 22 .(1)如图,连接OD,BD .T 在OO 中,OD OB ,•/ AB 是OO 的直径,E解得r 3 ./. OA OD 3,FB 8.•/ F F, FDO FBE 90 ,FDO FBE . ......................................................... 4分.FD OD…FB BE .二BE 6.TE为BC中点,.BC 2BE 12. ................................................................... 5 分五、解答题(本题共22分,第23题7分,第24题8分,第25题7 分)23.解:(1)(注:直接等分不给分,在等距平行线上有正确痕迹的给分,作出一个给1分.)(2)①②4分24 .解:(1 )解法一:T抛物线y mx2 (m 3)x 3(m 0)与y轴交于点C , C(0, 3).分…订T抛物线与x轴交于A、B两点,OB=OC ,••• B(3,0)或B(-3,0).T点A在点B的左侧,m 0,•抛物线经过点B(3,0). .............. 分- (2)•0 9m 3(m 3) 3.•m 1.•抛物线的解读式为y x2 2x 3. .................................................. 3分解法二:令y 0,2•mx (m 3)x 3=0.•(x 1)(mx 3) 0 .•彳 3…x 1,x= .mQm 0,点A在点B的左侧,•A( 1,0), B(-,0) . .................................. 1 分m令x 0 ,可得y 3 .•C(0, 3).•OC 3. .................................... 2 分QOB OC ,3.• y x2 2x 3.(2)①由抛物线y x2 2x 3可知对称轴为x 1. ................ 分•点P(N,b)与点Q(X2,b)在这条抛物线上,且X j X2, PQ n ,• X1 1 n,X212n2.2 n... 分5• 2x12n ,2x2•原式二(2 n)2(2 n)n 6n 3 7..... 分②4 b2或b0. ............................. ... 分8(注:答对一部分给1分•)25 .解:(1丿①1 ; ..................................................... 1分②k;............................................. 2分2(2)解:连接AE.T ABC, DEF均为等腰直角三角形,DE 2, AB 1 ,/. EF 2,BC 1, DEF 90 , 4 5 45 ./. DF 2 2, AC 、2, EFB 90 ./. DF 2AC, AD 2.•••点A为CD的中点................ 3分•EA DF ,EA平分DEF .•MAE 90 , AEF 45 , AE•/ BEM 45 ,•1+ 2= 3+ 2=45 .•- 1= 3.•AEM s FEB..AM AEBF EF2.AM DM(3)过B 作BE 的垂线交直线EM 于点G ,连接AG 、BG . 「• EBG 90 .•/ BEM 45 ,「• EGB BEM 45 . 「• BE BG .ABC 为等腰直角三角形, /. BA BC, ABC 90 .1 2.ABGCBE. ............................................ 6 分:.AG EC k,3 4.T 3+ 65+ 4=45 ,二 65.二 AG // DE .AGM DEM .AM AG k DM DE 2(注:本卷中许多问题解法不唯一,请老师根据评分标准酌情给分.)二AM_/22二DMAD AME€。
