数字电路第七章答案
北京理工大学数字电路第七章答案

北京理工大学数字电路第七章答案二进制数10101转换为十进制数后为() [单选题] *A.15B.21(正确答案)C.18D.10逻辑函数式D+D,简化后结果是() [单选题] *A.2DB.D(正确答案)C.D²D.0一位十六进制数可以用二进制数来表示,需要二进制的位数是() [单选题] *A.1B.2C.4(正确答案)D.16当决定某个事件的全部条件都具备时,这件事才会发生。
这种关系称为() [单选题] *A.或逻辑B.与逻辑(正确答案)C.非D.异或010*********的8421码为() [单选题] *A.496(正确答案)B.495C.598D.4694位二进制数可用十六进制数来表示,需要十六进制的位数是() [单选题] *A.1(正确答案)B.2C.3D.48421BCD码用4位二进制数表示十进制数的位数是() [单选题] *A.1(正确答案)B.2C.3D.4在数字电路中,不属于基本逻辑门是() [单选题] *A.与门B.或门C.非门D.与非门(正确答案)如图所示门电路,电路实现的逻辑式Y= [单选题] *A.Y=(AB)\B.Y=ABC.Y=A+B(正确答案)D.Y=(A+B)\如图所示的波形图表示的逻辑关系是()[单选题] *A.F=A·B(正确答案)B.F=A+BC.F=(A·B)\D.F=(A+B)\异或门F=A⊕B两输入端A、B中,A=1,则输出端F为() [单选题] *A.A⊕BB.B\(正确答案)C.BD.0下列表所示的真值表完成的逻辑函数式为()[单选题] *A.F=ABB.F=ABC.F=A⊕BD.F=A+B(正确答案)当A=B=0时,能实现F=1的逻辑运算是() [单选题] *A.F=A·BB.F=A+BC.F=A⊕BD.F=(A+B)\(正确答案)八位二进制数能表示十进制数的最大值是() [单选题] *A.255(正确答案)B.248C.192D.168将(01101)2转换为十进制数为() [单选题] *A.13(正确答案)B.61C.51D.25逻辑函数式Y=A+A,化简后的结果是() [单选题] *A.2AB.A(正确答案)C.1D.A2逻辑函数式Y=EF+E\+F\的逻辑值为() [单选题] *A.EFB.(EF)\C.0D.1(正确答案)以下表达式中符合逻辑运算法则的是() [单选题] *=C2B.1+1=10C.A·1=1D.A+1=1(正确答案)当逻辑函数有n个变量时,取值组合有() [单选题] *A.nB.2nC.n²D.2"(正确答案)二进制数码为(11101),则对应的十进制数为() [单选题] *A.29(正确答案)B.28C.13D.14下列说法中与BCD码的性质不符的是() [单选题] *A.一组四位二进制组成的码只能表示一位十进制B.BCD码是一种人为选定的0~9十个数字的代码C.BCD码是一组四位二进制数,能表示十六以内的任何一个十进制数(正确答案)D.BCD码有多种数字信号和模拟信号的不同之处是() [单选题] *A.数字信号在大小上不连续,时间上连续,而模拟信号则相反B.数字信号在大小上连续,时间上不连续,而模拟信号则相反C.数字信号在大小、时间上均不连续,而模拟信号则相反(正确答案)D.数字信号在大小、时间上均连续,而模拟信号则相反“与非”运算的结果是逻辑“0”的输入是() [单选题] *A.全部输入是“0”B.任一输入是“0”C.仅一输人是“0”D.全部输入是“1”(正确答案)相同为“0”不同为“1”,它的逻辑关系是() [单选题] *A.或逻辑B.与逻辑C.异或逻辑(正确答案)D.同或逻辑一只四输入端或非门,使其输出为“1”的输入变量取值组合有种。
数字电子技术第七章作业及答案

第七章(脉冲波形的产生与整形)作业1、简述单稳态触发器的功能特点,举例说明其应用。
由CMOS 门组成的微分型单稳态触发器如图7-1所示。
设电阻R =1k Ω,电容C =0.1μF ,试计算该电路的暂稳态时间。
图7-1 微分型单稳态触发器 解:单稳态触发器只有一个稳定状态,一个暂稳态。
在外加脉冲的作用下,单稳态触发器可以从一个稳定状态翻转到一个暂稳态。
由于电路中RC 延时环节的作用,该暂态维持一段时间又回到原来的稳态,暂稳态维持的时间取决于RC 的参数值。
利用单稳态触发器的特性可以实现脉冲整形,脉冲定时等功能。
暂稳态时间为:ms RC tw 069.0101.01069.02ln 63=⨯⨯⨯==-2、简述施密特触发器的功能特点,举例说明其应用。
图7-2所示的是施密特触发器74LS14与其输入端电压V I 的波形,试画出输出电压V O 的波形。
图7-2 施密特触发器 解:施密特触发器也有两个稳定状态,但与一般触发器不同的是,施密特触发器采用电位触发方式,其状态由输入信号电位维持;对于负向递减和正向递增两种不同变化方向的输入信号,施密特触发器有不同的阈值电压。
1. 波形变换2. 脉冲波的整形3. 脉冲鉴幅 4、构成多谐振荡器3、用定时器555组成多谐振荡器,要求输出电压V O 的方波周期为1ms ,试选择电阻与电容的数值,并画出电路图。
解:周期T 计算如下:121269.0C R R T )(+=取C 1=0.1μF ,R 2=5.1k Ω则有:Ω=⨯-⨯=⨯⨯-⨯⨯=-=--k R C T R 3.4102.101045.1101.52101.069.010269.0343632114、试分析如图7-3所示脉冲信号产生电路。
(1)说明该电路各部分的功能。
(2)画出A 、B 、C 和v O 各点波形。
(3)已知施密特触发器CT4014的V T+=1.6V ,V T -=0.8V 。
求电路的输出脉宽t W 。
数字电子技术第7章习题答案

数字电子技术第7章习题答案
1. 什么是逻辑门?
答:逻辑门是数字电路中的基本组件,用于对输入进行逻辑运算并产生输出。
2. 列举几种常见的逻辑门。
答:与门、或门、非门、异或门、与非门、或非门等。
3. 什么是真值表?
答:真值表是一种用来展示逻辑函数输入与输出关系的表格,其中列出了所有可能的输入和对应的输出。
4. 什么是逻辑电路?
答:逻辑电路是指由逻辑门组成的电路,用于对输入进行逻辑运算并产生输出。
5. 什么是卡诺图?
答:卡诺图是一种用于最小化逻辑函数的图形化工具,通过将函数的真值表转化为图形,可快速找到最小化的逻辑表达式。
6. 什么是多路复用器?
答:多路复用器是一种数字电路,可以选择不同的输入并将其发送到一个输出线上。
7. 什么是解码器?
答:解码器是一种数字电路,用于将二进制数字输入转换为对应的输出,通常用于驱动其他数字电路中的寄存器、计数器等。
8. 什么是编码器?
答:编码器是一种数字电路,用于将多个输入端连接到一个二进制数字输出端,也可以实现将多个开关等输入转换为一个数字信号输出。
9. 什么是计数器?
答:计数器是一种数字电路,可用于记录电路所经过的时间或事件数量,通常用于计时器、频率计等应用。
10. 什么是触发器?
答:触发器是一种数字电路,可用于存储和控制数字信号,通常用于存储器、寄存器等应用。
《数字电路-分析与设计》第七章习题及解答(部分1) 北京理工大学出版社
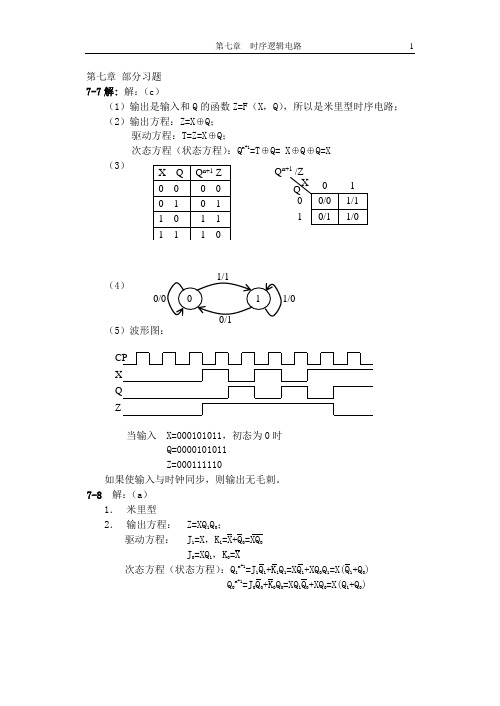
第七章 部分习题 7-7解: 解:(c )(1)输出是输入和Q 的函数Z=F (X ,Q ),所以是米里型时序电路; (2)输出方程:Z=X ⊕Q ;驱动方程:T=Z=X ⊕Q ;次态方程(状态方程):Q n+1=T ⊕Q= X ⊕Q ⊕Q=X(3)(4)(5)波形图:当输入 X=000101011,初态为0时 Q=0000101011 Z=000111110如果使输入与时钟同步,则输出无毛刺。
7-8 解:(a ) 1. 米里型2. 输出方程: Z=XQ 1Q 0;驱动方程: J 1=X ,K 1=X+Q 0=XQ 0J 0=XQ 1,K 0=X次态方程(状态方程):Q 1n+1=J 1Q 1+K 1Q 1=XQ 1+XQ 0Q 1=X(Q 1+Q 0)Q 0n+1=J 0Q 0+K 0Q 0=XQ 1Q 0+XQ 0=X(Q 1+Q 0)Q n+1CP X Q Z3.4.7-12某同步时序电路的逻辑方程如下:驱动方程:nQ X T 01⊕=,n Q X T 10=;输出方程:n Q X Z 1=。
要求: 解:1.同步时序电路的逻辑图示于图,这是米里型的状态机。
2.(a )状态方程: Q 1n+1=T 1⊕Q 1=X ⊕Q 0⊕Q 1Q 0n+1=T 0⊕Q 0=XQ 1⊕Q 0=XQ 1Q 0+XQ 0+Q 1Q 0(b )状态转换表: (c )状态转换图:(Q 1Q 0n+1Q7-15解:(a )“11”检测器,不重叠。
S 0:初始状态,输出0; S 1:输入一个“1”,输出0; S 2:输入两个“1”,输出1;(b ) “101”检测器,可重叠。
S 0:初始状态;S 1:输入序列为“1”;S 2:输入序列为“10”;S 3:输入序列为“101”;(c )(d )略7-34 “011”序列检测器,可重叠。
解:1.采用D(a ) 米里型状态图: S 0:初始状态;S 1:输入序列为“0”; S 2:输入序列为“01”;S 3:输入序列为“011”; (b ) 状态表(两种画法均可):(c ) 状态化简:由观察法知,S 0、S 3等价。
《数字电路-分析与设计》第七章习题及解答(部分2) 北京理工大学出版社

第七章 习题答案7-111、米里型状态机2、输出方程: 01Q XQ Z =驱动方程: 011Q Q X D = 10Q X D =状态方程: 01111Q Q X D Q n ==+ 1010Q X D Q n ==+ 3、状态转换表:4、状态转换图:5、时序图:已知:X=1011111001110 初始: 0001=Q Q0/0X Q 1n Q 0n ZCP7-147-32 一、次态K 图,D 触发器: 1、根据状态转换表,有:1212313Q XQ Q Q Q X Q n +=+1212122312Q XQ Q Q X Q Q X Q Q X Q n +++=+ 111Q X Q n =+2、求驱动方程:对于D 就是状态方程: 12123133Q XQ Q Q Q X Q D n +==+12121223122Q XQ Q Q X Q Q X Q Q X Q D n +++==+ 1111Q X Q D n ==+3、检查启动特性:Z Q Q Q n n n /111213+++能够自启动。
二、次态K 图,JK 触发器:1、求状态方程:1212313Q XQ Q Q Q X Q n +=+ 1212122312Q XQ Q Q X Q Q X Q Q X Q n +++=+ 111Q X Q n =+与采用D 触发器一样。
与JK 触发器的特性方程相比Q K Q J Q n +=+1 2、得JK 触发器的驱动方程: 12312313Q Q Q X Q Q Q X Q n +=+∴ )(123Q Q X J ⊕= 13=K132XQ Q X J += 1112Q X Q X Q X K ⊕=+= X J =1 11=K 3、检查启动特性: (与前相同,略)7-38 设计一个二位多功能计数器: 1、列状态转换驱动表:2、从四变量K 图求驱动方程:00100011Q C C Q C Q C J ++=其它K 图略: 001001001011Q C C Q C C Q C C C C K +++= 1110Q C Q J += 1110Q C C K +=逻辑电路图,略。
数字电路第7章习题解答
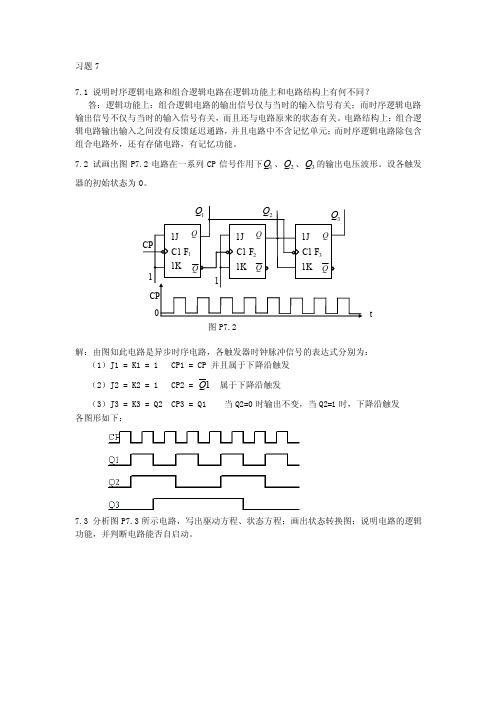
习题77.1 说明时序逻辑电路和组合逻辑电路在逻辑功能上和电路结构上有何不同?答:逻辑功能上:组合逻辑电路的输出信号仅与当时的输入信号有关;而时序逻辑电路输出信号不仅与当时的输入信号有关,而且还与电路原来的状态有关。
电路结构上:组合逻辑电路输出输入之间没有反馈延迟通路,并且电路中不含记忆单元;而时序逻辑电路除包含组合电路外,还有存储电路,有记忆功能。
7.2 试画出图P7.2电路在一系列CP 信号作用下1Q 、2Q 、3Q 的输出电压波形。
设各触发器的初始状态为0。
解:由图知此电路是异步时序电路,各触发器时钟脉冲信号的表达式分别为:(1)J1 = K1 = 1 CP1 = CP 并且属于下降沿触发 (2)J2 = K2 = 1 CP2 = 1Q 属于下降沿触发(3)J3 = K3 = Q2 CP3 = Q1 当Q2=0时输出不变,当Q2=1时,下降沿触发 各图形如下:7.3 分析图P7.3所示电路,写出驱动方程、状态方程;画出状态转换图;说明电路的逻辑功能,并判断电路能否自启动。
图P7.2CP1JC1 F 3 1K 1J C1 F 2 1K 1J C1 F 1 1K 1Q2Q3Q1 QQQ Q QQ1CP 0t解:由电路图可知:该电路是同步时序电路 它的驱动方程为:J0 = 2n Q K0 = 1 J1 = 1n Q K1=1状态方程为: 11n Q + = 2n Q *1nQ 12n Q + = 1nQ*2n Q状态表如下:2n Q 1n Q12n Q + 11n Q +0 0 0 10 1 1 01 0 0 01 1 0 0 由状态表可以得状态转换图如下:由其状态图可知,此电路具有计数功能。
并且可以看出,若此电路由于某种原因进入无效状态时,在CP 脉冲作用后,电路能够回到有效序列,因而具有自启动能力。
7.4 分析图P7.4所示电路,写出各触发器的驱动方程、状态方程;画出状态转换图;当X=1和X=0时,电路分别完成什么逻辑功能?CP11Q2Q图P7.3 1J1K C1 1J C11K Q QQQ00 011110解:由电路图可知,这是一个同步时序电路输出方程: nn n n Q Q X Q XQ Y 0101+= 驱动方程: J0 = K0 = 1 J1 = K1= 0n Q X ⊕状态方程: 10n Q += 0n Q 11n Q += ()01n n Q X Q ⊕⊕11n Q +10n Q + X 0 1 1n Q0n Q0 0 0 1 1 10 1 1 0 0 01 0 1 1 0 1 1 1 0 0 1 0由状态图可以画出其状态表如下图:由状态图可以看出,此电路是一个可控计数器。
数字集成电路分析与设计 第七章答案
CHAPTER 7P7.1. Assume that all nodes start at 0V. The first row outputs will be at DD T V V -. Since thesenodes are also the gate nodes of the second row of transistors, their source nodes will be at 2DD T V V -. Likewise, the last row of transistors have voltages of 3DD T V V -. However, this value is below 0V so we leave them at 0V.1.2V1.2V0.73V 0.73V 0.73V0.33V0.33V0.33V0V0V0VP7.2. (a)(b)(c)(d)P7.3. (a) First calculate V Q .()01.80.51.15Q DD T DD T V V V V V Vγ=-=-+=--=Since this is slightly below 1.3V (voltage at which the PMOS turns on), we assume that the PMOS is slightly on. Since the PMOS’s V GS is quite low (because Q is high) and its V DS is quite high (because Q is low), the transistor is very likely in saturation. Similarly for the NMOS, because its V GS is high and its V DS is low, it’s likely in the linear region. Equating the two currents:()()()()()()()()22,,222211DSNDSN CN NQ Q CN NSDP sat DSN linV N N OX GSN T DSN P sat OX GSP T V GSP T CP PN V N N OX Q T Q P sat OX DD Q T V DD Q T CP PE L N I I W C V V V W v C V V V V E L L W C V V V W v C V V V V V V E L L μμ=---=-++----=--++For simplicity we shall assume that 11Q CN NV E L +≈ and220QV ≈.()()()2N N OX Q T QP sat OX DD Q T DD Q T CP P NW C V V V W v C V V V V V V E L L μ---≈--+Solve to produce:0.0080V Q V ≈When the CLK goes low, the intermediate output suffers from clock feedthough. To calculate the effects of clock feedthrough, let us first compute the capacitances involved. The capacitance from the clock signal to Q is:(.2/)(.2)0.0.4fF GS OL C C fF um um ===The capacitance from the Q to ground is:()()()(),310.2320.2 1.4fF Q DN IN inv d g C C C C W C W =+=+=+=The capacitive feedthrough equation is:()210.04 1.80.05V 0.04 1.41.150.05 1.1VGS CLK Q GS Q Q Q Q C V V C C V V V -∆∆===-++=+∆=-=To get the new value of Q V , first determine the determine the regions of operation of the transistors in the inverter by calculating V S . Then, once again, use the currentequations to determine Q V .Since the new voltage of V Q is still greater than the switching voltage, the transistors are in the same regions:()()()()()()2000460.4100.2810P N sat OX DD Q T Q N N OX Q T DD Q T CP P OXW L v C V V V V W C V V V V V E L C μ---≈---+⨯⨯≈()()()21.8 1.10.50.2270OX C --()()0.016V1.10.5 1.8 1.10.5 4.8≈---+(b) In this case 1.8Q DD V V V == and 0Q V =. Clock feedthrough has no effect since the transmission gate CLK signals cancel each other out.()()()()()()()(),3151515315(23)312.5102100.2110(2)0.23(210)(0.2)312.5101100.2257.532.5pass pass inv d inv eqn g eff g eqn d t R C R C R C W C W C W R C Wps ps ps----=+=+++⎡⎤=⨯⨯+⨯+⨯+⎣⎦⨯⨯=+=P7.4.a. Out A BC =+BBOutb. Out AB BC C =++Outc. ()Out A B C AB ABC AB =+++=+BBOutd. ()()1Out A B C AB ABC AB AB C AB A B =+++=+=+==+OutP7.5.a. ()Out A B C =+b. ()()Out A B C D E =+++ P7.6.a. Out A BC =+c bclkclkV DDb. Out AB BCC =++a bclkclkV DDc.()Out A B C AB ABC AB =+++=+V DDd.()()()Out A B C AB A B C A B AB=+++=+++=+aclkclkV DDP7.7.Assuming that one of the transistors in each transmission gate is being driven by a min-sized inverter:a.()()()()122333passinvRC R R RLERC R R+====b.()()()()()()()()313133313133AAinvCCinvRRC RLERC R RRRC RLERC R R========()()()()339333BBinvRRC RLERC R R====P7.8.a. Out A sel B sel =⋅+⋅b.R inv 6.25k ΩC inv,diff 1.2fF C pass,gate 0.8fF C pass,diff0.8fFR pass 6.25k ΩCpass,diff0.8fFCpass,gate0.8fFfC inv,gate2.4f fFCpass,diff0.8fFc. ()()(),,,,,,2A C inv inv diff pass gate pass diff inv pass inv gate pass gate pass diff t R C C C R R fC C C -=++++++ d. (),,inv inv LOADC out inv diff LOAD inv inv diffR R C t fC C R C f f-=+=+ e.()()()()(),,,,,,,,220inv inv diff pass gate pass diff inv pass inv gate pass gate pass diff inv LOADinv inv diff inv LOAD inv pass inv gate t R C C C R R fC C C R C R C fR C dtR R C df f f =++++++++=+-===3.2=P7.9. In both of these cases, the logical effort is the same due to the fact that the longest pathfrom output to ground is three transistors long. Assume that the CLK arrives ahead of the signals. Then,12()26663R R LE R λλ+== P7.10. We will use 0.18um technology and the node names below:W=4W=4OutFor the two inverter inputs:()()()3230.2 1.2fF inv g C C W ===For the pass gate inputs:()0.4fF pass g C C W ==At node x:()(3)(2) 1.4x eff eff g C C W C W C W fF =++=At node y:()2((2))(2)2y eff g eff C C W C W C W fF =++=At node Out:()((2))(2) 1.2out eff g eff C C W C W C W fF =++=The shortest path is through the one of the G ND input nodes to the output:()()()()min 212.5 1.4212.5 1.247.5x out t RC RC k fF k fF ps =+=+=The longest path is through one of the inverters to the output.()()()()()()max 2312.5 1.4212.52312.5 1.2112.5sx y out t RC RC RC k fF k fF k fF p =++=++=P7.11. At 0t =: DD F V =0X =?Y =.When the a goes high the first time, the voltage at X would be computed using the charge-sharing formula:()101.21V 210F DDX X F C V V C C ===++But because the maximum allowable voltage at node x is 0.734V, set 0.734V X V = Then recomputed V F :()()()()10 1.220.734 1.05V 10F DD X X F F C V C V V C --===When Phi goes down, F DD V V = and V X and V Y remains the same. The next time the Phi goes up, all the internal nodes are 0. When Phi goes down, F DD V V = and V X and V Y remains at 0. P7.12.P7.13.a. The input settings that give you the worst-case charge sharing are any of 1a c e === and both of 0b d ==. Essentially, what you are doing it trying to create the greatest amount of parasitic capacitances without creating a path to G ND .b. Assuming that transistors share nodes to reduce capacitance.()()()()()()()12*11125(3)(5) 5.2fF 333190.2 1.8fF 5.2 1.8 1.34V 5.2 1.8g d g d C C W C W C W C C W W W C V V C C =++==++=====++ The actual voltage would be larger than this since the internal node cannot rise above V DD -V T .c. This circuit fails if the worse case voltage falls below the switching voltage which can be computed to be V S =0.92V. Therefore, the circuit will operate properly. P7.14. Both of these circuits act as latches. When EN is on, there is a path from the output toeither V DD or G ND . The first latch is better than the second because the second latch suffers from charge sharing. When EN is off, there is no path from the output to either of the sources, if IN is switching it is possible for whatever charge that is held on OUT to be shared with the internal nodes between the two NMOS’s or the two PMOS’s. Therefore, the second one is not as good as the first one. P7.15.a.OUT OL X DD TV V V V V ==-b. First, let ’s find the required change in voltage:()()2OUT DD OLX DD T DD T TV V V V V V V V V ∆=-∆=+--=Now, let’s set up the clock feedthrough equation and solve for C b :22b OUT X b XX X T Xb OUT X DD OL TC V V C C V C V C C V V V V V ∆∆=+∆==∆-∆--。
数字电子技术基础数电第六版阎石课后答案第七章
数字电子技术基础数电第六版阎石课后答案第七章第七章:逻辑门和逻辑代数1. 本章节内容概述本章介绍了逻辑门和逻辑代数的基础知识。
首先介绍了逻辑电平和逻辑门的概念,然后详细介绍了与门、或门、非门等基本逻辑门的原理、特性和应用。
接着介绍了与非门、或非门、异或门等组合逻辑门的原理和应用。
最后介绍了逻辑代数的基本概念和运算规则。
2. 逻辑门逻辑门是数字电子电路中使用的基本元件,用于进行逻辑运算。
逻辑门有多种类型,其中最基本的有与门(AND)、或门(OR)和非门(NOT)。
2.1 与门(AND)与门是一种逻辑门,其输出信号仅在所有输入信号都为高电平时才为高电平,否则为低电平。
与门的逻辑符号如下:AND gateAND gate2.2 或门(OR)或门是一种逻辑门,其输出信号在任何输入信号中有一个或多个为高电平时就为高电平,只有所有输入信号都为低电平时才为低电平。
或门的逻辑符号如下:OR gateOR gate2.3 非门(NOT)非门是一种逻辑门,其输出信号和输入信号相反。
当输入信号为低电平时,输出信号为高电平;当输入信号为高电平时,输出信号为低电平。
非门的逻辑符号如下:NOT gateNOT gate3. 组合逻辑门除了基本逻辑门之外,还有一些由基本逻辑门组合而成的组合逻辑门,例如与非门(NAND)、或非门(NOR)和异或门(XOR)等。
3.1 与非门(NAND)与非门是由与门和非门组成的组合逻辑门。
其输出信号在所有输入信号都为高电平时为低电平,否则为高电平。
与非门的逻辑符号如下:NAND gateNAND gate3.2 或非门(NOR)或非门是由或门和非门组成的组合逻辑门。
其输出信号在任何输入信号中有一个或多个为高电平时为低电平,只有所有输入信号都为低电平时才为高电平。
或非门的逻辑符号如下:NOR gateNOR gate3.3 异或门(XOR)异或门是一种比较特殊的组合逻辑门,其输出信号在输入信号中有奇数个高电平时为高电平,否则为低电平。
数字电路课后题参考答案
习题参考答案注:参考答案,并不是唯一答案或不一定是最好答案。
仅供大家参考。
第一章习题2. C B A D B A C B A F ⋅⋅+⋅⋅+⋅⋅=3. 设:逻辑变量A 、B 、C 、D 分别表示占有40%、30%、20%、10%股份的四个股东,各变量取值为1表示该股东投赞成票;F 表示表决结果,F =1表示表决通过。
F =AB +AC +BCD4. 设:A 、B 开关接至上方为1,接至下方为0;F 灯亮为1,灯灭为0。
F =A ⊙B5. 设:10kW 、15kW 、25kW 三台用电设备分别为A 、B 、C ,设15kW 和25kW 两台发电机组分别为Y 和Z ,且均用“0”表示不工作,用“1”表示工作。
C AB Z BA B A Y ⋅=⋅=6.输入为余3码,用A 、B 、C 、D 表示,输出为8421BCD 码,用Y 0、Y 1、Y 2、Y 3表示。
D C A B A Y CB DC BD B Y DC Y DY ⋅⋅+⋅=⋅+⋅⋅+⋅=⊕==32107. 设:红、绿、黄灯分别用A 、B 、C 表示,灯亮时为1,灯灭时为0;输出用F 表示,灯正常工作时为0,灯出现故障时为1。
C A B A C B A F ⋅+⋅+⋅⋅=8. D C B D A H DC B AD C B A D C B A D C B A G DC B AD C A B A F DC B A E ⋅⋅+⋅=⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅=⋅⋅⋅+⋅⋅+⋅=⋅⋅⋅=第二章习题1. 设:红、绿、黄灯分别用A 、B 、C 表示,灯亮时其值为1,灯灭时其值为0;输出报警信号用Y 表示,灯正常工作时其值为0,灯出现故障时其值为1。
AC AB C B A Y ⋅⋅=2. 设:烟、温度和有害气体三种不同类型的探测器的输出信号用A 、B 、C 表示,作为报警信号电路的输入,有火灾探测信号时用1表示,没有时用0表示。
报警信号电路的书躇用Y 表示,有报警信号时用1表示,没有时用0表示。
数字电子技术基础课后习题答案第7章习题答案
题7.1.1 可编程阵列逻辑(PAL)由、和组成。
答:输入缓冲器、与阵列、或阵列输出题7.1.2 通用阵列逻辑(GAL)由、和组成。
答:输入缓冲器、与阵列、或阵列输出逻辑宏单元题7.1.3 可编程阵列逻辑(PAL)可组成种典型的输出组态。
(A)2 (B)3 (C)4 (D)5答:C题7.1.4 通用阵列逻辑(GAL)的输出逻辑宏单元可组成种典型的输出组态。
(A)2 (B)3 (C)4 (D)5答:D题7.1.5 在系统编程器件(isp)和早期的EEPROM在编程方面,前者脱离了束缚。
(A)软件平台(B)编程器(C)电源(D)刷新电路答:B题7.1.6 单片通用阵列逻辑(GAL)的输出逻辑宏单元编程为寄存器组态时,只能应用在场合。
(A)同步时序电路(B)异步时序电路(C)复位电路(D)移位寄存器答:A、D题7.2.1 在系统可编程逻辑器件采用编程单元。
(A)E2CMOS (B)熔丝(C)SRAM (D)隧道型浮栅单元答:A题7.2.2 EPM7000S系列提供的共享乘积项有和。
(A)共享扩展(B)并联扩展(C)串联扩展(D)缓冲扩展答A、B题7.2.3 输入输出单元即可以编程为输入或输出,还可以编程为。
答:双向题7.2.4 编程I/O控制块输出缓冲器的输出电压摆率,可提供较高的。
(A)克服毛刺(B)并联扩展(C)转换速度(D)减低功耗答:C题7.2.5 ispLSI1000系列的ORP可提供GLB到IOC的信号。
(A)输入(B)中间(C)输出(D)时钟答:C题7.2.6 CPLD具有较高的性能,并具有如下特点。
(A)单片多系统(B)异步时序电路(C)动态刷新(D)丰富的查找表8081题7.3.1 现场可编程门阵列(FPGA )静态时无 ,称之为 。
(A) 功耗 (B) 电流(C) 零功耗器件 (D) 有源器件答:A 、C题7.3.2 CPLD 的信号通路固定,系统速度可以 。
FPGA 的内连线是分布在逻辑单元周围,而且编程的种类和编程点很多,使布线相当灵活,但在系统速度方面低于 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章可编程逻辑器件PLD第一节基本内容一、基本知识点(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD是70年代发展起来的新型逻辑器件,相继出现了只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL 和可擦写编程逻辑器件EPLD等多个品种,它们的组成和工作原理基本相似。
PLD的基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
在PLD中,输入电路中为了适应各种输入情况,每一个输入信号都配有一缓冲电路,使其具有足够的驱动能力,同时产生原变量和反变量输出,为与门阵列提供互补信号输入。
输出电路的输出方式有多种,可以由或阵列直接输出,构成组合方式输出,也可以通过寄存器输出,构成时序方式输出。
输出既可以是低电平有效,也可以是高电平有效;既可以直接接外部电路,也可以反馈到输入与阵列,由此可见PLD的输出电路根据不同的可编程逻辑器件有所不同。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程(2)与或阵列均可编程(3)与阵列可编程,或阵列固定归纳上述PLD的结构特点,列于表7-1。
表7-1 各种PLD的结构特点2.按编程方式分类(1)掩膜编程(2)熔丝与反熔丝编程(3)紫外线擦除、电可编程(4)电擦除、电可编程(5)在系统编程(Isp)(三)高密度可编程逻辑器件HDPLD243通常衡量可编程逻辑器件芯片的密度是以芯片能容纳等效逻辑门的数量,一般是以2000为界限,即芯片容纳等效逻辑门小于2000门,称它为低密度可编程逻辑器件或简单的可编程逻辑器件(SPLD),若大于2000等效逻辑门,称为高密度可编程逻辑器件(HDPLD)。
在前面按编程部位分类可编程逻辑器件中提及的通用阵列逻辑(GAL)的等效逻辑门一般不超过2000门,习惯上称其为低密度可编程逻辑器件。
通用阵列逻辑GAL是在PAL基础上发展起来的一种具有较高可靠性和灵活性的新型可编程逻辑器件,它采用E2CMOS工艺和灵活的输出结构,能将数片中小规模集成电路集成在芯片内部,并具有电擦写反复编程的特性。
在基本阵列结构上仍是与阵列可编程,或阵列固定的结构。
GAL在输出结构配置了8个可以任意组态的输出逻辑宏单元OLMC(Output Logic Macro Cell),适当地为输出逻辑宏单元进行编程组态,GAL就可以在功能上代替编程阵列逻辑PAL。
输出逻辑宏单元OLMC 由或门、异或门、D触发器、多路选择器MUX、时钟控制、使能控制和编程元件等组成。
高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device)从芯片密度上有了很大的改进,单片芯片内可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD器件在结构上仍延续GAL的结构原理,因而还是电擦写、电编程的EPLD器件。
(四)现场可编程逻辑器件FPGA可编程逻辑器件基本组成是与阵列、或阵列和输出电路。
对这些基本组成电路进行编程就可以实现任何积之和的逻辑函数,再加上触发器则可实现时序电路。
现场可编程门阵列的编程单元是基于静态存储器(SRAM)结构,不像PLD那样受结构的限制,它可以靠门与门的连接来实现任何复杂的逻辑电路,更适合实现多级逻辑功能。
现场可编程门阵列FPGA与HDPLD相比较特点如下:(1)FPGA的编程单元是基于SRAM结构,可以无限次编程,它为易失性元件,掉电后芯片内信息丢失。
通电之后,要为FPGA重新配置逻辑。
(2)FPGA中实现逻辑功能的CLB比HDPLD实现逻辑功能的OLMC规模小,制作一个OLMC的面积可以制作多个CLB,因而FPGA内的触发器要多于HDPLD的触发器,使得FPGA在实现时序电路时要强于HDPLD。
(3)HDPLD的信号汇总于编程内连矩阵,然后分配到各个宏单元,因此信号通路固定,系统速度可以预测。
而FPGA的内连线是分布在CLB周围,而且编程的种类和编程点很多,使得布线相当灵活。
(4)由于FPGA的CLB规模小,可分为两个独立的电路,又有丰富的连线,所以系统综合时可进行充分的优化,以达到逻辑最高的利用。
(五)随机存取存储器RAM随机存取是指可以随时将数据存入(称写入), 和取出(称读出)。
随机存储器(RAM)的主要指标是存储器容量和存取时间(周期)。
存储容量表示一片RAM存储数据的能力。
存放一个二进制数码需要一个存储单元,所以存储容量常用存储单元的总数(bit)来表示。
存取时间表示从存储器中开始存取第一个字到能够存取第二个字为止所需的时间,或称为存取周期。
存取时间越短,表示存储器的存取速度越高。
RAM的基本结构可以分为三个部分:存储矩阵,地址译码器及读写控制电路。
存储矩阵244是用来存储要存放的代码,矩阵中每个存储单元都用一个二进制码给以编号,以便查询此单元。
译码器可以将输入地址译为电平信号,以选中存储矩阵中的相应的单元。
存储器根据工作原理的不同可分为静态RAM和动态RAM两大类。
(1)静态RAM静态RAM是在触发器的基础上附加控制线或门控制管构成的,它们是靠电路状态来存储数据。
根据使用的器件不同,静态存储单元又分为MOS型和双极型两种。
(2)动态RAM动态RAM是利用MOS管栅级电容能够存储电荷的原理制成的。
电路结构比较简单,但由于栅极电容的容量很小,而漏电流不可能为零,所以电荷的存储时间有限。
为了及时补充泄露掉的电荷以避免存储信号丢失,必须定时给栅极电容补充电荷。
通常把这种操作叫做刷新或再生。
因此,工作时必须辅以比较复杂的刷新电路。
二、重点1.可编程逻辑器件PLD的基本结构与工作原理基于任何组合逻辑函数均可化为与或式,从而实现与门—或门两级电路实现,而任何时序电路又都是由组合电路加上存储元件(触发器)构成。
2.可编程逻辑器件PLD按编程部位分类、编程方法分类的基本概念及其特征。
3.多次可擦写的可编程逻辑器件PLD主要基于浮栅技术,这种编程方法是一只多晶硅浮栅浮于控制栅和衬底之间的半导体中。
当控制栅上的电压加大时,产生很强的电场,足以使电子获得能量穿过半导体进入浮栅住留。
这样MOS管因为浮栅上存储负电荷作用使开启电压改变,从而达到逻辑编程“0”和“1”的目的。
4.单片可编程逻辑器件容量总是有限的,所以在设计时,应考虑利用多片PLD,按一定方法连接以扩展其容量。
(1)字长扩展字长又称为数据位数,对字长的扩展即是地址的位数保持不变,而对数据位增加。
(2)字扩展字又称为地址位数,对字的扩展即是数据的位数保持不变,而对地址位增加。
在实际应用中,往往需要同时进行地址扩展和数据扩展,例如存储器总容量为16K X16bit,用2K X8bit芯片构成存储器时,必须同时进行地址扩展和数据扩展,用16片2K X8bit的芯片,依据一定的连接方式连接,便可得到总容量为16K X16bit=256Kbit的存储器。
5.可编程逻辑阵列PLA电路的分析方法:(1)根据题意或者电路图,写出逻辑与-或表达式;(2)若时序电路,则写出激励、驱动和输出方程;(3)写出真值表或者状态图;(4)根据真值表或者状态图分析其工作原理。
6.可编程阵列逻辑PAL和通用阵列逻辑GAL的基本组成和PAL的各种组态、GAL的输出宏单元各种组态及其特点。
7.高密度可编程逻辑器件HDPLD的基本组成和其工作原理。
8.现场可编程门阵列FPGA工作原理是靠门与门的连接实现任何复杂的逻辑电路,较适于多级逻辑设计。
重点在于掌握工作原理及其特点。
9. 可编程逻辑器件设计实质上是设计专用集成电路ASIC,整个设计过程必须伴随着电子245246设计自动化(EDA )软件平台。
本教材第二篇指导读者利用Foundation 软件设计平台设计高密度PLD 器件,完成可编程逻辑器件的设计。
三、难点1.可编程逻辑器件的不同分类方法及其各种基本概念。
2.PLA 电路的设计方法:(1)根据题意写出真值表或者状态图; (2)选择触发器;(3)写出驱动、激励和输出方程; (4)画出PLA 电路图。
3.现场可编程门阵列FPGA 中的可配置逻辑块CLB 不仅可以完成组合逻辑、时序逻辑电路的功能,而且还可以作为RAM 使用。
当作为RAM 使用时,不仅可以配置成电平触发的16位双口或32位单口RAM ,而且还可以配置成边沿触发的16位双口或32位单口RAM 。
第二节 典型题解例7-1 试用SD805 32×8bitPROM 构成容量为32×32bit 的PROM 。
解:此题为扩展存储器的数据位(字长),方法比较简单。
在驱动器的负载能力允许之内,将每个存储器地址输入端对应连接,且允许输入端S 接在一起既可。
采用四片SD805PROM 构成32×32bit 的PROM ,其电路连接图如图7-1所示,因为每片SD805输出8位,其中SD805-(1)输出0~7位(32位中的低8位),SD805-(4)输出24~31位(32位中的高8位)。
例7-2 试用SD805 32×8bit PROM 构成容量为512×8bit PROM 。
解:此题为扩大存储器的地址(字数),一个SD805 容量是32字×8位,可利用允许输入来扩展字数,即每片一个字组,通过外加译码器T1154来分别选中每一片,也就将该字组的32个字选中,这样SD805 本来只有五位地址输入,可选中32个字,现采用16片SD80524 .……… 31 15 .……….23 输出32位数据 S A B C D E 地址输入图7-1数据扩展(扩展成32×32bitPROM)连接图与一片译码器T1154,经扩展成九位地址输入后,可选中512个字,其电路连接图如图7-2所示。
九位地址码ABCDEFGHI中,I为最高位,A为最低位。
当T1154译码器输入FGHI=0000时,Y0输出有效,选中SD805-(1),决定0~31字,当FGHI=1000时,选中SD805-(2),决定32~63字......,其余类推。
当FDHI=1111时,选中SD805-(16),即决定479~511字。
12345678F G H I S地址输入图7-2 扩大存储器地址连接图例7-3 试用SD805 32×8bit PROM构成容量为128×2 bit PROM。
