倍角公式和半角公式
三角函数公式凑角

三角函数公式凑角
三角函数公式凑角是指通过已知的三角函数值,利用三角函数的和差角公式、倍角公式、半角公式等,将给定的角度变换为易于计算的角度。
常见的凑角方法包括:
1.和差角公式:sin(α+β)=sinαcosβ+cosαsinβ;
cos(α+β)=cosαcosβ-sinαsinβ;tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)。
2.倍角公式:sin2α=2sinαcosα;cos2α=cos²α-sin²α;
tan2α=(2tanα)/(1-tan²α)。
3.半角公式:sin(α/2)=±√[(1-cosα)/2];
cos(α/2)=±√[(1+cosα)/2];tan(α/2)=±√[(1-
cosα)/(1+cosα)]。
4.辅助角公式:sinx=(2tan(x/2))/(1+tan²(x/2));cosx=(1-
tan²(x/2))/(1+tan²(x/2));tanx=(2tan(x/2))/(1-tan²(x/2))。
通过这些公式,可以将给定的角度变换为易于计算的角度,例如将角度转换为正弦值、余弦值或正切值,或将角度转换为半角或辅助角等。
这样可以简化三角函数的计算,提高计算效率和准确性。
倍角公式和半角公式口诀

倍角公式和半角公式口诀倍角公式口诀:正弦二倍,正负取决;余弦二倍,正负不同;正切二倍,正负相同;余切二倍,正负取决。
半角公式口诀:正弦半角,加减号;余弦半角,加减号;正切半角,加减号;余切半角,加减号。
正文:在三角函数中,倍角公式和半角公式是非常重要的公式之一。
它们可以帮助我们简化复杂的三角函数表达式,从而更方便地进行计算和推导。
下面我们将分别介绍倍角公式和半角公式的口诀,并举例说明其应用。
倍角公式口诀是一种简单易记的口诀,可以帮助我们快速记忆倍角公式的变化规律。
首先我们来看倍角公式口诀:正弦二倍,正负取决;余弦二倍,正负不同;正切二倍,正负相同;余切二倍,正负取决。
这个口诀告诉我们,在倍角公式中,正弦和余切的正负取决于原角的正负,而余弦和正切的正负则与原角的正负相反。
这个口诀的记忆方式非常简单直观,让人很容易就能记住倍角公式的正负变化规律。
接下来我们通过一个具体的例子来说明倍角公式的应用。
假设我们需要计算sin(2x)的值,其中x是一个已知的角度。
根据倍角公式sin(2x) = 2sin(x)cos(x),我们可以利用已知角度x的正弦值和余弦值来求得sin(2x)的值,而无需直接求解sin(2x)的正弦值。
这样一来,我们可以大大简化计算的复杂度,提高计算效率。
接下来我们来看半角公式口诀:正弦半角,加减号;余弦半角,加减号;正切半角,加减号;余切半角,加减号。
这个口诀告诉我们,在半角公式中,正弦、余弦、正切和余切的正负变化规律。
根据这个口诀,我们可以很容易地记住半角公式的正负变化规律,从而在实际计算中更加得心应手。
接下来我们通过一个具体的例子来说明半角公式的应用。
假设我们需要计算sin(x/2)的值,其中x是一个已知的角度。
根据半角公式sin(x/2) = ±√[(1-cos(x))/2],我们可以利用已知角度x的余弦值来求得sin(x/2)的值,而无需直接求解sin(x/2)的正弦值。
倍角公式和半角公式-拔高难度-讲义

倍⾓公式和半⾓公式-拔⾼难度-讲义倍⾓公式和半⾓公式知识讲解⼀、倍⾓公式sin 22sin cos ααα=;2222cos 2cos sin 12sin 2cos 1ααααα=-=-=-22tan tan 21tan ααα=- 3sin 33sin 4sin ααα=-;3cos34cos 3cos ααα=-;323tan tan tan 313tan αααα-=- ⼆、半⾓公式1cos sin22αα-=±;1cos cos 22αα+=±; 1cos 1cos sin tan21cos sin 1cos ααααααα--=±==++ 三、万能公式22tan2sin 1tan 2ααα+;221tan 2cos 1tan 2ααα-=+;22tan2tan 1tan 2ααα=-四、公式的推导sin 2sin()sin cos cos sin 2sin cos ααααααααα=+=+=22cos2cos()cos cos sin sin cos sin ααααααααα=+=?-?=- 再利⽤22sin cos 1αα+=,可得:2222cos2cos sin 2cos 112sin ααααα=-=-=- ()2tan tan 2tan tan 2tan 1tan tan 1tan ααααααααα+=+==-?-sin 2tan2cos2ααα===sin 2sinsin1cos 222tan2sin cos 2sin cos 222αααααα-=== sin 2cossinsin 222tan21cos cos2cos cos222ααααααααα===+ 【说明】这⾥没有考虑cossin22αα==,实际处理题⽬的时候需要把等于0的情况分出来单独讨论⼀下.五、综合运⽤1.倍⾓、半⾓、和差化积、积化和差等公式的运⽤1)并项功能: 2221sin 2sin cos 2sin cos (sin cos )ααααααα±=+±=± 2)升次功能: 2222cos 2cos sin 2cos 112sin ααααα=-=-=- 3)降次功能: 221cos 21cos 2cos ,sin 22αααα+-== 2.三⾓变换中常⽤的数学思想⽅法技巧有:1)⾓的变换:和、差、倍、半、互余、互补的相对性,有效沟通条件与结论中⾓的差异,⽐如:3015453060452? =-=-=ααββαββ=-+=+-=?()()()()ππ2()()44ααβαβαββααα=++-=+--=+--()()222βαβαβαααβα?-=-+=-=--ππππππ244362αααααα+-=++-=++-= ? ? ? ? ???????????π3ππ2ππ5ππ443366αααααα++-=++-=++-= ? ? ? ? ? ?2)函数名称的变换:三⾓变形中,常常需要变函数名称为同名函数,在三⾓函数中正余弦是基础,通常化切为弦,变异名为同名;有时可以使⽤万能公式将所有函数名化为正切; 3)常数代换:在三⾓函数运算、求值、证明中,有时需要将常数转化为三⾓函数值,例如:2222ππππ1sin cos sec tan sintan 2sin 2464αααα=+=-===; 4)幂的变换:降幂是三⾓变换时常⽤的⽅法常⽤的降幂公式有:21cos2cos 2αα+=,21cos2sin 2αα-=但降幂并⾮绝对,有时也需要对某些式⼦进⾏升幂处理,⽐如221cos22cos ,1cos22sin αααα+=-=;21sin 2(sin cos )ααα±=±;5)公式变形:三⾓公式是变换的依据,应熟练掌握三⾓公式的顺⽤,逆⽤及变形应⽤,例如:tan tan tan()(1tan tan)αβαβαβ±=±??m ; 6)辅助⾓公式的运⽤:在求值问题中,要注意辅助⾓公式() sin cos y a b ααα?=++的应⽤,其中tan b a=,?所在的象限由,a b 的符号确定.⼀.填空题(共1⼩题)1.(2012?北京模拟)如果函数y=cos2ωx﹣sin2ωx的最⼩正周期是4π,那么正数ω的值是.【解答】解:因为函数y=cos2ωx﹣sin2ωx=cos2ωx,它的最⼩正周期是4π,所以,解得ω=.故答案为:⼆.解答题(共12⼩题)2.(2018春?晋江市校级期中)已知向量、是两个相互垂直的单位向量,向量=2﹣,=﹣+2.(1)求以及向量在向量⽅向上的投影;(2)设向量与的夹⾓为α,求tan2α;(3)若t∈R,求|﹣t|的最⼩值.【解答】解:(1)分别以、的⽅向为x,y轴的正⽅向,建⽴平⾯直⾓坐标系,则=(2,﹣1),=(﹣1,2),所以?=﹣2﹣2=﹣4,||=||=,故向量在向量⽅向上的投影为||cos<,>==﹣;(2)cosα==﹣,由α∈[0,π],可得sinα==,则tanα==﹣,tan2α===﹣;(3)由(1)﹣t=(2+t,﹣1﹣2t),|﹣t|2=(2+t)2+(﹣1﹣2t)2=5t2+8t+5=5(t+)2+,当t=﹣时,|﹣t|取得最⼩值.3.(2018?辽宁模拟)已知函数f(x)=2cos2x+sin2x.(Ⅰ)求f()的值;(Ⅱ)求f(x)的最⼤值和最⼩值.【解答】解:(Ⅰ)函数f(x)=2cos2x+sin2x,f()=2cos+sin2==﹣﹣﹣﹣(5分)(Ⅱ)f(x)=2cos2x+sin2x=2cos2x+=,所以f(x)的最⼤值为2,最⼩值为﹣1﹣﹣﹣﹣﹣﹣(10分)4.(2017春?殷都区校级期末)已知函数f(x)=sin2(x+)﹣cos2x﹣(x∈R).(1)求函数f(x)最⼩值和最⼩正周期;(2)若A为锐⾓,且向量=(1,5)与向量=(1,f(﹣A))垂直,求cos2A.﹣=cos2x﹣1=,∴函数f(x)最⼩值是﹣2,最⼩正周期T==π;(2)∵向量=(1,5)与向量=(1,f(﹣A))垂直,∴1+5f(﹣A)=0,则1+5[]=0,∴=>0,∵A为锐⾓,∴,则,∴==,则cos2A=cos[()﹣]=+=×+=.5.(2017?青⽺区校级模拟)设a,b,c分别是△ABC三个内⾓∠A,∠B,∠C 的对边,若向量,,且.(1)求tanA?tanB的值;(2)求的最⼤值.【解答】解:(1)由得,,即4cos(A﹣B)=5cos(A+B),解得,.(2)因为=,⼜=,所以,tan(A+B)有最⼩值,当且仅当时,取得最⼩值.⼜tanC=﹣tan(A+B),则tanC有最⼤值,故的最⼤值为.6.(2015秋?硚⼝区期末)当α≠(2k+1)π,k∈Z时,等式恒成⽴,我们把这个恒等式叫“半⾓公式”.(1)证明上述半⾓公式;(2)若α,β都是锐⾓,,试求的值.【解答】解:(1)右边==左边,(2)∵α,β都是锐⾓,?,∵0<α+β<π?,∴sinβ=sin(α+β﹣α)=sin(α+β)cosα﹣cos(α+β)sinα=,∴,∴=.【解答】解:∵0<β<<α<,∴<2α<π,﹣<﹣β<0,∴<2α﹣β<π.∵cos(2α﹣β)=﹣,∴sin(2α﹣β)=.同理可得:﹣<α﹣2β<.⼜∵sin(α﹣2β)=,∴cos(α﹣2β)=.∴cos(α+β)=cos[(2α﹣β)﹣(α﹣2β)] =cos(2α﹣β)cos(α﹣2β)+sin(2α﹣β)sin(α﹣2β)=(﹣)×+×=,∵<α+β<,∴α+β=,∴sin=.8.(2011春?天河区校级期中)已知sinα=,sin(α+β)=,α与β均为锐⾓,求cos.(cos)【解答】解:∵0<α<,∴cosα=.…(2分)⼜∵0<α<,0<β<,∴0<α+β<π.…(4分)若0<α+β<,∵sin(α+β)<sinα,∴α+β<α不可能.故<α+β<π.∴cos(α+β)=﹣.…(6分)∴cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα=﹣??,…(10分)∵0<β<,∴0<<.故cos.…(13分)9.已知,求证:y=x2﹣4x+5.【解答】证明:由x=2+tan得x﹣2=tan=,故(x﹣2)2====﹣1⼜故(x﹣2)2=y﹣1整理得y=x2﹣4x+5证毕10.(2017秋?烟台期中)设△ABC的内⾓A,B,C的对应边分别为a,b,c,若(1)求a:b:c;(2)若△ABC外接圆的半径为14,求△ABC的⾯积.【解答】解:(1)由m,n共线,得,,所以:2b=a+c设a=b﹣d,c=b+d,由已知,,即,∴,从⽽,∴a:b:c=7:5:3.(2)由正弦定理,得:,由(1)设即,所以:所以:,所以:△ABC的⾯积为.11.(2016秋?黄陵县校级⽉考)已知向量与为共线向量,且α∈[﹣π,0].(Ⅰ)求sinα+cosα的值(Ⅱ)求的值.【解答】解:(Ⅰ)∵与为共线向量,∴(cosα﹣)?1﹣(﹣1)?sinα=0,∴sinα+cosα=.(Ⅱ)∵1+sin2α=(sinα+cosα)2=,∴sin2α=﹣,∴(sinα﹣cosα)2=(sinα+cosα)2﹣4sinαcosα=﹣2×(﹣)=.⼜∵α∈[﹣π,0],sinα?cosα<0,∴α∈[﹣,0],∴sinα﹣cosα<0,∴sinα﹣cosα=﹣.∴=.12.(2016春?长治校级期中)已知函数f(x)=sin(3x+).若α是第⼆象限的⾓,f()=cos(α+)cos2α,求cosα﹣sinα的值.∴f()=sin(α+),⼜f()=cos(α+)cos2α=cos(α+)sin(2α+),∴cos(α+)×2cos(α+)sin(α+)=sin(α+),依题意知sin(α+)=0或=;①∵α是第⼆象限的⾓,∴cosα<0,sinα>0,∴cosα﹣sinα=cos(α+)<0,②由①②得:cos(α+)=﹣或﹣1,∴cosα﹣sinα=×(﹣)=﹣或﹣.13.(2015秋?临河区校级期末)已知,.(1)求cos2α的值;(2)求的值.【解答】解:(1)∵,.cos2α=2cos2α﹣1=﹣1=﹣.(2)∵,.∴sinα==.∴=sinα+cosα==.。
倍角公式和半角公式1

倍角公式和半角公式1倍角公式和半角公式1倍角公式和半角公式是代数中常用的一组公式,用于求解角度的相关问题。
倍角公式用于在已知角度的情况下求解角度的两倍大小,而半角公式则用于在已知角度的情况下求解角度的一半大小。
这两个公式在几何学、三角学以及物理学中都有广泛的应用。
倍角公式是指将一个角度的两倍写成其他三个角度的函数形式。
对于任意角度θ,倍角公式可以用以下两种形式来表示:1.正弦倍角公式:sin(2θ) = 2sin(θ)cos(θ)2.余弦倍角公式:cos(2θ) = cos²(θ) - sin²(θ)在实际应用中,正弦倍角公式和余弦倍角公式通常是成对使用的。
其中,正弦倍角公式是通过将2θ拆解成θ+θ并利用正弦函数的和角公式推导而得,而余弦倍角公式则是通过将2θ拆解成θ+θ并利用余弦函数的和角公式推导而得。
半角公式是指将一个角度的一半写成其他两个角度的函数形式。
对于任意角度θ,半角公式可以用以下两种形式来表示:sin(θ/2) = ±√[(1 - cos(θ))/2]cos(θ/2) = ±√[(1 + cos(θ))/2]半角公式同样可以成对使用,分别应用于正弦函数和余弦函数。
这两个公式可以通过将θ拆解成2(θ/2)并利用正弦函数和余弦函数的倍角公式推导而得。
举例来说,假设我们需要求解sin(150°) 的值。
根据正弦半角公式,sin(150°) 可以写成sin(75°/2) 的形式。
再根据正弦半角公式,sin(75°/2) 可以表示为±√[(1 - cos(75°))/2]。
我们可以使用三角函数表或计算器来查找cos(75°) 的值,然后代入公式计算sin(75°/2) 的值。
再举一个例子,假设我们需要证明sin(3θ) = 3sin(θ) -4sin³(θ) 的恒等式。
倍角公式和半角公式

半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
si n^2(α/2)=(1-cosα)/2c os^2(α/2)=(1+c osα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=si nα/(1+c osα)=(1-cosα)/si nα=+或-[1-cosα)/(1+c osα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαco sαt an2α=2t anα/(1-tan^2(α))c os2α=c os^2(α)-si n^2(α)=2c os^2(α)-1=1-2si n^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=si nα/(1+c osα)=(1-c osα)/si nαtan(2α)=2tanα/[1-tan^2(α)]·倍角公式:si n(2α)=2sinα·c osαc os(2α)=c os^2(α)-sin^2(α)=2c os^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:si n3α=3sinα-4si n^3(α)c os3α=4c os^3(α)-3c osαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:si n^2(α/2)=(1-cosα)/2c os^2(α/2)=(1+c osα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=si nα/(1+c osα)=(1-c osα)/si nα·万能公式:si nα=2tan(α/2)/[1+tan^2(α/2)]c osα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:si nα·cosβ=(1/2)[si n(α+β)+sin(α-β)]c osα·si nβ=(1/2)[si n(α+β)-sin(α-β)]c osα·c osβ=(1/2)[c os(α+β)+c os(α-β)]si nα·si nβ=-(1/2)[c os(α+β)-cos(α-β)]·和差化积公式:si nα+si nβ=2si n[(α+β)/2]cos[(α-β)/2]si nα-si nβ=2cos[(α+β)/2]si n[(α-β)/2]c osα+c osβ=2c os[(α+β)/2]c os[(α-β)/2]c osα-c osβ=-2si n[(α+β)/2]si n[(α-β)/2]·其他:si nα+si n(α+2π/n)+sin(α+2π*2/n)+si n(α+2π*3/n)+……+si n[α+2π*(n-1)/n]=0c osα+c os(α+2π/n)+c os(α+2π*2/n)+cos(α+2π*3/n)+……+c os[α+2π*(n-1)/n]=0 以及si n^2(α)+si n^2(α-2π/3)+si n^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:si n4A=-4*(cosA*si nA*(2*si nA^2-1))c os4A=1+(-8*c os A^2+8*c os A^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:si n5A=16si nA^5-20si nA^3+5si nAc os5A=16c os A^5-20c os A^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:si n6A=2*(cosA*si nA*(2*si nA+1)*(2*sinA-1)*(-3+4*si nA^2))c os6A=((-1+2*c os A^2)*(16*c os A^4-16*c os A^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:si n7A=-(sinA*(56*si nA^2-112*si nA^4-7+64*si nA^6))c os7A=(c osA*(56*c osA^2-112*c osA^4+64*c os A^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:si n8A=-8*(cosA*si nA*(2*si nA^2-1)*(-8*si nA^2+8*sinA^4+1))c os8A=1+(160*c os A^4-256*c os A^6+128*c os A^8-32*c os A^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:si n9A=(sinA*(-3+4*si nA^2)*(64*sinA^6-96*si nA^4+36*si nA^2-3))c os9A=(c osA*(-3+4*cosA^2)*(64*c os A^6-96*cosA^4+36*c os A^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:si n10A=2*(c os A*sinA*(4*sinA^2+2*si nA-1)*(4*sinA^2-2*si nA-1)*(-20*si nA^2+5+16*si nA^4))c os10A=((-1+2*c os A^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*c os A^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
三角形倍角公式和半角公式

三角形倍角公式和半角公式大家好,今天我们来聊聊三角形倍角公式和半角公式。
这两个公式可是数学里的小宝贝哦!它们可以帮助我们解决很多三角形的问题。
不过,别看它们小小的,可是个个都是“大腕儿”呢!让我们来认识一下三角形倍角公式。
三角形倍角公式是这样的:sin2A + sin2B +sin2C = 2sin(A + B)cos(A B)。
你看,这个公式里面有三个角A、B、C,而且这三个角都是三角形的内角。
这个公式的意思是说,一个三角形的两个角的正弦值的平方之和等于另外两个角的正弦值的两倍乘以这两个角的余弦值之差。
这个公式可厉害了,它可以帮助我们求出三角形的各个角度,还可以用来判断一个三角形是不是直角三角形。
接下来,我们来说说半角公式。
半角公式是这样的:cos(A/2) = (1 tan(A/2)) / (1 + tan(A/2))。
这个公式里面只有一个角A,而且这个角也是三角形的一个内角。
这个公式的意思是说,一个三角形的一个角度的一半的余弦值等于这个角度一半的正切值减一除以这个角度一半的正切值加一。
这个公式可神奇了,它可以帮助我们求出一个三角形的一个角度的一半的余弦值,还可以用来判断一个三角形是不是等腰三角形。
那么,这两个公式有什么用呢?其实,它们在我们的日常生活中也有很多应用。
比如说,我们在装修房子的时候,需要测量墙角的角度,这时候就可以用到这两个公式了。
还有,我们在玩游戏的时候,如果要让角色沿着一个圆弧走,也可以用到这两个公式。
这两个公式可是我们生活中的小助手哦!学会了这两个公式还不够,我们还需要知道它们的逆运算。
比如说,我们知道了sin2A + sin2B + sin2C = 2sin(A + B)cos(A B),那么它的逆运算就是什么呢?没错,就是sin(A + B)cos(A B) = sin2A + sin2B + sin2C。
同样地,我们知道了cos(A/2) = (1 tan(A/2))/ (1 + tan(A/2)),那么它的逆运算就是什么呢?没错,就是tan(A/2) = (1 cos(A/2)) / (1 + cos(A/2))。
倍角公式和半角公式
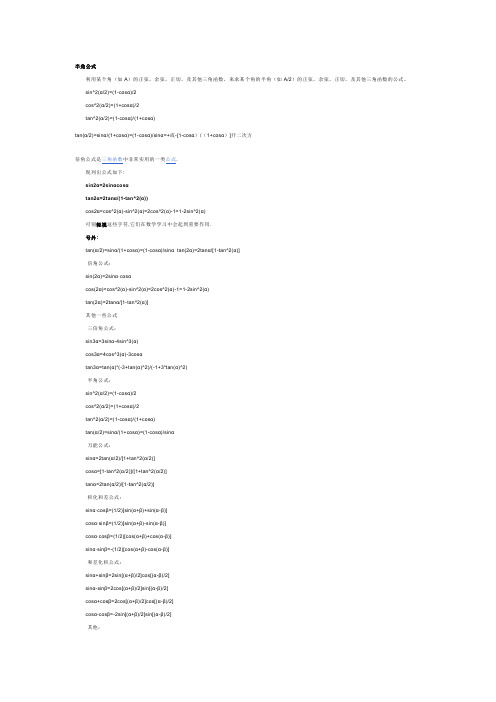
半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα=+或-[1-cosα)/(1+cosα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα tan(2α)=2tanα/[1-tan^2(α)]·倍角公式:sin(2α)=2sinα·cosαcos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:sin4A=-4*(cosA*sinA*(2*sinA^2-1))cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4))cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
三角函数的倍角与半角公式的应用

三角函数的倍角与半角公式的应用三角函数的倍角与半角公式是数学中常用的公式,它们在解题和推导过程中起着重要的作用。
本文将围绕三角函数的倍角与半角公式展开论述,并介绍其在实际应用中的具体运用。
一、倍角公式的应用1. 正弦函数的倍角公式正弦函数的倍角公式表示为:sin(2θ) = 2sinθcosθ,其中θ为任意实数。
倍角公式的应用一般涉及到解决与角度相关的问题,比如三角函数的值、图形的旋转等。
以一个样例进行说明:已知sinθ = 1/2,求sin(2θ)的值。
解:根据已知条件sinθ = 1/2,可以得到θ = π/6 或θ = 5π/6(这里以弧度制为例)。
代入倍角公式sin(2θ) = 2sinθcosθ,可以求得当θ = π/6 时,sin(2θ) = 1/2。
同理,当θ = 5π/6 时,sin(2θ) = -1/2。
因此,sin(2θ)的值为±1/2,具体取决于θ的取值。
2. 余弦函数的倍角公式余弦函数的倍角公式表示为:cos(2θ) = cos^2θ - sin^2θ = 1 - 2sin^2θ = 2cos^2θ - 1,其中θ为任意实数。
解:根据已知条件cosθ = 3/5,可以得到sinθ = 4/5(通过勾股定理)或sinθ = -4/5(考虑到θ在第一、二象限时是正值)。
代入余弦函数的倍角公式cos(2θ) = cos^2θ - sin^2θ,可以求得当sinθ = 4/5 时,cos(2θ) = -7/25;当sinθ = -4/5 时,cos(2θ) = -9/25。
因此,cos(2θ)的值为-7/25 或-9/25。
二、半角公式的应用1. 正弦函数的半角公式正弦函数的半角公式表示为:sin(θ/2) = ±√[(1 - cosθ)/2],其中θ为任意实数。
半角公式的应用一般用于将角度减半,从而简化计算过程。
以一个样例进行说明:已知cosθ = 4/5,求sin(θ/2)的值。
