高二数学倍角公式和半角公式
半角与倍角公式

半角与倍角公式在我们的数学世界里,半角与倍角公式就像是神秘的魔法咒语,虽然它们看起来有些复杂,但一旦掌握,就能为我们解决很多难题,打开神奇的数学大门。
还记得我上高中那会,有一次数学考试,最后一道大题就是关于半角与倍角公式的应用。
当时我瞅着那道题,心里就有点打鼓。
题目说:已知角α的正弦值为 3/5,且α在第一象限,求α/2 的余弦值。
我深吸一口气,开始在草稿纸上写写画画。
先根据已知条件,利用三角函数的平方关系算出α的余弦值是 4/5 。
然后呢,就该轮到半角公式登场啦。
半角的余弦公式是:cos(α/2) = ±√[(1 + cosα) / 2] 。
因为α/2也在第一象限,所以取正号。
把cosα = 4/5 代入公式,经过一番计算,终于算出了答案。
当我算出结果的那一刻,心里那叫一个美,就好像攻克了一座坚固的城堡。
咱们先来说说半角公式。
半角公式包括正弦、余弦和正切的半角公式。
就拿正弦的半角公式来说吧,sin(α/2) = ±√[(1 - cosα) / 2] 。
这里为啥有个正负号呢?这就得看角所在的象限啦,如果在第一、二象限就是正的,如果在第三、四象限就是负的。
可别小瞧这个正负号,一不小心就容易出错哟!再看看余弦的半角公式,cos(α/2) = ±√[(1 + cosα) / 2] 。
同样要注意正负号的判断。
还有正切的半角公式,tan(α/2) = ±√[(1 - cosα) / (1 + cosα)] 或者tan(α/2) = (1 - cosα) / sinα 或者tan(α/2) = sinα / (1 + cosα) 。
是不是感觉有点眼花缭乱?别慌,多做几道题,熟练了就好。
说完半角公式,咱们再来聊聊倍角公式。
倍角公式那也是相当重要的。
比如正弦的倍角公式sin2α = 2sinαcosα 。
想象一下,一个角变成了它的两倍,正弦值也跟着有了新的变化。
余弦的倍角公式就有三种形式:cos2α = cos²α - sin²α ,cos2α =2cos²α - 1 ,cos2α = 1 - 2sin²α 。
倍角公式和半角公式

半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
si n^2(α/2)=(1-cosα)/2c os^2(α/2)=(1+c osα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=si nα/(1+c osα)=(1-cosα)/si nα=+或-[1-cosα)/(1+c osα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαco sαt an2α=2t anα/(1-tan^2(α))c os2α=c os^2(α)-si n^2(α)=2c os^2(α)-1=1-2si n^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=si nα/(1+c osα)=(1-c osα)/si nαtan(2α)=2tanα/[1-tan^2(α)]·倍角公式:si n(2α)=2sinα·c osαc os(2α)=c os^2(α)-sin^2(α)=2c os^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:si n3α=3sinα-4si n^3(α)c os3α=4c os^3(α)-3c osαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:si n^2(α/2)=(1-cosα)/2c os^2(α/2)=(1+c osα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=si nα/(1+c osα)=(1-c osα)/si nα·万能公式:si nα=2tan(α/2)/[1+tan^2(α/2)]c osα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:si nα·cosβ=(1/2)[si n(α+β)+sin(α-β)]c osα·si nβ=(1/2)[si n(α+β)-sin(α-β)]c osα·c osβ=(1/2)[c os(α+β)+c os(α-β)]si nα·si nβ=-(1/2)[c os(α+β)-cos(α-β)]·和差化积公式:si nα+si nβ=2si n[(α+β)/2]cos[(α-β)/2]si nα-si nβ=2cos[(α+β)/2]si n[(α-β)/2]c osα+c osβ=2c os[(α+β)/2]c os[(α-β)/2]c osα-c osβ=-2si n[(α+β)/2]si n[(α-β)/2]·其他:si nα+si n(α+2π/n)+sin(α+2π*2/n)+si n(α+2π*3/n)+……+si n[α+2π*(n-1)/n]=0c osα+c os(α+2π/n)+c os(α+2π*2/n)+cos(α+2π*3/n)+……+c os[α+2π*(n-1)/n]=0 以及si n^2(α)+si n^2(α-2π/3)+si n^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:si n4A=-4*(cosA*si nA*(2*si nA^2-1))c os4A=1+(-8*c os A^2+8*c os A^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:si n5A=16si nA^5-20si nA^3+5si nAc os5A=16c os A^5-20c os A^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:si n6A=2*(cosA*si nA*(2*si nA+1)*(2*sinA-1)*(-3+4*si nA^2))c os6A=((-1+2*c os A^2)*(16*c os A^4-16*c os A^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:si n7A=-(sinA*(56*si nA^2-112*si nA^4-7+64*si nA^6))c os7A=(c osA*(56*c osA^2-112*c osA^4+64*c os A^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:si n8A=-8*(cosA*si nA*(2*si nA^2-1)*(-8*si nA^2+8*sinA^4+1))c os8A=1+(160*c os A^4-256*c os A^6+128*c os A^8-32*c os A^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:si n9A=(sinA*(-3+4*si nA^2)*(64*sinA^6-96*si nA^4+36*si nA^2-3))c os9A=(c osA*(-3+4*cosA^2)*(64*c os A^6-96*cosA^4+36*c os A^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:si n10A=2*(c os A*sinA*(4*sinA^2+2*si nA-1)*(4*sinA^2-2*si nA-1)*(-20*si nA^2+5+16*si nA^4))c os10A=((-1+2*c os A^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*c os A^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
三角形半角公式和倍角公式

三角形半角公式和倍角公式
三角形半角公式:
假设在三角形ABC中,已知A角的大小为α,B角的大小为β,C 角的大小为γ,则三角形ABC中任意一条边对应的半角记作β/2,则该半角所对应的角度θ可以用以下公式计算:
tan(θ/2) = √[(s-a)(s-b)/(s-c)(s)]
其中,s为半周长,即(s-a+b+c)/2,a、b、c分别为三角形ABC 中的三边长。
三角形倍角公式:
假设在三角形ABC中,已知A角的大小为α,则A角的倍角为
2α,则三角形ABC中任意一条边对应的倍角记作2α/2=α,则该倍角所对应的角度θ可以用以下公式计算:
sin 2α = 2 sin α cos α
另外,还存在余弦和正弦的倍角公式,它们分别如下:
cos 2α = cos²α - sin²α
sin 2α = 2sinα cosα
至于拓展,三角函数公式有很多,比如三角形的正弦余弦定理,三角形的面积公式等等,都是很重要的数学公式。
三角形倍角公式和半角公式

三角形倍角公式和半角公式大家好,今天我们来聊聊三角形倍角公式和半角公式。
这两个公式可是数学里的小宝贝哦!它们可以帮助我们解决很多三角形的问题。
不过,别看它们小小的,可是个个都是“大腕儿”呢!让我们来认识一下三角形倍角公式。
三角形倍角公式是这样的:sin2A + sin2B +sin2C = 2sin(A + B)cos(A B)。
你看,这个公式里面有三个角A、B、C,而且这三个角都是三角形的内角。
这个公式的意思是说,一个三角形的两个角的正弦值的平方之和等于另外两个角的正弦值的两倍乘以这两个角的余弦值之差。
这个公式可厉害了,它可以帮助我们求出三角形的各个角度,还可以用来判断一个三角形是不是直角三角形。
接下来,我们来说说半角公式。
半角公式是这样的:cos(A/2) = (1 tan(A/2)) / (1 + tan(A/2))。
这个公式里面只有一个角A,而且这个角也是三角形的一个内角。
这个公式的意思是说,一个三角形的一个角度的一半的余弦值等于这个角度一半的正切值减一除以这个角度一半的正切值加一。
这个公式可神奇了,它可以帮助我们求出一个三角形的一个角度的一半的余弦值,还可以用来判断一个三角形是不是等腰三角形。
那么,这两个公式有什么用呢?其实,它们在我们的日常生活中也有很多应用。
比如说,我们在装修房子的时候,需要测量墙角的角度,这时候就可以用到这两个公式了。
还有,我们在玩游戏的时候,如果要让角色沿着一个圆弧走,也可以用到这两个公式。
这两个公式可是我们生活中的小助手哦!学会了这两个公式还不够,我们还需要知道它们的逆运算。
比如说,我们知道了sin2A + sin2B + sin2C = 2sin(A + B)cos(A B),那么它的逆运算就是什么呢?没错,就是sin(A + B)cos(A B) = sin2A + sin2B + sin2C。
同样地,我们知道了cos(A/2) = (1 tan(A/2))/ (1 + tan(A/2)),那么它的逆运算就是什么呢?没错,就是tan(A/2) = (1 cos(A/2)) / (1 + cos(A/2))。
倍角公式和半角公式
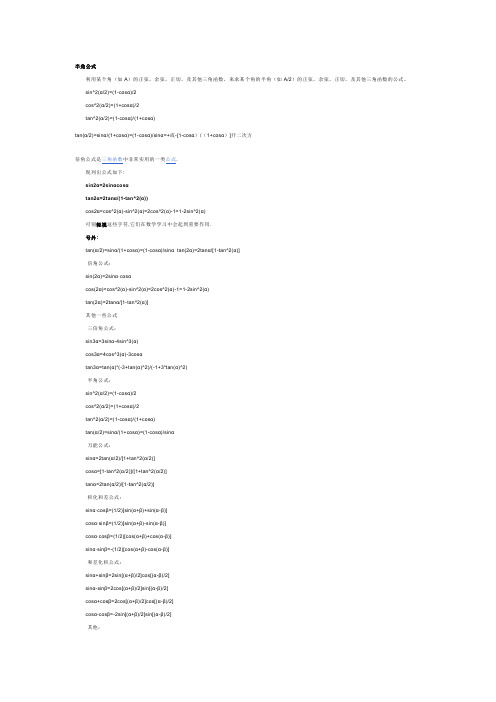
半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα=+或-[1-cosα)/(1+cosα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα tan(2α)=2tanα/[1-tan^2(α)]·倍角公式:sin(2α)=2sinα·cosαcos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:sin4A=-4*(cosA*sinA*(2*sinA^2-1))cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4))cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
三角函数的倍角公式与半角公式应用

三角函数的倍角公式与半角公式应用三角函数是数学中重要的一部分,广泛应用于科学、工程和金融等领域。
在三角函数的应用中,倍角公式和半角公式是常见且重要的部分。
它们能够帮助我们简化复杂的计算,提高计算的效率和准确性。
本文将介绍三角函数的倍角公式和半角公式,并应用于实际问题中。
一、三角函数的倍角公式倍角公式是指将一个角的两倍用另外一个角的三角函数表达出来的公式。
对于正弦函数、余弦函数和正切函数而言,它们的倍角公式如下:1. 正弦函数的倍角公式:sin(2θ) = 2sinθcosθ2. 余弦函数的倍角公式:cos(2θ) = cos^2θ - sin^2θ = 2cos^2θ - 1 = 1 - 2sin^2θ3. 正切函数的倍角公式:tan(2θ) = 2tanθ / (1 - tan^2θ)倍角公式的应用十分广泛。
例如,在几何图形的计算中,我们可以利用倍角公式简化角的计算,从而简化问题的解决过程。
此外,在信号处理和电路分析中,倍角公式也能够帮助我们分析和处理复杂的信号。
二、三角函数的半角公式半角公式是指将一个角的一半用另外一个角的三角函数表达出来的公式。
与倍角公式类似,正弦函数、余弦函数和正切函数都有对应的半角公式:1. 正弦函数的半角公式:sin(θ/2) = ±√[(1 - cosθ) / 2]2. 余弦函数的半角公式:cos(θ/2) = ±√[(1 + cosθ) / 2]3. 正切函数的半角公式:tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)]在实际问题中,半角公式也经常被使用。
例如,在概率论和统计学中,我们可以利用半角公式计算概率密度函数和累积分布函数,从而分析和解决与随机变量相关的问题。
三、三角函数公式的应用举例1. 应用倍角公式的例子:假设有一个直角三角形,已知一个角度θ的正弦函数值为0.6,我们想要计算该角的余弦函数值。
利用倍角公式,我们可以将该问题简化为计算2θ的正弦函数值和余弦函数值。
高二数学倍角公式和半角公式

cos2 cos sin
2 2
tan tan tan( ) 1 tan tan tan tan tan( ) 1 tan tan
2 tan tan 2 1 tan 2
一、倍角公式
sin 2 2 sin cos (S2 )
公式左端的角是右端角的二倍
在这两个公式中分别 2a和cos2a 求出sin 2
1 cos 2 cos 2 2 2 cos 1 sin 2 2 sin 1 cos 2 2 2 2 cos2 cos sin (1 sin ) sin 2 2 2 cos (1 cos ) 1 2 sin 2 2 cos 1
三、公式应用:
例1、(公式巩固性练习)求值
1、 sin 22。 30, cos22。 30,
2 2、 2 cos 1 8 2
2
2 4
2 3、 sin cos 8 8 2
2 2
试试看 伴你学134页8题
1 4、 8 sin cos cos cos 2 48 48 24 12
3.2.1倍角公式
复习回顾:
• 完成下列和角公式
sin cos sin cos cos( ) cos cos sin sin tan( ) tan tan 1 tan tan 思考:
若 我们可以得到怎样的结论?
cos10 3 sin10 sin 50 cos10 2 sin 40 sin 50 cos10 2sin 40 cos 40 cos10 sin 80 1 cos10
高二数学倍角公式和半角公式

3 (1) 当m=0时,求 f x 在 , 上的取值范围; 8 4 3 (2) 当 tan a 2 时,f a ,求m的值。 5
真题试炼
2.(2010山东文)已知函数
f ( x) sin( x)cos x cos2 x ( 0)
f (x ) max =
2+ 2
f (x ) min = 1
例2 已知函数
f (x ) = 2a cos x ( 3 sin x + cos x ) + a (a > 0)
2
(1)若对任意x∈R都有 f (x ) < 4 成立, 求a的取值范围; p (2)若 f (- ) = 4 ,求关于x的不等式 6 f (x ) > 8 的解集.
a Î [0, 1]
p (k p , k p + )(k ? Z ) 3
例3
3 3 已知向量a = (cos x , - sin x ) , 2 2
p x x b = (cos , sin ) ,其中 x Î [0, ] ,求函 2 2 2
数f(x)=a· b-|a+b|的值域.
3 [- , - 1] 2
若函数y=f(x)的图象关于直线x a ( a 0) 对称,求a的最小值.
f ( x ) [2 sin( x ) sin x]cos x 3 sin x 3
2
例4 已知函数
amin
12
真题试炼
1.(2010江西理)已知函数
2
f x 1 cot x sin x m sin x sin x 4 4
22sinsincos3sin3fxxxxx?????0xaa??min12a??????21cotsinsinsin44fxxxmxx?????????????????????fx384????????tan2a???35fa?1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
