人教版数学高一B版必修1同步精练 函数(一)
人教b版高一数学必修一：2.1.1《函数(1)》学案(含答案)
二、填空题
6．将集合 { x|x＝1 或 2≤ x≤8} 表示成区间为 ____________ ． 7．若 f(2x)＝ x3，则 f(1)＝ ________. 8．函数 y＝ x2－ 2 的定义域为 { － 1,0,1,2} ，则其值域为 ________．
三、解答题 9．求下列函数的定义域：
－x (3)y＝ 2x2－ 3x－2；
(2) y＝
3；
1－ 1－x
(4) y＝
2x＋ 3－
1＋ 2－x
1 x.
规律方法 求函数定义域的原则： (1)分式的分母不等于零； (2)偶次根式的被开方数 (式 )
为非负数ቤተ መጻሕፍቲ ባይዱ (3)零指数幂的底数不等于零等．
变式迁移 1 求下列函数的定义域：
(1)
f
(
x)＝
第二章 函 数
§2.1 函 数 2.1.1 函数 (一 )
自主学习
学习目标 1．理解函数的概念，能用集合与对应的语言刻画函数，体会对应关系在刻画函数概念 中的作用． 2．通过实例领悟构成函数的三要素；会求一些简单函数的定义域． 3．了解区间的概念，体会用区间表示数集的意义和作用．
自学导引
1．函数的有关概念 设集合 A 是一个 ____________ ，对 A 中的 ____________，按照确定的法则 f，都有
(4)两个函数是否相同，与自变量是什么字母无关． 变式迁移 2 试判断下列函数是否为同一函数：
(1)f(x)＝ x· x＋ 1与 g( x)＝ x x＋ 1 ； (2)f(x)＝ x2－ 2x 与 g(t)＝ t2－ 2t； (3)f(x)＝ 1 与 g(x)＝ x0(x≠ 0)．
知识点三 求函数解析式
人教B版数学高一版必修1练习一次函数的性质与图象
2.2 一次函数和二次函数 2．2.1 一次函数的性质与图象知识点一：一次函数的概念1．函数y ＝(m 2－4)x ＋2m 是关于x 的一次函数，则m 的取值范围是 A ．m≠2 B ．m≠－2C ．m≠±2D ．m 为任意实数2．若函数y ＝(t －2)xt 2－t －1是正比例函数，则t 的值是A ．2B ．－1C ．2或－1D ．0或2 3．如果ab>0，bc<0，那么一次函数ax ＋by ＋c ＝0的图象的大致形状是4．当m ＝__________时，函数y ＝(2m －1)x ＋1－3m 与y ＝x ＋1图象的交点在x 轴上． 知识点二：一次函数的性质5．已知y ＝(m －1)xm 2－3m ＋3是一次函数，且y 随x 的增大而增大，则m 的值为 A ．1 B ．2 C ．大于1 D ．1或26．已知一次函数的解析式为x －2y ＋7＝0，则其对应直线的斜率与y 轴上的截距分别为A.12，72 B ．1，－7 C ．1，72 D ．－12，72 7．如果一次函数y ＝kx ＋b 的图象经过第一、三、四象限，那么 A ．k>0，b>0 B ．k>0，b<0 C ．k<0，b>0 D ．k<0，b<08．两条直线y 1＝ax ＋b 与y 2＝bx ＋a 在同一坐标系中的图象可能是下图中的9．已知点A(－4，a)，B(－2，b)都在直线y ＝12x ＋k(k 为常数)上，则a 和b 的大小关系为a__________b.10．已知y ＋5与3x ＋4成正比例，当x ＝1时，y ＝2. (1)求y 与x 的函数关系式．(2)求当x ＝－1时，y 的值；当y ＝8时，x 的值． (3)如果y 的取值范围为[0,5]，求x 的取值范围．11．已知函数y ＝(2m －1)x ＋1－3m ，m 为何值时， (1)这个函数为一次函数？ (2)函数在定义域上是减函数？(3)这个函数的图象与直线y ＝x ＋1的交点在x 轴上？能力点一：一次函数的概念及性质的应用12．若k ，b 是一元二次方程x 2＋px －|q|＝0的两个实根(k·b≠0)，在一次函数y ＝kx ＋b 中，y 随x 的增大而减小，则一次函数的图象一定经过A ．第一、二、四象限B ．第一、三、四象限C ．第二、三、四象限D ．第一、二、三象限 13．下列函数中，是一次函数的为__________．(1)y ＝x 2＋1 (2)y ＝|x| (3)y ＝kx ＋3 (4)y ＝2x ＋6 (5)y ＝x (6)y ＝3x(7)y ＝7x (8)y ＝x 2x ＋114．已知一次函数y ＝(m －2)x ＋m 2－3m －2，它的图象在y 轴上的截距为－4，则m ＝__________.15．若函数y ＝ax －2与y ＝bx ＋3的图象与x 轴交于同一点，则ab ＝__________.16．已知一次函数y ＝(n －2)x ＋n 的图象与y 轴交点的纵坐标为－1，判断函数y ＝(3－5)x n ＋2是什么函数，写出这两个函数的解析式，并指出这两个函数在直角坐标系中的位置及增减性．17.已知函数f(x)的图象关于y 轴对称，当－1≤x<0时，f(x)＝x ＋1，求当0<x≤1时，f(x)的表达式．能力点二：一次函数的综合问题18．设一次函数图象经过点A(2,0)和B(－2,1)，则该函数的解析式为__________． 19．教师给出一个函数y ＝f(x)，让甲、乙、丙、丁四位同学各指出这个函数的一个性质：甲：函数图象不经过第三象限； 乙：函数图象经过第一象限；丙：在区间(－∞，2)上，函数y ＝f(x)为减函数； 丁：当x<2时，y>0.已知这四位同学的叙述都正确，请构造满足上述所有性质的一个函数为__________．20．已知直线y ＝－b 4x －4和直线y ＝1a x ＋2a 交于点P(1,3)，求a 、b 的值，并求出两直线与x 轴所围成的三角形的面积．21．设f(x)＝2－ax ，若在[1,2]上，f(x)>1恒成立，求a 的取值范围．22．已知一次函数y ＝(6＋3m)x ＋(n －4)，求： (1)m 为何值时，y 随x 的增大而减小？(2)m ，n 为何值时，函数图象与y 轴的交点在x 轴下方？ (3)m ，n 分别为何值时，函数图象过原点O(0,0)?答案与解析基础巩固1．C2．B 由⎩⎪⎨⎪⎧t －2≠0，t 2－t －1＝1，解得t ＝－1.3．A 由ax ＋by ＋c ＝0，得y ＝－a b x －cb.∵ab>0，bc<0，∴－a b <0，－cb >0，即一次函数的斜率小于0且在y 轴上的截距大于0，故选A.4.25设交点为(x 0,0)， 则⎩⎪⎨⎪⎧x 0＋1＝0，2m －1x 0＋1－3m ＝0，解得m ＝25.5．B 由⎩⎪⎨⎪⎧m 2－3m ＋3＝1，m －1>0，得⎩⎪⎨⎪⎧m ＝1或2，m>1，∴m＝2.6．A 7.B 8.A 9.<10．解：(1)由题意，设y ＋5＝k(3x ＋4)，把x ＝1，y ＝2代入，得7＝k(3＋4)， ∴k＝1.∴y＋5＝3x ＋4， 即y ＝3x －1.(2)由题意可得，当x ＝－1时，y ＝3×(－1)－1＝－4；当y ＝8时，8＝3x －1，得x ＝3.(3)由0≤y≤5，可得0≤3x－1≤5，即1≤3x≤6.∴13≤x≤2.11．解：(1)当m≠12时，这个函数为一次函数．(2)根据一次函数的性质，可知当2m －1<0，即m<12时，函数在其定义域上是减函数．(3)∵直线y ＝x ＋1与x 轴交于点(－1,0)，代入y ＝(2m －1)x ＋1－3m 中，得1－2m ＋1－3m ＝0.∴m＝25.能力提升12．A 由条件知，k·b＝－|q|<0， 又∵y＝kx ＋b 为减函数， ∴k<0，故b>0.∴选A. 13．(4)(6)14．1 由⎩⎪⎨⎪⎧m 2－3m －2＝－4，m －2≠0，得m ＝1.15.83 由方程组⎩⎪⎨⎪⎧y ＝ax －2，y ＝bx ＋3，可得⎩⎪⎨⎪⎧x ＝－5a －b ，y ＝3a －8ba －b ，由于两函数交点在x 轴上，所以y ＝0，即3a －8b ＝0. 因此a b ＝83.16．解：当x ＝0时，y ＝n.∵y＝(n －2)x ＋n 的图象与y 轴交点纵坐标为－1，∴n＝－1.此时，一次函数y ＝(n －2)x ＋n 为y ＝－3x －1；y ＝(3－5)x n ＋2为y ＝(3－5)x.∵－3<0,3－5>0，∴y＝(n －2)x ＋n 在R 上递减，y ＝(3－5)x n ＋2在R 上递增，两函数图象如图．17．解：当0<x≤1时，－1≤－x<0， ∴f(－x)＝－x ＋1.又∵f(x)的图象关于y 轴对称， ∴f(x)为偶函数．∴f(x)＝f(－x)＝－x ＋1， 即当0<x≤1时，f(x)＝－x ＋1.18．y ＝－14x ＋1219.y ＝－x ＋2(只要是形如y ＝kx －2k(k<0)的函数即可)20．解：由已知，得⎩⎪⎨⎪⎧－b4－4＝3，1a ＋2a ＝3，解得⎩⎪⎨⎪⎧a ＝1，b ＝－28.∴已知直线分别为y ＝7x －4，y ＝x ＋2.分别令y ＝0，得A(－2,0)，B(47，0)，∴S △PAB ＝12|47－(－2)|×3＝277，即两直线与x 轴所围成的三角形面积为277.21．解：要使f(x)>1在[1,2]上恒成立，只需f(x)的最小值大于1. ∴当a<0时，f(x)在[1,2]上单调递增． ∴f(x)的最小值为f(1)＝2－a. ∴2－a>1，即a<1.∴a<0；当a>0时，f(x)在[1,2]上单调递减， ∴f(x)的最小值为f(2)＝2－2a.∴2－2a>1.解得a<12.∴0<a<12.当a ＝0时，f(x)＝2>1恒成立．综上，a 的取值范围为(－∞，0)∪(0，12)∪{0}＝(－∞，12)．拓展探究22．解：(1)∵y＝(6＋3m)x ＋(n －4)随x 的增大而减小， ∴6＋3m<0.∴m<－2. (2)当x ＝0时，y ＝n －4.当函数图象与y 轴的交点在x 轴下方时，y<0，得n －4<0， 所以n<4.∴当m∈R ，n<4时，函数图象与y 轴的交点在x 轴下方．(3)当一次函数y ＝(6＋3m)x ＋n －4的图象过点(0,0)时，应有0＝n －4，解得n ＝4. ∴当m∈R ，n ＝4时，函数图象过原点(0,0)． 2．2.2 二次函数的性质与图象 ～2.2.3 待定系数法基础巩固1．B2．D y ＝x 2＋2x －2＝(x ＋1)2－3，∴顶点为(－1，－3)． 3．C4．(1)C (2)D (3)B5．A 由题意，知1≤2a2×－1≤2，∴1≤a≤2.6．C ∵f(x)＝－(x －2)2＋a ＋4， ∴f(x)图象的对称轴为x ＝2. ∴f(x)在[0,1]上单调递增． ∵f(x)min ＝－2，即f(0)＝－2，即a ＝－2， ∴f(x)max ＝f(1)＝1.7．m>928．(－14，14)9．解：∵y＝－3x 2＋5x －6＝－3(x －56)2－4712，∴函数图象的对称轴是x ＝56，顶点是(56，－4712)，在(－∞，56]上是增函数，在[56，＋∞)上是减函数．10．2x －5 设g(x)＝kx ＋b(k>0)，f[g(x)]＝f(kx ＋b)＝(kx ＋b)2＝k 2x 2＋2kbx ＋b 2＝4x 2－20x ＋25，比较两边系数得k ＝2，b ＝－5，所以g(x)＝2x －5.11．y ＝15x 2＋85x ＋312．解：设f(x)＝ax 2＋bx ＋c(a≠0)，则f(3x ＋1)＝a(3x ＋1)2＋b(3x ＋1)＋c ＝9ax 2＋(6a ＋3b)x ＋a ＋b ＋c.∴9ax 2＋(6a ＋3b)x ＋a ＋b ＋c ＝9x 2－6x ＋5. 比较两边系数，得⎩⎪⎨⎪⎧9a ＝96a ＋3b ＝－6a ＋b ＋c ＝5⎩⎪⎨⎪⎧a ＝1，b ＝－4，c ＝8.∴f(x)＝x 2－4x ＋8.能力提升13．A 由题意，知－－m2×2＝2， ∴m＝8.∴f(1)＝2×12－8×1＋3＝－3. 14．D15．D 由f(－x)＝f(x)，得m 2－1＝0，∴m＝±1.故f(x)＝1或f(x)＝－2x 2＋1. ∴选D. 16.43 ∵f(x)＝11－x 1－x ＝1x 2－x ＋1＝1x －122＋34， ∴f(x)≤43，即f(x)有最大值43.17．解：y ＝f(x)＝3x 2＋2x ＋1＝3(x ＋13)2＋23.(1)顶点坐标为(－13，23)，对称轴是直线x ＝－13.(2)当x ＝－13时，y min ＝23.(3)∵函数图象关于直线x ＝－13对称，∴f(－13－x)＝f(－13＋x)．∴f(0)＝f(－13＋13)＝f(－13－13)＝f(－23)＝1.(4)∵f(－34)＝f(－13－512)＝f(－13＋512)＝f(112)，而函数在[－13，＋∞)上是增函数，112<154，∴f(112)<f(154)，即f(－34)<f(154)．18．解：(1)当a ＝－2时，f(x)＝x 2－2x ＋2＝(x －1)2＋1，∴f(x)的图象的对称轴是x ＝1.∴f(x)在[－2,1]上递减，在(1,3]上递增． ∴当x ＝1时，y min ＝1. ∵f(－2)＝10，f(3)＝5， ∴f(－2)>f(3)>f(1)． ∴当x ＝－2时，y max ＝10.(2)∵f(x)＝[x ＋(a ＋1)]2＋2－(a ＋1)2， ∴函数f(x)的图象对称轴为x ＝－(a ＋1)．当f(x)在[－2,3]上单调递减时，有－(a ＋1)≥3，即a≤－4； 当f(x)在[－2,3]上单调递增时，有－(a ＋1)≤－2，即a≥1.综上所述，当a≤－4或a≥1时，函数f(x)在[－2,3]上是单调函数．19．解：解法一：设抛物线解析式为y ＝ax 2＋bx ＋c.则⎩⎪⎨⎪⎧c ＝123，100a ＋10b ＋c ＝0，4ac －b 24a ＝3，解得⎩⎪⎨⎪⎧a ＝－112，b ＝23，c ＝53.∴y＝－112x 2＋23x ＋53.解法二：设抛物线解析式为y ＝a(x －h)2＋3. 则⎩⎪⎨⎪⎧123＝ah 2＋3，0＝a 10－h 2＋3，解得⎩⎪⎨⎪⎧a ＝－112，h ＝4.∴y＝－112(x －4)2＋3，即y ＝－112x 2＋23x ＋53.20．解：(1)∵CD＝10， ∴DF＝12CD ＝5.AB ＝20，BE ＝12AB ＝10.设抛物线方程为y ＝ax 2，则D(5，y 0)． ∴B 的坐标为(10，y 0－3)．又∵点D 、B 都在抛物线y ＝ax 2上，∴⎩⎪⎨⎪⎧y 0＝25a ，y 0－3＝100a.解得⎩⎪⎨⎪⎧a ＝－125，y 0＝－1.∴抛物线解析式为y ＝－125x 2.(2)∵点D 的坐标为(5，－1)， ∴警戒线到拱桥顶的距离为1 m. ∴水面从警戒线到拱顶用的时间为10.2＝5(h)． 答：若洪水到来时，水面以0.2 m/h 的速度上升，再持续5个小时，才能到达拱桥顶．21．D 由⎩⎪⎨⎪⎧3k ＋b ＝－2，－k ＋b ＝2，解得k ＝－1，b ＝1. 22．y ＝23x 2－43x －2 设二次函数为y ＝a(x ＋1)(x －3)，由于点(0，－2)在图象上，∴－2＝a(0＋1)(0－3)． 解得a ＝23.∴y＝23(x ＋1)(x －3)＝23x 2－43x －2.拓展探究23．解：当x∈[1,4]时，由题意，可设f(x)＝a(x －2)2－5(a>0)，由f(1)＋f(4)＝0，得a(1－2)2－5＋a(4－2)2－5＝0，解得a ＝2.∴f(x)＝2(x －2)2－5(1≤x≤4)． ∵y＝f(x)(－1≤x≤1)是奇函数， ∴f(0)＝－f(－0)． ∴f(0)＝0.又y ＝f(x)(0≤x≤1)是一次函数， ∴可设f(x)＝kx(0≤x≤1)．∵f(1)＝2(1－2)2－5＝－3， 又f(1)＝k·1＝－3， ∴k＝－3.∴当0≤x≤1时，f(x)＝－3x. 当－1≤x<0时，0<－x≤1， ∴f(x)＝－f(－x)＝－3x.∴当－1≤x≤1时，f(x)＝－3x. ∴函数的解析式为f(x)＝⎩⎪⎨⎪⎧－3x ，－1≤x ≤1，2x －22－5，1<x ≤4.。
人教B版数学高一版必修1练习函数的单调性
2.1.3 函数的单调性知识点一：函数的单调性 1．下列命题正确的是A ．定义在R 上的函数f(x)，若存在x 1，x 2∈(a，b)，使得x 1<x 2时，有f(x 1)<f(x 2)，那么f(x)在(a ，b)上为增函数B ．定义在(a ，b)上的函数f(x)，若有无穷多对x 1，x 2∈(a，b)，使得x 1<x 2时，有f(x 1)<f(x 2)，那么f(x)在(a ，b)上为增函数C ．若f(x)在区间I 1上为增函数，在区间I 2上为增函数，那么f(x)在I 1∪I 2上也一定为增函数D ．若f(x)在区间I 上为增函数，且f(x 1)<f(x 2)(x 1，x 2∈I)，那么x 1<x 22．定义在R 上的函数f(x)对任意两个不相等实数a 、b ，总有f a －f ba －b >0成立，则必有A ．函数f(x)是先增加后减少B ．函数f(x)是先减少后增加C ．f(x)在R 上是增函数D ．f(x)在R 上是减函数 3．下列函数中，在区间(0,2)上为增函数的是A ．y ＝3－xB ．y ＝x 2＋1C ．y ＝1xD ．y ＝－|x|4．关于函数y ＝2x单调性的表达正确的是A ．在(－∞，0)上递增，在(0，＋∞)上递减B ．在(－∞，0)∪(0，＋∞)上递减C ．在[0，＋∞)上递减D ．在(－∞，0)和(0，＋∞)上都递减5．已知函数f(x)＝4x 2－mx ＋1在(－∞，－2]上递减，在[－2，＋∞)上递增，则f(1)＝__________.6．设函数f(x)＝(2a －1)x ＋b 是R 上的增函数，则实数a 的取值范围是__________． 知识点二：函数的单调区间与最值7．函数f(x)＝11＋x 2(x∈R )的值域是A ．(0,1)B ．(0,1]C ．[0,1)D ．[0,1] 8．函数f(x)＝－1－2x 的单调区间为__________，在此区间上是__________(填“增函数”或“减函数”)．9．函数f(x)＝xx ＋2在区间[2,4]上的最大值为__________，最小值为__________．10．画出函数y ＝－x 2＋2|x|＋3的图象，并指出函数的单调区间． 11．讨论函数f(x)＝x ＋x －1的单调性，并求其值域．能力点一：函数单调性的判定与证明12．如果函数f(x)在区间(a ，b)和(c ，d)上都是增函数，且x 1∈(a，b)，x 2∈(c，d)，x 1<x 2，那么A ．f(x 1)<f(x 2)B ．f(x 1)>f(x 2)C ．f(x 1)＝f(x 2)D ．无法确定 13．下列命题中正确命题的序号是__________．①函数y ＝2x 2＋x ＋1在(0，＋∞)上不是增函数②函数y ＝1x ＋1在(－∞，－1)∪(－1，＋∞)上是减函数③y＝－5－4x －x 2的单调区间是[－2，＋∞)④已知f(x)在R 上是增函数，若a ＋b>0，则有f(a)＋f(b)>f(－a)＋f(－b)14．已知f(x)<0(x>0)，且f(x)单调递增，试判断F(x)＝1f x 在(0，＋∞)上的单调性并证明．能力点二：函数单调性的简单应用15．已知y ＝f(x)在[0，＋∞)上是减函数，则f(34)与f(a 2－a ＋1)的大小关系为__________．16．f(x)，g(x)都是单调函数，有如下四个命题：①若f(x)单调递增，g(x)单调递增，则f(x)－g(x)单调递增； ②若f(x)单调递增，g(x)单调递减，则f(x)－g(x)单调递增； ③若f(x)单调递减，g(x)单调递增，则f(x)－g(x)单调递减； ④若f(x)单调递减，g(x)单调递减，则f(x)－g(x)单调递减． 则上述说法中正确的是__________．17．已知f(x)是定义在[－1,1]上的增函数，且f(x －2)<f(1－x)，求x 的取值范围．18．已知f(x)＝－x 3＋ax 在(0,1)上是增函数，求实数a 的取值范围．19.已知f(x)是定义在(0，＋∞)上的增函数，且f(xy )＝f(x)－f(y)，f(2)＝1，解不等式：f(x)－f(1x －3)≤2.能力点三：函数最值的求法及应用20．函数f(x)＝1x －1在区间[2,6]上的最大值和最小值分别是A.15，1 B ．1，15 C.17，1 D ．1，1721．已知函数f(x)＝x 2＋2x ＋a x ，x∈[1，＋∞)．(1)当a ＝12时，求函数f(x)的最小值；(2)若对任意x∈[1，＋∞)，f(x)>0恒成立，试求实数a 的取值范围．22．已知函数f(x)＝x －1x ＋1，x∈[1,3]，证明函数的单调性，并求其最大值和最小值．23．设函数f(x)是实数集R 上的单调增函数，令F(x)＝f(x)－f(2－x)． (1)求证：F(x)在R 上是单调增函数； (2)若F(x 1)＋F(x 2)>0，求证：x 1＋x 2>2.24．讨论函数y ＝x 2－2(2a ＋1)x ＋3在[－2,2]上的单调性．答案与解析基础巩固1．D2．C 由条件知，f(a)－f(b)与a －b 同号，故f(x)在R 上为增函数． 3．B 4.D5．21 由已知，－－m2×4＝－2，∴m＝－16，f(x)＝4x 2＋16x ＋1. ∴f(1)＝21.6．a>12 由2a －1>0，得a>12.7．B ∵x 2≥0，∴1＋x 2≥1.∴0<11＋x 2≤1.8．(－∞，12] 增函数9.23 12 ∵f(x)＝x x ＋2＝1－2x ＋2， ∴f(x)在[2,4]是增函数，∴f(x)min ＝f(2)＝12，f(x)max ＝f(4)＝23.10．解：y ＝－x 2＋2|x|＋3＝函数图象如图所示．由图象可知：函数在(－∞，－1]，[0,1]上是增函数； 函数在[－1,0]，[1，＋∞)上是减函数．∴函数的单调递增区间是(－∞，－1]，[0,1]；单调递减区间是[－1,0]，[1，＋∞)．11．解：由故x≥1，即函数f(x)的定义域是[1，＋∞)． 对于任意的x 1，x 2∈[1，＋∞)，且x 1<x 2，有f(x 1)－f(x 2)＝(x 1＋x 1－1)－(x 2＋x 2－1) ＝(x 1－x 2)＋(x 1－1－x 2－1)＝x 1－x 2x 1＋x 2＋x 1－1－x 2－1x 1－1＋x 2－1＝(x 1－x 2)(1x 1＋x 2＋1x 1－1＋x 2－1)．∵1≤x 1<x 2， ∴x 1－x 2<0，1x 1＋x 2＋1x 1－1＋x 2－1>0.∴f(x 1)－f(x 2)<0，即f(x 1)<f(x 2)．∴函数f(x)＝x ＋x －1在[1，＋∞)上单调递增． ∴当x ＝1时，y min ＝1＋1－1＝1，无最大值． 故所求函数的值域是[1，＋∞)．能力提升12．D 例如y ＝－1x 在(－∞，0)和(0，＋∞)都为增函数，但f(－1)>f(1)；而对于y＝x(x≠0)在(－∞，0)和(0，＋∞)上都是增函数，但是f(－1)<f(1)，故选D.13．④ ①因为函数在(－14，＋∞)上为增函数，所以在(0，＋∞)上也是增函数，故①错；②应该在区间(－∞，－1)和(－1，＋∞)上均为减函数，故②错；③函数y ＝－5－4x －x 2的定义域为[－5,1]，所以增区间为[－2,1]，故③错；④∵f(x)为R 上的增函数，又a ＋b>0，∴a>－b 且b>－a.∴f(a)>f(－b)且f(b)>f(－a)，两式相加，得f(a)＋f(b)>f(－a)＋f(－b)，故④正确． 14．解：F(x)在(0，＋∞)上为减函数，下面给出证明： 任取x 1、x 2∈(0，＋∞)，且Δx＝x 2－x 1>0，∵F(x 2)－F(x 1)＝1f x 2－1f x 1＝fx 1－f x 2f x 2f x 1，又y ＝f(x)在(0，＋∞)上为增函数且Δx＝x 2－x 1>0， ∴Δy＝f(x 2)－f(x 1)>0， 即f(x 2)>f(x 1)． ∴f(x 1)－f(x 2)<0. 而f(x 1)<0，f(x 2)<0， ∴f(x 1)f(x 2)>0. ∴F(x 2)－F(x 1)<0.又Δx>0，∴F(x)在(0，＋∞)上为减函数．15．f(34)≥f(a 2－a ＋1) ∵a 2－a ＋1＝(a －12)2＋34≥34>0，且y ＝f(x)在[0，＋∞)上是减函数， ∴f(34)≥f(a 2－a ＋1)．16．②③17．解：x 应满足解得∴1≤x<32.∴x 的取值范围是1≤x<32.18．解：在(0,1)上任取x 1，x 2，使0<x 1<x 2<1.∵f(x)＝－x 3＋ax 在(0,1)上是增函数， ∴有f(x 1)－f(x 2)<0，即－x 31＋ax 1－(－x 32＋ax 2) ＝x 32－x 31＋a(x 1－x 2)＝(x 2－x 1)(x 21＋x 1x 2＋x 22)＋a(x 1－x 2)＝(x 2－x 1)(x 21＋x 1x 2＋x 22－a) <0.∵0<x 1<x 2<1，∴x 2－x 1>0. ∴x 21＋x 1x 2＋x 22－a<0.∴a>x 21＋x 1x 2＋x 22恒成立，即a>(x 21＋x 1x 2＋x 22)max.又∵x 21＋x 1x 2＋x 22<3， ∴a≥3.∴a 的取值范围是a≥3. 19．解：f(2)＋f(2)＝2.∵f(xy )＝f(x)－f(y)，∴f(y)＋f(xy)＝f(x)．在以上等式中取x ＝4，y ＝2， 则有f(2)＋f(2)＝f(4)， ∵f(2)＝1，∴f(4)＝2.∴f(x)－f(1x －3)≤2可变形为f[x(x －3)]≤f(4)．又∵f(x)是定义在(0，＋∞)上的增函数，∴解得3<x≤4.∴原不等式的解集为{x|3<x≤4}． 20．B21．(1)解：当a ＝12时，f(x)＝x ＋12x ＋2，因为f(x)在区间[1，＋∞)上为增函数，所以f(x)在区间[1，＋∞)上的最小值为f(1)＝72.(2)解法一：在区间[1，＋∞)上，f(x)＝x 2＋2x ＋a x >0恒成立x 2＋2x ＋a>0恒成立．设y ＝x 2＋2x ＋a ，∵y＝(x ＋1)2＋a －1在[1，＋∞)上递增，∴当x ＝1时，y min ＝3＋a ，于是当且仅当y min ＝3＋a>0时，函数f(x)>0恒成立，∴a>－3.解法二：f(x)＝x ＋ax＋2，x∈[1，＋∞)，当a≥0时，函数f(x)的值恒为正； 当a<0时，函数f(x)递增． 故当x ＝1时，f(x)min ＝3＋a.于是当且仅当f(x)min ＝3＋a>0，函数f(x)>0恒成立， ∴－3<a<0.故a>－3.22．解：f(x)＝x －1x ＋1＝x ＋1－2x ＋1＝1－2x ＋1.设x 1，x 2是区间[1,3]上的任意两个实数，且x 1<x 2，则Δx＝x 1－x 2<0， Δy＝f(x 1)－f(x 2)＝1－2x 1＋1－1＋2x 2＋1＝2x 2＋1－2x 1＋1 ＝2x 1＋1－2x 2＋1x 1＋1x 2＋1＝2x 1－x 2x 1＋1x 2＋1.由1≤x 1<x 2≤3，得(x 1＋1)(x 2＋1)>0， 又因为Δx＝x 1－x 2<0， 所以Δy<0.所以，函数f(x)＝x －1x ＋1是区间[1,3]上的增函数．因此，函数f(x)＝x －1x ＋1在区间[1,3]的两个端点上分别取得最小值与最大值，即在x ＝1时，取得最小值，最小值是0，在x ＝3时取得最大值，最大值是12.拓展探究23．证明：(1)任取x 1<x 2， ∵f(x)在R 上为单调增函数，∴f(x 1)<f(x 2)，f(2－x 1)>f(2－x 2)，即f(x 1)－f(x 2)<0，f(2－x 1)－f(2－x 2)>0.∴F(x 1)－F(x 2)＝[f(x 1)－f(2－x 1)]－[f(x 2)－f(2－x 2)]＝[f(x 1)－f(x 2)]＋[f(2－x 2)－f(2－x 1)]<0，即F(x 1)<F(x 2)．∴F(x)在R 上是单调增函数． (2)∵F(x 1)＋F(x 2)>0， ∴F(x 1)>－F(x 2)．而－F(x 2)＝－[f(x 2)－f(2－x 2)]＝f(2－x 2)－f(x 2)＝f(2－x 2)－f[2－(2－x 2)]＝F(2－x 2)，∴F(x 1)>F(2－x 2)．又∵F(x)在R 上是增函数， ∴x 1>2－x 2，即x 1＋x 2>2.24．解：由题意，函数的对称轴方程为x ＝2a ＋1；(1)当2a ＋1≤－2，即a≤－32时，函数在[－2,2]上为增函数．(2)当－2<2a ＋1<2，即－32<a<12时，函数在[－2,2a ＋1]上是减函数，在[2a ＋1,2]上是增函数．(3)当2a ＋1≥2，即a≥12时，函数在[－2,2]上是减函数．综上所述：当a≤－32时，函数在[－2,2]上为增函数；当－32<a<12时，函数在[－2，2a ＋1]上是减函数，在[2a ＋1,2]上是增函数；1当a≥2时，函数在[－2,2]上是减函数．。
人教新课标版数学高一B版必修1同步训练 2.3函数的应用(Ⅰ)
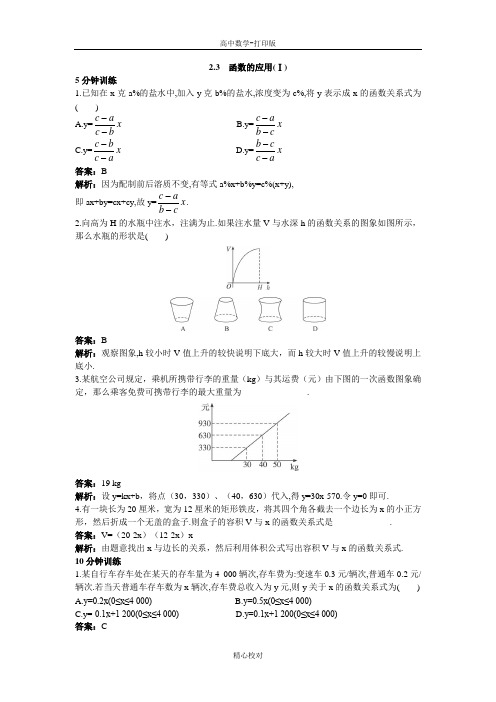
2.3 函数的应用(Ⅰ)5分钟训练1.已知在x 克a%的盐水中,加入y 克b%的盐水,浓度变为c%,将y 表示成x 的函数关系式为( )A.y=x b c a c -- B.y=x cb ac -- C.y=x a c b c -- D.y=x a c c b -- 答案：B解析：因为配制前后溶质不变,有等式a%x+b%y=c%(x+y),即ax+by=cx+cy,故y=x cb ac --. 2.向高为H 的水瓶中注水，注满为止.如果注水量V 与水深h 的函数关系的图象如图所示，那么水瓶的形状是( )答案：B解析：观察图象,h 较小时V 值上升的较快说明下底大，而h 较大时V 值上升的较慢说明上底小.3.某航空公司规定，乘机所携带行李的重量（kg ）与其运费（元）由下图的一次函数图象确定，那么乘客免费可携带行李的最大重量为_______________.答案：19 kg解析：设y=kx+b ，将点（30，330）、（40，630）代入,得y=30x-570.令y=0即可.4.有一块长为20厘米，宽为12厘米的矩形铁皮，将其四个角各截去一个边长为x 的小正方形，然后折成一个无盖的盒子.则盒子的容积V 与x 的函数关系式是_____________. 答案：V=（20-2x ）（12-2x ）x解析：由题意找出x 与边长的关系，然后利用体积公式写出容积V 与x 的函数关系式. 10分钟训练1.某自行车存车处在某天的存车量为4 000辆次,存车费为:变速车0.3元/辆次,普通车0.2元/辆次.若当天普通车存车数为x 辆次,存车费总收入为y 元,则y 关于x 的函数关系式为( )A.y=0.2x(0≤x≤4 000)B.y=0.5x(0≤x≤4 000)C.y=-0.1x+1 200(0≤x≤4 000)D.y=0.1x+1 200(0≤x≤4 000)答案：C解析：由题意,得y=0.3(4 000-x)+0.2x(0≤x≤4 000),即y=-0.1x+1 200(0≤x≤4 000).2.某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x 2(0<x<240, x ∈N *),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量为( )A.100台B.120台C.150台D.180台答案：C解析：设生产者不亏本时的最低产量为x 台,依题意,得25x-3 000-20x+0.1x 2≥0,即x 2+50x-30 000≥0.解得x≤-200(舍)或x≥150.所以生产者不亏本时的最低产量为150台.3.某地的中国移动“神州行”卡与中国联通130网的收费标准如下表：网络 月租费 本地话费 长途话费甲:联通130网 12元 每分钟0.36元 每6秒钟0.06元 乙:移动“神州行”卡 无 每分钟0.6元 每6秒钟0.07元 (注:本地话费以分钟为单位计费,长途话费以6秒钟为单位计费)若某人每月拨打本地电话时间是长途电话时间的5倍,且每月通话时间(分钟)的范围在区间(60,70)内,则选择较为省钱的网络为( )A.甲B.乙C.甲、乙均一样D.分情况确定 答案：A解析：(1)若按甲网络计费,则需支出的费用为y 1=12+5×0.36x+660x ×0.06=2.4x+12. 当60<x<70时,156<y 1<180.(2)若按乙网络计费,则需支出的费用为y 2=5x×0.6+60x×607.0=3.7x. 当60<x<70时,222<y 2<259.由(1)(2)可知选择甲网络省钱.4.对于每一个实数x ，f （x ）是y=2-x 2和y=x 这两个函数值中的较小者，则f （x ）的最大值是( )A.1B.2C.0D.-2答案：A解析：由数形结合的思想，比较两函数图象在同一坐标系下的位置关系.5.一辆汽车在某段路程中的行驶速度v 与时间t 的关系如图所示,则该汽车在前3小时内行驶的路程为________km,假设这辆汽车的里程表在汽车行驶这段路程前的读数为2 006 km,那么在t ∈［1,2］时,汽车里程表读数s 与时间t 的函数解析式为_______________.答案：220 s=1 976+80t(t≥0)解析：该汽车在前3个小时内行驶的路程为50×1+80×1+90×1=220 km.由于这辆汽车在行驶这段路程前的里程表的读数为2 006 km,所以当t ∈［1,2］时,汽车里程表的读数s 与时间t 的函数关系式是s=2 006+50×1+80(t-1)=1 976+80t(t≥0).6.绿缘商店每月按出厂价每瓶3元购进一种饮料.根据以前的统计数据,若零售价定为4元,每月可销售400瓶;若每瓶售价降低0.05元,则可多销售40瓶.在每月的进货量当月销售完的前提下,请你给该商店设计一个方案:销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?解：设销售价为x 元/瓶,则根据题意(销售量等于进货量),正好当月销售完的进货量为05.04x -×40+400,即400×(9-2x)瓶. 此时所得的利润为f(x)=400(9-2x)(x-3)=400(-2x 2+15x-27)(元),根据函数的性质,当x=3.75时,f(x)取得最大值450,这时进货量为400×(9-2x)=400×(9-2×3.75)=600(瓶).获得最大利润为450元.30分钟训练1.为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”.计费方法如下表:每户每月用水量 水价不超过12 m 3的部分 3元/m 3超过12 m 3但不超过18 m 3的部分 6元/m 3超过18 m 3的部分 9元/m 3若某户居民本月交纳的水费为48元,则此户居民本月用水量( )A.比12 m 3少B.比12 m 3多,但不超过18 m 3C.比18 m 3多D.恰为12 m 3答案：B解析：设每户每月用水量为x,水价为y,则y=⎪⎩⎪⎨⎧>⨯-++≤<⨯-+≤<,18,9)18(3636,1812,6)12(36,120,3x x x x x x 即⎪⎩⎪⎨⎧>-≤<-≤<=.18,909,1812,366,120,3x x x x x x y∴48=6x-36,x=14,故选B.2.如图,是一份统计图表,根据此图表得到的以下说法中,正确的有( )①这几年人民的生活水平逐年得到提高;②人民生活费收入增长最快的一年是2003年;③虽然2005年生活费收入增长最缓慢,但由于生活价格指数也略有降低,因而人民的生活仍有较大改善.A.1项B.2项C.3项D.0项答案：C解析：根据题图,“生活费收入指数”减去“生活价格指数”的差是逐年增大的，故①正确.“生活费收入指数”2003-2004年最“陡”，②正确.生活价格指数下降,而“生活费收入指数”的曲线呈上升趋势，故③正确.3.(探究题)如图,△ABO为正三角形,直线x=t截三角形得△ABO左侧的阴影图形,当直线自左向右匀速移动时(0≤t≤a),阴影图形面积S关于t的函数图象大致是( )答案：A解析：S=⎪⎪⎩⎪⎪⎨⎧≤<+-≤≤.2,323,22322ataattatt4.为了稳定市场,确保农民增收,某农产品的市场收购价格a与其前三个月的市场收购价格有关,且使a与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格：月份 1 2 3 4 5 6 7价格(元/担) 68 78 67 71 72 70则7月份该产品的市场收购价格应为( )A.69元B.70元C.71元D.72元答案：C解析：f(a)=(a-71)2+(a-72)2+(a-70)2=3(a-71)2+2.当a=71时,f(a)最小.5.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断：①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水. 则一定能确定正确的论断序号是____________.答案：①解析：由题中甲、乙两图可知,一个水口单位时间内的出水量是进水量的2倍.对于①,由于蓄水量持续增加,所以它是正确的;对于②,由于单位时间内的出水量同进水量一致,所以它表示同时打开一个进水口和一个出水口;对于③,也可表示同时打开两个进水口和一个出水口.6.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元的14%纳税；超过4 000元的按全稿酬的11%纳税.某人出版了一书共纳税420元,这个人的稿费为____________元.答案：3 800解析：∵3 200×14%=448>420,∴稿费超出800元的部分为420÷14%=3 000,即可求出.7.用4 m 长的合金条做一个“日”字形的窗户.当窗户的长和宽各为多少时,透过的光线最多?解：设“日”字形窗户的长为x m ，则宽为324x - m ，其面积为 S=x x x x 34323242+-=-•=32)1(322+--x . 所以当窗户的长为1 m ，宽为32m 时，窗户的面积最大为32m 2，即透过的光线最多. 8.某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台.现销售给A 地10台,B 地8台.已知从甲地调运1台至A 地、B 地的运费分别为400元和800元,从乙地调运1台至A 地、B 地的运费分别为300元和500元.(1)设从乙地调运x 台至A 地,求总运费y 关于x 的函数关系式.(2)若总运费不超过9 000元,问共有几种调运方案?(3)求出总运费最低的调运方案及最低的费用.解：由甲、乙两地调运至A 、B 两地的机器台数及费用列表如下：调出地 甲地 乙地调至地 A 地 B 地 A 地 B 地台数 10-x 12-(10-x) x 6-x每台运费 400 800 300 500 运费合计 400(10-x) 800［12-(10-x)］ 300x500·(6-x) (1)依题意,得y=400(10-x)+800［12-(10-x)］+300x+500(6-x),即y=200(x+43)(0≤x≤6,x ∈Z ).(2)由y≤9 000,解得x≤2.∵x ∈Z ,0≤x≤6,∴x=0,1,2.∴共有三种调运方案.(3)由一次函数的单调性,知当x=0时,总运费y 最低,y min =8 600元,即从乙地调6台给B 地,甲地调10台给A 地、调2台给B 地的调运方案的总运费最低,最低运费为8 600元.9.某商场经营一批进价为12元/个的小商品,在4天的试销中,对此商品的单价x(元)与相应的日销量y(个)作了统计,其数据如下：x 16 20 24 28y 42 30 18 6(1)能否找到一种函数,使它反映y 关于x 的函数关系?若能,写出函数解析式.(2)设经营此商品的日销售利润为P(元),求P 关于x 的函数解析式,并指出当此商品的销售价每个为多少元时,才能使日销售利润P 取最大值?最大值是多少?解：(1)观察x 、y 的关系,可大体看到y 与x 是一次函数,令y=kx+b.代入当x=16时,y=42;x=20时,y=30.得⎩⎨⎧+=+=)2(.2030)1(,1642b k b k由②-①,得-12=4k,∴k=-3.代入②,得b=90.所以y=-3x+90,显然当x=24时,y=18.当x=28时,y=6.对照数据,可以看到y=-3x+90即为所求解析式.(2)利润P=(x-12)·(-3x+90)=-3x 2+126x-1 080=-3(x-21)2+243.∵二次函数开口向下,∴当x=21时,P 最大为243.即每件售价为21元时,利润最大,最大值为243元.。
人教版数学高一-人教B版必修一规范训练 函数(一)
双基达标 (限时20分钟)1．与函数y ＝－2x 3为同一函数的是 ( )．A ．y ＝x －2xB ．y ＝－x －2xC ．－2x 3D ．y ＝x2－2x解析 函数y ＝－2x 3的定义域为(－∞，0]，则化简为－2x 3＝－x－2x .答案 B2．函数f (x )＝(x －12)0＋|x 2－1|x ＋2的定义域为( )．A ．(－2，12)B ．(－2，＋∞)C ．(－2，12)∪(12，＋∞)D ．(12，＋∞)解析由⎩⎨⎧x －12≠0x ＋2>0，得⎩⎨⎧x ≠12，x >－2，即x >－2且x ≠12.答案 C3．函数f (x )＝x 2－1x 2＋1，则f (2)f (12)＝( )．A ．1B ．－1 C.35D ．－35解析 ∵f (x )＝x 2－1x 2＋1，∴f (12)＝122－1122＋1＝1－221＋22＝－35， f (2)＝22－122＋1＝35，∴f (2)f (12)＝－1.故选B.答案 B4．已知f (x )＝x 3－8，则f (x －2)＝________.解析f(x)＝x3－8，∴f(x－2)＝(x－2)3－8＝x3－6x2＋12x－16.答案x3－6x2＋12x－165．已知函数f(x)的定义域为[0,3]，则函数f(3x＋6)的定义域是________．解析由0≤3x＋6≤3，得－2≤x≤－1，故定义域为[－2，－1]．答案[－2，－1]6．已知f(x)＝11＋x(x∈R，且x≠－1)，g(x)＝x2＋2(x∈R)．(1)求f(2)、g(2)的值；(2)求f[g(2)]的值；(3)求f[g(x)]的解析式．解(1)f(2)＝11＋2＝13，g(2)＝22＋2＝6.(2)f[g(2)]＝f(6)＝11＋6＝17.(3)f[g(x)]＝f(x2＋2)＝11＋(x2＋2)＝1x2＋3.综合提高(限时25分钟)7．设f(x)＝2x＋3，g(x＋2)＝f(x)，则g(0)的值为()．A．1 B．－1C．－3 D．7解析∵g(x＋2)＝f(x)，∴g(0)＝f(－2)＝2×(－2)＋3＝－1.答案 B8．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝f(2x)x－1的定义域是()．A．[0,1] B．[0,1) C．[0,1)∪(1,4] D．(0,1) 解析∵y＝f(x)的定义域是[0,2]，故f(2x)中，0≤2x≤2，即0≤x≤1，又x－1≠0，∴x≠1，∴0≤x<1.答案 B9．设f (x )＝x －1x ＋1，则f (x )＋f (1x )等于________． 解析 f (1x )＝1x －11x ＋1＝1－x x ＋1，∴f (x )＋f (1x )＝x －11＋x ＋1－x1＋x ＝0.答案 010．函数f (x )＝(x ＋1)0|x |－x的定义域为________．解析 要使解析式有意义，当且仅当⎩⎪⎨⎪⎧x ＋1≠0，|x |－x >0.解得定义域为{x |x <0且x ≠－1}(区间表示：(－∞，－1)∪(－1,0))．答案 (－∞，－1)∪(－1,0) 11．已知函数f (x )＝x 21＋x 2，x ∈R .(1)求f (x )＋f (1x )的值；(2)计算：f (1)＋f (2)＋f (3)＋f (4)＋f (12)＋f (13)＋f (14)的值． 解 (1)f (x )＋f (1x )＝x 21＋x 2＋1x 21＋1x 2＝x 21＋x 2＋11＋x 2＝1＋x 21＋x 2＝1. (2)f (1)＋f (2)＋f (3)＋f (4)＋f (12)＋f (13)＋f (14)＝f (1)＋[f (2)＋f (12)]＋[f (3)＋f (13)][f (4)＋f (14)]＝12＋3＝72. 12．(创新拓展)已知f (x －1)＝x 2－2x ＋7. (1)求f (2)和f (a )的值； (2)求f (x )和f (x ＋1)的解析式； (3)求f (x ＋1)的值域．解 (1)f (2)＝f (3－1)＝9－6＋7＝10，f (a )＝f [(a ＋1)－1]＝(a ＋1)2－2(a ＋1)＋7＝a 2＋6. (2)法一(配凑法)：∵f(x－1)＝(x－1)2＋6，∴f(x)＝x2＋6.∴f(x＋1)＝(x＋1)2＋6＝x2＋2x＋7.法二(换元法)：令x－1＝t，则x＝t＋1，则f(t)＝(t＋1)2－2(t＋1)＋7＝t2＋6，∴f(x)＝x2＋6，∴f(x＋1)＝(x＋1)2＋6＝x2＋2x＋7.(3)∵f(x＋1)＝x2＋2x＋7＝(x＋1)2＋6≥6，∴f(x＋1)的值域为[6，＋∞)．。
倾力打造人教B版数学必修1同步练习-2.1.1 函 数 含答
1．函数23x y +=的定义域是( )． A ．{x |x ＜0，且32x ≠-} B ．{x |x ＜0}C ．{x |x ＞0}D ．{x |x ≠0，且32x ≠-，x ∈R } 2．设集合M ＝R ，从M 到P 的映射21:1f x y x →=+，则映射f 的值域为( )． A ．{y |y ∈R }B ．{y |y ∈R ＋}C ．{y |0≤y ≤2}D ．{y |0＜y ≤1}3．若1()x f x x -=，则方程f (4x )＝x 的根是( )． A. 12 B ．12- C ．2 D ．－24．下列从集合A 到集合B 的对应法则为映射的是( )． A ．A ＝B ＝N ＋，对应法则:3f x y x →=-B ．A ＝R ，B ＝{0,1}，对应法则()()10:00x f x y x ≥⎧⎪→=⎨<⎪⎩ C ．A＝B ＝R ，对应法则:f x y →=D ．A ＝Z ，B ＝Q ，对应法则1:f x y x→= 5．已知集合A ＝[1,4]，B ＝(－∞，a )，若A ⊆B ，则实数a 的取值范围是________．(用区间表示)6．(拓展题)若函数y ＝f (x )对于一切实数a ，b 都满足f (a ＋b )＝f (a )＋f (b )，且f (1)＝8，则f (－12)＝________. 7．若f ：y ＝3x ＋1是从集合A ＝{1,2,3，k }到集合B ＝{4,7，a 4，a 2＋3a }的一个映射，求自然数a ，k 及集合A 、B .8．(1)已知1)f x =-f (x )；(2)已知f (3x ＋1)＝3x 2－x ＋1，求f (x )；(3)已知213()()f x f x x -=，求f (x )．参考答案1. 答案：A解析：由2300x x x +≠⎧⎪⎨->⎪⎩得x ＜0且32x ≠-. 2. 答案：D解析：∵x ∈R ，x 2＋1≥1， ∴(]210,11y x =∈+． 3. 答案：A 解析：41(4)4x f x x x -==， ∴4x 2－4x ＋1＝0， ∴12x =. 4. 答案：B解析：在A 项中，当x ＝3时，|x －3|＝0，于是集合A 中有一个元素在集合B 中没有元素和它对应，故不是映射；在C 项中，集合A 中的负数在集合B 中没有元素和它对应，故也不是映射；在D 项中，集合A 中的元素0，其倒数不存在，因而0在集合B 中无对应元素，故同样不是映射；只有B 项符合定义，故选B.5. 答案：(4，＋∞)解析：∵A ⊆B ，∴a ＞4.6. 答案：－4解析：令a ＝b ＝0得f (0＋0)＝f (0)＋f (0)，∴f (0)＝0.令12a b ==，得11(1)()()22f f f =+， ∴1()42f =. 令12a =，12b =-，则11()()(0)022f f f -+==， ∴11()()422f f -=-=-.7. 解：∵1的象是4,7的原象是2，∴可判断A 中元素3的象10要么是a 4，要么是a 2＋3a . 由a 4＝10且a ∈N ，知不存在a .∴a 2＋3a ＝10，即a 1＝－5(舍去)，a 2＝2.又集合A 中元素k 的象只能是a 4＝16，∴3k ＋1＝16.∴k ＝5.∴A ＝{1,2,3,5}，B ＝{4,7,16,10}．8. 解：(1)凑配法：∵21)1)1)3f x =-=-+， ∴f (x )＝x 2－4x ＋3.11≥，∴f (x )＝x 2－4x ＋3(x ≥1)．(2)换元法：∵f (3x ＋1)＝3x 2－x ＋1，令3x ＋1＝t ， ∴13t x -=. ∴221135()3()1333t t t t f t ---+=-+= ＝21533t t -+. ∴215()33f x x x =-+. (3)构造法： ∵213()()f x f x x -=， ① ∴2113()()f f x x x-=. ② ①×3＋②，得2218()3f x x x =+， ∴2231()88f x x x=+. 又x ≠0，∴2231()88f x x x =+ (x ≠0)．。
数学人教B版必修1同步训练：2-1-1函数 含解析 精品
第二章 函数2.1 函数 2.1.1 函数5分钟训练1.给出下列四个对应，其中构成映射的是()A.(1)(2)B.(1)(4)C.(1)(3)D.(3)(4) 答案：B解析：紧扣映射的定义进行判断.2.已知映射f:A→B,集合A 中元素n 在对应法则f 下的象是2n -n,则121的原象是( ) A.8 B.7 C.6 D.5 答案：B解析：可把备选的答案代入2n -n=121中进行验证.3.下列过程中,变量之间是否存在依赖关系?其中哪些是函数关系?(1)设一长方体盒子高为10 cm,底面是正方形,求这个长方体的体积V(cm 3)与底面边长a(cm)的关系;(2)秀水村的耕地面积是106(m 2),求这个村人均占有耕地面积x(m 2)与人数n 的关系;(3)设地面气温是20 ℃,如果每升高1 km,气温下降6 ℃,求气温t(℃)与高度h(km)的关系. 答案：(1)长方体的体积V(cm 3)与边长a(cm)之间存在函数关系,其中边长是自变量,体积是因变量;反之亦行.(2)秀水村的人均占有耕地面积x(m 2)与人数n 之间存在函数关系,其中人数是自变量,人均占有耕地面积是因变量;反之亦行.(3)气温t(℃)与高度h(km)之间存在函数关系,其中气温是自变量,高度是因变量;反之亦行. 4.以下给出的同组函数中,是否表示同一函数?为什么? (1)f 1：y=xx;f 2:y=1. (2)f 1：y=|x|;f 2:y=⎩⎨⎧<->.0,,0,x x x x(3)f 1：y=⎪⎩⎪⎨⎧≥<<≤;2,3,21,2,1,1x x xf 2： X x≤1 1<x<2 x≥2 y123(4)f 1：y=2x; f 2:如图.解：(1)不同函数.f 1(x)的定义域为{x ∈R |x≠0},f 2(x)的定义域为R. (2)不同函数.f 1(x)的定义域为R,f 2(x)的定义域为{x ∈R |x≠0}.(3)同一函数.x 与y 的对应关系完全相同,它们是同一函数的不同表示形式. (4)同一函数.理由同(3). 10分钟训练1.对于函数y=f(x),有以下说法:①y 是x 的函数;②对于不同的x 、y 的值也不同; ③f(a)表示当x=a 时函数f(x)的值,是一个常量;④f(x)一定可以用一个具体的式子表示出来.其中正确命题的个数是( ) A.1 B.2 C.3 D.4 答案：B提示：①③正确.2.设集合A={a ，b ，c}，B={1，0，-1}，映射f ：A→B 满足f （a ）-f （b ）=f （c ），则映射f ：A→B 的个数有( )A.4个B.5个C.6个D.7个 答案：D解析：f （a ）-f （b ）=f （c ），即f （a ）=f （b ）+f （c ），根据映射的定义，对f （a ）=1、0、-1三种情况讨论.（1）f （a ）=1时，f （b ）=1，f （c ）=0或f （b ）=0，f （c ）=1两种情况；（2）f （a ）=0时，f （b ）=1，f （c ）=-1或f （b ）=-1，f （c ）=1或f （b ）=f （c ）=0三种情况；（3）f （a ）=-1时，f （b ）=-1，f （c ）=0或f （b ）=0，f （c ）=-1两种情况.所以共有7种情况，故选D.3.若函数f （x ）的定义域是［0，1］，则f （x+a ）+f （x-a ）（0＜a ＜21）的定义域是( ) A.∅ B.［a ，1-a ］ C.［-a ，1+a ］ D.［0，1］ 答案：B解析：函数f （x+a ）+f （x-a ）的定义域是函数f （x+a ）和f （x-a ）定义域的交集，分别求出后利用数轴合并.∵⎩⎨⎧+≤≤-≤≤-⇒⎩⎨⎧≤-≤≤+≤.1,11010a x a a x a a x a x 如图，得函数f （x+a ）+f （x-a ）（0＜a ＜21)的定义域［a ，1-a ］，故选B.4.求下列函数的定义域：(1)f(x)=21-x ；(2)f(x)=23+x ；(3)f(x)=xx -++211. 解：(1)∵x-2=0，即x=2时，分式21-x 无意义，而x≠2时，分式21-x 有意义，∴这个函数的定义域是{x|x≠2}. (2)∵3x+2<0，即x<32-时，根式23+x 无意义，而3x+2≥0，即x≥32-时，根式23+x 才有意义，∴这个函数的定义域是{x|x≥32-}. (3)∵当x+1≥0且2-x≠0，即x≥-1且x≠2时，根式1+x 和分式x-21同时有意义， ∴这个函数的定义域是{x|x≥-1且x≠2}.5.（1）若函数y=f （x ）的定义域为［1，2］，求f （2x+1）的定义域； （2）若函数y=f （2x+1）的定义域为［1，2］，求f （x ）的定义域. 解析：（1）1≤2x+1≤2⇒0≤x≤21⇒f （2x+1）的定义域是［0，21］. （2）f （2x+1）的定义域为［1，2］是指x 的取值范围是［1，2］，1≤x≤2，∴2≤2x≤4. ∴3≤2x+1≤5.∴f （x ）的定义域为［3，5］. 30分钟训练1.下列函数中,与y=x 表示同一函数的是( )A.y=xx 2B.y=2xC.y=tD.y=x 0·x 答案：C解析：y=xx 2=x(x≠0),y=2x =|x|,y=x 0·x=x(x≠0).显然A 、D 与y=x 的定义域不同, B 与y=x 的对应关系不同.2.(创新题)设f,g 都是由A 到A 的映射〔其中A={1,2,3}〕其对应法则如下表:1 2 3 f 1 1 2 g 3 21则f ［g(3)］等于( )A.1B.2C.3D.不存在 答案：A解析：f ［g(3)］=f(1)=1.3.(探究题)已知函数y=f(x)的定义域为［a,b ］,{(x,y)|y=f(x),a≤x≤b}∩{(x,y)|x=0}只有一个子集,则( )A.ab>0 B .ab≥0 C.ab<0 D .ab≤0 答案：A解析：依题意,得{(x,y)|y=f(x),a≤x≤b}∩{(x,y)|x=0}=∅, 故函数y=f(x)(x ∈［a,b ］)与y 轴不相交, 所以ab>0.4.已知f(21x-1)=2x+3,f(m)=6,则m 等于( ) A.41- B.41 C.23 D.23-答案：A 解析：方法一:设21x-1=t,则x=2t+2, f(t)=2×(2t+2)+3=4t+7, 即f(x)=4x+7. 令4x+7=6,得x=41-, 即m=41-. 方法二:令2x+3=6,得x=23. ∴m=21x-1=21×23-1=41-.5.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d 对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( ) A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7 答案：C解析：由题意,可知⎪⎪⎩⎪⎪⎨⎧====⎪⎪⎩⎪⎪⎨⎧==+=+=+.7,1,4,6.284,2332,92,142d c b a d d c c b b a 解得 6.函数f(x)=6||22--x x的定义域是_________________.答案：{x|x≤2,且x≠-3}解析：要使函数有意义,当且仅当⎩⎨⎧±≠≥-,3,02x x解得x≤2且x≠-3.7.已知g （x ）=1-2x ，f ［g （x ）］=221xx -（x≠0），则f （21）等于____________. 答案：15 解析：令g （x ）=21，解得x=41. 代入f ［g （x ）］=221xx -，得f ［g （41）］=f （21）=22)41()41(1-=15. 8.已知映射f:A→B 中,A=B={(x,y)|x ∈R ,y ∈R },其中f:(x,y)→(3x -2y+1,4x+3y-1). (1)求A 中元素(1,2)的象; (2)求B 中元素(1,2)的原象;(3)是否存在这样的元素(a,b),使它的象仍是自己?若有,求出这个元素. 解：(1)由题意,得x=1,y=2,代入象的表达式,得3×1-2×2+1=0,4×1+3×2-1=9, 即(1,2)的象是(0,9).(2)由题意,得⎪⎪⎩⎪⎪⎨⎧==⎩⎨⎧=-+=+-.179,176.2134,1123y x y x y x 解得所以象(1,2)的原象是(179,176). (3)假设存在以自己为象的元素(a,b),则满足方程组⎪⎩⎪⎨⎧==⎩⎨⎧=-+=+-.21,0,134,123b a b b a a b a 解得所以存在这样的元素(a,b),使它的象仍是自己,这个元素是(0,21). 9.如图,△ABC 是一等腰直角三角形,AB=AC=1,EF ∥BC.当E 从A 移向B 时,写出线段EF 的长度l 与它到点A 的距离h 之间的函数关系式,并作出函数图象.解：在Rt △ABC 中,∠A=90°,AB=AC=1, EF ∥BC,EF=l,设A 到EF 的距离为h, 则l=2h,0≤h≤22. 图象如图所示.。
高一数学人教B版(2019)必修第一册最新同步练习(附详解)：3.3函数的应用(一)
高一数学人教B 版（2019）必修第一册同步课时作业3.3函数的应用(一）1.某商场以每件30元的价格购进一种商品，试销中发现，这种商品每天的销量m (件)与售价x (元)满足一次函数1623m x =-，若要每天获得最大的销售利润，每件商品的售价应定为( )A.30元B.42元C.54元D.越高越好2.某公司在甲、乙两地销售一种品牌车，利润(单位：万元)分别为21 5.060.15L x x =-和22L x =，其中x 为销售量(单位：辆).若该公司在这两地共销售15辆车，则能获得的最大利润为( )A.45.606B.45.6C.45.56D.45.513.某商店出售,A B 两种价格不同的商品，由于商品A 连续两次提价20%，同时商品B 连续两次降价20%，结果都以每件23元售出，若商店同时售出这两种商品各一件，则与价格不升不降时的情况比较，商店盈利情况是( )A.多赚约6元B.少赚约6元C.多赚约2元D.盈利相同4.某汽车运输公司，购买了一批豪华大客车投入客运，据市场分析，每辆客车营运的总利润y 万元与营运年数()*x x ∈N 的关系式为21225y x x =--+，则为使其营运年平均利润最大，每辆客车营运年数为( )A.2B.4C.5D.65.某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是( )A.10%B.15%C.18%D.20%6.出租车按如下方法收费:起步价7元,可行3km(不含3km);3km 到7km(不含7km)按1.6元/km 计价(不足1km 按1km 计算);7km 以后按2.2元/km 计价,到目的地结算时还需付1元的燃油附加费.若从甲地坐出租车到乙地(路程12.2km),需付车费(精确到1元)( )A.28元B.27元C.26元D.25元7.将进货单价为80元的商品按90元出售时,能卖出400个.若该商品每个涨价1元,其销售量就减少20个,为了赚取最大的利润,售价应定为每个( )A.115元B.105元C.95元D.85元8.某产品的总成本y (万元)与产量x (台)之间的函数关系式是23000200.1,(0,240)y x x x =+-∈.若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是( )A.100台B.120台C.150台D.180台9..某工厂八年来某种产品总产量C 与时间t 的函数关系如图所示.下列说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度保持稳定;③第三年后产量增长的速度保持稳定;④第三年后,年产量保持不变;⑤第三年后,这种产品停止生产.其中说法正确的是 ( )A.②⑤B.①③C.①④D.②④10.某公司在甲乙两地销售同一种品牌车,利润(单位:万元)分别为21 5.060.15L x x =-和22,L x =其中x 为销售量(单位:辆). 若该公司在这两地共销售15辆车,则能获得的最大利润为( )A.45.606万元B.45.6万元C.45.56万元D.45.51万元11.某种商品进货价每件50元，据市场调查，当销售价格(每件x 元)在区间[]50,80时，每天售出的件数2100000(40)P x =-，当销售价格定为__________元时所获利润最大. 12.国家对出书所得的稿费纳税作如下规定：不超过800元的不纳税；超过800元而不超过4000元的按超过部分的14%纳税；超过4000元的按全稿酬的11%纳税.某人出版了一本书共纳税420元，则这个人的稿费为________.13.某公司购买一批机器投入生产，据市场分析，每台机器生产的产品可获得的总利润y （单位：万元）与机器运转时间x （单位：年）的关系式为()21825y x x x *=-+-∈N ，则当每台机器运转______年时，年平均利润最大，最大值是________万元.14.如图所示,折线是某电信局规定打长途电话所需要付的电话费y (元)与通话时间t (分钟)之间的函数关系图象,根据图象填空:1.通话2分钟,需付电话费__________元;2.通话5分钟,需付电话费__________元;3.如果3t ≥,则电话费y (元)与通话时间t (分钟)之间的函数关系式为__________15.在某服装批发市场，某种品牌的时装当季节即将来临时，价格呈上升趋势，设这种时装开始时定价为20元，并且每周(7天)涨价2元，从第6周开始保持30元的价格平稳销售；从第12周开始，当季节即将过去时，平均每周减价2元，直到第16周周末，该服装不再销售.(1)试建立销售价y 与周次x 之间的函数关系式；(2)若这种时装每件进价Z 与周次x 次之间的关系为()20.125812,116Z x x =--+≤≤，且x 为整数，试问该服装第几周出售时，每件销售利润最大？最大利润为多少？答案以及解析1.答案：B解析：设当每件商品的售价为x 元时，每天获得的销售利润为y 元.由题意得，()()()30301623y m x x x =-=--.上式配方得()2342432y x =--+.∴当42x =时，利润最大.故选B. 2.答案：B解析：设甲地销售x 辆，则乙地销售()15x -辆，从而总利润为()()()225.060.152150.15 3.06300015S x x x x x x x x =-+-=-++≥≤≤∈，，N ， 显然，当10x =时，S 取得最大值45.6S =.3.答案：B解析：设,A B 两种商品的原价为,a b ， 则2223252325(120%)(120%)23,,4663616a b a b a b ⨯⨯+=-=⇒==+-≈(元). 4.答案：C 解析：平均利润212252512y x x x x x x -+-⎛⎫==-+ ⎪⎝⎭， 由对勾函数的性质得，当05x <，且*x ∈N ，y x为增函数； 当5x >，且*x ∈N 时，y x 为减函数， 故当5x =时，年平均利润最大，故选C.5.答案：D解析：设平均每次降价的百分率为x ,则22000(1)1280x ⋅-=,所以20%x =,故选D.6.答案：C解析：设路程为x ,需付车费为y 元,则有7,037 1.6(3),3714.4 2.2(7),7x y x x x x <<⎧⎪=+-≤<⎨⎪+-≥⎩.由题意知,从甲地坐出租车到乙地,需付车费14.4 2.2(12.27)25.8426y =+⨯-=≈(元).7.答案：C解析：设售价定为(90)x +元,卖出商品后获得的利润为2(9080)(40020)20(10200)y x x x x =+--=-++,∴当5x =时,y 取得最大值,即售价应定为90595+=(元).8.答案：C解析：设产量为x ,则总售价为25x .使生产者不亏本,则必须满足总售价大于或等于总成本,即2250.1x x x ≥3000+20-,即20.153000x x +-≥0,化为250300000x x +-≥,解得150x ≥或200x ≤-(舍去).故最低产量是150台.9.答案：A解析：解:前三年总产量C 与t 是一条直线,增长熟读保持稳定,3年后由于总产量不变,故没有继续生产.选A.10.答案：B解析：设在甲地销售x 辆车,则在乙地销售()15x -辆车,获得的利润为()25.060.15215y x x x =-+-20.15 3.0630,x x =-++ 当 3.0610.22(0.15)x ==⨯-时, y 最大, 但*x N ∈,所以当10x =时, 1530.63045.6,max y =-++=故选B.11.答案：60解析：设销售价格每件x 元()5080x ≤≤，每天获利润y 元， 则2100000(50)(50)(5080)(40)x y x P x x -=-=≤≤-， 问题转化为250(5080)(40)x u x x -=≤≤-的最大值即可， 22250110101(40)40(40)(40)40x u x x x x x -==-=-+-----，这是一个u 关于140x -的二次函数，当111402(10)20x ==-⨯-，即[]6050,80x =∈时，u 取得最大值. 所以当销售价格每件为60元时所获利润最大.12.答案：3800元解析：设稿费为x 元时，纳税y 元，则由题意得0,080014%(800),800400011%,4000x y x x x x ≤≤⎧⎪=-<≤⎨⎪>⎩，即0,08000.14112,80040000.11,4000x x x x x ≤≤⎧-<≤>⎪⎨⎪⎩.由0.14112420x -=，解得3800x =；由0.11420x =，解得2381811x = (舍去). 13.答案：5；8解析：每台机器运转x 年的年平均利润为2518y x x x ⎛⎫=-+ ⎪⎝⎭，而0x >，故182258y x -，当且仅当5x =时等号成立，此时年平均利润最大，最大值为8 万元.14.答案：1.3.6; 2.6; 3. ()1.23y t t =≥解析：1.由图象可知,当3t ≤时,电话费都是3.6元.2.由题中图象可知,当5t =时,6y =,需付电话费6元3.当3t ≥时, y 关于t 的图象是一条直线, 且经过()3,3.6和()5,6两点, 故设函数关系式为y kt b =+,解得 1.2,0.k b ==故电话费y (元)与通话时间t (分钟)之间的函数关系式为()1.23.y t t =≥15.答案：(1)218,16, 30,612,254,1216,x x x y x x x x x +≤≤∈⎧⎪=<<∈⎨⎪-+≤≤∈⎩Z Z Z .(2)设每件销售利润为w 元，当16x ≤≤时，()22180.125812w y Z x x =-=++--21148x =+， 当6x =时，w 取得最大值18.5；当612x <<时，()2300.125812w y Z x =-=+--()20.125818x =-+， 当8x =时，w 取得最大值18；当1216x ≤≤时，()()222540.1258120.1251618w y Z x x x =-=-++--=-+， 当16x =时，w 取得最大值18.综上所述，在第6周时出售，每件销售利润最大，最大销售利润为18.5元. 解析：。
人教B版数学高一版必修1同步训练2.1.2函数的表示方法
2.1.2 函数的表示方法5分钟训练1.一个面积为100 cm2的等腰梯形，上底长为x cm，下底长为上底长的3倍，则把它的高y 表示成x的函数为( )A.y=50x(x＞0)B.y=100x(x＞0)C.y=x50(x＞0) D.y=x100(x＞0)答案：C解析：由23xx+·y=100,得2xy=100.∴y=x50(x＞0).2.小明离家去学校,由于怕迟到,一开始就跑步,等跑累了再步行走完余下的路程(跑步的速度与步行的速度均为定值).若以纵轴表示离家的路程,路程用d表示;横轴表示出发后的时间,时间用t表示,则下列图形中能反映小明运动规律的是( )答案：D解析：因为跑步的速度与步行的速度均为定值,且前者大,故选D.3.设一个函数的解析式为f(x)=2x+1,它的值域为{-1,2,3},则该函数的定义域为_____________.答案：{-1,21,1}解析：f(x)=2x+1是单调函数,令2x+1=-1,2,3,得x=-1,21,1.4.已知函数f(x)=⎪⎩⎪⎨⎧<=>+,0,0,0,,0.1xxxxπ则f［f(-1)］的值是______________.答案：π解析：分段函数是一个函数而不是几个函数，求函数值时,首要的是确定自变量的数值属于哪一个区间段，从而选取相应的对应法则.f(-1)=0,f(0)=π，由此可得结果.10分钟训练1.等腰三角形的周长是20,底边长y是一腰长x的函数,则y=f(x)等于( )A.20-2x(0<x≤10)B.20-2x(0<x<10)C.20-2x(5≤x≤10)D.20-2x(5<x<10) 答案：D解析：函数的定义域易写成⎩⎨⎧>->,0220,0x x 得0<x<10,而错选B.因由构成三角形的条件可知2x>20-2x,得x>5.所以函数的定义域为{x|5<x<10}.2.如图,在△ABC 中,底BC=a,高AD=h,MNPQ 为一边在底边上的内接矩形,设MN=x,矩形周长为y,把y 表示成x 的函数应为( )A.y=2(a+x x h a -)(0<x<h)B.y=(a+x x h a-)(x>0) C.y=2(a+x x h a -)(0<x≤2h ) D.y=(a+x x ha-)(0<x<h)答案：A解析：由平行线分线段成比例定理,得ADMNAD BC MQ -=, 即h x h a MQ -=.解得MQ=hx h a )(-. ∴y=2［x+h x h a )(-］=2(a+x x ha-).由MQ>0,得x<h.又∵x>0,∴0<x<h.3.设M=｛x ｜-2≤x≤2｝，N=｛y ｜0≤y≤2｝，如图给出4个图形，其中能表示以集合M 为定义域，N 为值域的函数关系的是( )答案：B解析：要构成函数必须是定义域中的每一个自变量值对应唯一一个函数值.A 中，当0＜x≤2时，N 中没有元素与x 对应，不符合函数概念.C 中每个x 值有两个y 值与之对应，也不符.D 中的对应是映射，值域与要求不符.故选B.4.已知函数f(x)的图象如右图所示,则f(x)的函数解析式是____________.答案：f(x)=⎩⎨⎧≤≤-<≤-+10,1,1xxxx解析：f(x)的图象由两条线段组成，∴该函数是一分段函数,特别要注意端点值是否可以取到.5.已知函数f(x)=⎪⎪⎩⎪⎪⎨⎧<-=>.0,1,0,1,0,2xxxxx(1)画出函数的图象;(2)求f(1),f(-1),f［f(-1)］的值.解：(1)分别作出f(x)在x>0,x=0,x<0段上的图象,如图,作法略.(2)f(1)=12=1,f(-1)=11--=1,f［f(-1)］=f(1)=1.6.某人驱车以52千米/时的速度从A地驶往260千米远处的B地,到达B地并停留1.5小时后,再以65千米/时的速度返回A地.试将此人驱车走过的路程s表示为时间t的函数.解：从A地到B地,路上的时间为52260=5(小时);从B地回到A地,路上的时间为65260=4(小时).所以走过的路程s(千米)与t(小时)的关系为⎪⎩⎪⎨⎧≤<-+≤≤<≤=.5.105.6),5.6(65260,5.65,260,5,52ttttts30分钟训练1.如图所示的图形中，不可能是函数y=f(x)的图象的是( )答案：D解析：因为D中的一个变量x对应两个y值，所以它不表示函数.2.由于水污染日益严重，水资源变得日益短缺.为了节约用水，某市政府拟自2007年始对居民自来水收费标准调整如下：每户每月用水不超过4吨时，每吨6元；当用水超过4吨时，超过部分每吨增收3元.则某户居民所交水费y元与该月此户居民所用水量x吨之间的函数关系式为( )A.y=6xB.y=⎩⎨⎧>-≤≤4,12940,6xxxxC.y=⎩⎨⎧>+≤≤4,12640,9xxxxD.y=9x-12答案：B解析：当用水量0≤x≤4时，水费y=6x；当用水量x>4时，水费y=24+9×（x-4）=9x-12.故选B.3.已知函数f（x）=32+xcx（x≠23-），满足f［f（x）］=x，则c的值是( )A.3B.-3C.3或-3D.不存在答案：B解析：f［f（x）］=⇒=++•+•xxcxxcxc332232x（2c+6）=c2-9对任何x（x≠23-）成立，所以2c+6=c2-9=0，即c=-3.而323+-xx≠23-，故所求c=-3.4.(创新题)某地2006年的降雨量p(x)与时间x的图象如图所示,定义“落量差函数”q(x)为时间段［0,x］内的最大降雨量与最小降雨量的差,则q(x)的图象可能是( )答案：B解析：观察p(x)与时间x 的图象可知,当x ∈［0,6］时,q(x)随x 增大而增大;当x ∈(6,9)时,q(x)是常函数;当x ∈［9,12］时,q(x)又随x 增大而增大.5.如图，有一块边长为a 的正方形铁皮，将其四个角各截去一个边长为x 的小正方形，然后折成一个无盖的盒子，写出体积V 以x 为自变量的函数式是______________，这个函数的定义域为__________.答案：V=x （a-2x ）2 ｛x|0＜x ＜2a ｝ 解析：据长方体的体积公式，易得V=x （a-2x ）2，其中0＜x ＜2a . 6.函数f(x)对于任意实数x 满足条件f(x+2)=)(1x f ,若f(1)=-5,则f ［f(5)］=___________. 答案：51-解析：由f(x+2)=)(1x f ,得f(x+4)=)2(1+x f =f(x),所以f(5)=f(1)=-5,则f ［f(5)］=f(-5)=f(-1)=)21(1+-f =51-.7.(探究题)设［x ］是大于或等于x 的最小正整数(即数x 的整数部分),例如［4.25］=4,［0,82］=0,那么函数y=［21+x ］-［2x］(x ∈N )的值域为_____________. 答案：{0,1}解析：当x=2k(k ∈N )时, y=]2[]21[x x -+=［k+21］-［k ］=k-k=0;当x=2k+1(k∈N)时,y=]2[]21[xx-+=［k+1］-［k+21］=(k+1)-k=1.所以所求函数的值域为{0,1}.8.如图,用长为l的铁丝弯成下部为矩形，上部为半圆形的框架，若矩形底边长为2x，求此框架围成的面积y与x的函数关系式，并指出其定义域.解：由题意知此框架是由一个矩形和一个半圆组成的图形，而矩形的长AB=2x，宽为a,则有2x+2a+πx=l，即a=xxl--22π，半圆的直径为2x，半径为x.所以y=)22(22xxlx--+ππ·2x=-(22π+)x2+lx.根据实际意义知xxl--22π＞0，又∵x＞0，∴0＜x＜π+21，即函数y=-(2+2π)x2+lx的定义域是{x|0＜x＜π+21}.9.动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A.设x表示P 点的行程，f（x）表示PA的长，g（x）表示△ABP的面积，求f（x）和g（x），并作出g （x）的简图.解：(1)如图，当P在AB上运动时，PA=x；当P点在BC上运动时，由Rt△ABP可得PA=2)1(1-+x；当P点在CD上运动时，由Rt△ADP易得PA=2)3(1x-+；当P点在DA上运动时，PA=4-x.故f（x）的表达式为f（x）=⎪⎪⎩⎪⎪⎨⎧≤<-≤<+-≤<+-≤≤.43,4,32,106,21,22,10,22xxxxxxxxxx（2）由于P点在折线ABCD上的位置不同，△ABP的形状各有特征，计算它们的面积也有不同的方法，因此同样必须对P点的位置进行分类求解.如图，当P在线段AB上时，△ABP的面积S=0；当P在BC上时，即1＜x≤2时，S△ABP=21AB·BP=21（x-1）；当P在CD上时，即2＜x≤3时，S△ABP=21·1·1=21；当P在DA上，即3＜x≤4时，S△ABP=21（4-x）.故g （x ）=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤<-≤<≤<-≤≤.43),4(21,32,21,21),1(21,10,0x x x x x x g(x)的简图如下图.。
新教材人教B版高中数学必修第一册练习-函数及其表示方法答案含解析
3.1.1函数及其表示方法第三章函数3.1 函数的概念与性质3.1.1函数及其表示方法课时1 函数的概念考点1函数的概念1.下列说法正确的是()。
A.函数值域中每一个数在定义域中一定只有一个数与之对应B.函数的定义域和值域可以是空集C.函数的定义域和值域一定是数集D.函数的定义域和值域确定后,函数的对应法则也就确定了答案：C解析：由函数的定义可知,函数的定义域和值域为非空的数集。
2.下列四个图形中,不是以x为自变量的函数的图像是()。
图3-1-1-1-1答案：C解析：根据函数定义,知对自变量x的任意一个值,都有唯一确定的实数(函数值)与之对应。
显然选项A,B,D 满足函数的定义,而选项C不满足。
故选C。
3.(2018·河北衡水中学高一月考)下列四组函数中,表示同一函数的是()。
3 B.y=1与y=x0A.y=√x2与y=√x3C.y=2x+1与y=2t+1D.y=x与y=(√x)2答案：C3=x,它们的对应关系不同,不是同一函数;对于B,y=1(x∈R),y=x0=1(x≠0),它们的解析：对于A,y=√x2=|x|,y=√x3定义域不同,不是同一函数;对于C,y=2x+1与y=2t+1,它们的定义域相同,对应关系也相同,是同一函数;对于D,y=x(x∈R),y=(√x)2=x(x≥0),它们的定义域不同,不是同一函数。
【易错点拨】考查同一函数的问题,注意把握同一函数的定义,必须保证是三要素完全相同,才是同一函数。
4.(2019·西安高一检测)下列式子中不能表示函数y=f(x)的是()。
A.x=y2B.y=x+1C.x+y=0D.y=x2答案：A5.给出下列两个集合间的对应关系:①A={-1,0,1},B={-1,0,1},f:A中的数的平方;②A={0,1},B={-1,0,1},f:A中的数的开方;③A=Z,B=Q,f:A中的数的倒数;④A=R,B={正实数},f:A中的数取绝对值;⑤A={1,2,3,4},B={2,4,6,8},f:A中的数的2倍。
人教B版高中数学必修一函数的单调性同步练习名师解析
第2章 2.1.3 1．设f (x )，g (x )都是单调函数，有如下四个命题，其中正确的命题是( )①若f (x )单调递增，g (x )单调递增，则f (x )－g (x )单调递增；②若f (x )单调递增，g (x )单调递减，则f (x )－g (x )单调递增；③若f (x )单调递减，g (x )单调递增，则f (x )－g (x )单调递减；④若f (x )单调递减，g (x )单调递减，则f (x )－g (x )单调递减．A ．①③B ．①④C ．②③D ．②④答案：C解析：∵g (x )是单调增函数时，－g (x )是单调减函数，g (x )是单调减函数时，－g (x )是单调增函数，∴根据两个单调增函数相加是增函数，两个单调减函数相加是减函数这一原理，易知②③正确，故选C.2．设f (x )是定义在区间U 上的增函数，且f (x )>0，则下列函数中增函数的个数是( )①y ＝1－f (x ) ②y ＝1f (x )③y ＝f 2(x ) ④y ＝－f (x ) A ．1B ．2C ．3D ．4 答案：A解析：由于y ＝1－t ，y ＝1t，y ＝－t 均在(0，＋∞)上递减，而f (x )递增，且f (x )>0，∴函数y ＝1－f (x )、y ＝1f (x )、y ＝－f (x )均在U 上递减，又y ＝t 2在(0，＋∞)上递增，f 2(x )也递增．故选A.3．已知f (x )＝(3a －1)x ＋b 在(－∞，＋∞)上是增函数，则a 的取值范围是( )A.⎝⎛⎭⎫－∞，13 B.⎝⎛⎭⎫13，＋∞ C.⎝⎛⎦⎤－∞，13 D.⎣⎡⎭⎫13，＋∞ 答案：B解析：由3a －1>0，解得a >13，故选B. 4．已知f (x )在区间(－∞，＋∞)上是减函数，a ，b ∈R ，且a ＋b0，则下列选项正确的是( )A ．f (a )＋f (b )－[f (a )＋f (b )] B ．f (a )＋f (b )f (－a )＋f (－b ) C ．f (a )＋f (b )－[f (a )＋f (b )] D ．f (a )＋f (b ) f (－a )＋f (－b )答案：D解析：∵a ＋b0，∴a －b ，且b －a . 又∵f (x )在区间(－∞，＋∞)上是减函数． ∴f (a ) f (－b )，f (b )f (－a )， ∴f (a )＋f (b ) f (－a )＋f (－b )．故选D.5．已知函数f (x )＝4x 2－mx ＋1在(－∞，－2]上递减，在[－2，＋∞)上递增，则f (1)＝________.答案：21解析：由条件可知x ＝－2是f (x )的对称轴，∴－－m 2×4＝－2，解得m ＝－16. ∴f (x )＝4x 2＋16x ＋1，则f (1)＝21.6．若f (x )在R 上是增函数且f (x 1)>f (x 2)，则x 1、x 2大小关系为________．答案：x 1>x 2解析：由增函数的定义知若f (x 1)>f (x 2)，则x 1>x 2.7．指出f (x )＝2x 2＋4x 的单调区间，并对减区间情况给予证明．分析：对于基本初等函数可结合其图象，确定出单调区间．本题确定抛物线的开口方向和对称轴是关键．解：∵已知函数是开口向上的抛物线，且对称轴为x ＝－1.∴函数的单调增区间为[－1，＋∞)，单调减区间为(－∞，－1]．下面对减区间情况给予证明．设x 1<x 2－1，则f (x 1)－f (x 2)＝(2x 21＋4x 1)－(2x 22＋4x 2)＝2(x 21－x 22)＋4(x 1－x 2)＝2(x 1－x 2)(x 1＋x 2＋2)．∵x 1<x 2－1，∴x 1－x 2<0，x 1＋x 2＋2<0，∴f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)，∴f (x )在(－∞，－1]上是减函数．8．用定义证明：(1)函数f (x )＝kx ＋b (k <0，k ，b 为常数)在R 上是减函数；(2)函数g (x )＝k x(k <0，k 为常数)在(－∞，0)上是增函数． 证明：(1)设任意的x 1、x 2∈R ，且x 1<x 2，则f (x 1)－f (x 2)＝(kx 1＋b )－(kx 2＋b )＝k (x 1－x 2)，由x 1<x 2及k <0，得k (x 1－x 2)>0.∴f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)．∴f (x )＝kx ＋b (k <0)在R 上为减函数．(2)设x 1、x 2∈(－∞，0)，且x 1<x 2，则g (x 1)－g (x 2)＝k x 1－k x 2＝k (x 2－x 1)x 1x 2， ∵x 1<x 2<0，∴x 1x 2>0，x 2－x 1>0.又k <0，∴g (x 1)－g (x 2)<0，即g (x 1)<g (x 2)．∴g (x )＝k x(k <0)在(－∞，0)上为增函数．。
高中数学 第三章 函数 3.3 函数的应用(一)课后课时精练 新人教B版必修第一册-新人教B版高一第
3.3 函数的应用（一）A 级：“四基”巩固训练一、选择题1．某厂日产手套的总成本y (元)与日产量x (双)之间的关系为y ＝5x ＋40000.而手套出厂价格为每双10元，要使该厂不亏本至少日产手套( )A ．2000双B ．4000双C ．6000双D ．8000双答案 D解析 由题意得5x ＋40000≤10x ，解得x ≥8000，即日产手套至少8000双才不亏本． 2．某城市出租汽车的收费标准是：起步价为6元，行程不超过2千米者均按此价收费；行程超过2千米，超过部分按3元/千米收费(不足1千米按1千米计价)；另外，遇到堵车或等候时，汽车虽没有行驶，但仍按6分钟折算1千米计算(不足1千米按1千米计价)．陈先生坐了趟这种出租车，车费24元，车上仪表显示等候时间为11分30秒，那么陈先生此趟行程的取值X 围是( )A ．[5,6)B ．(5,6]C ．[6,7)D ．(6,7]答案 B解析 若按x 千米(x ∈N )计价，则6＋(x －2)×3＋2×3＝24，得x ＝6.故实际行程应属于区间(5,6]．3．某公司在甲、乙两地同时销售一种品牌车，利润(单位：万元)分别为L 1＝－x 2＋21x 和L 2＝2x ，其中x 为销售量(单位：辆)．若该公司在这两地共销售15辆车，则能获得的最大利润为( )A ．120.25万元B ．120万元C ．90.25万元D ．132万元答案 B解析 设在甲地销售了x 辆车，则在乙地销售了(15－x )辆车，令总利润为L ，则L ＝－x 2＋21x ＋2(15－x )＝－x 2＋19x ＋30＝－⎝⎛⎭⎪⎫x －1922＋12014.因为x ∈N ，所以当x ＝9或10时，L 有最大值，L max ＝120(万元)．所以在甲地销售9辆车，在乙地销售6辆车或在甲地销售10辆车，在乙地销售5辆车时可获得最大利润120万元．4．利民工厂某产品的年产量在150吨至250吨之间，年生产的总成本y (万元)与年产量x (吨)之间的关系可近似地表示为y ＝x 210－30x ＋4000，则每吨的成本最低时的年产量为( )A ．240吨B ．200吨C ．180吨D ．160吨答案 B解析 依题意，得每吨的成本为y x ＝x 10＋4000x －30，则yx ≥2x10·4000x－30＝10，当且仅当x 10＝4000x，即x ＝200时取等号，因此，当每吨成本最低时，年产量为200吨．5．某工厂的大门是一抛物线形水泥建筑物，大门的地面宽度为8 m ，两侧距地面 3 m 高处各有一个壁灯，两壁灯之间的水平距离为6 m ，如图所示，则厂门的高约为(水泥建筑物厚度忽略不计，精确到0.1 m)( )A ．6.9 mB ．7.0 mC ．7.1 mD ．6.8 m答案 A解析 建立如图所示的坐标系，由题设条件知抛物线对应的函数解析式为y ＝ax 2.设A 点的坐标为(4，－h )，则C 点的坐标为(3，3－h )．将这两点的坐标分别代入y ＝ax 2，可得⎩⎪⎨⎪⎧－h ＝a ·42，3－h ＝a ·32，解得⎩⎪⎨⎪⎧a ＝－37，h ＝487≈6.9.所以厂门的高约为6.9 m.二、填空题6．某航空公司规定，乘机所携带行李的重量x (kg)与运费y (元)之间的函数关系如图所示，那么乘客免费可携带行李的最大重量为________．答案 19 kg解析 设y 与x 之间的函数关系式为y ＝kx ＋b ，将点(30,330)，(40,630)代入得y ＝30x －570，令y ＝0可得x ＝19.7．某商品进货单价为45元，若按50元一个销售，能卖出50个；若销售单价每涨1元，其销售量就减少2个，为了获得最大利润，此商品的最佳售价应为每个________元．答案 60解析 设涨价x 元时，获得的利润为y 元，有y ＝(5＋x )·(50－2x )＝－2x 2＋40x ＋250.∴当x ＝10时，y 取得最大值，此时售价为60元．8．为净化水质，向一个游泳池加入某种化学药品，加药后池水中该药品的浓度C (单位：mg·L －1)随时间t (单位：h)的变化关系为C ＝20tt 2＋4，则经过________ h 后池水中该药品的浓度达到最大．答案 2 解析C ＝20tt 2＋4＝20t ＋4t.因为t >0，所以t ＋4t≥2t ·4t＝4⎝ ⎛⎭⎪⎫当且仅当t ＝4t ，即t ＝2时等号成立.所以C ＝20t ＋4t≤204＝5，即当t ＝2时，C 取得最大值． 三、解答题9．某商店出售茶壶和茶杯，茶壶每个定价20元，茶杯每个定价5元，该店推出以下两种优惠方法：①买一个茶壶赠送一个茶杯； ②按总价的92%付款．某顾客需购茶壶4个，茶杯若干(不少于4个)，若需茶杯x 个，付款数为y 元，试分别建立两种优惠方法中y 与x 的函数解析式，并讨论顾客选择哪种优惠方法更合算．解 由优惠方法①，得函数解析式y 1＝20×4＋5(x －4)＝5x ＋60(x ≥4)． 由优惠方法②，得函数解析式y 2＝(5x ＋4×20)×92%＝4.6x ＋73.6. 所以y 1－y 2＝0.4x －13.6(x ≥4)． 当0.4x －13.6>0，即x >34时，y 1>y 2， 则优惠方法②合算；当0.4x －13.6＝0，即x ＝34时，y 1＝y 2， 则两种优惠方法付款数一样；当0.4x －13.6<0，即4≤x <34时，y 1<y 2， 则优惠方法①合算．10．某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆，租出的车每月每辆需维护费150元，未租出的车每月每辆需维护费50元．(1)当每辆车的月租金定为3600元时，能租出多少辆车？(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益为多少？ 解 (1)当每辆车的月租金为3600元时，未租出的车辆数为3600－300050＝12，所以这时租出了88辆．(2)设每辆车的月租金定为x 元，则公司月收益为f (x )＝⎝⎛⎭⎪⎫100－x －300050(x －150)－x －300050×50， 整理，得f (x )＝－x 250＋162x －21000＝－150(x －4050)2＋307050，所以当x ＝4050时，f (x )最大，最大值为f (4050)＝307050.即当每辆车的月租金定为4050元时，租赁公司的月收益最大，最大月收益为307050元．B 级：“四能”提升训练1．某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y (件)与销售单价x (元)之间的关系可近似看作一次函数y ＝kx ＋b (k ≠0)，函数图像如图所示．(1)根据图像，求一次函数y ＝kx ＋b (k ≠0)的表达式；(2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S 元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？解 (1)由图像知，当x ＝600时，y ＝400；当x ＝700时，y ＝300，代入y ＝kx ＋b (k ≠0)中，得⎩⎪⎨⎪⎧400＝600k ＋b ，300＝700k ＋b ，解得⎩⎪⎨⎪⎧k ＝－1，b ＝1000.所以y ＝－x ＋1000(500≤x ≤800)．(2)销售总价＝销售单价×销售量＝xy ， 成本总价＝成本单价×销售量＝500y ，代入求毛利润的公式，得S ＝xy －500y ＝x (－x ＋1000)－500(－x ＋1000)＝－x 2＋1500x －500000＝－(x －750)2＋62500(500≤x ≤800)．所以当销售单价定为750元时，可获得最大毛利润62500元，此时销售量为250件． 2．住宅小区为了使居民有一个优雅、舒适的生活环境，计划建一个八边形的休闲小区，它的主体造型的平面图是由两个相同的矩形ABCD 和EFGH 构成的面积为200 m 2的十字形区域．现计划在正方形MNPQ 上建一花坛，造价为4200元/m 2，在四个相同的矩形(如图中阴影部分)上铺花岗岩地坪，造价为210元/m 2，再在四个空角上铺草坪，造价为80元/m 2.(1)设总造价为S 元，AD 的边长为x m ，试建立S 关于x 的函数关系式； (2)计划至少要投入多少元，才能建造这个休闲小区？ 解 (1)设DQ ＝y ，则x 2＋4xy ＝200，y ＝200－x24x.S ＝4200x 2＋210×4xy ＋80×4×12y 2＝38000＋4000x 2＋400000x2(0<x <102)． (2)S ＝38000＋4000x 2＋400000x2≥38000＋216×108＝118000，当且仅当4000x 2＝400000，即x＝10时，S min＝118000，即计划至少要投入11.8万元才能建造这个休闲小区．x2。
人教B版数学高一版必修1同步练习2.4函数与方程第一小节
第二章 函数与方程2．4.1 函数的零点1．函数f(x)＝2x ＋7的零点为( )A ．7 B.72 C ．－72 D ．－72．方程x －1x＝0的一个实数解的存在区间为……( )A ．(0,1)B ．(0,2)C ．(1,2)D ．(－1,1)3．观察下面的四个函数图象，则在(－∞，0)内，函数y ＝f i (x)(i ＝1,2,3,4)有零点的是… ( )A ．①B ．①②C ．①②③D ．②④4．已知函数y ＝x 2＋ax ＋3有一个零点为2，则a 的值为________．5．若函数f(x)的图象是连续不间断的，根据下面的表格，可以断定f(x)的零点所在的区间为__________．(只填序号)1．已知函数f(x)＝2ax ＋4，若在区间[－2,1]上存在x 0，使f(x 0)＝0，则实数a 的取值范围是…( )A ．(－∞，－2]∪[1，＋∞)B ．[－1,2]C ．[－1,4]D ．[－2,1]2．函数f(x)＝x2－3x＋2在区间(1,2)内的函数值()A．大于等于0 B．小于等于0C．大于0 D．小于03．对于函数f(x)＝x2＋mx＋n，若f(a)>0，f(b)>0，则函数f(x)在区间(a，b)内() A．一定有零点B．一定没有零点C．可能有两个零点D．至多有一个零点4．设函数，又g(x)＝f(x)－1，则函数g(x)的零点是________．5．二次函数y＝ax2x －3 －2 －1 0 1 2 3 4y 6 0 －4 －6 －6 －4 0 6 则不等式ax2＋bx＋c>0的解集是________．6．求证：方程5x2－7x－1＝0的根一个在(－1,0)上，另一个在(1,2)上．7．若函数f(x)＝ax2－x－1仅有一个零点，求实数a的取值范围．1．已知f(x)＝(x－a)(x－b)－2，并且α，β是方程f(x)＝0的两根，则实数a，b，α，β的大小关系可能是()A．α<a<b<βB．a<α<β<bC．a<α<b<βD．α<a<β<b2．若函数f(x)＝ax ＋b 有一个零点是2，那么函数g(x)＝bx 2－ax 的零点是( )A ．0,2B ．0，12C ．0，－12D ．2，－123．二次函数f(x)＝x 2＋px ＋q 的零点为1和m ，且－1<m<0，那么p 、q 满足的条件为( ) A ．p>0且q<0 B ．p>0且q>0 C ．p<0且q>0 D ．p<0且q<0 4．若函数y ＝f(x)是偶函数，定义域为{x ∈R |x ≠0}，且f(x)在(0，＋∞)上是减函数，f(2)＝0，则函数f(x)的零点有( )A ．唯一一个B ．两个C ．至少两个D ．无法判断5．函数f(x)＝ax 2＋2ax ＋m(a ≠0)的一个零点为1，则它的另一个零点为________． 6．函数f(x)＝x 2＋2(a ＋3)x ＋2a －9的两个零点中，一个大于3，一个小于－3，则a 的取值范围为________．7．函数y ＝7x 2－(k ＋13)x ＋3k －2的图象与x 轴的两个交点分别在(0,1)和(1,2)内，则k 的取值范围为________．8．试找出一个长度为1的区间，在这个区间上函数y ＝x －13x ＋2至少有一个零点．9．求函数y ＝x 3－4x 的零点，并画出它的图象．10．函数y ＝－2x 2＋x ＋3的自变量x 在什么范围内取值时，函数值大于0，小于0，等于0?答案与解析课前预习1．C 令f(x)＝2x ＋7＝0，解得x ＝－72.2．B 由x －1x＝0，得x ＝±1，显然1∈(0,2)．3．B 在(－∞，0)内，函数f 1(x)、f 2(x)的图象与x 轴有交点．4．－72 由题意x ＝2为方程x 2＋ax ＋3＝0的根，即4＋2a ＋3＝0，∴a ＝－72.5．③④⑤ 由表可知：f(2)·f(3)<0，f(3)·f(4)<0，f(4)·f(5)<0，且f(x)的图象是连续不间断的，∴f(x)在[2,3]，[3,4]，[4,5]上有零点．课堂巩固1．A 依题意f(－2)·f(1)≤0⇔(－4a ＋4)(2a ＋4)≤0，解得a ≤－2或a ≥1.2．D 令f(x)＝0，解得x 1＝1，x 2＝2，∴在(1,2)内函数值同号，又二次函数图象开口向上，∴f(x)在区间(1,2)内的函数值小于0. 3．C 如图所示．4．1，－5 当x ≥0时，g(x)＝f(x)－1＝2x －2，令g(x)＝0，得x ＝1；当x<0时g(x)＝x 2－4－1＝x 2－5，令g(x)＝0，得x ＝±5(正值舍去)，∴g(x)的零点为1和－ 5.5．{x|x<－2或x>3} 由表可知f(－2)＝f(3)＝0，且当x ∈(－2,3)时，y<0，∴当x ∈(－∞，－2)∪(3，＋∞)时ax 2＋bx ＋c>0.点评：只要利用表中数据，结合函数零点的性质，无须求出函数的解析式． 6．解：设f(x)＝5x 2－7x －1，则f(－1)·f(0)＝11×(－1)＝－11<0，f(1)·f(2)＝(－3)·5＝－15<0.且二次函数f(x)＝5x 2－7x －1是连续的．∴f(x)在(－1,0)和(1,2)上各有零点．即方程5x 2－7x －1＝0的根一个在(－1,0)上，另一个在(1,2)上．点评：判断f(x)是否在(x 1，x 2)上存在零点，除验算f(x 1)·f(x 2)<0是否成立外，还须考察函数在(x 1，x 2)上是否连续，若要判断根的个数，还须结合函数的单调性．7．解：(1)若a ＝0，则f(x)＝－x －1为一次函数，易知函数仅有一个零点；(2)若a ≠0，则函数f(x)为二次函数，若其只有一个零点，则方程ax 2－x －1＝0只有一个实根，故判别式Δ＝1＋4a ＝0，得a ＝－14.综上，当a ＝0或－14时函数仅有一个零点．点评：判断函数零点的个数就是判断相应方程的实根的个数．课后检测1．A 由题意，f(a)＝f(b)＝－2，f(α)＝f(β)＝0，且f(x)的图象开口向上，故a ，b 必在α，β之间．2．C 函数f(x)＝ax ＋b 的零点是2，∴2a ＋b ＝0，得ba＝－2，而g(x)＝bx 2－ax ＝bx(x －a b )＝bx(x ＋12)，∴g(x)的零点为0和－12.3．D ∵f(1)＝0，∴p ＋q ＋1＝0. 又f(0)<0，得q<0；f(－1)>0， 得1－p ＋q>0. 又q ＝－p －1，∴－2p>0，即p<0.4．B 由f(x)为偶函数且f(2)＝0得f(－2)＝0，画出f(x)的大致图象，可知f(x)只有两个零点．5．－3 由题意f(1)＝a ＋2a ＋m ＝0，即m ＝－3a ， ∴f(x)＝ax 2＋2ax －3a ＝a(x 2＋2x －3)＝a(x ＋3)(x －1)． 令f(x)＝0，易得x ＝1或x ＝－3.6．(－92，－94) 由题意，函数f(x)的图象为开口向上的抛物线，与x 轴的交点有两个：一个在(3,0)右侧，一个在(－3,0)左侧．∴⎩⎪⎨⎪⎧f(－3)<0，f(3)<0，解得a ∈(－92，－94)．7．(23，4) 开口向上的抛物线与x 轴的交点在(0,1)，(1,2)内，则⎩⎪⎨⎪⎧f(0)>0，f(1)<0，f(2)>0，解得k ∈(23，4)．8．解：函数f(x)＝x －13x ＋2的定义域为(－∞，－23)∪(－23，＋∞)．取区间[12，32]，则易证：f(12)＝12－132＋2＝－17<0，f(32)＝113>0，∴f(12)·f(32)<0，∴在区间[12，32]内函数f(x)至少有一个零点．∴区间[12，32]符合条件．9．解：∵x 3－4x ＝x(x 2－4)＝x(x －2)(x ＋2)，∴函数y ＝x 3－4x 的零点为0，－2,2，这三个零点把x 轴分成4个区间：(－∞，－2]，(－2,0]，(0,2]，(2，＋∞)，在这四个区间内，取x 的一些值(包括零点)．在直角坐标系中描点作图，图象如图所示．10．解：由－2x 2＋x ＋3＝0，得x 1＝－1，x 2＝32，所以函数的零点是－1和32，亦即当自变量x 取－1和32时函数值等于0.函数的两个零点－1和32将x 轴分成3个区间：(－∞，－1)，(－1，32)，(32，＋∞)，在区间(－1，32)内取特殊值x ＝0，得其函数值f(0)＝3>0，依函数零点的性质，知当x ∈(－1，32)时有f(x)>0；当x ∈(－∞，－1)和x ∈(32，＋∞)都有f(x)<0. 因此，当自变量x ∈(－1，32)时函数值大于0；当x ∈(－∞，－1)∪(32，＋∞)时函数值小于0；当x ＝－1和32时，函数值等于0.。
高中数学第二章函数2.1函数(1)同步练习新人教B版必修1(2021年整理)
高中数学第二章函数2.1 函数（1）同步练习新人教B版必修1 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第二章函数2.1 函数（1）同步练习新人教B版必修1）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第二章函数2.1 函数（1）同步练习新人教B版必修1的全部内容。
2．1.1 函数1．下列说法中，不正确的是( ）A．函数值域中每一个数都有定义域中的一个数与之对应B．函数的定义域和值域一定是无限集C．定义域和对应关系确定后，函数的值域也就确定了D．若函数的定义域中只有一个元素，则值域中也只有一个元素2．下列说法中，正确的个数是（）①定义域不同,两个函数就不同②对应法则不同,两个函数就不同③定义域和值域都分别相同的函数,一定是同一函数A．1 B．2 C．3 D．03．下列集合A到集合B的对应法则f是映射的是（）A．A＝｛－2，0,2}，B＝｛－4,0,4}，f：A中数的平方B．A＝{0，1｝，B＝{－1，0,1｝，f：A中数的平方根C．A＝Z，B＝Q，f：A中数的倒数D．A＝R，B＝｛x｜x〉0}，f：A中数的平方4．函数y＝错误!－错误!＋错误!的定义域为__________．5．把下列集合用区间表达出来:（1）｛x｜x≠2,且x≠1｝；(2)｛x|错误!≤x≤错误!｝；（3)｛x|x≥3或x≤－3};(4)｛x｜－2≤x≤2，且x≠1｝．1．下列四组函数中，表示同一函数的是( ）A．f（x)＝x，g（x）＝(错误!)2B．f（x）＝x，g（x）＝错误!C．f（x)＝x＋2,g（x）＝错误!D．f（x)＝x，g(x)＝3x32．下列四个命题正确的有（)①函数是定义域到值域的对应关系②f（x)＝错误!＋错误!是函数③f（x)＝5，因这个函数的值不随x的变化而变化，所以f（t2＋1)＝5④y＝2x(x∈N）的图象是一条直线A．1个 B．2个 C．3个 D．4个3．下列对应是集合A到集合B的一一映射的是…（)A．A＝B＝R,f:x→y＝错误!,x∈A，y∈BB．A＝B＝R,f:x→y＝x2，x∈A，y∈BC．A＝B＝R，f：x→y＝错误!,x∈A，y∈BD．A＝B＝R，f：x→y＝x3，x∈A，y∈B4．已知f(x）＝x2＋ax＋b，满足f（1)＝f(2）＝0，则f（－1)＝__________。
人教B版高中数学必修1同步章节训练题及答案全册汇编
人B版高中数学必修1同步习题目录1.1 集合与集合的表示方法1.2-集合与集合的运算第1章《集合》测试2.1.1《函数》测试题(1)(新人教B必修1)2.1.2《函数表示法》测试题(2)(新人教B必修1)2.1.3《函数的单调性》测试题(新人教B必修1)2.1.4《函数的奇偶性》测试题(新人教B必修1)2.2.1《一次函数的性质与图象》测试题2.2.2《二次函数综合题》测试2.2.3《待定系数法》同步测试2.3《函数的应用(Ⅰ)》同步测试2.4.1《函数的零点》同步测试2.4.2《求函数零点近似解的一种计算方法?二分法》同步测试第2章《函数》测试3.1.1《实数指数幂及其运算》同步测试3.1.2《指数函数》同步测试3.2.1《对数及其运算》同步测试3.2.2《对数函数》同步测试3.3《幂函数》同步测试3.4《函数的应用》测试第3章《基本初等函数1》测试1.1 集合与集合的表示方法1.下面四个命题正确的是 ( )A.10以内的质数集合是0,3,5,7B.“个子较高的人”不能构成集合C.方程的解集是1,1D.1是集合N中最小的数2.下面的结论正确的是 ( )A.若,则B.若,则自然数C.的解集是-1,1D.所有的正偶数组成的集合是有限集3.已知集合S中的三个元素可构成ABC的三条边长,那么ABC一定不是 ( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形4.下面四个关系式中,正确的是A.∈0B.aaC.a∈a,bD.a∈a,b5.下列语句:(1)0与0表示同一个集合;(2)由1,2,3组成的集合可表示为1,2,3或3,2,1;(3)方程(x-1)2x-220的所有解的集合可表示为1,1,2;(4)不等式的解集是有限集,正确的是 ()A.只有(1)和(4)B.只有(2)和(3)C.只有(2)D.以上语句都不对6.下列六个关系式①0 ②0 ③④ 0 ⑤0 ⑥其中正确的个数( )A.3B.4C.5D.67.若方程的解集中有且只有一个元素,则的取值集合是( )A.{1}B.{-1}C.{0,1}D.{-1,0,1}8.A面积为1的矩形,B{面积为1的正三角形},则( )A. A,B都是有限集B. A,B都是无限集C. A是有限集,B是无限集D. A是无限集,B是有限集9.若,则实数的值为( )A.-1B.0C.-1或0D.-1或0或-210.若方程和的解为元素的集合是M,则M中元素的个数( )A.1B.2C.3D.411.如果方程的解集是M, 方程的解集是N, 3∈M且3∈N,那么等于14B. 2 C. 11D. 712.方程组解集为 ( )A.0B.1C.1,0 D.(0,1)13.用数对的集合表示方程的一切正整数解为 .14.实数集中的元素应该满足的条件是 .15.已知数集 Aa+2,a+12,a2+3a+3, 且 1∈A, 求实数 a 的值1.1 集合与集合的表示方法1.1.1 集合的概念题号 1 2 3 4 5 6 7 8 9 10 11 12答案 B C D D C B D D C C A D13. ;1415.解: 若a+daq 解之得q1 a+2daq2当q1时,有aaqaq2与元素的互异性矛盾。
2021-2022年高中数学 2.1.1《函数》 同步练习一 新人教B版必修1
2021-2022年高中数学 2.1.1《函数》 同步练习一 新人教B 版必修1注意:本试卷共分两部分：第I 卷和第II 卷.其中第I 卷为客观题，共16小题，满分76分；第II 卷为主观题，共6小题，满分74分.试卷总分为150分，答题时间为120分钟.注意：本部分共16小题，其中1—12题每题5分，13—16题每题4分，共76分一、选择题（本题共12小题，每题5分，共60分）1、下列表述正确的是：（ D ） Ａ、 Ｂ、 Ｃ、 Ｄ、2、下列四个集合中，表示空集的是：（D ）Ａ、 Ｂ、},,),{(22R y R x x y y x ∈∈-= Ｃ、 Ｄ、},0232{2N x x x x ∈=-+ 3、函数在R 上是减函数，则（ D ） Ａ、 Ｂ、 Ｃ、Ｄ、4、已知为R 上的减函数，则满足的实数的取值范围是：（ D ） Ａ、Ｂ、 Ｃ、Ｄ、5、已知全集，则正确表示集合和 关系的韦恩图是（B ）6、设，，，则= ( B )A 、 B 、 C 、 D 、7、集合,,若,则的值为( D )A 、0B 、1C 、2D 、48、已知全集U ={1，2，3，4，5，6，7，8}，M ={1，3，5，7}，N ={5，6，7}， 则( C ）A 、{5，7}B 、{2，4}C 、{2.4.8}D 、{1，3，5，6，7} 9、设，则=(B) Ａ、 Ｂ、 Ｃ、Ｄ、10、函数的图像与直线的交点共有（ C ）Ａ、 个 Ｂ、 个 Ｃ、个或个 Ｄ、可能多于个 11、函数的图像关于（ C ）Ａ、轴对称 Ｂ、直线对称 Ｃ、坐标原点对称 Ｄ、直线对称12、若函数，则函数在其定义域上是（B ） Ａ、单调递减的偶函数Ｂ、单调递减的奇函数Ｃ、单调递增的偶函数 Ｄ、单调递增的奇函数 二、填空题（本小题共4题，共16分）13、某班共30人，其中15人喜爱篮球运动，10人喜爱兵乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为__ (12) 14、已知函数，则的解析式为：__ 15、设函数为偶函数，则__ （-1）16、设A 是整数集的一个非空子集，对于，如果且，那么是A 的一个“孤立元”，给定，由S的3个元素构成的所有集合中，不含“孤立元”的集合共有（6） 个13、 ； 14、 ；15、__ ； 16、 ；第II 卷（主观题部分）注意：本部分共6个小题，其中17—21小题每题12分，22题14分17、（12分）用列举法表示下列集合<1>},,3),{(N y N x y x y x ∈∈=+；<2>},2,1),{(2Z x x x y y x ∈≤-=解：<1>{(0,3),(1，2),(2，1),(3，0)} <2>{(-2,3),(-1,0),(0,-1),(1,0),(2,3)}18、（12分）<1>写出所有满足的集合<2>已知集合,其中集合至少有一个奇数，求满足这样的条件的集合有几个，请你一一写出.解：<1>{1，2，3} {1,2,4}, {1,2,3,4}<2>{1} {3} {0,1} {1,2} {1,3} {0,3} {2,3} {0,1,2} {1,2,3} {2,3,0} {0,1,3}{0,1,2,3}19、（12分）设集合2{},35{-<=≤≤-=x x B x x A 或，求 解：20、(12分)已知函数，求:<1>函数的定义域；<2>的值解：<1>定义域为；<2>21、（12分）已知为二次函数，若，且，求的表达式.解：设二次函数为)0()(2≠++=a c bx ax x f ，，1)1()2++=+++⇒x b b a x b a （112=++=+⇒b a b b a ，所以二次函数的解析式为22、（14分）已知函数在上是减函数，是比较与的大小.解：由题意可得：075.0)5.0122>+-=+-a a a （，又函数在上是减函数，而由75.075.0)5.0122≥+-=+-a a a （，所以24583 6007 怇33067 812B 脫36916 9034 逴Yi23606 5C36 尶28517 6F65 潥36470 8E76 蹶3423785BD 薽29495 7337 猷20118 4E96 亖•)20034 4E42 乂32620 7F6C 罬。
人教b版数学高一必修1同步练习-2.3_函数的应用(ⅰ)
1．已知直角梯形OABC中，AB∥OC，BC⊥OC，AB＝1，OC＝BC＝2，直线x＝t截这个梯形位于此直线左方的图形的面积(如图中阴影部分)为y，则函数y＝f(t)的大致图象为()．2．一个人以6 m/s的速度去追停在交通灯前的汽车，当他距汽车25 m时，交通灯由红变绿，汽车以1 m/s2的加速度匀加速开走，则()．A．人可在7 s内追上汽车B．人可在10 s内追上汽车C．人追不上汽车，其间最近距离为10 mD．人追不上汽车，其间最近距离为7 m3．为了稳定市场，确保农民增收，某农产品的市场收购价格a与其前三个月的市场收购价格有关，且使a与其前三个月的市场收购价格之差的平方和最小．若下表列出的是该产品前6个月的市场收购价格：则7月份该产品的市场收购价格应为()．A．69元B．70元C．71元D．72元4．北京电视台每星期六播出《东芝动物乐园》，在这个节目中曾经有这样一个抢答题：小蜥蜴体长15 c m，体重15 g，问：当小蜥蜴长到体长为20 c m时，它的体重大约是()．A．20 g B．25 gC．35 g D．40 g5．某商人购货，进价已按原价a扣去25%，他希望对货物订一新价，以便按新价让利20%销售后仍可获得售价25%的纯利，则此商人经营这种货物的件数x与按新价让利总额y之间的函数关系是________．6．如图，大海中的两艘船，甲船在A处，乙船在A处正东50 km的B处，现在甲船从A处以20 km/h 的速度向正北方向航行，同时乙船从B处以10 km/h的速度向正西方向航行，则经过______ h后，两船相距最近．7．某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程．下图的二次函数图象(部分)刻画了该公司年初以来累积利润S (万元)与时间t (月)之间的函数关系式．(1)根据图形求累积利润S (万元)与时间t (月)之间的函数关系式； (2)求截止到几月末公司累积利润可达到30万元； (3)求第8个月公司所获利润是多少万元？8．某工厂生产某产品所需要的费用为P 元，而卖出x 吨的价格为每吨Q 元．已知 211000510P x x =++，xQ a b=+.若生产出的产品能够全部卖掉，且在产量为150吨时利润最大，此时每吨价格为40元，求实数a 、b 的值．9.某私营企业老板对企业有突出贡献的某员工加薪，有两种加薪方案供员工选择：方案一：每年年末加薪1 000元；方案二：每半年加薪300元．[注：每年年末加薪a 元，即是原薪金为m 元，则加薪第一年总薪金应为m ＋a 元，第二年薪金应为(m ＋a )＋a 元等等，依次类推](1)设该员工在此私企再工作2年，试问该员工根据自己需继续工作的年限选择哪种加薪方案较实惠，请说明理由；(2)设该员工在此私企继续工作x 年，试问该员工根据自己需继续工作的年限选择哪种加薪方案较实惠，请说明理由．〔注：m ＋(m ＋a )＋(m ＋2a )＋(m ＋3a )＋…＋[m ＋(x －1)a ]＝mx ＋(1)2x x -a 〕参考答案1. 答案：C解析：当0≤t ≤1时，21()22f t t t t =⋅=； 当1＜t ≤2时，1()12(1)2212f t t t =⨯⨯+-⨯=-， ∴当t ∈[0,1]时的图象是抛物线的一段，当t ∈[1,2]时的图象是一条线段． 2. 答案：D 解析：如图，设汽车在C 点开始运动，此时人到达A 点，AC ＝25 m ，经t s 后，汽车到达D 点，有路程212CD at =，此时人追到B 点，有路程AB ＝v t ，依题意，汽车与人的距离222111252567(6)7222S AC CD AB at vt t t t =+-=+-=+-=+-≥.所以，人不能追上汽车，他与汽车最近的距离是在汽车开动6 s 后的瞬间，两者最近距离为7 m ，故选D.3. 答案： C解析：f (a )＝(a －71)2＋(a －72)2＋(a －70)2＝3(a －71)2＋2，当a ＝71时，f (a )最小． 4. 答案：C解析：假设小蜥蜴从15 c m 长到20 c m ，体形是相似的．这时蜥蜴的体重正比于它的体积，而体积与体长的立方成正比．记体长为l 的蜥蜴的体重为W 1，因此有3201532035.615W W =⋅≈，合理的答案为35 g ．故选C.5. 答案：4ay x =(x ∈N ＋) 解析：依题意，设新价为b ，则有b (1－20%)－a (1－25%)＝b (1－20%)·25%.化简得54b a =. ∴520%20%4y b x a x =⋅⋅=⋅⋅，即4ay x = (x ∈N ＋)． 6. 答案：1解析：设经过t h 后，甲船到达点M 处，乙船到达点N 处，此时AM ＝20t km ，AN ＝50－NB ＝50－10t ，这时两船相距y MN ====，∴当t ＝1时，y 取最小值，此时两船相距最近． 7. 解：(1)设S ＝at 2＋bt ＋c ，易知c ＝0，又42212222a b a b b a+=-⎧⎧=⎪⎪⇒⎨⎨-=⎪⎪=-⎩⎩∴212()2S t t t N =-∈)． (2)令2123010,6()2t t t t -=⇒==-舍去， 即截止到10月末公司累积利润达到30万元． (3) 2211(8)(7)828727 5.5()22S S ⎡⎤-=⨯-⨯-⨯-⨯=⎢⎥⎣⎦万元，即第八个月公司获利5.5万元． 8. 解：利润函数的解析式为21()(10005)10x y Qx P x a x x b =-=+-++211()(5)100010x a x b =-+--， 依题意，有5150112()10a b --=-，此时15040a b +=. 上述两式相减并整理，得b ＝－30.代入上述任何一式，有a ＝45.9. 解：(1)选择方案一，第1年加薪＝1 000，第2年加薪＝2 000，2年加薪总额＝3 000；选择方案二，第1年加薪＝900，第2年加薪＝2 100,2年加薪总额＝3 000，因此，该员工选择哪种加薪方案都一样．(2)选择方案一的加薪总额为2(1)100010005005002x x x x x ++⋅=+. 选择方案二的加薪总额为22(21)30023006003002x x x x x -⋅+⋅=+. ∵(500x 2＋500x )－(600x 2＋300x )＝－100x (x －2)，令－100x (x －2)＞0得0＜x ＜2，∴0＜x ＜2，即x ＝1(工作1年)时，选择方案一；x ＝2(工作2年)时，两种方案一样；x ＞2(工作3年及以上)时，选择方案二.。
2020新教材人教B版高中数学必修第一册精练：3.13.1.1函数及其表示方法第1课时课后课时精练含
课后课时精练A 级：“四基”巩固训练、选择题F 列函数中，与函数y =—%有相同定义域的是(A. f(x)_C . f(x)= XI 答案 A解析 函数的定义域为｛xX>0｝；函数f(x) = ¥的定义域为｛x|x>0｝；函X x 1数f(x) = x 的定义域为｛xx ^0, x € R ｝;函数f(x)= xi 的定义域为R ；函数f(x) =入 —x ―1的定义域为｛x|x > 1｝.所以与函数丫=丄有相同定义域的是f(x)= xx x x2. 下列各组函数中，表示同一函数的是()B. y = x 2 — 1 与 y = x - 1C. y =X °(X M 0)与 y = 1(X M 0)D. y = 2x + 1, x € Z 与 y = 2x — 1, x € Z 答案 C解析 A 中两函数的定义域不同；B , D 中两函数的对应关系不同；C 中定 义域与对应关系都相同.故选C.3. 函数y = ,x + 1的值域为( )A . [ — 1,+x )B . [0,+x )C . (— x, 0]D . ( — x,— 1]答案 B解析 由于.x + 1 >0,所以函数y =〔 x + 1的值域为[0,+ x ). 4.已知 f(x) = (x — 1)2+ 1,贝U f(x +B . f(x)= XD . f(x)=1)等于()2 2A. (x+ 2) + 1B. x + 12 2C. (x-2)2+ 1D. 4x2+ 1答案B解析••• f(x) = (x- 1)2+ 1,二f(x+ 1)= [(x+ 1) —1]2+ 1= x2+ 1.故选B.5. 若函数y=x2—3x—4的定义域为[0, m],值域为—晋，—4〔则m的取值范围是()7 25 1A. (0,4] B』—広，—41C. 2，3D. 2，+,丿答案C解析•••当x= 0 或x= 3 时，y= —4；当x=3时,y= —^5，- m€ ||，3〔故选C.二、填空题2 16. 设f(x)= 2x2+ 2, g(x)=后，则g[f(2)] = __________.1答案匕解析T f(2)= 2X 22+ 2= 10,1 1--g[ f(2)]= g(10)= 10+ 2=12.7. ____________________________________________________ 已知函数f(x)的定义域为[1,4]，则f(x+ 2)的定义域为___________________________ .答案[—1,2]解析由1w x+ 2w 4,得一1w x W 2.8. 若f$x != x3，则f(1) = _______ .答案8解析令*x= 1,则x = 2. A f(1)= 23= 8.三、解答题19. 已知函数f(x)= x+ 3+ ；,x+ 2(1) 求函数的定义域；(2) 求f(-3), ff 的值；⑶当a>0时，求f(a), f(a- 1)的值.x+ 3》0, 解(1)要使函数有意义，则x 应满足’/+ 2工0.解得—3w x< — 2 或x> — 2.即函数的定义域是［—3,—2)U (—2,+^)._____ 1(2)f(—3)= —3+ 3+ —3+ 2 =—1.(3) - a>0，…a, a —1 € [ —3, —2) U (—2，+ g). 即f(a), f(a—1)有意义.则f(a戶,a+ 3+ 土；f(a—1)= a—1 + 3+a—1 + 2 = a + 2 +a+ 1.x2+ ax 210. 求使函数y= x2 —x+〔的值恒小于2的a的取值范围.2 小x + ax—2 解令x2—+1<2,因为x2—x+ 1= x—2 2+ 3>0,所以x2 + ax—2<2x2 —2x+ 2,2即x —(a + 2)x+ 4>0对x€ R 恒成立.所以△二[—(a+ 2)] 2—4X 4<0,化简，得(a+ 6)(a —2)<0，解得-6<a<2.x + ax 2所以使函数y= ：2 —x+1的值恒小于2的a的取值范围是(—6,2).B级：“四能”提升训练2x1. 已知函数f(X)= —2.1 + x⑴求 f(2) + f 1 , f(3) + f 3 的值； ⑵求证：f(x) + f 1是定值；⑶求 f(2) + f 2 + f (3)+ f 3 +…+ f(2020)+ f 2020 的值•x 2解⑴：f")二右,2口 1 ⑴ 22b 丿•••f(2)+f 2 = 1, 1+亦 12⑴丄 3丿彳f(3) + f3 - 1 + 32+ 12- 1.1+3…2&2(2)证明：f(x) + f ；X 卜右+“' 1 + 定值.(3) 由(2),知 f(x) + f x 二 1, (1\••• f (2)+ f1 二 1, f(3)+ f 3 = 1， f(4) + f 1 二 1,(1 \ Af(2020)+ f 五二 1.⑴ ⑴ (1••• f(2)+ f 2 + f(3) + f 3 +…+ f(2020) + f 2020 二 2019.2. 已知函数f(x)= x 2- 16的定义域为集合 A,函数g(x) = x 2— 2x + a,x € [0,4] 的值域为集合B ,若A U B = R ,求实数a 的取值范围.解 由题意，函数f(x)= , x 2— 16的定义域需满足：X 2—16》0,解得x < — 4 或 x >4, 所以集合A= {x|x < - 4或x > 4}, 函数 g(x) = x 2- 2x + a = (x — 1)2+ a -1,x 2 1 x 2 +112_ l+?+ E = x ^ + 1 =x I J f(x)+专【是因为x€ [0,4],当x= 1时，函数g(x)取得最小值为a- 1; 当x= 4时，函数g(x)取得最大值为a+ 8;所以函数g(x)的值域为[a-1, a+ 8],所以集合B=[a—1, a+ 8],A L i f^rtA因为A U B= R，如图所示：a —1 w —4,所以需满足* 解得—4w a w- 3,a+8> 4,故实数a的取值范围为[—4,—3].。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
函数(一)
双基达标 (限时20分钟)
1．与函数y ＝－2x 3为同一函数的是 ( )．
A ．y ＝x －2x
B ．y ＝－x －2x
C ．－2x 3
D ．y ＝x
2
－2x
解析 函数y ＝－2x 3的定义域为(－∞，0]，则化简为
－2x 3＝－x
－2x .
答案 B
2．函数f (x )＝(x －12)0＋|x 2－1|
x ＋2的定义域为
( )．
A ．(－2，1
2)
B ．(－2，＋∞)
C ．(－2，12)∪(1
2，＋∞)
D ．(1
2，＋∞)
解析
由⎩⎨⎧
x －1
2≠0
x ＋2>0
，得⎩⎨
⎧
x ≠1
2，
x >－2，
即x >－2且x ≠1
2.
答案 C
3．函数f (x )＝x 2－1x 2＋1
，则f (2)
f (12)＝
( )．
A ．1
B ．－1 C.35
D ．－35
解析 ∵f (x )＝x 2
－1x 2＋1，∴f (12)＝1
22－1122＋1＝1－22
1＋2
2＝－3
5， f (2)＝22－122＋1＝35，∴f (2)f (12)＝－1.故选B.
答案 B
4．已知f (x )＝x 3－8，则f (x －2)＝________.
解析f(x)＝x3－8，∴f(x－2)＝(x－2)3－8＝x3－6x2＋12x－16.
答案x3－6x2＋12x－16
5．已知函数f(x)的定义域为[0,3]，则函数f(3x＋6)的定义域是________．解析由0≤3x＋6≤3，得－2≤x≤－1，故定义域为[－2，－1]．
答案[－2，－1]
6．已知f(x)＝
1
1＋x
(x∈R，且x≠－1)，g(x)＝x2＋2(x∈R)．
(1)求f(2)、g(2)的值；
(2)求f[g(2)]的值；
(3)求f[g(x)]的解析式．
解(1)f(2)＝
1
1＋2
＝
1
3，g(2)＝2
2＋2＝6.
(2)f[g(2)]＝f(6)＝
1
1＋6
＝
1
7.
(3)f[g(x)]＝f(x2＋2)＝
1
1＋(x2＋2)
＝
1
x2＋3
.
综合提高(限时25分钟)
7．设f(x)＝2x＋3，g(x＋2)＝f(x)，则g(0)的值为()．A．1 B．－1
C．－3 D．7
解析∵g(x＋2)＝f(x)，∴g(0)＝f(－2)＝2×(－2)＋3＝－1.
答案 B
8．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝f(2x)
x－1
的定义域是()．
A．[0,1] B．[0,1) C．[0,1)∪(1,4] D．(0,1) 解析∵y＝f(x)的定义域是[0,2]，
故f(2x)中，0≤2x≤2，
即0≤x≤1，又x－1≠0，∴x≠1，∴0≤x<1.
答案 B
9．设f (x )＝
x －1x ＋1
，则f (x )＋f (1
x )等于________． 解析 f (1x )＝1
x －11x ＋1＝1－x x ＋1，∴f (x )＋f (1x )＝x －11＋x ＋1－x
1＋x ＝0.
答案 0
10．函数f (x )＝(x ＋1)0
|x |－x
的定义域为________．
解析 要使解析式有意义，当且仅当⎩⎪⎨⎪⎧
x ＋1≠0，
|x |－x >0.解得定义域为{x |x <0且
x ≠－1}(区间表示：(－∞，－1)∪(－1,0))．
答案 (－∞，－1)∪(－1,0) 11．已知函数f (x )＝x 2
1＋x 2，x ∈R .
(1)求f (x )＋f (1
x )的值；
(2)计算：f (1)＋f (2)＋f (3)＋f (4)＋f (12)＋f (13)＋f (1
4)的值． 解 (1)f (x )＋f (1x )＝x 2
1＋x 2
＋
1x 2
1＋1x 2＝x 21＋x 2＋1
1＋x 2＝1＋x 21＋x 2＝1. (2)f (1)＋f (2)＋f (3)＋f (4)＋f (12)＋f (13)＋f (1
4)
＝f (1)＋[f (2)＋f (12)]＋[f (3)＋f (13)][f (4)＋f (14)]＝12＋3＝7
2. 12．(创新拓展)已知f (x －1)＝x 2－2x ＋7. (1)求f (2)和f (a )的值； (2)求f (x )和f (x ＋1)的解析式； (3)求f (x ＋1)的值域．
解 (1)f (2)＝f (3－1)＝9－6＋7＝10，
f (a )＝f [(a ＋1)－1]＝(a ＋1)2－2(a ＋1)＋7＝a 2＋6. (2)法一(配凑法)：
∵f(x－1)＝(x－1)2＋6，
∴f(x)＝x2＋6.
∴f(x＋1)＝(x＋1)2＋6＝x2＋2x＋7.
法二(换元法)：
令x－1＝t，则x＝t＋1，
则f(t)＝(t＋1)2－2(t＋1)＋7＝t2＋6，
∴f(x)＝x2＋6，
∴f(x＋1)＝(x＋1)2＋6＝x2＋2x＋7.
(3)∵f(x＋1)＝x2＋2x＋7＝(x＋1)2＋6≥6，∴f(x＋1)的值域为[6，＋∞)．。