数理统计第四章 方差分析
单因素试验的方差分析——概率论与数理统计(李长青版)
其次, 同一品种下数据表现出来的差异称为试验(随
机)误差, 这是由客观条件的偶然干扰造成, 与因素(品种) 无直接联系.
方差分析正是分析两类误差的有效工具.
本问题只考虑品种一种因素，故是单因素试验，即只有
一个因子，记为 A, 5个不同的品种就是该因子的5个不同 的水平，分别记为 A1 , A2 , A3 , A4 , A5 , 由于同一品种在不 同的田块上的亩产量不同，故可以认为一个品种的亩产 量 就是一个母体，在方差分析中，总是假定各母体相互独 立地服从同方差的正态分布，即第 j 个品种的亩产量是 一个随机变量，它服从正态分布:
nj
ns , 称为总平均,
它是从 s 个总体中抽得的样本的样本均值.
用样本值 xij 与总平均
x 之间的偏差平方和来反映
种子品种代 号 (水平)
重复试验序号及作物实测产量 1 128 125 148 2 126 137 132 3 139 125 139 4 130 117 125 5 142 106 151 133 122 139
A1 A2
A3
这里试验的指标是作物产量, 作物是因素, 三种种 子品种代表三个不同的水平. 首先,形成数据差异的直接原因是种子的不同品 种.因此, 每个品种下产量的均值差异检验是我们的主 要任务.这种由因素(种子品种)造成的差异称为条件(系 统)误差.
H 0 : 1 2 s 0, H1 : 1 , 2 , , s 不全为零.
(二) 离差平方和分解 引入记号
nj
1 xj nj
s
x
i 1
ij
( j 1, 2,
, s) 水平Aj下的样本均值,
称为组内平均(或列平均)
数理统计 单因素方差分析
表1 试验数据的形式
总体
观测值
样本容量
1 2 s
y11 , y12 , y1 n1 y 21 , y 22 , y 2 n2 y s 1 , y s 2 , y sn s
n1 n2 ns
1、方差分析的任务是： （1） 检验s 个总体均值是否相等，即
H 0 : 1 2 s H 1 : 1 , 2 , , s 不全相等
记
1 s ni i ，称为总平均， n i 1
i i 称为水平 Ai 的效应。
从而模型可以写为：
yij i ij 2 ~ N ( 0 , ) ij ni i 0 i
(i 1,2,, s; j 1,2,, ni )
来源
因子 误差 总和
平方和
318 .98
395 .46
714 .44
自由度
3
均方
106 .33 28.25
F 3.76
14
17
3.76 F0.05 (3,14) 3.34
拒绝H 0
例3
例4
5、未知参数的估计
不管 H 0 是否为真，
2
SE ˆ 因此 为 2 的无偏估计。 n s
因此，给定检验水平 时，拒绝域为：
F F ( s 1, n s )
表2 方差分析表 来源 因子 误差 总和 平方和
S A ni y ny
i 1 2 i s 2
自由度 均方
s 1
SA s1
SE n s
F
S A ( s 1) S E (n s)
S E ST S A
数理统计部分 方差分析与协方差分析 回归方程 非参数统计PPT课件
相应的观测值为x。
第26页/共54页
SST
(x i jk x••• ) 2
i jk
SSE
(x i jk x i j• ) 2
i jk
SSA
( x i •• x ••• ) 2
i jk
SSB
( x • j • x ••• ) 2
处理
苗高
1
19, 23, 21, 13
2
21, 24, 27, 20
3
20, 18, 19, 15
4
22, 25, 27, 22
第14页/共54页
data ex;do a=1 to 3;do i=1 to 5 ; input x @@; output;end;end; cards; 19 23 21 13 21 24 27 20 20 18 19 15 22 25 27 22 ; proc anova; class a;model x=a; means a/duncan cldiff;run;
第42页/共54页
第43页/共54页
四、双因素协方差分析
• （一）不考虑交互作用的双因素协方差分析
方差来源 平方和 自由 均方和 F值 度
A
QA
r-1 MQA FA
显著性
B
QB
s-1 MQB FB
误差
QE
rs-r-s MQE
总和
QT
rs-2
第44页/共54页
第45页/共54页
data ex;do a=1 to 3 ;do b=1 to 5 ; input x y @ @;output; end; end; cards; 8 2.85 10 4.24 12 3.00 11 4.94 10 2.88 10 3.14 12 4.50 7 2.75 12 5.84 10 4.06 12 3.88 10 3.86 9 2.82 10 4.94 9 2.89 ; proc glm;class a b ;model y=x a b/solution; lsmeans a b/stderr pdiff;run;
方差分析的基本思想
第一节方差分析的基本思想1、方差分析的意义前述的t检验和u检验适用于两个样本均数的比较，对于k个样本均数的比较，如果仍用t检验或u检验，需比较次，如四个样本均数需比较次。
假设每次比较所确定的检验水准=0.05，则每次检验拒绝H0不犯第一类错误的概率为1-0.05=0.95；那么6次检验都不犯第一类错误的概率为(1-0.05)6=0.7351，而犯第一类错误的概率为0.2649，因而t检验和u检验不适用于多个样本均数的比较。
用方差分析比较多个样本均数,可有效地控制第一类错误。
方差分析(analysis of variance,ANOVA)由英国统计学家R.A.Fisher首先提出，以F命名其统计量，故方差分析又称F检验。
2、方差分析的基本思想下面通过表5.1资料介绍方差分析的基本思想。
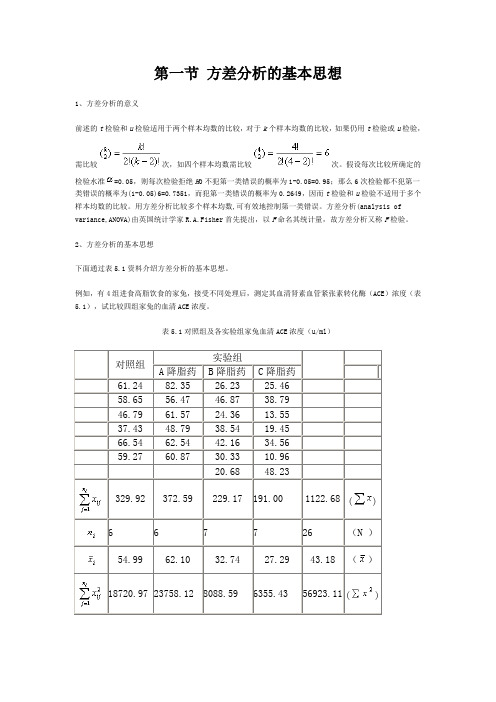
例如，有4组进食高脂饮食的家兔，接受不同处理后，测定其血清肾素血管紧张素转化酶（ACE）浓度（表5.1），试比较四组家兔的血清ACE浓度。
表5.1对照组及各实验组家兔血清ACE浓度（u/ml）对照组实验组A降脂药B降脂药C降脂药61.24 82.35 26.23 25.4658.65 56.47 46.87 38.7946.79 61.57 24.36 13.5537.43 48.79 38.54 19.4566.54 62.54 42.16 34.5659.27 60.87 30.33 10.9620.68 48.23329.92 372.59 229.17 191.00 1122.68 () 6 6 7 7 26 （N ）54.99 62.10 32.74 27.29 43.18 （）18720.97 23758.12 8088.59 6355.43 56923.11 ()由表5.1可见，26只家兔的血清ACE浓度各不相同，称为总变异；四组家兔的血清ACE浓度均数也各不相同，称为组间变异；即使同一组内部的家兔血清ACE 浓度相互间也不相同，称为组内变异。
方差分析(ANOVA)PPT参考课件
三、多个样本均数的两两比较
34
2020/1/15
方差分析能说明什么问题？
不拒绝H0，表示拒绝总体均数相等的证据不
足 分析终止
拒绝H0，接受H1, 表示总体均数不全相等
哪两两均数之间相等？哪两 两均数之间不等？
需要进一步作多重比较
35
2020/1/15
能否用T检验呢 当有k个均数需作两两比较时，比较的次数共 有c= ＝ k!/(2!(k-2)!)=k(k-1)/2
18~岁 21.65 20.66
… … 18.82 16 22.07 8.97
30~岁 27.15 28.58
… … 23.93 16 25.94 8.11
45~60岁 20.28 22.88 … … 26.49 16 25.49 27 7.19
2020/1/15
基本步骤
（1）建立假设，确定检验水准
2020/1/15
单因素方差分析 （1） 方差齐性检验
结果分析
2020/1/15
Test of Homogeneity of Variances
no
Levene Statistic 3.216
df1 2
df2 33
Sig. .053
Levene方法检验统计量为3.216，其P值为0.053，可 认为样本所来自的总体满足方差齐性的要求。
方差分析（ANOVA）
1
2020/1/15
n4
n3 n2 n1
Y4
Y3 Y2
Y1
2
2020/1/15
例子：某研究者在某单位工作人员中进行了体重指 数（BMI）抽样调查，随机抽取不同年龄组男性受试 者各16名，测量了被调查者的身高和体重值，由此按 照BMI=体重/身高2公式计算了体重指数，请问，不 同年龄组的体重指数有无差异。
数理统计课件-方差分析(zijiyong)
计算各水平样本均值： ①假定从第i个总体中抽取一个容量为ni的简单随机样本， 第i个总体的样本均值为该样本的全部观察值总和除 以观察值的个数 ni ②计算公式为
x
xi
j 1
ij
ni
(i 1,2,, k )
式中： ni为第 i 个总体的样本观察值个数 xij 为第 i 个总体的第 j 个观察值
通过对数据 误差来源的 分析来判断 不同总体的 均值是否相 等
四、方差分析的基本思想和原理
（一）两类误差 1. 组内误差 组内误差：在因素的同一水平(同一个总体)下，样本的各
2.
观察值之间的差异 比如，同一种颜色的饮料在不同超市上的销售量是不同的 不同超市销售量的差异可以看成是随机因素的影响，或者 说是由于抽样的随机性所造成的，称为随机误差 组间误差 组间误差：在因素的不同水平(不同总体)下，各观察值之 间的差异 比如，同一家超市，不同颜色饮料的销售量也是不同的 这种差异可能是由于抽样的随机性所造成的，也可能是由 于颜色本身所造成的，后者所形成的误差是由系统性因素 造成的，称为系统误差
然后加以比较进行统 计判断，得出结论。
ANOVA 由英国统 计学家R.A.Fisher首 创，为纪念Fisher， 以F命名，故方差分析 又称 F 检验 （F test）。
注：方差分析(Analysis of Variance，简称ANOVA)，又称 “变异数分析”或“F检验”.
学习目标：
本章的主要学习目标是要求学生在理解方差分 析基本思想的基础上，掌握单因素和双因素方差分 析的应用原理；重点是要学会方差分析的操作与应 用。
SST=SSE+SSA
实例
超市 (j)
1 2 3 4 5 合计
概率论与数理统计单因素试验的方差分析讲课文档
乙 1580 1640 1640 1700 1750
丙 1460 1550 1600 1620 1640 1740 1660 1820
丁
第三页，共21页。
1510 1520 1530 1570 1680 1600
第三页，共21页。
引例
灯泡的使用寿命——试验指标
灯丝的配料方案——试验因素（唯一的一个） 四种配料方案（甲乙丙丁）——四个水平
第十八页，共21页。
第十八页，共21页。
例2的上机实现步骤
1、输入原始数据列，并存到A，B，C列；
第十九页，共21页。
第十九页，共21页。
2、选择Stat>ANOVA>one-way(unstacked)
第二十页，共21页。
各水平数据放同一列 各水平数据放在不同列
第二十页，共21页。
第二十一页，共21页。
r
SSE
i1
ni
T 2 X ij n j1
r2 i
i1 i
第十五页，共21页。
ni
其中 T i X ij , j1 同一水平 下观测值 之和
r
T Ti i1
所以观测 值之和
第十五页，共21页。
例2 P195 2 以 A、B、C 三种饲料喂猪，得一个月后每猪 所增体重（单位：500g）于下表，试作方差分析。
饲料
增重
A
51
40
43
48
B
23
25
26
C
23
28
解：T1 51404348182,
T2 232526 74,
T 1 8 2 7 4 5 1 3 0 7
T3 232851
dfAr12, dfEnr936,
方差(概率论与数理统计)
方差分析通过比较不同组数据的分散程度，判断不同因素对数据变 异的贡献程度，从而进行多因素比较。
方差分析的适用条件
进行方差分析前需要满足独立性、正态性和方差齐性等条件，以确 保分析结果的准确性和可靠性。
方差分析的步骤
包括建立假设、计算自由度、计算F值、进行显著性检验等步骤，最 终得出各因素对数据变异的贡献程度和显著性水平。
统计学推断
在统计学中，方差分析、回归分析和生存分析等方法都涉及到方差的 概念和应用。
质量控制
在生产过程中，方差分析可以用于检测产品质量的一致性和稳定性。
社会科学研究
在社会学、心理学和经济学等社会科学领域，方差分析常用于研究不 同组别之间的差异和变化。
02
方差的计算方法
离差平方和的分解
离差平方和是由数据点与平均值的偏差平方和组成的，即每个数据点与平 均值的差的平方的总和。
其中，n是数据点的数量，组内离差平方和是每个数据点 与其所属类别的平均值的偏差平方和的总和，组间离差平 方和是不同类别的平均值之间的偏差平方和。
方差的计算实例
首先计算每个数据点与平均值的偏差的平方： {0, 1, 2, 3, 4}。
最后，根据方差的计算公式，方差 = (5-1) / 5 * 30 + 1 / 5 * 0 = 24。
假设有一个数据集{1, 2, 3, 4, 5}，其平均值为3。
然后求出偏差的平方的总和：0 + 1 + 4 + 9 + 16 = 30。
03
方差与其他统计量的关 系
方差与期望值的关系
方差是衡量数据离散程度的统计量，而期望值是数据的平均 水平。方差和期望值之间存在密切的关系，通常表示为方差 等于期望值的平方减去数据点的平方。
概率论与数理统计-方差
3. 若X1与X2 独立，则 D(X1+X2)= D(X1)+D(X2);
可推广为：若X1,X2,…,Xn相互独立,则
n
n
D[ Xi ] D( Xi )
i 1
i 1
n
n
D[ Ci Xi ] Ci2D( Xi )
i 1
i 1
4. D(X)=0 P(X= C)=1， 这里C=E(X)
P(X= x)
qp(
k 1
qk
)+E(X)
qp( q ) 1 q
1 p
qp
2 (1 q)3
1 p
2q p2
1 p
2
p p2
D(X)=E(X2)-[E(X)]2
2 p p2
1 p2
1
p p2
三、方差旳性质
1. 设C是常数,则D(C)=0;
X1 与X2不一定独立时， D(X1 +X2 )=？
请思索
2. 若C是常数,则D(CX)=C2 D(X);
解：设X为n 次试验中，事件A出现旳次数， 则 X~B(n, 0.75)
E(X)=0.75n, D(X)=0.75*0.25n=0.1875n
所求为满足 P(0.74 X 0.76) 0.90 n
旳最小旳n .
P(0.74 X 0.76) 可改写为 n
P(0.74n< X<0.76n )
有关系数
解得
n 1875 18750 1 0.9
即n 取18750时，能够使得在n次独立反复 试验中, 事件A出现旳频率在0.74~0.76之间旳 概率至少为0.90 .
我们简介了随机变量旳方差. 它是刻划随机变量取值在其中心附近离 散程度旳一种数字特征 .
概率论与数理统计PPT课件第四章数学期望与方差
在回归分析中，数学期望和方差 等统计指标用于描述因变量和自 变量之间的关系，以及预测未来
的趋势。
假设检验
在假设检验中，数学期望和方差等 统计指标用于比较两组数据或样本 的差异，判断是否具有显著性。
方差分析
方差分析利用数学期望和方差等统 计指标，分析不同组别或处理之间 的差异，确定哪些因素对数据变化 有显著影响。
质量控制
统计分析
在统计分析中，方差分析是一种常用 的统计方法，通过比较不同组数据的 方差，可以判断它们是否存在显著差 异。
在生产过程中，方差用于度量产品质 量波动的程度，通过控制产品质量指 标的方差，可以提高产品质量稳定性。
03
期望与方差的关系
期望与方差的关系式
期望值是随机变量取值的平均数 ，表示随机变量的“中心趋势”
方差的性质
方差具有可加性
当两个随机变量相互独立时，它们组 合而成的随机变量的方差等于它们各 自方差的线性组合。
方差与期望值的关系
方差与期望值之间存在一定的关系， 如方差等于期望值减去偏差的平方和 再求平均值。
方差的应用
风险评估
在金融和经济学中，方差被用来度量 投资组合的风险，通过计算投资组合 中各个资产的方差和相关系数，可以 评估投资组合的整体风险。
期望与方差的拓展
期望与方差在金融中的应用
金融风险评估
利用数学期望和方差计算 金融资产的风险，评估投 资组合的风险和回报。
资产定价
利用数学期望和方差等统 计指标，对金融资产进行 定价，确定其内在价值。
保险精算
通过数学期望和方差等统 计方法，评估保险产品的 风险和回报，制定合理的 保费和赔付方案。
期望与方差在统计学中
期望与方差在其他领域的应用
西安交大研究生课程之应用数理统计作业
研究生教材《应用数理统计》——课后习题答案详解学号：3113312042姓名：齐以年班级：硕3079班目录第一章数理统计的基本概念 (1)第二章参数估计 (18)第三章假设检验 (36)第四章方差分析与正交试验设计 (46)第五章回归分析 (51)第六章统计决策与贝叶斯推断 (56)对应书目：《应用数理统计》施雨编著西安交通大学出版第一章 数理统计的基本概念1.1 解：∵ 2~(,)X N μσ∴ 2~(,)n X N σμ∴~(0,1)N 分布∴(1)0.95P X P μ-<=<=又∵ 查表可得0.025 1.96u = ∴ 221.96n σ=1.2 解：(1) ∵ ~(0.0015)X Exp∴ 每个元件至800个小时没有失效的概率为：8000.001501.2(800)1(800)10.0015x P X P X e dxe -->==-<=-=⎰∴ 6个元件都没失效的概率为： 1.267.2()P e e --==(2) ∵ ~(0.0015)X Exp∴ 每个元件至3000个小时失效的概率为：30000.001504.5(3000)0.00151x P X e dxe--<===-⎰∴ 6个元件没失效的概率为： 4.56(1)P e -=-1.3解：(1) X ={(x 1,x 2,x 3)|x k =0,1,2,…,k =1,2,3},p (x 1,x 2,x 3)=λx 1+x 2+x 3x 1!x 2!x 3!e −3λ,x k =0,1,2,…;k =1,2,3(2) X ={(x 1,x 2,x 3)|x k ≥0;k =1,2,3},f (x 1,x 2,x 3)=λ3e −λ(x 1+x 2+x 3), x k ≥0;k =1,2,3(3) X ={(x 1,x 2,x 3)|a ≤x k ≤b;k =1,2,3},f (x 1,x 2,x 3)=1(b−a)3, a ≤x k ≤b;k =1,2,3(4) X ={(x 1,x 2,x 3)|−∞<x k <+∞;k =1,2,3}=R 3,f (x 1,x 2,x 3)=1(2π)3/2e −12∑(x k −μ)23k=1,−∞<x k <+∞;k =1,2,31.4 解：ini n x n x ex x x P ni i 122)(ln 2121)2(),.....,(122=--∏∑==πσμσ1.5证：21122)(na a x n x a x n i ni i i +-=-∑∑==∑∑∑===-+-=+-+-=ni i ni i n i i a x n x x na a x n x x x x 1222211)()(2221.6证明 (1) ∵22112211221()()()2()()()()()nnii i i nni i i i ni i XX X X X X X X X n X X X n X μμμμμ=====-=-+-=-+--+-=-+-∑∑∑∑∑(2) ∵2221112221221()22ii i nn ni i i i i ni ni XX X X X nX X nX nX X nX =====-=-+=-+=-∑∑∑∑∑1.7证明：a) 证：)(11111+=+++=∑n n i i n x x n x)(11)(1111n n n n n x x n x x x n n -++=++=++b ）证：221111()1nn n i i S x x n ++==-+∑ 221112211121111[()]11121[()()()()]11(1)n n n i n i nn n n n n i i n n i i x x x x n n n x x x x x x x x n n n +=++++===---+++=----+-+++∑∑∑221112112[()()((1))111() ]1n n n n n n n n n nS x x x x nx x n x n n x x n ++++=+---+-+++-+22n122n 11[nS ()] 111[S ()]11n n n n n x x n n n x x n n ++=+-++=+-++ 1.8证明：显然： Zm+n ̅̅̅̅̅̅̅=nX ̅+mY ̅m+nS Z2=1m +n[∑(X i −Z m+n ̅̅̅̅̅̅̅)2n i=1+∑(Y i −Z m+n ̅̅̅̅̅̅̅)2mi=1] =1m +n[∑X i 2ni=1−2Zm+n ̅̅̅̅̅̅̅∗nX ̅+∑Y i 2−2Z m+n ̅̅̅̅̅̅̅∗mY ̅+(m +n)mi=1Zm+n ̅̅̅̅̅̅̅2] 因为: nS X 2=∑X i 2n i=1−nX ̅2 nS Y 2=∑Y i 2n i=1−nY ̅2所以:S Z2=nS X2+nS Y2m+n+1m+n[nX̅2+nY̅2−(nX̅+mY̅)2m+n] =nS X2+nS Y2m+n+m∗n(n+m)2(X̅−Y̅)21.10解:(1).∑∑====niiniixEnxnEXE11)(1)1()(=1n∙n∙mp=mpnpmpxDnxnDXDniinii)1()(1)1()(121-===∑∑==))(1()(122∑=-=niixxnESE)1(1)])1(1())1(([1)])()(())()(([1])()([1])([12222212212212p mp nn p m p mp n n p m p mp n n x E x D n x E x D n x nE x E n x x E n n i i i n i i n i i --=+--+-=+-+=-=-=∑∑∑=== 同理，（2）.λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(λnx D n x n D X D ni ini i 1)(1)1()(121===∑∑==λnn x E x D n x E x D n x nE x E n S E n i i i n i i 1)])()(())()(([1])()([1)(2122122-=+-+=-=∑∑==(3).2)(1)1()(11ba x E n x n E X E n i i n i i +===∑∑==na b x D nx n D X D ni in i i 12)()(1)1()(2121-===∑∑==12)(1)])()(())()(([1])()([1)(22122122a b n n x E x D n x E x D n x nE x E n S E ni i i n i i -⋅-=+-+=-=∑∑==(4).λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx n D X D ni in i i 2121)(1)1()(λ===∑∑==221221221)])()(())()(([1])()([1)(λnn x E x D n x E x D n x nE x E n S E n i i i n i i -=+-+=-=∑∑==(5).μ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx n D X D ni in i i 2121)(1)1()(σ===∑∑==221221221)])()(())()(([1])()([1)(σ⋅-=+-+=-=∑∑==nn x E x D n x E x D n x nE x E n S E n i i i n i i1.11 解：由统计量的定义知，1，3，4，5，6，7为统计量，5为顺序统计量 1.12 解：顺序统计量：-4，-2.1，-2.1，-0.1，-0.1，0，0，1.2，1.2，2.01，2.22，3.2，3.21中位数Me=0 极差R=（3.21+4）=7.21 再抽一个样本2.7，则顺序统计量变为：-4，-2.1，-2.1，-0.1，-0.1，0，0，1.2，1.2，2.01，2.22，2.7，3.2，3.21 此时，样本中位数Me=(0+1.2)/2=0.61.13解： F 20x={ 0 , x <0620, 0≪x <11320, 1≪x <21620, 2≪x <31820, 3≪x <41 , x ≫41.14解:利用伽马分布的可加性 X~Γ(α,λ) 则Y =∑X i ~Γ(nα,λ)n i=1X ̅=Y nf Y (y )=λnαy nα−1Γ(nα)e −λy,y >0根据随机变量函数的概率密度公式得：f X ̅(x )=λnα(nx)nα−1Γ(nα)e −λnx∗n =λnαn nαx nα−1Γ(nα)e −λnx ,x >01.15解：运用顺序统计量的概率密度公式 (1) f (m)(x )=n!(m−1)!(n−m )![F (x )]m−1[1−F (x )]n−m f(x) 1≪m ≪n (2) f (k)(j)(x )=n!(k−1)!(j−k−1)!(n−j )![F (x )]k−1[F (y )−F (x )]j−k−1[1−F (y )]n−j f(x)f(y) 1≪k<j ≪n (3) 样本极差R =X (n)−X (1), 其中X (n)和X (1)的概率密度可由（1）得到，再根据函数关系可推出R 的概率密度函数 1.16解:X i −μσ~N(0,1)(X i −μσ)2~χ2(1)故：∑(X i −μσ)2~ni=1χ2(n )1.17 证：),(~ λαΓXx ex x f λαααλ--Γ=∴1)()( 令kXY =ke ky kke ky yf ky ky⋅Γ=⋅Γ=∴----λαααλαααλαλ11)()( )()()(即 ),(~ky Y αΓ1.18 证：),(~ b a X β),()1()( 11b a B x xx f b a ---=∴),(),( ),()1()( 11b a B b k a B b a B x x x X E b a k k +=-=∴⎰∞+∞---),(),1()( b a B b a B X E +=∴ba a ab a b a b a a a a b a b a a a b b a b a b a +=Γ+Γ++ΓΓ=Γ++Γ+Γ+Γ=ΓΓ+Γ⋅++ΓΓ+Γ=)()()()()()()1()()1()()()()1()()1(),(),2()(2b a B b a B X E +=))(1()1()()()()2()()2(b a b a a a a b b a b a b a ++++=ΓΓ+Γ⋅++ΓΓ+Γ= 22)]([)()( X E X E X D -=∴2))(1())(1()1(b a b a ab ba ab a b a a a +++=+-++++=1.19 解：∵ ~(,)X F n m 分布2212(1)022()((1))()(1)()()()(1)()()n n m n mn m yn m y n mn nP Y y P X X y m myP X y n n n x x dx m m m++--+≤=+≤=<-Γ=+ΓΓ⎰2222122221122()()()1()(1)()()11(1)(1)(,)n n m n m n mn m n mf y P Y y y y y y y yy B ++----'=≤Γ=+ΓΓ----=∴ 22(1)(,)n mn n Y X X m mβ=+分布1.20 解：∵ ~()X t n 分布122212()()(()2)n n P Y y P X y P X xdxn ++-≤=≤=≤≤Γ=+112211221212122()()()(1)()1()(1)()()()n n n n n f y P Y y y y n y y n n n+++--+--'=≤Γ=+Γ=+ΓΓ∴ 2~(1,)2nY X F =分布1.21 解: (1) ∵ ~(8,4)X N 分布∴ 4~(8,)25X N 分布，即5(8)~(0,1)2X N - ∴ 样本均值落在7.8~8.2分钟之间的概率为：5(7.88)5(8)5(8.28)(7.88.2)()2220.383X P X P ---≤≤=≤≤=(2) 样本均值落在7.5~8分钟之间的概率为：5(7.58)5(8)5(88)(7.58)()2225(8)(0 1.25)20.3944X P X P X P ---≤≤=≤≤-=≤≤=若取100个样品，样本均值落在7.5~8分钟之间的概率为：10(7.88)10(8)10(8.28)(7.88.2)()2222*(0.84130.5)0.6826X P X P ---≤≤=≤≤=-= 单个样品大于11分钟的概率为：P 1=1−0.9333=0.0667 25个样品的均值大于9分钟的概率为: P 2=1−0.9938=0.0062 100个样品的均值大于8.6分钟的概率为P 3=1−0.9987=0.0013 所以第一种情况更有可能发生1.22 解：μ=2.5 2σ=36 n=5 (1)44302<<s ⇔)955,625(22∈σns 而)1(~222-n ns χσ即 )4(36522χ∈s通过查表可得 P ＝0.1929(2)样本方差落在30~40的概率为0.1929 样品均值-x 落在1.3~3.5的概率即：P{1.3<-x <3.5} ⇔P{-0.4472<σμ)(--x n <0.3727}又σμ)(--x n ~N(0,1)查标准正态分布表可得：P{1.3<-x <3.5}＝0.3179 由于样本均值与样本方差相互独立，故：这样两者同时成立的概率为P ＝0.1929⨯0.3179=0.06131.23 解：(1) ∵2~(0,)X N σ分布 ∴ 2~(0,)X N nσ分布∴ 22()~(1)nXχσ∵ 22221()()ni i a X an X an σσ===∑∴ 21a n σ=同理 21b m σ= (2) ∵ 2~(0,)X N σ分布 ∴222~(1)X χσ分布由2χ分布是可加性得：2221~()ni i X n χσ=∑()nic X t m ==∑ ∴c =(3) 由(2)可知2221~()ni i X n χσ=∑ 2221122211~(,)nni ii i n mn mi ii n i n X d Xnn dF n m XmXmσσ==++=+=+=∑∑∑∑∴ m d n =1.24证明：X n+1~N(μ,σ2) X̅~N(μ,σ2/n) X n+1−X ̅~N(0,n +1n σ2)X n+1−X̅√n +1nσ2~N(0,1)(n −1)S n∗2σ2~χ2(n −1) 所以：Y =X n+1−X ̅S n ∗√n n +1~t(n −1) 1.25 证明：∵ 211~(,)X N μσ分布∴2211()~(1)i X μχσ-∴ 1221111()~()n i i X n μχσ=-∑同理 2222212()~()n i i Y n μχσ=-∑ 1122222112211111222221122112()()~(,)()()n n i i i i n n i i i i X n n X F n n Y n Y n μσμσμσμσ====--=--∑∑∑∑第二章 参数估计2.1 (1) ∵ ~()X Exp λ分布∴ ()1E X λ=令 ˆ1X λ= 解得λ的矩估计为:ˆ1X λ= (2) ∵ (,)X U a b 分布∴ ()2a bE X +=2()()12b a D X -=令 1ˆˆ2ab A X +==22221ˆˆˆˆ()()1124n i i b a a b A X n =-++==∑ （22211n i i X X S n =-=∑）解得a 和b 的矩估计为:ˆˆaX bX =-=(3) 110()1E X x x dx θθθθ-=*=+⎰令 1ˆˆ1A X θθ==+ ∴ˆ1XXθ=- (4) 110()(1)!kk x kE X x x e dx k βββ--=*=-⎰令 ˆkX β=∴ ˆkXβ=(5) 根据密度函数有2221()22()E X a aE X a λλλ=+=++根据矩估计有1222221ˆˆˆ22ˆˆˆa A X aa A S X λλλ+==++==+解得λ和a 的矩估计为:ˆˆaX λ==(6) ∵ (,)X B m p∴ ()E X mp =令 1ˆmpA X == 解得p 的矩估计为:ˆX pm= 2.2解：（1）X 服从指数分布，λ的似然函数为：L (λ)=λn e −λ∑x i n i=1, x i>0,i =1,2,⋯,nlnL (λ)=nlnλ−λ∑x i ni=1∂lnL (λ)∂λ=nλ−∑x i ni=1解得：λ̂=1x̅（2）f (x )=1b−a,a <x <b似然函数为：L (a,b )=1(b −a)n,a <x i <b显然：a ̂=X (1) b ̂=X (n) （3）f (x )={θ x θ−1 ,0<x <10, 其他似然函数为：L (θ)=θn ∗∏x i θ−1ni=1,0<x i <1lnL (θ)=nlnθ+(θ−1)∑lnx i ni=1∂lnL (θ)∂θ=nθ+∑lnx i ni=1=0 解得：θ̂=−n ∑lnx in i=1（4） f (x )={βk(k−1)!x k−1e −βx ,x >00, x ≤0似然函数为：L (β)=(βk(k −1)!)n ∗∏x i k−1ni=1∗e −β∑x i n i=1 ,x i >0 i =1,2,⋯,n lnL (β)=nk ∗lnβ−n ∗ln (k −1)!+(k −1)∑lnx i ni=1−β∑x i ni=1∂lnL (β)∂β=nkβ−∑x i ni=1=0解得：θ̂=−kx̅（5） f (x )={λ x −λ(x−a),x >a 0, x ≤a似然函数为：L (a,λ)=λn x −λ∑(x i ni=1−a) ,x i >a,i =1,2,⋯,nlnL (a,λ)=n ∗lnλ−λ∑x i ni=1+nλa ∂lnL (a,λ)∂λ=nλ−∑(x i ni=1−a)=0 解得：a ̂=X (1) , λ̂=−1X ̅−X (1)（6） X~B(m , P)P {X =k }=(m k)P k(1−P)m−k ,k =0,1,⋯,m似然函数为：L (p )=(m k)n P ∑xi n i=1(1−P)∑(m−x i )n i=1,x i =0,1,2,⋯,nlnL (p )=n ∗ln (mk)+∑x i n i=1∗lnp +∑(m −x i )ni=1∗ln (1−p)∂lnL (p )∂p=∑x in i=1p−∑(m −x i )n i=11−p=0解得：p ̂=−X̅m2.3解：∵ X 服从几何分布，其概率分布为：1()(1)k P X k p p -==-故p 的似然函数为： 1()(1)ni i x nnL p p p =-∑=-对数似然函数为：1ln ()ln ()ln(1)ni i L p n p x n p ==+--∑令 1ln ()1()01nii L p n x n p p p=∂=--=∂-∑ ∴ 1ˆpX= 2.4 解：由题知X 应服从离散均匀分布，⎪⎩⎪⎨⎧≤≤==其它01 1)(Nk N k x pE (X )=N+12矩估计： 令N ̂+12=710 ∴N̂=1419 极大似然估计：⎪⎩⎪⎨⎧≤≤=其它07101 1)(NN N L要使)(N L 最大，则710=N710=∴∧N2.5 解：由题中等式知：2196.196.196.1)025.01(025.0)(1S X +=+=∴+=+-Φ=∴=-Φ-∧∧∧-σμθσμμσθσμθ2.6 解：（1） 05.009.214.2=-=R0215.005.04299.05=⨯==∴∧d Rσ（2）将所有数据分为三组如下所示：0197.005.03946.005.0)05.005.005.0(316=⨯==∴=++=∴∧d R R σ 2.7 解：（1）⎩⎨⎧+<<=其它 01x 1)(θθx f θθθθθθ≠+==+=++=∴∧21)()(2121)(X E E X E ∴ X =∧θ不是θ的无偏估计，偏差为21=-∧θθ（2） θ=-)21(X E 21-=∴∧X θ是θ的无偏估计（3） 22))(()())(()(θθθθ-+=-+=∧∧X E X D E D M S E41121+=n 2.8 证：由例2.24，令2211x a x a +=∧μ，则∧μ 为μ无偏估计应 满足121=+a a因此1μ，2μ，3μ都是μ的无偏估计)()()()(21)()(2513)()(95)9491)(()())(()()(1233212221212∧∧∧∧∧∧=∧<<===+=∴+==∑μμμμμμμD D D X D D X D D X D X D D a a X D X D a D i i i2132121X X +=∴∧μ最有效2.9 证： )(~λp X λλ==∴)( )(X D X EX 是λ=)(X E 的无偏估计，2*S 是λ=)( X D 的无偏估计 )()1()())1((2*2*S E X E S X E αααα-+=-+∴λλααλ=-+=)1(∴ 2*)1(SX αα-+是λ的无偏估计2.10 解：因为2222((1))()(1)()(1)()1(1)()11(1)1E X S E X E S na E S n n a E S n n n a n nααααλαλαλαλλ**+-=+-=+--=+---=+-=- 所以 2(1)X S αα*+-是λ的无偏估计量2.11证明：X~P (λ)假设T(X 1)为θ=e −2λ的无偏估计，即： E[T(X 1)]= θ, E [T (X1)]=∑T (X )∞x=0∗λx x!e−λ=e −2λ=∑T (X )∞x=0∗λx x!=e−λ=∑(−λ)xx!∞x=0=∑(−1)x λx x!∞x=0（泰勒展开）所以T (X 1)=(−1)X 1是θ=e −2λ的唯一无偏估计。
方差分析PPT课件
方差分析的用途
1. 用于多个样本平均数的比较 2. 分析多个因素间的交互作用 3. 回归方程的假设检验 4. 方差的同质性检验
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
第一节 方差分析的基本问题
▪ 一、方差分析问题的提出 问题：为了探索简便易行的发展大学生心 血管系统机能水平的方法，在某年级各项 身体发育水平基本相同，同年龄女生中抽 取36人随机分为三组，用三种不同的方法 进行训练，三个月后，测得哈佛台阶指数 如表 1 ，试分析三种不同的训练方法对女 大学生心血管系统的影响有无显著性差异。
结果的好坏和处理效应的高低，实际中具体测 定的性状或观测的项目称为试验指标。常用的 试验指标例如有：身高、体重、日增重、酶活 性、DNA含量等等。
影响因素（ experimental factor）： 观测中所
研究的影响观测指标的定性变量称之为因素。 当考察的因素只有一个时，称为单因素试验； 若同时研究两个或两个以上因素的影响时，则 称为两因素或多因素试验。
N (3, 2)
A3
61.31 60.00
┆ 67.26 69.05
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
分析
根据研究目的，这里有三个正态总体 N (1, 2)，N (2, 2 )， N (3 , a2 ) 。三组数据分别为来自三个总体的样本，问题是 推断 1 ,2 和 3 之间有无显著差异。 由 x1, x2, x3不相等，不能直接得出1, 2, 3不尽相等的结论， 原因是：造成 x1, x2, x3不相等可能有两个方面因素：一是 1, 2, 3 不等，二是1 2 3，但由于抽样误差，造成 x1, x2, x3 之间有差异。现在的任务是通过样本推断1, 2, 3之间有无 显著性差异。
统计学方差分析ppt课件
水平
水平指因素的具体表现，如销售的 四种方式就是因素的不同取值等级。有 时水平是人为划分的，比如质量被评定 为好、中、差。
单元
单元指因素水平之间的组合。如销 售方式一下有五种不同的销售业绩，就 是五个单元。方差分析要求的方差齐就 是指的各个单元间的方差齐性。
元素
元素指用于测量因变量的最小单 位。一个单元里可以只有一个元素， 也可以有多个元素。
均衡
如果一个试验设计中任一因素各水 平在所有单元格中出现的次数相同，且 每个单元格内的元素数相同，则称该试 验是为均衡，否则，就被称为不均衡。 不均衡试验中获得的数据在分析时较为 复杂。
交互作用
如果一个因素的效应大小在另一 个因素不同水平下明显不同，则称为 两因素间存在交互作用。当存在交互 作用时，单纯研究某个因素的作用是 没有意义的，必须分另一个因素的不 同水平研究该因素的作用大小。如果 所有单元格内都至多只有一个元素， 则交互作用无法测出。
地点一 地点二 地点三 地点四 地点五
方式一
77
86
81
88
83
方式二
95
92
78
96
89
方式三
71
76
68
81
74
方式四
80
84
79
70
82
【解】设这四种方式的销售量的均值分别用 1•, 2•, 3•, 4• 表示，四 个销售地点的平均销售量用 •1, •2, •3, •4 表示；则要检验的假设为
例题
Excel操作
构造F统计量
判断与结论
例题
Excel操作
方差分析概述
因素和水平
单元和元素
均衡
交互作用
方差分析课件-PPT
增重表就是选用S-N-K法作均数多重两两比较得结果:
本例按a=0、05水准,将无显著性差异得数归为一类 (Subset for alpha=0、05)。可见
品种5、2、3得样本均数位于同一个子集( Subset )内,说 明品种5、品种2、品种3得样本均数两两之间无显著差异; 品种3、4、1位于同一个Subset内,她们之间无显著差异;而 品种5、2与品种4、1得样本均数有显著差异。
即三组均数间差异极显著,即不同时期切痂对大鼠肝脏 ATP含量有影响。
LSD法多重比较:
“*”显著性标注 两组均数得差
•S-N-K法:本例按0、5水平,将无显著差异得均数归为一类。
•第一组与第三组为一类,无显著差异,它们与第二组之间均数差 异显著。
•LSD与S-N-K法,不同得两两比较法会有不同。
如欲了解就是否达到极显著差异,需要将显著水平框中得 值输入0、01。
例、 为了研究烫伤后不同时间切痂对大鼠肝脏 ATP得影响,现将30只雄性大鼠随机分成3组,每组 10只:A组为烫伤对照组,B组为烫伤后24小时切痂 组,C组为烫伤后96小时切痂组。全部大鼠在烫伤 168小时候处死并测量器肝脏ATP含量,结果如下。 问试验3组大鼠肝脏ATP总数均数就是否相同。
该12个观察值得总得均值为91、5,标准差为34、 48。
上图为品系、剂量间均值得方差分析(F检验)结果
由表中可知,品系得F=23、771,P=0、001<0、01,差异极显著;
剂量得F=33、537,P=0、001<0、01,差异极显著。说明不同品系与 不同雌激素剂量对大鼠子宫得发育均有极显著影响,故有必要进一步对 品系、雌激素剂量两因素不同水平得均值进行多重比较。
数理统计第四章 方差分析
B1
B2
B3
B4
A1
A2
32
35
35.5
38.5
33.5
36
36.5
37.5
38
39.5
39.5
43
A3
• •
问不同促进剂、不同份量氧化锌分别对定强有无显著影响？ 此例中有Ａ，Ｂ二个因子，因而因子Ａ有三种水平Ａ1，Ａ2， Ａ3，因子Ｂ有四种水平Ｂ1，Ｂ2，Ｂ3，Ｂ4 ，在每种组合Ａi Ｂj上 作一次试验获得了试验值，问因子Ａ、Ｂ分别对试验结果有无显著 影响？
1
2
3
4
1
2
3
4
1
2
3
4
0
1
2
3
4
4
下面对更一般问题建立数学模型
母体
X X
1
子样
X X
11
子样均值
X X
12
X X
1 n1
X X
1
2
21
22
2 n2
2
X
r
X
r1
X
r2
X
rnr
X
r
2
假定 那么
X
i
N ( i ,
2
) ,
则
ij
X ij i N (0 , ).
t(n r )
13
•
给定置信概率 1 ，使 得
p { | T | t ( n r ) } 1 .
2
即
p{ X i X
j
t ( n r ) S E
统计学课件之方差分析
2.9850 2.9320
-1.8100 -1.8960
平均
2.0320 3.8850 2.9585 -1.8530
a1-a2
0.0960 0.0100 0.0530
单独效应 其他因素固定时，同一因素不同水平的差异 主效应 某一因素各水平的平均差别 交互效应 某因素的各单独效应随另一因素改变而变化
完全随机设计方案与随机区组设计方案的比较
方差齐性检验（Bartlett法，求一个卡方值）
方差不齐的处理——非参数检验
在设计阶段未预先考虑或预料到，经假设检验得 出多个总体均数不全相等的提示后，才决定的多 个均数的两两事后比较，多用于探索性研究 方法有：SNK-q test、Bonfferoni-t test等
xi
0.5542 0.4167 0.3438 0.1646 0.3698 （ x ）
xi2 3.9350 2.3925 1.7006 0.5906 8.6187 （ x2 ）
随机区组设计
方案 配伍组设计，为配对设计的扩展（1：m） 首先将受试对象按可能影响试验结果的属性
相同或相近分组（非随机），如按性别、体重、 年龄、职业、病情等。共形成b个区组，再分别将 各区组内的试验单位随机分配到各处理组。
试问：三组ATP总体均数是否存在差别？ 若三组间存在差别，则推论B组和C组的处理对ATP
的影响。
表1 大鼠烫伤后ATP的测量结果（mg）
A组
B组
C组
xij
7.76
11.14
10.85
7.71
11.60
8.58
8.43
11.42
7.19
8.47
13.85
9.36
10.30
方差分析_精品文档
2021/5/27
44
2.2 组内观测次数相等的方差分析 K组处理中，每一处理皆有n个观测值，其方
差分析方法同前。
表5. 组内观测次数相等的单因素方差分析
2021/5/27
45
例2.测定东北、内蒙古、河北、安徽、贵 州五个地区冬季针矛的长度，每个地区
随机抽取4个样本，测定结果如表示，试 比较各地区针毛长度差异显著性。
27
其中平均数差数标准误计算公式：
s x1x2
s12s22 n1 n2
se2(n11n12)
当n1=n2时，sx1x2
2se2 n
s e 2 为处理内误差方差，n为每一处理观察次数。
2021/5/27
28
例1. 表1. 氨氮含量(ppm)
2021/5/27
29
根据例1， s 2se2 2*9.112.13
2021/5/27
9
1.4.1 平方和的分解 总平方和=处理间平方和+处理内平方和
SSTSSt SSe
k
S S T 1
n(x x )2x 2 ( x )2x 2 T 2
1
k n
k n
令 C T 2 ，
kn
SST x2C
SSt =
Ti2 C n
SSe SSTSSt
2021/5/27
10
2021/5/27
39
例如，分析不同施肥量是否给农作物产
量带来显著影响，考察地区差异是否影 响妇女的生育率，研究学历对工资收入 的影响等。这些问题都可以通过单因素 方差分析得到答案。
2021/5/27
40
• 单因素方差分析的第一步是明确观测变 量和控制变量。例如，上述问题中的观
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
本章内容： 方差分析的有关概念、自由度的计算；柯赫伦分解定理 （不证）；单因素、双因素实验数据方差分析法。 重点： 单因素、双因素方差分析 本章课时： 6~8 课时
1
• •
引言： 在工农业生产及产品试制中，常常需要分析哪几种因素对生产的质量 和产量起显著影响，并希望知道起显著作用的因素在什么时候，对生产起最 好的影响。
t(n r )
13
•
给定置信概率 1 ，使 得
p { | T | t ( n r ) } 1 .
2
即
p{ X i X
j
t ( n r ) S E
2
1 ni
1 nj
i 1 ni 1 nj
j
Xi X
j
t ( n r ) S E
QE
r
2
( ( n i 1) ) ( n r ) .
2 2 i 1
则E ( Q E )
r
( n r ) .
2
2 )
• •
E (Q A )
i 1
ni E ( X i X )
r 2
2
( r 1)
i 1
ni ( i ) ,
0 0 0 0
•
解：据 r=4, n1 =7, n2 =5, n3 =8, n4 =6, n=26. 方差来源 组间 组内 离差平方和 44374.6 149970.8 自由度 3 22 均方离值 14791.5 6816.8 2.17 F值
总和
• •
194345.4
，据
25
F 0 F 0 .0 5 ( 3 , 2 2 )
X i,
X
j
相互独立
( X i X j ) (i j )
又
N ( 0 ,1) 1 1 ni nj 1 2 Q E (n r ) 2
T
( X i X j ) (i j ) SE 1 ni 1 nj
15
• • • •
一）下面介绍一般数学模型： 设因子Ａ有ｒ个不同水平Ａ1，Ａ2，…, Ａr ； 因子Ｂ有ｓ个不同水平Ｂ1，Ｂ2，…,Ｂs 。 pq 对每种情况Ａi Ｂj进行一次独立试验，共得 个试验结果 Xij ，由下表给出
因子B
因子A
B1 A1
A2
X 11 X
21
B2
X 12 X
22
: 1 2 r
Q A / ( ( r 1))
2
成立下，作统计量
SA SE
2 2
Q E / ( ( n r ))
2
Байду номын сангаас
Q A / ( r 1) Q E / (n r )
F ( r 1, n r ).
10
•
3 )
给定显著性水平 使得
Bs
X
1s
X
i
均值
1
X X
X
2s
2
Ar
X
r1
X
r2
X
X
rs
s
X
r
均值 X j
X
1
X
2
X
其中
X
i
1 s
s
j 1 r
X
ij
,
i 1, 2 , , r ,
X
j
1 r 1
i 1 r
X
s
ij
,
j 1, 2 , , s , 1 r
r
X
rs
ni
X ij ,
i 1, 2 , , r （组内平均）（1）
r
X
n
i 1
j 1 ni r
X ij ,
其中 n
j 1
i 1
n（总平均） i
•
•
因此 X
1 n
ni X
i
（2）
据（1），（2）可得
r
i 1 j 1
ni
(X
ij
X i )( X
i
X ) 0
Q Q 为总离方差 ； E 组内离方差； A 组间离方差。
Q T : 描述全部数据离散成都； :
•Q
•
E
描述 X i j 抽样误差的大小程度；
反映了各母体均值 i 之间差异程度。
QA :
7
• • • • • • •
二）为了作出假设 H 的统计量，下面讨论 Q 和Q 的统计性质。
0
E
A
1 )
QE
均值（x i ） 1680
A1 A2 A3 A4
1580
1460 1510
1640
1550 1520
1640
1600 1530
1700
1620 1570
1750
1640 1600
1662
1636.25 1568.33
希望通过上表推断：灯泡不同配料方案对灯泡寿命有无显著影响。 如果影响显著，那么用那一种配料为好。 在统计学上，称灯泡品种为因素，称因素的不同状态为水平。 这里有4种水平— A ， A， A， A 4 。 3 2 1
p { F F ( r 1, n r ) }
• •
4 )
得到拒绝域 F
F ( r 1, n r ) .
列出方差分析表，计算 方差来源 组间 组内 总和
F0
离差平方和
r
自由度
2
均方离值
SA
2 2
F值
F0 SA SE
2 2
QA
i 1
ni ( X i X )
2
1
r
n
ni i
8
i 1
• • • •
记
SE
2
QE nr
QA r 1
2
则 则
2
ESE ,
2 2
SA
2
ES A
2
2
r 1
1
r
ni ( i ) .
2
i 1
显然有
ESE ES A.
（柯赫伦定理） 设 X 从于 N ( 0 ,1) ，又设
的利用实验结果的信息，这就是方差分析。
2
一、一元方差分析
eg1. 某灯泡厂用四种不同配料方案制成的灯丝生产四批灯泡，在每 一批中取若干个做寿命实验，得如下数据（单位：小时）。
灯泡种类 （ Ai ）
寿命（单位：h）（ x ij ） 1600 1610 1650 1680 1700 1720 1660 1680 1800 1740 1800
X
可写作 ij
X
i ij , i 1, , r .
ij N ( 0 , )
2
2
其中，各 i j 相互独立 ， i , 为未知参数。
5
•
1）在上作假设： H 0 : 1 2 r
H 1 : 1 , 2 , r 不全相等
1
2
3
4
1
2
3
4
1
2
3
4
0
1
2
3
4
4
下面对更一般问题建立数学模型
母体
X X
1
子样
X X
11
子样均值
X X
12
X X
1 n1
X X
1
2
21
22
2 n2
2
X
r
X
r1
X
r2
X
rnr
X
r
2
假定 那么
X
i
N ( i ,
2
) ,
则
ij
X ij i N (0 , ).
6
r
•
因此 Q
T
i 1 r j 1 ni
ni
r
(X
ij
X )
2
i 1 r j 1
ni
[( X
ij
X i) (X
i
X )]
2
i 1 j 1
(X
ij
X i)
2
i 1
ni ( X
i
X )
2
•
• •
QT
QE QA
QT Q E Q A
F 0 .0 5 (3, 2 2 ) 3 .0 5
0
接受原假设 H ，无显著影响。
12
• 原假设不成立时，需要对未知参数作区间估计
拒绝
H
0
，作出
2
i k (i k )
)
区间估计
ni 2 X j N ( j , ) nj E (X i X j) i j 1 1 2 D(X i X j) ( ) ni nj X i N (i,
•
例如在农业科学试验中，为了提高农作物的收获量，因地制宜的选择 品种，常常需要比较不同品种的种子，施不同种类、不同数量的肥料对农作 物收获量的影响。并从中找出最适宜于该地区的作物品种、肥料的种类和数 量，以提高单位面积的产量。