最新浙教版第二章 一元二次方程复习题
浙教版八年级下册数学第二章 一元二次方程含答案(巩固)
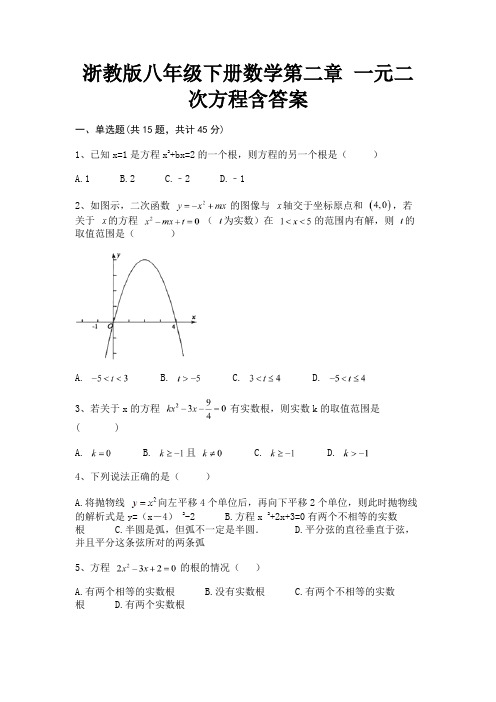
浙教版八年级下册数学第二章一元二次方程含答案一、单选题(共15题,共计45分)1、已知x=1是方程x2+bx=2的一个根,则方程的另一个根是()A.1B.2C.﹣2D.﹣12、如图示,二次函数的图像与轴交于坐标原点和,若关于的方程(为实数)在的范围内有解,则的取值范围是()A. B. C. D.3、若关于x的方程有实数根,则实数k的取值范围是( )A. B. 且 C. D.4、下列说法正确的是()A.将抛物线向左平移4个单位后,再向下平移2个单位,则此时抛物线的解析式是y=(x-4)2-2B.方程x 2+2x+3=0有两个不相等的实数根 C.半圆是弧,但弧不一定是半圆. D.平分弦的直径垂直于弦,并且平分这条弦所对的两条弧5、方程的根的情况()A.有两个相等的实数根B.没有实数根C.有两个不相等的实数根 D.有两个实数根6、一元二次方程2x2﹣3x﹣5=0的两个实数根分别为x1、x2,则x1+x2的值为()A. B.﹣ C.﹣ D.7、若关于y的一元二次方程ky2﹣4y﹣3=3y+4有实根,则k的取值范围是()A.k>﹣B.k≥﹣且k≠0C.k≥﹣D.k>且k≠08、已知x=﹣1是关于x的方程x2+mx﹣3=0的一个实数根,则此方程的另一个实数根为( )A.2B.﹣2C.3D.﹣39、若关于x的一元二次方程x2+5x+m2-1=0的常数项为0,则m等于()A.1B.2C.1或-1D.010、已知关于x的一元二次方程x2-2x+k-1=0有实数根,则实数k的取值范围是()A.k<0B.k≤0C.k≤2D.k<211、已知关于x的一元二次方程M为ax2+bx+c=0、N为cx2+bx+a=0(a≠c),则下列结论:①如果5是方程M的一个根,那么是方程N的一个根;②如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;③如果方程M与方程N有一个相同的根,那么这个根必是x=1.其中正确的结论是()A.①②B.①③C.②③D.①②③12、已知a、b、c分别为Rt△ABC(∠C=90°)的三边的长,则关于x的一元二次方程(c+a)x2+2bx+(c-a)=0根的情况是().A.方程无实数根B.方程有两个不相等的实数根C.方程有两个相等的实数根D.无法判断13、若方程x2﹣2x+m=0没有实数根,则实数m为()A.m≤1B.m<1C.m>1D.m≥114、一元二次方程x(x﹣2)=x﹣2的根是()A.0B.1C.1,2D.0,215、已知( 均为常数,且),则一元二次方程根的情况是()A.有两个不相等的实数根B.有两个实数根C.有两个相等的实数根 D.无实数根二、填空题(共10题,共计30分)16、如果是方程的一个根,则该方程的另一个根为________.17、一元二次方程x2﹣4x+6=0实数根的情况是________.18、若关于的一元二次方程总有两个不相等的实数根,则实数的取值范围是________.19、已知方程x2+mx+3=0的一个根是1,则它的另一个根是________,m的值是________。
浙教版八年级数学下册第二章一元二次方程练习(含答案)

第二章一元二次方程一、单选题1.下列方程中,关于X的一元二次方程是0A. ax1 +Z?x + c = OB. —+ —-2 = 0 厂xC. x(x-3)=2+x2D.小 x2-7=^x2.方程2x2-6x-5=0的二次项系数、一次项系数、常数项分别为( )A. 6、2、5B. 2、-6、5C. 2、-6、- 5D. -2、6、 53.已知x=l是关于x的一元二次方程x2+kx+4=0的一个根,则k的值为( )A. 5B. -5C. 3D. -34.关于1的一元二次方程V+ax —1=0的根的情况是( )A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.没有实数根5.用配方法解一元二次方程Y+3 = 4x时,原方程可变形为OA. (X-2)2=1B. (x-2)2 =7C. (X +2)2=2D.(X +2)2=16.用因式分解法解方程,下列方法中正确的是( )A.(2x-2)(3x-4) = 0, 口2-2x=0或3x-4 = 0B.(x + 3)(x-l) = l, Z:x + 3 = 0或x-l = lC.(x—2)(x-3) = 2x3f二x —2 = 2或x—3 = 3D.x(x + 2) = 0, Dx + 2 = 07.已知关于x的方程x2-x+m=0的一个根是3,则另一个根是(A. -6B. 6C. -2D. 28.设xl, x2是方程/一工一2016 = 0的两实数根,则蜡+ 2017占一2016的值是()A. 2015B. 2016C. 2017D. 20189.若一个三角形的两条边的长度分别为2和4,且第三条边的长度是方程6x + 8 = O的解,则它的周长是()A. 10B. 8 或10C. 8D. 610.某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )A. 560(1 + %)2 =1850B. 560+560(1 + 4 =1850C. 560(1 + x)+560( 1+ J:)2 =1850D. 560+560(1+ X)+560(1+ X)2 =1850二、填空题11.若方程〃7+3x - 4 = 2f是关于x的一元二次方程,则m的取值范围是12.关于"的一元二次方程9/_6x + k=0有两个不相等的实数根,则k的取值范圉是13.已知一元二次方程产+4工一3 = 0的两实数根为。
2024年浙教版数学八年级下学期第二章 一元二次方程 单元练习提高(含简单答案)

2024年浙教版数学八年级下学期第二章一元二次方程单元练习提高一、选择题(每题3分,共30分)1.下列方程属于一元二次方程的是( )A.2x+1=0B.x²−3x+1=0C.x²+y=1D.1=1x22.用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为( )A.(x+2)2=9 B.(x﹣2)2=9 C.(x+2)2=1 D.(x﹣2)2=13.方程x2+5x=0的解为( )A.x=5B.x=-5C.x₁=0,x₂=5D.x₁=0,x₂=−54.我们知道方程x2+2x-3=0的解是x1=1,x2=-3,现给出另一个方程(2x+3)2+2(2x+3)-3=0,它的解是( )A.x1=1,x2=3B.x1=1,x2=-3C.x1=-1,x2=-3D.x1=-1,x2=35.关于x的一元二次方程x2−4x−k=0没有实数根,则k的取值范围是( )A.k>4B.k<4C.k>−4D.k<−46.三角形两边长分别为2和4,第三边是方程x2−11x+30=0的解,则这个三角形的周长是( )A.11B.11或12C.12D.107.已知x₁,x₂是方程:x2−x−2024=0的两个实数根,则代数式x31−2024x1+x22的值是( )A.4 049B.4 047C.2 024D.18.假期老同学聚会,每两个人都握一次手,所有人共握手28次,则参加聚会的人数是( )A.7B.8C.9D.109.方程x2-2013|x|+2014=0的所有实数解的和是( )A.-2013B.0C.2 013D.2 01410.对于一元二次方程a x2+bx+c=0(a≠0),下列说法:①若a+b+c=0,则b2−4ac≥0;②若方程a x2+c=0有两个不相等的实根,则方程a x2+bx+c=0必有两个不相等的实根;③若c是方程a x2+bx+c=0的一个根,则一定有ac+b+1=0成立;②若x0是一元二次方程a x2+bx+c=0的根,则b2−4ac=(2ax0+b)2其中正确的( )A.只有①②④B.只有①②③C.①②③④D.只有①②二、填空题(每题4分,共24分)11.x=2是关于x的方程x2+mx+4=0的解,则m的值是 .12.若(x2+y2)(x2+y2-2)=8,则x2+y2的值为 .13.一个两位数,十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调,得到的两位数比原来的两位数小27,则原来的两位数是 .14.若实数a,b满足(4a+4b)(4a+4b-2)-8=0,则a+b=_________.15.已知关于x的一元二次方程,x2+ax+(m+1)(m+2)=0对任意的实数a均有实数根,则实数m的取值范围是_____.16.《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7−4=3.”小唐按此方法解关于x的方程x2+12x=m时,构造出如图2所示的图形,已知阴影部分的面积为64,则该方程的正数解为 .三、解答题(共8题,共66分)17.解下列方程.(1)x2-2=x;(2)2x2+x-1=018.已知关于x的方程x2−(m+2)x+(2m−1)=0.(1)求证:方程恒有两个不相等的实数根;(2)若此方程的一个根是1,求另一个根及m的值.19.已知方程x2-3x-1=0的两根也是方程x4+ax2+bx+c=0的根,求a+b-2c的值.20.已知关于x的方程k x2+(k+1)x+k=0有实数根.4(1)当k=4时,求解上述方程.(2)求k的取值范围.(3)是否存在实数k,使方程有两个根且两根的倒数和为1? 若存在,请求出k的值;若不存在,请说明理由.21.定义:若一元二次方程ax2+bx+c=0(a≠0)满足b=ac.则称此方程为“和美”方程.(1)当b<0时,判断此时“和美”方程ax2+bx+c=0(a≠0)解的情况,并说明理由.(2)若“和美”方程2x2+mx+n=0有两个相等的实数根,请解出此方程.22.已知a>0,b>a+c,判断关于x的方程ax2+bx+c=0的根的情况.23.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。
浙教版八年级下册数学第二章 一元二次方程含答案(考试真题)

浙教版八年级下册数学第二章一元二次方程含答案一、单选题(共15题,共计45分)1、方程(x﹣5)(x﹣6)=x﹣5的解是()A.x=5B.x=5或x=6C.x=7D.x=5或x=72、某商品原价为200元,为了吸引更多顾客,商场连续两次降价后售价为162元,求平均每次降价的百分率是多少?设平均每次降价的百分率为x,根据题意可列方程为()A. B. C.D.3、用配方法解一元二次方程x2﹣6x+1=0,则配方后所得的方程为()A.(x+3)2=10B.(x+3)2=8C.(x﹣3)2=10D.(x﹣3)2=84、关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为()A.﹣1B.0C.1D.﹣1或15、用配方法解方程x2-4x+1=0时,配方后所得的方程是( )A.(x-2) 2=1B.(x-2) 2=-1C.(x-2) 2=3D.(x+2) 2=36、已知x1, x2是一元二次方程x2+4x﹣3=0的两个实数根,则x1+x2﹣x1x2的值是()A.6B.0C.7D.-17、设a、b是整数,方程x2+ax+b=0的一根是,则的值为()A.2B.0C.-2D.-18、已知方程x2﹣2x﹣1=0,则此方程A.无实数根B.两根之和为﹣2C.两根之积为﹣1D.有一根为-1+9、若关于x的一元二次方程(k-1)x2+6x+3=0有实数根,则实数k的取值范围()A.k≤4且k≠1B.k<4且k≠1C.k<4D.k≤410、设x1, x2是方程x2+5x﹣3=0的两个根,则x12+x22的值是()A.19B.25C.31D.3011、若x1, x2是方程x2+px+q=0的两个实数根,则下列说法中正确的是()A.x1+x2=p B.x1•x2=﹣q C.x1+x2=﹣p D.x1•x2=p12、一元二次方程x2-9=0的根是()A.x=3B.x=4C.x1=3,x2=-3 D.x1= ,x2=-13、关于的方程有两实数根,则实数的取值范围是()A. B. C. D.14、方程的解是()A. B. C. , D. ,15、一元二次方程的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根 D.有两个实数根二、填空题(共10题,共计30分)16、为应对金融危机,拉动内需,吉祥旅行社3月底组织赴风凰古城、张家界风景区旅游的价格为每人1000元,为了吸引更多的人赴凤凰古城、张家界旅游,在4月底.、5月底进行了两次降价,两次降价后的价格为每人810元,那么这两次降价的平均降低率为________.17、有长为20m的铁栏杆,利用它和一面墙围成一个矩形花圃ABCD(如图),若花圃的面积为48m2,求AB的长.若设AB的长为xm,则可列方程为________.18、若关于x的一元二次方程(a-1)x2+ax+a2-1=0的一个根是0,则a的值是________。
浙教版初中数学第二章 一元二次方程专题复习1-一元二次方程的解法与应用(含答案)

专题复习一一元二次方程的解法与应用重点提示:一元二次方程的解法有四种:因式分解法;直接开平方法;配方法;公式法.对于不同的一元二次方程,要选择合适的方法以求快速并准确的解出方程,并注意配方法、整体换元、转化化归等数学方法和数学思想在解决问题中的应用.【夯实基础巩固】1.下面是小明同学在一次测验中解答的填空题,其中答对的是(C)A.若x2=4,则x=2B.方程x(2x﹣1)=2x﹣1的解为x=1C.若方程(m﹣2)x|m|+3mx﹣1=0是关于x的一元二次方程,则m=﹣2D.若分式的值为零,则x=1或x=22.已知三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的两根,则该三角形的周长为(A)3.方程x2﹣(+)x+=0的根是(A)A.x1=,x2=B.x1=1,x2=C.x1=﹣,x2=﹣D.x=±4.方程(x+)2+(x+)(2x﹣1)=0的较大根为(B)A.﹣B.C.D.5.一元二次方程(2x﹣1)2=(3﹣x)2的根是x1=,x2=﹣2.6.已知实数a≠b,且满足(a+1)2=3-3(a+1),3(b+1)=3-(b+1)2,则__-23___. 7.如图所示,在□ABCD中,AE⊥BC于点E,AE=EB=EC=a,且a是一元二次方程x2+2x ﹣3=0的根,则▱ABCD的周长是4+2.8.已知a为实数,且满足(a2+b2)2+2(a2+b2)﹣15=0,则代数式a2+b2的值为3.9.用适当的方法解下列方程:(1)2(x﹣1)2﹣4=0 (2)x2﹣4x+1=0(3)x2﹣8x+17=0 (4)x(x﹣2)+x﹣2=0.(1)x1=1+,x2=1﹣(2)x1=2+,x2=2﹣(3) =(﹣8)2﹣4×17<0,∴方程没有实数根.(4)x1=2,x2=﹣110.如图所示,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成.为方便进出,在垂直于住房墙的一边留一个1m宽的门.所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?设矩形猪舍垂直于住房墙的一边长为x(m),可以得出平行于墙的一边的长为(25﹣2x+1)m.由题意得x(25﹣2x+1)=80,解得x1=5,x2=8.当x=5时,26﹣2x=16>12(舍去).当x=8时,26﹣2x=10<12.∴所围矩形猪舍的长为10m,宽为8m.【能力提升培优】11.利用墙为一边,用长为13m的材料作另三边,围成一个面积为20m2的长方形小花园,这个长方形的长和宽各是(D)12.已知x2﹣8xy+15y2=0,那么x是y的(C).13.在正数范围内定义一种运算“*”,其规则为a*b=a+b2,根据这个规则,方程x*(x+1)=5的解是(B)14.如果关于x的一元二次方程x2+(k2﹣3)x+k=0的两个实数根互为相反数,则k15.已知非零实数x,y满足等式x2﹣2xy﹣3y2=0,则的值为3或﹣1.16.已知x为实数,(x2+4x)2+5(x2+4x)﹣24=0,则x2+4x的值为3.17.用适当的方法解下列方程:(1)4(x﹣1)2=36 (2)(3)(3x﹣1)(x+1)=4 (4)(2x﹣3)2﹣3(2x﹣3)+2=0(5)x2﹣(1+2)x++3=0 (6)3x2-10x+6=0(1)x1=4,x2=﹣2(2)x1=+2,x2=﹣2(3)x1=,x2=﹣1(4)x1=2,x2=(5)x1=,x2=1+18.如图所示,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:(1)第4个图形中阴影部分小正方形的个数为.(2)是否存在阴影部分小正方形的个数是整个图形中小正方形个数的?如果存在,是第几个图形;如果不存在,请说明理由.…(1)22(2)存在.理由如下:由题意得,解得个图形阴影部分小正方形的个数是整个图形中小正方形的个数的.【中考实战演练】19.【哈尔滨】今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加1600m2.设扩大后的正方形绿地边长为x(m),则下面所列方程正确的是(A)A.x(x﹣60)=1600 B.x(x+60)=1600C.60(x+60)=1600 D.60(x﹣60)=160020.【泰安】方程(2x+1)(x﹣1)=8(9﹣x)﹣1的根为﹣8或.【开放应用探究】21.阅读下列材料,并用相关的思想方法解决问题.计算:(1﹣﹣﹣)×(+++)﹣(1﹣﹣﹣﹣)×(++).令++=t,则原式=(1﹣t)×(t+)﹣(1﹣t﹣)×t=t+﹣t2﹣t﹣t+t2=.问题:(1)计算(1﹣﹣﹣﹣﹣…﹣)×(++++…++)﹣(1﹣﹣﹣﹣﹣…﹣﹣)×(++++…+).(2)解方程(x2+5x+1)(x2+5x+7)=7.(1)设++…+=t,则原式=(1﹣t)×(t+)﹣(1﹣t﹣)×t=t+﹣t2﹣t﹣t+t2+t=. (2)设x2+5x+1=t,则原方程化为t(t+6)=7,即t2+6t﹣7=0,解得t=﹣7或1.当t=1时,x2+5x+1=1,解得x1=0,x2=﹣5.当t=﹣7时,x2+5x+1=﹣7,即x2+5x+8=0,= 52﹣4×1×8<0,此时方程无解.∴原方程的解为x1=0,x2=﹣5.。
浙教版七年级数学下册第二章一元二次方程测试卷(Word版含答案)

浙教版七下第二章 一元二次方程测试卷(含解析)一.选择题(共10小题,满分30分,每小题3分)1.(3分)方程236ax y x -=+是二元一次方程,a 必须满足( ) A .0a ≠B .3a ≠-C .3a ≠D .2a ≠2.(3分)关于二元一次方程48x y +=的解,下列说法正确的是( ) A .任意一对有理数都是它的解 B .有无数个解 C .只有一个解D .只有两个解3.(3分)下列方程组中属于二元一次方程组的有( )(1)211x y y z -=⎧⎨=+⎩(2)03x y =⎧⎨=⎩(3)0235x y x y -=⎧⎨+=⎩(4)212 1.x y x y ⎧+=⎨+=-⎩.A .1个B .2个C .3个D .4个4.(3分)解方程组①216511y x x y =+⎧⎨+=-⎩;②2310236x y x y +=⎧⎨-=-⎩比较简便的方法是( )A .均用代入法B .均用加减法C .①用代入法,②用加减法D .①用加减法,②用代入法5.(3分)若2x y m=-⎧⎨=⎩是方程64nx y +=的一个解,则代数式31m n -+的值是( )A .3B .2C .1D .1-6.(3分)由方程组43x m y m +=⎧⎨-=⎩可得出x 与y 的关系是( )A .1x y +=B .1x y +=-C .7x y +=D .7x y +=-7.(3分)已知278ax by cx y +=⎧⎨-=⎩的解为32x y =⎧⎨=-⎩,某同学由于看错了c 的值,得到的解为22x y =-⎧⎨=⎩,则a b c ++的值为( )A .7B .8C .9D .108.(3分)已知x ,y 满足方程组36x m y m +=⎧⎨-=⎩,则无论m 取何值,x ,y 恒有关系式是( )A .1x y +=B .1x y +=-C .9x y +=D .9x y +=-9.(3分)《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.问:甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的23,那么乙也共有钱50.问:甲,乙两人各带了多少钱?设甲,乙两人持钱的数量分别为x ,y ,则可列方程组为()A.2502503x yx y+=⎧⎪⎨+=⎪⎩B.15022503x yy x⎧+=⎪⎪⎨⎪+=⎪⎩C.15022503x yx y⎧-=⎪⎪⎨⎪-=⎪⎩D.2502503x yx y-=⎧⎪⎨-=⎪⎩10.(3分)文峰超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入132元;第2天,卖出26支牙刷和14盒牙膏,收入264元;第3天,卖出39支牙刷和21盒牙膏,收入393元;第4天,卖出52支牙刷和28盒牙膏,收入528元;其中记录有误的是()A.第1天B.第2天C.第3天D.第4天二.填空题(共8小题,满分24分,每小题3分)11.(3分)已知95xy=⎧⎨=⎩是关于x、y的方程23x ay-=的一个解,则a的值是.12.(3分)试写出一个关于x、y的的二元一次方程,使它的一个解为12xy=⎧⎨=⎩,这个方程为.13.(3分)已知x、y满足方程组52723x yx y+=⎧⎨-=⎩,则x y+的值为.14.(3分)若22(24)()|4|0x x y z y-+++-=,则x y z++等于.15.(3分)若21xy=⎧⎨=⎩是方程组75ax bybx cy+=⎧⎨+=⎩的解,则a与c的关系是.16.(3分)请你阅读下面的诗句:“栖树一群鸦,鸦树不知数,三只栖一树,五只没去处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”若诗句中谈到的鸦为x只,树为y棵,则可列出方程组为.17.(3分)我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两.银子共有两.18.(3分)元旦期间,忠县永辉超市对三种风味的酸奶(原味、果粒味、大红枣味)进行A、B、C三种套餐的促销活动.已知A种套餐由3盒原味、4盒果粒味、5盒大红枣味搭配而成;B种套餐由2盒原味、8盒果粒味、8盒大红枣味搭配而成;C种套餐由5盒原味、4盒果粒味、6盒大红枣味搭配而成,每一种套餐的费用就是搭配该套餐的三种风味酸奶费用的总和.若一个A种套餐需35元,那么小明同学要买2个A种套餐、1个B种套餐和2个C种套餐共需费用元.三.解答题(共6小题,满分53分)19.(6分)已知方程1352x y+=,请你写出一个二元一次方程,使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩.20.(12分)解下列方程组:(1)124x yx y+=⎧⎨-=-⎩(2)1234()5()38x y x yx y x y+-⎧+=⎪⎨⎪+--=-⎩21.(7分)已知方程组27431x yx y+=⎧⎨-=-⎩的解也是关于x,y的二元一次方程3x y a=+的解,求(1)(1)7a a+-+的值.22.(8分)本地某快递公司规定:寄件不超过1千克的部分按起步价计费:寄件超过1千克的部分按千克计费.小文分别寄快递到上海和北京,收费标准及实际收费如表:收费标准:目的地起步价(元)超过1千克的部分(元/千克)上海7b北京104b+目的地质量(千克)费用(元)上海26a-北京37a+23.(10分)疫情期间为保护学生和教师的健康,某学校储备“抗疫物资”,用19000元购进甲、乙两种医用口罩共计900盒,甲、乙两种口罩的售价分别是20元/盒,25元/盒.(1)求甲、乙两种口罩各购进了多少盒?(2)现已知甲、乙两种口罩的数量分别是20个/盒,25个/盒,按照市教育局要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足市教育局的要求?24.(10分)为了提倡节约用水,某市制定了两种收费方式:当每户每月用水量不超过312m时,按一级单价收费;当每户每月用水量超过312m时,超过部分按二级单价收费.已知李阿姨家五月份用水量为310m,缴纳水费32元.七月份因孩子放假在家,用水量为314m,缴纳水费51.4元.(1)问该市一级水费,二级水费的单价分别是多少?(2)某户某月缴纳水费为64.4元时,用水量为多少?浙教版七下第二章一元二次方程测试卷(含解析)参考答案与试题解析一.选择题(共10小题,满分30分,每小题3分)1.(3分)方程236ax y x-=+是二元一次方程,a必须满足() A.0a≠B.3a≠-C.3a≠D.2a≠【解答】解:方程236ax y x-=+变形为(3)260a x y---=,根据二元一次方程的定义,得30a-≠,解得3a≠.故选:C.2.(3分)关于二元一次方程48x y+=的解,下列说法正确的是() A.任意一对有理数都是它的解B.有无数个解C.只有一个解D.只有两个解【解答】解:对于二元一次方程48x y+=,有无数个解,故选:B.3.(3分)下列方程组中属于二元一次方程组的有()(1)211x yy z-=⎧⎨=+⎩(2)3xy=⎧⎨=⎩(3)235x yx y-=⎧⎨+=⎩(4)212 1.x yx y⎧+=⎨+=-⎩.A.1个B.2个C.3个D.4个【解答】解:(1)本方程组中含有3个未知数;故本选项错误;(2)有两个未知数,方程的次数是1次,所以是二元一次方程组;(3)有两个未知数,方程的次数是1次,所以是二元一次方程组;(4)第一个方程未知项2x的次数为2,故不是二元一次方程组.共2个属于二元一次方程组.故选:B.4.(3分)解方程组①216511y xx y=+⎧⎨+=-⎩;②2310236x yx y+=⎧⎨-=-⎩比较简便的方法是()A.均用代入法B.均用加减法C.①用代入法,②用加减法D.①用加减法,②用代入法【解答】解:解方程组①216511y xx y=+⎧⎨+=-⎩比较简便的方法为代入法;②2310236x yx y+=⎧⎨-=-⎩比较简便的方法加减法,故选:C.5.(3分)若2x y m=-⎧⎨=⎩是方程64nx y +=的一个解,则代数式31m n -+的值是( )A .3B .2C .1D .1-【解答】解:2x y m =-⎧⎨=⎩是方程64nx y +=的一个解, ∴代入得:264n m -+=,32m n ∴-=, 31213m n ∴-+=+=,故选:A .6.(3分)由方程组43x m y m+=⎧⎨-=⎩可得出x 与y 的关系是( )A .1x y +=B .1x y +=-C .7x y +=D .7x y +=-【解答】解:原方程可化为43x m y m +=⎧⎨-=⎩①②,①+②得,7x y +=. 故选:C .7.(3分)已知278ax by cx y +=⎧⎨-=⎩的解为32x y =⎧⎨=-⎩,某同学由于看错了c 的值,得到的解为22x y =-⎧⎨=⎩,则a b c ++的值为( )A .7B .8C .9D .10【解答】解:根据题意得:322222a b a b -=⎧⎨-+=⎩,解得:45a b =⎧⎨=⎩,将3x =,2y =-代入得:3148c +=, 解得:2c =-,则4527a b c ++=+-=. 故选:A .8.(3分)已知x ,y 满足方程组36x m y m +=⎧⎨-=⎩,则无论m 取何值,x ,y 恒有关系式是( )A .1x y +=B .1x y +=-C .9x y +=D .9x y +=-【解答】解:36x m y m +=⎧⎨-=⎩①②,把②代入①得,63x y +-=,整理得,9x y+=,故选:C.9.(3分)《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.问:甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的23,那么乙也共有钱50.问:甲,乙两人各带了多少钱?设甲,乙两人持钱的数量分别为x,y,则可列方程组为()A.2502503x yx y+=⎧⎪⎨+=⎪⎩B.15022503x yy x⎧+=⎪⎪⎨⎪+=⎪⎩C.15022503x yx y⎧-=⎪⎪⎨⎪-=⎪⎩D.2502503x yx y-=⎧⎪⎨-=⎪⎩【解答】解:设甲需持钱x,乙持钱y,根据题意,得:15022503x yy x⎧+=⎪⎪⎨⎪+=⎪⎩,故选:B.10.(3分)文峰超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入132元;第2天,卖出26支牙刷和14盒牙膏,收入264元;第3天,卖出39支牙刷和21盒牙膏,收入393元;第4天,卖出52支牙刷和28盒牙膏,收入528元;其中记录有误的是()A.第1天B.第2天C.第3天D.第4天【解答】解:设每支牙刷x元,每盒牙膏y元.第1天:137132x y+=;第2天:2614264x y+=;第3天:3921393x y+=;第4天:5228528x y+=.假设第1天的记录正确,则第2天、第4天的记录也正确;假设第1天的记录错误,则第2天、第4天的记录也错误.故选:C.二.填空题(共8小题,满分24分,每小题3分)11.(3分)已知95xy=⎧⎨=⎩是关于x、y的方程23x ay-=的一个解,则a的值是3.5y =⎩移项得:5318a -=-, 合并得:515a -=-, 解得:3a =. 故答案为:3.12.(3分)试写出一个关于x 、y 的的二元一次方程,使它的一个解为12x y =⎧⎨=⎩,这个方程为3x y +=(答案不唯一) .【解答】解:根据题意:3x y +=(答案不唯一), 故答案为:3x y +=(答案不唯一)13.(3分)已知x 、y 满足方程组52723x y x y +=⎧⎨-=⎩,则x y +的值为 1 .【解答】解:527(1)23(2)x y x y +=⎧⎨-=⎩,(1)-(2)得:444x y +=, 1x y ∴+=,故答案为:1.14.(3分)若22(24)()|4|0x x y z y -+++-=,则x y z ++等于 12- .【解答】解:22(24)()|4|0x x y z y -+++-=, ∴240040x x y z y -=⎧⎪+=⎨⎪-=⎩, 解得:2212x y z ⎧⎪=⎪=-⎨⎪⎪=-⎩,则112222x y z ++=--=-. 故答案为:12-.15.(3分)若21x y =⎧⎨=⎩是方程组75ax by bx cy +=⎧⎨+=⎩的解,则a 与c 的关系是 49a c -= .1y =⎩5bx cy +=⎩得2725a b b c +=⎧⎨+=⎩①②,①2⨯-②,得49a c -=. 故答案为:49a c -=.16.(3分)请你阅读下面的诗句:“栖树一群鸦,鸦树不知数,三只栖一树,五只没去处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”若诗句中谈到的鸦为x 只,树为y 棵,则可列出方程组为 355(1)x y x y =+⎧⎨=-⎩.【解答】解:设诗句中谈到的鸦为x 只,树为y 棵,则可列出方程组为: 355(1)x y x y =+⎧⎨=-⎩. 故答案为:355(1)x y x y =+⎧⎨=-⎩.17.(3分)我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两.银子共有 46 两. 【解答】解:设有x 人,银子y 两, 由题意得:7498y x y x =+⎧⎨=-⎩,解得646x y =⎧⎨=⎩,故答案为46.18.(3分)元旦期间,忠县永辉超市对三种风味的酸奶(原味、果粒味、大红枣味)进行A 、B 、C 三种套餐的促销活动.已知A 种套餐由3盒原味、4盒果粒味、5盒大红枣味搭配而成;B 种套餐由2盒原味、8盒果粒味、8盒大红枣味搭配而成;C 种套餐由5盒原味、4盒果粒味、6盒大红枣味搭配而成,每一种套餐的费用就是搭配该套餐的三种风味酸奶费用的总和.若一个A 种套餐需35元,那么小明同学要买2个A 种套餐、1个B 种套餐和2个C 种套餐共需费用 210 元.【解答】解:设1盒原味的价格为x 元,1盒果粒味的价格为y 元,1盒大红枣味的结果为z 元, 由题意得:34535x y z ++=,则小明同学要买2个A 种套餐、1个B 种套餐和2个C 种套餐共需费用为: 2352882(546)x y z x y z ⨯++++++ 70121620x y z =+++ 704(345)x y z =+++ 70435=+⨯210=(元),故答案为:210.三.解答题(共6小题,满分53分)19.(6分)已知方程1352x y+=,请你写出一个二元一次方程,使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩.【解答】解:经验算41xy=⎧⎨=⎩是方程1352x y+=的解,再写一个方程,如3x y-=.20.(12分)解下列方程组:(1)124x yx y+=⎧⎨-=-⎩(2)1234()5()38x y x yx y x y+-⎧+=⎪⎨⎪+--=-⎩【解答】解:(1)在1(1)24(2)x yx y+=⎧⎨-=-⎩中,(1)+(2)得:33x=-,解得:1x=-,把1x=-代入(1)得:2y=.∴方程组的解为12xy=-⎧⎨=⎩.(2)在1(1)234()5()38(2)x y x yx y x y+-⎧+=⎪⎨⎪+--=-⎩中,由(1)得:56x y+=(3),由(2)得:938x y-+=-,938x y∴=+,将938x y=+代入(3)得:46184y=-, 4y∴=-.把4y=-代入938x y=+,得2x=.∴方程组的解为24xy=⎧⎨=-⎩.21.(7分)已知方程组27431x yx y+=⎧⎨-=-⎩的解也是关于x,y的二元一次方程3x y a=+的解,求(1)(1)7a a+-+的值.【解答】解:方程组27431x y x y +=⎧⎨-=-⎩①②, ①3⨯+②得:1020x =,即2x =,把2x =代入①得:3y =,把2x =,3y =代入方程得:63a =+,即3a =,则原式21791715a =-+=-+=.22.(8分)本地某快递公司规定:寄件不超过1千克的部分按起步价计费:寄件超过1千克的部分按千克计费.小文分别寄快递到上海和北京,收费标准及实际收费如表: 收费标准: 目的地起步价(元) 超过1千克的部分(元/千克) 上海7 b 北京10 4b + 目的地质量(千克) 费用(元) 上海2 6a - 北京3 7a +【解答】解:依题意得:7(21)610(31)(4)7b a b a +-=-⎧⎨+-+=+⎩, 解得:152a b =⎧⎨=⎩. 答:a 的值为15,b 的值为2.23.(10分)疫情期间为保护学生和教师的健康,某学校储备“抗疫物资”,用19000元购进甲、乙两种医用口罩共计900盒,甲、乙两种口罩的售价分别是20元/盒,25元/盒.(1)求甲、乙两种口罩各购进了多少盒?(2)现已知甲、乙两种口罩的数量分别是20个/盒,25个/盒,按照市教育局要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足市教育局的要求?【解答】解:(1)设甲种口罩购进了x 盒,乙种口罩购进了y 盒,依题意得:900202519000x y x y +=⎧⎨+=⎩, 解得:700200x y =⎧⎨=⎩,答:甲种口罩购进了700盒,乙种口罩购进了200盒.(2)207002520014000500019000⨯+⨯=+=(个),29001018000⨯⨯=(个), 1900018000>,∴购买的口罩数量能满足市教育局的要求.24.(10分)为了提倡节约用水,某市制定了两种收费方式:当每户每月用水量不超过312m时,按一级单价收费;当每户每月用水量超过312m时,超过部分按二级单价收费.已知李阿姨家五月份用水量为310m,缴纳水费32元.七月份因孩子放假在家,用水量为314m,缴纳水费51.4元.(1)问该市一级水费,二级水费的单价分别是多少?(2)某户某月缴纳水费为64.4元时,用水量为多少?【解答】解:(1)设该市一级水费的单价为x元,二级水费的单价为y元,依题意得:103212(1412)51.4xx y=⎧⎨+-=⎩,解得:3.26.5xy=⎧⎨=⎩.答:该市一级水费的单价为3.2元,二级水费的单价为6.5元.(2) 3.21238.4⨯=(元),38.464.4<,∴用水量超过312m.设用水量为a3m,依题意得:38.4 6.5(12)64.4a+-=,解得:16a=.答:当缴纳水费为64.4元时,用水量为316m.。
浙教版数学八年级下册第二章《一元二次方程》计算练习题(含答案)

浙教版数学八年级下册第二章《一元二次方程》计算练习题(含答案)1. x2=2x 2. x2=3x; 3. 2x2−4x−1=0 4. x2−2x=15. x2+3x+1=06. (x−3)2+4x(x−3)=0.7. 4x2−8x−1=08.(x+3)2=2x+6)10. x2−2x−24=011.x(x-2)=5(x-2) 12.x2-2x-3=0 9. x2=3(x+4313.x(3x-5)=6x-10 14.x2-4x-12=0; 15.x2+15=8x,16. x2−4x−1=0 17. x2−x−12=018. x2−3x+1=019. (x+1)2=2x+220.x2+2x−399=0 21. x2−4x−2=022. −3x2−4x+4=023. 3(x−5)2=10−2x24. (3x−1)2=(x+1)2 25.3x2-8x=3 26.3x(x-2)=4-2x 27.5x2-4x-1=0 28.4x(x-3)=x2-9 29.3(x+2)2=x(2+x)30.2x2+3x﹣2=0 31. 2(x+1)=x(x+1)32. x2+6x−27=0 33.x2-2x-3=0 34.x2-2x-1=0 35. 2x(x−2)=x2−336. x2−5x+1=037. (x−3)(x−1)=338. 2x2−2√2x−5=039. 2(x−3)2=x2−9.40.解关于x的方程:(a−1)x2=(2a−1)x−a(a是已知数)参考答案1.【答案】解:x2=2xx2−2x=0x(x−2)=0解得:x1=0,x2=22.【答案】(1)解:x2−3x=0,x(x-3)=0,x=0,x-3=0,∴x1=0,x2=3;(2)解:2x2−4x−1=0,∵a=2,b=-4,c=-1,∴b2-4ac=(-4)2-4×2×(-1)=24>0,∴x= −(−4)±√242×5,∴x1=2+√65,x2=2−√65.3.【答案】解:x2−2x=1,配方得:x2−2x+1=2,即(x−1)2=2,开方得:x−1=±√2,解得:x1=√2+1,x2=−√2+1.4.【答案】(1)解:x2+3x+1=0 a=1,b=3,c=1∵b2−4ac=32−4×1×1=5,∴x1=−b+√Δ2a =−3+√52;x2=−b−√Δ2a=−3−√52.(2)解:(x−3)(x−3+4x)=0,x−3+4x=0,x−3=0,x1=35,x2=3.5.【答案】(1)解:4x2−8x−1=0∵a=4,b=−8,c=−1∴Δ=b2−4ac=(−8)2−4×4×(−1)=80>0∴x=−b±√b2−4ac2a =−(−8)±√802×4=8±4√58∴x1=1+√52,x2=1−√52.(2)解:(x+3)2=2x+6 (x+3)2−2(x+3)=0(x+3)(x+1)=0x+3=0,x+1=0x1=−3,x1=−1.6.【答案】(1)解:x2=3(x+43),整理得:x2−3x−4=0,因式分解得:(x−4)(x+1)=0,∴x−4=0或x+1=0,∴x1=4,x2=−1;(2)解:x2−2x−24=0,因式分解得:(x−6)(x+4)=0,∴x−6=0或x+4=0,∴x1=6,x2=−4.7.【答案】解:x(x-2)-5(x-2)=0∴(x-5) (x-2) =0∴x1=5,x2=2.8.【答案】(1)解:(x-3)(x+1)=0 解得,x1=3,x2=-1(2)解:3x2-5x=6x-103x2-11x+10=0解得,x1=2,x2=539.【答案】(1)解:∵x2-4x-12=0.∴(x-6)(x+2)=0则x-6=0或x+2=0解得x1=6,x2=-1(2)解:∵x2-8x+15=0∴(x-3)(x-5)=0。
一元二次方程综合复习训练浙教版八年级数学下册

2021-2022学年浙教版八年级数学下册《第2章一元二次方程》期中综合复习训练(附答案)一.选择题1.下列方程中,是一元二次方程的是()A.+x﹣1=0B.3x+1=5x+42C.ax2+bx+c=0D.m2﹣2m+1=0 2.若关于x的一元二次方程(m+1)x2﹣x+m2﹣m﹣2=0有一根为0,则m的的值为()A.2B.﹣1C.2或﹣1D.1或﹣23.一元二次方程x2﹣6x+1=0配方后可化为()A.(x+3)2=2B.(x﹣3)2=8C.(x﹣3)2=2D.(x﹣6)2=35 4.已知方程x2+2x﹣8=0的解是x1=2,x2=﹣4,那么方程(x+1)2+2(x+1)﹣8=0的解是()A.x1=1,x2=5B.x1=1,x2=﹣5C.x1=﹣1,x2=5D.x1=﹣1,x2=﹣55.若关于x的一元二次方程(k+1)x2﹣2x+3=0有实数根,则k的取值范围是()A.B.C.k<﹣且k≠﹣1D.k≤﹣且k≠﹣16.电影《长津湖》于2021年9月30日在中国大陆上映,某地第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达7亿元,若把增长率记作x,则方程可以列为()A.2(1+x)=7B.2(1+x)2=7C.2+2(1+x)2=7D.2+2(1+x)+2(1+x)2=77.m是方程x2+x﹣2=0的根,则代数式2m2+2m﹣2022的值是()A.﹣2018B.2018C.﹣2026D.20268.某网店销售一批运动装,平均每天可销售20套,每套盈利45元;为扩大销售量,增加盈利,采取降价措施,一套运动服每降价1元,平均每天可多卖4套.若网店要获利2100元,设每套运动装降价x元,则列方程正确的是()A.(45﹣x)(20+4x)=2100B.(45+x)(20+4x)=2100C.(45﹣x)(20﹣4x)=2100D.(45+x)(20﹣4x)=2100二.填空题9.设a、b是方程x2+x﹣2022=0的两个实数根,则(a+1)2+b的值为.10.已知(x2+y2)2+6(x2+y2)﹣7=0,则x2+y2的值为.11.已知实数m、n满足m2﹣4=2m,n2=4+2n,则|m﹣n|=.12.等腰△ABC的底和腰分别是一元二次方程x2﹣5x+4=0的两根,则这个等腰三角形的周长为.13.若a2+1=3a,b2+1=3b,则代数式的值为.14.关于x的一元二次方程(m+1)x2+(2m+1)x+m﹣1=0有两个不相等的实数根,则m 的取值范围是.15.如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点C运动,点P到达终点后,P、Q两点同时停止运动,则秒时,△BPQ的面积是6cm2.16.关于x的一元二次方程ax2+bx+c=0(a≠0),现给出以下结论:①若a﹣b+c=0,则方程必有一根为﹣1;②若a﹣b+c=0,则方程一定有两个不相等的实数根;③若a、c异号,则方程一定有两个不相等的实数根;④若m是方程的根,则等式(2am+b)2=b2﹣4ac一定成立.其中正确的结论是.(写出所有正确结论的序号)三.解答题17.解下列方程.(1)2x2+5x=18﹣11x;(2)(3x﹣1)2=(x+1)2.18.已知关于x的一元二次方程x2﹣kx+k﹣1=0.(1)求证:无论k取何值,该方程总有实数根;(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.19.已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0.(1)求证:方程有两个不相等的实数根;(2)如果方程的两实根为x1、x2,且x12+x22﹣x1x2=13,求m的值.20.阅读以下材料:利用我们学过的完全平方公式及不等式知识能解决代数式一些问题,如a2+2a﹣4=a2+2a+12﹣12﹣4=(a+1)2﹣5∵(a+1)2≥0,∴a2+2a﹣4=(a+1)2﹣5≥﹣5,因此,代数式a2+2a﹣4有最小值﹣5.根据以上材料,解决下列问题:(1)代数式a2﹣2a+2的最小值为;(2)试比较a2+b2+11与6a﹣2b的大小关系,并说明理由;(3)已知:a﹣b=2,ab+c2﹣4c+5=0,求代数式a+b+c的值.21.如图,利用一面墙(墙EF最长可利用28m),围成一个矩形花园ABCD,与墙平行的一边BC上要预留2m宽的入口(如图中MN所示,不用砌墙),现有砌60m长的墙的材料.(1)当矩形的长BC为多少米时,矩形花园的面积为300m2;(2)能否围成面积为480m2的矩形花园,为什么?22.某商场以每千克20元的价格购进某种榴莲,计划以每千克40元的价格销售.为了让顾客得到更大的实惠,现决定降价销售,已知这种榴莲的销售量y(kg)与每千克降价x(元)(0<x<10)之间满足一次函数关系,其图象如图所示.(1)求y关于x的函数解析式.(2)该商场在销售这种榴莲中要想获利1105元,则这种榴莲每千克应降价多少元?参考答案一.选择题1.解:A.是分式方程,不是一元二次方程,故本选项不符合题意;B.是一元一次方程,不是一元二次方程,故本选项不符合题意;C.当a=0时,不是一元二次方程,故本选项不符合题意;D.是一元二次方程,故本选项符合题意;故选:D.2.解:把x=0代入方程,得(m+1)×02﹣x+m2﹣m﹣2=0,整理,得(m﹣2)(m+1)=0.解得m1=2,m2=﹣1.又∵方程(m+1)x2﹣x+m2﹣m﹣2=0是关于x的一元二次方程,∴m+1≠0,∴m≠﹣1,即m=2.故选:A.3.解:∵x2﹣6x+1=0,∴x2﹣6x=﹣1,则x2﹣6x+9=﹣1+9,即(x﹣3)2=8.故选:B.4.解:把方程(x+1)2+2(x+1)﹣8=0看作关于(x+1)的一元二次方程,∵方程x2+2x﹣8=0的解是x1=2,x2=﹣4,∴x+1=2或x+1=﹣4,解得x=1或x=﹣5,∴方程(x+1)2+2(x+1)﹣8=0的解为x1=1,x2=﹣5.故选:B.5.解:依题意得:,解得:k≤﹣且k≠﹣1.故选:D.6.解:若把增长率记作x,则第二天票房约为2(1+x)亿元,第三天票房约为2(1+x)2亿元,依题意得:2+2(1+x)+2(1+x)2=7.故选:D.7.解:∵实数m是关于x的方程x2+x﹣2=0的一个根,∴m2+m﹣2=0,∴m2+m=2,∴2m2+2m﹣2022=2(m2+m)﹣2022=﹣2018.故选:A.8.解:设每套书运动服降价x元时,则每天可出售(20+4x)套;由题意得:(45﹣x)(20+4x)=1200;故选:A.二.填空题9.解:∵a、b是方程x2+x﹣2022=0的两个实数根,∴a+b=﹣1,a2+a﹣2022=0,即a2+a=2022,则原式=a2+2a+1+b=(a2+a)+(a+b)+1=2022﹣1+1=2022.故答案为:2022.10.解:设x2+y2=z,则原方程换元为z2+6z﹣7=0,∴(z﹣1)(z+7)=0,解得:z1=1,z2=﹣7,∵x2+y2≥0,∴x2+y2=1故答案为:1.11.解:∵实数m、n满足m2﹣4=2m,n2=4+2n,∴m=n或m,n为一元二次方程x2﹣2x﹣4=0的两个不相等的实数根.当m=n时,|m﹣n|=0;当m,n为一元二次方程x2﹣2x﹣4=0的两个不相等的实数根时,m+n=2,mn=﹣4,∴|m﹣n|====2.故答案为:0或2.12.解:x2﹣5x+4=0,(x﹣4)(x﹣1)=0,x﹣4=0或x﹣1=0,所以x1=4,x2=1,因为1+1=2<4,不符合三角形三边的关系,所以等腰三角形的底边为1,腰为4,所以三角形的周长为4+4+1=9.故答案为:9.13.解:∵a2+1=3a,b2+1=3b,当a=b时,代数式的值为2,当a≠b时,根据题意a,b是方程x2﹣3x+1=0的两个根,故a+b=3,ab=1.则====7.故代数式的值为7或2,故答案为:7或2.14.解:根据题意得m+1≠0且Δ=(2m+1)2﹣4(m+1)(m﹣1)>0,解得m>﹣且m≠﹣1,即m的取值范围为m>﹣且m≠﹣1,故答案为:m>﹣且m≠﹣1,15.解:设运动时间为t秒,则PB=(10﹣2t)cm,BQ=tcm,依题意得:(10﹣2t)t=6,整理得:t2﹣5t+6=0,解得:t1=2,t2=3.∴2或3秒时,△BPQ的面积是6cm2.故答案为:2或3.16.解:①∵a﹣b+c=0,∴当x=﹣1时,ax2+bx+c=a﹣b+c=0,∴x=﹣1为方程ax2+bx+c=0的一根,故结论①正确;②∵a﹣b+c=0,∴b=a+c,∴Δ=b2﹣4ac=(a+c)2﹣4ac=(a﹣c)2≥0,∴方程有两个实数根,故结论②错误;③∵a、c异号,a≠0,∴Δ=b2﹣4ac=b2+4a2>0,∴方程一定有两个不相等的实数根,故结论③正确;④∵x=m方程的一个根,∴am2+bm+c=0,∴(2am+b)2﹣(b2﹣4ac)=4a2m2+4abm+b2﹣b2+4ac=4a(am2+bm+c)=0,∴(2am+b)2=b2﹣4ac,故结论④正确;故答案为:①③④.三.解答题17.解:(1)方程整理为x2﹣8x﹣9=0,(x﹣9)(x+1)=0,x﹣9=0或x+1=0,所以x1=9,x2=﹣1;(2)(3x﹣1)2﹣(x+1)2=0,(3x﹣1+x+1)(3x﹣1﹣x﹣1)=0,3x﹣1+x+1=0或3x﹣1﹣x﹣1=0,所以x1=0,x2=1.18.(1)证明:∵Δ=(﹣k)2﹣4(k﹣1)=k2﹣4k+4=(k﹣2)2≥0,∴无论k取何值,该方程总有实数根;(2)解:解方程x2﹣kx+k﹣1=0得x1=k﹣1,x2=1,当k﹣1=1时,k=2,因为1+1=2,不符合三角形三边的关系,舍去;当k﹣1=2时,即k=3,三角形的三边为2、2、1,综上所述,k的值为3.19.(1)证明:关于x的一元二次方程x2﹣(m﹣3)x﹣m=0,∵(m﹣1)2≥0,∴Δ=(m﹣3)2﹣4×(﹣m)=m2﹣6m+9+4m=m2﹣2m+1+8=(m﹣1)2+8≥8>0,则方程有两个不相等的实数根;(2)由根与系数的关系可得:x1+x2=m﹣3,x1x2=﹣m,∵x12+x22﹣x1x2=13,∴(x1+x2)2﹣3x1x2=13,即(m﹣3)2+3m=13,整理得:m2﹣3m﹣4=0,即(m﹣4)(m+1)=0,所以m﹣4=0或m+1=0,解得:m=4或m=﹣1.20.解:(1)a2﹣2a+2=(a2﹣2a+1)+1=(a﹣1)2+1,∵(a﹣1)2≥0,∴(a﹣1)2+1≥1,即代数式a2﹣2a+2的最小值为1;故答案为:1;(2)a2+b2+11>6a﹣2b,理由如下:a2+b2+11﹣(6a﹣2b)=a2+b2+11﹣6a+2b=(a2﹣6a+9)+(b2+2b+1)+1=(a﹣3)2+(b+1)2+1,∵(a﹣3)2≥0,(b+1)2≥0,∴a2+b2+11>6a﹣2b;(3)∵a﹣b=2,∴a=b+2,∵ab+c2﹣4c+5=0,∴b(b+2)+c2﹣4c+5=0,∴(b+1)2+(c﹣2)2=0,∴b+1=0,c﹣2=0,∴b=﹣1,c=2,∴a=﹣1+2=1,∴a+b+c=1﹣1+2=2.21.解:(1)设BC=xm,则AB=m,依题意得:x•=300,整理得:x2﹣62x+600=0,解得:x1=12,x2=50.又∵墙EF最长可利用28m,∴x=12.答:当矩形的长BC为12m时,矩形花园的面积为300m2.(2)不能围成面积为480m2的矩形花园,理由如下:设BC=ym,则AB=m,依题意得:y•=480,整理得:y2﹣62y+960=0,解得:y1=30,y2=32.又∵墙EF最长可利用28m,∴y1=30,y2=32均不符合题意,舍去,∴不能围成面积为480m2的矩形花园.22.解:(1)设y关于x的函数解析式为y=kx+b(k≠0),将(2,60),(4,70)代入y=kx+b得:,解得:,∴y关于x的函数解析式为y=5x+50(0<x<10).(2)依题意得:(40﹣x﹣20)(5x+50)=1105,整理得:x2﹣10x+21=0,解得x1=3,x2=7.又∵要让顾客得到更大的实惠,∴x=7.答:这种榴莲每千克应降价7元.11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章期末复习练习
1、在下列方程中,属于一元二次方程的是( )
A 、2x 2+x=x
1-5 B 3x=1 C -5x 2+3y-2=0 D (a+4)2=9 2、用因式分解法解方程(2x-1)(3x+4)=x-4
3、已知一元二次方程(x-a)(2x-3)=6的一个根是x=0,求a 的植和方程的另一个根
4、用因式分解法解下列方程 y(y+5)=-4
25 3(x-3)=(x-3)2
(2x+3)2=24x 1.2y-0.04=9y 2
5、已知a 是一元二次方程(x+5)(2x-3)=-15的根,你能求出代数式
442-a +a
-22的值吗?
6、用配方法解下列方程 x 2-6x=-5 y 2+3y-2=0 a 2=6a-1 x 2-4x+3=0 2y 2+8y+7=0 -
2
1x 2-3x=1
7、用配方法解方程:x 2-5=23x 4x(x-3)+3=x 2
8、我们可以用配方的方法将多项式x 2+bx+c 化成(x+m)2+n 的形式,例如x 2-4x-3=(x-2)2-7。
请将多项式k 2-3k+5化成(k+m)2+n 的形式,并说明取任意实数时,它的值一定大于零的理由。
9、用公式法解下列方程
X 2+2x-3=0 -2m 2+4=-3m 23a 2-a-4
1=0 8y 2-2y-15=0
10、选择合适的方法解下列方程: x 2-2x=99 (2x-1)2+3(2x-1)=0
11、请阅读下列解方程x 4-2x 2-3=0的过程
解:设x 2=y ,则原方程可变形为y 2-2y-3=0
由(y-1)2=4,得y 1=3,y 2=-1
当y=3 x 2=3 ∴x 1=3 x 2=3
当y=-1 ,x 2=-1, 无解
所以,原方程的解为x 1=3 x 2=3
这种解方程的方法叫做换元法
用上述方法解下面两个方程: x 4-x 2-6=0 (x 2+2)2-2(x 2+2)-3=0
12、某企业两年前创办时的资金是1000万元,现在已有资金1440万元,求该企业这两年内资金的年平均增长率。
13、截止2021年底,某城市自然保护区的覆盖率为4%,尚未达到国家A级标准,因此市政府决定加快绿化建设,力争到2021年底自然保护区的覆盖率达到8%以上,若要达到最低目标8%,则这个城市自然保护区的年平均增长率是多少?(保留2个有效数字)
14、某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,经调查表明,单价在60元以内,这种台灯的售价每上涨1元,其销量就减少10个,为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?这时售出台灯多少个?
15、小明用如图所示的正方形纸板,剪去角上四个小正方形后做一个无盖纸盒,做成的无盖纸盒高6厘米,容积为384立方厘米,那么这块正方形纸板的边长是多少厘米?
16、在宽20米,长32米的长方形耕地上修筑同样宽的三条道路(两纵一横),把耕地分成大小相等的6块实验地,问要使实验地的总面积为570平方米,道路宽为多少米?
17、如图,长方形面长4米,宽2米,一块长方形台布的面积是桌面面积的3倍,将这块台
18、如图,在△ABC中,∠A=900,AB=24cm,AC=16cm,现有动点P从点B出发,沿射线方向BA运动,动点Q从点C出发,沿射线CA方向运动,已知点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,问经过几秒,△APQ的面积是△ABC面积的一半?
19、如图,某公司计划用32米长的材料沿墙建造一个面积为120平方米的长方形仓库,仓库的一边靠墙,墙长16米,你认为这个计划可行吗?如果可行,请求出仓库的长和宽,如果不可行,请说明理由。
20、已知等腰三角形底边长为9,腰长是方程x2-10x+24=0的一个根,求这个三角形的周长。
21、某省2021年治理水土流失面积400平方千米,并逐年加大了治理力度,每年治理水土流失面积比前一年增长相同的白分点,到2021年底,这三年共治理水土流失面积1324平方千米,求该省2020-2021年每年治理水土流失面积比前一年增长的百分数。
22、大众旅行社吸引市民组团去某地旅游,特推出了如下收费标准:如果人数不超过25人,人均旅游费用降低20元,但人均旅游费用不低于700元,某单位组织员工去该地旅游,共支付给大众旅游费用27000元,请问该单位这次共有多少员工去该地旅游?。
