8 轮系 习题答案
8 轮系 习题答案
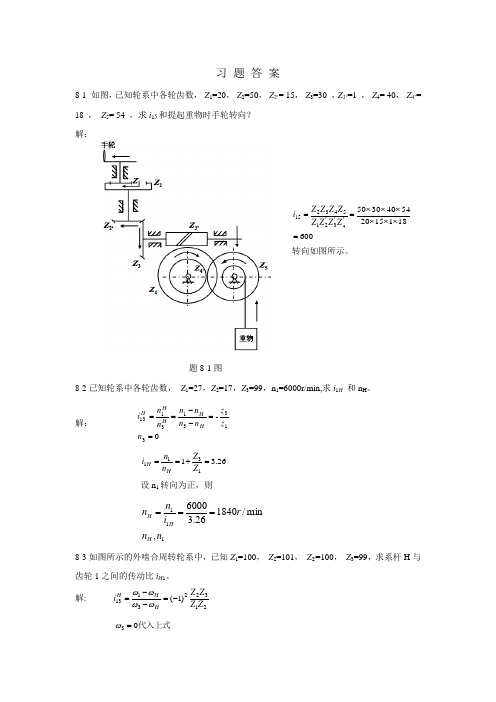
习 题 答 案8-1 如图,已知轮系中各轮齿数, Z 1=20, Z 2=50, Z 2‘= 15, Z 3=30 ,Z 3‘=1 , Z 4= 40, Z 4’= 18 , Z 5= 54 ,求i 15和提起重物时手轮转向?解:600181152054403050''3'215432154=⨯⨯⨯⨯⨯⨯==Z Z Z Z Z Z Z Z i转向如图所示。
题8-1图8-2已知轮系中各轮齿数, Z 1=27,Z 2=17,Z 3=99,n 1=6000r/min,求i 1H 和n H 。
解: 0-313313113==--==n z z n n n n n n i H H H HH26.311311=+==Z Z n n i H H 设n 1转向为正,则111,min /184026.36000n n r i n n H H H ===8-3如图所示的外啮合周转轮系中,已知Z 1=100, Z 2=101, Z 2'=100, Z 3=99,求系杆H 与齿轮1之间的传动比i H 1。
解:213223113)1(Z Z Z Z i H H H -=--=ωωωω 代入上式03=ω100100991011'21321⨯⨯=⨯⨯=-Z Z Z Z H ωω 100001100009999111=-==H H i ωω 1000011==∴ωωH H i 8-4 图示圆锥齿轮组成的周转轮系中,已知Z 1=20, Z 2=30, Z 2‘=50, Z 3=80,n 1=50r/min. 求系杆H 转速。
题8-4图解: '213231Z Z Z Z n n n n H H ⨯⨯-=-- 等式右边的符号是在转化轮系中确定的。
设n1转向为正,则50208030050⨯⨯-=--H H n n min /7.14r n H =∴ 与n1转向相同,方向的判定如图所示。
8-5 如图为标准圆柱直齿轮传动系统,已知Z 1=60, Z 2=20, Z 2‘=25,各轮模数相等,求:1)Z 3;2)若已知n 3=200r/min, n 1=50r/min, n 3,n 1转向如图,求系杆H 转速大小和方向;3)若n 1方向与图中相反时,则系杆H 转速大小和方向如何?解:1)首先根据同心条件求出Z 3)(21)(213'221Z Z m Z Z m +=- 153=Z 2)'21323113Z Z Z Z n n n n i H H H ⨯⨯-=--= 2560152020050⨯⨯-=--H H n n min /75r n H =∴ 转向与n1一致 3)当n1方向相反时,以-50r/min 代入,则2560152020050⨯⨯-=---H H n n min /33.8r n H -=∴ m i n /33.8r n H -=∴转向与n1一致8-6 图示轮系中,已知各轮齿数为Z 1=60,Z 2=20,Z 2‘=20,Z 3=20,Z 4=20,Z 5=100,试求传动比i 41。
机械原理轮系习题参考答案

一、解:(1)判断方向,蜗杆左旋用左手右旋用右手,四指握向蜗杆转动方向,拇指指向的反方向即为涡轮转向。
由此逆向判断图中蜗杆、涡轮和齿轮旋转方向如图中箭头所示。
手柄转向如图所示。
4001
601836186056341265432116=××=••=••=z z z z z z w w w w w w i 二、解:该轮系为周转轮系,由反转法对整个轮系加一个反向旋转角速度H w −,
由于齿轮4为定齿轮,角速度为零,即04=w ,所以H H i i 14
11−=; 又有 2.2)1(3423123
14−=•••−=z z z z z z i H
所以 2.32.211=+=H i
三、解:此轮系中假设轮1的方向向下,则行星轮2、2'和太阳轮4的转向都是
向下。
行星轮2、2'和行星架的角速度相同 在左边行星轮系中,1
3
1H 130z z H H −=−−=ωωωω 在右边行星轮系中,'2
444'2z z H ==ωωωω ∴4114ωω=i ==+4'2131z z z z z 25416
四、解:该轮系可以分为两部分,如图中虚线所分的左右两部分,左边为周转轮系,右边为定轴轮系;
分别求出两个轮系的传动比如下:
周转轮系:=H i 1414
1556601441===++z z n n n n H H ; 定轴轮系:7
63530566556====z z n n i ; 两轮系的关系是:
45n n =; 联立方程组求得min 9.741r n ≈; 转向与齿轮6转向相反。
第六章轮系测试题及答案

第六章轮系测试题及答案一、选择题1. 齿轮传动中,齿数比是指()。
A. 齿轮的齿数B. 两个齿轮的齿数之比C. 齿轮的直径比D. 齿轮的周长比答案:B2. 轮系中,行星轮的作用是()。
A. 传递动力B. 改变传动比C. 改变旋转方向D. 以上都是答案:D3. 在齿轮传动中,如果主动轮的转速为1000转/分钟,从动轮的齿数是主动轮的两倍,那么从动轮的转速为()。
A. 500转/分钟B. 2000转/分钟C. 1000转/分钟D. 无法确定答案:A二、填空题1. 轮系中,如果主动轮的齿数为30,从动轮的齿数为60,那么齿数比为______。
答案:1:22. 在一个行星轮系中,太阳轮的转速为200转/分钟,行星轮的转速为100转/分钟,那么行星架的转速为______。
答案:150转/分钟三、简答题1. 请简述轮系的基本组成。
答案:轮系通常由主动轮、从动轮、行星轮和行星架组成。
2. 轮系在机械传动中有什么作用?答案:轮系在机械传动中主要用于改变转速和扭矩,实现动力的传递和分配。
四、计算题1. 已知一个齿轮传动系统,主动轮齿数为40,从动轮齿数为80,求传动比。
答案:传动比为2:1。
2. 一个行星轮系中,太阳轮齿数为20,行星架固定,行星轮齿数为40,求行星轮的转速,如果太阳轮的转速为500转/分钟。
答案:行星轮的转速为1000转/分钟。
五、论述题1. 论述齿轮传动和轮系传动在机械设计中的重要性。
答案:齿轮传动和轮系传动在机械设计中具有至关重要的作用。
它们不仅可以实现动力的高效传递,还可以通过改变齿数比来调整转速和扭矩,满足不同的工作需求。
此外,轮系传动还可以实现复杂的运动控制,如改变旋转方向和实现多轴驱动等,对于提高机械设备的性能和灵活性具有重要意义。
第11章-轮系习题答案

一、填空题:1.轮系可以分为:定轴轮系和 周转轮系 。
2.定轴轮系是指:当轮系运动时,各轮轴线位置固定不动的轮系;周转轮系是指:轮系运动时,凡至少有一个齿轮的轴线是绕另一齿轮的轴线转动的轮系。
3.周转轮系的组成部分包括: 太阳轮 、 行星轮 和 行星架 。
4.行星轮系具有 1个自由度,差动轮系有 2自由度。
5、行星轮系的同心条件是指:要使行星轮系能正常运转,其基本构件的回转线必须在同一直线上。
6、确定行星轮系中各轮齿数的条件包括:传动比条件、同心条件、均布条件、邻接条件。
7、正号机构和负号机构分别是指:转化轮系的传动比H 1n i 为正号或者负号的周转轮系。
动力传动中多采用 负号 机构。
二、分析计算题 1、在图示的车床变速箱中,移动三联齿轮a 使3’和4’啮合。
双移动双联齿轮b 使齿轮5’和6’啮合。
已知各轮的齿数为z 1=42,582=z ,38'3=z ,42'4=z ,48'5=z ,48'6=z 电动机的转速为n 1=1445r/min ,求带轮转速的大小和方向。
解:3858483842484258'5'31'6'426116-=⨯⨯⨯⨯=-==z z z z z z n n i min /9466r n -=(与电动机转动方向相反)2、在图示的轮系中,已知各轮齿数为20z z z z z 65321=====, 已知齿轮1、4、5、7为同轴线,试求该轮系的传动比17i 。
(1)z z z z z 41231225520100=++==⨯=z z z z 75612332060=+==⨯=(2)iz z z z zz z z z z17323467123561=-()=-⨯⨯=-100602020153、在图示轮系中,已知:蜗杆为单头且右旋,转速n11440= r/min,转动方向如图示,其余各轮齿数为:402=z,20'2=z,303=z,18'3=z,544=z,试:(1)说明轮系属于何种类型;(2)计算齿轮4得转速n4;(3)在图中标出齿轮4的转动方向。
第六章 轮系计算题专项训练(附答案)

第六章轮系计算题专项训练(附答案)1、已知齿数和转速,求蜗轮的转速和各轮的回转方向。
齿数和转速的关系可以用传动比公式i=n1/n4来表示,因此先求出传动比i,再用i和n1求出n4.i的计算公式为i=z2z4z5z6/z1z2'z4'z5',代入数据计算得到i=220.7.然后代入i 和n1=800r/min,求得n4=3.62r/min。
回转方向可以根据齿轮的齿数和传动方式(直接传动或倒置传动)来确定。
2、已知各轮的齿数,求传动比i。
传动比的计算公式为i=z2z4z5z6/z1z2'z4'z5',代入数据计算得到i=16.3、已知各轮的齿数和蜗杆的参数,求传动比i。
传动比的计算公式同样为i=z2z4z5z6/z1z2'z4'z5',代入数据计算得到i=17.4、已知各轮的齿数和主动轴的转速,求齿轮5的转速和方向。
先用传动比公式i=n1/n5求得i=200,再用i和n1=500r/min求得n5=2.5r/min。
齿轮5的方向可以根据箭头来确定。
5、已知各轮的齿数,求传动比i。
传动比的计算公式同样为i=z2z4z5z6/z1z2'z4'z5',代入数据计算得到i=16.6、已知各轮的齿数和主动轴的转速,求传动比i和齿轮5的转动方向。
传动比的计算公式同样为i=z2z4z5z6/z1z2'z4'z5',代入数据计算得到i=40.齿轮5的方向可以根据箭头来确定。
7、已知各轮的齿数和蜗杆的参数,求传动比i和轮6的转速和方向。
传动比的计算公式同样为i=z2z4z5z6/z1z2'z4'z5',代入数据计算得到i=4.轮6的转速可以用传动比公式i=n1/n6求得,代入n1=1200r/min和i=4计算得到n6=300r/min。
轮6的方向可以根据蜗杆的旋转方向和箭头来确定。
朱明zhubob机械设计基础第7.8.9章轮系习题答案

第七章1.轮系的分类依据是什么?轮系在运转过程中各轮几何轴线在空间的相对位置关系是否变动2.怎样计算定轴轮系的传动比?如何确定从动轮的转向?定轴轮系的传动比等于组成轮系的各对齿轮传动比的连乘积,也等于从动轮齿数的连乘积与主动轮齿数的连乘积之比。
对于首末两轮的轴线相平行的轮系,其转向关系用正、负号表示。
还可用画箭头的方法来确定齿轮的转向3.定轴轮系和周转轮系的区别有哪些?定轴轮系是指在轮系运转过程中,各个齿轮的轴线相对于机架的位置都是固定的。
周转轮系是指在轮系运转过程中,其中至少有1个齿轮轴线的位置不固定,而是绕着其他齿轮的固定轴线回转4.怎样求混合轮系的传动比?分解混合轮系的关键是什么?如何划分?在计算复合轮系时,首要的问题是必须正确地将轮系中的各组成部分加以划分。
而正确划分的关键是要把其中的周转轮系部分找出来。
周转轮系的特点是具有行星轮和行星架,所以要找到轮系中的行星轮,然后找出行星架(行星架往往是由轮系中具有其他功用的构件所兼任)。
每一行星架,连同行星架上的行星轮和行星轮相啮合的太阳轮就组成一个基本的周转轮系,当周转轮系一一找出之后,剩下的便是定轴轮系部分了5.轮系的设计应从哪些方面考虑?考虑机构的外廓尺寸、效率、重量、成本等。
根据工作要求和使用场合合理地设计对应的轮系。
6.如图7-32所示为一蜗杆传动的定轴轮系,已知蜗杆转速n 1 = 750 r/min ,z 1 = 3,z 2 = 60,z 3 = 18,z 4 = 27,z 5 = 20,z 6 = 50。
试用画箭头的方法确定z 6的转向,并计算其转速。
答:齿轮方向向左,n6=75r/min7.如图7-33示为一大传动比的减速器,z 1 = 100,z 2 = 101,z 2 = 100,z 3 = 99。
求:输入件H 对输出件1的传动比i H1。
图7-32 蜗杆传动的定轴轮系 图7-33 减速器 答:100001 H i8.如图7-34所示为卷扬机传动示意图,悬挂重物G 的钢丝绳绕在鼓轮5上,鼓轮5与蜗轮4连接在一起。
学习情境8 轮系

2.代入已知转速时,必须带入符号,一般先假设某一方向正, 相同以正值带入, 相反以负值带入,求得的转速与哪个已知量的符号相同就与谁的转向相同。 3. i H 不是周转轮系的传动比.
GK
圆锥齿轮组成的周转轮系
2 O 1
Z 2 Z3 W1 WH i W3 WH Z1Z 2
H 13
H
3
温故而知新
1.齿轮传动比; 2.齿轮啮合的转动方向。
学习情境8
轮系
在生产实践中,一对齿轮传动往往无法满足大的传动比、多种转速、 多种转向等的要求,于是就发展了轮系。
(何谓轮系?)定义: 由一系列齿轮组成的传动系统称为轮系。
知识目标:
1.了解轮系的功用,熟悉轮系的类型; 2.掌握轮系的传动比的计算; 3.掌握轮系的传动方向的判定。
5分 5分ห้องสมุดไป่ตู้5分 5分 5分 5分 10分 10分 10分 10分 15分 15分
积极【5】;一般【3】;不积极【0】 全部【5】;一半【3】;没有【1】 全勤【5】;缺两次【3】;30%【0】 强【5】;一般【3】;不强【1】 强【5】;一般【3】;不强【0】 强【5】;一般【3】;不强【1】 强【10】;一般【6】;不强【2】 强【10】;一般【6】;不强【2】 积极【10】;一般【6】;较差【2】 好【10】;一般【6】;较差【2】 好【15】;一般【10】;较差【5】 【0】-【15】
答案: 14.5
轮系在生产实践中应用广泛,如减速器中、手表中、机床中等。具体的应用种类也很多, 为了便于识别和应用,先熟悉各种轮系。
1、按照各个齿轮的轴线是否全部平行分为:平行轴轮系和 非平行轴轮系。
3 1 2 4 2 5 (a) (b) 1 右旋蜗杆 3
机械设计基础课后习题答案(第五版)(完整版)

机械设计基础(第五版)课后习题答案(完整版 )高等教育出版社杨可桢、程光蕴、李仲生主编1-1 至 1-4 解机构运动简图如下图所示。
图 1.11 题 1-1 解图图 1.12题1-2解图图 1.13 题 1-3 解图图 1.14题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3 的角速比为:1-14解该正切机构的全部瞬心如图所示,构件 3 的速度为:,方向垂直向上。
1-15解要求轮 1 与轮 2 的角速度之比,首先确定轮1、轮 2和机架 4 三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16 解( 1)图 a 中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
( 2)图 b 中的CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b 中机构的自由度为:所以构件之间能产生相对运动。
题 2-1 答 : a),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题 2-2 解 : 要想成为转动导杆机构,则要求与均为周转副。
( 1 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
( 2 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题2-3 见图 2.16 。
图 2.16题 2-4 解 : (1)由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转/分钟题2-5解 : (1)由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 答 案
8-1 如图,已知轮系中各轮齿数, Z 1=20, Z 2=50, Z 2‘= 15, Z 3=30 ,Z 3‘=1 , Z 4= 40, Z 4’= 18 , Z 5= 54 ,求i 15和提起重物时手轮转向?
解:
600
181152054403050''3'215
432154=⨯⨯⨯⨯⨯⨯==Z Z Z Z Z Z Z Z i
转向如图所示。
题8-1图
8-2已知轮系中各轮齿数, Z 1=27,Z 2=17,Z 3=99,n 1=6000r/min,求i 1H 和n H 。
解: 0
-313313113==--==n z z n n n n n n i H H H H
H
26.311
311=+==Z Z n n i H H 设n 1转向为正,则
1
11,min /184026.36000n n r i n n H H H ===
8-3如图所示的外啮合周转轮系中,已知Z 1=100, Z 2=101, Z 2'=100, Z 3=99,求系杆H 与齿轮1之间的传动比i H 1。
解:
213223113)1(Z Z Z Z i H H H -=--=ωωωω 代入上式03=ω
100
100991011'21321⨯⨯=⨯⨯=-Z Z Z Z H ωω 10000
1100009999111=-==H H i ωω 1000011==
∴ωωH H i 8-4 图示圆锥齿轮组成的周转轮系中,已知Z 1=20, Z 2=30, Z 2‘=50, Z 3=80,n 1=50r/min. 求系杆H 转速。
题8-4图
解: '
213231Z Z Z Z n n n n H H ⨯⨯-=-- 等式右边的符号是在转化轮系中确定的。
设n1转向为正,则
50
208030050⨯⨯-=--H H n n min /7.14r n H =∴ 与n1转向相同,方向的判定如图所示。
8-5 如图为标准圆柱直齿轮传动系统,已知Z 1=60, Z 2=20, Z 2‘=25,各轮模数相等,求:
1)Z 3;
2)若已知n 3=200r/min, n 1=50r/min, n 3,n 1转向如图,求系杆H 转速大小和方向;
3)若n 1方向与图中相反时,则系杆H 转速大小和方向如何?
解:
1)首先根据同心条件求出Z 3
)(2
1)(213'221Z Z m Z Z m +=- 153=Z 2)'
21323113Z Z Z Z n n n n i H H H ⨯⨯-=--= 25
60152020050⨯⨯-=--H H n n min /75r n H =∴ 转向与n1一致 3)当n1方向相反时,以-50r/min 代入,则
25
60152020050⨯⨯-=---H H n n min /33.8r n H -=∴ m i n /33.8r n H -=∴转向与n1一致
8-6 图示轮系中,已知各轮齿数为Z 1=60,Z 2=20,Z 2‘=20,Z 3=20,Z 4=20,Z 5=100,试求传动比i 41。
解:为求解传动比,可以将该轮系划分为由齿轮1、2、2′、5和行星架H 所组成的行星轮系,
得: 3
5206010020'21525115-=⨯⨯-=-=--=z z z z i H H H ωωωω 由 ,05=ω 得
3
81=H ωω 8
31ωω=H (1) 由齿轮2′,3,4,5和行星架H 所组成得行星轮系,得
520
100455445===--=z z i H H H ωωωω 4514-=-=H ωω 所以:148
341ωω=- 传动比为:2
31441-==ωωi 8-7如图所示为用于自动化照明灯具上的周转轮系,已知输入轴转速n 1=19.5r/min ,各轮齿数Z 1=60, Z 2= Z 2‘= 30, Z 3=40, Z 4= 40, Z 5= 120,试求箱体转速?
解: n 5=0
4
'21532
35115)1(Z Z Z Z Z Z n n n n i H H H -=--= min /5.6r n H =∴ 转向与n1一致
8-8 已知图示轮系中各轮齿数,Z 1=30,Z 4= Z 5=21,Z 2=24,Z 3=Z 6=40,Z 7=30,Z 8=90,n 1=960r/min ,方向如图示,求n H 的大小和方向。
解:
6340)1(42
.096042.042.040
2130248467865186681434124114==-=-=--===∴====n n n z z z z n n n n i n n z z z z n n i H H H
由于其中
min /888r n H = n H 转向的箭头向上。
8-9已知 Z 1=30, Z 2=30, Z 2‘=20, Z 3=90,Z 3’=40, Z 4=30, Z 4’=30, Z 5=15 ,Z 1‘=40,求i ⅠⅡ。
解:i ⅠⅡ= i 4H
在周转轮系中:
1
331Z Z n n n n H H -=-- 31
3'3'1-=-=--Z Z n n n n H H
在定轴轮系中:
4'1'144'
14
3n n Z Z n n =⇒= 4'3'
344'343n n Z Z n n -=⇒-= 3
844-===III H H n n i i 8-10 已知 Z 1=12, Z 2=51, Z 3=76, Z 4=49, Z 5=12 ,Z 6=73,求此混合轮系传动比i 1H 。
解:在周转轮系中:
4
66446Z Z n n n n i H H H -=--= 在定轴轮系中:
1221Z Z n n -= 所以:14217
4n n n -== 1331Z Z n n = 所以:16319
3n n n == 3940611-==H
H n n i 8-11 如图所示轮系,已知锥齿轮齿数Z 1=Z 4=55, Z 5=50,其余各圆柱直齿轮齿数 Z 1‘=100, Z 2= Z 2’= Z 3= Z 4‘ =20, n 6=3000r/min ,转向如图,求n 4、 n 1大小和方向。
解:在周转轮系中:
5
13'2'1432'4'141'''==--=Z Z Z Z Z Z n n n n i H H H 在定轴轮系中:
11
4514514-=-=-=Z Z Z Z Z Z i 得:反向与同向
与6'446'11m in,/2000m in,/2000n r n n n r n n -====
8-12如图所示的轮系中,各齿轮均为标准齿轮,已知各齿轮齿数为z 1=18,z 1’=80,z 2=20,z 3=36,z 3’=24,z 4’=80,z 5=50,z 6=2(左旋),z 7=58,试求:
(1) 齿数z 4;
(2) 传动比17i ;
(3) 已知轮1转向如图所示,试确定轮7的转向。
解:(1) 根据同轴条件
433212r r r r r +=++
4'33212
222z m z m z m mz z m +=++ 702436202182'33244=-+⨯+=-++=z z z z z
(2) 划分轮系
1、2、3-3’、4、6组成周转轮系;
1’、5、4’组成定轴轮系;
6、7组成定轴轮系,于是有
6
3524187036'31436461614-=⨯⨯-=-=--=z z z z n n n n i (1) 180
80'1'441'4'1-=-=-==z z n n i (2) 29258677667====
z z n n i (3) 由式(2)得14n n -=,将其带入式(1)
6356161-=---n n n n 6
351/1/6161-=---n n n n 得
294161-=n n ,负号说明轮6与轮1方向相反,取其绝对值并将其与式(3)相乘得
412929
4176617117=⨯-=⨯==n n n n n n i (3) 1n 与6n 方向相反,在根据左手定则可确定蜗轮7顺时针方向回转。
