高中数学必修2第一章1-1-1课件
合集下载
北师大版高中数学选择性必修2第一章1.1数列的概念课件PPT
北师大版高中数学教材 选择性必修第二册
第一章 数列
§1：数列的概念
知识与技能：
（1）通过实例，理解数列的概念； （2）理解数列的项和项数,通项的含义,了解数列的分类， 理解数列与函数的关系。
过程与方法：
（1）让学生从日常生活中的实际问题出发，引导学生通 过视察，推导，归纳抽象出数列的概念； （2）通过实例说明项,项数,通项的含义。
（2）数列中的数是可以重复出现，而数集中的元素 具有互异性，不能有相同的元素出现。
情情境境导导入入 新课讲授 讲练巩固 课堂小结 课后作业
2、数列的项：数列中的每一个数都叫做这个数
列的项.各项依次叫做这个数列的第 1 项(或首
项)，第 2项，…，第 n 项，….
项 a1 a2
a3 a4 a5 a6
（－1）n或（－1）n＋1常常用来表示正负相间的变化规律． （4）对于周期出现的数列，考虑利用周期函数的知识解答．
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
➽目标检测
1、下列数列既是递增数列，又是无穷数列的是（ D ）
A．1，2，3，…，20 B．－1，－2，－3，…，－n，… C．1，2，3，2，5，6，…
《庄子·天下篇》
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
情境二：大自然是懂数学的.
树木的分杈、花瓣的数量、植物种子的排列...... 都遵循了某种数学规律.
斐波那契数
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
大自然是懂数学的.
树木的分杈、花瓣的数量、植物种子的排列...... 都遵循了某种数学规律. 斐波那契数 1，1，2，3，5，8，13，21，34，55，89，......
第一章 数列
§1：数列的概念
知识与技能：
（1）通过实例，理解数列的概念； （2）理解数列的项和项数,通项的含义,了解数列的分类， 理解数列与函数的关系。
过程与方法：
（1）让学生从日常生活中的实际问题出发，引导学生通 过视察，推导，归纳抽象出数列的概念； （2）通过实例说明项,项数,通项的含义。
（2）数列中的数是可以重复出现，而数集中的元素 具有互异性，不能有相同的元素出现。
情情境境导导入入 新课讲授 讲练巩固 课堂小结 课后作业
2、数列的项：数列中的每一个数都叫做这个数
列的项.各项依次叫做这个数列的第 1 项(或首
项)，第 2项，…，第 n 项，….
项 a1 a2
a3 a4 a5 a6
（－1）n或（－1）n＋1常常用来表示正负相间的变化规律． （4）对于周期出现的数列，考虑利用周期函数的知识解答．
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
➽目标检测
1、下列数列既是递增数列，又是无穷数列的是（ D ）
A．1，2，3，…，20 B．－1，－2，－3，…，－n，… C．1，2，3，2，5，6，…
《庄子·天下篇》
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
情境二：大自然是懂数学的.
树木的分杈、花瓣的数量、植物种子的排列...... 都遵循了某种数学规律.
斐波那契数
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
情境导入 新课讲授 讲练巩固 课堂小结 课后作业
大自然是懂数学的.
树木的分杈、花瓣的数量、植物种子的排列...... 都遵循了某种数学规律. 斐波那契数 1，1，2，3，5，8，13，21，34，55，89，......
第一章角的概念推广、象限角及其表示-【新】北师大版高中数学必修第二册PPT全文课件
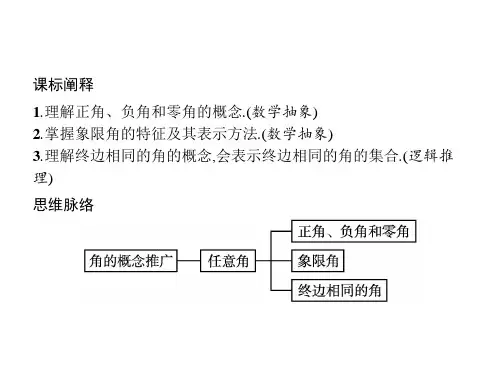
解得1294≤k<6274.
又k∈Z,所以k=1,或k=2. 当k=1时,β=435°; 当k=2时,β=795°.
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
激趣诱思
知识点拨
微思考1 60°,-660°,-300°,420°,780°的角的终边有什么关系? 提示相同.-660°=60°-2×360°,-300°=60°-360°, 420°=60°+360°,780°=60°+2×360°. 微思考2 如何表示与60°终边相同的角的集合? 提示S={β|β=60°+k·360°,k∈Z}.
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
探究一
探究二
探究三
当堂检测
反思感悟 概念辨析问题的求解方略 对于概念辨析题,一是利用反例排除错误答案,二是利用定义直接 判断.本题需要准确理解象限角、锐角、钝角、终边相同的角等基 本概念才能作出正确的判断.
探究三
当堂检测
反思感悟 象限角的判定 1.已知一个角的大小判断其所在象限时,可先根据终边相同的角的 表示方法,找到在[0°,360°)内与之终边相同的角,再确定其象限. 2.已知角的终边所在的象限,求待求角的终边所在的位置时,通常首 先根据所给已知角的范围,得到待求角的范围,然后判断待求角终 边所在的位置.
又k∈Z,所以k=1,或k=2. 当k=1时,β=435°; 当k=2时,β=795°.
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
激趣诱思
知识点拨
微思考1 60°,-660°,-300°,420°,780°的角的终边有什么关系? 提示相同.-660°=60°-2×360°,-300°=60°-360°, 420°=60°+360°,780°=60°+2×360°. 微思考2 如何表示与60°终边相同的角的集合? 提示S={β|β=60°+k·360°,k∈Z}.
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
第一章角的概念推广、象限角及其表 示-【新 】北师 大版高 中数学 必修第 二册PP T全文 课件【 完美课 件】
探究一
探究二
探究三
当堂检测
反思感悟 概念辨析问题的求解方略 对于概念辨析题,一是利用反例排除错误答案,二是利用定义直接 判断.本题需要准确理解象限角、锐角、钝角、终边相同的角等基 本概念才能作出正确的判断.
探究三
当堂检测
反思感悟 象限角的判定 1.已知一个角的大小判断其所在象限时,可先根据终边相同的角的 表示方法,找到在[0°,360°)内与之终边相同的角,再确定其象限. 2.已知角的终边所在的象限,求待求角的终边所在的位置时,通常首 先根据所给已知角的范围,得到待求角的范围,然后判断待求角终 边所在的位置.
新人教B版高中数学必修二教学课件 第一章 立体几何初步 1.2.3《(第2课时)平面与平面垂直》
∵PA⊥平面ABC，BC⊂平面ABC， ∴PA⊥BC， ∵AD∩PA＝A，∴BC⊥平面PAC， 又AC⊂平面PAC，∴BC⊥AC．
[点评]
已知条件是线面垂直和面面垂直，要证明两条直
线垂直，应将两条直线中的一条放入一平面中，使另一条直线 与该平面垂直，即由线面垂直得到线线垂直．在空间图形中， 高一级的垂直关系蕴含着低一级的垂直关系，通过本题可以看 到：面面垂直⇒线面垂直⇒线线垂直．
求证：平面ABC⊥平面SBC．
[ 解析]
解法一：取 BC 的中点 D，连接 AD、SD.
由题意知△ASB 与△ASC 是等边三角 形，则 AB＝AC． ∴AD⊥BC，SD⊥BC． 2 令 SA＝a，在△SBC 中，SD＝ 2 a， 2 又∵AD＝ AC －CD ＝ 2 a，
2 2
∴AD2＋SD2＝SA2. 即 AD⊥SD.又∵AD⊥BC，∴AD⊥平面 SBC． ∵AD⊂平面 ABC， ∴平面 ABC⊥平面 SBC．
[解析]
∵△ABC为正三角形，D为BC的中点，
∴AD⊥BC． 又∵CC1⊥底面ABC，AD⊂平面ABC， ∴CC1⊥AD. 又BC∩CC1＝C， ∴AD⊥平面BCC1B1. 又AD⊂平面AC1D，
∴平面AC1D⊥平面BCC1B1.
三棱锥 S －ABC 中，∠ BSC ＝ 90°，∠ ASB＝ 60°，∠ ASC ＝60°，SA＝SB＝SC．
当 F 为 PC 的中点时，满
足平面 DEF⊥平面 ABCD. 取 AD 的中点 G，PC 的中点 F，连 接 PG、BG、DE、EF、DF，则 PG⊥ AD，而平面 PAD⊥面 ABCD， 所以 PG⊥平面 ABCD.在△PBC 中， EF∥PB； 在菱形 ABCD 中，GB∥DE，而 EF⊂平面 DEF，DE⊂平面 DEF，EF∩DE ＝E，∴平面 DEF∥平面 PGB.又 PG⊥平面 ABCD，PG⊂平面 PGB， ∴平面 PGB⊥平面 ABCD，∴平面 DEF⊥平面 ABCD.
【同步课堂】人教A版高中数学必修2第一章1.1.1-2空间几何体的结构课件(共40张PPT)
棱柱 ２．其余各面都是四边形（侧面）
３．每相邻两个侧面的公共边（侧棱）都互 相平行
10
探究问题 1：
长方体按如图截去一角后所得的两部分还是棱柱 吗？
D’
C’
A’
B’
D C
A
B
11
探究问题 2：
有两个面互相平行,其余各面都是平行四边形的几 何体是棱柱吗? 定义: 1、有两个面互相平行，
2、其余各面都是四边形，
D
C 底面
的侧棱。
A
B
棱锥可以表示为：棱锥S-ABCD
底面是三角形，四边形，五边形----的棱锥分 别叫三棱锥，四棱锥，五棱锥---
13
思考：一个棱锥至少有几个面？一个N棱锥有分别 有多少个底面和侧面？有多少条侧棱？有多少个 顶点？
至少有4个面；1个底面，N个侧面，N条侧棱，1个顶 点.
14
练习：下列几何体是不是棱锥,为什么?
旋转体: 由一个平面图形绕它所在平面内的
一条定直线旋转所形成的封闭几何体
注：棱柱与圆柱统称为柱体
5
1.棱柱的结构特征：
①有两个面互相平行 ②其余各面都是四边形
③每相邻两个四边形的公共边互相平行
有两个面互相平行，其余各面都是四边形，每相邻两个四
边形的公共边互相平行，由这些面围成的图形叫做棱柱
6
1、棱柱 1、两个互相平行的面叫棱柱的底面。
3、每相邻两个四边形的公共边 都互相平行。
12
2.棱锥的结构特征
有一个面是多边形，其余各面都是有一个公共顶
点的三角形，由这些面所围成的多面体叫做棱锥.
底面：棱锥中的多边形面叫做棱锥的底面或底。 S 顶点
侧面：有公共顶点的各个三角形面叫做棱锥
３．每相邻两个侧面的公共边（侧棱）都互 相平行
10
探究问题 1：
长方体按如图截去一角后所得的两部分还是棱柱 吗？
D’
C’
A’
B’
D C
A
B
11
探究问题 2：
有两个面互相平行,其余各面都是平行四边形的几 何体是棱柱吗? 定义: 1、有两个面互相平行，
2、其余各面都是四边形，
D
C 底面
的侧棱。
A
B
棱锥可以表示为：棱锥S-ABCD
底面是三角形，四边形，五边形----的棱锥分 别叫三棱锥，四棱锥，五棱锥---
13
思考：一个棱锥至少有几个面？一个N棱锥有分别 有多少个底面和侧面？有多少条侧棱？有多少个 顶点？
至少有4个面；1个底面，N个侧面，N条侧棱，1个顶 点.
14
练习：下列几何体是不是棱锥,为什么?
旋转体: 由一个平面图形绕它所在平面内的
一条定直线旋转所形成的封闭几何体
注：棱柱与圆柱统称为柱体
5
1.棱柱的结构特征：
①有两个面互相平行 ②其余各面都是四边形
③每相邻两个四边形的公共边互相平行
有两个面互相平行，其余各面都是四边形，每相邻两个四
边形的公共边互相平行，由这些面围成的图形叫做棱柱
6
1、棱柱 1、两个互相平行的面叫棱柱的底面。
3、每相邻两个四边形的公共边 都互相平行。
12
2.棱锥的结构特征
有一个面是多边形，其余各面都是有一个公共顶
点的三角形，由这些面所围成的多面体叫做棱锥.
底面：棱锥中的多边形面叫做棱锥的底面或底。 S 顶点
侧面：有公共顶点的各个三角形面叫做棱锥
人教B版高中数学必修二课件第一章1.1.6棱柱、棱锥、棱台和球的表面积
法二：延长正四棱台的侧棱交于点 P， 如图设 PB1＝x， 则x＋x 8＝48，得 x＝8. ∴PB1＝B1B＝8， ∴E1 为 PE 的中点 ∴PE1＝ 82－22＝2 15， PE＝2PE1＝4 15.
∴S ＝S －S 正棱台侧
大正棱锥侧
小正棱锥侧
＝4×12×8×PE－4×12×4×PE1
＝4×12×8×4 15－4×12×4×2 15
[通一类] 4．(2012·枣庄高一检测)已知一个表面积为120cm2的正 方体的四个顶点在半球的球面上，四个顶点在半球的
底面上，求半球的表面积．
解：如图，为过正方体对角面的截面图．设正方体的棱长为 a， 半球的半径为 R， 由 6a2＝120 得 a2＝20， 在 Rt△AOB 中，AB＝a，OB＝ 22a， 由勾股定理，得 R2＝a2＋( 22a)2＝32a2＝30. 所以半球的表面积为 S＝2πR2＋πR2＝3πR2＝3×30π＝90π(cm2)．
＝48 15(cm2)．
∴正四棱台的侧面积为 48 15 cm2.
[研一题] [例3] 正四棱台两底面边长分别为a和b(a<b)．若侧棱所在 直线与上、下底面正方形中心的连线所成的角为45°，求 棱台的侧面积． [自主解答] 如图， 设O1，O分别为上、下底面的中心， 过C1作C1E⊥AC于E，过E作EF⊥BC 于F，连接C1F， 则C1F为正四棱台的斜高． 由题意知∠C1CO＝45°，
∴球的表面积 S＝4πR2＝4π×172a2＝73πa2. [答案] B
[悟一法] 与球有关的组合体共有两种，一种是内切，一种是外接．解 题时要认真分析图形，明确切点和接点的位置，灵活利用球的 对称性， ①若半径为 R 的球的内接正方体的棱长为 a，则 2R＝ 3a. ②若半径为 R 的球的内接长方体的长、宽、高分别为 a， b，c，则 2R＝ a2＋b2＋c2.
高中数学 1-1-2圆柱、圆锥、圆台、球的结构特征、简单组合体的结构特征课件 新人教A版必修2
自主预习 阅读材料P5－7，回答下列问题： 1．圆柱
以 矩形 的一边所在直线为旋转轴，其余三边旋转形 定义
成的面所围成的 旋转体 叫做圆柱 旋转轴叫做圆柱的 轴 ；垂直于轴的边旋转而成的 有关 圆面叫做圆柱的底面； 平行于轴的边旋转而成的曲 概念 面叫做圆柱的侧面；无论旋转到什么位置，不垂直 于轴的边都叫做圆柱侧面的母线
4．简单组合体 (1)概念：由 简单几何体 组合而成的几何体叫做简单组 合体．常见的简单组合体大多是由具有棱、锥、台、球等几 何结构特征的物体组成的． (2)基本形式：一种是由简单几何体 拼接 而成，另一种是 由简单几何体 截去 或 挖去 一部分而成．
[知识拓展]球与其他几何体形成的组合体问题 球与其他几何体组成的几何体在试题中通常以相切或相 接的形式出现，解决此类问题常常利用截面来分析这两个几 何体之间的关系，从而将空间问题转化成平面问题．
(4)以AD边为轴旋转所得的组合体：一个圆柱上部挖去一 个圆锥．如下图④所示．
规律总结：根据几何体的特征判断几何体的形状 (1)首先要熟练掌握各类几何体的概念，把握好它们的性 质，其次要有一定的空间想象能力． (2)圆柱、圆锥、圆台可以分别看作是以矩形的一边、直 角三角形的一直角边、直角梯形垂直于底边的腰所在的直线 为旋转轴，其余各边旋转而成的曲面所围成的几何体，其轴 截面(过轴的截面)分别是矩形、等腰三角形、等腰梯形．这些 轴截面集中反映了旋转体的各主要元素，处理旋转体的有关 问题时一般要作出其轴截面．
图形
有关 概念
原圆锥的底面和截面分别叫做圆台的下 底面和上 底面．与圆柱和圆锥一样，圆台也有轴、 侧面 、 母线，如上图所示，轴为 OO′ ，AA′为母线
表示 用表示的轴的 字母 表示，上图中的圆台可记作 法 圆台 OO′ 规定 圆台 与 棱台 统称为台体
人教B版高中数学必修第一册 1-2-1《命题与量词》课件PPT
（2）含有存在量词“有些”，是存在量词命题.
（3）含有存在量词“有些”，是存在量词命题.
（4）含有存在量词“至少有一个”，是存在量词命题.
1.命题真假的判断
例1 判断下列命题的真假.
（1）∀ ∈ ，2 + 4 > 0.（2）∀ ∈ {1， − 1，0}，2 + 1 > 0.
解 （1）这是全称量词命题，∵
（7）-2不是整数.（8）4>3.
【解】
（1）是疑问句，不能判断真假，不是命题.（2）是命题，是假命题.
（3）是开语句，无法判断真假，不是命题.
（4）和（5）都是祈使句，不能判断真假，不是命题.（6）是感叹句，不能判断真假，不是命题.
（7）是命题，是假命题.（8）是命题，是真命题.
量词——全称量词及全称量词命题
（2）∀ ∈N，2 > 0.
（3）∀ ∈Q，32 + 6 − 1是有理数.
1
量词——存在量词及存在量词命题
存在
量词
存在
定义
符号表示
定义
“存在”“有”“至少有一个”在陈述中表示所述事物的个体或
部分，称为存在量词
∃
含有存在量词的命题，称为存在量词命题
量词 一般形式 存在集合中的元素，（）
求的取值范围.
解：当为真命题时， ≥ 6或 ≤ −1.
当为真命题时， > −1.又是假命题，∴ ≤ −1.
故当是真命题且是假命题时，的取值范围为 ≤ −1.
反思感悟
已知含参命题的真假，求参数的思路
此类型题目一般与不等式相结合.
求解此类型题目的思路往往是在给出命题真假的前提下，分别求出各命题中参数
课堂小结
2020-2021学年高一数学人教A版高中数学必修2第一章1.2.1中心投影与平行投影课件
探究二 ：空间几何体的三视图 长
正视图
方
体
的
三
视
侧 视
图
c（高）
图
b（宽）
a(长)
俯视图
三视图能反映物体真实的形状和长、宽、高.
正
视 图
c（高）
a(长)
高 平
长对正 齐
侧
c（高）
视 图
b（宽）
俯
a(长)
视
b（宽）
图
宽相等
c（高）
b（宽）
a(长)
正侧俯 视视视 图图图 反反反 映映映 了了了 物物物 体体体 的的的 高高长 度度度 和和和 长宽宽 度度度
（D）三棱柱
2020-2021学年高一数学人教A版高中 数学必 修2第一 章1.2. 1中心 投影与 平行投 影课件 【精品 】
2020-2021学年高一数学人教A版高中 数学必 修2第一 章1.2. 1中心 投影与 平行投 影课件 【精品 】
5、一空间几何体的三视图如图所示, 则该几何体是___
巩固提高:简单组合体的三视图
例2：画出下面几何体的三视图。
正视图
侧视图
俯视图 注意：不可见的轮廓线，用虚线画出。
正视图
侧视图
俯视图
正视图
侧视图
俯视图
2020-2021学年高一数学人教A版高中 数学必 修2第一 章1.2. 1中心 投影与 平行投 影课件 【精品 】
例3：（1）一个几何体的三视图如下,你 能说出它是什么立体图形吗?
2020-2021学年高一数学人教A版高中 数学必 修2第一 章1.2. 1中心 投影与 平行投 影课件 【精品 】
俯视图
2020-2021学年高一数学人教A版高中 数学必 修2第一 章1.2. 1中心 投影与 平行投 影课件 【精品 】
人教A版高中数学必修二课件第一章1.3.2球的体积和表面积(共41张PPT)
3
答案：288πcm3
5.(2013·新课标全国卷Ⅱ)已知正四棱锥O-ABCD的体积为
底3面2边，长为，则以O为3 球心，OA为半径的球的表面积为
2
_______.
【解析】设正四棱锥的高为h，则 1
3
2
h
3
2，
3
2
解得高h=则3 底2 .面正方形的对角线长为
2
2 3 6，
所以OA=所(3以2球)2的 (表6面)2积为6,
(3)此类问题的具体解题流程：
【变式训练】正方体的内切球和外接球的半径之比为()
A.∶31B.∶2C.2∶3 D.∶3
3
3
【解析】选D.设正方体的棱长为a,则内切球半径为 a ,
2
外接球半径为所以3a 半, 径之比为1∶=∶3. 3 3
2
【规范解答】有关球的计算问题 【典例】【条件分析】
【规范解答】设圆锥的底面半径为r，高为h，母线长为l，
3
3
答案：(1)√(2)√(3)×(4)√
【知识点拨】 1.对球的三点说明 (1)球的表面是曲面,不能展开在一个平面上,因此没有展开图. (2)球既是中心对称的几何体,又是轴对称的几何体,它的任何 截面均为圆面,它的三视图也都是圆. (3)球是一个封闭的几何体,既包括球的表面,又包括球面所包 围的空间.
【解题探究】1.求球的体积和表面积的关键是什么？ 2.两个球的体积之比和表面积之比分别与半径有何关系？ 3.两个铁球熔化为一个球后,哪一个量是不变的？ 探究提示： 1.关键是确定球的半径. 2.两个球的体积之比等于两个球的半径比的立方,表面积之比 等于两个球的半径比的平方. 3.体积不变，即两个小球的体积和应与大球的体积相同.
答案：288πcm3
5.(2013·新课标全国卷Ⅱ)已知正四棱锥O-ABCD的体积为
底3面2边，长为，则以O为3 球心，OA为半径的球的表面积为
2
_______.
【解析】设正四棱锥的高为h，则 1
3
2
h
3
2，
3
2
解得高h=则3 底2 .面正方形的对角线长为
2
2 3 6，
所以OA=所(3以2球)2的 (表6面)2积为6,
(3)此类问题的具体解题流程：
【变式训练】正方体的内切球和外接球的半径之比为()
A.∶31B.∶2C.2∶3 D.∶3
3
3
【解析】选D.设正方体的棱长为a,则内切球半径为 a ,
2
外接球半径为所以3a 半, 径之比为1∶=∶3. 3 3
2
【规范解答】有关球的计算问题 【典例】【条件分析】
【规范解答】设圆锥的底面半径为r，高为h，母线长为l，
3
3
答案：(1)√(2)√(3)×(4)√
【知识点拨】 1.对球的三点说明 (1)球的表面是曲面,不能展开在一个平面上,因此没有展开图. (2)球既是中心对称的几何体,又是轴对称的几何体,它的任何 截面均为圆面,它的三视图也都是圆. (3)球是一个封闭的几何体,既包括球的表面,又包括球面所包 围的空间.
【解题探究】1.求球的体积和表面积的关键是什么？ 2.两个球的体积之比和表面积之比分别与半径有何关系？ 3.两个铁球熔化为一个球后,哪一个量是不变的？ 探究提示： 1.关键是确定球的半径. 2.两个球的体积之比等于两个球的半径比的立方,表面积之比 等于两个球的半径比的平方. 3.体积不变，即两个小球的体积和应与大球的体积相同.
高中数学 第一章 立体几何初步 1.1.6 棱柱、棱锥、棱
探究一
探究二
探究三
探究四
【典型例题 2】 已知正六棱台的两底面边长分别为 1 cm 和 2 cm,高是 1 cm,求它的侧面积.
解:如图所示是正六棱台的一个侧面及其高组成 的一部分(其余部分省略),则侧面 ABB1A1 为等腰梯 形,OO1 为高,且 OO1=1 cm,AB=1 cm,A1B1=2 cm,取 AB 和 A1B1 的中点 C,C1,连接 OC,CC1,O1C1,则 CC1 为正六 棱台的斜高,且四边形 OO1C1C 为直角梯形.
探究一
探究二
探究三
探究四
【典型例题 1】 如图所示,正四棱锥底面正方形的边长为 4 cm,高与斜 高的夹角为 30°,求该正四棱锥的侧面积和表面积.
思路分析:根据多面体的侧面积公式,必须求出相应多面体的底面边长 和各侧面的斜高,我们可以把问题转化到三角形内加以分析求解.
探究一
探究二
探究三
探究四
解:正四棱锥的高 PO,斜高 PE,底面边心距 OE 组成一个 Rt△POE. 因为 OE=2 cm,∠OPE=30°, 所以 PE=sin���3������0��� °=4(cm).
思考 1 斜棱柱的侧面展开图是什么?它的侧面积如何求解?
提示:斜棱柱的侧面展开图是一些平行四边形连接起来的不规则图形, 它的侧面积等于各个侧面面积之和,也等于直截面(与侧棱垂直相交的截面) 的周长与侧棱长的乘积.
2.圆柱、圆锥的侧面积 几何体 侧面展开图 圆柱
圆锥
侧面积公式
S 圆柱侧=2πrl r 为底面半径 l 为侧面母线长
1.1.6 棱柱、棱锥、棱台和球的表面积
课程目标
1.掌握棱柱、棱锥和棱台的表面积公式 的推导方法,进一步加强空间问题与平 面问题相互转化的思想,并熟练运用公 式求面积. 2.了解棱柱、棱锥和棱台的侧面积的求 法——侧面展开图. 3.了解球的表面积公式,并会熟练运用公 式求球的表面积. 4.了解旋转体的构成,并会求旋转体的表 面积.
湘教版高中数学必修第一册第1章1-1-1第1课时集合与元素课件
以集合中元素的确定性和互异性为切入点，思考求解a值的方法．
[解] 由题意可知，a＝1或a2＝a， (1)若a＝1，则a2＝1，这与a2≠1相矛盾，故a≠1． (2)若a2＝a，则a＝0或a＝1(舍去)，又当a＝0时，A中含有元素1和0， 满足集合中元素的互异性，符合题意． 综上可知，实数a的值为0．
三个元素．]
5
题号
1
√
2
3
D [由题意可知，a∈R且a∉Q，所以a是无理数．故选D．]
4
5
题号
4．若1∈A，且集合A与集合B相等，则1___∈_____B(填“∈”或 1
“∉”)．
2
∈ [由集合相等的定义可知，1∈B．]
3
4
5
5．已知集合A由a2－a＋1，|a＋1|两个元素构成，若3∈A，则a的 值为___－__1_或__－__4___．
√A．一切很大的数
√B．好心人
题号
√C．漂亮的小女孩
D．不小于3的自然数
1 2
ABC [“很大”“好”“漂亮”等词没有严格的标准，故选项A，3
4
B，C中的元素均不能构成集合．故选ABC．]
5
2．用“book”中的字母构成的集合中元素个数为( )
题号
A．1
B．2
1
√C．3
D．4
2
3
C [由集合中元素的互异性可知，该集合中共有“b”“o”“k” 4
[母题探究] 本例若去掉条件“a∈A”，其他条件不变，求实数a的取值范围． [解] 由集合中元素的互异性可知a2≠1，即a≠±1．
反思领悟 根据集合中元素的基本属性求值的3个步骤
[跟进训练] 3．设集合A中含有三个元素3，x，x2－2x． (1)求实数x应满足的条件； (2)若－2∈A，求实数x的值．
[解] 由题意可知，a＝1或a2＝a， (1)若a＝1，则a2＝1，这与a2≠1相矛盾，故a≠1． (2)若a2＝a，则a＝0或a＝1(舍去)，又当a＝0时，A中含有元素1和0， 满足集合中元素的互异性，符合题意． 综上可知，实数a的值为0．
三个元素．]
5
题号
1
√
2
3
D [由题意可知，a∈R且a∉Q，所以a是无理数．故选D．]
4
5
题号
4．若1∈A，且集合A与集合B相等，则1___∈_____B(填“∈”或 1
“∉”)．
2
∈ [由集合相等的定义可知，1∈B．]
3
4
5
5．已知集合A由a2－a＋1，|a＋1|两个元素构成，若3∈A，则a的 值为___－__1_或__－__4___．
√A．一切很大的数
√B．好心人
题号
√C．漂亮的小女孩
D．不小于3的自然数
1 2
ABC [“很大”“好”“漂亮”等词没有严格的标准，故选项A，3
4
B，C中的元素均不能构成集合．故选ABC．]
5
2．用“book”中的字母构成的集合中元素个数为( )
题号
A．1
B．2
1
√C．3
D．4
2
3
C [由集合中元素的互异性可知，该集合中共有“b”“o”“k” 4
[母题探究] 本例若去掉条件“a∈A”，其他条件不变，求实数a的取值范围． [解] 由集合中元素的互异性可知a2≠1，即a≠±1．
反思领悟 根据集合中元素的基本属性求值的3个步骤
[跟进训练] 3．设集合A中含有三个元素3，x，x2－2x． (1)求实数x应满足的条件； (2)若－2∈A，求实数x的值．
【名师一号】(新课标版)高二数学必修2课件 第一章 第一节 空间几何体的结构-1[ 高考]
![【名师一号】(新课标版)高二数学必修2课件 第一章 第一节 空间几何体的结构-1[ 高考]](https://img.taocdn.com/s3/m/e40a6f9b960590c69ec3764b.png)
第15页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
4．棱柱、棱锥、棱台的关系 棱柱、棱锥、棱台的关系如图所示．
第16页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
课堂互动探究
剖析归纳 触类旁通
第17页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
解析
如图，所得截面为六边形．
答案 6
第36页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
5.如图，四边形ABCD是一个正方形，E，F分别是AB和BC 的中点，沿折痕DE，EF，FD折起得到一个空间几何体，请你 动手折一折，看看这个空间几何体是什么几何体．
第37页
返回导航
第8页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
名 师 讲 解 1.棱柱的概念与分类 多面体是由若干个平面多边形所围成的几何体．棱柱就是 一个多面体，它是由一个平面多边形沿某一方向平移形成的空 间几何体，它的形成使之具备如下几个特点：
第9页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
第28页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
【解】 ①五棱柱；②五棱锥；③三棱台． 如图所示．
第29页
返回导航
第一章
空间几何体
·高中同步学习方略 ·新课标A版 ·数学 ·必修2
高中数学课件-1-2-1-1等差数列的概念和通项公式 课件(北师大版必修5)
§2 等差数列
第一章 数列
进入导航
2.1 等差数列
第一章 数列
进入导航
第1课时 等差数列的概念和通项公式
预习篇 课堂篇 提高篇
巩固篇 课时作业
第一章 数列
进入导航
学习目标
1.理解等差数列的特点与定义，掌握等差数列的判断 方法.
2.记住等差数列的概念、等差数列的通项公式，并能 运用通项公式解决一些简单问题.
第一章 数列
进入导航
进入导航
【尝试解答】 数列5,8,11，…记为{an}，数列 3,7,11，…记为{bm}，则an＝5＋(n－1)·3＝3n＋2，bm＝3＋ (m－1)·4＝4m－1.
令an＝bm，得3n＋2＝4m－1(n，m∈N＋)， 即n＝43m－1(n，m∈N＋)． 要使n为正整数，m必须是3的倍数，记m＝3k(k∈N＋)． ∴n＝43·3k－1＝4k－1.
第一章 数列
进入导航
理解等差数列的定义需注意以下问题： (1)注意定义中“从第2项起”这一前提条件的两层含 义：其一，第1项前面没有项，无法与后续条件中“与前一 项的差”相吻合；其二，定义中包括首项这一基本量，且 必须从第2项起，以便保证数列中各项均与其前一项作差． (2)注意定义中“每一项与它的前一项的差”这一运算 要求，它的含义也有两个：其一是强调作差的顺序，即后 面的项减前面的项；其二是强调这两项必须相邻．
第一章 数列
进入导航
规律方法 求解时要紧紧抓住“同一个常数”这个条件，本例中 的第2小题是从第2项开始的等差数列，即1，2，3，…n构 成等差数列，但整个数列不是等差数列.
第一章 数列
进入导航
根据下列数列的通项公式an，判断各数列是否为等差 数列：
(1)an＝3n＋5；(2)an＝n2.
第一章 数列
进入导航
2.1 等差数列
第一章 数列
进入导航
第1课时 等差数列的概念和通项公式
预习篇 课堂篇 提高篇
巩固篇 课时作业
第一章 数列
进入导航
学习目标
1.理解等差数列的特点与定义，掌握等差数列的判断 方法.
2.记住等差数列的概念、等差数列的通项公式，并能 运用通项公式解决一些简单问题.
第一章 数列
进入导航
进入导航
【尝试解答】 数列5,8,11，…记为{an}，数列 3,7,11，…记为{bm}，则an＝5＋(n－1)·3＝3n＋2，bm＝3＋ (m－1)·4＝4m－1.
令an＝bm，得3n＋2＝4m－1(n，m∈N＋)， 即n＝43m－1(n，m∈N＋)． 要使n为正整数，m必须是3的倍数，记m＝3k(k∈N＋)． ∴n＝43·3k－1＝4k－1.
第一章 数列
进入导航
理解等差数列的定义需注意以下问题： (1)注意定义中“从第2项起”这一前提条件的两层含 义：其一，第1项前面没有项，无法与后续条件中“与前一 项的差”相吻合；其二，定义中包括首项这一基本量，且 必须从第2项起，以便保证数列中各项均与其前一项作差． (2)注意定义中“每一项与它的前一项的差”这一运算 要求，它的含义也有两个：其一是强调作差的顺序，即后 面的项减前面的项；其二是强调这两项必须相邻．
第一章 数列
进入导航
规律方法 求解时要紧紧抓住“同一个常数”这个条件，本例中 的第2小题是从第2项开始的等差数列，即1，2，3，…n构 成等差数列，但整个数列不是等差数列.
第一章 数列
进入导航
根据下列数列的通项公式an，判断各数列是否为等差 数列：
(1)an＝3n＋5；(2)an＝n2.
高中数学人教A版必修2第一章1.2.3空间几何体的直观图-斜二侧画法 课件教学课件
（2）已知图形中平行于x轴或y轴的线段，在直观图 中分别画成平行于x′轴或y′轴的线段。
（3）已知图形中平行于x轴的线段，在直观图中保持 原长度不变；平行于y轴的线段，长度为原来的一半。
例2.用斜二测画法画长,宽,高分别是4cm,3cm, 2cm的长方体的直观图。
思考：直观图
画法的步骤是 怎样的？
上 分 别 截 取 2 c m 长 的 线 段 A A , B B , C C , D D .
Z
D
C y
A D
BQ C
MO
Nx
AP B
4成 图 .顺 次 连 接 A,B,C,D,并 加 以 整 理
去 掉 辅 助 线 ,将 被 遮 挡 住 的 部 分 改 为 虚 线 ,
就 可 得 到 长 方 体 的 直 观 图 .
1、画轴； 2、画底面； 3、画侧棱；（直棱柱的侧棱和z轴平行，长度保持不变） 4、成图。注意:去掉辅助线,将被遮挡的部分改为虚线.
1 画 轴 . 画 x 轴 , y 轴 , z 轴 , 三 轴 交 于 点 O , 使 x O y = 4 5 ,
x O z 9 0 .
Z
y
O
x
2画 底 面 .以 O为 中 心 ,在 x轴 上 取 线 段 MN,使 MN=4 cm;在
脚踏实地过好每一天，最简单的恰恰是最难的。拿梦想去拼，我怎么能输。只要学不死，就往死里学。我会努力站在万人中央成为别人的光。行为决定性格， 性格决定命运。不曾扬帆，何以至远方。人生充满苦痛，我们有幸来过。如果骄傲没有被现实的大海冷冷拍下，又怎么会明白要多努力才能走到远方。所有的 豪言都收起来，所有的呐喊都咽下去。十年后所有难过都是下酒菜。人生如逆旅，我亦是行人。驾驭命运的舵是奋斗，不抱有一丝幻想，不放弃一点机会，不 停止一日努力。失败时郁郁寡欢，这是懦夫的表现。所有偷过的懒都会变成打脸的巴掌。越努力，越幸运。每一个不起舞的早晨，都是对生命的辜负。死鱼随 波逐流，活鱼逆流而上。墙高万丈，挡的只是不来的人，要来，千军万马也是挡不住的既然选择远方，就注定风雨兼程。漫漫长路，荆棘丛生，待我用双手踏 平。不要忘记最初那颗不倒的心。胸有凌云志，无高不可攀。人的才华就如海绵的水，没有外力的挤压，它是绝对流不出来的。流出来后，海绵才能吸收新的 源泉。感恩生命，感谢她给予我们一个聪明的大脑。思考疑难的问题，生命的意义；赞颂真善美，批判假恶丑。记住精彩的瞬间，激动的时刻，温馨的情景， 甜蜜的镜头。感恩生命赋予我们特有的灵性。善待自己，幸福无比，善待别人，快乐无比，善待生命，健康无比。一切伟大的行动和思想，都有一个微不足道 的开始。在你发怒的时候，要紧闭你的嘴，免得增加你的怒气。获致幸福的不二法门是珍视你所拥有的、遗忘你所没有的。骄傲是胜利下的蛋，孵出来的却是 失败。没有一个朋友比得上健康，没有一个敌人比得上病魔，与其为病痛暗自流泪，不如运动健身为生命添彩。有什么别有病，没什么别没钱，缺什么也别缺 健康，健康不是一切，但是没有健康就没有一切。什么都可以不好，心情不能不好；什么都可以缺乏，自信不能缺乏；什么都可以不要，快乐不能不要；什么 都可以忘掉，健身不能忘掉。选对事业可以成就一生，选对朋友可以智能一生，选对环境可以快乐一生，选对伴侣可以幸福一生，选对生活方式可以健康一生。 含泪播种的人一定能含笑收获一个有信念者所开发出的力量，大于个只有兴趣者。忍耐力较诸脑力，尤胜一筹。影响我们人生的绝不仅仅是环境，其实是心态 在控制个人的行动和思想。同时，心态也决定了一个人的视野、事业和成就，甚至一生。每一发奋努力的背后，必有加倍的赏赐。懒惰像生锈一样，比操劳更 消耗身体。所有的胜利，与征服自己的胜利比起来，都是微不足道。所有的失败，与失去自己的失败比起来，更是微不足道挫折其实就是迈向成功所应缴的学 费。在这个尘世上，虽然有不少寒冷，不少黑暗，但只要人与人之间多些信任，多些关爱，那么，就会增加许多阳光。一个能从别人的观念来看事情，能了解 别人心灵活动的人，永远不必为自己的前途担心。当一个人先从自己的内心开始奋斗，他就是个有价值的人。没有人富有得可以不要别人的帮助，也没有人穷 得不能在某方面给他人帮助。时间告诉你什么叫衰老，回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵，昨天的太阳，晒不干今天的衣裳。今天做别人不 愿做的事，明天就能做别人做不到的事。到了一定年龄，便要学会寡言，每一句话都要有用，有重量。喜怒不形于色，大事淡然，有自己的底线。趁着年轻， 不怕多吃一些苦。这些逆境与磨练，才会让你真正学会谦恭。不然，你那自以为是的聪明和藐视一切的优越感，迟早会毁了你。无论现在的你处于什么状态， 是时候对自己说：不为模糊不清的未来担忧，只为清清楚楚的现在努力。世界上那些最容易的事情中，拖延时间最不费力。崇高的理想就像生长在高山上的鲜 花。如果要搞下它，勤奋才能是攀登的绳索。行动是治愈恐惧的良药，而犹豫、拖延将不断滋养恐惧。海浪的品格，就是无数次被礁石击碎又无数闪地扑向礁 石。人都是矛盾的，渴望被理解，又害怕被看穿。经过大海的一番磨砺，卵石才变得更加美丽光滑。生活可以是甜的，也可以是苦的，但不能是没味的。你可
（3）已知图形中平行于x轴的线段，在直观图中保持 原长度不变；平行于y轴的线段，长度为原来的一半。
例2.用斜二测画法画长,宽,高分别是4cm,3cm, 2cm的长方体的直观图。
思考：直观图
画法的步骤是 怎样的？
上 分 别 截 取 2 c m 长 的 线 段 A A , B B , C C , D D .
Z
D
C y
A D
BQ C
MO
Nx
AP B
4成 图 .顺 次 连 接 A,B,C,D,并 加 以 整 理
去 掉 辅 助 线 ,将 被 遮 挡 住 的 部 分 改 为 虚 线 ,
就 可 得 到 长 方 体 的 直 观 图 .
1、画轴； 2、画底面； 3、画侧棱；（直棱柱的侧棱和z轴平行，长度保持不变） 4、成图。注意:去掉辅助线,将被遮挡的部分改为虚线.
1 画 轴 . 画 x 轴 , y 轴 , z 轴 , 三 轴 交 于 点 O , 使 x O y = 4 5 ,
x O z 9 0 .
Z
y
O
x
2画 底 面 .以 O为 中 心 ,在 x轴 上 取 线 段 MN,使 MN=4 cm;在
脚踏实地过好每一天，最简单的恰恰是最难的。拿梦想去拼，我怎么能输。只要学不死，就往死里学。我会努力站在万人中央成为别人的光。行为决定性格， 性格决定命运。不曾扬帆，何以至远方。人生充满苦痛，我们有幸来过。如果骄傲没有被现实的大海冷冷拍下，又怎么会明白要多努力才能走到远方。所有的 豪言都收起来，所有的呐喊都咽下去。十年后所有难过都是下酒菜。人生如逆旅，我亦是行人。驾驭命运的舵是奋斗，不抱有一丝幻想，不放弃一点机会，不 停止一日努力。失败时郁郁寡欢，这是懦夫的表现。所有偷过的懒都会变成打脸的巴掌。越努力，越幸运。每一个不起舞的早晨，都是对生命的辜负。死鱼随 波逐流，活鱼逆流而上。墙高万丈，挡的只是不来的人，要来，千军万马也是挡不住的既然选择远方，就注定风雨兼程。漫漫长路，荆棘丛生，待我用双手踏 平。不要忘记最初那颗不倒的心。胸有凌云志，无高不可攀。人的才华就如海绵的水，没有外力的挤压，它是绝对流不出来的。流出来后，海绵才能吸收新的 源泉。感恩生命，感谢她给予我们一个聪明的大脑。思考疑难的问题，生命的意义；赞颂真善美，批判假恶丑。记住精彩的瞬间，激动的时刻，温馨的情景， 甜蜜的镜头。感恩生命赋予我们特有的灵性。善待自己，幸福无比，善待别人，快乐无比，善待生命，健康无比。一切伟大的行动和思想，都有一个微不足道 的开始。在你发怒的时候，要紧闭你的嘴，免得增加你的怒气。获致幸福的不二法门是珍视你所拥有的、遗忘你所没有的。骄傲是胜利下的蛋，孵出来的却是 失败。没有一个朋友比得上健康，没有一个敌人比得上病魔，与其为病痛暗自流泪，不如运动健身为生命添彩。有什么别有病，没什么别没钱，缺什么也别缺 健康，健康不是一切，但是没有健康就没有一切。什么都可以不好，心情不能不好；什么都可以缺乏，自信不能缺乏；什么都可以不要，快乐不能不要；什么 都可以忘掉，健身不能忘掉。选对事业可以成就一生，选对朋友可以智能一生，选对环境可以快乐一生，选对伴侣可以幸福一生，选对生活方式可以健康一生。 含泪播种的人一定能含笑收获一个有信念者所开发出的力量，大于个只有兴趣者。忍耐力较诸脑力，尤胜一筹。影响我们人生的绝不仅仅是环境，其实是心态 在控制个人的行动和思想。同时，心态也决定了一个人的视野、事业和成就，甚至一生。每一发奋努力的背后，必有加倍的赏赐。懒惰像生锈一样，比操劳更 消耗身体。所有的胜利，与征服自己的胜利比起来，都是微不足道。所有的失败，与失去自己的失败比起来，更是微不足道挫折其实就是迈向成功所应缴的学 费。在这个尘世上，虽然有不少寒冷，不少黑暗，但只要人与人之间多些信任，多些关爱，那么，就会增加许多阳光。一个能从别人的观念来看事情，能了解 别人心灵活动的人，永远不必为自己的前途担心。当一个人先从自己的内心开始奋斗，他就是个有价值的人。没有人富有得可以不要别人的帮助，也没有人穷 得不能在某方面给他人帮助。时间告诉你什么叫衰老，回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵，昨天的太阳，晒不干今天的衣裳。今天做别人不 愿做的事，明天就能做别人做不到的事。到了一定年龄，便要学会寡言，每一句话都要有用，有重量。喜怒不形于色，大事淡然，有自己的底线。趁着年轻， 不怕多吃一些苦。这些逆境与磨练，才会让你真正学会谦恭。不然，你那自以为是的聪明和藐视一切的优越感，迟早会毁了你。无论现在的你处于什么状态， 是时候对自己说：不为模糊不清的未来担忧，只为清清楚楚的现在努力。世界上那些最容易的事情中，拖延时间最不费力。崇高的理想就像生长在高山上的鲜 花。如果要搞下它，勤奋才能是攀登的绳索。行动是治愈恐惧的良药，而犹豫、拖延将不断滋养恐惧。海浪的品格，就是无数次被礁石击碎又无数闪地扑向礁 石。人都是矛盾的，渴望被理解，又害怕被看穿。经过大海的一番磨砺，卵石才变得更加美丽光滑。生活可以是甜的，也可以是苦的，但不能是没味的。你可
新教材高中数学1-1-1空间向量及其运算课件新人教B版选择性必修一
2021
第一章
1.1.1 空间向量及其运算
内
容
索
引
01
课前篇 自主预习
02
课堂篇 探究学习
核心素养
1.理解空间向量的概念,掌握空间向量
的表示方法.(数学抽象)
2.学会空间向量的线性运算及它们的
运算律.(数学运算)
3.能用空间向量的线性运算解决简单
的立体几何问题.(逻辑推理)
4.理解空间向量夹角的概念,并掌握两
(2)减法:a-b=.
(3)数乘:λa,
①当λ≠0,a≠0时,
|λa|=|λ||a|,而且λa的方向:
当λ>0时,λa与a方向相同;
当λ<0时,λa与a方向相反;
②当λ=0或a=0时,λa=0.
(4)线性运算律
①加法交换律:a+b=b+a;
②加法结合律:(a+b)+c=a+(b+c);
③分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
)
(4)模相等的向量不一定是相等向量.(
)
(5)表示两个平行向量的有向线段所在的直线一定不重合.(
答案 (1)√ (2)×
(3)√ (4)√
(5)×
)
微练习
在平行六面体ABCD-A1B1C1D1中,与向量 AD 相等的向量共有(
A.1个
B.2个
C.3个
D.4个
答案 C
解析 与AD相等的向量有A1 D1 , BC, B1 C1 ,共 3 个.
)
答案 ×
微思考
两个非零向量共线时,其夹角分别是多少?
提示 两个非零向量共线且同向时,<a,b>=0;两个非零向量共线且反向
第一章
1.1.1 空间向量及其运算
内
容
索
引
01
课前篇 自主预习
02
课堂篇 探究学习
核心素养
1.理解空间向量的概念,掌握空间向量
的表示方法.(数学抽象)
2.学会空间向量的线性运算及它们的
运算律.(数学运算)
3.能用空间向量的线性运算解决简单
的立体几何问题.(逻辑推理)
4.理解空间向量夹角的概念,并掌握两
(2)减法:a-b=.
(3)数乘:λa,
①当λ≠0,a≠0时,
|λa|=|λ||a|,而且λa的方向:
当λ>0时,λa与a方向相同;
当λ<0时,λa与a方向相反;
②当λ=0或a=0时,λa=0.
(4)线性运算律
①加法交换律:a+b=b+a;
②加法结合律:(a+b)+c=a+(b+c);
③分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
)
(4)模相等的向量不一定是相等向量.(
)
(5)表示两个平行向量的有向线段所在的直线一定不重合.(
答案 (1)√ (2)×
(3)√ (4)√
(5)×
)
微练习
在平行六面体ABCD-A1B1C1D1中,与向量 AD 相等的向量共有(
A.1个
B.2个
C.3个
D.4个
答案 C
解析 与AD相等的向量有A1 D1 , BC, B1 C1 ,共 3 个.
)
答案 ×
微思考
两个非零向量共线时,其夹角分别是多少?
提示 两个非零向量共线且同向时,<a,b>=0;两个非零向量共线且反向
2020-2021学年高中数学 第一章 立体几何初步 1.1 简单几何体 1.1.1 简单旋转体课件 北师大版必修2
所围成的几何体 侧面：不垂直于旋转
叫作圆柱
轴的边旋转而成的 ____曲__面_____；
名 称
定义
相关概念
圆 锥
以直角三角形的 __一__条__直__角__边___ 所在的直线为旋 转轴，其余各边 旋转而形成的曲 面所围成的几何 体叫作圆锥
高：在旋转轴上这 条边的长度； 底面：垂直于旋转 轴的边旋转而成的 ____圆__面_____； 侧面：不垂直于旋 转轴的边旋转而成 的__曲__面_______；
步
§1 简单几何体
1．1 简单旋转体
1．问题导航 (1)连接圆柱(圆台)两底面的圆心的连线与其底面有怎样的位 置关系？ (2)有同学说：“直角三角形绕其一边所在的直线旋转一周所 形成的几何体是圆锥．”这种说法对吗？ (3)圆台中，上底面半径r、下底面半径R、高h与母线l之间有 怎样的关系？
图形表示
名
定义
相关概念
称
以_直__角__梯__形__垂_直___ _于__底__边__的__腰___所
母线：无 论转到什
在的直线为旋转
圆
么位置，
轴，其余各边旋
台
这条边都
转而形成的曲面
叫作侧面
所围成的几何体
的母线
叫作圆台
图形表示
1．判断正误．(正确的打“√”，错误的打“×”) (1)矩形绕其一边所在直线旋转一周而形成的曲面所围成的几何 体是圆柱．( √ ) (2)直角三角形绕其一边所在直线旋转一周而形成的曲面所围成 的几何体是圆锥．( × ) (3)直角梯形绕其腰所在直线旋转一周而形成的曲面所围成的几 何体是圆台．( × ) (4)圆以一条直径所在的直线为轴，旋转180°围成的几何体是 球．( √ )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
①过球面上任意两点只能作一个球的大圆；(注：球大
圆是以球心为圆心，球半径为半径的圆)
②连接球的任意两个大圆的交点的线段是球的直径；
人 教
A
③球是与定点的距离等于定长的所有点的集合．
版 数
学
其中正确的是
()
A．①② B．②③ C．②
D．①③
[答案] C
第一章 空间几何体
[解析] 若两点为球的直径的端点，可做无数个大
点的集合．
②球面被经过球心的平面截得的圆叫做球的大圆；被
不经过球心的平面截得的圆叫做球的小圆．
人 教
A
③球
小圆
的
圆心
O′
，
球心
O，
|OO′|
＝
d，
球小
圆
半径
r
，版 数
学
球半径为R，则d2＝R2－r2.
5．圆台可看作直角梯形以其垂直于两底的腰所在直线
为旋转轴，其余三边旋转所形成的曲面所围成的旋转体．
6．用运动变化的观点来认识柱、锥、台之间的关系：
截面A1B1C1D1与底面虽然平行，但各侧棱AA1，BB1，CC1，
DD1延长后不能相交于一点；图(2)中显然各侧棱延长后能
交 于 一 点 ， 即 原 几 何 体 为 棱 锥 ， 但 截 面 A1B1C1D1 与 底 面
人 教 A
ABCD不平行．
版 数
学
第一章 空间几何体
4．①球面也可以看作空间中到定点的距离等于定长的
[例2] 将下列几何体按结构特征分类填空
①课本 ②篮球 ③量筒 ④三棱镜 ⑤金字塔
人
教
⑥滤纸卷成漏斗 ⑦量杯 ⑧羽毛球
A 版
数
(1)棱柱结构特征的有：________________；
学
(2)圆柱结构特征的有：__________________；
(3)棱锥结构特征的有：________________；
绕其斜边旋转时形成同底的两个圆锥．
第一章 空间几何体
矩形ABCD中，AB＝4，AD＝2，分别以AB、AD所在
直线为轴旋转所形成的圆柱相同吗？________.
人 教
A
[答案] 不相同
版 数
学
[解析] 以AB为轴旋转形成的圆柱底面半径为2，以
AD为轴旋转所形成圆柱的底面半径为4.
第一章 空间几何体
∴AO1＝
OA2－OO21＝
23R，∴截面圆面积
S＝π(
3 2
R)2＝34πR2.
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
[例6] 将直角梯形ABCD以它的一条边AB所在直线为
轴旋转一周，所形成的几何体为
()
A．圆柱
B．圆锥
C．圆台
D．以上都不对
人 教
A
[错解] C
版 数
学
[辨析] 只有将直角梯形ABCD绕它垂直于两底的腰所
在直线旋转时，形成的几何体才是圆台，由于直角梯形
ABCD未指出哪两边平行，哪条腰与底垂直，故以AB边所
在直线为轴旋转，形成的几何体形状不确定．
[正解] D
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
1．下列命题：
2．一般地：有两个面
互相平行
，其余各面都是
人 教
A
四边形
，并且相邻两个四边形的公共边互相平行 ，
版 数
学
这些面围成的几何体叫做棱柱． 互相平行 的 两 个 平
面叫做棱柱的底面，其余各面叫做侧面；相邻两个侧面的
公共边叫做侧棱，侧面与底面的公共顶点叫做顶点，底面
是n边形的棱柱叫做n棱柱．我们可以用表示底面各顶点的
字母来表示棱柱．
第一章 空间几何体
3．一般地：有一个面是多边形，其余各面是 有一个公共顶点的三角形 ，这些面围成的几何体叫做棱
锥；多边形面叫做棱锥的底面；其余各面叫做侧面；相邻
侧面的公共边叫做侧棱，各侧面的公共顶点叫做顶点，底
人 教
A
面是n边形的棱锥叫做n棱锥，其中三棱锥又常叫做
版 数
四面体 ，我们可以用顶点和底面各顶点来表示棱锥． 学
圆．球是一个几何体，包括到球心的距离小于半径的点，
到定点的距离等于定长的所有点的集合组成球面，而不是
球，球与球面是不同的两个概念，∴①③错，②正确，故
人 教
A
选C.
版 数
学
第一章 空间几何体
2．以下棱柱中，最多只有一对面互相平行的是( )
A．三棱柱
B．四棱柱
人 教
A
C．五棱柱
D．六棱柱
版 数
学
[答案] A
(2)平行平面共有四对，但能作为棱柱底面的只有一对，人教
A
即上下两个平行平面.
版 数
学
第一章 空间几何体
[例 5] 用一个平面截半径为 R 的球，截面到球心的
距离为R2，则截面圆面积为________．
人 教 A
版
[解析] 如图，O 为球心，O1 为截面圆心，AB 为截
数 学
面圆的直径，则 OA＝R，OO1＝R2，
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
人
教
1．1 空间几何体的结构
A 版
数
学
第一章 空间几何体
人
1．1.1 柱、锥、台、球的结构
教 A
版
数
特征
学
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
阅读教材P2－6，回答下列问题： 1．(1)只考虑物体占有空间部分的 形状和大小 ，
柱的底面， 平行于轴的边
旋转而成的曲面叫做圆
人 教
A
柱的侧面，无论旋转到什么位置，不垂直于轴的边都叫做
版 数
学
圆柱侧面的母线，圆柱可用表示它轴的字母表示．
第一章 空间几何体
6．以 直角三角形 的一条 直角 边 所 在 直
线为旋转轴，其余两边旋转所形成的曲面所围成的旋转体
叫做圆锥．圆锥常用表示它轴的字母来表示．
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
[例4] 如图，过BC的截面截去长方体的一角，截后剩
余几何体中，A′B′＝D′C′，问剩余的几何体是不是棱柱？
人 教
A
版
数
学
第一章 空间几何体
[解析] 选择平面ABB′A′与平面DCC′D′为两个平行平
面 ， 则 它 符 合 棱 柱 的 结 构 特 征 ， 故 它 是 四 棱 柱 ABB′A′ －
球心， 半圆的半径
叫做球的半径， 半圆的直径
叫做球的直径．球常用表示球心的字母来表示．
人 教
A
版
数
学
第一章 空间几何体
人 教 A 版 数 学
第一章 空间几何体
本节学习重点：柱、锥、台、球的概念与结构特征．
人 教
A
本节学习难点：棱柱及台体的结构特征．
版 数
学
第一章 空间几何体
人 教 A 版 数 学
面的有几对？
人 教
A
(2)观察螺杆头部模型，有多少对平行的平面？能作为
版 数
学
棱柱底面的有几对？
第一章 空间几何体
[解析] (1)有三对平行平面，有三对平面可作为棱柱
的 底 面 ． 它 们 分 别 为 平 面 ABCD 与 平 面 A′B′C′D′ 、 平 面
ADD′A′与平面BCC′B′、平面ABB′A′与平面DCC′D′.
DCC′D′.
[点评]
几何体这一节主要是使学生通过几何直观，
人 教
A
形成和发展空间想象能力，不要求严格证明．一些有待证
版 数
学
明的结论可提醒学生学过后续课程内容后再严格证明，为
后续学习埋下伏笔，但后面学到相应内容时，一定要再回
扣证明一下，以形成完整知识链，也进一步巩固前面知
识．
第一章 空间几何体
(1)观察长方体，共有多少对平行平面？能作为棱柱底
7．用
平行
于圆锥底面的平面去截圆锥，底面与
人 教
A
截面间的部分叫做圆台，截面叫做圆台的上底面，圆锥的
版 数
学
底面叫做圆台的下底面，圆锥的母线被截后余下的部分叫
做圆台的母线．
圆柱和棱柱统称为 柱体 ； 圆 锥 和 棱 锥 统 称 为
锥体 ；棱台和圆台统称为
台体 ．
第一章 空间几何体
8．以半圆的 直径 所在直线为轴，旋转一周，所 形成的旋转体叫做球体，简称 球 ， 半圆的圆心 叫
[例3] 指出所给三个几何图形的底面、侧面、顶点、
棱，并指出它们分别由几个面围成，各有多少条棱？多少
人 教
A
个顶点？
版 数
学
第一章 空间几何体
[ 解 析 ] 图 (1) 中 ， 底 面 A1C1 、 AC 、 侧 面 A1B1BA 、
B1C1CB、C1D1DC、DD1A1A共有6个面；顶点A1、B1…共8
(4)圆锥结构特征的有：________________；
(5)球体结构特征的有：________________；
(6)其它结构特征的有：________________.
第一章 空间几何体
[解析] (1)①④ (2)③ (3)⑤ (4)⑥ (5)② (6)⑦ ⑧
人 教 A 版 数 学
第一章 空间几何体
[解析] 三棱柱只有两个底面互相平行，四、五、六
棱柱的侧面中也可以有相互平行的．