数值分析3-4(最小二乘法)
最小二乘法数值分析实验报告

最小二乘法数值分析实验报告最小二乘法数值分析实验报告篇一:数值分析+最小二乘法实验报告数学与信息工程学院实课程名称:实验室:实验台号:班级:姓名:实验日期:验报告数值分析 201X年 4 月 13日篇二:数值分析上机实验最小二乘法数值分析实验报告五最小二乘法一、题目设有如下数据用三次多项式拟合这组数据,并绘出图形。
二、方法最小二乘法三、程序M文件:sy ms x f; xx=input( 请输入插值节点 as [x1,x2...]\n ff=i nput( 请输入插值节点处对应的函数值 as [f1,f 2...]\n m=input(请输入要求的插值次数m= n=leng th(xx); fr i=1:(m+1) syms faix; fai=x^(i-1); fr j=1:n x=xx(j);H(i,j)=eval(fai); end endA=ff*(H) *inv(H*(H) syms x; f=0; fr i=1:(m+1) f=f+A(i)*x^(i-1); end f plt(xx,ff, * ) hldnezplt(f,[xx(1),xx(n)])四、结果 sav e and run之后:请输入插值节点 as [x1,x2...] [-3 -2-1 0 1 2 3] 请输入插值节点处对应的函数值 as[f1,f2...] [-1.76 0.42 1.21.341.432.254.38]请输入要求的插值次数m=3 f =133/100+121469856021/35184372088832*x-8042142191733/450359 9627370496*x^2+1020815915537309/9007199254740992*x^3五、拓展:最小二乘法计算方法比较简单,是实际中常用的一种方法,但是必须经计算机来实现,如果要保证精度则需要对大量数据进行拟合,计算量很大。
一个最小二乘问题的三种解法

一个最小二乘问题的三种解法发布时间:2022-08-30T01:58:08.890Z 来源:《教学与研究》2022年第4月第8期作者:肖燏[导读] 线性非齐次方程组无解时,寻找,使得达到极小,此处,实矩阵、向量均已给定. 这是一个高等数学和线肖燏湖南中医药大学信息科学与工程学院湖南长沙 410208)摘要线性非齐次方程组无解时,寻找,使得达到极小,此处,实矩阵、向量均已给定. 这是一个高等数学和线性代数的综合性问题.本文分别从多元函数、向量函数、和向量射影出发,得出这个最小二乘问题的三种解法。
关键词最小二乘多元函数极值向量函数极值向量射影Abstract When there is no solution to the linear non-homogeneous equation system , find , so that reaches the minimum. Here, the real matrix and vector have been given. This is a comprehensive problem of advanced mathematics and linear algebra. Starting from multivariate function, vector function and vector projection, this paper obtains three solutions to the least square problem.Key words least square; extremum of multivariate function; extremum of vector function; projection of vector参考文献[1] 蔡大用,白峰杉. 高等数值分析[M]. 北京:清华大学出版社,1996.[2] 方保镕,周继东,李医民. 矩阵论[M]. 北京:清华大学出版社,2013.[3] 吴赣昌. 高等数学[M]. 北京:中国人民大学出版社,2017.[4] 同济大学数学系. 工程数学.线性代数[M]. 北京:高等教育出版社,2014.作者简介:肖燏(1974—),女,硕士,讲师,研究方向为计算数学.。
数值分析简明教程课后习题答案(第二版)
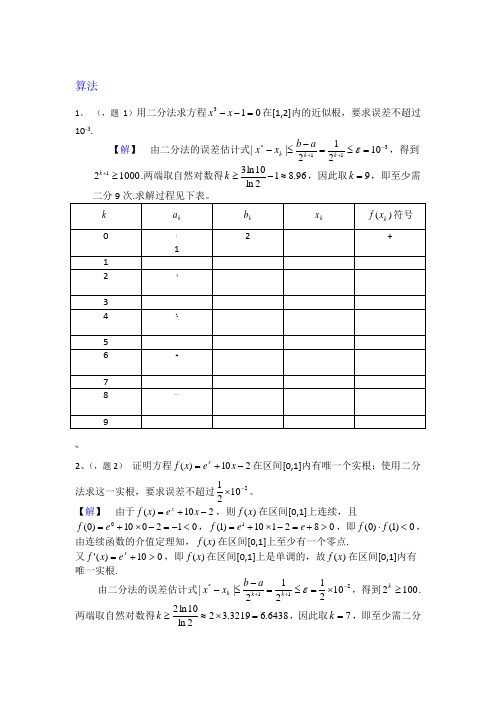
算法1、 (,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需%2、(,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分【误差1.(,题8)已知e=…,试问其近似值7.21=x ,71.22=x ,x 2=,718.23=x 各有几位有效数字并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
最小二乘法的基本原理

最小二乘法的基本原理最小二乘法是一种常用的数学工具,用于拟合数据和估计参数。
它在各个领域都有广泛的应用,包括统计学、经济学、工程学等。
最小二乘法的基本原理是通过最小化观测数据的残差平方和来找到最佳拟合曲线或估计参数。
在本文中,我们将介绍最小二乘法的基本原理及其在实际问题中的应用。
首先,让我们来了解最小二乘法的基本思想。
假设我们有一组观测数据,表示为(x1, y1), (x2, y2), ... , (xn, yn),我们希望找到一个模型来描述这些数据。
通常情况下,我们会选择一个函数形式来拟合这些数据,比如线性函数、多项式函数等。
我们的目标是找到最佳的函数参数,使得该函数与观测数据的残差平方和最小。
为了实现这一目标,我们首先定义拟合函数的形式,比如线性函数y = ax + b。
然后,我们需要定义一个衡量拟合效果的指标,通常选择残差平方和作为衡量标准。
残差即观测数据与拟合函数值之间的差异,将每个观测数据的残差平方求和,得到残差平方和。
最小二乘法的核心思想就是通过调整函数参数,使得残差平方和达到最小。
在实际应用中,最小二乘法可以用于拟合数据、估计参数以及解决最优化问题。
比如在统计学中,我们可以利用最小二乘法来拟合回归模型,估计回归系数;在工程学中,最小二乘法可以用于信号处理、滤波器设计等领域。
总之,最小二乘法是一种非常强大的工具,可以帮助我们处理各种数据分析和建模问题。
最小二乘法的优点在于它简单易用,计算效率高,而且有较好的数学性质。
但是,最小二乘法也有一些局限性,比如对异常值比较敏感,对数据分布有一定的要求等。
在实际应用中,我们需要结合具体问题的特点来选择合适的拟合方法,有时候可能需要借助其他工具来处理特殊情况。
总之,最小二乘法是一种非常重要的数学工具,它在数据分析、参数估计、模型拟合等方面都有着广泛的应用。
通过对最小二乘法的基本原理和应用进行深入理解,我们可以更好地应用它来解决实际问题,提高数据分析和建模的效率和准确性。
最小二乘法曲线拟合原理

最小二乘法曲线拟合原理最小二乘法曲线拟合是一个重要的数值分析方法,它是通过最小二乘法对样本点与直线或曲线之间的关系进行拟合和分析,从而估算出一个函数的一组参数。
最小二乘法曲线拟合是一种经典的数值分析方法,可以用来拟合函数和曲线,估算出参数,预测数据,分析函数,优化模型,甚至可以分析复杂多变量函数。
最小二乘法曲线拟合的核心方法是使用最小二乘法把拟合的曲线拟合到观察到的数据,通过求解方程的最小二乘法,把一系列的观察数据点拟合为最小二乘法曲线,计算出拟合曲线的最佳系数,满足拟合效果的最佳拟合曲线。
最小二乘法曲线拟合的核心目标是通过计算拟合曲线的最小均方误差(SSE)、平均均方误差(MSE)、最大均方误差(MAXE)等方法,使拟合曲线与观察数据点之间的差距最小,从而求解出最佳拟合曲线系数。
最小二乘法曲线拟合具有很强的解析性,可以用数学计算方法快速求解,可以满足各种不同应用场景的需求,因而被广泛应用于科学研究、工程设计、市场分析等领域。
最小二乘法曲线拟合最常见的应用场景有:根据观察数据拟合和估计函数的参数;分析函数的性质;优化模型的能力;预测数据等等。
当应用最小二乘法拟合函数时,首先需要把观察数据用直线或曲线拟合,然后使用极小化残差平方和的方法,来求解参数,这是一个典型的最优化问题,利用一般最优化算法来求解,如梯度下降算法、牛顿法等。
此外,在应用最小二乘法曲线拟合的过程中,还可以考虑几种情况,比如样本数据受到误差的影响,具有某种偏差性;偏差是否服从正态分布;样本数据的分布是否同分布;拟合曲线的拟合是否收敛,参数计算是否准确等等。
总之,最小二乘法曲线拟合是一种重要的数值分析方法,可以用来拟合函数和曲线、估算参数、预测数据、优化模型等。
在应用最小二乘法曲线拟合时,需要考虑一些影响因素,比如样本数据受到误差的影响、偏差是否服从正态分布等,因此,它是一种有效的数值分析方法。
数值分析答案

x0
x1
y
f(x0)
f(x1)
y’
f’(x0)
建立差商表:
自变量
函数值
一阶差商
二阶差商
x0
f(x0)
x0
f(x0)
f’(x0)
x1
f(x1)
则由newton插值公式可得:
整理得:
其中R(x)由以下计算得到:
构造辅助函数:
有 , , 三个零点, 有 , , 三个零点,则 至少有一个零点,记作 。
则
。
(2)S”(0)=0,S”(4)=24
解:用三转角算法计算:
(1) , ,
, ,
, ,
列方程组:
则三次样条插值函数为:
=x3-8, 。
=x3-8, 。
=x3-8, 。
=x3-8, 。
(2)
列方程组:
则三次样条插值函数为:
=x3-8, 。
=x3-8, 。
=x3-8, 。
=x3-8, 。
用三弯矩算法计算:
具体计算如下:
解得最小二乘解:x1=26/11,x2=15/11
(2)
简化为:
两边同乘以系数矩阵的转置矩阵,就得到所需要的法方程组:
具体计算如下:
解得最小二乘解:x=1450/487=2.9774,y=597/487=1.2259
第四章数值积分与数值微分
4-1用四节点复化梯形公式计算积分
(1) ,(2)
误差
则用二次插值的步长应:
2-6对区间[a,b]作步长为h的剖分,且 ,证明:在任意相邻两节点间做线性插值,其误差限为 。
证明:区间上的误差限:
误差限:
2-7设 ,计算差商 , 及 .
数值分析之最小二乘法与最佳一致逼近

就要求矩阵 G非奇异,
而 0 ( x), 1 ( x), , n ( x)在 [a, b]上线性无关不能推出 矩阵 G非奇异,必须加上另外的条件.
8
定义10
设 0 ( x), 1 ( x), , n ( x) [a, b]的任意线
性组合在点集 {xi , i 0,1,, m}(m n) 上至多只有 n 个
只在一组离散点集 {xi , i 0,1,, m} 上给定,这就是科
学实验中经常见到的实验数据 {( xi , yi ), i 0,1,, m}的
曲线拟合.
1
问题为利用 yi f ( xi ), i 0,1,, m, 求出一个函数
y S * ( x) 与所给数据{( xi , yi ), i 0,1,, m} 拟合.
13
令 S1 ( x) a0 a1 x, 这里 m 4, n 1, 0 ( x) 1, 1 ( x) x, 故
( 0 , 0 ) i 8,
i 0 4
( 0 , 1 ) (1 , 0 ) i xi 22,
i 0
4
(1 , 1 ) i xi2 74,
这样就变成了线性模型 .
19
例2
设数据 ( xi , yi )(i 0,1,2,3,4) 由表3-1给出,
表中第4行为 ln yi yi ,通过描点可以看出数学模型为 及 b. y aebx , 用最小二乘法确定 a
表3 1 i xi yi 0 1.00 5.10 1 1.25 5.79 2 1.50 6.53 3 1.75 7.45 4 2.00 8.46
4
S ( x ) 的一般表达式为线性形式.
若 k ( x)是 k 次多项式,S ( x ) 就是 n 次多项式. 为了使问题的提法更有一般性,通常在最小二乘法中 S ( x) a00 ( x) a11 ( x) ann ( x) (n m) 考虑加权平方和
常用数值分析方法

常用数值分析方法1.插值方法插值是通过已知数据点的近似值,获得未知位置上的函数值。
常用的插值方法包括拉格朗日插值、牛顿插值和分段线性插值等。
插值方法通常用于数据的光滑处理、曲线拟合和函数逼近等问题。
2.数值微分与积分方法数值微分是通过有限差分等方法,对实际问题的函数进行求导。
数值积分则是通过数值方法求解复杂函数的积分。
常用的数值微分与积分方法包括欧拉法、龙格-库塔法和辛算法等。
3.非线性方程求解非线性方程求解是求解形如f(x)=0的方程,其中f(x)是一个非线性函数。
常用的非线性方程求解方法包括二分法、牛顿法和割线法等。
这些方法基于不同的数学原理来逼近方程的根。
4.线性方程组求解线性方程组求解是求解形如Ax=b的方程组,其中A是一个矩阵,b 是一个向量。
常用的线性方程组求解方法包括高斯消元法、LU分解和迭代法等。
这些方法可以高效地求解大规模的线性方程组。
5.最小二乘法最小二乘法是一种用于拟合实验或观测数据的方法。
它通过最小化观测数据与理论模型之间的残差平方和,得到最佳的参数估计。
最小二乘法广泛应用于曲线拟合、回归分析和信号处理等领域。
6.数值优化数值优化是在约束条件下求解最优化问题的方法。
常用的数值优化方法包括梯度下降法、共轭梯度法和拟牛顿法等。
这些方法可以在函数复杂或维度高的情况下,有效地寻找最优解。
7.偏微分方程数值解法偏微分方程数值解法是用数值方法解决偏微分方程的方法。
常用的数值解法包括有限差分法、有限元法和谱方法等。
这些方法广泛应用于物理学、工程学和金融学等领域,可以模拟和预测复杂现象。
总之,数值分析方法在科学和工程领域中起着重要的作用。
通过数学和计算机的结合,数值分析使得复杂计算变得简单,从而有效解决各种实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求如下多元函数的最小值
I (a0 , a1,..., an ) = ∑ω(xi )[∑ajϕj (xi ) − f (xi )]2
i=0 j =0
m
n
由多元函数 求极值的必 要条件
∂I = 0, (k = 0,1,⋯, n) ∂ak
即
m n ∂I = 2∑ω(xi )[∑ajϕ j (xi ) − f (xi )]ϕk (xi ) ∂ak i=0 j =0
S1( x) = a0 + a1 x
得法方程为
8a0 + 22a1 = 47 22a0 + 74a1 = 145.5
解得
a0 = 2.77, a1 = 1.13
于是所求拟合曲线为
∗ S1 ( x) = 2.77 + 1.13x
在某化学反应里, 例2. 在某化学反应里,根据实验所得生成物的 浓度与时间关系如下表, 求浓度y与时间 与时间t的拟 浓度与时间关系如下表 , 求浓度 与时间 的拟 合曲线y=F(t). 合曲线
; (1) y是t的增函数 (2)当t →0 + 时,y = 0; (3)t →∞时,y趋于一个定值
根据这些条件,可设想两种形式的函数关系: 根据这些条件,可设想两种形式的函数关系: y = F(t) 是双曲线型
1 b t = a + ,即y = y t (at + b)
y = F(t) 是指数形式
结论: 结论:
选择拟合曲线的数学模型, 选择拟合曲线的数学模型,并不一定开始 就能选好,往往需要通过分析若干模型后, 就能选好,往往需要通过分析若干模型后, 经过实际计算才能选到较好的模型, 经过实际计算才能选到较好的模型,如本 例的指数模型就比双曲线模型好得多。 例的指数模型就比双曲线模型好得多。
δ = ∑δi2 = ∑[S∗ ( xi ) − yi ]2
2 2 i=0 i=0
m
m
= min ∑[S( xi ) − yi ]2
S( x)∈ ϕ
m
这里
i=0
S( x) = a0 + a1x +... + an x
n
(n < m)
3. 一般定义 已知: 一组数据( 已知: 一组数据(xi,yi)(i=0,1,…,m), , 求: 在函数类 ϕ = span{ϕ0 ,ϕ1 ,...,ϕn }中找一 ∗ 使误差平方和最小, 个函数 y = S (x) ,使误差平方和最小, 即
但遗憾的是, 但遗憾的是 , 在实际中噪声的形式往往是 未知的。 在上个世纪60年代 年代, 未知的 。 在上个世纪 年代 , Tukey说明了在 说明了在 现实情况中, 现实情况中,噪声的形式与高斯或拉普拉斯规 律都相去甚远。 律都相去甚远。
回到起点! 回到起点!
作业: 作业: 习题 16,17,18 16,17,
2 2
即
δ = ∑ω( xi )[S∗ ( xi ) − yi ]2
2 2 i=0
m
ω( x) ≥ 0
其中
S( x) = a0ϕ0 ( x) + a1ϕ1( x) + ... + anϕn ( x) (n < m)
注:权函数在实际问题中有重要作用! 权函数在实际问题中有重要作用!
二、求解方法
求S*(x)
展开
∑a j ∑ω( xi )ϕ j ( xi )ϕk ( xi ) = ∑ω( xi ) f ( xi )ϕk ( xi )
j=0 i =0 i =0
n
m
m
法方程
解方程组
∗ a 有唯一解 k = ak (k = 0,1,..., n)
则S
∗
∗ ∗ ∗ ( x) = a0 0 ( x) + a1 1( x) + ... + an n ( x)
2 2
+ ( x + 2 y − 6)2 + (2x + y − 7)2
达到最小
则(x,y)应满足 )
∂Q( x, y) =0 ∂x ∂Q( x, y) =0 ∂y
即 6x − y = 17
− 3x + 46 y = 48
解得
x = 3.0403 y = 1.2408
高斯提出了最小二乘法,而拉普拉斯提出了
最小模方法。从那时起就有了下面的问题: 从那时起就有了下面的问题:
那种方法更好呢? 世纪和20世纪初 那种方法更好呢?在19世纪和 世纪初,人 世纪和 世纪初, 们更趋向于最小二乘法。 们更趋向于最小二乘法。 在1953年,L.Le Cam定义了 定义了ML方法一致收 年 定义了 方法一致收 敛的一些充分条件后,人们发现: 敛的一些充分条件后,人们发现:如果离散 数据点的噪声是服从高斯(正态)规律的, 数据点的噪声是服从高斯(正态)规律的, 则最小二乘法给出最好的结果; 则最小二乘法给出最好的结果;若噪声是服 从拉普拉斯规律的,则最小模法给出最好的 从拉普拉斯规律的, 结果。 结果。
例3. 用最小二乘法解超定方程组
2x + 4 y = 11 3x − 5 y = 3 x + 2 y = 6 2x + y = 7
欲求( ) 解 欲求(x,y)使得其尽可能使四个等式成 立,即使
Q( x, y) = (2x + 4 y − 11) + (3x − 5 y − 3)
b<0
b/ t
y = ae
y = F(t) 是双曲线型
1 b t = a + ,即y = y t (at + b)
为了确定a、 , 为了确定 、b,令
1 1 y= , x= y t
于是可用 x 的线性函数 S1( x) = a + bx 拟合 数据 ( xi , yi )
(i = 1,...,16) 。 xi , yi ) 可由原始 (
(数据有删减) 数据有删减)
δ = ∑δi2 = ∑[S∗ ( xi ) − yi ]2
2 2 i=0 i=0
m
m
= min ∑[S( xi ) − yi ]2
S( x)∈ ϕ
m
这里
i=0
S( x) = a0ϕ0 ( x) + a1ϕ1( x) + ... + anϕn ( x)
(n < m)
4. 广义定义 通常把最小二乘法 δ 都考虑为加权平方和
i i
(2)使残差的绝对值之和为最小 使残差的绝对值之和为最小
∑e
i
i
= min
最小二乘法
(3)使残差的平方和为最小 使残差的平方和为最小
∑e
i
2 i
= min
2. 多项式拟合的一般定义 已知: 一组数据( 已知: 一组数据(xi,yi)(i=0,1,…,m), , 求: 在函数类 ϕ = span{ , x,..., xn} 中找一 1 ∗ 使误差平方和最小, 个函数 y = S (x) ,使误差平方和最小, 即
第3章 函数逼近与曲线拟合 §4 曲线拟合的最小二乘法
一、最小二乘法的定义 二、求解方法 三、求解步骤 四、举例
一、最小二乘法的定义
1. “曲线拟合”问题 曲线拟合” 曲线拟合 已知: 一组实验数据( 已知 : 一组实验数据 ( xi , yi ) (i=0,1,…,m), , 且观测数据有误差 求:自变量x与因变量y之间的函数关系 y=F(x) ,不要求y=F(x)经过所有点,而只要 经过所有点, 不要求 经过所有点 求在给定点上误差
计算出来。 数据 (ti , yi ) 计算出来。
这里ϕ0 ( x) = 1,ϕ1( x) = x
可求得 (ϕk ,ϕ j ), ( y,ϕ j ), j, k = 0,1 代入法方程得
16a + 3.38073b = 1.8372×103 3 3.38073a + 1.58435b = 0.52886×10
δi = F( xi ) − yi
最小。 按某种标准最小。
(i = 0,1,..., m)
度量标准不同,将导致不同的拟合结果, 度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种: 的准则有如下三种: (1)使残差的最大绝对值为最小 使残差的最大绝对值为最小
maxei = max yi − F(xi ) = min
t Y t y 1
4.00
2
6.40
3
8.00
4
8.80
5
9.22
6
9.50
7
9.70
8
9.86
9
10
11
12
13
14
15
16
10.00 10.20 10.32 10.42 10.50 10.55 10.58 10.60
根据所给数据,在坐标纸上标出, 解 根据所给数据,在坐标纸上标出,得下图 y
t 从图中可以看出开始时浓度增加较快, 从图中可以看出开始时浓度增加较快 , 后来 逐渐减弱, 逐渐减弱 , 到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 趋于某个常数, 值上,即当 时 趋于某个常数 水平渐近线。 反应未开始, 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为 度为 。
b ln y = lna + t
ˆ 于是由 (ti , yi ) 计算出 ( xi , yi ) ,拟合数 据 ( xi , yi ) 的曲线仍设为 ˆ
S1( x) = A+ bx
得法方程
16A+ 3.38073b = −75.26394 3.38073A+ 1.58435b = −16.82229
解得 从而得到
