5-6稳定裕度和稳定性能、动态性能分析
王划一-自动控制原理-5-3稳定裕度
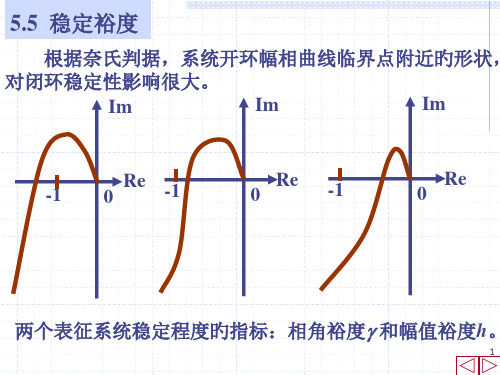
= 37.4
当(g) = 180时
180 = arctang 180 2arctan0.1g
求得
arctang =2arctan0.1g g = 8.94
20 lg h
20 lg A(g )
20
lg
k g g2 12
9.03dB
因为 > 0，所以闭环系统是稳定旳。
0
0 20 40 60 80
能够看出，调整时间与相角裕度和幅值穿越频率都有 关系。假如两个二阶系统旳相同，则它们旳超调量也相同， 这时比较大旳系统，调整时间较短。
17
例5-19 一单位反馈控制系统，其开环传递函数
G(s)
7
s(0.087s 1)
试用相角裕度估算过渡过程指标p% 与ts。
解：系统开环伯德图如图示
33
四 、奈奎斯特稳定判据
内容 应用
5.5 稳定裕度
根据奈氏判据，系统开环幅相曲线临界点附近旳形状，
对闭环稳定性影响很大。
Im
Im
Im
-1
Re 0
-1
Re 0
-1
Re 0
两个表征系统稳定程度旳指标：相角裕度 和幅值裕度h。
1
（1）幅值裕度h ：令相角为180时相应旳频率为g （相角穿越频率），频率为g 时相应旳幅值A(g)旳倒数，
定义为幅值裕度h ，即 h 1 A(g )
10 11.5
0
1
20
40dB/dec
()/()
0
90
180
19
2) 高阶系统
近似旳关系式
p
0.16 0.4( 1
频域性能指标和时域性能指标的关系
5.7 频域性能指标和时域性能指标的关系频率响应法是通过系统的开环频率特性和闭环频率特性的一些特征量间接地表征系统的瞬(暂)态响应的性能，因而这些特征量又被称为频域性能指标。
常用的频域性能指标有幅值裕度、相位裕度、谐振峰值、谐振频率和频带宽度等。
虽然这些指标没有时域性能指标那样直观，但在二阶系统中，它们与时域性能指标有着确定的对应关系，对于高阶系统，也有近似的关系。
5.7.1频域指标和二阶系统的过渡过程指标设二阶单位反馈系统的方框图如图5-80所示。
图 5-80 二阶单位反馈系统的方框图此系统的闭环传递函数为2222)()(nn n s s s X s Y ωξωω++= 其中ξ为阻尼比，n ω为无阻尼自然振荡频率。
令s j =ω代入上式，可得系统的闭环频率响应为:ja n nM j j X j Y e 2)1(1)()(22=+-=ωωξωωωω式中 M nn =-+1122222()()ωωξωω2212a r c t a n nn ωωωωξα--= 根据式(5-67)可知，当00707≤≤ξ.时，在谐振频率ωr 处，M 出现峰值ωωξr n =-122M r =-1212ξξ二阶系统的闭环频率特性如图5-81所示。
图 5-81 图5-80所示系统的闭环频率特性对于二阶系统，在012≤<ξ时，频率特性的谐振峰值M r 可以反映系统的阻尼系数ξ，而其谐振频率ωr 可以反映给定ξ对应的自然频率ωn ,从而也能反映响应速度。
这样就可把二阶系统闭环频率特性的M r 和ωr 当作性能指标用。
系统的频带宽度(带宽)由图5-81可见，当ωω>r 时，闭环频率特性的幅值M 单调下降。
当闭环频率特性的幅值下降到707.021==M 时，或者说，当闭环频率特性的分贝值下降到零频率时分贝值以下3分贝时，对应的频率ωb 称为截止频率，又称带宽频率。
此时有b j M j M ωωω>-<3)0(lg 20)(lg 20对于0)0(lg 20=j M ，有b j M ωωω>-<3)(lg 20系统对频率高于ωb 的输入衰减很大，只允许频率低于ωb 的输入通过。
自动控制原理试题
4.以下不属于非线性系统特点的是（ ）
A. 满足叠加性 B. 存在自激振荡 C.有多个平衡点 D. 频率响应会畸变
5.设系统开环传递函数为 ，则开环放大倍数为（ ）
A. ； B. 6； C. 12； D. ２
三、判断题（每小题２分，共10分）
1）系统的闭环脉冲传递函数；（4分）
2）判定系统的稳定性；（4分）
3）说明零阶保持器对系统的影响。（4分）
六、控制系统两种结构方案如图所示。(12分)
１）如何调整K1，K2和K3，使系统获得良好动态性能？
２）比较两种方案的特点。
七、已知单位反馈系统传递函数为 ，（14分）
１）试绘制概略根轨迹。
２）分析各参数变化对系统性能的影响。
A. zpk B. tf C. ss D. sos
2.关于开环放大倍数对系统性能的影响，错误的是（ ）
A. 提高开环放大倍数，系统的快速性提高，稳定性增强；
B. 开环放大倍数与开环相频特性无关；
C. 提高开环放大倍数，能够提高系统的稳态精度；
D. 开环放大倍数等于０型系统的静态位置误差系数。
3. 控制系统结构如图所示，则系统属于（ ）
则T =秒，A =。
二、求图示系统的传递函数。（10分）
三、稳定性分析（共2题，5分/题，共10分）
1.已知系统的特征方程如下，应用劳斯稳定判据判定稳定性。
2.设二阶非线性系统 ，判定系统奇点的类型并给出Matlab仿真程序。
四、已知渐进对数幅频特性曲线如图所示，求开环传递函数，并求截止频率、相角裕度。
（16分）
五、设带理想继电特性的非线性控制系统如图所示。设系统的初始状态为零，利用相轨迹法分析系统在阶跃信号作用下的运动过程（10分）。
5.67稳定裕度
点尚可增加的迟后相
1
g
c
( c )
与Bode图中的对应关系：
L( )
1
g
c
( c )
c g K g dB
( )
(c )
二、增益裕量 K g (幅值稳定裕度) ①定义
A( g )
g ：相位交界频率
1
g
1 Kg | G jg H jg |
-20vdB/dec
L1 ( )
1
②当 1 时，k也可由 L1 ( ) 与横轴的交点 0来求。 当
0
，L(0 ) 0 ，有：
0 20 lg k 20 lg 0 , k 0
20 lg k
0
1
四、系统Bode图中频段、高频段分析
1、中频段： Bode图中幅频特性曲线在截止
频率正弦输入信 号响应的平稳性。
谐振峰值与最大超调量之间的关系
（2） b 与 t s 的关系
由带宽的定义知当 带宽频率。得：
1 1 M ( ) M (0) 时的频率为 2 2
幅频特性为：
M ( )
n 2
(n 2 2 )2 (2n ) 2
b n 1 2 2 2 4 2 4 4
ts 3
n
3 bt s 1 2 2 2 4 2 4 4
结论：对于给定的谐振峰值，调整时间与闭 环带宽成反比。则系统有较大的带宽，则系 统响应的快速性好。
（3） c 与 t s 关系
n n G ( S ) H S S ( S 2 n ) 2 n
值为：
均为正值。且通常取
第五章_频域特性
，半径为
1 2
。
16
A（）—— 幅频特性；G（j）的模，它等于稳态 的输出分 量与输入分量幅值之比. （）—— 相频特性；G（j）的幅角，它等于稳态输出分 量与输入分量的相位差。 G ( j ) U（）—— 实频特性； j V V（）—— 虚频特性； V ( ) 都是的函数，之间的 A ( ) 关系用矢量图来表示。
10
R
极坐标图
c 1 G ( j ) r R C j 2
r (t )
i (t )
C
c (t )
1 1 j T e
j a rc ta n T
e
j
1 1 j T
1 /( 2 T )
1/ 1 T
G ( j ) 9 0
由于幅角是常数，且幅值随ω增大而减小。因此，积分 环节是一条与虚轴负段相重合的直线。
14
典型环节的极坐标图
4. 惯性环节
G ( j ) 1 1 j T 1 1 ω T
2 2
1 1 T
2 2
j
T
1 T
2 2
G jω
取三个特殊点
（RC=T）
5
即为无源RC网络的频率特性。
频率特性的性质
1、与传递函数一样，频率特性也是一种数学模型。 它描述了系统的内在特性，与外界因素无关。当系统 结构参数给定，则频率特性也完全确定。 2、频率特性是一种稳态响应。 系统稳定的前提下求得的，不稳定系统则无法直接观 察到稳态响应。从理论上讲，系统动态过程的稳态分量总 可以分离出来，而且其规律并不依赖于系统的稳定性。因 此，我们仍可以用频率特性来分析系统的稳定性、动态性 能、稳态性能等。 3、系统的稳态输出量与输入量具有相同的频率。 当频率改变，则输出、输入量的幅值之比A（）和相 位移（）随之改变。这是系统中的储能元件引起的。
系统频率测试实验报告(3篇)
第1篇一、实验目的1. 了解系统频率特性的基本概念和测试方法。
2. 掌握使用示波器、频谱分析仪等设备进行系统频率测试的操作技巧。
3. 分析测试结果，确定系统的主要频率成分和频率响应特性。
二、实验原理系统频率特性是指系统对正弦输入信号的响应，通常用幅频特性（A(f)）和相频特性（φ(f)）来描述。
幅频特性表示系统输出信号幅度与输入信号幅度之比，相频特性表示系统输出信号相位与输入信号相位之差。
频率测试实验通常包括以下步骤：1. 使用正弦信号发生器产生正弦输入信号；2. 将输入信号输入被测系统，并测量输出信号；3. 使用示波器或频谱分析仪观察和分析输出信号的频率特性。
三、实验设备1. 正弦信号发生器2. 示波器3. 频谱分析仪4. 被测系统（如放大器、滤波器等）5. 连接线四、实验步骤1. 准备实验设备，将正弦信号发生器输出端与被测系统输入端相连；2. 打开正弦信号发生器，设置合适的频率和幅度；3. 使用示波器观察输入信号和输出信号的波形，确保信号正常传输；4. 使用频谱分析仪分析输出信号的频率特性，记录幅频特性和相频特性；5. 改变输入信号的频率，重复步骤4，得到一系列频率特性曲线；6. 分析频率特性曲线，确定系统的主要频率成分和频率响应特性。
五、实验结果与分析1. 幅频特性曲线：观察幅频特性曲线，可以发现系统存在一定频率范围内的增益峰值和谷值。
这些峰值和谷值可能对应系统中的谐振频率或截止频率。
通过分析峰值和谷值的位置，可以了解系统的带宽和选择性。
2. 相频特性曲线：观察相频特性曲线，可以发现系统在不同频率下存在相位滞后或超前。
相位滞后表示系统对输入信号的相位延迟，相位超前表示系统对输入信号的相位提前。
通过分析相位特性，可以了解系统的相位稳定性。
六、实验总结1. 通过本次实验，我们掌握了系统频率特性的基本概念和测试方法。
2. 使用示波器和频谱分析仪等设备，我们成功地分析了被测系统的频率特性。
3. 通过分析频率特性曲线，我们了解了系统的主要频率成分和频率响应特性。
5-5 频域：稳态分析
M
p
0.16 0.4(
1 sin γ
1)
(35 γ 90 )
ts
Kπ ωc (s)
(35 90 )
式中
K 2 1 .5 (
1 sin
1) 2.5(
1 sin γ
Gm>1，系统稳定。 Gm<1，系统不稳定。 Gm=1，系统临界稳定。
4
(1)增益裕度Gm
Gm
1 G(j ω g )H(j ω g )
以分贝表示时
G M dB 20lgGm 20lg G(j ω g )H(j ω g ) dB
GM>0 (Gm>1) ，系统稳定。 GM<0 (Gm<1) ，系统不稳定。
2
2
2.587
2.587 3.14 12
5.4.3 基于闭环频率特性的 系统性能分析
22
讨论二阶系统闭环频域指标谐振峰值Mr ,谐振角频率r ,带宽 b对系统动态性能的影响.
二阶系统的闭环频率特性
M(j ) ωn (j ) 2 ζ n (j ) ω
2 2 n 2
M 00 0 .7 0 7 M 0 -3
0
r
b
23
M (dB)
谐振峰值Mr：
M
r
闭环幅频最大值。
Mr对应Mp ,越小越好。 谐振角频率r： 谐振峰值频率。
00 0 .7 0 7 M 0 -3
0
M
r
b
对|M(jω)|求导,令导数为0,可求得
稳定裕度
m
(1 ij )
j
(1 T j )
闭环传递函数和频率特性可表示为：
GK ( s ) ( s) 1 GK ( s ) K (1 i s ) s
m i 1 j
(1 T s) K (1 s)
j 1 i 1 i m
n
|M(j|下降到
[0, b ]称为系统带宽。
2 M 0 时，对应的频率 b 称为带宽频率。频率范围 2
5.8 闭环系统性能分析
16
一、稳态性能指标分析：
如果通过频率特性曲线能确定系统的无差度阶数 v（即积分环节的个数） 和开环放大系数 K 的话，则可求得系统的稳态误差。（见3.6 稳态误差分析） 在波德图上，低频渐近线的斜率 和 的关系如下： 由 20 (dB / Dec),可求得 值； 也可由
|M(j|下降到
② 对典型欠阻尼二阶系统而言，性能指标与系统的特征参数有关。欠 阻尼二阶系统的特征参数是阻尼系数z 和无阻尼震荡频率。
tp 2 d n 1z
d%e
z
1z 2
100%
4 z ，当Δ 2时 n ts 3 ，当Δ 5时 z n
③ 对临界阻尼和过阻尼二阶系统而言，性能指标只有ts 。
60 40 20 0 -20 -40 -60 -80 -100 -120 -90 -120 -150 -180 -210 -240
10
K=30 K=3 K=0.3
－20dB/dec
当K=3，c=1.583， 23.3° 当K=30， －40dB/dec c=5.12， 16° －60dB/dec
20 0 -20 -40 -60 -80 -100 -120 -140 -90 -120 -150 -180 -210 -240 -270 0.01 0.1 1 10 100 1000
基于MATLAB的系统稳定性能判定
在对系统进行 动态性能分析 时， 其 中 一 种 方 式 是 对 闭 环 阶 跃 响应分析 。 系统 分 析 最 直 接 的 方 法 是 求 取 系 统 的 阶 跃 响 应 并 画 出 响 应 曲线 ， 这 在 人 工 分 析 时 很难 办 到 ， 但 是 用Ｍ Ａ ＴＬ ＡＢ 软 件 来 完 成却很容易， 而且 还 便 于 研 究 某 些 参 数对 系统 性 能 的 影 响 。 我们 仍
特性 ， 从 图 中得 到 穿越 频率 ∞ｃ （ 计 算 或 图解 均可 ） ， 计 算 出对 应 于 ∞
计算就更为复杂麻烦 ， 但是 利 用 ＭＡＴＬ ＡＢ 仿 真 软 件 就 显 的 比 较 简
具。
单。 参考文献 利 用ｍａ ｒ ｇ ｉ ｎ （ ） 函 数 可 以计 算 给 定 线 性 系统 的 相 位 裕 度 和 幅值 ［ １ ］熊新 民 ． 自动控 制原 理 与 系统 Ｉ Ｎ］ ． 北京 ： 电子 工业 出版 社 ， ２ ０ ０ ３ 裕度 。 该 函数 的 调 用 格 式 是 ：
ａＩ Ｉ Ｓ ＝
Ｓ Ｃ Ｉ Ｅ Ｎ Ｃ Ｅ ＆Ｔ Ｅ Ｃ Ｈ Ｎ ０ Ｌ ０ ０ Ｙ Ｉ Ｎ Ｆ Ｏ Ｒ Ｍ Ａ Ｑ Ｔ Ｉ ： Ｏ 坠 Ｎ
４ห้องสมุดไป่ตู้． ０ ０ ００
８５． ０ ４ ０４
４． ８９ ９ ０
０． ２ ０ ７ ９
因此 ， 该 系统的 相位 裕度 是 ８ ５ ． ０ ４ ０ ４ 。 ， 对 应 幅 值 穿 越 频 率 为 ０ ． ２ ０ ７ ９ ｒ ａ ｄ ／ ｓ ； 幅值裕 度为４ ８ ． ０ ０ ０ ０ ， 对应 相位穿越 频率 为４ ． ８ ９ ９ ０ ｒ ａ ｄ ／ ｓ 。 ２． ４ 利用 开 环频 率 特性 图形 判 定 系统 的稳 定性 在 ＭＡ ＴＬ ＡＢ中 ， 可 以直 接 画 出 系统 的开 环 奈 奎斯 特 图 ， 然 后根 据 频 域 稳 定 判 据 就 可 判 明 系统 的 稳 定 性 。 例 如 已知 某 系 统 的 开 环
北京理工大学自动控制原理考研知识点
本资料由理硕教育整理，理硕教育是全国唯一专注于北理工考研辅导的学校，相对于其它机构理硕教育有得天独厚的优势。
丰富的理工内部资料资源与人力资源确保每个学员都受益匪浅，确保理硕教育的学员初试通过率89%以上，复试通过率接近100%，理硕教育现开设初试专业课VIP 一对一，初试专业课网络小班，假期集训营，复试VIP 一对一辅导，复试网络小班，考前专业课网络小班，满足学员不同的需求。
因为专一所以专业，理硕教育助您圆北理之梦。
详情请查阅理硕教育官网北京理工大学自动控制原理考研考点第二章 控制系统的数学模型一 主要知识点传递函数会求各类传递函数：开环传递函数、闭环传递函数、误差传递函数、典型环节传递函数。
针对典型系统结构图来记：图结构图化简。
把握住等效原则即可。
等效原则，即化简前后回路上传递函数的乘积不变、且前向通道上传递函数的乘积不变。
信号流图熟练运用Mason 公式：（关键是每一个量代表的含义）二 需要记忆的：常见的拉氏变换、拉式反变换（掌握留数法）三 备考策略本章内容较简单且单独出题的可能性不大，注意与其他章节的结合，尤其是非线性那章中结构图的化简。
第三章一 主要知识点1 二阶系统的时域分析数学模型单位阶跃响应取不同值时对应的单位阶跃响应曲线：不同情况下系统的根。
欠尼阻二阶系统的动态过程分析动态性能指标公式，要记住并理解各公式的由来。
2 稳定性分析)s s 1i （）（∑∆∆=i i P P 2n n 22n s 2s )()(s ωζωω++==ΦS R S C ）（ζ理解稳定的充要条件劳斯判断：列劳斯表（两种特殊情况的处理）；稳定性判断及稳定范围的确定。
3 稳态误差（首先想到以稳定性为前提）稳态误差的计算：终值定理、由稳态误差系数确定。
扰动作用下的稳态误差：主要取决于扰动作用点前的传递函数。
降低稳态误差的方法：增大系统开环总增益，以降低给定输入作用下的稳态误差；增大扰动作用点前系统前向通路的增益，以降低扰动作用所引起的稳态误差第四章根轨迹法一 主要知识点理解根轨迹的含义、根轨迹增益与开环增益的区别、两个基本条件根轨迹的绘制根轨迹图的分析二 需要记忆的：根轨迹绘制规则三 备考策略本章内容是每年单独出题的章节，是比较重要的章节。
稳定裕度的定义
5.5 稳定裕度5.5.1 稳定裕度的定义控制系统稳定与否是绝对稳定性的概念。
而对一个稳定的系统而言，还有一个稳定的程度，即相对稳定性的概念。
相对稳定性与系统的动态性能指标有着密切的关系。
在设计一个控制系统时，不仅要求它必须是绝对稳定的，而且还应保证系统具有一定的稳定程度。
只有这样，才能不致因系统参数的小范围漂移而导致系统性能变差甚至不稳定。
对于一个最小相角系统而言，)(ωj G 曲线越靠近点（0,1j −），系统阶跃响应的振荡就越强烈，系统的相对稳定性就越差。
因此，可用)(ωj G 曲线对点（）的接近程度来表示系统的相对稳定性。
通常，这种接近程度是以相角裕度和幅值裕度来表的。
0,1j −相角裕度和幅值裕度是系统开环频率指标，它们与闭环系统的动态性能密切相关。
1．相角裕度相角裕度是指开环幅相频率特性)(ωj G 的幅值1)()(==ωωj G A 时的向量与负实轴的夹角，常用希腊字母γ表示。
图5-47 相角裕度和幅值裕度的定义 图 5-48 稳定裕度在Bode 图上的表示在G 平面上画出以原点为圆心的单位圆，见图5-47。
)(ωj G 曲线与单位圆相交，交点处的频率c ω称为截止频率，此时有1)(=c A ω。
按相角裕度的定义180()c γϕω=+o （5-69）由于01lg 20)(lg 20)(===c c A L ωω，故在伯德图中，相角裕度表现为dB L 0)(=ω处的相角)(c ωϕ与水平线之间的角度差，如图5-48所示。
上述两图中的o 180−γ均为正值。
2．幅值裕度)(ωj G 曲线与负实轴交点处的频率g ω称为相角交界频率，此时幅相特性曲线的幅值为)(g A ω，如图5-47所示。
幅值裕度是)(ωj G 与负实轴交点至虚轴距离的倒数，即1()g A ω，常用h 表示，即)(1g A h ω=（5-70）在对数坐标图上20lg 20lg ()()g g h A L =−ω=−ω （5-71）即的分贝值等于h )(g L ω与之间的距离（下为正）。
稳定性分析与稳定裕度
稳定性分析与稳定裕度稳定性是指系统在受到内外部扰动时能否回到平衡状态的能力。
稳定裕度则是指系统能够容忍的扰动大小。
在工程领域中，稳定性分析和稳定裕度的研究对于保障系统的安全可靠性至关重要。
本文将介绍稳定性分析与稳定裕度的概念、计算方法以及其在不同领域的应用。
一、稳定性分析的概念稳定性分析是一种评估系统稳定性的方法。
它可以通过分析系统的特性和参数来判断系统在遭受外界扰动时是否能够保持平衡。
在稳定性分析中，常用的方法包括等效线性化、Bifurcation分析、Lyapunov稳定性分析等。
等效线性化是一种常见的稳定性分析方法。
它通过将非线性系统在某一特定工作点附近进行线性化处理，得到等效线性系统，并通过研究其特征根来判断系统的稳定性。
Bifurcation分析则是研究系统在参数变化过程中平衡点的分岔情况，以此来判断系统是否存在稳定性转变。
而Lyapunov稳定性分析则是利用Lyapunov函数的性质来评估系统的稳定性。
二、稳定裕度的计算稳定裕度是评估系统稳定性的指标之一。
它是指系统在遭受一定范围内的扰动时能够保持稳定的能力。
稳定裕度的计算通常涉及到系统的摄动响应和性能指标的定义。
摄动响应是指系统在受到扰动时的响应情况。
常见的稳定裕度指标包括幅值裕度和相位裕度。
幅值裕度是指系统在受到特定幅值的扰动时，输出信号的幅值与输入信号幅值之间的差值。
相位裕度则是指系统在受到特定相位的扰动时，输出信号相位与输入信号相位之间的差值。
稳定裕度的计算与系统的数学模型和特性密切相关。
在实际工程中，可以通过仿真实验或实际测试来获取系统的摄动响应，从而计算稳定裕度。
此外，还可以通过建立数学模型，利用控制理论和信号处理方法来计算稳定裕度。
三、稳定性分析与稳定裕度的应用稳定性分析与稳定裕度的研究在众多领域中都有广泛的应用。
以下是几个典型的应用案例：1.电力系统稳定性分析：电力系统中存在较大的复杂性和不确定性，稳定性分析可以帮助评估系统的动态响应和抗干扰能力，为电力系统的设计和运行提供指导。
控制系统的性能指标与评价方法
控制系统的性能指标与评价方法控制系统是现代工业生产中不可或缺的一部分，它能够对生产过程进行监测和调节，以保持系统运行在稳定、高效的状态下。
为了评估控制系统的性能，我们需要定义一些指标，并采用相应的评价方法进行分析。
本文将介绍控制系统的性能指标以及常用的评价方法。
一、响应速度响应速度是指控制系统对输入信号的改变作出相应的速度。
在工业生产过程中，由于生产环境的变化，输入信号也会发生变化，控制系统需要能够及时地对这些变化作出反应，以保持系统的稳定性。
常用的评价方法有系统的动态特性和稳态误差。
动态特性可以通过系统的阶跃响应来评估，而稳态误差则可以通过系统的静态特性来评估。
二、稳定性稳定性是指控制系统在面对干扰或变化时的抵抗能力。
一个稳定的控制系统应该能够保持输出信号在一定范围内波动，不会出现震荡或过度调节的情况。
稳定性的评价方法主要包括系统的零极点分布、伯德图和罗斯特曼图等。
三、精度精度是指控制系统输出信号与期望信号之间的差异程度。
对于某些特殊的生产过程，精度要求非常高，一般要求系统的输出信号能够与期望信号完全匹配。
常用的评价方法有系统的静态误差和误差曲线。
四、鲁棒性鲁棒性是指控制系统对于参数变化和外部干扰的抵抗能力。
在实际工程中，控制系统的参数往往会受到各种因素的影响而发生变化，同时系统也会面临来自外界的各种干扰。
鲁棒性评价方法包括系统的灵敏度函数和鲁棒边界。
五、稳定裕度稳定裕度是指控制系统距离稳定临界点的距离。
在实际工程中，由于参数变化、外部干扰等因素的存在，控制系统可能会临界失稳。
稳定裕度评价方法主要有相角裕度和增益裕度。
六、能耗能耗是指控制系统在完成一定任务的过程中所消耗的能量。
对于一些特殊的应用场景，如能源稀缺或环境要求苛刻的情况下，我们需要评价控制系统的能耗情况。
能耗评价方法主要包括系统的能耗模型和功耗曲线。
综上所述，控制系统的性能评价涉及多个指标，包括响应速度、稳定性、精度、鲁棒性、稳定裕度和能耗。
自动控制原理计算题题库
自动控制原理计算题题库 1 某系统结构如图二所示，求系统的开环传递函数和闭环传递函数。
当C 值为200时，求R 的值。
2 已知单位反馈系统的开环传递函数为)3)(1(22)(++=s s s G 系统输入量为r(t)，输出量为C(t)，试求：(1) 当r(t)=1(t)时，输出C(t)的稳态值和最大值;(2) 为了减少超调量，使阻尼比等于0.6，对系统实施速度反馈控制，试画出速度反馈系统方框图，并确定速度反馈系数。
3 已知系统的开环传递函数)10)(2()()(++=s s s K s H s G 为保证系统稳定，并且在)(2)(1)(t t t r +=作用下的稳态误差2.0≤ss e ，试确定K 的取值范围。
4 已知某系统的开环传递函数为)7)(2()()(++=s s s K s H s G ， （1）画出以K 为参数的闭环系统根轨迹图；（2）求出使系统不出现衰减振荡的K 值范围。
5 已知某最小相角系统的对数幅频特性如图六中)(0ωL 所示：(1) 求系统的开环传递函数并计算相角裕量γ，判别闭环系统稳定性；(2) 为了改善系统性能，采用1100110)(++=s s s G c 的校正装置进行串联校正，试画出校正后系统的Bode 图，求出相角裕量γ'；(3) 在Bode 图上标出相角裕量γ'及幅值裕量)(dB h 。
6 系统微分方程如下：试画出结构图，并求传递函数)()(s R s C7 某系统的结构图如图所示，图中放大器参数4=p k ，电动机参数1.0,1==m d T k 秒, 01.0=d T 秒,（１） 求系统的单位阶跃响应及其s t %,σ和ss e ；（２） 如要求稳态误差小于或等于%)5(e 5%ss ≤，应该变哪一参数，并计算该参数的值。
试分析该参数变化对系统性能的影响。
8 设单位反馈系统的闭环传递函数为n n n n n n a s a s a s a s a s ++++=---1111.......)(φ，试证明系统在单位斜坡函数作用下，稳态误差为零。
稳定裕度和稳定性能动态性能分析
时间都比较大，稳定性和快速性都比较差。
若L()的中频段斜率为-60dB/dec，中频段对应 的传函的分母比分子高三阶，相角裕量必定小于0， 系统不稳定。
在中频段，为了使系统具有较高的动态 指标，中频段的斜率最好为-20dB/dec，且具 有足够的频宽，这样，系统容易得到大于450 相角裕量。同时，穿越频率要满足系统快速性 的要求。
稳定裕度和稳定性能动态性能分析
5-3 稳定裕度
项目
内容
教学目的
掌握幅值裕度和相角裕度的概念，明确幅值裕度 和相角裕度对系统性能的影响。
教 学 重 点 幅值裕度和相角裕度的概念。
教 学 难 点 幅值裕度和相角裕度对系统性能的影响。
讲授技巧及注 意事项
注重图形和公式推导的结合。
K=4 K=1
Imaginary Axis
0
10
1
10
2
10
Frequency (rad/sec)
二、闭环系统的频域性能指标 1、带宽频率 闭环幅频特性下降到频率为零时的分贝值 以下3分贝时，对应的频率称为带宽频率b。
2 0 lg (j b) 2 0 lg (j0 ) 3
频率范围(0,b )称为系统的带宽。
2、谐振峰值 闭环幅频特性的最大值20lgMr所对应的Mr 值。 (Mr=1/|sinγ| ）
0 0
Step Response
5
10
15
Time (sec)
由以上可以看出：极坐标图离开（-1，j0） 点的远近程度是系统的相对稳定性的一种度量， 这种度量常用相角裕量（度）和幅值裕量（度） 来描述。
一.稳定裕度的定义
稳定裕度包括相角裕度和幅值裕度两个概念
系统的开环幅相曲线如图： a点： | A(c)|1
频域法分析典型II型系统动态性能和稳态性能
邢台学院物理系《自动控制理论》课程设计报告书设计题目:频域法分析典型II系统的动态性能和稳性能专业:自动化班级:学生姓名:学号:指导教师:2013 年 4 月7 日邢台学院物理系课程设计任务书专业：自动化年月日摘要频率特性法是经典控制理论中对系统进行分析与综合的又一重要方法。
与时域分析法和根轨迹法不同。
频率特性法不是根据系统的闭环极点和零点来分析系统的时域性能指标，而是根据系统对正弦信号的稳态响应，即系统的频率特性来分析系统的频域性能指标。
它内容丰富，包含了很多实用的方法对系统稳定性进行判断，不用计算出具体的系统的传递函数。
因此，从某种意义上讲，频率特性法与时域分析法和根轨迹法有着本质的不同。
频率特性虽然是系统对正弦信号的稳态响应，但它不仅能反映系统的稳态性能，而且可以用来研究系统的稳定性和动态性能。
关键词：随动系统串联校正相角裕度幅值裕度超调量调节时间目录1-1、频率特性的基本概念 ------------------------------- 4 1-2、获取系统频率特性的途径和表示方法------------------- 51、获取频率特性的途径----------------------------------- 52、系统频率特性的表示方法------------------------------- 5 1-3、频域稳定判据 ------------------------------------- 61、奈奎斯特稳定性判据----------------------------------- 62、伯德图----------------------------------------------- 73、相位裕量与幅值裕量----------------------------------- 7 1-4、典型系统的分析 ----------------------------------- 71、Ⅱ型系统的开环奈氏曲线------------------------------- 72、设控制系统的开环传递函数为--------------------------- 8总结体会--------------------------------------------- 11 参考文献1-1、频率特性的基本概念讨论线性定常系统（包括开环、闭环系统）在正弦输入信号作用下的稳态输出。
机械控制工程资料-----5-6频域稳定判据奈氏判据
(c)由于ν＝2，从 0点逆时针
＝0 补画半径为无穷大的半园。
Re
P=0, N=-1，Z=2
0
K 该闭环不系统稳定。
Gc (S) S 2 (TS 1)
Im
Gd
(S)
10 S(TS 1)
(d)ν=1,从 0 点逆时针
补画半径为无穷大的1/4园。
记为半次正(半次负)穿越。
右图中 N 2 N 2
N N N 22 0
- +- + -1 0
Re
幅相曲线在负实轴(-.-1)
区间的正负穿越如图所示 R 2N
4
Nyquist稳定判据
闭环系统稳定的充要条件是：闭合曲线ГGH曲线不穿 过（-1，j0） ，且逆时针绕（-1，j0）点的圈数R等于 G(s)H(s)位于s右半平面的极点数P圈。
( x ) G jx H jx 180 0
h
1
G jx H jx
00
h
1
Im
1
h
x
- ＋
1 c
00
h1
Im
c
Re x
－
-1
Re
G( j)
G( j)
1 h
（a）稳定系统
（b）不稳定系统 20
20lg G( jc )H( jc ) 0dB
Im
-1
0 Re
Im
-1 0 Re
Im
-1
0 Re
Im
-1 0 Re
h(t)
h(t)
自动控制原理 第五章(第六次)
• 指开环幅相特性曲线在截止频率 附c 近的区段。
22
从开环频率特性研究闭环系统性能
自动控制原理
(1)截止频率 的c 斜率为-20dB/dec 宽度2 c 3
系统是稳定的，并近似认为整个开环特性为-20dB/dec
则，开环传递函数为 G(s) K c
ss
相位裕度约为90°，幅值裕度为无穷大，超调量 为零，调节时间 3 。
n2
1
c2 4 2n2
29
从开环频率特性研究闭环系统性能
自动控制原理
A(c ) c
n2
1
c 2
4
2 2 n
n4 c2 (c2 4
2 2 n
)
1
n4
c4
1
4
2
n2 c2
1
c ( 4 2 1 2 2 )1/ 2 n
阻尼比一定，截止频率随自然频率的增大 而增大。
30
从开环频率特性研究闭环系统性能
A( jc )
(
K 1
1 c2 )3
c
K
1/
3
1
1.233, K 1.908, K
4 10
相角裕度:
180
K=4时:
() 180 3arctgc Kg>1, γ>0 闭环系统稳定
27.1 7.0
K=10时: Kg<1,γ <0 闭环系统不稳定
K 4 K 10
பைடு நூலகம்10
5.6 频域稳定裕度—相对稳定性
幅值裕度为
Kg
1
G jg H jg
1 4
0.34
0.98 1 0.982
该闭环系统不稳定。
《自动控制原理》 胡寿松 第05#6章 频域稳定裕度.ppt
?
0.69
?b
上升时间：
tr
?
2 .202 T
?
2.202
?b
调节时间：
ts
?
3T
?
3
?b
说明 ? b和延迟
时间、上升时间、 调节时间也成反比。
（2）二阶系统带宽 ? b
设二阶系统的闭环传递函数为
? (s) ?
s2
?
?
2 n
2??
n
s
?
?
2 n
故有 | ? ( j0) |? 1。
系统的幅频特性： |? ( j? ) |?
贝时，对应的频率 ? b称为带宽频率， 即带宽频率 ? b为 满足下列方程的解：
20 lg ? ( j? b ) ? 20 lg ? ( j0) ? 3
对于Ⅰ型和Ⅰ型以上系统，由于 ? ( j0) ? 1 故有：
20 lg ? ( j? b ) ? ? 3(dB )
显然，当 ? >? b时，有 20 lg ? ( j? ) ? 20 lg ? ( j0) ? 3
③物理意义： 稳定系统在 截止频率 ωc处若相角再迟 后一个γ角度，则系统处于 临界状态 ；若相角迟后 大于γ ，系统将变成不稳定。
j
-1 ωx
1
γ ωc
0
∠G(jω c)Ｈ(jω c) G(jω)Ｈ(jωc)
上述两图中， γ均为正值
（2）幅值裕度
①在开环幅相频率特性曲线中定义
幅值裕度 是指在(-1,j0)点处的幅值1与开环幅相
d? (1? 2? 2 )2 ? 1
即A与ζ成反比关系，根据假设，又 A与? b成正比 关系，故可得， ? b与阻尼比 ζ成反比关系 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
( jw ) M (w )e
j (w )
A(w )e j (w ) 1 A(w )e j (w )
由闭环频率特性可得：
sin( ) 20 lg A(w ) 20 lg sin
给定一确定的值，若从00~3600连续变 化，则存在和20lgA(w)连续的一一对应值， 在(, 20lgA)平面获得一等线，改变的值， 可获得等曲线簇。
-1
0.8 0.6 0.4
-2
-3 0.2 -4 -2 0
0
5
10 Time (sec)
15
Nyquist Diagram
Step Response 1.4 1.2
K=0.5
Imaginary Axis
1
0
1
Amplitude
-1 0 Real Axis 1 2 -1
0.8 0.6 0.4
-2
-3
t s 0
w 0
由时域分析法可知：系统稳态误差和系统 的型别 n 、开环放大倍数 K 以及输入信号 R(s) 有关。
系统型别n的确定：极坐标图的低频段的斜率为 -20n，由此可确定n的值。 系统开环放大倍数 K 的确定：由于 L(w)=20lgK20nlgw ， 低 频 渐 近 线 或 延 长 线 过 (w=wc ， 0) 或 (w=1,20lgK)点，由此可确定K的值。
Amplitude
-2 -1 0 Real Axis 1 2
-1
1
-2
0.5 -3
-4
0
0
10
20
30 Time (sec)
40
50
60
K=1
Imaginary Axis
Nyquist Diagram 1 1.4 1.2 1
Step Response
0
Amplitude
-1 0 Real Axis 1 2
若L(w)的中频段斜率为-40dB/dec，并且占据的 频率区间较宽，可认为中频段对应的开环传函为：
K wc2 G ( s) 2 2 s s
G (s) 则闭环传函： ( s) 1 G ( s)
wc2
s2 1
wc2 2 2 wc s wc2
s2
相当于一个z0二阶系统，对应的阶跃响应为等 幅振荡的。实际系统即使稳定，一般超调量和调节 时间都比较大，稳定性和快速性都比较差。
控制系统的稳定与否是绝对稳定性的概 念，稳定系统的稳定程度是相对稳定性(稳定 裕度 ) 的概念，一般说来， G(jw)H(jw) 越接近 于(-1，j0)点，系统的相对稳定性越差。下面 以典型三阶系统为例进行说明。
K G( s) s( s 1)( s 2)
K=8
Imaginary Axis
Nyquist Diagram 0.5 0 -0.5 -1 -1.5 -2 -2.5 -4
Step Response 15
10
Amplitude
-2 0 Real Axis 2 4
5
0
-5
-10
0
5
10
15 Time (sec)
20
25
30
K=6
Nyquist Diagram 0.5 0 -0.5 1.5 2 Step Response
在穿越频率处，A(w ) 1 ，所以w 2 (1 w 2 )(1 0.04w 2 ) 4 ，解 此方程较困难，可采用近似解法。由于 wc较小（小于2），所以： 2 A(w ) 1, 解得：w c 1.25 w 1 w 2 精确值：wc=1.227
10
8dB
21
穿越频率处的相角为： (wc ) 90 tg 1wc tg 1 0.2wc 155.38
得： 1 0.2wg 2 1, 解得：wg 2.24 2 A(w g ) 0.33216 2 2 w g 1 w g 1 0.04w g 所以，幅值裕度为： Lg 20log A(w g ) 9.6(dB)
12
当增益从k=10增大到k=100时，幅值特性曲线上移20dB，相位 特性曲线不变。这时系统的相位稳定裕度和幅值裕度分别是12dB和-30度。因此系统在k=10时是稳定的，在k=100时是不稳 定的。
L(w )
1
wg
A(w g )
wc w g w
(w c )
(w )
Lg
wc
w
(w g )
1 180 (wc ) 为幅值稳定裕度和相位稳定裕 [定义]： 和 kg A(w g ) 度。 在对数坐标图上，用 Lg表示 k g 的分贝值。即 Lg 20logkg 20log A(wg )
12dB
30
Saturday, June 28, 2014
13
5-7 开环频率特性与稳态性能、 动态性能的关系 稳态性能分析
稳态误差是描述系统稳态性能的性能指 标，由终值定理知稳态误差由频率特性的低 频段决定。
ess lim e(t ) lim se( s) lim jw e( jw )
第五章 线性系统的频域分析法
第六节 稳定裕度
5-6 稳定裕度
项目 内 容
教 学 目 的 和相角裕度对系统性能的影响。
掌握幅值裕度和相角裕度的概念，明确幅值裕度
教 学 重 点 幅值裕度和相角裕度的概念。
教 学 难 点 幅值裕度和相角裕度对系统性能的影响。
讲授技巧及注 注重图形和公式推导的结合。 意事项
由闭环频率特性可得：
cos cos2 M 2 1 20lg A(w ) 20lg M 2 1
给定一确定的 M 值，若 从 00~3600 连续 变化，则存在和20lgA(w)连续的一一对应值， 在 (, 20lgA) 平面获得一等 M 线，改变 M 的值， 可获得等M曲线簇。 在(, 20lgA)平面上等曲线簇和等M曲线 簇组合成尼克尔斯图线。
0.2
-4 -2
0
0
5 Time (sec)
10
15
由以上可以看出：极坐标图离开（-1，j0） 点的远近程度是系统的相对稳定性的一种度量， 这种度量常用相角裕量（度）和幅值裕量（度） 来描述。
当频率特性曲线穿过(-1,j0)点时，系统处于临界稳定状态。 A ( w ) 1 , ( w ) 180 ,wc wg 。对于最小相位系统， 这时： g c 可以用 A(w g )和 (wc )来表示频率特性曲线接近(-1,j0)点的程度， 或称为稳定裕度。稳定裕度越大，稳定性越好。
比如，若增加开环放大系数K，则对数幅频特性曲线将上升，而 相角特性曲线不变。可见，开环放大系数太大，容易引起系统 的不稳定。 [相位稳定裕度的物理意义]：稳定系统在幅值穿越频率wc 处将 相角减小 度，则系统变为临界稳定；再减小，就会变为不稳 定。
8
[例]设控制系统如下图所示 R( s ) k=10和k=100时，试求系统 的相位稳定裕度和幅值裕度。
已知单位反馈系统开环传函如下，绘制闭 环系统的频率特性图：
11.7 G( s) s(1 0.05s)(1 0.1s)
>> g=zpk([],[0,-20,-10],2340) >> bode(feedback(g,1))
Bode Diagram 10 5
System: untitled1 Peak gain (dB): 6.76 At f requency (rad/sec): 9.05
高频段： L(w)在中频段以后的频段
由于高频段远离开环截止频率，所以对系统的动 态性能影响不大高频段的形状主要影响系统的抗干扰 性能。
20lg A(w) 0 A(w) 1
( jw) G( jw) 1 G( jw) A(w)
A(w)在高频段的幅值，直接反映了系统对高频 干扰信号的抑制能力。高频部分的幅值越低，系统 的抗干扰能力就越强。高频段的斜率一般设置为-60 或-80dB/dec。
Imaginary Axis
-1 -1.5 -2 -2.5 -3 -3
Amplitude
-2 -1 0 Real Axis 1 2 3
1
0.5
0
0
5
10
15
20
25
30
35
Time (sec)
K=4
Imaginary Axis
Nyquist Diagram 1 2
Step Response
0 1.5
180 (wc ) 180155.38 24.6 相角裕度为：
精确值： =25.389
11
幅值裕度：先求相角穿越频率w g
相角穿越频率处w g的相角为： (wg ) 90 tg 1wg tg 1 0.2wg 180
即：tg 1wg tg 1 0.2wg 90 1 1.2w g tg 90 2 1 0.2w g
频域分析法总结
稳定性分析：Nyquist判据(绝对稳定性)、稳
定裕度(和h) (相对稳定性) 稳态性能分析：由对数坐标图的低频段确定 系统的型别ν和开环放大系数K。 动态性能分析（定性）：三频段法
5-8闭环系统频域性能指标
一、闭环频率特性的图解法
设系统开环频率特性为：
G( jw ) A(w )e j (w )
若 L(w) 的中频段斜率为 -60dB/dec ，中频段对应 的传函的分母比分子高三阶，相角裕量必定小于 0 ， 系统不稳定。
在中频段，为了使系统具有较高的动态 指标，中频段的斜率最好为 -20dB/dec ，且具 有足够的频宽，这样，系统容易得到大于 450 相角裕量。同时，穿越频率要满足系统快速性 的要求。