九年级数学专题复习四边形
九年级数学中考复习专题:四边形综合(考察全等证明、长度与面积计算等)

九年级数学中考复习专题:四边形综合(考察全等证明、长度与面积计算等)(一)1.综合与实践问题情境在数学活动课上,老师提出了这样一个问题:如图①,已知正方形ABCD,点E是边上一点,连接AE,以AE为边在BC的上方作正方形AEFG.数学思考(1)连接GD,求证:△ABE≌△ADG;(2)连接FC,求∠FCD的度数;实践探究(3)如图②,当点E在BC的延长线上时,连接AE,以AE为边在BC的上方作正方形AEFG,连接FC,若正方形ABCD的边长为4,CE=2,则CF的长是.2.如图,正方形ABCD的边长是2厘米,E为CD的中点,Q为正方形ABCD边上的一个动点,动点Q以每秒1厘米的速度从A出发沿A→B→C→D运动,最终到达点D,若点Q运动时间为x秒.(1)当x=1时,S△AQE=平方厘米;当x=时,S△AQE=平方厘米.(2)在点Q的运动路线上,当点Q与点E相距的路程不超过厘米时,求x的取值范围.(3)若△AQE的面积为平方厘米,直接写出x值.3.如图,在平行四边形ABCD中,∠BAD的平分线交C于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.(1)求证:四边形ECFG是菱形;(2)连结BD、CG,若∠ABC=120°,则△BDG是等边三角形吗?为什么?(3)若∠ABC=90°,AB=10,AD=24,M是EF的中点,求DM的长.4.如图1,正方形ABCD沿GF折叠,使B落在CD边上点E处,连接BE,BH.(1)求∠HBE的度數;(2)若BH与GF交于点O,连接OE,判断△BOE的形状,说明理由;(3)在(2)的条件下,作EQ⊥AB于点Q,连接OQ,若AG=2,CE=3,求△OQR 的面积.5.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.(1)求证:BD、EF互相平分;(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.6.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD于点M,MN⊥CM,交AB于点N,(1)求∠BMN的度数;(2)求BN的长.7.如图,四边形OABC为矩形,其中O为原点,A、C两点分别在x轴和y轴上,B点的坐标是(4,6),将矩形沿直线DE折叠,使点C落在AB边上点F处,折痕分别交OC,BC于点E、D,且D点坐标是(,6).(1)求F点的坐标;(2)如图2,P点在第二象限,且△PDE≌△CED,求P点的坐标;(3)若M点为x轴上一动点,N点为直线DE上一动点,△FMN为以FN为底边的等腰直角三角形,求N点的坐标.8.已知,在平行四边形ABCD中,点F是AB上一点,连接DF交对角线AC于E,连接BE.(1)如图1,若∠EBC=∠EFA,EC平分∠DEB,求证:平行四边形ABCD是菱形;(2)如图2,对角线AC与BD相交于点O,当点F是AB的中点时,直接写出与△ADF 面积相等的三角形(不包括以AD为边的三角形).9.如图,四边形ABCD是平行四边形,∠BAC=90°,AB=AC,点H为边AB的中点,点E在CH的延长线上,且AE⊥BE.点F在线段AE上,且BF⊥CE,垂足为G.(1)若BF=AF,且EF=3,BE=4,求AD的长;(2)求证:BF+2EH=CE.10.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,则线段AE与DF的关系是;(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(3)如图2,连接AC,当△ACE为等腰三角形时,请你求出CE:CD的值.参考答案1.(1)证明:∵四边形ABCD和四边形AEFG是正方形,∴AB=AD,AE=AG,∠ABE=∠ADG=90°,∴∠BAE+∠EAD=∠DAG+∠EAD,∴∠BAE=∠DAG,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS);(2)解:如图①,过点F作FH⊥BC,交BC的延长线于点H,∵∠AEF=∠ABE=90°,∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,∴∠FEH=∠BAE,又∵AE=EF,∠EHF=∠ABE=90°,∴△EHF≌△ABE(SAS),∴FH=EB,EH=AB=BC,∴CH=BE,∴CH=FH,∴∠FCH=45°,∴∠FCD=45°;(3)解:过点F作FH⊥BC,交BC的延长线于点H,如图②,由(2)知△EHF≌△ABE,∴EH=AB,FH=BE,∵AB=BC=4,CE=2,∴BE=FH=6,CH=CE+EH=6,∴CF==6.故答案为:6.2.解:(1)①∵E为CD的中点,∴DE=1,∵动点Q以每秒1厘米的速度从A出发沿A→B→C→D运动,∴当x=1时,AQ=1,∴S△AQE=×AQ×AD=×1×2=1,②∵AQ=,∴点Q在AB上,∴S△AQE=×AQ×AD=;故答案为:①1;②.(2)根据题意,得,解得:.∴x的取值范围是.(3)①当点Q在AB上,∵S△AQE=×x×2=,∴x=,②当点Q在BC上时,∵S△AQE=S梯形ABCE﹣S△ABQ﹣S△CQE=×2×(x﹣2)﹣×1×(4﹣x)=.∴x=,③当点Q在CD上时,∵S△AQE=,∴x=.综合以上可得x=或或.3.证明:(1)∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形;(2)△BDG是等边三角形,理由如下:∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,AD∥BC,∵∠ABC=120°,∴∠BCD=60°,∠BCF=120°,由(1)知,四边形CEGF是菱形,∴CE=GE,∠BCG=∠BCF=60°,∴CG=GE=CE,∠DCG=120°,∵EG∥DF,∴∠BEG=120°=∠DCG,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD,∴△BEG≌△DCG(SAS),∴BG=DG,∠BGE=∠DGC,∴∠BGD=∠CGE,∵CG=GE=CE,∴△CEG是等边三角形,∴∠CGE=60°,∴∠BGD=60°,∵BG=DG,∴△BDG是等边三角形;(3)如图2中,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=10,AD=24,∴BD===26,∴DM=BD=13.4.解:(1)如图1中,过点E作EN⊥AB于N,过点B作BM⊥EA′于M.由翻折可知,∠ABF=∠FEA′=90°,FB=FE,∴∠FBE=∠FEB,∴∠EBN=∠BEM,∵∠ENB=∠BME=90°,BE=EB,∴△ENB≌△BME(AAS),∴EN=BM,∵四边形ABCD是正方形,∴∠NBC=∠C=∠A=∠ENB=90°,AB=BC,∴AB=BM=BC,∵BH=BH,BE=BE,∴Rt△BAH≌Rt△BMH(HL),Rt△BME≌Rt△BCE,∴∠ABH=∠MBH,∠EBM=∠EBC,∴∠HBE=∠MBH+∠EBM=∠ABC=45°.(2)结论:△BOE是等腰直角三角形.理由:如图2中,由翻折的旋转可知,FG垂直平分线段BE,∴∠OBE=∠OEB=45°,∴OB=OE,∠BOE=90°,∴△BOE是等腰直角三角形.(3)如图3中,过点O作OM⊥EQ于M,ON⊥AB于N,过点G作GJ⊥BC于J.∵∠A=∠ABJ=∠BJG=90°,∴四边形ABJG是矩形,∴AG=BJ=2,AB=GJ=BC,∵FG⊥BE,∴∠EBC+∠BFG=90°,∠BFG+∠JGF=90°,∴∠CBE=∠JGF,∵∠C=∠GJF=90°,BC=GJ,∴△GJF≌△BCE(AAS),∴FJ=CE=3,∴BF=EF=5,CF==4,∴BC=BF+CF=9,∴BE===3,∴OB=OE=3,∵EQ⊥AB,∴∠ONB=∠OME=∠OMQ=∠MQN=90°,∴四边形MQNO是矩形,∴∠MON=∠BOE=90°,∴∠BON=∠EOM,∴△ONB≌△OME(AAS),∴ON=OM,∴四边形MQNO是正方形,设OM=OM=NQ=MQ=x,∵∠C=∠CBQ=∠BQE=90°,∴四边形BCEQ是矩形,∴BQ=EC=3,EQ=BC=9,在Rt△BON中,则有x2+(x+3)2=(3)2,解得x=3或﹣6(舍弃),∴OM=QM=3,EM=BN=6,∵∠BQR=∠OMR=90°,∠BRQ=∠ORM,BQ=OM=3,∴△BQR≌△OMR(AAS),∴QR=MR=∴S△OQR=•QR•OM=××3=.5.(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC,∵DE、BF分别是∠ADC和∠ABC的角平分线,∴∠ADE=∠CDE,∠CBF=∠ABF,∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,∴∠AED=∠ADE,∠CFB=∠CBF,∴AE=AD,CF=CB,∴AE=CF,∴AB﹣AE=CD﹣CF即BE=DF,∵DF∥BE,∴四边形DEBF是平行四边形.∴BD、EF互相平分;(2)∵∠A=60°,AE=AD,∴△ADE是等边三角形,∵AD=4,∴DE=AE=4,∵AE=2EB,∴BE=GE=2,∴BG=4,过D点作DG⊥AB于点G,在Rt△ADG中,AD=4,∠A=60°,∴DG=AD cos∠A=4×=2,∴BD===2.6.解:(1)∵正方形ABCD的面积是8,∴BC=CD==2,∴BD=×2=4.∵四边形ABCD为正方形,∴∠DCO=∠BCO=∠CDO=∠MBN=45°,∵CM平分∠ACD,∴∠DCM=∠MCO=22.5°,∴∠BMC=∠CDO+∠DCM=45°+22.5°=67.5°.∵MN⊥CM,∴∠CMN=90°,∴∠BMN=90°﹣67.5°=22.5°,∴∠BMN的度数为22..5°.(2)∵∠MCO=22.5°,∠BCO=45°,∴∠BCM=∠BCO+∠MCO=67.5°,又∵∠BMC=67.5°,∴∠BCM=∠BMC,∴BM=BC=CD=2,∴DM=BD﹣BM=4﹣2.∵∠DCM=22.5°,∠BMN=22.5°,∴∠DCM=∠BMN.∴在△DCM和△BMN中,,∴△DCM≌△BMN(ASA),∴BN=DM=4﹣2,∴BN的长为4﹣2.7.解:(1)∵点D坐标是(,6),B点的坐标是(4,6),四边形OABC为矩形,∴BC=AO=4,OC=AB=6,CD=,BD=BC﹣CD=,∵将矩形沿直线DE折叠,∴DF=CD=,∴BF===2,∴AF=6﹣2=4,∴点F(4,4).(2)如图2中,连接PF交DE于J.当四边形EFDP是矩形时,△PDE≌△FED≌△CED,∵C(0,6),F(4,4),∴直线CF的解析式为y=﹣x+6,∵DE垂直平分线段CF,∴直线DE的解析式为y=2x+1,∴E(0,1),D(,6),∵DJ=JE,∴J(,),∵PJ=JF,∴P(﹣,3).(3)如图3中,连接FN,以FN为对角线构造正方形NMFM′,连接MM′交FN于K.设N(m,2m+1),则K(,),M(,),M′(,),当点M落在x轴上时,=0,解得m=﹣,当点M′落在X轴上时,=0,解得m=﹣9,∴满足条件的点N的坐标为(﹣,)或(﹣9,﹣17).8.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠EDC=∠EFA,∵∠EBC=∠EFA,∴∠EBC=∠EDC,∵EC平分∠DEB,∴∠DCE=∠BCE,在△CED和△CEB中,,∴△CED≌△CEB(AAS),∴CD=CB,∵四边形ABCD为平行四边形,∴平行四边形ABCD为菱形;(2)解:与△ADF面积相等的三角形(不包括以AD为边的三角形)为△AOB、△BOC、△COD、△DFB;理由如下:∵四边形ABCD是平行四边形,∴OA=OB,OC=OD,∴△AOB的面积=△BOC的面积=△COD的面积=△ABD的面积,∵点F是AB的中点,∴△ADF的面积=△DFB的面积=△ABD的面积,∴△AOB的面积=△BOC的面积=△COD的面积=△DFB的面积=△ADF的面积.9.解:(1)∵AE⊥BE.EF=3,BE=4,∴BF=,∵BF=AF,∴AF=5,∴AE=3+5=8,∴AB,∵∠BAC=90°,AB=AC,∴BC=,∵四边形ABCD是平行四边形,∴AD=BC=4;(2)在CH上截取HM=HE,连接BM和AM,如图,∵BE⊥AE,∴∠AEB=90°,∵点H为边AB的中点,∴EH=AH=BH=MH,∴四边形AEBM是矩形,∴∠EAM=90°,∵∠BAC=90°,∴∠BAF=∠CAM,∵BF⊥CE,∴∠EGB=90°,∴∠EBG+∠BEG=90°,∵∠EBG+∠BFE=90°,∴∠BEG=∠BFE,∵矩形AEBM中,BE∥AM,∴∠BEG=∠AMH,∴∠BFE=∠AMH,∴∠AFB=∠AMC,∵AB=AC,∴△ABF≌△ACM(AAS),∴BF=CM,∵CM+EM=CE,EM=EH+MH=2EH,∴BF+2EH=CE.10.解:(1)结论:AE=DF,AE⊥DF,理由:如图1中,∵四边形ABCD是正方形,∴AD=DC,∠ADE=∠DCF=90°,∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,∴DE=CF,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS),∴AE=DF,∠DAE=∠FDC,∵∠ADE=90°,∴∠ADP+∠CDF=90°,∴∠ADP+∠DAE=90°,∴∠APD=180°﹣90°=90°,∴AE⊥DF;故答案为:AE=DF,AE⊥DF.(2)成立.理由如下:如图2中,∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠DCF=90°,∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,∴DE=CF,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS),∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°,∴AE⊥DF.(3)有两种情况:①如图3﹣1中,当AC=CE时,设正方形ABCD的边长为a,由勾股定理得:AC=CE==a,则CE:CD=a:a=.②如图3﹣2中,当AE=AC时,设正方形ABCD的边长为a,由勾股定理得:AC=AE==a,∵四边形ABCD是正方形,∴∠ADC=90°,即AD⊥CE,∴DE=CD=a,∴CE:CD=2a:a=2,即CE:CD=或2.。
中考数学一轮复习专题突破练习—四边形

中考数学一轮复习专题突破练习—四边形一、单选题1.(2022·上海嘉定·九年级)下列命题:①等腰梯形的两个底角相等;①两个底角相等的梯形是等腰梯形;①等腰梯形的对角线等;①对角线相等的梯形是等腰梯形,其中真命题的个数是()A.0B.2C.3D.4【答案】D【分析】根据等腰梯形的性质对①①进行判断;根据等腰梯形的判定方法对①①进行判断.【详解】解:等腰梯形的两个底角相等,所以①为真命题;两个底角相等的梯形是等腰梯形,所以①为真命题;等腰梯形的对角线相等,所以①为真命题;对角线相等的梯形是等腰梯形,所以①为真命题.故选:D.2.(2022·临沂第九中学九年级月考)如图,在□ABCD中,对角线BD①AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连接DE、BF,下列结论不成立的是()A.四边形DEBF为平行四边形B.若AE=3.6,则四边形DEBF为矩形C.若AE=5,则四边形DEBF为菱形D.若AE=4.8,则四边形DEBF为正方形 【答案】D 【分析】根据平行四边形的判定方法,矩形的判定方法,菱形的判定方法,正方形的判定方法解答即可. 【详解】解:①O 为BD 的中点, ①OB =OD ,①四边形ABCD 为平行四边形, ①DC //AB ,①①CDO =①EBO ,①DFO =①OEB , ①①FDO ①①EBO (AAS ), ①OE =OF ,①四边形DEBF 为平行四边形, 故A 选项不符合题意, 若AE =3.6,AD =6, ①3.6365AE AD ==, 又①63105ADAB ==, ①AE ADAD AB=, ①①DAE =①BAD , ①①DAE ①①BAD ,①①AED=①ADB=90°.①四边形DEBF为矩形.故B选项不符合题意,①AB=10,AE=5,①BE=5,又①①ADB=90°,①DE=1AB=5,2①DE=BE,①四边形DEBF为菱形.故C选项不符合题意,①AE=3.6时,四边形DEBF为矩形,AE=5时,四边形DEBF为菱形,①AE=4.8时,四边形DEBF不可能是正方形.故选项D符合题意.故选:D.3.(2022·重庆字水中学九年级)下列命题是假命题的是()A.有一组邻边相等的矩形是正方形B.对角线相等的平行四边形是矩形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直的四边形是菱形【答案】D【分析】根据正方形、矩形、平行四边形、菱形的判定定理逐一判断即可.【详解】A:是真命题,是正方形的判定定理;B:是真命题,是矩形的判定定理;C:是真命题,是平行四边形的判定定理;D:不正确,是假命题,对角线互相垂直平分的平行四边形是菱形;故选:D.4.(2022·沙坪坝·重庆八中九年级月考)如图,正方形ABCD和正方形CEFG中,点D在CG上,2AD=,423DG=,H是AF的中点,那么CH的长是()A.3B.583C.15D.974【答案】B【分析】连接AC、CF,根据正方形性质求出AC、CF,①ACD=①GCF=45°,再求出①ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边中线的性质解答即可.【详解】如图,连接AC、CF,①正方形ABCD 和正方形CEFG ,2AD =,423DG =, ①①ACD =①GCF =45°,723CG =, ①()222222AC AD ==⨯=,2271422233CF CG ⎛⎫==⨯=⎪⎝⎭,①ACF =90°, ①在Rt ACF 中,222214258233AF AC CF ⎛⎫=+=+= ⎪⎝⎭, ①H 是AF 的中点, ①11258582233CH AF ==⨯=.故选:B .5.(2022·广东九年级期末)如图,将矩形ABCD 绕点B 顺时针旋转90°至矩形EBGF 的位置,连接AC 、EG ,取AC 、EG 的中点M 、N ,连接MN ,若AB =8,BC =6,则MN =( )A .8B .6C .5D .52【答案】D 【分析】连接BD ,BF ,DF ,由矩形的性质可以得到MN 是①BDF 的中位线,即12MN DF =,由旋转的性质可以得到BF =BD ,①DBF =90°,利用勾股定理求出DF 的长即可得到答案.【详解】解:如图所示,连接BD ,BF ,DF ,①四边形ABCD 和四边形BGFE 都是矩形,M ,N 分别是AC 和EG 的中点, ①M 和N 分别也是BD 和BF 的中点, ①MN 是①BDF 的中位线, ①12MN DF =①AB =8,BC =6,①ABC =90°, ①2210BD AC AB BC ==+=,①将矩形ABCD 绕点B 顺时针旋转90°至矩形EBGF 的位置, ①BF =BD =10,①DBF =90°, ①22102DF BD BF =+=, ①1522MN DF ==, 故选D .6.(2022·深圳市宝安中学(集团)九年级)下列判断正确的是( ). A .对角线相等的四边形是矩形B .将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似C .如果两个相似多边形的面积比为16①9,那么这两个相似多边形的周长比可能是4①3D.若点C是AB的黄金分割点,且6cmAB=,则BC的长为()3cm【答案】C【分析】A.利用矩形的判定定理对角线相等的平行四边形可判断;B.一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似应满足长与宽相等时可以,而矩形的长与宽一般不等;C.利用相似图形的性质即可;D.利用黄金分割法可求出BC有两个值即可.【详解】解:A、对角线相等的平行四边形是矩形,故此选项错误;B、将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形不一定相似,故此选项错误;C、如果两个相似多边形的面积比为16:9,则两个相似多边形的相似比为4:3,那么这两个相似多边形的周长比等于相似比是4:3,故此选项正确;D、若点C是AB的黄金分割点,且AB=6cm,则BC的长为()3cm或(-,故此选项错误;9cm故选C.7.(2022·山东济宁学院附属中学)如图,矩形纸片ABCD,6cmBC=,AB=,8cmE为边D上一点,将BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F 处,过点F作FM BE⊥,垂足为点M,取AF的中点N,连接MN,则MN=()cm.A .5B .6C .245D .27【答案】A 【分析】连接AC ,MC ,可求得M 为CF 的中点,根据中位线的性质可得12MN AC =,勾股定理求得AC 即可. 【详解】解:连接AC ,MC由折叠的性质可得CF EB ⊥,CE EF = 又①FM BE ⊥①点M 在线段FC 上,90EMF EMC ∠=∠=︒ 又①ME ME = ①()EMF EMC HL △≌△ ①FM MC = 又①AF 的中点N①MN 为ACF 的中位线 ①12MN AC =在Rt ACB 中,2210cm AC AB BC =+= ①5cm MN = 故选A8.(2022·全国九年级专题练习)如图,在平行四边形ABCD 中,AD =2AB ,作CE ①AB 于点E ,点F 是AD 的中点,连接CF ,EF .关于下列四个结论:①①BCF =①DCF ;①①FEC =①FCE ;①①AEF =①CFD ;①S ①CEF =S ①BCE ,则所有正确结论的序号是( )A .①①①①B .①①①C .①①①D .①①【答案】B 【分析】由平行四边形的性质结合等腰三角形的判定与性质可得①DFC =①BCF ,①DFC =①DCF ,可证明①;取EC 的中点G ,连接FG ,则FG 为梯形AECD 的中位线,再证明 FG ①CE ,可证明①;根据平行线的性质可得①AEC =①DCE =90°,进而可证明①;而无法证明①. 【详解】解:①四边形ABCD 为平行四边形, ①AB ①CD ,AD ①BC ,AB =CD , ①①DFC =①BCF ,①点F是AD的中点,①AD=2DF,①AD=2AB,①AD=2CD,①DF=CD,①①DFC=①DCF,①①BCF=①DCF,故①正确;取EC的中点G,连接FG,则FG为梯形AECD的中位线,①FG①AB,①CE①AB,①FG①CE,①EF=CF,①①FEC=①FCE,故①正确;①CE①AB,AB①CD,①CE①CD,①①AEC=①DCE=90°,即①AEF+①FEC=①DCF+①FCE=90°,①①AEF=①DCF,①①DCF=①CFD,①①AEF=①CFD,故①正确;①1•2CEFS CE BE =()()()11111112222222••••2BCESCE FG CE AE CD CE AE AB CE AE BE ==+=+=+ 而2AE BE +不一定等于2BE ①CEF S △不一定等于BCES ,故①错误;故选:B .9.(2022·全国九年级专题练习)如图,在梯形ABCD 中,AD ①BC ,EF 是梯形ABCD 的中位线,若①BEF 的面积为4cm 2,则梯形ABCD 的面积为( )A .8cm 2B .12cm 2C .16cm 2D .20cm 2【答案】C 【分析】如图,过A 作AN①BC 于N ,交EF 于M ,根据梯形的中位线性质得出AD+BC =2EF ,AM =MN ,由此再根据已知三角形的面积得出EF×AM =8,由此进一步根据梯形面积公式变形求解即可. 【详解】如图,过A 作AN①BC 于N ,交EF 于M , ①EF 是梯形ABCD 的中位线,①AD+BC =2EF ,EF①AD①BC , ①AM①EF ,AM =MN , ①①BEF 的面积为4cm 2, ①12EF×AM =4, ①EF×AM =8,①梯形ABCD 的面积为12(AD+BC)×AN =12×2EF×2AM =2EF×AM =16cm 2, 故选:C .10.(2022·珠海市文园中学九年级)如图,在边长为2的正方形ABCD 中,,E F 分别为,BC CD 的中点,连接AE BF ,交于点G ,将BCF ∆沿BF 对折,得到BPF ∆,延长FP 交BA 延长线于点Q .下列结论①QB QF =; ①AE BF ⊥;①4BGE ECFG S S ∆=四边形; ①4sin 5BQP ∠=,正确的有( )A .4B .3C .2D .1【答案】A 【分析】①①BCF 沿BF 对折,得到①BPF ,利用角的关系求出QF =QB ;①首先证明①ABE ①①BCF ,再利用角的关系求得①BGE =90°,即可得到AE ①BF ; ①利用QF =QB ,解出BP ,QB ,根据正弦的定义即可求解;①可证①BGE 与①BCF 相似,进一步得到相似比,再根据相似三角形的性质即可求解. 【详解】解:①根据题意得,FP =FC ,①PFB =①BFC ,①FPB =90°①CD ①AB , ①①CFB =①ABF , ①①ABF =①PFB , ①QF =QB ,故正确;①①E ,F 分别是正方形ABCD 边BC ,CD 的中点, ①CF =BE ,在①ABE 和①BCF 中,AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩, ①①ABE ①①BCF (SAS ), ①①BAE =①CBF , 又①①BAE +①BEA =90°, ①①CBF +①BEA =90°, ①①BGE =90°,①AE ①BF ,故正确; ①由①知,QF =QB , 令PF =k (k >0),则PB =2k 在Rt ①BPQ 中,设QB =x , ①x 2=(x ﹣k )2+4k 2, ①x =52k,①sin①BQP =45BPQB ,故正确; ①①①BGE =①BCF ,①GBE =①CBF , ①①BGE ①①BCF ,①BE =12BC ,BF BC ,①BE :BF =1①①BGE 的面积:①BCF 的面积=1:5, ①S 四边形ECFG =4S ①BGE ,故正确. 综上所述,共有4个结论正确. 故选A . 二、填空题11.(2022·上海崇明·九年级)如果一个等腰梯形的周长为50厘米,一条腰长为12厘米,那么这个梯形的中位线长为_____厘米. 【答案】13 【分析】根据梯形的周长公式列式进行计算即可得到两底的和,再根据梯形的中位线等于两底和的一半求出中位线的长即可.【详解】①等腰梯形的周长为50厘米,一条腰长为12厘米,①两底的和为5012226-⨯=(厘米),①这个梯形的中位线长为126132⨯=(厘米),故答案为:13.12.(2022·浙江九年级月考)如图,已知ABCD的对角线4cmBD=,将ABCD绕其对称中心O旋转180︒,则点D所转过的路径长为______cm.【答案】2π【分析】点D所转过的路径是一段圆心角为180°,半径为OD的弧,根据平行四边形的性质可得OD=12BD,根据弧长公式计算即可得答案.【详解】①四边形ABCD是平行四边形,4cmBD=,①OD=12BD=2cm,①将ABCD绕其对称中心O旋转180︒,①点D所转过的路径是一段圆心角为180°,半径为OD的弧,①点D所转过的路径长=122ODπ⨯⋅=2π,故答案为:2π13.(2022·哈尔滨市虹桥初级中学校九年级开学考试)如图,矩形ABCD 的对角线AC 、BD 相交于点O ,过点O 作OE ①BC ,垂足为点E ,过点A 作AF ①OB ,垂足为点F ,若BC =2AF ,OD =6,则BE 的长为____.【答案】33【分析】证明ABF BOE △≌△,进而证明ABO 是等边三角形,结合矩形的性质以及全等三角形的性质,勾股定理,进而即可求得BE . 【详解】四边形ABCD 是矩形6AO BO OD OC ∴====,90ABC ∠=︒90ABF OBE ∴∠+∠=︒ AF OB ⊥,90ABF BAF ∴∠+∠=︒,90AFB ∠=︒BAF OBE ∴∠=∠OE ①BC ,OB OC =12BE EC BC ∴==,90BEO ∠=︒ BC =2AF ,12AF BC BE ∴==∴ABF BOE △≌△AB BO ∴=,BE AF = OB OA =ABO ∴是等边三角形AF BO ⊥1302BAF BAO ∴∠=∠=︒12BF AB ∴=2232AF AB BF AB ∴=-= 6AB OA == 33∴=AF 33BE AF ∴==.故答案为:33.14.(2022·广东)如图,在梯形ABCD 中,AB ①CD ,BD ①AD ,BC =CD ,①A =60°,CD =2,则下底AB 的长等于__.【答案】4 【分析】由已知可得梯形为等腰梯形,从而可得AD =2,再根据含30°角直角三角形的性质可以得到AB 的值 . 【详解】解:①①A =60°,BD ①AD ,①①ABD=30°,又①AB①CD,①①CDB=①ABD=30°,①BC=CD,①①CBD=①CDB=30°,①①ABC=60°=①A,①AD=BC=CD=2,①AB=2AD=4.故答案为:4.15.(2022·哈尔滨市虹桥初级中学校九年级开学考试)已知矩形ABCD中,BE 平分①ABC交矩形的一条边于点E,若BD=10,①EBD=15°,则AB=___.【答案】5或53【分析】画出符合条件的两种情况,根据矩形性质求出①A=①ABC=①BCD=90°,①ABE =①CBE=45°,求出①DBC的度数,求出CD即可得出结论.【详解】解:有两种情况:①BE与边AD相交时,如图1,①四边形ABCD 是矩形,①①A =①ABC =①BCD =90°,AB =CD , ①BE 平分①ABC , ①①CBE =12①ABC =45°, ①①EBD =15°,①①DBC =①CBE −①DBE =30°, ①CD =12BD =12×8=5, ①AB=5;①BE 与边CD 相交时,如图2,①四边形ABCD 是矩形, ①①A =∠ABC =①C =90°, ①BE 平分①ABC , ①①ABD =12①ABC =45°, ①①EBD =15°,①①ABD =①CBE -①DBE =30°, ①152AD BD ==, ①2253AB BD AD =-=故答案为:5或53.三、解答题16.(2022·福建省同安第一中学九年级)如图,已知四边形ABCD是矩形,(1)尺规作图,求作正方形BECF,使得顶点E在矩形ABCD内;(2)连接DE,若AB=6,AD=8,求DE的长.【答案】(1)见解析;(2)25【分析】(1)要使得正方形BECF的顶点E在矩形ABCD内,则应考虑以BC为对角线,因为①B=①C=90°,要构成正方形则E点应为①B和①C的角平分线的交点,所以可先作①B与①C的角平分线,然后再根据正方形的对称性作图即可;(2)连接FE交BC于G点,并延长FE交AD于H点,根据矩形和正方形的性质分别求出DH和HE的长度,从而利用勾股定理求解即可.【详解】解:(1)如图所示,先作①B和①C的角平分线,交于E点,则此时①BEC为等腰直角三角形,然后分别以B,C两点为圆心,BE,CE为半径作圆弧在BC下方交于F点,①此时四边形BECF即为所求正方形;(2)如图所示,连接FE交BC于G点,并延长FE交AD于H点,①四边形ABCD为矩形,①①ADC=①BCD=90°,CD=AB=6,AD=BC=8,由(1)可知四边形BECF为正方形,BC=4,EG①BC,①EG=GC=12①①ADC=①BCD=①EGC=90°,即四边形CDHG为矩形,①DH=CG=4,GH=CD=6,①DHE=90°,①HE=GH-GE=2,在Rt①HDE中,根据勾股定理得:DE=22+=25.DH HE17.(2022·西安市铁一中学九年级开学考试)如图,在ABC中,AB AC=,D是边BC延长线上的一点,连接AD,过点A、D分别作//DE AB,AE、DEAE BD、//交于点E ,连接CE .求证:AD CE =. 【答案】见解析 【详解】证明:①AB =AC , ①①B =①ACB , ①//AE BD 、//DE AB ,①四边形AEDB 是平行四边形, ①DE =AB ,①EDB +①B =180°, ①DE =AC ,①①ACB +①ACD =180°, ①①ACD =①EDC , 在①ADC 与①EDC 中AC DE ACD EDC CD DC =⎧⎪∠=∠⎨⎪=⎩, ①①ADC ①①EDC (SAS ), ①AD =CE .18.(2022·宜兴市实验中学九年级)如图所示,ABCD 的对角线AC 的垂直平分线与边AD ,BC 分别相交于点E ,F .求证:四边形AFCE 是菱形.【答案】见解析 【分析】根据题意先证明()ASA AOE COF ≌△△,即可证明四边形AFCE 为平行四边形,根据EF AC ⊥可得结果. 【详解】证明:①四边形ABCD 是平行四边形 ①//AE FC ,AO CO =, ①EAC FCA ∠=∠,①EF 是AC 的垂直平分线, ①EF AC ⊥,在AOE △与COF 中,EAO FCO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩①()ASA AOE COF ≌△△, ①EO FO =,①四边形AFCE 为平行四边形, 又①EF AC ⊥, ①四边形AFCE 为菱形.19.(2022·长沙市雅礼实验中学九年级月考)如图所示,正方形ABCD 的边长是4,点E 是边BC 上的一个动点且90AEF ∠=︒,EF 交DC 于点G ,交正方形外角平分线CF 于点F ,点M 是AB 的中点,连按EM . (1)求证:BAE FEC ∠=∠;(2)若E 为BC 的中点,求证:AE EF =;(3)点E 在何位置吋线段DG 最短,并求出此时DG 的值.【答案】(1)见解析;(2)见解析;(3)E 为BC 中点时,DG =3 【分析】(1)由正方形性质可得90AEB BAE ∠+∠=︒,由90AEF ∠=︒得90AEB CEF ∠+∠=︒,由同角的余角相等即可求证结论;(2)由正方形的性质求证()AME ECF ASA ≌△△,继而即可求证结论; (3)易知ABE GEC ∽△△,设设BE x =,4CE x =-,利用已知边表示出关于DG 的二次函数关系,继而求得DG 的值. 【详解】解:(1)四边形ABCD 是正方形 ①90B ∠=︒,90AEB BAE ∠+∠=︒, ①90AEF ∠=︒,①90AEB CEF ∠+∠=︒, ①BAE CEF ∠=∠, (2)如图①四边形ABCD 是正方形,①AB BC =,90B BCD DCG ∠=∠=∠=︒, ①点E 是边BC 的中点, ①AM EC BE ==,①45BME BEM ∠=∠=︒,①135AME ∠=︒, ①CF 平分DCG ∠,①45DCF FCG ∠=∠=︒, ①180135ECF FCG ∠=︒-∠=︒,①AME ECF ∠=∠, ①90AEF ∠=︒,①90AEB CEF ∠+∠=︒, 又90AEB MAE ∠+∠=︒,①MAE CEF ∠=∠, ①()AME ECF ASA ≌△△,①AE EF =;(3)设BE x =,4CE x =-,由(1)知BAE GEC ∠=∠,又90B ECG ∠=∠=︒ ①ABE GEC ∽△△,①AB BE EC GC =,①44xx GC=- ①()144GC x x =-①()()2211144423444DG x x x x x =--=-+=-+当2x =即E 为BC 中点时,DG 的最小值为3.20.(2022·福建厦门双十中学思明分校九年级期末)如图,已知四边形ABCD是平行四边形.(1)请用直尺和圆规在AB上取一点E,使得EA=ED;(2)在(1)的条件下,连接CE,若①A=60°,AB=6,AD=4,求线段CE的长.【答案】(1)作图见解析;(2)27.【分析】(1)作线段AD的垂直平分线交AB于E即可;(2)过点E作EH①CD于H,求出E H,CH,即可解决问题.【详解】解:(1)如图,线段DE即为所求作,(2)过点E作EH①CD于H,①①A=60°,EA=ED,①①ADE是等边三角形,①①AED=60°,AE=AD=DE=4,①四边形ABCD是平行四边形,①AB①CD,①①CDE=①AED=60°,①①DHE=①CHE=90°,①①DEH=30°,①DH=1DE=2,2由勾股定理得EH=22-=,4223①AB=CD=6,①CH=CD-DH=4,①EC=()2222+=+=.CH EH4232721.(2022·长沙市开福区青竹湖湘一外国语学校九年级开学考试)如图,E为长方形ABCD的边AB上一点,将长方形沿CE折叠,使点B恰好落在ED上的点F处.(1)求证:AE=DF;(2)若BE=1,BC=3,求CD的长.【答案】(1)见解析;(2)5【分析】(1)根据矩形的性质和折叠性质证得①AED=①CDF,AD=CF,①A=①CFD=90°,进而证明①ADE①①FCD即可;(2)设CD x==,利用勾股定=,则1=-,根据全等三角形性质得到ED CD xAE x理列出x的方程,解之即可解答.【详解】解:(1)①四边形ABCD是长方形,①AD=BC,AB=CD,①A=①B=90°,AB①CD,①①AED=①CDF,由折叠可知:AD=BC=CF,①B=①CFE=90°,①①A=①CFD=90°,①①ADE①①FCD(AAS),①AE=DF;(2)设CD x=,则1=-,AE x由折叠得:AD=CF=BC=3,①①ADE①①FCD,①ED CD x==,Rt①AED中,222+=,AE AD ED①222-+=,(x1)3x解得:5x=,即CD=5.22.(2022·上海九年级专题练习)如图,在梯形ABCD中,AD BC∥,AC DB⊥,∠=︒,DBCAC=,305(1)求对角线BD 的长度; (2)求梯形ABCD 的面积. 【答案】(1)3;(2253. 【分析】(1)如图,过A 作AE DB 交CB 延长线于E ,①AC①DB ,AE①DB ,①AC①AE ,①AEC=①DBC=30°,即①EAC 为直角三角形,四边形AEBD 为平行四边形,根据勾股定理求解;(2)记梯形ABCD 的面积为S ,过A 作AF①BC 于F ,则①AFE 为直角三角形,求出梯形的高AF ,根据梯形面积公式即可求解. 【详解】解;(l )如图,过A 作AE DB 交CB 延长线于E , ①AC DB ⊥,AE DB .①AC AE ⊥,30AEC DBC ∠=∠=︒, ①90EAC ∠=︒,即EAC ∆为直角三角形, ①210EC AC ==,①222210553AE EC AC =--= ①AD BC ∥且AE DB . ①四边形AEBD 为平行四边形.①53DB AE ==;(2)记梯形ABCD 的面积为S ,过A 作AF BC ⊥于F ,则AFE ∆为直角三角形. ①30AEF ∠=︒ ①15322AF AE ==,即梯形ABCD 的高532AF =, ①四边形AEBD 为平行四边形, ①AD EB =.1()2S AD BC AF =+⨯1153253102222EC AF =⨯=⨯⨯=.23.(2020·浙江)已知:如图,四边形ABCD 中,AD ①BC ,对角线BD 平分①ABC ,且BD ①DC ,E 为BC 中点,AB =DE . (1)求证:四边形ABED 是菱形;(2)若①C =60°,CD =4,求四边形ABCD 的面积.【答案】(1)详见解析;(2)3【解析】 【分析】(1)由直角三角形斜边上的中线等于斜边的一半推出BE =ED =EC ,再由边关系推出角相等进而推出平行,由双平行推出平行四边形,加上邻边相等的平行四边形是菱形,可以推出结论.(2)作DF①BC于F,利用30的直角三角形,求出DF的长度,再由梯形的面积公式即可求出.【详解】证明:(1)①BD①DC,E为BC中点,①BE=ED=EC,①①DBE=①BDE;又AD①BC,①①ADB=①DBE,①①ADB=①BDE,①AB=AD,①①ABD=①ADB①①BDE=①ABD①DE①AB又①AD①BC,即AD①BE,①四边形ABCD为平行四边形又AB=AD,①平行四边形ABCD为菱形.(2)由(1)得,BE=EC=AD=DE,①①C=60°,①①DEC 为等边三角形.作DF①BC 于F ,则DF DC , BC =2BE =2AD =8, ①S梯形ABCD =12 (AD+BC )×DF =12×(4+8)=。
2023中考数学复习-专题22 四边形(讲通)(学生版)

专题22 四边形1.掌握平行四边形、菱形、矩形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性.2.探索并掌握平行四边形的有关性质和四边形是平行四边形的条件.3.探索并了解等腰梯形的有关性质和四边形是等腰梯形的条件.一、四边形的相关概念1.多边形的定义:在平面内,由不在同一直线上的一些线段首尾顺次相接组成的封闭图形叫做多边形.2.多边形的性质:(1)多边形的内角和定理:n边形的内角和等于(n-2)·180°;(2)推论:多边形的外角和是360°;(3)对角线条数公式:n边形的对角线有条;(4)正多边形定义:各边相等,各角也相等的多边形是正多边形.3.四边形的定义:同一平面内,由不在同一条直线上的四条线段首尾顺次相接组成的图形叫做四边形.4.四边形的性质:(1)定理:四边形的内角和是360°;(2)推论:四边形的外角和是360°.例1.一个多边形的外角和是内角和的,这个多边形的边数为()A.5B.6C.7D.8二、平行四边形的定义、性质与判定1.定义:两组对边分别平行的四边形是平行四边形.2.性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等,邻角互补;(3)平行四边形的对角线互相平分;(4)平行四边形是中心对称图形,对角线的交点是它的对称中心.3.判定:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.4.两条平行线间的距离:定义:夹在两条平行线间最短的线段的长度叫做两条平行线间的距离.性质:夹在两条平行线间的平行线段相等.5.平行四边形的面积:1.平行四边形的面积=底×高;2.同底(等底)同高(等高)的平行四边形面积相等.例2.如图,已知在▭ABCD中,对角线AC、BD相交于点O,AE▭BD,BM▭AC、DN▭AC,CF▭BD垂足分别是E、M、N、F,求证:EN▭MF.三、矩形的定义、性质与判定1.矩形的定义:有一个角是直角的平行四边形叫做矩形.2.矩形的性质矩形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:①边的性质:对边平行且相等.②角的性质:四个角都是直角.③对角线性质:对角线互相平分且相等.④对称性:矩形是中心对称图形,也是轴对称图形.直角三角形斜边上的中线等于斜边的一半.直角三角形中,角所对的边等于斜边的一半.点评:这两条直角三角形的性质在教材上是应用矩形的对角线推得,用三角形知识也可推得.3.矩形的判定判定①:有一个角是直角的平行四边形是矩形.判定②:对角线相等的平行四边形是矩形.判定③:有三个角是直角的四边形是矩形.四、菱形的定义、性质与判定1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质①菱形的四条边都相等;②菱形的对角线互相垂直,并且每一条对角线平分一组对角.注意:菱形也具有平行四边形的一切性质.3.菱形的判定①有一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形④有一条对角线平分一组对角的平行四边形是菱形⑤对角线互相垂直且平分的四边形是菱形4.菱形的面积①对角线乘积的一半(只要是对角线互相垂直的四边形都可用);②设菱形的边长为a,一个夹角为x°,则面积公式是:S=a²·sinx5.菱形的周长菱形周长=边长×4用“a”表示菱形的边长,“C”表示菱形的周长,则C=4a例3.如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,CE与BF相交于点H.(1)判断四边形EHFG的形状;(2)在什么情况下,四边形EHFG为菱形?五、梯形1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.(1)互相平行的两边叫做梯形的底;较短的底叫做上底,较长的底叫做下底.(2)不平行的两边叫做梯形的腰.(3)梯形的四个角都叫做底角.2.直角梯形:一腰垂直于底的梯形叫做直角梯形.3.等腰梯形:两腰相等的梯形叫做等腰梯形.4.等腰梯形的性质:(1)等腰梯形的两腰相等;(2)等腰梯形同一底上的两个底角相等. (3)等腰梯形的对角线相等.5.等腰梯形的判定方法:(1)两腰相等的梯形是等腰梯形(定义);(2)同一底上的两个角相等的梯形是等腰梯形;(3)对角线相等的梯形是等腰梯形.6.梯形中位线:连接梯形两腰中点的线段叫梯形的中位线.7.面积公式:S=(a+b)h(a、b是梯形的上、下底,h是梯形的高).六、平面图形1.平面图形的镶嵌的定义:用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片,这就是平面图形的镶嵌,又称做平面图形的密铺.2.平面图形镶嵌的条件:(1)同种正多边形镶嵌成一个平面的条件:周角是否是这种正多边形的一个内角的整倍数.在正多边形里只有正三角形、正四边形、正六边形可以镶嵌.(2)n种正多边形组合起来镶嵌成一个平面的条件:▭n个正多边形中的一个内角的和的倍数是360°;▭n个正多边形的边长相等,或其中一个或n个正多边形的边长是另一个或n个正多边形的边长的整数倍.1.(2022·泉州市东海中学)在四边形ABCD中,E,F,G,H分别为各边的中点,顺次连结E,F,G,H,得到中点四边形EFGH.当AC=BD时,则四边形EFGH是()A.平行四边形B.矩形C.菱形D.正方形2.(2022·黑龙江九年级期末)如图,矩形ABCD中8AB=把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.若254AF=,则AD的长为()A.4B.5C.6D.7 3.(2022·重庆实验外国语学校九年级月考)下列命题中,真命题是()A.对角线互相垂直的四边形是菱形B.对角线互相垂直平分的四边形是正方形C.四条边相等的四边形是矩形D.有一组对边平行且相等的四边形是平行四边形4.(2022·深圳市罗湖区翠园初级中学)如图,平行四边形ABCD中,对角线AC、BD相交于点O,则下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC▭BD时,它是菱形C.当AC=BD时,它是矩形D.当AC垂直平分BD时,它是正方形5.(2022·沙坪坝·重庆八中九年级月考)如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定ABE ADF≌的是()A.BE DF∠=∠∠=∠C.AE AF=B.BAF DAE=D.AEB AFD 6.(2022·重庆实验外国语学校九年级开学考试)下列说法不正确的是()A.平行四边形两组对边分别平行B.平行四边形的对角线互相平分C.平行四边形的对角互补,邻角相等D.平行四边形的两组对边分别平行且相等7.(2020·浙江杭州市·九年级)若一个梯形的中位线长为15,一条对角线把中位线分成两条线段.这两条线段的比是3:2,则梯形的上、下底长分别________.8.(2022·沈阳市第四十三中学九年级月考)如图,在▭ABC中,▭A=50°,AB=AC,点D 在AC边上,以CB、CD为边作平行四边形BCDE,则▭E的度数为_____.9.(2022·济南市章丘区实验中学九年级月考)已知:如图,平行四边形ABCD中,AC,BD⊥于点F.交于点O,AE BD⊥于点E,CF BD求证:OE OF=.10.(2019·宁波市慈湖中学九年级)如图,在梯形ABCD中,AD▭BC,AB=DC,若点M为线段AD上任意一点(M与A、D不重合).问:当点M在什么位置时,MB=MC,请说明理由.。
九年级中考数学专题复习-平行四边形专题
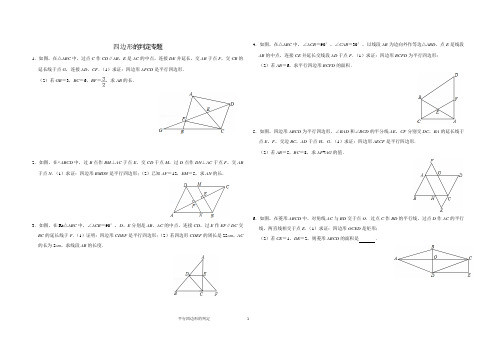
四边形的判定专题1.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF =,求AB的长.2.如图,在▱ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB 于点N.(1)求证:四边形BMDN是平行四边形;(2)已知AF=12,EM=5,求AN的长.3.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是25cm,AC 的长为5cm,求线段AB的长度.4.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形BCFD的面积.5.如图,四边形ABCD为平行四边形,∠BAD和∠BCD的平分线AE,CF分别交DC,BA的延长线于点E,F,交边BC,AD于点H,G.(1)求证:四边形AECF是平行四边形.(2)若AB=5,BC=8,求AF+AG的值.6.如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是.7.如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD 的平分线于点E、F.(1)若CE=8,CF=6,求OC的长;(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.8.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD =°时,四边形BECD 是矩形.9.如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.(1)求tan∠DBC的值;(2)求证:四边形OBEC是矩形.10.如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.11.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.12.如图,矩形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E、F.(1)求证:四边形BEDF是平行四边形;(2)只需添加一个条件,即,可使四边形BEDF为菱形.13.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.14.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD、AC、BC于点E、O、F,连接CE 和AF.(1)求证:四边形AECF为菱形;(2)若AB=4,BC=8,求菱形AECF的周长.15.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.(1)求证:四边形ABCD是菱形;(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.16.如图,在△ABC中,∠ACB=90°,O、D分别是边AC、AB的中点,过点C作CE∥AB交DO的延长线于点E,连接AE.(1)求证:四边形AECD是菱形;(2)若四边形AECD的面积为24,tan∠BAC =,求BC的长.17.如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.(1)求证:四边形AECD是菱形;(2)若AB=6,BC=10,求EF的长.18.如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若DC =,tan∠DCB=3,求菱形AEBD 的面积.19.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.20.如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.21.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.22.如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.(1)求证:AF=CE;(2)若DE=2,BE=4,求sin∠DAF的值.23.如图,已知▱ABCD中,AB=AC,CO⊥AD,垂足为点O,延长CO、BA交于点E,联结DE.(1)求证:四边形ACDE是菱形;(2)联结OB,交AC于点F,如果OF=OC,求证:2AB2=BF•BO.24.如图,在▱ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,且AE=AF.(1)求证:▱ABCD是菱形;(2)若∠EAF=60°,CF=2,求菱形ABCD的面积.25.如图,菱形ABCD 的边长为,对角线AC、BD交于O,且DE∥AC,AE∥BD.(1)判断四边形AODE的形状并给予证明;(2)若四边形AODE的周长为14,求四边形AODE的面积.26.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,F是AD的中点,连接EC.(1)求证:四边形ADCE是平行四边形;27.如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.(1)求证:四边形OBCE是平行四边形;(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.。
九年级中考数学平行四边形专题复习(含答案)

九年级中考数学平行四边形专题复习一、选择题:1.已知四边形ABCD是平行四边形,再从①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ) A.选①② B.选②③ C.选①③ D.选②④2.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )A.△EBD是等腰三角形,EB=ED B.折叠后∠ABE和∠CBD一定相等C.折叠后得到的图形是轴对称图形 D.△EBA和△EDC一定是全等三角形3.有下列说法:①由许多条线段连接而成的图形叫做多边形;②多边形的边数是不小于4的自然数;③从一个多边形(边数为n)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成(n-2)个三角形;④半圆是扇形.其中正确的结论有( )A.1个 B.2个 C.3个 D.4个4.如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )95°D D.85°105°C C.95°A.115°115°B B.105°5.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )A.1.8B.2.4C.3.2D.3.66.现有纸片:4张边长为a的正方形,3张边长为b的正方形,8张宽为a、长为b的长方形,用这15张纸片重新拼出一个长方形,那么该长方形的长为( )A.2a+3b B.2a+b C.a+3b D.无法确定7.如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形 ENCM 的面积之比为( )A.9:4 B.12:5 C.3:1 D.5:28.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )A. B.2 C. +1 D.2+19.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )A.1 B.2 C.3 D.410.如图,已知矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )A.6cm2 B.8cm2 C.10cm2 D.12cm2二、填空题:11.如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形______.12.如图,在▱ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD度数为 .13.如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG 木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为______m.14.如图,正方形ABCD的长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是 cm2.15.在中,,其面积为,则的最大值是.16.已知平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+0.5m-0.25=0的两个实数根.当m= 时,四边形ABCD是菱形.三、解答题:17.如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.求平行四边形ABCD的周长.18.如图,已知在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.19.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上, 顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.(1)求证:△AEH∽△ABC;(2)求这个正方形的边长与面积.20.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的九分之一?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.21.下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长为 ;(2)在图中画出两条裁剪线,并画出将此六边形剪拼成的正方形.22.如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45°,交直线BC边于点F,连结EF.探究:当点E在边AB上,求证:EF=AE+CF.应用:(1)当点E在边AB上,且AD=2时,则△BEF的周长是 .(2)当点E不在边AB上时,EF,AE,CF三者的数量关系是 .参考答案1.B2.B3.B4.C5.D6.A7.D8.B9.C10.A11.答案为:△AFE(答案不唯一).12.答案为:120°.13.答案为:.14.答案为:32.15.答案为:16.答案为:1.17.解:在平行四边形ABCD中,∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABE=∠EBC,∠BCE=∠ECD.,∴∠EBC+∠BCE=90°,∴∠BEC=90°, ∴BC22=BE22+CE22=1222+522=1322∴BC=13cm,∵AD∥BC,∴∠AEB=∠EBC,∴∠AEB=∠ABE,∴AB=AE,同理CD=ED,∵AB=CD,∴AB=AE=CD=ED=0.5BC=6.5cm,∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm18.提示:取BE的中点P,证明四边形EFPC是平行四边形.19.(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.(2)解:如图设AD与EH交于点M.∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM,设正方形EFGH的边长为x,∵△AEH∽△ABC,∴=,∴=,∴x=,∴正方形EFGH的边长为cm,面积为cm2.20.21.答案为:(1);(2)如图:22.探究:证明:如图,延长BA到G,使AG=CF,连接DG,∵四边形ABCD 是正方形,∴DA=DC ,∠DAG=∠DCF=90°, ∴△DAG ≌△DCF (SAS ),∴∠1=∠3,DG=DF ,∵∠ADC=90°,∠EDF=45°,∴∠EDG=∠1+∠2=∠3+∠2=45°2=45°==∠EDF , ∵DE=DE ,∴△GDE ≌△FDE (SAS ),∴EF=EG=AE+AG=AE+CF ; 应用:解:(1)△BEF 的周长=BE+BF+EF ,由探究得:EF=AE+CF , ∴△BEF 的周长=BE+BF+AE+CF=AB+BC=2+2=4,故答案为:4; (2)当点E 不在边AB 上时,分两种情况:①点E 在BA 的延长线上时,如图2,EF=CF ﹣AE ,理由是:在CB 上取CG=AE ,连接DG , ∵∠DAE=∠DCG=90°,AD=DC ,∴△DAE ≌△DCG (SAS )∴DE=DG ,∠EDA=∠GDC ∵∠ADC=90°,∴∠EDG=90°∴∠EDF+∠FDG=90°,∵∠EDF=45°,∴∠FDG=90°﹣45°45°=45°=45°,∴∠EDF=∠FDG=45°, 在△EDF 和△GDF 中,∵,∴△EDF ≌△GDF (SAS ),∴EF=FG ,∴EF=CF ﹣CG=CF ﹣AE ;②当点E 在AB 的延长线上时,如图3,EF=AE ﹣CF ,理由是:把△DAE 绕点D 逆时针旋转90°至△DCG ,可使AD 与DC 重合,连接DG , 由旋转得:DE=DG ,∠EDG=90°,AE=CG ,∵∠EDF=45°,∴∠GDF=90°﹣45°45°=45°=45°,∴∠EDF=∠GDF , ∵DF=DF ,∴△EDF ≌△GDF ,∴EF=GF ,∴EF=CG ﹣CF=AE ﹣CF ;综上所述,当点E 不在边AB 上时,EF ,AE ,CF 三者的数量关系是:EF=CF ﹣AE 或EF=AE ﹣CF ;故答案为:EF=CF ﹣AE 或EF=AE ﹣CF .。
2021年九年级数学中考复习专题:四边形综合(考察全等证明、长度与面积计算等)(五)

2021年九年级数学中考复习专题:四边形综合(考察全等证明、长度与面积计算等)(五)1.在正方形ABCD中,点E是BC边上一点,连接AE.(1)如图1,点F为AE的中点,连接CF.已知tan∠FBE=,BF=5,求CF的长;(2)如图2,过点E作AE的垂线交CD于点G,交AB的延长线于点H,点O为对角线AC的中点,连接GO并延长交AB于点M,求证:AM+BH=BE.2.阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD 是垂美四边形吗?请说明理由;(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC =,AB=2,求GE的长.3.已知:如图,长方形ABCD中,∠A=∠B=∠B=∠D=90°,AB=CD=4米,AD=BC=8米,点M是BC边的中点,点P从点A出发,以1米/秒的速度沿AB方向运动再过点B沿BM方向运动,到点M停止运动,点O以同样的速度同时从点D出发沿着DA方向运动,到点A停止运动,设点P运动的时间为x秒.(1)当x=2秒时,线段AQ的长是米;(2)当点P在线段AB上运动时,图中阴影部分的面积发生改变吗?请你作出判断并说明理由.(3)在点P,Q的运动过程中,是否存在某一时刻,使得BP=DQ?若存在,求出点P的运动时间x的值;若不存在,请说明理由.4.A,B,C,D是长方形纸片的四个顶点,点E、F、H分别是边AB、BC、AD上的三点,连结EF、FH.(1)将长方形纸片ABCD按图①所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B'、C'、D',点B'在FC'上,则∠EFH的度数为;(2)将长方形纸片ABCD按图②所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B'、C'、D',若∠B'FC'=18°,求∠EFH的度数;(3)将长方形纸片ABCD按图③所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B'、C'、D',若∠EFH=m°,求∠B'FC'的度数为.5.勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.(1)连接BI、CE,求证:△ABI≌△AEC;(2)过点B作AC的垂线,交AC于点M,交IH于点N.①试说明四边形AMNI与正方形ABDE的面积相等;②请直接写出图中与正方形BCFG的面积相等的四边形.(3)由第(2)题可得:正方形ABDE的面积+正方形BCFG的面积=的面积,即在Rt△ABC中,AB2+BC2=.6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD 于点E,交CB于点F.(1)若∠B=30°,AC=6,求CE的长;(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明原因.7.已知:在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.(1)当点D在线段BC上时(与点B,C不重合),如图1,求证:CF=BD;(2)当点D运动到线段BC的延长线上时,如图2,第(1)问中的结论是否仍然成立,并说明理由.8.我们知道:在小学已经学过“正方形的四条边都相等,正方形的四个内角都是直角”,试利用上述知识,并结合已学过的知识解答下列问题:如图1,在正方形ABCD中,G是射线DB上的一个动点(点G不与点D重合),以CG为边向下作正方形CGEF.(1)当点G在线段BD上时,求证:∠DCG=∠BCF;(2)连接BF,试探索:BF,BG与AB的数量关系,并说明理由;(3)若AB=a(a是常数),如图2,过点F作FT∥BC,交射线DB于点T,问在点G 的运动过程中,GT的长度是否会随着G点的移动而变化?若不变,请求出GT的长度;若变化,请说明理由.9.如图,在矩形ABCD中,AB=6,BC=13,BE=4,点F从点B出发,在折线段BA﹣AD上运动,连接EF,当EF⊥BC时停止运动,过点E作EG⊥EF,交矩形的边于点G,连接FG.设点F运动的路程为x,△EFG的面积为S.(1)当点F与点A重合时,点G恰好到达点D,此时x=,当EF⊥BC时,x =;(2)求S关于x的函数解析式,并直接写出自变量x的取值范围;(3)当S=15时,求此时x的值.10.把一副三角板按如图1所示放置,其中点E在BC边上,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=CD=6,将三角板DCE绕点C顺时针旋转,记旋转角为α(0°≤α≤180°).(1)在图1中,设AB与DE的交点为F,则线段AF的长为;(2)当α=15°时,三角板DCE旋转到△D1CE1的位置(如图2所示),连接D1A,D1B,请判断四边形ACBD1的形状,并证明你的结论;(3)当三角板DCE旋转到△D2CE2的位置(如图3所示)时,此时点D2恰好在AB延长线上.①求旋转角α的度数;②求线段AD2的长.参考答案1.解:(1)Rt△ABE中,BF为中线,BF=5,∴AE=10,FE=5,作FP⊥BC于点P,Rt△BFP中,,∴BP=3,FP=4,在等腰三角形△BFE中,BE=2BP=6,由勾股定理求得,∴CP=8﹣3=5,∴;(2)∵∠ACD=∠BAC=45°,AO=CO,∠AOM=∠COG,∴证明△AMO≌△CGO(ASA),∴AM=GC,过G作GP垂直AB于点P,得矩形BCGP,∴CG=PB,∵AB=PG,∠AEB=∠H,∠ABE=∠GPH,∴△ABE≌△GPH(ASA),∴BE=PH=PB+BH=CG+BH=AM+BH.2.解:(1)如图2,四边形ABCD是垂美四边形;理由如下:连接AC、BD交于点E,∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;(2)猜想结论:AB2+CD2=AD2+BC2,证明:如图1,在四边形ABCD中,∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得:AB2+CD2=AO2+BO2+OD2+OC2AD2+BC2=AO2+BO2+OD2+OC2∴AB2+CD2=AD2+BC2,(3)如图3,连接CG,BE,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,∵∠AEC+∠AME=90°,∴∠ABG+∠BMN=90°,∴∠BNC=90°,即BG⊥CE,∴四边形CGEB是垂美四边形,由(2)得:EG2+BC2=CG2+BE2∵,AB=2,∴BC=1,,,∴EG2=CG2+BE2﹣BC2=6+8﹣1=13,∴.3.解:(1)∵四边形ABCD是矩形,∴AD=BC=8,∵DQ=2,∴AQ=AD﹣DQ=8﹣2=6,故答案为6.(2)结论:阴影部分的面积不会发生改变.理由:连结AM,作MH⊥AD于H.则四边形ABMH是矩形,MH=AB=4.∵S阴=S△APM+S△AQM=×x×4+(8﹣x)×4=16,∴阴影面积不变;(3)当点P在线段AB上时,BP=4﹣x,DQ=x.∵BP=DQ,∴4﹣x=x,∴x=3.当点P在线段BM上时,BP=x﹣4,DQ=x.∵BP=DQ,∴x﹣4=x,∴x=6.所以当x=3或6时,BP=DQ.4.解:(1)∵沿EF,FH折叠,∴∠BFE=∠B'FE,∠CFH=∠C'FH,∵点B′在FC′上,∴∠EFH=(∠BFB'+∠CFC')=×180°=90°,故答案为:90°;(2)∵沿EF,FH折叠,∴可设∠BFE=∠B'FE=x,∠C'FH=∠CFH=y,∵2x+18°+2y=180°,∴x+y=81°,∴∠EFH=x+18°+y=99°;(3)∵沿EF,FH折叠,∴可设∠BFE=∠B'FE=x,∠C'FH=∠CFH=y,∴∠EFH=180°﹣∠BFE﹣∠CFH=180°﹣(x+y),即x+y=180°﹣m°,又∵∠EFH=∠EFB'﹣∠B'FC'+∠C'FH=x﹣∠B'FC'+y,∴∠B'FC'=(x+y)﹣∠EFH=180°﹣m°﹣m°=180°﹣2m°,故答案为:180°﹣2m°.5.(1)证明:∵四边形ABDE、四边形ACHI是正方形,∴AB=AE,AC=AI,∠BAE=∠CAI=90°,∴∠EAC=∠BAI,在△ABI和△AEC中,,∴△ABI≌△AEC(SAS);(2)①证明:∵BM⊥AC,AI⊥AC,∴BM∥AI,∴四边形AMNI的面积=2△ABI的面积,同理:正方形ABDE的面积=2△AEC的面积,又∵△ABI≌△AEC,∴四边形AMNI与正方形ABDE的面积相等.②解:四边形CMNH与正方形BCFG的面积相等,理由如下:∵Rt△ABC中,AB2+BC2=AC2,∴正方形ABDE的面积+正方形BCFG的面积=正方形ACHI的面积,由①得:四边形AMNI与正方形ABDE的面积相等,∴四边形CMNH与正方形BCFG的面积相等;(3)解:由(2)得:正方形ABDE的面积+正方形BCFG的面积=正方形ACHI的面积;即在Rt△ABC中,AB2+BC2=AC2;故答案为:正方形ACHI,AC2.6.解:(1)∵∠ACB=90°,∠B=30°,∴∠CAB=60°,∵CD⊥AB,∴∠ADC=90°,∴∠ACD=30°,∵AF平分∠CAB,∴∠CAF=∠BAF=30°,∴CE=AE,过点E用EH垂直于AC于点H,∴CH=AH∵AC=6,∴CE=2答:CE的长为2;(2)∵FG⊥AB,FC⊥AC,AF平分∠CAB,∴∠ACF=∠AGF=90°,CF=GF,在Rt△ACF与Rt△AGF中,AF=AF,CF=GF,∴Rt△ACF≌Rt△AGF(HL),∴∠AFC=∠AFG,∵CD⊥AB,FG⊥AB,∴CD∥FG,∴∠CEF=∠EFG,∴∠CEF=∠CFE,∴CE=CF,∴CE=FG,∴四边形CEGF是菱形7.(1)证明:∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∴∠DAC+∠CAF=90°,∵∠ABC=90°,∴∠DAC+∠BAD=90°,∴∠BAD=∠CAF,在△BAD和△CAF中,∴△BAD≌△CAF(SAS),∴BD=CF,即CF=BD;(2)当点D运动到线段BC的延长线上时,如图2,第(1)问中的结论仍然成立.理由:∵∠BAC=∠DAF=90°,∴∠BAC+∠CAD=∠DAF+∠CAD,∴∠BAD=∠CAF,在在△BAD和△CAF中,∴△BAD≌△CAF(SAS),∴BD=CF,即CF=BD.8.解:(1)∵四边形ABCD和四边形EFCG是正方形,∴CD=CB,CG=CF,∠BCD=∠FCG=90°,∵∠DCG=90°﹣∠BCG,∠BCF=90°﹣∠BCG,∴∠DCG=∠BCF;(2)BF+BG=AB,理由:在Rt△CDG和△CBF中,,∴△CDG≌CBF(SAS),∴DG=BF,在Rt△ABD中,AD=AB,∴BD=AB,∵BD=DG+BG=BF+BG,∴BF+BG=AB;(3)∵BD是正方形ABCD的对角线,∴∠CBD=∠CDB=45°,由(2)知,△CDG≌CBF(SAS),∴DG=BF,∠CDG=∠CBF=45°,∴∠DBF=∠CBD+∠CBF=90°,∴∠FBT=90°,∵FT∥CB,∴∠BTF=∠CBD=45°,∴∠BFT=45°=∠BTF,∴BF=BT,∴DG=BT,∴GT=BG+BT=BG+DG=BD=AB=a.9.解:(1)当点F与点A重合时,x=AB=6;当EF⊥BC时,AF=BE=4,x=AB+AF=6+4=10;故答案为:6;10;(2)∵四边形ABCD是矩形,∴∠B=∠C=∠D=90°,CD=AB=6,AD=BC=13,分两种情况:①当点F在AB上时,如图1所示:作GH⊥BC于H,则四边形ABHG是矩形,∴GH=AB=6,AG=BH,∠GHE=∠B=90°,∴∠EGH+∠GEH=90°,∵EG⊥EF,∴∠FEB+∠GEH=90°,∴∠FEB=∠EGH,∴△EFB∽△GEH,∴=,即==,∴EH=x,∴AG=BH=BE+EH=4+x,∴△EFG的面积为S=梯形ABEG的面积﹣△EFB的面积﹣△AGF的面积=(4+4+x)×6﹣×4x﹣(6﹣x)(4+x)=x2+9x+12,即S=x2+9x+12(0<x≤6);②当点F在AD上时,如图2所示:作FM⊥BC于M,则FM=AB=6,AF=BM,同①得:△EFM∽△GEC,∴=,即=,解得:GC=15﹣x,∴DG=CD﹣CG=x﹣9,∵EC=BC﹣BE=9,AF=x﹣6,DF=AD﹣AF=19﹣x,∴△EFG的面积为S=梯形CDFE的面积﹣△CEG的面积﹣△DFG的面积=(9+19﹣x)×6﹣×9×(15﹣x)﹣(19﹣x)(x﹣9)=x2﹣21x+102 即S=x2﹣21x+102(6<x≤10);(3)当x2+9x+12=15时,解得:x=﹣6±2(负值舍去),∴x=﹣6+2;当x2﹣21x+102=15时,解得:x=14±4(不合题意舍去);∴当S=15时,此时x的值为﹣6+2.10.(1)解:(1)在Rt△ABC中,∠A=45°,AB=6,∴BC=AB=3,在Rt△CDE中,∠D=30°,CD=6,∴CE=3,∴BE=BC﹣CE=﹣3,在Rt△BEF中,∠B=90°﹣∠A=45°,∴BF=BE=6﹣3,∴AF=AB﹣BF=3,故答案为:3;(2)四边形ACBD1是正方形,理由:∵∠BCE1=α=15°,∴∠D1CB=45°=∠BAC,由旋转知,CD1=CD,∵CD=AB,∴CD1=AB,∵BC=AC,∴△D1CB≌△BAC(SAS),∴D1B=BC,同理可证:D1A=AC,又∴AC=BC,∴D1A=AC=BC=BD1,∴四边形ACBD1是菱形,又∠ACB=90°,∴菱形ACBD1是正方形.(3)①取AB边的中点H,连接CH,∵△ABC是等腰直角三角形,且斜边AB=6,∴CH⊥AB,且AH=CH=AB=3,∵△D2CE2是直角三角形,且斜边CD2=6,∠CD2E2=30°,∴CE2=3,又∵∠CHD2=∠E2=90°,∴Rt△D2CH≌Rt△D2CE2(HL),∴∠HD2C=∠E2D2C=30°,又∵∠ABC=45°,∴∠BCD2=15°,又∵∠E2CD2=60°,则旋转角α=∠BCE2=75°;②在Rt△D2CE2中,D2E2=CE2=3,∵Rt△D2CH≌Rt△D2CE2,∵D2H=D2E2=,AH=3,∴AD 2=AH+D2H=3+.。
2021年九年级数学中考复习分类压轴大题专题:四边形综合(三)

2021年九年级数学中考复习分类压轴大题专题:四边形综合(三)1.问题探究:小红遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使DE=AD,连接BE,证明△BED≌△CAD,经过推理和计算使问题得到解决.请回答:(1)小红证明△BED≌△CAD的判定定理是:;(2)AD的取值范围是;方法运用:(3)如图2,AD是△ABC的中线,在AD上取一点F,连结BF并延长交AC于点E,使AE =EF,求证:BF=AC.(4)如图3,在矩形ABCD中,=,在BD上取一点F,以BF为斜边作Rt△BEF,且=,点G是DF的中点,连接EG,CG,求证:EG=CG.2.点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F.点O为AC的中点.(1)如图1,当点P与点O重合时,线段OE和OF的关系是;(2)当点P运动到如图2所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立?(3)如图3,点P在线段OA的延长线上运动,当∠OEF=30°时,试探究线段CF、AE、OE之间的关系.3.在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.(1)如图1,若BC=2BA,求∠CBE的度数;(2)如图2,当AB=5,且AF•FD=10时,求BC的长;(3)如图3,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD时,求的值.4.在正方形ABCD中,线段EF交对角线AC于点G.(1)如图1,若点E、F分别在AB、CD边上,且AE=CF,求证:FG=EG;(2)如图2,若点E在AB边上,点F在BC边的延长线上,且AE=CF.(1)中结论是否依然成立?请说明理由;(3)在(2)的条件下,连结DG并延长交BC于点H,若BH=5,BE=12.求正方形ABCD 的面积.5.如图1,将矩形OABC放在直角坐标系中,O为原点,点C在x轴上,点A在y轴上,OA =4,OC=8.把矩形OABC沿对角线OB所在直线翻折,点C落到点D处,OD交AB于点E.(1)求点E坐标.(2)如图2,过点D作DG∥BC,交OB于点G,交AB于点H,连接CG,试判断四边形BCGD 的形状,并说明理由.(3)在(2)的条件下,点M是坐标轴上一点,直线OB上是否存在一点N,使以O、D、M、N为顶点的四边形是平行四边形?若存在,请直接写出点N坐标;若不存在,请说明理由.6.如图①,在菱形ABCD中,∠ABC=60°,P、Q是对角线BD上的两个动点,点P从点D 出发沿BD方向以1cm/s的速度向点B运动,运动终点为B;点Q从点B出发沿着BD的方向以2cm/s的速度向点D运动,运动终点为D.两点同时出发,设运动时间为x(s),以A、Q、C、P为顶点的图形面积为y(cm2),y与x的函数图象如图②所示,根据图象回答下列问题:(1)BD=,a=;(2)当x为何值时,以A、Q、C、P为顶点的图形面积为4cm2?(3)在整个运动的过程中,若△AQP为直角三角形,请直接写出符合条件的所有x的值:.7.在矩形ABCD中,连结AC,点E从点B出发,以每秒1个单位的速度沿着B→A的路径运动,运动时间为t(秒).以BE为边在矩形ABCD的内部作正方形BEHG.(1)如图,当四边形ABCD为正方形且点H在△ABC的内部,连结AH,CH,求证:AH=CH;(2)经过点E且把矩形ABCD面积平分的直线有条;(3)当AB=9,BC=12时,若直线AH将矩形ABCD的面积分成1:3两部分,求t的值.8.在数学的学习中,有很多典型的基本图形.(1)如图①,△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为D、E.试说明△ABD≌△CAE:(2)如图②,△ABC中,∠BAC=90°,AB=AC,点D、A、F在同一条直线上,BD⊥DF,AD=3,BD=4.则菱形AEFC面积为;(3)如图③,分别以Rt△ABC的直角边AC、AB向外作正方形ACDE和正方形ABFG,连接EG,AH是△ABC的高,延长HA交EG于点I,若AB=6,AC=8,求AI的长度.9.定义:如果四边形的一条对角线的中点到另外两个顶点的距离都等于这条对角线的长一半,那么我们称这样的四边形为“等距四边形”.(1)在下列图形中:①等腰梯形、②矩形、③菱形,是“等距四边形”的是.(填序号)(2)如图1,在菱形ABCD中,AB=4,∠A=60°,BE⊥CD于点E,点F是菱形ABCD边上的一点,顺次连接B、E、D、F,若四边形BEDF为“等距四边形”,求线段EF的长.(3)如图2,已知等边△ABC边长为4,点P是△ABC内一点,若过点P可将△ABC恰好分割成三个“等距四边形”,求这三个“等距四边形”的周长和.10.▱ABCD中,AE⊥BC于E,且AD=AE.(1)如图1,连结DE,过A作AF⊥AB交ED于F,在AB上截取AG=AF,连结DG,点H 为GD中点,连接AH,求证:4AH2+DF2=2AF2;(2)如图2,连结BD,把△ABD沿直线BD方向平移,得到△A′B′D′,若CD=,EC=2,求在平移过程中A'C+B'C的最小值.参考答案1.解:(1)∵AD是中线,∴BD=CD,又∵∠ADC=∠BDE,AD=DE,∴△BED≌△CAD(SAS),故答案为:SAS;(2)∵△BED≌△CAD,∴AC=BE=4,在△ABE中,AB﹣BE<AE<AB+BE,∴2<2AD<10,∴1<AD<5,故答案为:1<AD<5;(3)如图2,延长AD至H,使AD=DH,连接BH,∵AD是△ABC的中线,∴BD=CD,又∵∠ADC=∠BDH,AD=DH,∴△ADC≌△HDB(SAS),∴AC=BH,∠CAD=∠H,∵AE=EF,∴∠EAF=∠AFE,∴∠H=∠BFH,∴BF=BH,∴AC=BF;(4)如图3,延长CG至N,使NG=CG,连接EN,CE,NF,∵点G是DF的中点,∴DG=GF,又∵∠NGF=∠DGC,CG=NG,∴△NGF≌△CGD(SAS),∴CD=NF,∠CDB=∠NFG,∵=,=,∴tan∠ADB=,tan∠EBF=,∴∠ADB=∠EBF,∵AD∥BC,∴∠ADB=∠DBC,∴∠EBF=∠DBC,∴∠EBC=2∠DBC,∵∠EBF+∠EFB=90°,∠DBC+∠BDC=90°,∴∠EFB=∠BDC=∠NFG,∠EBF+∠EFB+∠DBC+∠BDC=180°,∴2∠DBC+∠EFB+∠NFG=180°,又∵∠NFG+∠BFE+∠EFN=180°,∴∠EFN=2∠DBC,∴∠EBC=∠EFN,∵=,且CD=NF,∴∴△BEC∽△FEN,∴∠BEC=∠FEN,∴∠BEF=∠NEC=90°,又∵CG=NG,∴EG=NC,∴EG=GC.2.解:(1)∵四边形ABCD是平行四边形,∴AO=CO,又∵∠AEO=∠CFO=90°,∠AOE=∠COF,∴△AEO≌△CFO(AAS),∴OE=OF,故答案为:OE=OF;(2)补全图形如图所示,结论仍然成立,理由如下:延长EO交CF于点G,∵AE⊥BP,CF⊥BP,∴AE∥CF,∴∠EAO=∠GCO,∵点O为AC的中点,∴AO=CO,又∵∠AOE=∠COG,∴△AOE≌△COG(AAS),∴OE=OG,∵∠GFE=90°,∴OE=OF;(3)点P在线段OA的延长线上运动时,线段CF、AE、OE之间的关系为OE=CF+AE,证明如下:如图,延长EO交FC的延长线于点H,由(2)可知△AOE≌△COH,∴AE=CH,OE=OH,又∵∠OEF=30°,∠HFE=90°,∴HF=EH=OE,∴OE=CF+CH=CF+AE.3.解:(1)∵四边形ABCD是矩形,∴∠C=90°,∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,∴BC=BF,∠FBE=∠EBC,∠C=∠BFE=90°,∵BC=2AB,∴BF=2AB,∴∠AFB=30°,∵四边形ABCD是矩形,∴AD∥BC,∴∠AFB=∠CBF=30°,∴∠CBE=∠FBC=15°;(2)∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,∴∠BFE=∠C=90°,CE=EF,又∵矩形ABCD中,∠A=∠D=90°,∴∠AFB+∠DFE=90°,∠DEF+∠DFE=90°,∴∠AFB=∠DEF,∴△FAB∽△EDF,∴,∴AF•DF=AB•DE,∵AF•DF=10,AB=5,∴DE=2,∴CE=DC﹣DE=5﹣2=3,∴EF=3,∴DF===,∴AF==2,∴BC=AD=AF+DF=2=3.(3)过点N作NG⊥BF于点G,∵NF=AN+FD,∴NF=AD=BC,∵BC=BF,∴NF=BF,∵∠NFG=∠AFB,∠NGF=∠BAF=90°,∴△NFG∽△BFA,∴,设AN=x,∵BN平分∠ABF,AN⊥AB,NG⊥BF,∴AN=NG=x,AB=BG=2x,设FG=y,则AF=2y,∵AB2+AF2=BF2,∴(2x)2+(2y)2=(2x+y)2,解得y=x.∴BF=BG+GF=2x+x=x.∴=.4.(1)证明:∵四边形ABCD是正方形,∴AB∥CD,∴∠EAG=∠FCG,又∵∠FGC=∠AGE,AE=CF,∴△CFG≌△AEG(AAS),∴FG=EG;(2)(1)中结论依然成立.理由如下:如图2,过点E作EM⊥AB交AC于点M,∵四边形ABCD是正方形,∴∠CAB=45°,∠ABC=90°,∴∠MAE=∠AME=45°,∴AE=EM,又∵AE=FC,∴EM=CF,∵∠AEM=∠ABC,∴ME∥CF,∴∠MEG=∠GFC,又∵∠MGE=∠FGC,∴△MEG≌△CFG(AAS),∴EG=FG;(3)解:如图3,连接DE,DF,EH,∵正方形ABCD中,∠DAE=∠DCB=90°,DC=AD,∴∠DAE=∠DCF=90°,又∵AE=CF,∴△ADE≌△DCF(SAS),∴DE=DF,由(2)知EG=GF,∴DG⊥EF,∴DH是EF的中垂线,∴EH=FH,∵BE=12,BH=5,∴EH===13,∴FH=13,设AE=x,则CF=x,∴AB=CB=12+x,∴CH=7+x,∴FH=CF+CH=x+7+x=2x+7,∴2x+7=13,解得x=3,∴AB=15,∴正方形ABCD的面积为225.5.解:(1)如图1中,∵四边形OABC是矩形,∴AB=OC=8,AB∥OC,∴∠ABO=∠BOC,由翻折可知,∠BOC=∠BOD,∴∠EOB=∠EBO,∴EO=BE,设AE=x,则EB=EO=8﹣x,在Rt△OAE中,∵∠OAE=90°,∴OA2+AE2=OE2,∴42+x2=(8﹣x)2,∴x=3,∴E(3,4).(2)如图2中,四边形BCGD是菱形.∵DG∥BC,∴∠DGB=∠CBG,由翻折的性质可知,∠CBG=∠DBG,BC=BD,∴∠DGB=∠DBG,∴DG =BD =BC ,∵DG ∥BC ,∴四边形BCGD 是平行四边形,∵BD =BC ,∴四边形BCGD 是菱形.(3)当点N 与G 重合,点M 与A 重合,四边形DM 1ON 1是平行四边形, ∵DH ==,∴EH ===, ∴AH =3+=,∴D (,),N 1(,), 当四边形ODN 1M 是平行四边形时,N 1(,), 当四边形ODN 2M 2是平行四边形时,N 2(), 当四边形ODM 1N 3是平行四边形时,N 3((﹣,﹣), 当四边形ODM 4N 4是平行四边形时,N 4(﹣,﹣)综上所述,满足条件的点N的坐标为N1(,),N2(,),N3((﹣,﹣),N4(﹣,﹣).6.解:(1)如图①中,连接AC交BD于点O.由题意:点N的实际意义表示x=3时,点Q运动到点D,∴BD=2×3=6,∵四边形ABCD是菱形,∠ABC=60°,∴∠ABD=∠ADB=30°,OB=OD=3,∴OA=OC=,AB=2AO=2,∴S菱形ABCD=×BD×AC=×6×2=6.∴a=6,故答案为:6,6;(2)设x秒后P,Q相遇.则3x=6,x=2,∴M(2,0),∴直线EM的解析式为:y=﹣3x+6,当y=4时,x=,∵N(3,3),F(6,6),∴直线NF的解析式为y=x,当y=4时,x=4,综上所述,满足条件的x的值为s或4s;(3)a:当0≤x≤3时,PQ=(6﹣3x)2,AQ2=3+(3﹣2x)2,AP2=3+(3﹣x)2,①当∠PAQ=90°时,PQ2=AP2+AQ2,(6﹣3x)2=3+(3﹣x)2+3+(3﹣2x)2,解得x=或(舍去),②当∠APQ=90°时,AP2+PQ2=AQ2,即3+(3﹣x)2+(6﹣3x)2=3+(3﹣2x)2,解得x=2或x=3,③当∠AQP=90°时,AP2=PQ2+AQ2,即3+(3﹣x)2=(6﹣3x)2+3+(3﹣2x)2,解得:x=2(不合题意,舍去),x=,b:3<x≤6时,此时Q已经到达终点,所以,AQ2=(2)2=12,此时PQ2=x2,AP2=3+(x﹣3)2,此时,∠AQP=30°,∴当∠APQ=90°时,AQ2=AP2+PQ2,即12=x2+3+(x﹣3)2,解得:x=3或0(舍去)当∠PAQ=90°时,PQ2=AP2+AQ2,即x2=12+3+(x﹣3)2,解得:x=4,综上所述,满足条件的x的值为或或3或4,故答案为:或或3或4.7.(1)证明:∵四边形ABCD、四边形BEHG是正方形,∴AB=BC,BE=BG=EH=GH,∠B=∠BEH=∠BGH=90°,∴AB﹣BE=BC﹣BG,∠AEH=∠CGH=90°,∴AE=CG,在△AEH和△CGH中,,∴△AEH≌△CGH(SAS),∴AH=CH;(2)解:连接BD交AC于O,如图1所示:作直线OE,则直线OE矩形ABCD面积平分,即经过点E且把矩形ABCD面积平分的直线有1条,故答案为:1;(3)解:分两种情况:①如图2所示:连接AH交BC于M,∵四边形ABCD是矩形,∴△ABC的面积=△ADC的面积,∵直线AH将矩形ABCD的面积分成1:3两部分,∴△ABM的面积=△ACM的面积,∴BM=CM=BC=6,由题意得:BE=BG=EH=GH=t,则AE=9﹣t,GM=6﹣t,∵△ABM的面积=△AEH的面积+正方形BEHG的面积+△GHM的面积,∴×6×9=x(9﹣t)+t2+t(6﹣t),解得:t=;②如图3所示:连接AH交CD于M,交BC的延长线于K,∵四边形ABCD是矩形,∴∠MCK=∠B=∠D=∠BCD=90°,AD=BC=12,CD=AB=9,△ABC的面积=△ADC的面积,∵直线AH将矩形ABCD的面积分成1:3两部分,∴△ADM的面积=△ACM的面积,∴DM=CM=CD=,在△KCM和△ADM中,,∴△KCM≌△ADM(ASA),∴CK=DA=12,∴BK=BC+CK=24,由题意得:BE=BG=EH=GH=t,则AE=9﹣t,GK=24﹣t,∵△ABK的面积=△AEH的面积+正方形BEHG的面积+△GHK的面积,∴×24×9=t(9﹣t)+t2+t(24﹣t),解得:t=;综上所述,若直线AH将矩形ABCD的面积分成1:3两部分,t的值为或.8.(1)证明:∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中,,∴△ABD ≌△CAE (AAS );(2)解:连接CE ,交AF 于O ,如图②所示:∵四边形AEFC 是菱形,∴CE ⊥AF ,∴∠COA =∠ADB =90°,同(1)得:△ABD ≌△CAO (AAS ),∴OC =AD =3,OA =BD =4,∴S △AOC =OA •OC =×4×3=6,∴S 菱形AEFC =4S △AOC =4×6=24,故答案为:24;(3)解:过E 作EM ⊥HI 的延长线于M ,过点G 作GN ⊥HI 于N ,如图③所示:∴∠EMI =∠GNI =90°,∵四边形ACDE 和四边形ABFG 都是正方形,∴∠CAE=∠BAG=90°,AC=AE=8,AB=AG=6,同(1)得:△ACH≌△EAM(AAS),△ABH≌△GAN(AAS),∴EM=AH=GN,在△EMI和△GNI中,,∴△EMI≌△GNI(AAS),∴EI=GI,∴I是EG的中点,∵∠CAE=∠BAG=∠BAC=90°,∴∠EAG=90°,在Rt△EAG中,由勾股定理得:EG===10,∵I是EG的中点,∴AI=EG=×10=5.9.解:(1)①等腰梯形对角线相等,但一条对角线的中点到另外两个顶点的距离的和大于另一条对角线,不符合题意;②矩形的对角线相等且互相平分,一条对角线的中点到另外两个顶点的距离等于这条对角线的一半,符合题意;③菱形的对角线互相平分,对角线不一定相等,因此一条对角线的中点到另外两个顶点的距离不等于另一条对角线的一半,不符合题意;故答案为:②;(2)根据等距四边形的定义,当点F在AD上且BF⊥AD时,四边形BFDE是等距四边形,如图1,取BD的中点O,连接OF,OE,EF,∵BF⊥AD,BE⊥DC,∴∠BFD=∠BED=90°,∴OF=OE=BD,∴四边形BFDE是等距四边形,在菱形ABCD中,AB=4,∠A=60°,AD∥BC,∴∠C=∠A=60°,∠ABC=120°,∴∠ABF=∠CBE=30°,∴∠EBF=∠ABC﹣∠ABF﹣∠CBE=60°,根据菱形的对称性得,BF=BE,∴△BEF是等边三角形,在Rt△ABF中,∠ABF=30°,∴AF=AB=2,根据勾股定理得,BF=2,∴EF=BF=2,当点F在AB上且DF⊥AB时,四边形DFBE是等距四边形,如图1﹣1,连接BD,EF,交于点O,∵DF⊥AB,DE⊥CD,∴∠BFD=∠BED=90°,∵AB∥CD,∴∠FBE=180°﹣∠BED=90°,∴∠BFD=∠BED=∠FBE,∴四边形BFDE是矩形,∴BD=EF,在菱形ABCD中,AB=AD=4,∠A=60°,∴BD=AB=4,∴EF=4;(3)过点P分别作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,如图2,同(2)的方法得,四边形ADPF,四边形BEPD,四边形ECFP是等距四边形,过点A作AG ⊥BC于G,在Rt△ABG中,∠ABC=60°,AB=4,∴∠BAG=30°,∴BG=AB=2,根据勾股定理得,AG=2,∴S△ABC=BC•AG=×4×2=4,∴S△ABC =S△APB+S△BPC+S△APC=4,∴(AB•PD+BC•PE+AC•PF)=4,∵AB=BC=AC=4,∴PD+PE+PF=2∴四边形ADPF,四边形DBEP,四边形PEFC的周长的和为AB+BC+AC+2(PD+PE+PF)=12+4.10.(1)证明:如图1中,延长AH交CD于T,连接EG,GF.∵四边形ABCD是平行四边形,∴AB∥CD,∴∠AGH=∠TDH,∵∠AHG=∠THD,HG=HD,∴△AHG≌△THD(ASA),∴AH=TH,AG=DT,∵AE⊥BC,AD∥BC,∴AE⊥AD,∵AF⊥AG,∴∠EAD=∠GAF.∴∠GAE=∠FAD,∵AD=AE,AF=AG,∴△GAE≌△FAD(SAS),∴DF=GE,∠AEG=∠ADE=45°,∵∠AED=45°,∴∠GEF=90°,∴EG2+EF2=FG2=2AF2,∵∠BAE+∠B=90°,∠BAE+∠EAF=90°,∴∠B=∠EAF,∵∠B=∠ADT,∴∠EAF=∠ADT,∵AG=AF,AG=DT,∴AF=DT,∵AE=AD,∴△EAF≌△ADT(SAS),∴EF=AT=2AH,∴DF2+4AH2=2AF2.(2)如图2中,∵A′B′=CD,A′B′∥AB∥CD,∴四边形A′B′CD是平行四边形,∴A′D=B′C,∴A'C+B'C的最小值=A′C+A′D的最小值,∵点A′在过点A且平行于BD的定直线上,∴作点D关于定直线的对称点E,∵A′C+B′C=A′C+A′D=A′C+A′E≥CE,则CE的长度即为A'C+B'C的最小值,过点E作EH⊥BC于H,交AD于J,过点A作AT⊥BD于T,设DE交AA′于K,过点C作CR⊥AD于R.∵∠AEC=∠EAR=∠ARC=90°,∴四边形AECR是矩形,∴AR=EC=2,设AE=AD=x,在Rt△CRD中,则有x2+(x﹣2)2=10,解得x=3或﹣1(舍弃),∴AD=AE=BC=3,BE=BC﹣EC=1,过点B作BQ⊥DA交DA的延长线于Q,则AQ=BE=1,DQ=AQ+AD=4,BQ=AE=3,∴BD===5,=•BD•AT=•AD•BQ,∵S△ABD∴AT=,∵四边形ATDK是矩形,∴DK=AT=KD′=,在Rt△ADK中,AK===,∵S=•AD•EJ=•DE•AK,△ADE∴EJ=,在Rt△DJD′中,DJ==,∴AJ=EH=AD﹣DJ=3﹣=,∴CH=EC﹣EH=2﹣=,∵EH=EJ+JH=+3=,在Rt△CEH中,CE==,∴A'C+B'C的最小值为.。
2020年九年级数学中考复习: 四边形专题复习教案

2020年九年级数学中考复习:四边形专题复习教案一、教学目标通过本教案的学习,学生将能够:1.了解四边形的定义和性质;2.掌握四边形的分类和特征;3.理解四边形的面积和周长的计算方法;4.能够解决与四边形相关的问题。
二、知识概述四边形是指由四条线段组成的封闭图形。
常见的四边形包括矩形、正方形、平行四边形和菱形等。
在九年级数学中,掌握四边形的定义、分类和性质是非常重要的,同时还需要熟练掌握四边形的面积和周长的计算方法。
2.1 四边形的定义和性质四边形是由四条线段构成的封闭图形,它有以下性质:•四边形的内角和等于360°;•对角线互相垂直的四边形是矩形;•有一对对边相等且互相平行的四边形是平行四边形;•有4个边长相等的四边形是正方形;•有一对对边相等且对角线互相垂直的四边形是菱形。
2.2 四边形的分类和特征根据边长和角度的特征,四边形可以分为以下几类:•矩形:具有四个内角都是直角的四边形;•正方形:具有四个边长相等且四个内角都是直角的四边形;•平行四边形:具有相对的两边平行的四边形;•菱形:具有四个边长相等且对角线互相垂直的四边形。
2.3 四边形的面积和周长的计算方法•矩形的面积等于长乘以宽;•正方形的面积等于边长的平方;•平行四边形的面积等于底边乘以高;•菱形的面积等于对角线的乘积的一半。
四边形的周长等于各边长的和。
三、教学重点与难点3.1 教学重点•四边形的定义和性质;•四边形的分类和特征;•四边形的面积和周长的计算方法。
3.2 教学难点•理解和应用四边形的性质;•熟练计算不同类型四边形的面积和周长。
4.1 导入与导入教师通过原生实例或者图片,引入四边形的概念,让学生了解四边形的定义。
4.2 教学内容4.2.1 四边形的定义和性质1.讲解四边形的定义和性质,介绍四边形的内角和等于360°的性质;2.分类介绍矩形、正方形、平行四边形和菱形的特征和性质。
4.2.2 四边形的面积和周长的计算方法1.讲解不同类型四边形的面积计算方法:矩形、正方形、平行四边形和菱形;2.讲解四边形的周长计算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总复习四边形【考纲要求】1.探索并了解多边形的内角和与外角和公式,了解正多边形的概念.2.掌握平行四边形、矩形、菱形、正方形、梯形、直角梯形、等腰梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性.3.探索并掌握平行四边形的有关性质和四边形是平行四边形的条件.4.探索并掌握矩形、菱形、正方形的有关性质和四边形是矩形、菱形、正方形的条件.5.探索并了解等腰梯形的有关性质和四边形是等腰梯形的条件.6.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计.【知识网络】【考点梳理】考点一、四边形的相关概念1.多边形的定义:在平面内,由不在同一直线上的一些线段首尾顺次相接组成的封闭图形叫做多边形.2.多边形的性质:(1)多边形的内角和定理:n边形的内角和等于(n-2)·180°;(2)推论:多边形的外角和是360°;(3)对角线条数公式:n边形的对角线有条;(4)正多边形定义:各边相等,各角也相等的多边形是正多边形.3.四边形的定义:同一平面内,由不在同一条直线上的四条线段首尾顺次相接组成的图形叫做四边形.4.四边形的性质:(1)定理:四边形的内角和是360°; (2)推论:四边形的外角和是360°.考点二、特殊的四边形1.平行四边形及特殊的平行四边形的性质2. 平行四边形及特殊的平行四边形的判定【要点进阶】面积公式:S 菱形 =21ab=ch.(a 、b 为菱形的对角线 ,c 为菱形的边长 ,h 为c 边上的高) S 平行四边形 =ah. a 为平行四边形的边,h 为a 上的高)考点三、梯形1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.(1)互相平行的两边叫做梯形的底;较短的底叫做上底,较长的底叫做下底. (2)不平行的两边叫做梯形的腰. (3)梯形的四个角都叫做底角.2.直角梯形:一腰垂直于底的梯形叫做直角梯形.3.等腰梯形:两腰相等的梯形叫做等腰梯形.4.等腰梯形的性质:(1)等腰梯形的两腰相等; (2)等腰梯形同一底上的两个底角相等. (3)等腰梯形的对角线相等. 5.等腰梯形的判定方法:(1)两腰相等的梯形是等腰梯形(定义);(2)同一底上的两个角相等的梯形是等腰梯形; (3)对角线相等的梯形是等腰梯形.6.梯形中位线:连接梯形两腰中点的线段叫梯形的中位线.7.面积公式: S=(a+b)h(a 、b 是梯形的上、下底,h 是梯形的高).【要点进阶】解决四边形问题常用的方法(1)有些四边形问题可以转化为三角形问题来解决.(2)有些梯形的问题可以转化为三角形、平行四边形问题来解决. (3)有时也可以运用平移、轴对称来构造图形,解决四边形问题. 考点四、平面图形1.平面图形的镶嵌的定义:用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片,这就是平面图形的镶嵌,又称做平面图形的密铺.2.平面图形镶嵌的条件:(1)同种正多边形镶嵌成一个平面的条件:周角是否是这种正多边形的一个内角的整倍数.在正多边形里只有正三角形、正四边形、正六边形可以镶嵌.(2)n 种正多边形组合起来镶嵌成一个平面的条件: ①n 个正多边形中的一个内角的和的倍数是360°;②n 个正多边形的边长相等,或其中一个或n 个正多边形的边长是另一个或n 个正多边形的边长的整数倍.【典型例题】类型一、特殊的四边形例1.如图所示,已知P 、R 分别是矩形ABCD 的边BC 、CD 上的点,E 、F 分别是PA 、PR 的中点,点P 在BC 上从B 向C 移动,点R 不动,那么下列结论成立的是( )A .线段EF 的长逐渐增大B .线段EF 的长逐渐变小C .线段EF 的长不变D .无法确定ABCD EF PR例2.正方形ABCD 中,P 为AB 边上任一点,AE⊥DP 于E ,点F 在DP 的延长线上,且DE=EF ,连接AF 、BF ,∠BAF 的平分线交DF 于G ,连接GC . (1)求证:△AEG 是等腰直角三角形; (2)求证:AG+CG=;(3)若AB=2,P 为AB 的中点,求BF 的长.【变式】如图,E 是正方形ABCD 外的一点,连接AE 、BE 、DE ,且∠EBA=∠ADE ,点F 在DE 上,连接AF ,BE=DF .(1)求证:△ADF ≌△ABE ;(2)小明还发现线段DE 、BE 、AE 之间满足等量关系:DE-BE=2AE .请你说明理由.例3.如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,AB=8,34tan =∠CAD ,CA=CD ,E 、F 分别是线段AD 、AC 上的动点(点E 与点A 、D 不重合),且∠FEC=∠ACB ,设DE=x ,CF=y. (1)求AC 和AD 的长; (2)求y 与x 的函数关系式;(3)当△EFC 为等腰三角形时,求x 的值.F CBDAE【变式】在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连结EF、EC、BF、CF.⑴判断四边形AECD的形状(不证明);⑵在不添加其它条件下,写出图中一对全等的三角形,用符号“≌”表示,并证明.⑶若CD=2,求四边形BCFE的面积.类型二、四边形与其他知识的综合运用例4. 有矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.(1)如果折痕FG分别与AD、AB交于点F、G,AF=23,求DE的长;(2)如果折痕FG分别与CD、DA交于点F、G,△AED的外接圆与直线BC相切,求折痕FG的长.例5.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A 时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当t为何值时,DE∥AB?(2)求四边形BQPC的面积s与t的函数关系式;(3)是否存在某一时刻t,使四边形BQPC的面积与Rt△ABC的面积比为13:15?若存在,求t的值.若不存在,请说明理由;(4)若DE经过点C,试求t的值.例6 .如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转а度得到四边形OAB'C',此时直线OA’、直线B’C’分别与直线BC相交于点P、Q.(1)四边形OABC的现状是,当а=90°时,BP:PQ的值是;(2)①如图,当四边形OA’B’C’的顶点B’落在y轴正半轴时,求BP:BQ的值;②如图,当四边形OA’B’C’的顶点B’落在直线BC上时,求△OPB'的面积;(3)在四边形OA’B’C’旋转过程中,当0<а°≤180°时,是否存在这样的点P和点Q,使BP=0.5BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.举一反三:【变式】如图,直角梯形ABCD 中,BC AD ∥,90BCD ∠=°,且2tan 2CD AD ABC =∠=,,过点D 作AB DE ∥,交BCD ∠的平分线于点E ,连接BE .(1)求证:BC CD =;(2)将BCE △绕点C ,顺时针旋转90°得到DCG △,连接EG..求证:CD 垂直平分EG. (3)延长BE 交CD 于点P .求证:P 是CD 的中点.【巩固练习】 一、选择题 1.如图,在中,,是上异于、的一点,则的值是( ).A .16 B .20 C .25 D .302. 如图1,在矩形中,动点从点出发,沿→→→方向运动至点处停止.设点运动的路程为,的面积为,如果关于的函数图象如图2所示,则当时,点应运动到( ). A .处 B .处 C .处 D .处ADGECB3.如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=AB2其中正确的结论有(). A.1个 B.2个 C.3个 D.4个4.一个正方形纸片,用剪刀沿一条不过任何顶点的直线将其剪成两部分;拿出其中一部分,再沿一条不过任何顶点的直线将其剪成两部分;又从得到的三部分中拿出其中之一,还是沿一条不过任何顶点的直线将其剪成两部分……如此下去,最后得到了34个六十二边形和一些多边形纸片,则至少要剪的刀数是().A. 2004 B. 2005 C. 2006 D. 20075.如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是.若反比例函数的图象经过点B,则此反比例函数表达式为().A.B. C.D.6.如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为()A.B.4﹣πC.πD.二、填空题7. 如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是_________.第7题第8题8. 如图,在等腰梯形中,,= 4=,=45°.直角三角板含45°角的顶点在边上移动,一直角边始终经过点,斜边与交于点.若为等腰三角形,则的长等于____________.9.如图,正方形A1B1B2C1,A2B2B3C2,A3B3B4C3,…,A n B n B n+1C n,按如图所示放置,使点A1、A2、A3、A4、…、A n 在射线OA上,点B1、B2、B3、B4、…、B n在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1,S2,S3,…,S n,则S n=________________-.第9题第10题10.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为.11.如图,已知正方形ABCD的边长为1,以顶点A、B为圆心,1为半径的两弧交于点E,以顶点C、D为圆心,1为半径的两弧交于点F,则EF的长为.12.如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是.三、解答题13.如图,在边长为4cm的正方形ABCD中,点E,F,G,H分别按A⇒B,B⇒C,C⇒D,D⇒A的方向同时出发,以1cm/s的速度匀速运动.在运动过程中,设四边形EFGH的面积为S(cm2),运动时间为t (s).(1)试证明四边形EFGH是正方形;(2)写出S关于t的函数关系式,并求运动几秒钟时,面积最小,最小值是多少?(3)是否存在某一时刻t,使四边形EFGH的面积与正方形ABCD的面积比是5:8?若存在,求出t 的值;若不存在,请说明理由.14.如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片还原,使点D与P重合,得折痕EF(点E、F为折痕与矩形边的交点,再将纸片还原。
