弹性力学讲义(徐芝纶版)
弹性力学徐芝纶版第一章ppt

03
应变分析
应变状态和应变分量
应变状态
描述物体在受力后形状的变化,包括 线应变和角应变。
应变分量
根据直角坐标系或极坐标系的选取, 将应变状态量分解为具体的应变分量 ,如正应变和剪应变。
土木工程
桥梁、隧道、高层建筑等土木 工程的设计和施工都需要考虑 材料的弹性和结构的稳定性。
弹性力学的基本假设和概念
连续性假设
均匀性假设
假设物质没有空隙或裂 纹,整个物质是连续的。
假设物质在各个方向上 的性质是均匀的,没有
局部变化。
各向同性假设
假设物质在各个方向上 假设
变形梯度和变形速率
变形梯度
描述物体在受力后形状变化的程度和 方向,由物质导数和变形梯度张量表 示。
变形速率
描述物体在单位时间内形状变化的程 度,由变形梯度的导数表示。
几何方程和应变边界条件
几何方程
描述物体在受力后形状变化的规律,包 括连续性方程、运动方程和几何方程。
VS
应变边界条件
描述物体在边界处的应变状态,包括位移 边界条件、应力边界条件和应变边界条件 。
弹性力学徐芝纶版第一章
• 引言 • 应力分析 • 应变分析 • 弹性本构关系 • 弹性力学的基本方程
01
引言
弹性力学的发展历程
古代弹性理论的萌芽
古希腊和中国的学者开始研究材料的弹性和 结构。
弹性力学理论的完善和发展
19世纪,科学家们开始深入研究弹性力学, 并取得了一系列重要成果。
弹性力学理论的初步形成
来。
弹性力学问题的求解方法
(完整版)徐芝纶弹性力学主要内容及知识点

(完整版)徐芝纶弹性力学主要内容及知识点1.弹性力学是研究弹性体由于受到外力作用、边界约束或温度改变等原因而引起的应力、形变和位移。
2外力分为体积力和面积力。
体力是分布在物体体积内的力,重力和惯性力。
体积分量,以沿坐标轴正方向为正,沿坐标轴负方向为负。
面力是分布在物体表面上的力,面力分量以沿坐标轴正方向为正,沿坐标轴负方向为负。
3内力,即物体本身不同部分之间相互作用的力。
3弹性力学中的基本假定:连续性,完全弹性,均匀性,各向同性,小变形假定。
凡是符合连续性、完全弹性、均匀性、各向同性等假定的物体称之为理想弹性体。
连续性,假定整个物体的体积被组成这个物体的介质所填满,不留下任何空隙。
完全弹性,指的是物体能完全恢复原形而没有任何剩余形变。
均匀性,整个物体时统一材料组成。
各向同性,物体的弹性在所有各个方向都相同。
4求解弹性力学问题,即在边界条件上,根据平衡微分方程、几何方程、物理方程求解应力分量、形变分量和位移分量。
弹性力学、材料力学、结构力学的研究对象分别是弹性体,杆状构件和杆件系统。
解释在物体内同一点,不同截面上的应力是不同的。
应力的符号不同:在弹性力学和材料力学中,正应力规定一样,拉为正,压为负。
切应力:弹性力学中,正面沿坐标轴正方向为正,沿负方向为负。
负面上沿坐标轴负方向为正,沿正方向为负。
材料力学中,所在的研究对象上任一点弯矩转向顺时针为正,逆时针为负。
5.形变:所谓形变,就是形状的改变。
包括线应变(各各线段每单位长度的伸缩,即单位伸缩和相对伸缩,伸长时为正,收缩时为负);切应变(各线段直接直角的改变,用弧度表示,以直角变小时为正,变大为负)6试述弹性力学平面应力问题与平面应变问题的主要特征及区别:平面应力问题:几何形状,等厚度薄板。
外力约束,平行于板面且不沿厚度变化。
平面应变问题:几何形状,横断面不沿长度变化,均匀分布。
外力约束,平行于横截面并不沿长度变化。
7.主应力:设经过P点的某一斜面上的切应力等于0,则该斜面上的正应力称为P点的一个主应力;应力主向:该斜面的法线方向称为该斜面的一个应力主向。
弹性力学讲义(徐芝纶版)-知识归纳整理

求知若饥,虚心若愚。 第 74 页/共 111 页
千里之行,始于足下。 第 75 页/共 111 页
求知若饥,虚心若愚。 第 76 页/共 111 页
千里之行,始于足下。 第 77 页/共 111 页
求知若饥,虚心若愚。 第 78 页/共 111 页
千里之行,始于足下。 第 79 页/共 111 页
求知若饥,虚心若愚。 第 110 页/共 111 页
千里之行,始于足下。 第 111 页/共 111 页
求知若饥,虚心若愚。 第 104 页/共 111 页
千里之行,始于足下。 第 105 页/共 111 页
求知若饥,虚心若愚。 第 106 页/共 111 页
千里之行,始于足下。 第 107 页/共 111 页
求知若饥,虚心若愚。 第 108 页/共 111 页
千里之行,始于足下。 第 109 页/共 111 页
求知若饥,虚心若愚。 第 80 页/共 111 页
千里之行,始于足下。 第 81 页/共 111 页
求知若饥,虚心若愚。 第 82 页/共 111 页
千里之行,始于足下。 第 83 页/共 111 页
求知若饥,虚心若愚。 第 84 页/共 111 页
千里之行,始于足下。 第 85 页/共 111 页
求知若饥,虚心若愚。 第 92 页/共 111 页
千里之行,始于足下。 第 93 页/共 111 页
求知若饥,虚心若愚。 第 94 页/共 111 页
千里之行,始于足下。 第 95 页/共 111 页
求知若饥,虚心若愚。 第 96 页/共 111 页
千里之行,始于足下。 第 97 页/共 111 页
知识归纳整理 第 1 页/共 111 页
弹性力学(徐芝纶四版)-第3章

—— 与材力中结果相同
(2)悬臂梁
边界条件
u x l 0 v x l 0
h y 2
h 2
由式(f)可知,此边界条件无法满足。 边界条件改写为:
M u xy y u0 EI (f) M 2 M 2 v y x x v0 2 EI 2 EI
第三章
平面问题的直角坐标解答
力学问题。
要点 —— 用逆解法、半逆解法求解平面弹性
主要内容
§3-1 多项式解答
§3-2 位移分量的求出
§3-3 简支梁受均布载荷
§3-4 楔形体受重力和液体压力
§3-5 级数式解答
§3-6 简支梁受任意横向载荷
§3-1 多项式解答
适用性:由一些直线边界构成的弹性体。 目的: 考察一些简单多项式函数作为应力函数φ(x,y) ,能解决什么样的 力学问题。 ——逆解法
说明: (1) 求位移的过程:
(a)将应力分量代入物理方程
xy 1 1 x ( x y) y ( y x) xy E G E
(b)再将应变分量代入几何方程
u x x
v y y
xy
u v y x
(c)再利用位移边界条件,确定常数。
M
l
M y
x
1
h
y 0 xy 0
M y My x I h3 / 12
(a)
1 My My xy 0 x y E I E I
(b)
(2)位移分量
将式(b)代入几何方程得:
平面应力情况下的物理方程:
x 1 ( x y)
E y 1 ( y x) E xy xy
弹性力学__徐芝纶版第三章

4 f
y4
0
4 f 0
一、逆解法和半逆解法 (一)逆解法的基本步骤:
取满足相容方程的 f
求出应力分量 x , y , xy
根据边界条件求出面力
考察能解决什么问题
§3-1 逆解法与半逆解法 多项式解答
(二)半逆解法的基本步骤:
根据问题的特 点设出部分应 力分量
是 结束
否
求出应力函数 f
x
§3-3 位移分量的求出
0 u0 v0 0
y
z
u P x Eh
P x
v P y
Eh
习题
[1]写出边界条件。 解:
x x0,xb g( y h1)
0 xy x0,xb y y0 gh1, xy y0 0
y
P
hE
xy 0
u P x Eh
v P
y Eh
u v 0 y x
u
P Eh
x
f1y
v
P
Eh
y
f2 x
代入第三式得: df1 y df2 x 0
dy
dx
移项得: df1 y df2 x
u yh2 0
v yh2 0
hx1
g
b
h2
bb
y 22
FN gbh1
b
下边的等效应力边界条件: 0 y yh2 dx gbh1
b
0
xy
dx 0
y h2
b 0
y
y h2
弹性力学 徐芝纶版第二章
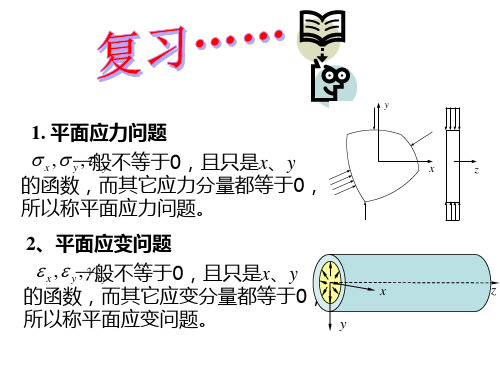
第二章 平面问题的基本理论
2.位移边界条件 在边界S上有:
us u , vs v
如图: (u ) x a 0
o
a
x
3.混合边界条件
l x s m xy s f x
在边界S上同时有:
y
l ( xy ) s m( y ) s f y
us u , vs v
f1 y y u0 u y u0
f 2 x x v0 v x v0
可见: 当形变完全确定时,位移分量 不能完全确定;反之,位移分量 确定时,形变分量可以完全确定。 上式中,u0,v0是物体沿x,y轴 的刚体平移。
x
x
y
x
xy
u v 0 y x
u f1 y
v f 2 x
df1 y df2 x 0 dy dx df1 y dy
df1 y df2 x dy dx
df2 x dx
第二章 平面问题的基本理论
例题2:试证明 1 , 2 是一点最大和最小的正应力。
n l x m y 2ml xy
2 2
证:令 x 1 y 2 则: xy 0
n l 2 x m 2 y 2ml xy l 2 1 m 2 2
l 2 1 (1 l 2 ) 2 l 2 ( 1 2 ) 2
gh1 , xy y 0 0
y
第二章 平面问题的基本理论
§2-7 圣维南原理及其应用 复习:圣维南原理:
如果把物体的一小部分边界上的面力, 变换为分布不同但静力等效的面力(主矢 量相同,对同一点的主矩也相同),那么, 近处的应力分量将有显著的改变,但远处
弹性力学双语讲义(chapter1)

extbook: Applied Elasticity 徐芝纶 中文教材: 中文教材: 弹性力学简明教程 徐芝纶
Chapter 1. Introduction 第一章 绪论
•A prismatical tension member with a small hole •It is assumed in mechanics of materials that the tensile stresses are uniformly distributed across the net section of the member. •The analysis in elasticity shows that the stresses are by no means uniform, but are concentrated near the hole.
Three branches of solid mechanics 固体力学的三个分枝 固体力学的三个分枝
• Mechanics of materials 材料力学, 材料力学, Structural Mechanics 结构力学 Elasticity 弹性力学
•
•
What does the Elasticity deal with? It deals with the stresses, deformations and displacements in elastic solids produced by external forces or changes in temperature. 研究弹性体由于外力和温度改变而引起的应力, 由于外力和温度改变而引起的应力 研究弹性体由于外力和温度改变而引起的应力, 形变和位移。 形变和位移。 It analyzes the stresses, deformations and displacements of structural elements within the elastic range and thereby to check the sufficiency of their strength, stiffness and stability. 分析结构的应力,形变和位移, 分析结构的应力,形变和位移,检查是否满足强 刚度和稳定性条件。 度,刚度和稳定性条件。
徐芝纶版弹性力学第五章精品课件张量分析

三.Ricci 符号
定义:
ei j k
1 1 0
ei j k
即:
e123 e231 e312 1 e213 e132 e321 1 e111 e112 e113 ... 0
a11
比较:
a12 a22 a32
a13 a23 ei j k a1i a2 j a3k erst a1r a2 s a3t a33
A a21 a31
特别地:
e1 e2 e12 k ek e123e3 e3
2
两个任意矢量的叉积
a b ai ei b j e j aib j ei e j aib j ei j k ek ei j k aib j ek c ( A2 5)
共27个分量,亦称为排列符号、置换符号
ei j k e j k i ek i j ei k j ek j i e j i k
e123 e231 e312 1
a11 A a21 a31 a12 a22 a32 a13
e213 e132 e321 1
由此得
( A1 8)
ei j k ei j s jj ks js kj 3 ks ks 2 k s ei j k ei j k jj kk jk kj 3 3 jj 6
§A-2 矢量的基本运算
矢量a 分量ai
a a1e1 a2e2 a3e3 ai ei
3.混合积
1
基矢量混合积
(ei e j ) ek ei j r er ek ei j r δr k ei j k
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应力公式
代入式 ( f ) ,得出 σ ρ 的公式。 (4) 应用应力变换公式(下节),
σ x σ ρ cos υσ υ sin υ2τ ρυ cosυsin υ,
2 2
2Φ 2Φ sin 2 υ( 1 Φ 1 2Φ )cos 2 υ 而 σx 2 2 ρ ρ ρ 2 ρ 2 y ρ
0,
F
0,
M
c
0。
注意:
d cos 1, 2
d d sin . 2 2
M
C
0 --通过形心C的力矩为0,当
考虑到二阶微量时,得
F
ρ
0 --通过形心C的 ρ 向合力为0,
)( d )d d d )d d d sin d sin 2 2
u
物理方程
4 1
, u 1 u , u u 1 u 。
4 2
1 ( ), E 1 ( ), E 2(1 ) 。 E
1 xy 2 y
sin cos
cos sin
T
sin cos
sin cos
1 xy cos 2 y sin
sin cos 1 2
u 注意: u cos u sin
可求得
u u u 1 u u u u 2 2 1 x cos sin sin cos x
y
1 zy 2
l11 l21 l31
l12 l22 l32
l13 l23 l33
对平面问题: ij x
cos sin
x 1 yx 2
yx
xy x 1 y yx 2
( ( (
d d d )d cos d cos f d d 0, 2 2
整理,略去三阶微量,得 1 f 0。 (a)
同理,由 Fυ 0 通过形心C的 υ向合力为0 可得:
物理方程
对于平面应变问题,只须将物理方程作如下 的变换即可。
。 1
E E , 2 1
§4-3 极坐标中的应力函数
与相容方程
以下建立直角坐标系与极坐标系的变 换关系,用于: 1、 物理量的转换; 2、从直角坐标系中的方程导出极坐标 系中的方程。
坐标变换
1.从直角坐标系到极坐标系的变换 坐标变量的变换:
1 2
f 0。
(b)
极坐标下的平衡微分方程:
1 f 0 1 2 f 0
1 Φ 2[ ( )]cosυsin υ, ρ ρ
比较两式的 cos2 υ,sin2 υ,cosυsinυ 的系数,便 得出 σ ρ ,σ υ ,τ ρυ 的公式。
应力公式
当不计体力时应力用应力函数表示的公式
2 1 1 2 σ x 0 2 y 0 2 2 σ y 0 2 x 2 0 2 1 xy 0 xy 0 2 2 (4 5)
4 2
物理方程
极坐标中的物理方程
直角坐标中的物理方程是代数方程, 且 x 与 y 为正交,
极坐标中的物理方程也是代数方程,且
ρ 与 υ 为正交,
故物理方程形式相似。
物理方程
平面应力问题的物理方程:
1 ( ), E 1 ( ), E 2(1 ) 。 E
的量纲为L, 的量纲为1。这些区别将引
起弹性力学基本方程的区别。 对于圆形,弧形,扇形及由径向线和
环向围成的物体,宜用极坐标求解。用极
坐标表示边界简单,使边界条件简化。
§4-1 极坐标中的平衡微分方程
在A内任一点( , )取出一个微分 体,考虑其平衡条件。
微分体--由夹角为 d υ 的两径向线和距离
第一节 第二节 第三节 第四节
极坐标中的平衡微分方程 极坐标中的几何方程及物理方程 极坐标中的应力函数与相容方程 应力分量的坐标变换式
第五节
轴对称应力和相应的位移
第六节
第七节 第八节 第九节 第十节 例题
圆环或圆筒受均布压力
压力隧洞 圆孔的孔口应力集中 半平面体在边界上受集中力 半平面体在边界上受分布力
Φ Φ ρ Φ υ. y ρ y υ y
一阶导数
而
cos , x
sin , x
sin ; y
cos 。 y
代入,即得一阶导数的变换公式,
Φ sin Φ sinυ Φ cosυ (cosυ )Φ , x ρ ρ υ ρ ρ υ
为 d ρ 的两环向线围成。
注意:
两 面不平行,夹角为 d υ ; 两 面面积不等,分别为ρd υ , d ρ dυ 。 ρ
从原点出发为正, 从 x 轴向 y 轴方向
转动为正。
平衡条件
平衡条件: 考虑通过微分体形心 C 的 , 向及矩的平
衡,列出3个平衡条件:
F
4 1
§4-2 几何方程及物理方程
几何方程--表示微分线段上形变和位移 之间的几何关系式 。 极坐标系中的几何方程可以通过微元变 形分析直接推得,也可以采用坐标变换的方 法得到。下面讨论后一种方法。根据直角坐 标与极坐标之间的关系,有
x sin cos , sin , , x y x cos y
Φ σ ρ (σ x ) υ0 ( 2 ) υ0 , y
2
(3) 应用应力变换公式(下节)
σ ρ σ x cos 2 υ σ y sin 2 υ 2τ xy cosυsin υ Φ cos υ Φ sin υ 2 Φ cosυsin υ. 2 2 xy y x
x cos ,
反之
2 2 2
y sin ;
(a)
y (b) x y , arctan 。 x
Φ( x, y) Φ( ρ,υ).
函数的变换:将式(a) 或 (b) 代入,
坐标变换
矢量的变换:位移 d (u, v) (u ρ , uυ ),
或
u u cos u sin , v u sin u cos 。 u u cos v sin , u u sin v cos 。
1 cos 2 sin
几何方程
由此可得 x cos 2 sin 2 sin cos
比较可知
, u 1 u , u u 1 u 。 u
直角坐标(x,y)与极坐标 ( , ) 比较:
相同:两者都是正交坐标系。
区别:直角坐标中, x和y坐标线都是直线,有 固定的方向, x 和y 的量纲均为L。 极坐标中, 坐标线( =常数)和 坐标线( =常数)在不同点有不同的方向;
应用
坐标线为直线, 坐标线为圆弧曲线;
对于平面应变问题,只须作如下同样变 换,
E E , 2 1
。 1
边界条件
边界条件--应用极坐标时,弹性体的 边界面通常均为坐标面,即:
常数,或 常数,
故边界条件形式简单。
平面应力问题在极坐标下的基本方程
1 f 0 2 1 f 0
展开即得:
二阶导数
(f)
拉普拉斯算子的变换:由式(f)得
2 2 2 1 1 2 2 2 2 ( 2 2 )。 (g ) 2 x y
相容方程应力公式
2.极坐标中的相容方程
Φ Φ 0
4 2 2
按 Φ求解
4.极坐标系中按应力函数 Φ 求解,应满足:
(1) A 内相容方程 4Φ 0.
(2) s s 上的应力边界条件(设全部为应 力边界条件)。 (3) 多连体中的位移单值条件。
§4-4 应力分量的坐标变换式
应力分量不仅具有方向性,还与其作 用面有关。 应力分量的坐标变换关系: 1、已知 σ x , σ y , τ xy ,求 σ ρ , σ υ , τ ρυ 。
(c)
(d)
坐标变换
导数的变换: 将对 x, y的导数,变换为对 ρ,υ 的导数:
Φ( x, y) 可看成是 Φ Φ(ρ,υ) ,而 ρ,υ 又
是 x, y的函数,即 Φ是通过中间变量 ρ,υ, 为 x, y 的复合函数。 有:
Φ Φ ρ Φ υ , x ρ x υ x
根据张量的坐标变换公式
' ij kmlki lmj ,
T T T ,
T T T
1 xy 2 1 xz 2 1 yz 2 z
x ij yx zx
xy y zy
x xz 1 yz yx 2 z 1 2 zx
(4 6)
