人教版初一数学上册400道计算题及练习题
数学计算题七年级上册

数学计算题七年级上册一、有理数运算。
1. 计算:(-2)+3 - (-5)- 解析:- 首先去括号,根据去括号法则,−(−5)=5,所以原式变为-2 + 3+5。
- 然后按照从左到右的顺序计算,-2+3 = 1,1 + 5=6。
2. 计算:(-3)×(-4)÷(-2)- 解析:- 先计算乘法,根据有理数乘法法则,两数相乘,同号得正,异号得负,并把绝对值相乘,所以(-3)×(-4)=12。
- 再计算除法,12÷(-2)= - 6。
3. 计算:-2^2+(-3)^3÷(-1)^2023- 解析:- 先计算指数运算,根据幂的运算法则,−2^2=-4(这里要注意指数运算的优先级高于负号),(-3)^3=-27,(-1)^2023=-1。
- 然后计算除法,-27÷(-1)=27。
- 最后计算加法,-4 + 27 = 23。
4. 计算:<=ft((1)/(2)-(2)/(3)+(5)/(6))×(-18)- 解析:- 根据乘法分配律a(b + c)=ab+ac,这里a=-18,b=(1)/(2),c =-(2)/(3),d=(5)/(6)。
- 则原式=(1)/(2)×(-18)-(2)/(3)×(-18)+(5)/(6)×(-18)。
- 计算可得:-9+12 - 15=-12。
5. 计算:0.25×(-2)^3-<=ft[4÷<=ft(-(2)/(3))^2+1]- 解析:- 先计算指数运算,(-2)^3=-8,<=ft(-(2)/(3))^2=(4)/(9)。
- 然后计算乘法和除法,0.25×(-8)=-2,4÷(4)/(9)=4×(9)/(4)=9。
- 最后计算括号内的式子和减法,-(9 + 1)=-10,-2-10=-12。
二、整式的加减。
人教版初一数学上册400道计算题及练习题
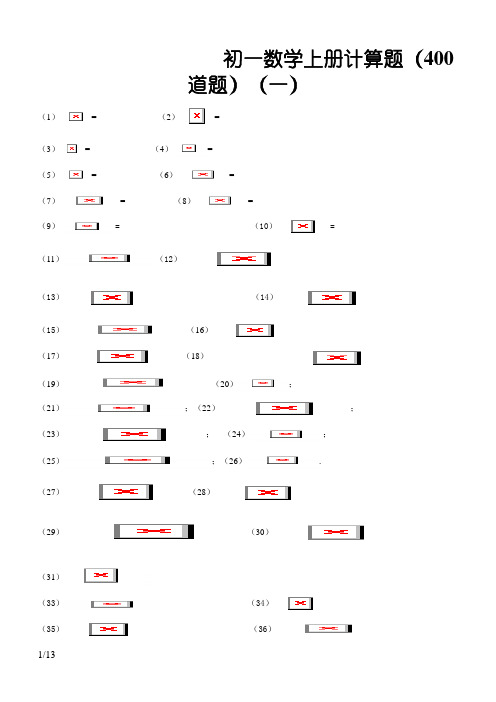
初一数学上册计算题(400道题)(一)(1)= (2)=(3) = (4) =(5)= (6)=(7)= (8) =(9)= (10)=(11)(12)(13)(14)(15)(16)(17)(18)(19)(20);(21);(22);(23);(24);(25);(26).(27)(28)(29)(30)(31)(32)(33)(34)(35)(36)(37)(38)如果,求的值(39)已知与互为相反数,求的值。
(40)(41)(42)(43)(44)(45)(46)(47)(48)(49)(50)100(51)(52)(53)(54)(55)(56)(57)(58)(59)若,,求a + b的值.(60)已知│a+1│与│b-2│互为相反数,求a-b的值.(61)(-12)÷4×(-6)÷2; ;(62)(62)(63);(64);(64);(68)(-5)×(-7)-5×(-6)(69)(70).(71)(72)(73)(74);(75);(76)(-5)×(-8)×0×(-10)×(-15);(77)(-3)×(-4)×(-5)+(-5)×(-7)(78)(-0.1)×(-1)×(-100)-0.•01×(1000).(79)2×(-1)×(-)×(-);(80)- + --)×(-20);(81)(-3)×(-0.12)×(-2)×33;(82)(- + -)×(-36).(83)-×(12-2-0.6)(84)(+)×|-|×2×(-5);(85)(-1)×3(-)×(-1)(86)(87)(-2)×(-)= (88)0×(-13.52)= (89)(-1)×a = (90)(-3.25)×(+)=(91)(-185.8)×(-36)×0×(-25)=(93)(94)(95)(96)(-)×0.125×(-2)×(-8);97)(98)(-0.25)×0.5×(-4)×4;(99)(-4)×(-18.36)×2.5;(100)(-)×(-18)+(-)×(-3)×2;(101)(-47.65)×2+(-37.15)×(-2)+10.5×(-7).(102)[(-2)×(-4)+(-5)]×[-3-(-2)×(-3)].(103)(104)(105)(106)(107)(-23)+7+(-152)+65 (108)|+(-)|(109)(-)+|―|(112)38+(-22)+(+62)+(-78)(113)(-8)+(-10)+2+(-1)(114)(-)+0+(+)+(-)+(-)(115)(-8)+47+18+(-27)(116)(-5)+21+(-95)+29 (117)(-8.25)+8.25+(-0.25)+(-5.75)+(-7.5)(118) 6+(-7)+(9)+2 (119) 72+65+(-105)+(-28)(120)(-23)+|-63|+|-37|+(-77)(121)19+(-195)+47 (122)(+18)+(-32)+(-16)+(+26)(122)(-3)-5(123)(-0.8)+(-1.2)+(-0.6)+(-2.4)(124)(-8)+(-3)+2+(-)+12 (125)5+(-5)+4+(-)(126)(-6.37)+(-3)+6.37+2.75(127)(-12.5)-(-7.5) (128)(-26)―(-12)―12―18 (129)―1―(-)―(+) (130)(-20)-(+5)-(-5)-(-12) (131)(-23)―(-59)―(-3.5) (132)|-32|―(-12)―72―(-5)(133)(-)―(-)―(134)(+)―(-)―(-)―(135)(-)―3―(-3.2)―7 (136)(+)―(-)―(137)(+6.1)―(-4.3)―(-2.1)―5.1 (138)(-)―(-1)―(-1)―(+1.75) (139)(-3)―(-2)―(-1)―(-1.75) (140)-8-5+4-3(141)-4++(-)―(142) 0.5+(-)-(-2.75)+(143)(+4.3)-(-4)+(-2.3)-(+4)(144)(-0.5)-(-3)+6.75-5(145)(-9)×(146)(-)×(-0.26)(147)(-2)×31×(-0.5)(148)×(-5)+×(-13)(149)(-4)×(-10)×0.5×(-3)(150)(-)××(-1.8)(151)(-0.25)×(-)×4×(-7)(152)(-)×(-)×(-)(153)(-8)×4×(-)×(-0.75)(154)4×(-96)×(-0.25)×(155)(-1+)×56(156)(――)×36 (157)(-36)×(+-)(158)(-)×(8--0.4)(159)(-66)×〔1-(-)+(-)〕(160)25×-(-25)×+25×(161)(+-+)×72(162)×(2-)×(-)×(-) (163)18÷(-3)(164)(-24)÷6 (165)(-57)÷(-3)(166)(-)÷(167)(-42)÷(-6)(168)(+)÷(-)(169)(-)÷9 (170)0.25÷(-)(171)-36÷(-1)÷(-)(172)(-1)÷(-4)÷(173)3÷(-)×(-) (174)0÷[(-3)×(-7)](175)-3÷(-)(176)(-24)÷(-6)(177) 2÷(5-18)×(178)1÷(-3)×(-)(179)-×(-)÷(-)(180)(-)÷(-)(181)(-+)÷(-)(182)-3.5 ×(-0.5)×÷(183)-1÷(-1)×1×(-7)(184)×(--)÷(185)÷(-2)-×-÷4(186)0.8×+4.8×(-)-2.2÷+0.8×(187)2÷(-)×÷(-5)(188)(-)×(-15×4)(189)(-2.4)(190)[15-(1÷1+3]÷(-1)(191)×(-5)÷(-)×5 (192)-(-+-)÷(-)(193)-13×-0.34×+×(-13)-×0.34(194) 8-(-25)÷(-5)(195)(-13)×(-134)××(-)(196)(-4)-(-5)+(-4)-3(197)(-16-50+3)÷(-2)(198)(-0.5)-(-3)+6.75-5(199)178-87.21+43+53-12.79(200)(-6)×(-4)+(-32)÷(-8)-3 (201)--(-)+|-1|(202)(-9)×(-4)+ (-60)÷12 (203) [(-)-1+]÷(-) (204)-|-3|÷10-(-15)×(205)-1×(-)÷2(206)(2-3+1)÷(-1)×(-7)(207)-×(8-2-0.04)(208)-2×( 209)--(210)-(211)-2×(212)÷(213)×(214)+(215)××(216)×-(217)++(218)-×-(219)+(220)0-÷3×(221)×÷(222)-×-÷(223)×(-+1) ×0 (224)6+×(225)-10+8÷-4×3 (226)--(227)-(1-0.5)×(228)××(229)4×+6 (230)×××(231)-+2×+(-6)÷(232)÷(-8)-×(-)(233)×()×(234)-2[-3×]÷(235)÷9÷(236)36×(237)-{}(238)-+(1-0.5)××[2×](239)-4×+(240)--+×÷(241)(-5.3)-(+4.8)+(-3.2)-(-2.5);(242)(243)-10+8÷(-2)2-3×(-4)-15;(244)-14-(1-0.5)××[2-(-3)2].(245)(246)(247)(248)(249)(250)(251)(252)(253); (254)(x+1)-3(x-1)=1-3x; (255)(x-2)-2(4x-1)=3(1-x).(256)(257);(258)(259)(260)(261)(262)(263)(264)(265)(266)(267)(268)(269)(270)(271)(272)(273)(274)(275)(276)(277)错误!未找到引用源。
七年级上册数学计算题库

七年级上册数学计算题库一、有理数运算。
1. 计算:(-3)+5- 解析:异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
|5| = 5,| - 3|=3,5>3,所以结果为正,5 - 3=2。
2. 计算:4-(-2)- 解析:减去一个数等于加上这个数的相反数,所以4-(-2)=4 + 2 = 6。
3. 计算:(-2)×3- 解析:两数相乘,异号得负,并把绝对值相乘,所以(-2)×3=-6。
4. 计算:(-4)÷2- 解析:两数相除,异号得负,并把绝对值相除,所以(-4)÷2=-2。
5. 计算:(-2)^3- 解析:表示3个-2相乘,(-2)^3=(-2)×(-2)×(-2)=-8。
二、整式加减。
6. 化简:3a + 2b - 5a - b- 解析:先找同类项,3a和-5a是同类项,2b和-b是同类项。
合并同类项得(3a - 5a)+(2b - b)=-2a + b。
7. 计算:(2x^2 - 3x+1)-(x^2 - 2x - 3)- 解析:去括号时,括号前是正号,去掉括号不变号;括号前是负号,去掉括号要变号。
所以原式=2x^2-3x + 1 - x^2+2x + 3=(2x^2 - x^2)+(-3x+2x)+(1 + 3)=x^2 -x+4。
8. 化简:4(a - b)+3(b - a)- 解析:先将3(b - a)变形为-3(a - b),则原式=4(a - b)-3(a - b)=(4 - 3)(a - b)=a - b。
三、一元一次方程。
9. 解方程:2x+3 = 7- 解析:首先移项,把常数项移到等号右边,得到2x=7 - 3,即2x = 4,然后两边同时除以2,解得x = 2。
10. 解方程:3(x - 1)=2x+1- 解析:先去括号得3x-3 = 2x + 1,再移项得3x-2x=1 + 3,合并同类项得x = 4。
七年级上册计算题数学

七年级上册计算题数学一、有理数运算。
1. 计算:(-3)+5 - (-2)- 解析:- 首先去括号,根据去括号法则,-(-2)=2。
- 则原式变为-3 + 5+2。
- 按照从左到右的顺序计算,-3+5 = 2,2 + 2=4。
2. 计算:-2×(-3)÷(1)/(2)- 解析:- 先计算乘法,-2×(-3)=6。
- 再计算除法,6÷(1)/(2)=6×2 = 12。
3. 计算:(-2)^3+(-3)×[(-4)^2 - 2]- 解析:- 先计算指数运算,(-2)^3=-8,(-4)^2 = 16。
- 则(-4)^2-2=16 - 2=14。
- 再计算乘法-3×14=-42。
- 最后计算加法-8+(-42)=-8-42=-50。
4. 计算:(1)/(2)-<=ft(-(1)/(3))+<=ft(-(1)/(4))- 解析:- 去括号得(1)/(2)+(1)/(3)-(1)/(4)。
- 通分,分母的最小公倍数是12,(1)/(2)=(6)/(12),(1)/(3)=(4)/(12),(1)/(4)=(3)/(12)。
- 则原式变为(6 + 4-3)/(12)=(7)/(12)。
5. 计算:-1^2023-(1 - 0.5)×(1)/(3)×[2 - (-3)^2]- 解析:- 先计算指数运算,1^2023=1,所以-1^2023=-1。
- 再计算括号内的式子,1-0.5 = 0.5=(1)/(2),(-3)^2 = 9,2-9=-7。
- 然后计算乘法(1)/(2)×(1)/(3)×(-7)=-(7)/(6)。
- 最后计算减法-1-<=ft(-(7)/(6))=-1+(7)/(6)=(1)/(6)。
二、整式的加减。
6. 化简:3a + 2b-5a - b- 解析:- 合并同类项,3a-5a=-2a,2b - b=b。
人教版数学七年级上册整式计算专项练习200题及答案详解

1当2已知,当3当4当5当当6若代数式7已知当8当9 C. D.如图所示的运算程序中,若开始输入的10B.C. D.按如图所示的程序计算:若开始输入的11 B.C.D.已知,则代数式的值是().12 B.C.D.已知,则式子的值为().13不能确定已知代数式的值是,则代数式的值是().14当时,代数式值为,那么当时,代数式的值是 ().1516化简17当18已知19已知代数式20化简21若22已知23如果24已知代数式25若代数式26整式化简求值:先化简,再求值:27已知整式化简求值:先化简,再求值:28已知三个有理数29已知30先化简,再求值31已知代数式32按照如图的运算顺序,输入33如图是一个数值转换机.若输入的34当35若36已知37已知多项式时,多项式的值是38已知.3940设41用整体思想解题:为了简化问题,我们往往把一个式子看成一个数42已知当43已知当44已知45先化简再求值:46设若代数式47若48已知49先化简再求值50若51已知52先化简,再求值:53先化简,在求值:5456当57化简求值:58化简:59请回答下列各题:60已知62已知63先化简,再求值:64先化简,再求值:65先化简,再求值:66回答下面问题;67先化简,再求值:68先化简,再求值:69化简再求值:70阅读框图并回答下列问题:.71先化简,再求值:72先化简,再求值.求73对于74先化简,再求值:75若76已知77已知78已知79奕铭在化简多项式80先化简,再求值81先化简,再求值:82先化简,再求值:83若84已知:85先化简再求值:86先化简,再求值:87已知88已知89已知90先化简,再求值:91已知92先化简,再求值:93若单项式94求多项式95设96已知97已知98求99若100若代数式1 23 4 5 67 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 26 2728 29 30 31 32 33 34 3536 37 38 39 40 41 4243 44 45 46 47 48 4950 51 52 53 54 55 5657 58 59 60 61 62 63 6465 66 67 68 69 70 7173 74 75 76 77 78 7981 82 83 84 85 8687 88 89 90 91 9293 94 9596 9798 99 100。
初一上册计算题精选集

初一上册计算题精选集初一的学习是为整个初中阶段打下坚实基础的重要时期,而数学中的计算题更是锻炼思维和提升能力的关键。
下面为大家精选了一些初一上册常见的计算题,通过练习和掌握这些题目,相信能帮助同学们更好地理解和运用所学知识。
一、有理数的运算1、计算:(-5) + 3这道题考查有理数的加法。
异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
在这道题中,|-5|>|3|,所以结果为负,用 5 3 = 2,最终答案为-2 。
2、计算:(-8) (-5)这是有理数的减法运算,减去一个数等于加上这个数的相反数。
所以原式可转化为-8 + 5 =-3 。
3、计算:(-2)×(-3)有理数乘法,同号得正,异号得负。
所以这道题的结果为 6 。
4、计算:(-12)÷(-3)两数相除,同号得正,异号得负。
所以答案为 4 。
二、整式的运算1、化简:3x + 2x同类项合并,系数相加,字母和指数不变。
所以结果为 5x 。
2、化简:(2x²+ 3x 5) (x² 2x + 1)去括号,然后合并同类项。
原式= 2x²+ 3x 5 x²+ 2x 1 = x²+5x 6 。
3、计算:2x(3x 1)使用乘法分配律,原式= 2x×3x 2x×1 = 6x² 2x 。
三、一元一次方程1、解方程:2x + 3 = 7首先,将 3 移到等号右边得到 2x = 7 3 ,即 2x = 4 ,然后两边同时除以 2 ,解得 x = 2 。
2、解方程:3(x 1) = 2x + 1先去括号得到 3x 3 = 2x + 1 ,然后将 2x 移到左边,-3 移到右边,得到 3x 2x = 1 + 3 ,解得 x = 4 。
四、综合计算题1、计算:(-2)³ ×(-4) 6 ÷(-3)先计算指数运算,(-2)³=-8 ,然后计算乘法-8×(-4) = 32 ,再计算减法 32 6 = 26 ,最后除以-3 ,得到-26/3 。
七年级上册数学计算题专练

七年级上册数学计算题专练一、有理数运算类。
1. 计算:(-3)+5 - (-2)- 解析:- 根据有理数加减法法则,减去一个数等于加上这个数的相反数。
- 所以(-3)+5 - (-2)=(-3)+5 + 2。
- 先计算(-3)+5 = 2,再计算2+2 = 4。
2. 计算:-2×(-3)÷(1)/(2)- 解析:- 根据有理数乘除法法则,先算乘法-2×(-3)=6。
- 再算除法6÷(1)/(2)=6×2 = 12。
3. 计算:(-2)^3+(-3)×[(-4)^2 - 2]- 解析:- 先计算指数运算,(-2)^3=-8,(-4)^2 = 16。
- 然后计算括号内的式子(-4)^2-2 = 16 - 2=14。
- 接着计算乘法-3×14=-42。
- 最后计算加法-8+(-42)=-8 - 42=-50。
二、整式加减类。
4. 化简:3a + 2b-5a - b- 解析:- 合并同类项,对于a的同类项3a-5a=(3 - 5)a=-2a。
- 对于b的同类项2b - b=(2 - 1)b = b。
- 所以化简结果为-2a + b。
5. 计算:(2x^2 - 3x + 1)-(3x^2 - 5x - 2)- 解析:- 去括号,得到2x^2-3x + 1-3x^2 + 5x+2。
- 合并同类项,2x^2-3x^2=(2 - 3)x^2=-x^2,-3x+5x=( - 3+5)x = 2x,1 + 2=3。
- 所以结果为-x^2+2x + 3。
三、一元一次方程类。
6. 解方程:2x+3 = 5x - 1- 解析:- 移项,将含x的项移到一边,常数项移到另一边,得到2x-5x=-1 - 3。
- 合并同类项-3x=-4。
- 系数化为1,x=(4)/(3)。
7. 解方程:(x+1)/(2)-(2x - 1)/(3)=1- 解析:- 先去分母,等式两边同时乘以6,得到3(x + 1)-2(2x - 1)=6。
七年级上册数学计算题。

七年级上册数学计算题。
一、有理数运算。
1. 计算:(-2)+3 - (-5)- 解析:- 首先去括号,根据去括号法则,“−(−5)=5”。
- 原式变为-2 + 3+5。
- 按照从左到右的顺序计算,-2+3 = 1,1 + 5=6。
2. 计算:(-3)×4+(-2)×(-5)- 解析:- 先算乘法,根据有理数乘法法则,“同号得正,异号得负”。
- (-3)×4=-12,(-2)×(-5) = 10。
- 再算加法,-12+10=-2。
3. 计算:(-4)÷2×(-(1)/(2))- 解析:- 按照从左到右的顺序计算,先算除法(-4)÷2=-2。
- 再算乘法-2×(-(1)/(2)) = 1。
4. 计算:(-2)^3+(-3)^2- 解析:- 先计算乘方,(-2)^3=-8(表示3个 - 2相乘),(-3)^2 = 9(表示2个 - 3相乘)。
- 再算加法,-8 + 9=1。
5. 计算:-1 - 2×(-3)^2- 解析:- 先算乘方,(-3)^2 = 9。
- 再算乘法,2×9 = 18。
- 最后算减法,-1-18=-19。
二、整式加减。
6. 化简:3a+2b - 5a - b- 解析:- 合并同类项,同类项是指所含字母相同,并且相同字母的指数也相同的项。
- 3a-5a=(3 - 5)a=-2a,2b - b=(2 - 1)b = b。
- 所以化简结果为-2a + b。
7. 计算:(2x^2 - 3x+1)-(3x^2 - 2x - 1)- 解析:- 去括号,括号前是“-”号,去括号后括号内各项要变号。
- 原式变为2x^2-3x + 1-3x^2+2x + 1。
- 合并同类项,2x^2-3x^2=(2 - 3)x^2=-x^2,-3x+2x=-x,1 + 1 = 2。
- 结果为-x^2 - x+2。
8. 化简:4(a - b)+3(b - a)- 解析:- 先将(b - a)变形为-(a - b)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ainy 晴初一數學上冊計算題(400道題)(1)= (2)=()22--3112⎛⎫⎪⎝⎭-(3) = (4) =()91-()42--(5)=(6)=()20031-()2332-+-(7)=(8) =()33131-⨯--()2233-÷-(9)= (10)=)2()3(32-⨯-22)21(3-÷-(11)(12)()()3322222+-+--235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(13) (14) ()34255414-÷-⎪⎭⎫ ⎝⎛-÷()⎪⎭⎫ ⎝⎛-÷----721322246(15) (16) ()()()33220132-⨯+-÷---[]24)3(2611--⨯--(17)(18)])3(2[)]215.01(1[2--⨯⨯--(19)(20);()()()33220132-⨯+-÷---22)2(3---(21);(22);]2)33()4[()10(222⨯+--+-])2(2[31)5.01()1(24--⨯⨯---332222()(3)(3)33÷--+-Ainy 晴(23); (24);94)211(42415.0322⨯-----+-20022003)2()2(-+-(25);(26).)2()3(]2)4[(3)2(223-÷--+-⨯--200420094)25.0(⨯-(27) (28)()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥()()----⨯-221410222(29) (30)()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325..()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.(31)(32)(56)(79)---(33) (34)(3)(9)(8)(5)-⨯---⨯-3515(26÷-+(35) (36)()()22431)4(2-+-⨯---5231591736342--+-(37)411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--Ainy 晴(38)如果,求の值0)2(12=-++b a 20112010()-3ab a b a a ++-()(39)已知與互為相反數,求の值。
|1|a +|4|b -b a (40)2234.0)2.1()211(922÷---⨯(41)12111110|11101211|-+-(42) (43)5]36)65121197(45[÷⨯+--)41()35(12575)125(72-⋅-+⨯--⨯ (44) )32()87()12787431(-+-÷--(45)4131211-+-(46) (47)()1-⎪⎭⎫⎝⎛-÷213122128(2)2⎛⎫-⨯-+÷- ⎪⎝⎭Ainy 晴(48)(49)1564358-÷⨯)4955.5(1416.34955.61416.3-⨯+⨯(50)100 (51) ()()222---÷3)2(32-+⎪⎭⎫ ⎝⎛-÷113(5)77(712()3322-⨯+⨯--÷-(52) (53)2012201313(2)(0.5)(6714-⨯-+-⨯322012111(((1)(2)(1)2216⎡⎤--÷--⨯-÷-⎢⎥⎣⎦(54)(55)222121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭)12()4332125(-⨯-+(56)(57)(20)(3)(5)(7)-++---+3712(()14263-+----(58)1( 6.5)(2)((5)3-⨯-÷-÷-(59)若,,求a + b の值. (60)已知│a +1│與│b -2│互為相反數,求a -b の7a =3b =值.Ainy 晴(61) (-12)÷4×(-6)÷2; ; (62) (62)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(63);111311123124244⎛⎫⎛⎫⎛⎫⎛⎫--+----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(64) ; (64)222121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭;206137+-+-(67);532)2(1---+-+(68)(-5)×(-7)-5×(-6)(69) ()25.05832-÷⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛-(70).()⎪⎭⎫⎝⎛----+⎪⎭⎫ ⎝⎛-⋅-21221232(71)222121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭Ainy 晴(72))12(4332125(-⨯-+(73)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(74);111311123124244⎛⎫⎛⎫⎛⎫⎛⎫--+----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(75);222121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭(76)(-5)×(-8)×0×(-10)×(-15);(77)(-3)×(-4)×(-5)+(-5)×(-7)(78)(-0.1)×(-1)×(-100)-0. 01×(1000).(79)2×(-1)×(-)×(-); 14342387(80)-+ --)×(-20);12131415Ainy 晴(81)(-3)×(-0.12)×(-2)×33;131413(82)(- + - )×(-36). 795634718(83)-×(12-2-0.6) 5625(84)(+)×|-|×2×(-5);12231413(85)(-1)×3(-)×(-1)182313(86) )8(12)11(9-⨯-+⨯-(87)(-2)×(-)= (88)0×(-13.52)= (89)(-1)×a = 1337(90)(-3.25)×(+)= (91)(-185.8)×(-36)×0×(-25)=21345(92))25()7()4(-⨯-⨯-(93) 34(853(-⨯⨯-Ainy 晴(94)1514348(43--⨯(95))8(45201(-⨯⨯-(96)(-)×0.125×(-2)×(-8);371397)53)8()92()4(52(8⨯-+-⨯---⨯(98)(-0.25)×0.5×(-4)×4;27(99)(-4)×(-18.36)×2.5;(100)(-)×(-18)+(-)×(-3)×2;2951115(101)(-47.65)×2+(-37.15)×(-2)+10.5×(-7).611611511Ainy 晴(102)[(-2)×(-4)+(-5)]×[-3-(-2)×(-3)].(103) )533()6.0(34521321----+-(104)(105))31()21()54(32(21+--+---+1(2)235+-+--(106)27()1333-+----(107)(-23)+7+(-152)+65 (108)|+(-)| (109)(-)+|―|52315231Ainy 晴(112)38+(-22)+(+62)+(-78) (113)(-8)+(-10)+2+(-1)(114)(-)+0+(+)+(-)+(-) (115)(-8)+47+18+(-27) 32416121(116)(-5)+21+(-95)+29 (117)(-8.25)+8.25+(-0.25)+(-5.75)+(-7.5) (118) 6+(-7)+(9)+2 (119) 72+65+(-105)+(-28) (120)(-23)+|-63|+|-37|+(-77) (121)19+(-195)+47(122)(+18)+(-32)+(-16)+(+26) (122)(-3)-52141 (123)(-0.8)+(-1.2)+(-0.6)+(-2.4) (124)(-8)+(-3)+2+(-)+122121(125)5+(-5)+4+(-) (126)(-6.37)+(-3)+6.37+2.755332523143(127)(-12.5)-(-7.5) (128)(-26)―(-12)―12―18(129)―1―(-)―(+) (130)(-20)-(+5)-(-5)-(-12)2123(131)(-23)―(-59)―(-3.5) (132)|-32|―(-12)―72―(-5)(133)(-)―(-)― (134)(+)―(-)―(-)― 4185811037452710(135)(-)―3―(-3.2)―7 (136)(+)―(-)―516717273(137)(+6.1)―(-4.3)―(-2.1)―5.1 (138)(-)―(-1)―(-1)―(+1.75)324332(139)(-3)―(-2)―(-1)―(-1.75) (140) -8-5+4-3 32433243976192(141) -4++(-)― (142) 0.5+(-)-(-2.75)+ 436132254121 (143)(+4.3)-(-4)+(-2.3)-(+4) (144)(-0.5)-(-3)+6.75-54121(145)(-9)× (146)(-)×(-0.26) (147)(-2)×31×(-0.5)32132(148)×(-5)+×(-13) (149)(-4)×(-10)×0.5×(-3) 3131(150)(-)××(-1.8) (151)(-0.25)×(-)×4×(-7) 833474(152)(-)×(-)×(-) (153)(-8)×4×(-)×(-0.75)735412721(154)4×(-96)×(-0.25)× (155)(-1+)×564817481143Ainy 晴(156)(――)×36 (157)(-36)×(+-) 6543979465127(158)(-)×(8--0.4) (159)(-66)×〔1-(-)+(-)〕4334222131115(160)25×-(-25)×+25× (161)(+-+)×72432141187436597(162)×(2-)×(-)×(-) (163)18÷(-3) (164)(-24)÷6 311437258165(165)(-57)÷(-3) (166)(-)÷ (167)(-42)÷(-6)5352(168)(+)÷(-) (169)(-)÷9 (170)0.25÷(-)2157313981(171)-36÷(-1)÷(-) (172)(-1)÷(-4)÷313274(173)3÷(-)×(-) (174)0÷[(-3)×(-7)] (175)-3÷(-)7697413141(176)(-24)÷(-6) (177) 2÷(5-18)× (178)1÷(-3)×(-)761813131Ainy 晴(179) -×(-)÷(-) (180)(-)÷(-) (181)(-+)÷(-) 871438343876529834343(182) -3.5 ×(-0.5)×÷ (183) -1÷(-1)×1×(-7) 617321726583(184)×(--)÷ (185)÷(-2)-×-÷4 5631214575527512535(186)0.8×+4.8×(-)-2.2÷+0.8× (187)2÷(-)×÷(-5)1127273119737471(188)(-)×(-15×4) (189)(-2.4)1275420361-+-()⨯⨯-73187(190)[15-(1÷1+3]÷(-1) (191)×(-5)÷(-)×5 21415221815151(192) -(-+-)÷(-)(193) -13×-0.34×+×(-13)3121114372421327231-×0.3475(194) 8-(-25)÷(-5) (195)(-13)×(-134)××(-)131671(196)(-4)-(-5)+(-4)-3 (197)(-16-50+3)÷(-2) 8721418152(198)(-0.5)-(-3)+6.75-5 (199)178-87.21+43+53-12.79 41212122119(200)(-6)×(-4)+(-32)÷(-8)-3 (201)--(-)+|-1|722121(202)(-9)×(-4)+ (-60)÷12 (203) [(-)-1+]÷(-)14975218421(204)-|-3|÷10-(-15)× (205)-1×(-)÷2315332716521(206)(2-3+1)÷(-1)×(-7) (207)-×(8-2-0.04)31211817614331(208)-2× ( 209)-- (210)-2322()31-4334(211)-2× (212)÷ (213)×31-()31-()23-()24-2-()22-(214) + (215) ×× (216)×-232-()34-()32-()42-()52-2-23()232⨯-Ainy 晴(217)++ (218)-×-()22-2-()32-3222-3)3(-()31-()31-(219)+ (220)0-÷3× ()[]221--()221-()23-()32-(221)×÷ (222)-×-÷22-()221-()38.0-23()231-()32-()221-(223)×(-+1) ×0 (224)6+×()243-3222()51-(225)-10+8÷-4×3 (226)--()22-51()()[]55.24.0-⨯-(227)-(1-0.5)×(228)××()251-31()32-()232-()323-(229)4×+6 (230)×××()23-()1321-83()122-()731-(231) -+2×+(-6)÷ (232)÷(-8)-×(-)27()23-()231-()42-()321-22(233)×()× (234)-2[-3×]÷ ()()[]222345----11587÷()47-()22-()221-4351(235)÷9÷ (236)36×()26-()296÷-()23121-(237)-{} (238)-+(1-0.5)××[2×]()⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛-⨯+--)2(2114.03334131()23-(239)-4×+ (240)--+×÷()[]3671÷-()[]()33235-÷--33()[]1283--÷()23-()32-25.01(241)(-5.3)-(+4.8)+(-3.2)-(-2.5); (242)⎪⎭⎫ ⎝⎛-+-⨯⎪⎭⎫ ⎝⎛-3132843(243)-10+8÷(-2)2-3×(-4)-15; (244)-14-(1-0.5)×13×[2-(-3)2].(245) (246)5244361832411÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+-36727199⨯-(247) (248)x x x 10415-+222pp p ---(249)(250))3()7(5nn n n a a a a -+----x y yx xy y x 222223-+- (251)(252)222252214.041ab b a ab b a +--]}68()(6[2{3)-+++----b a c b c a c aod (256) (257); (258)1524213-+=-x x 22)5(54-=--+x x x 46333-=+--x x x (259)⎪⎩⎪⎨⎧=+=-57502y x x y (260)(261)359236x y x y -=⎧⎨-+=-⎩()()()()31445135x y y x -=-⎧⎪⎨-=+⎪⎩(262)(263)(264)3262317x y x y -=⎧⎨+=⎩1323334m nm n ⎧+=⎪⎪⎨⎪-=⎪⎩83206570u v u v ++=⎧⎨++=⎩(265) (266) (267)x x 4923+≥-)1(5)32(2+<+x x 0)7(319≤+-x (268)(269)(270)31222+≥+x x 223125+<-+x x 5223-<+x x (271)(272) (273)234->-x )1(281)2(3--≥-+y y 14321<--<-x(274) (275) (276)2(1)41413x x x x +-<⎧⎪+⎨>-⎪⎩95)31(27≤-≤-x 532(1)314(2)2x xx -≥⎧⎪⎨-<⎪⎩(277)錯誤!未找到引用源。
