华侨大学大学物理练习题答案
大学物理下习题册答案详解

解 : a 30cm ,d 0.6m m , b=2.2m
D =a+b 2.5m ,
x 2.25m m
x D dx 5400 A
d
D
第 4级 明 纹 至 中 心 距 离 满 足 :
dx 4 x 4 D 9.00m m
D
ቤተ መጻሕፍቲ ባይዱ
d
练习34 光的干涉(2)
1.在双缝装置中,用一折射率为n的薄云母片覆盖其中
光的程亮差度2 分,, 2别则. 5为 有 , :3 .5
,比较 P、Q、R 三点
(1)P点最亮、Q点次之、R点最暗;
注意。单击此处添加正文,文字是您思想的提炼,为了演示发布的良好效果,请言简意赅地阐述您的观点。您的 内容已经简明扼要,字字珠玑,但信息却千丝万缕、错综复杂,需要用更多的文字来表述;但请您尽可能提炼思
20D 想 的 精 髓 , 否 则 容 易 造 成 观 者 的 阅 读 压 力 , 适 得 其 反 。 正 如 我 们 都 希 望 改 变 世 界 , 希 望 给 别 人 带 去 光 明 , 但 更 多
x 20x= 0.11m 时候我们只需要播下一颗种子,自然有微风吹拂,雨露滋养。恰如其分地表达观点,往往事半功倍。当您的内容 a 到 达 这 个 限 度 时 , 或 许 已 经 不 纯 粹 作 用 于 演 示 , 极 大 可 能 运 用 于 阅 读 领 域 ; 无 论 是 传 播 观 点 、 知 识 分 享 还 是 汇 报
n 1 题 目 中 k=-7
所 以 : e 7 n 1
答案为:(1)
2.迈克耳逊干涉仪可用来测量单色光的波长,当干涉仪
的动镜M2移动d距离时,测得某单色光的干涉条纹移 动N条,则该单色光的波长为:( )
华侨大学 大学物理作业本(下)答案

大学物理作业本(下)姓名班级学号江西财经大学电子学院2005年10月第九章 稳恒磁场练 习 一1. 已知磁感应强度为20.2-⋅=m Wb B 的均匀磁场,方向沿x 轴正方向,如图所示。
求:(1) 通过图中abcd 面的磁通量;(2) 通过图中befc 面的磁通量;(3) 通过图中aefd 面的磁通量。
2. 如图所示,在被折成钝角的长直导线通中有20安培的电流。
求A 点的磁感应强度。
设a=2.0cm , 120=α。
3.有一宽为a的无限长薄金属片,自下而上通有电流I,如图所示,求图中P点处的磁感应强度B。
4.半径为R的圆环,均匀带电,单位长度所带的电量为 ,以每秒n转绕通过环心并与环面垂直的轴作等速转动。
求:(1)环心的磁感应强度;(2)在轴线上距环心为x处的任一点P的磁感应强度。
练习二1.一载有电流I的圆线圈,半径为R,匝数为N。
求轴线上离圆心x处的磁感应强度B,取R=12cm,I=15A,N=50,计算x=0cm,x=5.0cm, x=15cm各点处的B值;2.在一半径R=1.0cm的无限长半圆柱形金属薄片中,自上而下通有电流I=5.0A,如图所示。
求圆柱轴线上任一点P处的磁感应强度。
3.如图所示,两无限大平行平面上都有均匀分布的电流,设其单位宽度上的电流分别为1i 和2i ,且方向相同。
求:(1) 两平面之间任一点的磁感应强度;(2) 两平面之外任一点的磁感应强度;(3) i i i ==21时,结果又如何?4.10A 的电流均匀地流过一根长直铜导线。
在导线内部做一平面S ,一边为轴线,另一边在导线外壁上,长度为1m ,如图所示。
计算通过此平面的磁通量。
(铜材料本身对磁场分布无影响)。
练习三1.半径为R 的薄圆盘上均匀带电,总电量为q ,令此盘绕通过盘心且垂直盘面的轴线匀速转动,角速度为ω,求轴线上距盘心x 处的磁感应强度。
2.矩形截面的螺绕环,尺寸如图所示。
(1) 求环内磁感应强度的分布;(2) 证明通过螺绕环截面(图中阴影区)的磁通量,210ln 2D D NIh πμ=Φ 式中N 为螺绕环总匝数,I 为其中电流强度。
大学物理C1练习题答案(新版)

大学物理C1练习题答案(新版)大学物理C1练习题答案力学练习题(一)一、选择题1.D2.B3.B4.D二、填空题1. 2sin A t -ωω 210,1,2,2k k +=πω2. 17.27 2.73(m)r i j ?=+ 0.350.06(m /i j =+v 1.16(m /s)=v3. (1)10 m ,(2)15.7 m三、计算题1. 232210(SI)3t x t ==+v 2./s)=±v力学练习题(二)一、选择题1.D2.D3.C 二、填空题1. sin g -θ cos g θ 2c o s g θv2. 3243t t - 2126t t -3. 55.9/min v m = '东偏北2636或26.6 4. 1212()F m m g m m +-+ 2112(2)m F m g m m ++ 三、计算题1. (1)0mg2. 00(1)R R t μ=+v v v 0(2)ln 2R R t s μμ==v3. (1)7m /s (2)11m /s 222(3)4m/s 605m/s 605m/s t n a a a ===力学练习题(三)一、选择题1.C2.A3.A4.D二、填空题1. 6m /s2. 12J3. 18N s ?三、计算题1. (1)26.49N (2)4.7N s ?2. 12.96m /s3. 0.301m /s力学练习题(四)一、选择题1.C2.B3.B D二、填空题1. 4s 15m/s2.12Ma 3. ln 2J k三、计算题1. 2(1)0.5rad /s - (2)0.25N m -? (3)75rad2. 2(1)10.3rad /s 1(2)9.08rad s -? 力学练习题(五)一、选择题1.C2.D3.B二、填空题1. 0.4rad /s2. 2112(kg m s )k -?? 3(N m)k ?三、计算题1. 21212()m t g m μ+=v v 2. 0(1)78.8=θ (2)4.87m /s (3)3.95J3. 0(1)4ω 22003(2)2W mr =ω 振动和波动练习题(一)一、选择题1.B 2.B 3.D二、填空题1.2,4,12s π-,2π-,2cos()22t ππ-,sin()22t πππ--,2cos()222t πππ--,π2.4T ,12T ,6T3.1︰1三、计算题1.(1)22.010cos(4)3x t m ππ-=?+(2)242.010cos(4)3x t m ππ-=?+ 2.(1)200/k N m =(2)0,0.1,0t x m ===v (3)0.1cos(10)x t m =振动和波动练习题(二)一、选择题1.C 2.C二、填空题1111221122sin sin cos cos A A tg A A -++,2,0,1,2k k ?π?=±=,(21),0,1,2k k ?π?=±+= 2.3cos(5)6t π+,)2t π+ 3.F kx =-,cos[()]x y A t uω?=-+,波沿传播方向传播x 距离落后的时间,波沿传播方向传播x 距离落后的相位。
11-12-2厦门工学院期中考试物理试题及答案

华侨大学厦门工学院2011—2012学年第二学期期中考试《大学物理A (一)》考试试卷1、(本题3分) (0604)某物体的运动规律为d v /dt = -k v 2t ,式中的k 为大于零的常量。
当t = 0时,初速为v 0,则速度v 与时间t 的函数关系是(A) 0221v v +=kt (B) 0221v v +-=kt(C) 021211v v +=kt (D) 021211v v +-=kt [ C ]2、(本题3分)(0094)如图所示,假设物体沿着竖直面上圆弧形轨道下滑,轨道是光滑的,在从A 至C 的下滑过程中,下面哪个说法是正确的?(A) 它的加速度大小不变,方向永远指向圆心。
(B) 它的速度均匀增加。
(C) 它的合外力大小变化,方向永远指向圆心。
(D) 它的合外力大小不变。
(E) 轨道支持力的大小不断增加。
[ E ]解 如上图受力分析可见 A能转化为动能可知,下滑过程动能应越来越大,可见答案B也是错误的。
对于答案E有: Rv m mg N R v m mg N 22+==-θθsin sin3、(本题3分) (0412)如图,一质量为m 的物体,位于质量可以忽略的直立弹簧正上方高度为h 处,该物体从静止开始落向弹簧,若弹簧的劲度系数为k ,不考虑空气阻力,则物体下降过程中可能获得的最大动能是(A) mgh (B) mgh +22m g k(C) mgh -222m g k (D) mgh +222m g k解答: 选物体 弹簧 地球为系统,系统只有保守力做功,机械能守恒。
最大动能应该是物体压缩弹簧下降过程中重力等于弹性力的时候,设此时最大动能为E max 。
据机械能守恒定律有----------------------------------------------------------------------------------------------------------------------------------------密-----------------封----------------线-------------------内------------------------------------封----------------线-------------------内-------------------不封----------------线-------------------内-------------------不----------------线-------------------内-------------------不__________________________________系______级系______级________________________专_______专业______班 姓班 姓名:__________________________ 学号:()mzx E kx x h mg +=+221式中x 满足kx =mg,即x =mg/k 代入前式即得答案D4、(本题3分) (0367)质量为20g 的子弹沿X 轴正向以500 m/sX 轴正向以50 m/s 的速率前进,在此过程中木块所受冲量大小为(A) 9N ·s (B) -9N ·s (C) 10N ·s (D) -10N ·s [ A ]解答 根据动量定理,有()S N mv mv I ⋅-=-⨯=-=95005002012.式中负号表示方向。
(完整版)大学物理课后习题答案详解

第一章质点运动学1、(习题1.1):一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线 (2)质点的位置 : 22(48)r ti t j =+- 由d /d v r t =则速度: 28v i tj =+ 由d /d a v t =则加速度: 8a j =则当t=1s 时,有 24,28,8r i j v i j a j =-=+= 当t=2s 时,有 48,216,8ri j v i j a j =+=+=2、(习题1.2): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dt dv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式. 解: =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程; (3)落地前瞬时小球的d d r t ,d d v t ,tv d d . 解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t = 而落地所用时间 gh2t = 所以 0d -2gh d r v i j t =d d v g j t=- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
华侨大学741大学物理12-16年真题
y
u
B
x
O |x|
招生专业 光学 科目名称 普通物理(电磁学、振动与波)
科目代码 741
10.(本题 3 分)
一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中 (A) 它的势能转换成动能. (B) 它的动能转换成势能. (C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加. (D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.
5.(本题 3 分)
附图中,M、P、O 为由软磁材料制成的棒,三者在同一平面内,当 K 闭合后,
(A) M 的左端出现 N 极. (C) O 的右端出现 N 极.
(B) P 的左端出现 N 极. (D) P 的右端出现 N 极.
M
P
O
K
6.(本题 3 分)
如图,长度为
l
的直导线
ab
在均匀磁场
B
中以速度v
13.(本题 10 分)
在强度的大小为 E,方向竖直向上的匀强电场中,有一半径为 R 的半球形光滑绝缘槽放在光滑水平面上(如图所示).槽的质量为 M,一质量为 m 带有电荷+q 的小球从槽的顶点 A 处由静止释放.如 果忽略空气阻力且质点受到的重力大于其所受电场力,求:
(1) 小球由顶点 A 滑至半球最低点B时相对地面的速度; (2) 小球通过 B 点时,槽相对地面的速度; (3) 小球通过 B 点后,能不能再上升到右端最高点 C?
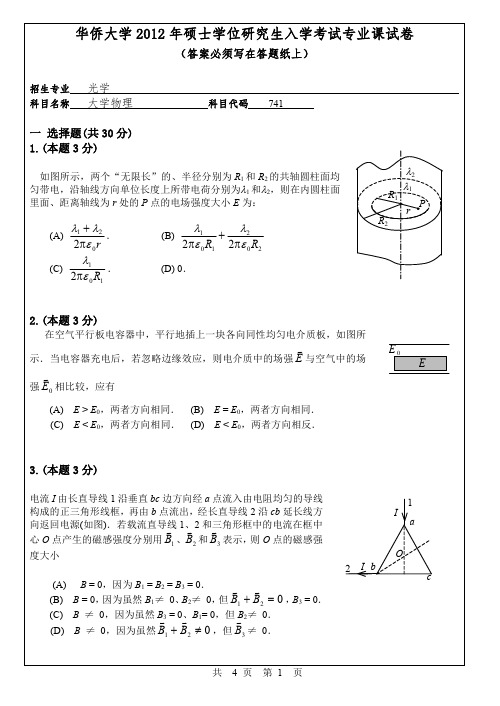
里面、距离轴线为 r 处的 P 点的电场强度大小 E 为:
(A)
1 2 . 2 0 r
(C)
1 . 2 0 R1
(B)
1 2 2 0R1 2 0R2
(D) 0.
华侨大学大学2013年大学物理考试题AB卷试题及答案

eg
a= r b T=11mg / 8
第 2页
21. ( 本题 5分)(0423)
T2-mg=ma 1 T1 r-T r= mr 2 b 2 1 T r-T2 r= mr 2 b 2 解上述 5 个联立方程得:
is
2分 1分 1分 1分 1分
a
根据牛顿第三定律,球对槽压力大小同上,方向沿半径向外. a t = g sin q 由②式得
三 计算题 (共38分)
20. ( 本题 5分)(5391)
re
① ②
T m
v v 解:球 A 只受法向力 N 和重力 mg ,根据牛顿第二定律 N - mg cos q = mv 2 / R 法向: mg sin q = ma t 切向:
d
1分 1分 1分 1分 1 分
2分
b
T1
由①式可得
(B)
3. ( 本题 3分)(0344)
(B)
4. ( 本题 3分)(0247)
(C)
5. ( 本题 3分)(4552)
(B)
6. ( 本题 3分)(4453)
(B)
7. ( 本题 3分)(5052)
(B)
8. ( 本题 3分)(1443)
(D)
9. ( 本题 3分)(1475)
(A)
10. ( 本题 3分)(1525)
te
b
T2
v P1
2m
a
v P2
2分 2分
23. ( 本题10分)(4598)
解:设 c 状态的体积为 V2,则由于 a,c 两状态的温度相同,p1V1= p1V2 /4 故 V2 = 4 V1 循环过程 ΔE = 0 , Q =W . 而在 a→b 等体过程中功 W1= 0. 在 b→c 等压过程中功 W2 =p1(V2-V1) /4 = p1(4V1-V1)/4=3 p1V1/4 在 c→a 等温过程中功 W3 =p1 V1 ln (V2/V1) = -p1V1ln 4 ∴ W =W1 +W2 +W3 =[(3/4)-ln4] p1V1 Q =W=[(3/4)-ln4] p1V1
华侨大学2013大物期中考试卷答案

d
在无限大平面上沿 z 轴方向上取长 dl,沿 x 轴方向取宽 da,则其面积为
re
1分 2分 1分
18. ( 本题12分)(2278)
解∶电流密度
J=
I p( R - a 2 )
2
1分
v J r1 Pr
y v B1 q1 qC v 2 B 2 P
B 与 r1, r2 无关,可知圆柱孔内为匀强场,方向沿 y 轴正向.
场的磁感强度,作安培环路 abcda,由安培环路定理得: v v 1分 B ò × d l = m 0 ih ∴
Bh + Bh = m 0 ih 1 B = m0 I 2 B1 = B0 - B , B2 = B0 + B 1 1 B0 = ( B1 + B2 ) , B = ( B2 - B1 ) 2 2 i = ( B2 - B1 ) / m 0
nR
eg
第 3页
is
P 点场强为充满圆柱并与 I 同向的电流 I10,及充 2 ⊙ Ä 满孔并与 I 反向的电流 I20 的场叠加而成.取垂直 r1 C O OC r2 ′ 于圆柱轴并包含 P 点的平面,令柱轴与孔轴所在 C x q1 q2 C v J O O′ C 处分别为 O 与 O¢, P 点与两轴的距离分别为 r1 与 r2,并建立坐标如图.利用安培环路定理可知 P 点场强为与 I 同向的 I1 和与 I 反向的 I2 的场的叠加,且有 I 1 = Jpr12 , I 2 = Jpr22 m I m B1 = 0 1 = 0 r1 J 2分 2pr1 2 m I m B2 = 0 2 = 0 r2 J 2分 2pr2 2 v v B1 , B2 方向如图所示. P 点总场 v v v B = B1 + B2 m B x = B2 sin q 2 - B1 sin q 1 = 0 J (r2 sin q 2 - r1 sin q 1 ) = 0 3分 2 m m B y = B1 cos q 1 + B2 cos q 2 = 0 J (r1 cos q 1 + r2 cos q 2 ) = 0 Jb 3分 2 2 m m 0 bI B = B y = 0 Jb = 1分 2 2p( R 2 - a 2 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习一 (磁)1. (C)2.a 4I 0πμ,⊗3.)412(R 2I 0ππμ+-, ⊗4. 可看成许多平行的无限长载流直导线组成,其中一宽为θRd dl =的直导线载有电流dl RIdI π=θθπμθπd sin R2I)2cos(dB dB 20x -=+=⎰-=-=ππμθθπμ02020x RI d sin R 2I Bθθπμθπd cos R 2I )2sin(dB dB 20y =+= 0d cos R2I B 020y ==⎰πθθπμ )T (i1037.6i RI B 620O -⨯-=-=πμ5. 将此盘看成无数同心带电圆环组成,半径为r的圆环带电rdr2dq πσ⋅=圆环转动形成的电流为rdr dq 2dI ωσπω==则 dr r dIdB ωσμμ00212== 各B d 同向R 21dr 21dB B 00R 0σωμωσμ===∴⎰⎰练习二 (磁)1. (B)2. 变量 ,I ομ-3. 1∶1, 304. 在横截面上以轴点为圆心,作半径为r 的圆形环路则 (1) a r < ⎰=⋅Ll d B 0, 0=∴B(2) b r a << I a b a r rB l d B L )()(22222--==⋅⎰ππμπο , ra b Ia r B )(2(22)22--=∴πμο (3) b r <I rB l d B L⎰==⋅ομπ2,rIB πμο2=∴ 5. 取电流元 dI=(I/b)dx则 )x r b (b 2Idx)x r b (2dIdB 00-+=-+=πμπμrbr ln b 2I )x r b (b 2IdxB b00+=-+=⎰πμπμ 方向向里练习三 (磁)1.(B )2. 03. 1∶14.取面积元xdx ahydx dS ==,它距长直载流导线为 (b+x )m d φ=S d B ⋅=xdx ahx b I⋅+)(2πμο=dx xb ba hI )1(2+-πμο ∴ m φ=⎰m d φ=ahIπμο2dx xb ba)1(0⎰+-=ahI πμο2[b ab ln b a +-]5. 在横截面上以轴点为圆心作半径为r 的圆形环路,由环路定理可得:R r < 222r R I rB ππμπο⋅= r R I B 22πμο=内R r ≥ I rB ομπ=2 rIB πμο2=外 矩形纵截面 外内S S S +=,其总磁通量为:⎰⎰⋅+⋅=S 外S 内m S d B S d Bφ)m 1l (2ln 212I ldr r 2I ldr R2Ir R 2R 0R20=+=+=⎰⎰)(πμπμπμο 练习四 (磁)1. (D)2. (B)3. (B)4. AB 处的B )6a3b (2IB AB -=πμο,⊗,受力)6a3b (2aI I F 211-=πμο, 方向AB ⊥向左1I 在BC 上与1I 相距x 的电流元l d I 2处的xIB πμο21=,⊗,由B l d I F⨯=⎰22 及 2330cos dxdx dl ==得6a 3b 3a 3b ln 3I I 23dx x 2I I F 21a 33b a63b 212-+=⋅=⎰+-πμπμοο 方向:在∆平面里BC ⊥向外 同理知23F F =,CA F ⊥3向外(在∆平面里)。
由对称性知合力无y 分量60cos 6a 3b 3a 3b ln 3I I 2)a 63b (2I aI F F 2121x -+⨯+--==∴πμπμοο 5.(1)由安培环路定律和磁场叠加原理,可得导线间的B 为)x d 3(2Ix 2I B -+=πμπμοο, 滑块受到的磁力 5ln I IBdx f 2d 52d 2⎰==πμο常量===∴5ln 2πμοm I m fa又00=U 5ln 212ομπmlIa l t ==∴(2) 215ln 2)(πμοm l I at V t ⋅==练习五 (磁)1. (C)2. (D)3. 矫顽力大,剩磁也大 永久磁铁4. I R 221π, IB R 221π,ϕsin RIB 2 5. B 垂直于y 轴而与x 轴成锐角6. (1) 朝东(2) 已知电子的能量 E k =(1/2)mv 2=1.2×104eV所以电子的速度 v=(2E k /m)1/2(1)电子的电量 e=1.6×19-19 C 电子的质量 m=9.11×10-31kg 设电子通过的距离为s 、偏转间距为 x 则有Rmv evB f 2== (2)222)x R (s R -+= (3) 联解(1),(2),(3)得 m 1098.2mE 8eBs R 2s x 3k22-⨯==≈7. 证: 将此盘看成无数同心带电圆环组成,半径为r 的圆环带电 rdr 2dq πσ⋅=圆环转动形成的电流为 rdr dq 2dI ωσπω==该圆电流的磁矩为 rdr r SdI dp 2m ωσπ⋅== 方向沿盘面轴线 该圆电流在磁场中受到的磁力矩为 dr r B B dp dM 3m πωσ==各M d同向 4BR dr r B M 4R3σωππωσ==⎰证毕.练习六 (磁)1.(B )2.(D )3. ① (D),② (B),③ b , 2RBv4.-VBL 215. dx Kxl S d B d m 1=⋅=φθφθθcos l Kl 21xdx Kl 221)cos 1(l 2)cos 1(l 1m 22==⎰+- θωθθφεsin 21sin 21221221l Kl dt d l Kl dt d m i =⋅=-= 练习七 (磁)1.(A )2.(D )3. 0.15T4.(1)自感 212ln 212D Dh N S d B INI N L D D ⎰=⋅==πμφο (2)H D D h N L 138.0ln 2212==πμο5. 在棒上取一长度元dl ,该长度元的速度 θωsin l v =,该长度元上的电动势为ldl sin B dl sin vB d 2i θωθε==OP 棒上的电动势为 2L2i )sin L (B 21ldl sin B θωθωε==⎰练习八 (磁)1. 变化的磁场,E q F=2. 导体在磁场中运动(切割磁力线)时,自由电荷受洛仑兹力而在导体内定向移动所致;磁场随时间变化所产生的涡旋电场可对载流子做功。
3. 0 4. 3.7 H 5. -800 Wb/s6. 在正方形线圈取一长条形面积元dr d dS ⋅= ,其所在处的磁感强度dr )r1d r 1(2I B 0--=πμ )34ln(2Id dr )r 1d r 1(2Id BdS 0d3d 20m πμπμφ=--==⎰⎰dtdI )34ln(2d dt d 0m i πμφε==7. (1) 取面积元 ldr dS = ldr r2IBdS d 0m πμφ== ada ln 2Il ldr r 2I 0da a0m +==⎰+πμπμφ (2) ad a ln 2l N I N M 0m +==πμφ (3) t cos )ada ln(2l NI dt dI M00M ωπωμε+-=-= 练习九 (磁)1. (C)2. 0 ,42228R r I πμο 3. 略4. R 2vB i ⋅=ε P 端电势高5. (1)两线圈内电流绕向相反,各点B=0,则0=ψ 0==∴IL ψ(2)此时两线圈完全耦合 121L L L M ==IL 4)M L M L (I 121122211=+++=+++=ψψψψψH L I L 2.041===ψ(3) 此时也为完全耦合,但二者磁通不能相加 21ψψψ==I L L IM L I LI 11122)(2=⋅=+=H L L 05.01== 练习十 (磁)1. (C)2. 0 ,221ab B ωε=,高 3. 1.5 mH 4. 22.6 J/m 3 5. 线框中只有两条坚直边切割磁力线,以顺时针方向为正,线框中的感应电动势为 ))l d (2I d 2I (vl l vB l vB 10022221i +-=-=πμπμε)l d (d 2vl Il 1210+=πμ, 顺时针方向6. (1) 00I i ,x2i B ==πμ10l l l 0000l l l l l l ln 2I v dx x 2I vvBdx 100100+===⎰⎰++πμπμε V a >V b (2) t cos I i 0ω=, 以abcda 作为回路正方向1020l l l 202l l l ln 2il dx x 2il dx Bl 100+===⎰⎰+πμπμφ )t cos v t sin l (l l l ln 2I ]il [dt d l l l ln 2dt d 20100020100ωωωπμπμφε-+=+-=-=练习十一 (磁)1. B2. D3. B4.t cos a 2r I 20ωμπt sin Ra 2r I 20ωωμπ 5.θtg BL mgRaθtg BLmg由b 向a6. 解:(1) 设线圈转至任意位置时圆线圈的法向与磁场之间的夹角为θ,则通过该圆线圈平面的磁通量为θcos r πB 2=Φ, nt 2t π==ωθ∴nt 2cos r πB 2π=Φ在任意时刻线圈中的感应电动势为nt 2sin n 2r NB td d N2πππ=-=Φε nt 2sin n BNr 222ππ=t Τ2sin I nt 2sin R n NBr 2R i m 2πππ2===E当线圈转过π /2时,t =T /4,则 987.0R /NBn r 2I i 2m ===2π A(2) 由圆线圈中电流I m 在圆心处激发的磁场为==')r 2/(NI B m 0μ 6.20×10-4T 方向在图面内向下,故此时圆心处的实际磁感强度的大小500.0)B B (B 2/1220≈'+= T 方向与磁场B的方向基本相同.解:筒以ω旋转时,相当于表面单位长度上有环形电流π2L Q ω⋅,它和通电流螺线管的nI 等效.按长螺线管产生磁场的公式,筒内均匀磁场磁感强度为: Lπ2Q B 0ωμ=(方向沿筒的轴向)筒外磁场为零.穿过线圈的磁通量为: L2a Q B a π202ωμΦ==在单匝线圈中产生感生电动势为=-=t d d ΦE )t d d (L 2Qa20ωμ-0020Lt 2Qa ωμ= 感应电流i 为 020RLt 2Qa R i ωμ==Ei 的流向与圆筒转向一致.练习一(振动)1.(C ) 2.(B ) 3.(B ) 4. km 2π5. 15×10-2COS (6πt+π/2) 6.(1) t=0时, a=2.5ms -2N 5ma F == (2) 5a max =, 其时1)t 5sin(=-πN 10a m F max max == x=±0.2m7. 由曲线可知A =10cm.t=0 ⎩⎨⎧<-==-=0sin 10cos 105ϕωϕVo Xo ⇒=ϕ32π由图可知质点由位移为Xo =-5cm 和Vo<0的状态,到x =0和V>0的状态所需时间t=2s ,代入方程得 O=10cos (2ω+2π/3)即 2ω+2π/3=3π/2 ∴ ω=5π/12故得 X = 0.1cos (5πt/12+2π/3) (SI )练习二(振动)1. (B)2. (C)3. (A)4. (1) s 19.4T s5.1A /v Av 1m m =⇒==∴=-ωω(2) 222m s /m 105.4A a -⨯==ω(3) )SI ()2/t 5.1cos(02.0x 2/ππφ+==5. (1) 对小物体在竖直方向有 mg-N=ma N=m (g-a )当N=0,即 a=g 时,小物体开始脱离振动物体.已知 A=10cm . =ωmk=50 rad ·s-1∴amax = A ω2= 5ms -2< g 故小物体不会离开.(2)若a max >g 小物体与振动物体分离,开始分离的位置由N=0求得:g= a max = -ω-2x x=-g/ω2=-19.6cm 即在平衡位置上方19.6cm 处开始分离.由 a max =ω2A >g可得 A >g/ω2=19.6cm练习三(振动)1. (E )2.(C )3.43,g l ∆π24.(1)令22P kA 412E kx 21E ===, 则 x 2=A 2/2 ∴)m (54.3A 22x ±=±= (2)令=t ∆ωπ/4,则 43)3/(44t =⨯==ππωπ∆(S ), 5, 解:(1) 由题意 kA F m =,m x A =,m m x F k /=.16.021212===m m m x F kx E J (2) π===2mm m x A vv ω rad /s由 t = 0, φcos 0A x ==0.2 m , 0sin 0<-=φωA v可得 π=31φ则振动方程为)312cos(4.0π+π=t x练习四(振)1. (B)2. (B)3. 5×10-2m 4. 4×10-2m ,2π 5. 依题画出旋转矢量图,由图可知两谐振动的相位差为π/2. 6. 解:设合成运动(简谐振动)的振动方程为 )cos(φω+=t A x 则 )cos(2122122212φφ-++=A A A A A ① 以 A 1 = 4 cm ,A 2 = 3 cm ,π=π-π=-212112φφ代入①式,得5cm 3422=+=A cm又 22112211cos cos sin sin arctg φφφφφA A A A ++= ②≈127°≈2.22 rad ∴)22.22cos(05.0+π=t x (SI)练习五(波)1.(C )2.(B )3. 2π/54. 0.06sin(πt/2-5π/4)5. (1) 由P 点的运动方向,则可判定该波向左传播.对原点O 处质点,t=0时,有⎪⎩⎪⎨⎧<-==0sin A V cos A 2/A 20ϕωϕ∴4πϕ= ∴O 处振动方程为:y 0=Acos (500πt+π/4)波动方程为:y=Acos[2π(250t+x/200)+π/4] (SI ) (2)距O 点100m 处质点振动方程是: y 1=Acos (500πt+5π/4) (SI )振动速度为 V=-500πAsin (500πt+5π/4) (SI ) 6.练习六(波)1. (C)2. (A)3. (D)4. a/b5. 解:(1) O 处质点,t = 0 时 0cos 0==φA y , 0sin 0>-=φωA v 所以 π-=21φ 又 ==u T /λ (0.40/ 0.08) s= 5 s 故波动表达式为 ]2)4.05(2cos[04.0π--π=x t y (SI) (2) P 处质点的振动方程为 ]2)4.02.05(2cos[04.0π--π=t y P )234.0cos(04.0π-π=t (SI) 6. 解:由图,λ = 2 m , 又 ∵u = 0.5 m/s ,∴ ν = 1 /4 Hz ,T = 4 s .题图中t = 2 s =T 21.t = 0时,波形比题图中的波形倒退λ21,见图. 此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动,∴ π=21φ ∴ )2121cos(5.0π+π=t y (SI)练习七(波)1. (B )2. (B )3. R 22/R 21 4. 1.27×10-2Wm -2, 3.18×10-3Wm -25.(1) P=ω/t=2.7×10-3J ·S -1(2) I = P/S = 9.00×10-2Js -1m -2(3)341065.2/--⨯==Jm u I ω6. 已知 A=0.1m , T=1S , λ=8m 波沿x 轴负向传播,则波函数y=0.1cos[2π(t+x/λ)+ϕ]在x=λ/2处有 )t 2cos(1.0y 0ϕππ++=而4/0πϕπ=+ 4/30πϕ-=∴x (m)y (m)0u 0.512t = 0-1∴ 波函数为y=0.1cos[2π(t+x/8)-3π/4]于是有 (1)x=λ/4处的振动方程为 y=0.1cos (2πt-π/4)(2)x=-λ/4处的振动方程为 y=0.1cos (2πt-5π/4)其振动速度为 )45t 2sin(2.0dt dy πππ--= 且 12/T t ms 444.0)45sin(2.0dt dy -==--=πππ练习八(波)1.(D )2. 03. 0.5m4. 4. 相同,相同,2π/35. 解:=-π--=∆)(21212r r λφφφ422412/r r π-=π+π-πλλ464.0)cos 2(2/1212221=++=∆φA A A A A m 6. (1) )/x 2t cos(A y λππω-+= (2) )/x 2/L 4t cos(A y λπλπω+-'='练习九(波)1. (B )2. (B)3. Acos2π(t/T-x/λ),A4. 1×102,0.15.(1)L=3×λ/2, λυ= u ∴L=3u/2υ=(3/2)×(320/400)=1.2m (2)弦的中点是波腹,故 y=3×10-3cos (2πx/0.8)cos (800πt+ϕ) 式中ϕ可由初始条件来选择.6.(1)由图知B 点的初相为ϕ=π,波向x 轴正向 传播,则波动方程为y=cos[2πυ(t-x/u )+π](2)若以反射点为D 为原点,并以此时刻为t=0,由条件X o =0,υ0﹥0, 得ϕ=-π/2则入射波波函数为y 1=Acos[2πυ(t-x/μ)-π/2]因反射点为节点,有半波损失,故反射波的波函数为y 2=Acos[2πυ(t+x/μ)+π/2](3)合成波的波函数为:y= y 1+y 2=2Asin(2πx/λ)cos2πυt 波腹位置:当,2)1K 2(x2,1x2sinπλπλπ+== 4)1k 2(x λ+= (k=0,1,2,····)因原点在反射点,x ﹤0, ∴波腹坐标为x=-λ/4,-3λ/4,-5λ/4,…… 波节位置:当sin(2πx/λ)=0,,2kx ,K x2λπλπ==(k=0,1,2,····)∴波节坐标为 x=0,-λ/2,-λ,-3λ/2,……练习十(波)1. (A)2. ωλSw/2π3. 5π4. 由0Su uννυ-=知驶向观察者时有 440=3300ν/(330-s ν) (1)离开观察者时有 392=3300ν/(330+s ν) (2)两式解得392(330+s ν)=440(330-s ν)。
