(完整word)高中数学双曲线经典例题.doc
(完整word版)双曲线讲义

圆锥曲线第二讲 双曲线一 双曲线的定义平面内到两个定点12,F F 的距离之差的绝对值等于常数2a (小于12F F )的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点.两焦点之间的距离叫做双曲线的焦距.注:(1)定义中的限制条件1202a F F <<.当122a F F =时,点的轨迹是分别以12,F F 为端点的两条射线;当122a F F >时,轨迹不存在;当20a =时,点的轨迹是线段12F F 的垂直平分线.(2)定义中的绝对值必不可少.若没有绝对值符号则点的轨迹表示双曲线的一支.例 1 已知1(5,0)F -,2(5,0)F ,动点P 满足122PF PF a -=,当a 为3和5时,P 的轨迹分别是_________.双曲线的一支和一条射线.例2 已知点(,)P x y 的坐标满足下列条件,是判断下列各条件下点P 的轨迹是什么图形:(16=;(26=练习1 已知平面上定点1F ,2F 及动点M ,命题甲:22()MF MF a a -=为常数,命题乙:M 点轨迹是以1F ,2F 为焦点的双曲线,则甲是乙的____条件.必要不充分条件练习2 若平面内一动点(,)P x y 到两定点1(1,0)F -,2(1,0)F 的距离之差的绝对值为定值(0)a a ≥,讨论点P 的轨迹方程.二 双曲线的标准方程(1)设(,)M x y 是双曲线上任意一点,焦点1F ,2F 的坐标分别为(,0)c -,(,0)c ,M 与1F 和2F 的距离之差的绝对值等于常数2(0)a c a >>,则双曲线的标准方程为 :22221(0,0)x y a b a b-=>>其中:①222c a b =+; ②a c b c <<且,a 和b 大小关系不明确(2)设(,)M x y 是双曲线上任意一点,焦点1F ,2F 的坐标分别为(0,)c ,(0,)c -,M 与1F 和2F 的距离之差的绝对值等于常数2(0)a c a >>,则双曲线的标准方程为 :22221(0,0)y x a b a b-=>>其中:①222c a b =+; ②a c b c <<且,a 和b 大小关系不明确例1 若方程22123x y m m +=--表示双曲线,则实数m 的取值范围为______.(3,2)(3,)-+∞U例2 若1k >,则关于,x y 的方程222(1)1k x y k -+=-所表示的曲线是____.焦点在y 轴上的双曲线.例3 方程221cos 2010sin 2010x y ︒︒-=所表示的曲线为_______.焦点在y 轴上的双曲线.练习1 若方程2221523x y m m m +=---表示焦点在y 轴上的双曲线,则实数m 的取值范围为_____.(5,)+∞练习2 已知双曲线2288kx ky -=的一个焦点为(0,3),则k =_____.-1三 双曲线的定义及其标准方程的应用例1 若12,F F 是双曲线221916x y -=的两个焦点,若双曲线上一点M 到它的一个焦点的距离等于16,则点M 到另一个焦点的距离为____(4或28),若P 是双曲线左支上的点,且1232PF PF =g ,则12F PF V 的面积为_____.16例2 在ABC V 中,,,a b c 为其三边边长,点B ,C 的坐标分别为(1,0)B -,(1,0)C ,则满足1sin sin sin 2C B A -=的顶点A 的轨迹方程为______.224141()32x y x -=>例 3 已知(3,0)M -,(3,0)N ,(1,0)B ,动圆C 与直线MN 切于点B ,过,M N 与圆C 相切的两直线相交于P ,则点P 的轨迹方程为________.221(1)8y x x -=>例4 已知F 是双曲线221412x y -=的左焦点,点(1,4)A ,P 是双曲线右支上的动点,则PF PA +的最小值为_____.9练习1在平面直角坐标系xoy 中,已知ABC V 的顶点(6,0),(6,0)A C -,若顶点B在双曲线2212511x y -=的左支上,则sin sin sin A C B -=______.56练习2若点P 是以(A B 为焦点,实轴长为2210x y +=的一个交点,则PB PA +的值为______.例3 已知2225:(2)4A x y ++=e ,221:(2)4B x y -+=e ,动圆P 与A e ,B e 都外切,则动圆P 圆心的轨迹方程为_____.221(0)3y x x -=>练习4 已知双曲线的方程2214y x -=,点A 的坐标为(0),B 是圆2x +2(1y =上的点,点C 为其圆心,点M 在双曲线的右支上,则MA MB +的最小值为1四 双曲线的简单几何性质注:(1)标准方程中参数,,a b c ,其中c 最大,,a b 大小关系不确定.(2)我们把ce a=称为双曲线的离心率且1e >.22221x y a b -=的渐近线方程为b y x a=±.(3)如果12,F F 是双曲线的两个焦点,P 是双曲线上的任意一点,则121cos 1F PF -≤∠<.(求离心率的范围)(4)122PF PF c +≥,122PF PF c -<.(求离心率范围)(5)等轴双曲线:虚轴长和实轴长相等的双曲线.等轴双曲线的离心率e =(6)共轭双曲线:两个实轴和虚轴互为对调的双曲线称为共轭双曲线.三 双曲线的定义练习(5.3)已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=,与222222:1sin sin tan y x C θθθ-=的()D .A 实轴长相等 .B 虚轴长相等 .C 焦距相等 .D 离心率相等 四 双曲线标准方程的求解(先定位后定量)例1(调研)设双曲线与椭圆2212736x y +=有共同的焦点,且与椭圆相交,一个交点的坐标为4),则此双曲线的标准方程是______.22145y x -=例2 (调研)已知双曲线的渐近线方程为230x y ±=,(0,5)F -为双曲线的一个焦点,则双曲线的标准方程为________.22131********y x -= 练习1(简单)设椭圆1C 的离心率为513,焦点在x 轴上且长轴长为26.若曲线2C 上的点到椭圆的两个焦点的距离之差的绝对值等于8,则曲线2C 的标准方程为_______.221169x y -= 例2(5.3)已知双曲线:C 22221x y a b -=的焦距为10,点(2,1)P 在C 的渐近线上,则C 的方程为_______.221205x y -= 五 双曲的简单几何性质双曲线的几何性质的实质是围绕双曲线中的“六点”(两个焦点,两个定点,两个虚轴的端点),“四线”(两条对称轴,两条渐近线),“两形”(中心,焦点以及虚轴端点构成的三角形,双曲线是一点和两个焦点构成的三角形)研究它们之间的相互关系.例 1(简单)设双曲线22221x y a b-=,的虚轴长为2,焦距为近线的方程为_______.y x =例2(练透)已知双曲线22221x y a b-=的离心率为2,则双曲线的渐近线方程为_____.12y x =±.练习1(调研)设12,F F 是双曲线22124y x -=的两个焦点,P 是双曲线上的一点,1234PF PF =,则12PF F V 的面积等于_____.24例2(简单)若直线1y kx =+与双曲线221916y x -=的一条渐近线垂直,则实数k=____.43±六 双曲线的离心率 离心率的取值问题例1(练透)12,F F 是双曲线:C 22221x y a b-=的左右焦点,过1F 的直线l 与C 的左右两支分别交于,A B 两点,若22::3:4:5AB BF AF =,则双曲线的离心率为例2(练透)过双曲线2222:1(0,0)x y C a b a b-=>>的一个焦点F 作双曲线的一条渐近线的垂线,若垂足恰好在线段OF 的垂直平分线,则双曲线的离心率为____.练习1(练透)设12,F F 是双曲线2222:1(0,0)A x y C a b a b-=>>的两个焦点,P 是C 上的一点,若126PF PF a +=,且12PF F V 的最小内角为30︒,则C 的离心率为练习2(练透) 设12,F F 分别为双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,A 为双曲线的左顶点,以12,F F 为直径的圆交双曲线的某条渐近线于,M N 两点,且满足120MAN ︒∠=,则该双曲线的离心率为________.3练习3(练透)设12,F F 分别是双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,若双曲线右支上存在一点P ,使得22()0OP OF F P +=u u u r u u u u r u u u u rg ,O为坐标原点,且12PF =u u u r u u u r,则该双曲线的离心率为1离心率的范围问题双曲线的离心率范围问题主要考查两点:(1)利用三角形的三边关系得到关于,a c 的齐次不等式,解不等式得到离心率范围.(2)若果12,F F 是双曲线的两个焦点,P 是双曲线上的任意一点,则121cos 1F PF -≤∠<.通过余弦定理得到关于,a c 的齐次不等式,解不等式得到离心率范围.例1 (调研)已知双曲线2222:1(0,0)A x y C a b a b-=>>的左右焦点为12,F F ,点P在双曲线的右支上,且124PF PF =,则此双曲线的离心率e 的最大值为_____.53. 例2(调研)已知(1,2),(1,2)A B -,动点P 满足AP BP ⊥u u u r u u u r ,若双曲线22221x y a b-=的渐近线与动点P 的轨迹没有公共点,则双曲线离心率的取值范围是____.12e <<练习1(5.3)已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为12,F F ,P 为双曲线右支上任意一点,若212PF PF 的最小值为8a ,则双曲线的离心率的取值范围是_____.(1,3]练习2(练透)点P 是双曲线22221(0,0)x y a b a b-=>>左支上的一点,其右焦点为(,0)F c ,若M 为线段FP 的中点,且M 到坐标原点的距离为8c,则双曲线的离心率取值范围是_______.4(1,]3练习3(练透)已知点F 是双曲线22221(0,0)x y a b a b-=>>的左焦点,点E 是右顶点,过F 且垂直于x 轴的直线与双曲线交于,A B 两点,若ABE V 是锐角三角形,则双曲线的离心率取值范围为______.(1,2) 七 双曲线的综合问题例1 (练透)设双曲线22143x y -=的左右焦点分别为12,F F ,过1F 的直线l 交双曲线左支于,A B 两点,则22BF AF +的最小值为____.11。
《双曲线》练习题经典(含答案)

2, 1.
消去
y
得:(λ+2)x2-4
2x+4-λ=0.
∵方程组有两解,∴λ+2≠0 且 Δ>0,
4-λ ∴λ>2 或 λ<0 且 λ≠-2,x1·x2=λ+2,
3(4-λ)
uuur uuur 而 MAgMB =x1x2+(y1+2)·(y2+2)=x1x2+ 2x1· 2x2=3x1x2= λ+2 ,
4-λ 3
y2
∴λ+2=-2,解得 λ=-14.∴曲线 C 的方程是 x2-14=1.
31.(本题满分 12 分) 已知中心在原点的双曲线 C 的右焦点为 2, 0,右顶点为 3, 0 .
(Ⅰ)求双曲线 C 的方程
uuur uuur (Ⅱ)若直线 l : y kx 2 与双曲线恒有两个不同的交点 A 和 B 且 OA OB 2 (其中 O 为原点),求 k 的
3.在平面直角坐标系中,双曲线 C 过点 P(1,1),且其两条渐近线的方程分别为 2x+y=0 和 2x﹣y=0,则双曲 线 C 的标准方程为( B )
A.
B.
C.
或
D.
x2
y2
x2 y2
4.已知椭圆 2a 2 + 2b 2 =1(a>b>0)与双曲线 a 2 - b 2 =1 有相同的焦点,则椭圆的离心率为( A )
为 ,则双曲线的离心率为( A )
A.2 B.
C.
D.
7.已知双曲线
y2 a2
x2 9
1 的两条渐近线与以椭圆 x2 25
y2 9
1
的左焦点为圆心、半径为
16 5
的圆相切,则双曲
线的离心率为( A )
A. 5 B. 5 C. 4 D. 6
高中数学 双曲线范例例题共42页

1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,教育 最重要 的部分 。—— 陈鹤琴
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
42
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
高三数学2轮复习精选试题汇编:双曲线 Word版含答案

双曲线一、选择题1 .双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为12,F F ,在双曲线右支上存在一点P 满足12PF PF ⊥且126PF F π∠=,那么双曲线的离心率是( )A .2B .3C .31+D .51+2 .设F 是抛物线)0(2:21>=p px y C 的焦点 ,点A 是抛物线与双曲线22222:by a x C - =1)0,0(>>b a 的一条渐近线的一个公共点 ,且x AF ⊥轴 ,那么双曲线的离心率为( )A .2B .3C .25D .53. 双曲线1412222222=+=-by x y x 的准线经过椭圆 (b >0 )的焦点 ,那么b = A.3 B.5 C.3 D.24. 设双曲线()222200x y a b a b-=1>,>的渐近线与抛物线21y =x +相切 ,那么该双曲线的离心率等于(A )3 (B )2 (C )5 (D )6 5.双曲线的两条渐近线与直线围成一个三角形区域 ,表示该区域的不等式组是 ( )A. B. C. D.6. 假设双曲线的两焦点为F 1、F 2 ,以F 1F 2为直径的圆与双曲线交于A 、B 、C 、D ,假设此6点构成正六边形 ,那么双曲线的离心率为 ( ) A . B .C .D .7.双曲线的右焦点为F ,假设过点F 且倾斜角为的直线与双曲线的右支有且只有一个交点 ,那么此双曲线离心率的取值范围是 (A )(B )(C )(D )8.假设双曲线上的点到左准线的距离是到左焦点距离的 ,那么(A) (B) (C) (D)9. 在正△ABC 中 ,D ∈AB ,E ∈AC ,向量 ,那么以B ,C 为焦点 ,且过D ,E 的双曲线的离心率为 ( )A .B .C .D .10.如图 ,B 地在A 地的正东方向4 km 处 ,C 地在B 地的北偏东30º方向2 km 处 ,河流的没岸PQ (曲线 )上任意一点到A 的距离比到B 的距离远2 km .现要在曲线PQ 上选一处M 建一座码头 ,向B 、C 两地转运货物 .经测算 ,从M 到B 、M 两地修建公路的费用分别是a 万元/km 、2a 万元/km ,那么修建这两条公路的总费用最|低是 (A )(2 -2)a 万元 (B )5a 万元 (C )(2+1)a 万元 (D )(2+3)a 万元11.双曲线2221(0)2x y b b -=>的左右焦点分别为12,F F ,其一条渐近线方程为y x = ,点0(3,)P y 在该双曲线上 ,那么12PF PF • =A. 12-B. 2- C .0 D. 412.双曲线24x-212y=1的焦点到渐近线的距离为(A )23(B )2 (C )3(D )1二、填空题13.过双曲线左焦点的直线交曲线的左支于两点 ,为其右焦点 ,那么的值为______.14.双曲线的顶点到渐近线的距离为2 ,焦点到渐近线的距离为6 ,那么该双曲线的离心率为.15. 点P (-1 ,-3 )在双曲线的左准线上 ,过点P且方向为的光线经直线y =2反射后通过双曲线的左焦点 ,那么此双曲线的离心率为 .16. 假设双曲线的渐近线方程为 ,那么实数的值为_________.三、解答题17.设双曲线C:相交于两个不同的点A、B.(I )求双曲线C的离心率e的取值范围:(II )设直线l与y轴的交点为P ,且求a的值.18.双曲线的中|心在原点 ,右顶点为A (1 ,0 )点P、Q在双曲线的右支上 ,支M (m,0 )到直线AP的距离为1 .(Ⅰ )假设直线AP的斜率为k ,且 ,求实数m的取值范围;(Ⅱ )当时 ,ΔAPQ的内心恰好是点M ,求此双曲线的方程 .19.双曲线 ,为上的任意点 .(1 )求证:点到双曲线的两条渐近线的距离的乘积是一个常数; (2 )设点的坐标为,求的最|小值;20.某中|心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响 ,正东观测点听到巨响的时间比其他两个观测点晚 ,各观测点到中|心的距离都是,试确定该巨响的位置 . (假定当时声音传播的速度为,各相关点均在同一平面上 )答案一、选择题1. C因为12PF PF ⊥且126PFF π∠= ,所以21,3PF c PF c =,又1232PF PF c c a --= ,所以22(31)31(31)(31)c a +===-+ ,即双曲线的离31 ,选C.2. D解:由题意知(,0)2p F ,不妨取双曲线的渐近线为b y x a = ,由22b y xa y px⎧=⎪⎨⎪=⎩得222pa x b =.因为x AF ⊥ ,所以2A p x = ,即2222pa p x b == ,解得224b a = ,即22224b a c a ==- ,所以225c a = ,即25e = ,所以离心率5e = ,选D.3. C详细分析:可得双曲线的准线为21a x c=±=±,又因为椭圆焦点为2(4,0)b ±-所以有241b -=.即b 2 =3故b =3.故C.4. C5. 答案:A 详细分析:双曲线的两条渐近线方程为,与直线围成一个三角形区域时有 .应选A6. 答案:A7. 答案:C详细分析:双曲线的右焦点为F ,假设过点F 且倾斜角为的直线与双曲线的右支有且只有一个交点 ,那么该直线的斜率的绝|对值小于等于渐近线的斜率,∴ ≥,离心率e 2 = ,∴ e ≥2 ,选C.8. 答案:C详细分析:由题离心率 ,由双曲线的第二定义知,应选择C .【名师点拔】此题在条件中有意识的将双曲线第二定义 "到左焦点距离与到左准线的距离是定值〞中比的前后项颠倒为 "到左准线的距离是到左焦点距离的〞 ,如此题改为填空题 ,没有了选择支的提示 ,那么难度加大 .【考点分析】此题考查双曲线的第二定义 ,根底题 . 9. 答案:D10. 答案:B 11. C详细分析:由题知22=b ,故)0,2(),0,2(,123210F F y -±=-±= , ∴0143)1,32()1,32(21=+-=±-•±--=•PF PF ,应选择C .解析2:根据双曲线渐近线方程可求出双曲线方程22122x y -= ,那么左、右焦点坐标分别为12(2,0),(2,0)F F - ,再将点0(3,)P y 代入方程可求出(3,1)P ± ,那么可得120PF PF ⋅= ,应选C .12. A详细分析:双曲线24x -212y =1的焦点(4,0)到渐近线3y x =的距离为34023d ⨯-==,选A二、填空题13. 答案:8详细分析:根据双曲线定义有|MF 2| -|MF| =2a ,|NF 2| -|NF| =2a ,两式相加得|MF 2| +|NF 2| -|MN| =4a =8点评:此题主要考查双曲线定义的灵活运用 . 14. 答案:3详细分析:如图 ,过双曲线的顶点A 、焦点F 分别向其渐近线作垂线 ,垂足分别为B 、C ,那么:15. 答案:16. 答案:三、解答题17. 详细分析: (I )由C与t相交于两个不同的点 ,故知方程组有两个不同的实数解.消去y并整理得(1-a2 )x2 +2a2x-2a2 =0. ①双曲线的离心率(II )设由于x1 +x2都是方程①的根 ,且1-a2≠0 ,18. 详细分析:(Ⅰ)由条件得直线AP的方程(即.又因为点M到直线AP的距离为1,所以得.∵∴≤≤2,解得+1≤m≤3或- -1≤m≤1 - -.∴m的取值范围是(Ⅱ)可设双曲线方程为由得.又因为M是ΔAPQ的内心,M到AP的距离为1,所以∠MAP =45º,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1 .因此 , (不妨设P在第|一象限 )直线PQ方程为 .直线AP的方程y =x -1,∴解得P的坐标是 (2 + ,1 + ) ,将P点坐标代入得 ,所以所求双曲线方程为即19. (1 )设是双曲线上任意一点 ,该双曲的两条渐近线方程分别是和.点到两条渐近线的距离分别是和 ,…它们的乘积是.点到双曲线的两条渐线的距离的乘积是一个常数. ……(2 )设的坐标为 ,那么…,当时 ,的最|小值为 ,即的最|小值为. …20. 详细分析:如图 ,以接报中|心为原点O ,正东、正北方向为x轴、y轴正向 ,建立直角坐标系.设A、B、C分别是西、东、北观测点 ,那么A (-1020 ,0 ) ,B (1020 ,0 ) ,C (0 ,1020 )设P (x,y )为巨响为生点 ,由A、C同时听到巨响声 ,得|PA| =|PB| ,故P在AC的垂直平分线PO上 ,PO的方程为y =-x ,因B点比A点晚4s听到(爆|炸)声 ,故|PB|-|PA| =340×4 =1360由双曲线定义知P点在以A、B为焦点的双曲线上 ,依题意得a =680, c =1020 ,用y =-x代入上式 ,得 ,∵|PB|>|PA|,答:巨响发生在接报中|心的西偏北450距中|心处.。
双曲线 Word版含解析

课时规范练A 组 基础对点练1.(2018·新余摸底)双曲线x 2a 2-y 24a 2=1(a ≠0)的渐近线方程为( ) A .y =±2x B.y =±12x C .y =±4xD.y =±2x2.(2018·开封模拟)已知l 是双曲线C :x 22-y 24=1的一条渐近线,P 是l 上的一点,F 1,F 2是C 的两个焦点,若PF 1→·PF 2→=0,则P 到x 轴的距离为( ) A.233 B. 2 C .2D.2633.双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为y =2x ,则双曲线C 的离心率是( ) A. 5 B. 2 C .2D.524.(2018·贵阳期末)已知双曲线C 的两个焦点F 1,F 2都在x 轴上,对称中心为原点O ,离心率为 3.若点M 在C 上,且MF 1⊥MF 2,M 到原点的距离为3,则C 的方程为( ) A.x 24-y 28=1 B.y 24-x 28=1 C .x 2-y 22=1D.y 2-x 22=15.若双曲线C 1:x 22-y 28=1与C 2:x 2a 2-y 2b 2=1(a >0,b >0)的渐近线相同,且双曲线C 2的焦距为45,则b =( ) A .2 B.4 C .6D.86.(2018·德州模拟)在平面直角坐标系中,经过点P (22,-2)且离心率为3的双曲线的标准方程为( ) A.x 24-y 22=1 B.x 27-y 214=1 C.x 23-y 26=1D.x 214-y 27=17.(2016·高考天津卷)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的焦距为25,且双曲线的一条渐近线与直线2x +y =0垂直,则双曲线的方程为( ) A.x 24-y 2=1 B.x 2-y 24=1C.3x 220-3y 25=1D.3x 25-3y 220=18.若双曲线E :x 29-y 216=1的左,右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|=3,则|PF 2|等于( ) A .11 B.9 C .5D.39.(2018·洛阳统考)若圆锥曲线C :x 2+λy 2=1的离心率为2,则λ=10.(2018·福州模拟)已知直线y =kx -1和双曲线x 2-y 2=1的右支交于不同两点,则k 的取值范围是 k < 2.11.双曲线Γ:y 2a 2-x 2b 2=1(a >0,b >0)的焦距为10,焦点到渐近线的距离为3,则Γ的实轴长等于____.12.已知抛物线y 2=8x 与双曲线x 2a 2-y 2=1(a >0)的一个交点为M ,F 为抛物线的焦点,若|MF |=5,则该双曲线的渐近线方程为B 组 能力提升练1.已知A ,B 分别为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为( ) A. 5 B.2 C. 3D. 22.(2016·高考全国卷Ⅱ)已知F 1,F 2是双曲线E :x 2a 2-y 2b 2=1的左,右焦点,点M在E 上,MF 1与x 轴垂直,sin ∠MF 2F 1=13,则E 的离心率为( ) A. 2 B.32 C. 3D.23.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点是F ,左,右顶点分别是A 1,A 2,过F 作A 1A 2的垂线与双曲线交于B ,C 两点.若A 1B ⊥A 2C ,则该双曲线的渐近线的斜率为( ) A .±12 B.±22 C .±1D.±24.(2018·广州调研)在平面直角坐标系xOy 中,设F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点,P 为双曲线C 的右支上一点,且△OPF 为正三角形,则双曲线C 的离心率为( ) A .1+ 3 B. 3 C.233D.2+ 35.设双曲线x 2a 2-y 2b 2=1(b >a >0)的半焦距为c ,且直线l 过(a,0)和(0,b )两点.已知原点到直线l 的距离为3c4,则双曲线的离心率为( ) A.223 B. 2 C. 3D.26.过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点与对称轴垂直的直线与渐近线交于A ,B 两点,若△OAB 的面积为13bc3,则双曲线的离心率为( )A.52B.53C.132D.1337.如图,F 1,F 2分别是双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,过F 1的直线l 与双曲线的左、右两支分别交于点B ,A .若△ABF 2为等边三角形,则双曲线的离心率为( )A.7B.4C.233D. 38.已知P 是双曲线x 23-y 2=1上任意一点,过点P 分别作双曲线的两条渐近线的垂线,垂足分别为A ,B ,则P A →·PB →的值是( ) A .-38 B.316 C .-38D.不能确定9.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)与函数y =x 的图象交于点P ,若函数y =x 的图象在点P 处的切线过双曲线左焦点F (-2,0),则双曲线的离心率是( ) A.5+12B. 2C.3+12D.3210.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)满足条件:(1)焦点为F 1(-5,0),F 2(5,0);(2)离心率为53,求得双曲线C 的方程为f (x ,y )=0.若去掉条件(2),另加一个条件求得双曲线C 的方程仍为f (x ,y )=0,则下列四个条件中,符合添加条件的共有( )①双曲线C 上的任意一点P 都满足||PF 1|-|PF 2||=6; ②双曲线C 的虚轴长为4;③双曲线C 的一个顶点与抛物线y 2=6x 的焦点重合;④双曲线C 的渐近线方程为4x ±3y =0. A .1个 B.2个 C .3个D.4个11.(2016·高考浙江卷)设双曲线x 2-y 23=1的左,右焦点分别为F 1,F 2.若点P 在双曲线上,且△F 1PF 2为锐角三角形,则|PF 1|+|PF 2|的取值范围是12.(2018·郑州质检)已知双曲线C :x 2a 2-y 2b 2=1的右焦点为F ,过点F 向双曲线C的一条渐近线引垂线,垂足为M ,交另一条渐近线于N ,若2MF →=FN →,则双曲线C 的渐近线方程为13.(2018·湖北八校联考)我国南北朝时期的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”是几何体的高,“幂”是截面面积.其意:如果两个等高的几何体在同高处的截面面积恒等,那么这两个几何体的体积相等.已知双曲线C 的渐近线方程为y =±2x ,一个焦点为(5,0).直线y =0与y =3在第一象限内与双曲线及渐近线围成如图所示的图形OABN ,则它绕y 轴旋转一圈所得几何体的体积为____.14.(2016·高考山东卷)已知双曲线E :x 2a 2-y 2b 2=1(a >0,b >0).若矩形ABCD 的四个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB |=3|BC |,则E 的离心率是____.。
双曲线函数的最值问题举例(附练习、答案)

双曲线函数的最值问题举例(附练习、答案)双曲线函数是数学中常见的一类函数,对于这类函数的最值问题,我们可以通过一些实际例子来加深理解。
下面提供了一些练题和相应的答案,帮助读者更好地掌握双曲线函数的最值问题。
练题1. 设函数 $f(x) = e^x - e^{-x}$,求函数 $f(x)$ 在定义域内的最小值和最大值。
2. 函数 $g(x) = \sinh(x)$ 在 $[-1, 1]$ 区间上是增函数还是减函数?并求其最小值和最大值。
3. 对于任意正实数 $a$,函数 $h(x) = \cosh(ax)$ 在定义域内的最大值是否存在?如果存在,是多少?答案1. 解答:首先求函数的一阶导数:$$f'(x) = e^x + e^{-x}$$然后求导数为零的点,即:$$e^x + e^{-x} = 0$$由于 $e^x$ 恒大于零,所以 $e^x + e^{-x}$ 恒大于零,即不存在导数为零的点。
因此函数 $f(x)$ 在定义域内没有极值点,也就是没有最小值和最大值。
2. 解答:首先求函数的一阶导数:$$g'(x) = \cosh(x)$$函数 $g(x)$ 的一阶导数为 $\cosh(x)$,根据双曲函数的性质可知 $\cosh(x) > 0$,即在定义域内函数 $g(x)$ 是增函数。
当 $x = 0$ 时,$\sinh(0) = 0$,所以函数 $g(x)$ 在 $[-1, 1]$ 区间上最小值为 0。
当 $x = 1$ 时,$\sinh(1) \approx 1.1752$,所以函数 $g(x)$ 在$[-1, 1]$ 区间上最大值为约 1.1752。
3. 解答:函数 $h(x) = \cosh(ax)$ 为双曲余弦函数,其定义域为实数集。
双曲余弦函数的最大值为 $\cosh(0) = 1$,当且仅当 $ax = 0$ 时取到最大值。
因此,函数 $h(x)$ 在定义域内的最大值为 1。
(完整word版)打印双曲线基础训练题(含答案),推荐文档

双曲线基础训练题(一)1.到两定点()0,31-F 、()0,32F 的距离之差的绝对值等于6的点M 的轨迹 ( D )A .椭圆B .线段C .双曲线D .两条射线2.方程11122=-++k y k x 表示双曲线,则k 的取值范围是(D ) A .11<<-k B .0>k C .0≥k D .1>k 或1-<k3. 双曲线14122222=--+m y m x 的焦距是( C ) A .4 B .22 C .8 D .与m 有关4.已知m,n 为两个不相等的非零实数,则方程m x -y+n=0与n x 2+my 2=mn 所表示的 曲线可能是 ( C )5.焦点为()6,0,且与双曲线1222=-y x 有相同的渐近线的双曲线方程是( B )A .1241222=-y xB .1241222=-x yC .1122422=-x yD .1122422=-y x6.若a k <<0,双曲线12222=+--k b y k a x 与双曲线12222=-by a x 有 ( D )A .相同的虚轴B .相同的实轴C .相同的渐近线D . 相同的焦点7.过双曲线191622=-y x 左焦点F 1的弦AB 长为6,则2ABF ∆(F 2为右焦点)的周长是( A )A .28B .22C .14D .128.双曲线方程为152||22=-+-ky k x ,那么k 的取值范围是 ( D )A .k >5B .2<k <5C .-2<k <2D .-2<k <2或k >59.双曲线的渐近线方程是y=±2x ,那么双曲线方程是( D )A .x 2-4y 2=1 B .x 2-4y 2=1 C .4x 2-y 2=-1 D .4x 2-y 2=110.设P 是双曲线19222=-y a x 上一点,双曲线的一条渐近线方程为1,023F y x =-、F 2分别是双曲线的左、右焦点,若3||1=PF ,则=||2PF(C )A .1或5B . 6C . 7D . 911.已知双曲线22221,(0,0)x y a b a b-=>>的左,右焦点分别为12,F F ,点P 在双曲线的右支上,且12||4||PF PF =,则双曲线的离心率e 的最大值为 ( B )A .43B .53C .2D .7312.设c 、e 分别是双曲线的半焦距和离心率,则双曲线12222=-by a x (a>0, b>0)的一个顶点到它的一条渐近线的距离是 ( D )A .caB .c bC .ea D .eb 13.双曲线)1(122>=-n y nx 的两焦点为F 1,F 2,P 在双曲线上,且满足|PF 1|+|PF 2|=,22+n 则△PF 1F 2的面积为 ( B )A .21 B .1 C .2 D .414.二次曲线1422=+my x ,]1,2[--∈m 时,该曲线的离心率e 的取值范围是( C )A .]23,22[B .]25,23[C .]26,25[D .]26,23[15.直线1+=x y 与双曲线13222=-y x 相交于B A ,两点,则AB =_____6416.设双曲线12222=-by a x 的一条准线与两条渐近线交于A 、B 两点,相应的焦点为F ,若以AB 为直径的圆恰好过F17.双曲线122=-by ax 的离心率为5,则a :b= 4或4118.求一条渐近线方程是043=+y x ,一个焦点是()0,4的双曲线标准方程,并求此双曲线的离心率.(12分)[解析]:设双曲线方程为:λ=-22169y x ,∵双曲线有一个焦点为(4,0),0>∴λ双曲线方程化为:2548161691169222=⇒=+⇒=-λλλλλy x ,∴双曲线方程为:1251442525622=-y x ∴455164==e .19.(本题12分)已知双曲线12222=-by a x 的离心率332=e ,过),0(),0,(b B a A -的直线到原点的距离是.23求双曲线的方程; [解析]∵(1),332=a c 原点到直线AB :1=-by a x 的距离.3,1.2322==∴==+=a b c ab b a ab d .故所求双曲线方程为 .1322=-y x双曲线基础练习题(二)一. 选择题1.已知双曲线的离心率为2,焦点是(4,0),(4,0)-,则双曲线的方程是A. 221412x y -=B. 221124x y -= C. 221106x y -= D. 221610x y -=2.设椭圆1C 的离心率为513,焦点在x 上,长轴长为26,若曲线2C 上的点到椭圆1C 的两个焦点距离差的绝对值等于8,则曲线2C 的标准方程是A. 2222143x y -=B. 22221135x y -=C. 2222134x y -= D. 222211312x y -=3. 已知双曲线22221x y a b -=的一条渐近线方程为43y x =,则双曲线的离心率等于A .53B .43C .54D .324. 已知双曲线22112x y n n+=-,则n = A.2- B .4 C.6 D.8-5.设1F 、2F 是双曲线22221x y a b-=的两个焦点,若1F 、2F 、(0,2)P b 是正三角形的三个顶点,那么其离心率是A.32 B. 52C. 2D. 3 6.已知双曲线2239x y -=,则双曲线右支上的点P 到右焦点的距离与点P 到右准线距离之比等于A C. 2 D.4 7.如果双曲线22142x y -=上一点P 到双曲线右焦点的距离是2,那么点P 到y 的距离是A.B. C. D. 8.设12F F ,是双曲线22221x y a b-=的左、右焦点,若其右支上存在一点P 使得1290F PF ∠=o,且12PF =,则e =A.B. 1C.D . 19. 若双曲线22221x y a b-=的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是A .3B .5C D10. 设ABC △是等腰三角形,120ABC ∠=o ,则以A B ,为焦点且过点C 的双曲线的离心率为A .221+ B .231+ C .21+D .31+11. 双曲线22221x y a b-=的左、右焦点分别是12F F ,,过1F 作倾斜角为30o的直线交双曲线右支于M 点,若2MF 垂直于x 轴,则双曲线的离心率为 ABCD .312. 设1,a >则双曲线22221(1)x y a a -=+的离心率e 的取值范围是A .B .C .(25),D .(213.已知双曲线()222102x y b b-=>的左、右焦点分别为1F 、2F ,它的一条渐近线方程为y x =,点0)P y 在该双曲线上,则12PF PF =u u u r u u u u rgA .12-B .2-C .0D .414.双曲线22221x y a b-=的两个焦点为1F 、2F ,若P 为其上一点,且122PF PF =,则离心率e 的取值范围是A .(1),3B .(1,3]C .(3)∞,+D .)+[3,∞15.设P 为双曲线22112y x -=上一点,1F 、2F 是双曲线的两个焦点,若1PF :2PF =3:2,则12PF F ∆的面积为A .B .12C .D .2416.设1F 、2F 是双曲线2219y x -=的左、右焦点,P 为该双曲线上一点,且120PF PF =u u u r u u u u r g ,则12PF PF +=u u u r u u u u rA .B .CD .二.填空题17.已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线方程是y x =,若顶点到渐近线的距离为1,则双曲线方程为18.以1(60)F -,,2(60)F ,为焦点,离心率2e =的双曲线的方程是19.中心在原点,一个焦点是1(30)F -,20y ±=的双曲线的方程为20.过点(20)N ,且与圆2240x y x ++=外切的动圆圆心的轨迹方程是21.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 22. 已知双曲线22291(0)ym x m -=>的一个顶点到它的一条渐近线的距离为15,则m =23.已知双曲线2221(2x y a a -=>的两条渐近的夹角为3π,则双曲线的离心率为24.已知双曲线22221x y a b -=的右焦点为F ,右准线与一条渐近线交于点A ,OAF ∆的面积为22a ,(O 为坐标原点),则该双曲线的两条渐近线的夹角为25.过双曲线22143x y -=左焦点1F 的直线交双曲线的左支于M N ,两点,2F 为其右焦点,则22MF NF MN+-=26. 若双曲线22221x y a b-=的右支上存在一点,它到右焦点及左准线的距离相等,则e 取值范围是27..P是曲线22221x y a b-=的右支上一点,F为其右焦点,M 是右准线:x l 与x 轴的交点,若60,PMF ∠=o 45PFM ∠=o ,则双曲线方程是28.过双曲线221916x y -=的右焦点F 且平行双曲线的一条渐近线的直线与双曲线交于点B, A 为右顶点,则FAB ∆的面积等于 三.解答题29.分别求满足下列条件的双曲线方程(1)中心在原点,一条准线方程是x=,离心率e =(2)中心在原点,离心率e =30.已知双曲线22221(00)x y C a b a b-=>>:,的两个焦点为1(20)F -,,2(20)F ,,点(3P 在双曲线C 上.⑴求双曲线C 的方程; ⑵记O 为坐标原点,过点(02)Q ,的直线l 与双曲线C 相交于不同的两点E F ,,若OEF =△S l 方程.双曲线练习题答案(二)一.选择题1.A 2. A3.A4. B 5. C6.C7.A8D9. D10. B11. B12. B13.C14.B15.B16B 二.填空题17.223144x y-=18.221927x y-=19.22145x y-=20.()22113yx x-=≥21.322.423.324.2π25.826.(11⎤⎦27.2211260x y-=28.3215二.解答题29.分别求满足下列条件的双曲线方程(1)中心在原点,一条准线方程是5x=,离心率e=2214yx-=(2)中心在原点,离心率2e=顶点到渐近线的距离为5;2214xy-=30. 已知双曲线22221(00)x yC a ba b-=>>:,的两个焦点为1(20)F-,,2(20)F,,点(3P在双曲线C上.⑴求双曲线C的方程;⑵记O为坐标原点,过点(02)Q,的直线l与双曲线C相交于不同的两点E F,,若OEF=△S l方程.⑴解略:双曲线方程为22122x y-=.⑵解:直线:l2y kx=+,代入双曲线C的方程并整理,得22(1)460k x kx---=. ①Q直线l与双曲线C相交于不同的两点E F,,222110(4)46(1)0kkkk k≠±⎧⎧-≠⎪⎪∴⇔⎨⎨<<∆=-+⨯->⎪⎪⎩⎩,,,,(1)(11)(1k∴∈--U U,.②设1122()()E x yF x y,,,,则由①式得12241kx xk+=-,12261x xk=--,EF ∴21k -而原点O 到直线l 的距离d =1122OEFS d EF ∴=⋅==△.若OEFS =△,即422201k k k=⇔--=-,解得k =此满足②故满足条件的直线l 有两条,其方程分别为2y =+和2y =+双曲线基础练习题(三)一、选择题(每题5分)1.已知a=3,c=5,并且焦点在x 轴上,则双曲线的标准程是( )A .116922=+y x B. 116922=-y x C. 116922=+-y x 1916.22=-y x D 2.已知,5,4==c b 并且焦点在y 轴上,则双曲线的标准方程是( )A .191622=-y x B. 191622=+-y x C.116922=+y x D.116922=-y x 3..双曲线191622=-y x 上P 点到左焦点的距离是6,则P 到右焦点的距离是( ) A. 12 B. 14 C. 16 D. 184..双曲线191622=-y x 的焦点坐标是 ( ) A. (5,0)、(-5,0)B. (0,5)、(0,-5) C. (0,5)、(5,0) D.(0,-5)、(-5,0) 5、方程6)5()5(2222=++-+-y x y x 化简得:A .116922=-y x B. 191622=+-y x C.116922=+y x D. 191622=-y x 6.已知实轴长是6,焦距是10的双曲线的标准方程是( )A ..116922=-y x 和116922=+-y x B. 116922=-y x 和191622=+-y x C.191622=-y x 和191622=+-y x D. 1162522=-y x 和1251622=+-y x 7.过点A (1,0)和B ()1,2的双曲线标准方程( )A .1222=-y x B .122=+-y x C .122=-y x D. 1222=+-y x8.P 为双曲线191622=-y x 上一点,A 、B 为双曲线的左右焦点,且AP 垂直PB ,则三角形PAB 的面积为( ) A . 9 B . 18 C . 24 D . 369.双曲线191622=-y x 的顶点坐标是 ( ) A .(4,0)、(-4,0) B .(0,-4)、(0,4)C .(0,3)、(0,-3) D .(3,0)、(-3,0)10.已知双曲线21==e a ,且焦点在x 轴上,则双曲线的标准方程是( )A .1222=-y x B .122=-y x C .122=+-y x D. 1222=+-y x11.双曲线191622=-y x 的的渐近线方程是( ) A . 034=±y x B .043=±y x C .0169=±y x D .0916=±y x 12.已知双曲线的渐近线为043=±y x ,且焦距为10,则双曲线标准方程是( )A .116922=-y x B. 191622=+-y x C.116922=+y x D. 191622=-y x 二、填空题(每题5分共20分)13.已知双曲线虚轴长10,焦距是16,则双曲线的标准方程是________________. 14.已知双曲线焦距是12,离心率等于2,则双曲线的标准方程是___________________.15.已知16522=++-t y t x 表示焦点在y 轴的双曲线的标准方程,t 的取值范围是___________.16.椭圆C 以双曲线122=-y x 焦点为顶点,且以双曲线的顶点作为焦点,则椭圆的标准方程是___________________三、解答题17.(本小题(10分)已知双曲线C :191622=+-y x ,写出双曲线的实轴顶点坐标,虚轴顶点坐标,焦点坐标,准线方程,渐近线方程。
(完整word版)用几何画板画双曲线
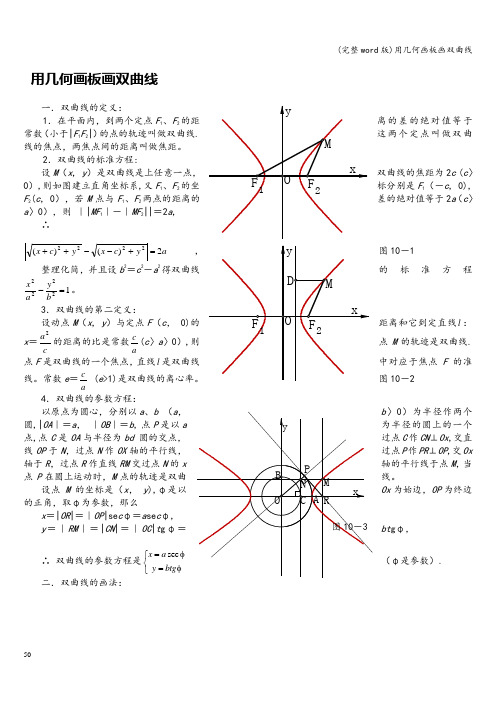
用几何画板画双曲线一.双曲线的定义:1.在平面内,到两个定点F 1、F 2的距离的差的绝对值等于常数(小于|F 1F 2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距。
2.双曲线的标准方程:设M (x , y )是双曲线是上任意一点,双曲线的焦距为2c (c 〉0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的差的绝对值等于2a (c 〉a 〉0),则 ||MF 1|-|MF 2||=2a ,∴ay c x y c x 2)()(2222=+--++图10-1整理化简,并且设b 2=c 2-a 2得双曲线的标准方程12222=-b y a x 。
3.双曲线的第二定义: 设动点M (x , y )与定点F(c , 0)的距离和它到定直线l : x =c a 2的距离的比是常数a c(c 〉a 〉0),则点M 的轨迹是双曲线.点F 是双曲线的一个焦点,直线l 是双曲线中对应于焦点F 的准线。
常数e =ac(e >1)是双曲线的离心率。
图10-24.双曲线的参数方程:以原点为圆心,分别以a 、b (a , b 〉0)为半径作两个圆,|OA |=a , |OB |=b , 点P 是以a 为半径的圆上的一个点,点C 是OA 与半径为bd 圆的交点,过点C 作CN ⊥Ox ,交直线OP 于N ,过点N 作OX 轴的平行线,过点P 作PR ⊥OP ,交Ox 轴于R ,过点R 作直线RM 交过点N 的x 轴的平行线于点M ,当点P 在圆上运动时,M 点的轨迹是双曲线。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OP 为终边的正角,取φ为参数,那么x =|OR |=|OP |se c φ=a se c φ,y =|RM |=|CN |=|OC |t g φ=bt g φ, ∴ 双曲线的参数方程是⎩⎨⎧φ=φ=btg y a x sec(φ是参数).二.双曲线的画法:画法1:图10-41.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段AB ,使|AB |=2a ,(|AB |<|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|AB |;4.在AB 延长线上分别取C ',使|BC '|=|A 1F 1|;在ABC '的延长线方向上作射线C 'C ,并用“作图”菜单中的“对象上的点”功能在C 'C 上作点C ;5.分别以F 1、F 2为圆心,用|BC |、|AC |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|AC |、|BC |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点";6.依次选中点C 、点P 1 (或点C 、点P 2 , 或点C 、点P 3, 或点C 、点P 3),用“作图”菜单中的“轨迹”功能,作出双曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学双曲线经典例题一、双曲线定义及标准方程1.已知两圆 C1:(x+4)2+y2=2,C2:(x﹣ 4)2+y2=2,动圆 M 与两圆C1,C2都相切,则动圆圆心M 的轨迹方程是()A.x=0B.C.D.2、求适合下列条件的双曲线的标准方程:(1)焦点在x 轴上,虚轴长为12,离心率为;(2)顶点间的距离为6,渐近线方程为.3、与双曲线有相同的焦点,且过点的双曲线的标准方程是4、求焦点在坐标轴上,且经过点A(,﹣2)和B(﹣2,)两点的双曲线的标准方程.5、已知 P 是双曲线=1 上一点, F1,F2是双曲线的两个焦点,若| PF1 2| =17,则| PF | 的值为.二、离心率1、已知点 F 、F 分别是双曲线的两个焦点, P 为该双曲线上一点,1 2若△ PF1 2F 为等腰直角三角形,则该双曲线的离心率为.2、设 F1,F2是双曲线 C:( a>0,b>0)的两个焦点.若在 C上存在一点 P.使PF1 2 1 2⊥PF ,且∠ PF F =30°,则 C的离心率为.3、双曲线的焦距为 2c,直线 l 过点( a,0)和(0,b),且点( 1,0)到直线 l 的距离与点(﹣ 1,0)到直线 l 的距离之和.则双曲线的离心率 e 的取值范围是()A.B.C.D.3、焦点三角形1、设 P 是双曲线 x2﹣=1 的右支上的动点, F 为双曲线的右焦点,已知 A(3,1),则 |PA|+|PF| 的最小值为.2、.已知 F1,F2分别是双曲线 3x2﹣5y2=75 的左右焦点, P 是双曲线上的一点,且∠ F1PF2 =120°,求△ F1 PF2的面积.3、已知双曲线焦点在y 轴上, F1,F2为其焦点,焦距为10,焦距是实轴长的 2 倍.求:(1)双曲线的渐近线方程;(2)若 P 为双曲线上一点,且满足∠ F1PF2=60°,求△ PF1F2的面积.4、直线与双曲线的位置关系已知过点 P(1,1)的直线 L 与双曲线只有一个公共点,则直线 L 的斜率 k= ____5、综合题型如图,已知椭圆x 2y221(a>b>0)的离心率为2,以该椭圆上的点和a2 b2椭圆的左、右焦点F1、F2 为顶点的三角形的周长为4( 2+1) ,一等轴双曲线的顶点是该椭圆的焦点,设 P 为该双曲线上异于顶点的任一点,直线 PF1和 PF2与椭圆的交点分别为 A、B和 C、D.(1)求椭圆和双曲线的标准方程;(2)设直线 PF1、PF2的斜率分别为 k1、k2,证明: k1·k2=1;(3)是否存在常数λ,使得 |AB| +|CD| =λ |AB| ·|CD| 恒成立?若存在,求λ的值;若不存在,请说明理由.高中数学双曲线经典例题参考答案与试题解析一.选择题(共 2 小题)1.(2015 秋?洛阳校级期末)已知两圆 C 1:(x+4)2+y 2=2,C 2:(x ﹣4)2+y 2=2, 动圆 M 与两圆 C 1, 2 都相切,则动圆圆心 M 的轨迹方程是( )C A .x=0 B .C .D .【解答】解:由题意,①若两定圆与动圆相外切或都内切, 即两圆 C 1:(2 2, x+4 )+y=2C 2:(x ﹣4)2+y 2=2,动圆 M 与两圆 C 1,C 2 都相切,∴ | MC 1| =| MC 2| ,即 M 点在线段 C 1, C 2 的垂直平分线上又 C 1,C 2 的坐标分别为(﹣ 4,0)与( 4, 0)∴其垂直平分线为 y 轴,∴动圆圆心 M 的轨迹方程是 x=0②若一内切一外切,不妨令与圆C 1:( x+4)2+y 2=2 内切,与圆 C 2 :(x ﹣4)2+y 2=2外切,则有 M 到( 4,0)的距离减到(﹣ 4, 0)的距离的差是 2,由双曲线的定义知,点 M 的轨迹是以(﹣ 4,0)与( 4, 0)为焦点,以为实半轴长的双曲线,故可得 b 2=c 2﹣a 2=14,故此双曲线的方程为综①②知,动圆 M 的轨迹方程为应选 D .2.(2014?齐齐哈尔三模)双曲线 的焦距为 2c ,直线 l过点( a ,0)和( 0,b ),且点( 1,0)到直线 l 的距离与点(﹣ 1,0)到直线 l的距离之和.则双曲线的离心率 e 的取值范围是()A.B.C.D.【解答】解:直线 l 的方程为+=1,即 bx+ay﹣ab=0.由点到直线的距离公式,且 a>1,得到点( 1,0)到直线 l 的距离,同理得到点(﹣ 1,0)到直线 l 的距离 .,.由,得..于是得5≥2e2,即4e4﹣25e2+25≤0.解不等式,得≤e2≤ 5.由于 e>1>0,所以 e 的取值范围是.故选 D.二.填空题(共 5 小题)3.(2013 秋?城区校级期末)已知P 是双曲线=1 上一点, F1,F2是双曲线的两个焦点,若 | PF1 ,则 2 的值为33 .| =17 | PF |【解答】解:由双曲线方程知,a=8,b=6,则c==10.∵ P 是双曲线上一点,∴|| PF1| ﹣ | PF2||=2a=16,又 | PF1| =17,∴| PF2| =1 或 | PF2|=33.又 | PF2| ≥c﹣a=2,∴| PF2| =33.故答案为 334.(2008 秋?海淀区期末)已知点 F1、F2分别是双曲线的两个焦点,P 为该双曲线上一点,若△ PF1 2为等腰直角三角形,则该双曲线的离心率为.F【解答】解:由题意,角 F1或角 F2为直角,不妨令角F2为直角,双曲线方程﹣=1此时 P(c,y),代入双曲线方程﹣=1解得 y=又三角形 PF1F2为等腰三角形得PF2=F1F2,故得=2c,即 2ac=c2﹣a2,即e2﹣2e﹣1=0,解得 e=1故双曲线的离心率是故答案为..(2014 秋象山县校级月考)设P是双曲线x2﹣ =1 的右支上的动点, F 为5 ?双曲线的右焦点,已知 A(3, 1),则 | PA|+| PF| 的最小值为﹣2 .【解答】解:设双曲线左焦点为 F2,由双曲线的定义可得 | PF2﹣,即 2 ﹣,| | PF| =2a | PF| =| PF | 2a则| PA|+| PF| =| PF2|+| PA| ﹣2a≥| F2A| ﹣2a,当P、F2、A 三点共线时, | PF2|+| PA| 有最小值,此时 F2(﹣ 2,0)、 A( 3, 1),则 | PF2 2,|+| PA| =| AF | =而对于这个双曲线, 2a=2,所以最小值为﹣ 2.故答案为:﹣2.6.(2011 秋 ?张家港市校级期末)与双曲线 有相同的焦点,且过点的双曲线的标准方程是 .【解答】 解:设所求双曲线的方程为,∵已知双曲线的焦点为(± ,0)∴所求双曲线中的 c 2=5①∵双曲线过点∴②且 c 2=a 2+b 2③联立①②③解得 a 2=4, b 2=1,∴双曲线的方程为.故答案为:.7.( 2013?湖南)设 F 1,F 2 是双曲线 C : (a >0,b >0)的两个焦点.若在 C 上存在一点 P .使 PF 1⊥ 2,且∠ 1 2 °,则 C 的离心率为.PF PF F =30【解答】 解:依题意可知∠ F 1PF 2=90°|F 1F 2| =2c ,∴ | PF 1| = | F 1F 2| = c , | PF 2| = | F 1F 2| =c ,由双曲线定义可知 | PF 1| ﹣| PF 2| =2a=( ﹣1)c∴ e= =.故答案为:.三.解答题(共 4 小题)8.已知 F 1,F 2 分别是双曲线 3x 2﹣5y 2 =75 的左右焦点, P 是双曲线上的一点,且∠ F 1PF 2=120°,求△ F 1PF 2 的面积.【解答】 解:由题意,双曲线 3x 2﹣ 5y2,可化为 =1=75由 余 弦 定 理 可 得160=PF 2+PF 22 ﹣ 2PF 1?PF 2cos120 °= ( PF 1 ﹣ PF 2 )2+3PF 1 ?PF 2=100+3PF 1?PF 2,∴ PF 1?PF 2=20.△ F1PF2= PF 1 2 ° × ×=5 . S ?PF sin120 = 20故答案为: A .9.(2014 春?湄潭县校级期中)已知双曲线焦点在 y 轴上, F 1, F 2 为其焦点,焦距为 10,焦距是实轴长的 2 倍.求:( 1)双曲线的渐近线方程;( 2)若 P 为双曲线上一点,且满足∠ F 1PF 2=60°,求△ PF 1F 2 的面积.【解答】 解:(1)设双曲线方程为( a > 0, b > 0),则∵焦距是实轴长的 2 倍,∴ c=2a ,∴ b== a ,∴双曲线的渐近线方程为 y=±x ;( 2 ) 由 余 弦 定 理 可 得 4c 2=PF 1 2+PF 22 ﹣ 2PF 1?PF 2cos60 °=( PF 1 ﹣ PF 2 )2+PF 1?PF 2=4a 2+PF 1?PF 2,∵焦距为 10,∴ 2c=10,2a=5∴ PF 1?PF 2=75.∴ S △ F1PF2= PF 1 2°=. ?PF sin60 = ?75?10.( 2008 秋?岳阳校级期末)求焦点在坐标轴上,且经过点A(,﹣2)和 B (﹣ 2 ,)两点的双曲线的标准方程.【解答】解:设所求双曲线方程为: mx2﹣ ny2,(mn >),=1 0因为点 A(,﹣ 2)和 B(﹣ 2 ,)在双曲线上,所以可得:,解得,故所求双曲线方程为.11.( 2009 秋?天心区校级期末)求适合下列条件的双曲线的标准方程:( 1)焦点在x 轴上,虚轴长为12,离心率为;( 2)顶点间的距离为6,渐近线方程为.【解答】解:(1)焦点在 x 轴上,设所求双曲线的方程为=1.由题意,得解得 a=8, c=10.∴b2=c2﹣ a2=100﹣ 64=36.所以焦点在 x 轴上的双曲线的方程为.( 2)当焦点在 x 轴上时,设所求双曲线的方程为=1由题意,得解得 a=3,b= .所以焦点在 x 轴上的双曲线的方程为.同理可求当焦点在y 轴上双曲线的方程为.。
