基本初等函数总复习
基本初等函数复习课

基本初等函数一、知识点回顾1.设]1,(,2),1(,log 81{)(-∞∈+∞∈-=x x x x x f ,则满足41)(=x f 的x 的值为2.下列函数中,既是奇函数,又在定义域内为减函数的是 ( )x y A )21(.= 2x y .B -= 3x y .C -= x log y .D 32=3.不论a 为何正实数,函数12x y a+=-的图象一定通过一定点,则该定点的坐标是_________4.如果,10<<a 那么下列不等式中准确的是( )2131)1()1.(a a A ->- 0)1(log .1>+-a B a 23)1()1.(a a C +>- 1)1.(1>-+a a D5.已知函数()()()f x x a x b =--(其中a b >)的图象如下面右图所示,则函数()xg x a b =+的图象是( )三、典型例题:例1.已知函数)1a ,0a (,1])21[(log )x (f x 3≠>-= (1)求函数的定义域;(2)求使0)x (f >的x 的取值范围。
例2.已知函数).1(log )1(log )x (f x x a a +--=(1)求)x (f 的定义域; (2)求使0)(>x f 的x 的取值范围。
(3) 并判断其奇偶性;例3.已知m x f x +-=132)(是奇函数, (1)求函数的定义域 (2)求常数m 的值;例4.已知定义在R 上的奇函数f(x),且当x ∈),0(+∞时,1)(2log )x (f x2-=. (1)求f (x)在R 上的解析式;(2)判断f(x)在),0(+∞的单调性并用定义证明.四、当堂检测:1.幂函数53m x )x (f -=( N m ∈)在)(0,+∞是减函数,且x)(f )x (f =-,则m=2.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围 ( ) A .)1,1(- B . ),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或3.已知2)(x x e e x f --=,则下列准确的是( )A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数 4.函数210)2()5(--+-=x x y 的定义域( )A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或 5.设指数函数)1,0()(≠>=a a a x f x,则下列等式中不准确的是( )A .f (x +y )=f(x )·f (y )B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈= D .)()]([·)]([)(+∈=N n y f x f xy f nnn6.下列关系式中,成立的是( )A .10log 514log 3103>⎪⎭⎫⎝⎛>B . 4log 5110log 3031>⎪⎭⎫⎝⎛>C . 03135110log 4log ⎪⎭⎫⎝⎛>>D .0331514log 10log ⎪⎭⎫⎝⎛>>7.当a ≠0时,函数y ax b =+和y b ax=的图象只可能是 ( )8.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称基本初等函数复习卷一、选择题 1. ·等于( )A.-B.-C.D.2.函数y=(m 2+2m-2)是幂函数,则m=( ) A.1B.-3C.-3或1D.23.设y 1=40.9,y 2=lo4.3,y 3=()1.5,则( ) A.y 3>y 1>y 2B.y 2>y 1>y 3C.y 1>y 2>y 3D.y 1>y 3>y 24.已知log 2m=2.013,log 2n=1.013,则等于( ) A.2B.C.10D.5.函数f(x)=+lg(2x +1)的定义域为( ) A.(-5,+∞)B.[-5,+∞)C.(-5,0)D.(-2,0)6.已知f(x)是函数y=log 2x 的反函数,则y=f(1-x)的图象是( )7.下列函数中,图象关于y 轴对称的是( ) A.y=log 2xB.y=C.y=x|x|D.y=8.下列各函数中,值域为(0,+∞)的是( ) A.y=B.y=C.y=x 2+x+1D.y=9. x=+的值属于区间( ) A.(-3,-2)B.(-2,-1)C.(-1,0)D.(2,3)10.设函数f(x)=已知f(a)>1,则实数a 的取值范围是( )A.(-2,1)B.(-∞,-2)∪(1,+∞)C.(1,+∞)D.(-∞,-1)∪(0,+∞) 二、填空题11.已知=(a>0),则lo a= .12.若函数f(x)=(3-a)x 与g(x)=log a x 的增减性相同,则实数a 的取值范围是 . 13.函数f (x )=a x -2+1的图象一定过定点P ,则P 点的坐标是________.14.已知函数f (x )=⎩⎨⎧log 2x ,x >03x ,x ≤0则f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫14的值是________.三、解答题15.计算下列各题:(1)0.008+()2+(-16-0.75.(2)(lg5)2+lg2·lg50+.16.已知函数f(x)=log3(ax+b)的图象经过点A(2,1),B(5,2),(1)求函数f(x)的解析式及定义域.(2)求f(14)÷f()的值.17.已知函数f(x)=log a(x2+1)(a>1).(1)判断f(x)的奇偶性;(2)求函数f(x)的值域.18. 函数f(x)=log a(1-x)+log a(x+3),(0<a<1).(1)求函数f(x)的定义域;(2)若函数f(x)的最小值为-2,求a的值.答案预习自测 3 C (-1,-- 1) A A 例1解:(1)由题意得(12)x -1>0(12)x >1=(12)0 解得x<0,即f(x)的定义域为(-∞,0) (2)由题意得log 3((12)x -1)> log 3 1所以1()1021()112x x ⎧->⎪⎪⎨⎪->⎪⎩,即0111()()2211()()22xx -⎧>⎪⎪⎨⎪>⎪⎩ 解得x<-1,所以x 的取值范围是(-∞,-1)例2 解:(1)由题意得1010x x ->⎧⎨+>⎩解得-1<x<1,所以f(x)的定义域为(-1,1)(2) f(x)>0即log a (1-x)>log a (1+x)当a>1时,101011x x x x ->⎧⎪+>⎨⎪->+⎩,解得x ∈(-1,0)当0<a<1时,101011x x x x ->⎧⎪+>⎨⎪-<+⎩,解得x ∈(0,1)综上所述,当a>1时,x 的取值范围是(-1,0);当0<a<1时,x 的取值范围是(0,1) (3)∵f(x)的定义域 (-1,1)关于原点对称,以及f(-x)= log a (1+x)-log a (1-x)= -(log a (1-x) -log a (1+x)) = -f(x) 所以f(x)是奇函数。
基本初等函数复习题型最全最细最精

根本初等函数复习一、根底复习:1、a 的次方根: , x 叫a 的n 次方根根式的性质:(1)n n a )(= ,(),1+∈>N n n 且;〔2〕⎩⎨⎧=为偶数时当为奇数时当n a n a a nn|,|,2、分数指数幂与根式:=mna =-n a =1a =0a3、幂的运算性质:=⋅s r a a =÷s r a a =s r a )( =r ab )(4、指数式与对数式的互化:⇒=N a b5、对数的性质:〔1〕N 〔2〕=1log a 〔3〕=a a log6、对数恒等式:=Naa log=b a a log7、对数的运算法那么:=⋅)(log N M a =)(log NMa =αM a log 8、换底公式:=b a log =b a log =n a b mlog 9、常用对数:=N 10log 自然对数:=N e log 10、幂、指、对函数函数的性质 二、典型例题: 1、指数、对数运算: 1、以下各式中,正确的选项是〔 〕A .100=B .1)1(1=--C .74471aa=-D .53531aa=-2. 计算:210319)41()2(4)21(----+-⋅- = ;)31()3)((656131212132b a b a b a ÷-的结果〔 〕A .a 6B .a -C .a 9-D .29a4.2x =72y =A ,且1x +1y=2,那么A 的值是 A .7 B .7 2 C .±72 D .98 a 、b 、c ∈R +,那么3a =4b =6c,那么( )A .bac111+=B .b a c 122+=C .b a c 221+= D .ba c 212+=6. 假设a<12,那么化简4(2a -1)2的结果是A.2a -1 B .-2a -1 C.1-2a D .-1-2a7、计算以下各式的值〔1〔2〕;21lg5(lg8lg1000)(lg lg lg 0.066++++8、设1245100,2()a b a b==+求的值.9、4(),01,42xx f x a =<<+且(1)()(1)f a f a +-求的值;1231000(2)()()()...()1001100110011001f f f f ++++求的值.说明:如果函数()xf x =,那么函数()f x 满足()(1)1f x f x +-=2、指数函数、对数、幂函数的图像:〔1〕定义考察:1、以下函数中指数函数的个数是 ( ). ①②③④A .0个 2.以下函数是指数函数的是〔 〕A. x y 5=B. x y +=25C. x y 52⋅=D. 15-=x y〔2〕定点问题1.函数0.(12>+=-a a y x 且)1≠a 的图像必经过点〔 〕)1,0.(A )1,1.(B )0,2.(C )2,2.(D2. 函数恒3()25x f x a -=+过定点 ( )A .(3 , 5)B .( 3, 7 )C .( 0, 1 )D .( 1, 0 )1log )()2(2+=-x x f 恒过定点___________〔3〕图像问题1.当a >1时,函数y=log a x 和y=(1-a)x 的图像只可能是( )2如图中函数21-=xy 的图象大致是〔 〕图3-73.在统一平面直角坐标系中,函数ax x f =)(与x a x g =)(的图像可能是〔 〕4.设d c b a ,,,都是不等于1的正数,x x x x d y c y b y a y ====,,,在同一坐标系中的图像如下图,那么d c b a ,,,的大小顺序是〔 d c b a A <<<. c d b a B <<<. c d a b C <<<. d c a b D <<<.5.图中所示曲线为幂函数n x y =在第一象限的图象,那么1c 、2c 、3c 、4c 大小关系为 〔 〕A.4321c c c c >>>B.3412c c c c >>>C.3421c c c c >>>D.2341c c c c >>> 3、指数函数、对数函数的单调性、奇偶性 〔1〕单调性1、比拟以下每组中两个数的大小0.30.4 1.3 1.60.3 1.3111(1)2.1_____2.1; (2)()_____(); (3)2.1_____()555-550.70.543(4)log 1.9_____log 2; (5)log 0.2_____log 2; (6)log 2_____log 4xyo 1Axyo1B xyo1Cxyo1Dxa =xby =xc y =xd y =yo2、031log 31log >>b a ,那么a 、b 的关系是 〔 〕 A .1<b <a B .1<a <b C .0<a <b <1 D .0<b <a <1 3.设10<<a ,使不等式531222+-+->x x x x a a 成立的x 的集合是4.以下函数中,在区间(0,1)上是增函数的是 ( ) A.y=-xB.y=log 21xC.y=31x D.y=-x 2+2x+15.〔1〕函数)26(log 21.0x x y -+=的单调增区间是________〔2〕log (2)a y ax =-在[0,1]是减函数,那么a 的取值范围是_________6.(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数,那么a 的取值范围是 〔 〕〔A 〕(0,1) 〔B 〕1(0,)3 〔C 〕11[,)73〔D 〕1[,1)77、 解以下不等式:(1)22332<-+x x ; 〔2〕2332)21(2--+<x x x ; 〔3〕)1,0(5213222≠>>-++-a a a a x x x x2()(1)x f x a R a =-在上是减函数,求实数的取值范围9、求以下函数的单调区间。
2024年高考数学总复习第二章《函数与基本初等函数》函数的单调性与最值

2024年高考数学总复习第二章《函数与基本初等函数》§2.2函数的单调性与最值最新考纲1.通过已学过的函数特别是二次函数,理解函数的单调性、最大(小)值及其几何意义.2.学会运用函数图象理解和研究函数的性质.1.函数的单调性(1)单调函数的定义增函数减函数定义一般地,设函数f (x )的定义域为I ,如果对于定义域I 内某个区间D 上的任意两个自变量的值x 1,x 2当x 1<x 2时,都有f (x 1)<f (x 2),那么就说函数f (x )在区间D 上是增函数当x 1<x 2时,都有f (x 1)>f (x 2),那么就说函数f (x )在区间D 上是减函数图象描述自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数y =f (x )在区间D 上是增函数或减函数,那么就说函数y =f (x )在这一区间具有(严格的)单调性,区间D 叫做y =f (x )的单调区间.2.函数的最值前提设函数y =f (x )的定义域为I ,如果存在实数M 满足条件(1)对于任意的x ∈I ,都有f (x )≤M ;(2)存在x 0∈I ,使得f (x 0)=M(3)对于任意的x ∈I ,都有f (x )≥M ;(4)存在x 0∈I ,使得f (x 0)=M结论M 为最大值M 为最小值概念方法微思考1.在判断函数的单调性时,你还知道哪些等价结论?提示对∀x 1,x 2∈D ,f (x 1)-f (x 2)x 1-x 2>0⇔f (x )在D 上是增函数,减函数类似.2.写出对勾函数y =x +ax (a >0)的增区间.提示(-∞,-a ]和[a ,+∞).题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若定义在R 上的函数f (x ),有f (-1)<f (3),则函数f (x )在R 上为增函数.(×)(2)函数y =f (x )在[1,+∞)上是增函数,则函数的单调递增区间是[1,+∞).(×)(3)函数y =1x的单调递减区间是(-∞,0)∪(0,+∞).(×)(4)如果一个函数在定义域内的某几个子区间上都是增函数,则这个函数在定义域上是增函数.(×)(5)所有的单调函数都有最值.(×)题组二教材改编2.函数f (x )=x 2-2x 的单调递增区间是____________.答案[1,+∞)(或(1,+∞))3.函数y =2x -1在[2,3]上的最大值是______.答案24.若函数f (x )=x 2-2mx +1在[2,+∞)上是增函数,则实数m 的取值范围是________.答案(-∞,2]解析由题意知,[2,+∞)⊆[m ,+∞),∴m ≤2.题组三易错自纠5.函数y =12log (x 2-4)的单调递减区间为________.答案(2,+∞)6.若函数f (x )=|x -a |+1的增区间是[2,+∞),则a =________.答案2解析∵f (x )=|x -a |+1的单调递增区间是[a ,+∞),∴a =2.7.函数y =f (x )是定义在[-2,2]上的减函数,且f (a +1)<f (2a ),则实数a 的取值范围是________.答案[-1,1)解析-2≤a+1≤2,-2≤2a≤2,a+1>2a,解得-1≤a<1.8.函数f(x)1x,x≥1,-x2+2,x<1的最大值为________.答案2解析当x≥1时,函数f(x)=1x为减函数,所以f(x)在x=1处取得最大值,为f(1)=1;当x<1时,易知函数f(x)=-x2+2在x=0处取得最大值,为f(0)=2.故函数f(x)的最大值为2.题型一确定函数的单调性命题点1求函数的单调区间例1(1)函数f(x)=ln(x2-2x-8)的单调递增区间是()A.(-∞,-2)B.(-∞,1)C.(1,+∞)D.(4,+∞)答案D解析函数y=x2-2x-8=(x-1)2-9图象的对称轴为直线x=1,由x2-2x-8>0,解得x>4或x<-2,所以(4,+∞)为函数y=x2-2x-8的一个单调递增区间.根据复合函数的单调性可知,函数f(x)=ln(x2-2x-8)的单调递增区间为(4,+∞).(2)函数y=-x2+2|x|+3的单调递减区间是__________________.答案[-1,0],[1,+∞)解析由题意知,当x≥0时,y=-x2+2x+3=-(x-1)2+4;当x<0时,y=-x2-2x+3=-(x+1)2+4,二次函数的图象如图.由图象可知,函数y=-x2+2|x|+3的单调递减区间为[-1,0],[1,+∞).命题点2讨论函数的单调性例2判断并证明函数f (x )=ax 2+1x (其中1<a <3)在[1,2]上的单调性.解函数f (x )=ax 2+1x(1<a <3)在[1,2]上单调递增.证明:设1≤x 1<x 2≤2,则f (x 2)-f (x 1)=ax 22+1x 2-ax 21-1x 1=(x 2-x 1)a (x 1+x 2)-1x 1x 2,由1≤x 1<x 2≤2,得x 2-x 1>0,2<x 1+x 2<4,1<x 1x 2<4,-1<-1x 1x 2<-14.又因为1<a <3,所以2<a (x 1+x 2)<12,得a (x 1+x 2)-1x 1x 2>0,从而f (x 2)-f (x 1)>0,即f (x 2)>f (x 1),故当a ∈(1,3)时,f (x )在[1,2]上单调递增.引申探究如何用导数法求解本例?解f ′(x )=2ax -1x 2=2ax 3-1x 2,因为1≤x ≤2,所以1≤x 3≤8,又1<a <3,所以2ax 3-1>0,所以f ′(x )>0,所以函数f (x )=ax 2+1x (其中1<a <3)在[1,2]上是增函数.思维升华确定函数单调性的方法:(1)定义法和导数法,证明函数单调性只能用定义法和导数法;(2)复合函数法,复合函数单调性的规律是“同增异减”;(3)图象法,图象不连续的单调区间不能用“∪”连接.跟踪训练1(1)下列函数中,满足“∀x 1,x 2∈(0,+∞)且x 1≠x 2,(x 1-x 2)·[f (x 1)-f (x 2)]<0”的是()A .f (x )=2xB .f (x )=|x -1|C .f (x )=1x -xD .f (x )=ln(x +1)答案C解析由(x 1-x 2)·[f (x 1)-f (x 2)]<0可知,f (x )在(0,+∞)上是减函数,A ,D 选项中,f (x )为增函数;B 中,f (x )=|x -1|在(0,+∞)上不单调;对于f (x )=1x -x ,因为y =1x与y =-x 在(0,+∞)上单调递减,因此f (x )在(0,+∞)上是减函数.(2)函数f (x )=(a -1)x +2在R 上单调递增,则函数g (x )=a |x -2|的单调递减区间是______________.答案(-∞,2]解析因为f (x )在R 上单调递增,所以a -1>0,即a >1,因此g (x )的单调递减区间就是y =|x -2|的单调递减区间(-∞,2].(3)函数f (x )=|x -2|x 的单调递减区间是________.答案[1,2]解析f (x )2-2x ,x ≥2,x 2+2x ,x <2.画出f (x )图象,由图知f (x )的单调递减区间是[1,2].题型二函数的最值1.函数y =x 2-1x 2+1的值域为____________.答案[-1,1)解析由y =x 2-1x 2+1,可得x 2=1+y 1-y.由x 2≥0,知1+y1-y≥0,解得-1≤y <1,故所求函数的值域为[-1,1).2.函数y =x +1-x 2的最大值为________.答案2解析由1-x 2≥0,可得-1≤x ≤1.可令x =cos θ,θ∈[0,π],则y =cos θ+sin θ=2sin θ∈[0,π],所以-1≤y ≤2,故原函数的最大值为 2.3.函数y =|x +1|+|x -2|的值域为________.答案[3,+∞)解析函数y 2x +1,x ≤-1,,-1<x <2,x -1,x ≥2.作出函数的图象如图所示.根据图象可知,函数y =|x +1|+|x -2|的值域为[3,+∞).4.函数y =3x +1x -2的值域为________________.答案{y |y ∈R 且y ≠3}解析y =3x +1x -2=3(x -2)+7x -2=3+7x -2,因为7x -2≠0,所以3+7x -2≠3,所以函数y =3x +1x -2的值域为{y |y ∈R 且y ≠3}.5.函数f (x )-log 2(x +2)在区间[-1,1]上的最大值为________.答案3解析由于y 在[-1,1]上单调递减,y =log 2(x +2)在[-1,1]上单调递增,所以f (x )在[-1,1]上单调递减,故f (x )在[-1,1]上的最大值为f (-1)=3.6.若函数f (x )=x 2+ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M -m ()A .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关答案B 解析方法一设x 1,x 2分别是函数f (x )在[0,1]上的最小值点与最大值点,则m =x 21+ax 1+b ,M =x 22+ax 2+b .∴M -m =x 22-x 21+a (x 2-x 1),显然此值与a 有关,与b 无关.故选B.方法二由题意可知,函数f (x )的二次项系数为固定值,则二次函数图象的形状一定.随着b 的变动,相当于图象上下移动,若b 增大k 个单位,则最大值与最小值分别变为M +k ,m +k ,而(M +k )-(m +k )=M -m ,故与b 无关.随着a 的变动,相当于图象左右移动,则M -m 的值在变化,故与a 有关,故选B.思维升华求函数最值的五种常用方法及其思路(1)单调性法:先确定函数的单调性,再由单调性求最值.(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值.(3)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值.(4)分离常数法:形如求y=cx+dax+b(ac≠0)的函数的值域或最值常用分离常数法求解.(5)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值.题型三函数单调性的应用命题点1比较函数值的大小例3已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)-f(x1)]·(x2-x1)<0恒成立,设a=f -12,b=f(2),c=f(3),则a,b,c的大小关系为()A.c>a>b B.c>b>aC.a>c>b D.b>a>c答案D解析根据已知可得函数f(x)的图象关于直线x=1对称,且在(1,+∞)上是减函数,因为a=f -12f522<52<3,所以b>a>c.命题点2解函数不等式例4(2018·四川成都五校联考)设函数f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则f(x)<0的解集是()A.{x|-3<x<0或x>3}B.{x|x<-3或0<x<3}C.{x|x<-3或x>3}D.{x|-3<x<0或0<x<3}答案B解析∵f(x)是奇函数,f(-3)=0,∴f(-3)=-f(3)=0,解得f(3)=0.∵函数f(x)在(0,+∞)内是增函数,∴当0<x<3时,f(x)<0;当x>3时,f(x)>0.∵函数f(x)是奇函数,∴当-3<x<0时,f(x)>0;当x<-3时,f(x)<0.则不等式f (x )<0的解集是{x |0<x <3或x <-3}.命题点3求参数的取值范围例5(1)(2018·全国Ⅱ)若f (x )=cos x -sin x 在[0,a ]上是减函数,则a 的最大值是()A.π4B.π2C.3π4D .π答案C解析∵f (x )=cos x -sin x =-2sin∴当x -π4∈-π2,π2,即x ∈-π4,3π4时,y =sinf (x )=-2sin ∴-π4,3π4是f (x )在原点附近的单调减区间,结合条件得[0,a ]⊆-π4,3π4,∴a ≤3π4,即a max =3π4.(2)已知函数f (x )2+12a -2,x ≤1,x -a ,x >1,若f (x )在(0,+∞)上单调递增,则实数a 的取值范围为________.答案(1,2]解析由题意,得12+12a -2≤0,则a ≤2,又y =a x -a (x >1)是增函数,故a >1,所以a 的取值范围为1<a ≤2.(3)(2018·安徽滁州中学月考)已知函数f (x )=log 2(x 2-ax +3a )在[2,+∞)上是增函数,则实数a 的取值范围是______________.答案(-4,4]解析设g (x )=x 2-ax +3a ,根据对数函数及复合函数的单调性知,g (x )在[2,+∞)上是增函数,且g (2)>0,2,a >0,∴-4<a ≤4,∴实数a 的取值范围是(-4,4].思维升华函数单调性应用问题的常见类型及解题策略(1)比较大小.(2)解不等式.利用函数的单调性将“f ”符号脱掉,转化为具体的不等式求解,应注意函数的定义域.(3)利用单调性求参数.①依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较;②需注意若函数在区间[a ,b ]上是单调的,则该函数在此区间的任意子集上也是单调的;③分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值.跟踪训练2(1)如果函数f (x )2-a )x +1,x <1,x ,x ≥1满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2>0成立,那么a 的取值范围是________.答案32,解析对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2>0,所以y =f (x )在(-∞,+∞)上是增函数.-a >0,>1,2-a )×1+1≤a ,解得32≤a <2.故实数a 的取值范围是32,(2)已知函数f (x )是定义在区间[0,+∞)上的函数,且在该区间上单调递增,则满足f (2x -1)<f x 的取值范围是______________.答案12,解析因为函数f (x )是定义在区间[0,+∞)上的增函数,且满足f (2x -1)<所以0≤2x -1<13,解得12≤x <23.1.下列函数中,在区间(0,+∞)上为增函数的是()A .y =ln(x +2)B .y =-x +1C .yD .y =x +1x答案A解析函数y=ln(x+2)的增区间为(-2,+∞),所以在(0,+∞)上一定是增函数.2.已知函数f(x)=x2-2x-3,则该函数的单调递增区间为()A.(-∞,1]B.[3,+∞)C.(-∞,-1]D.[1,+∞)答案B解析设t=x2-2x-3,由t≥0,即x2-2x-3≥0,解得x≤-1或x≥3,所以函数f(x)的定义域为(-∞,-1]∪[3,+∞).因为函数t=x2-2x-3的图象的对称轴为x=1,所以函数t在(-∞,-1]上单调递减,在[3,+∞)上单调递增,所以函数f(x)的单调递增区间为[3,+∞).3.设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是()A.f(π)>f(-3)>f(-2)B.f(π)>f(-2)>f(-3)C.f(π)<f(-3)<f(-2)D.f(π)<f(-2)<f(-3)答案A解析因为f(x)是偶函数,所以f(-3)=f(3),f(-2)=f(2).又因为函数f(x)在[0,+∞)上是增函数,所以f(π)>f(3)>f(2),即f(π)>f(-3)>f(-2).4.已知函数f(x)-2a)x,x≤1,a x+13,x>1,当x1≠x2时,f(x1)-f(x2)x1-x2<0,则a的取值范围是(),13 B.13,12,12 D.14,13答案A解析当x1≠x2时,f(x1)-f(x2)x1-x2<0,∴f(x)是R上的减函数.∵f(x)-2a)x,x≤1,a x+13,x>1,-2a<1,a<1,-2a≥13,∴0<a≤13.5.设f (x )x -a )2,x ≤0,+1x +a ,x >0,若f (0)是f (x )的最小值,则a 的取值范围为()A .[-1,2]B .[-1,0]C .[1,2]D .[0,2]答案D 解析∵当x ≤0时,f (x )=(x -a )2,f (0)是f (x )的最小值,∴a ≥0.当x >0时,f (x )=x +1x +a ≥2+a ,当且仅当x =1时取“=”.要满足f (0)是f (x )的最小值,需2+a ≥f (0)=a 2,即a 2-a -2≤0,解得-1≤a ≤2.∴a 的取值范围是0≤a ≤2.故选D.6.已知函数f (x )2x ,x ≥1,+c ,x <1,则“c =-1”是“函数f (x )在R 上单调递增”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件答案A 解析若函数f (x )在R 上单调递增,则需log 21≥c +1,即c ≤-1.由于c =-1,即c ≤-1,但c ≤-1不能得出c =-1,所以“c =-1”是“函数f (x )在R 上单调递增”的充分不必要条件.7.已知奇函数f (x )在R 上是增函数.若a =-b =f (log 24.1),c =f (20.8),则a ,b ,c 的大小关系为________________.答案a >b >c 解析∵f (x )在R 上是奇函数,∴a =-log f (log 25).又f (x )在R 上是增函数,且log 25>log 24.1>log 24=2>20.8,∴f (log 25)>f (log 24.1)>f (20.8),∴a >b >c .8.如果函数f (x )=ax 2+2x -3在区间(-∞,4)上单调递增,则实数a 的取值范围是______________.答案-14,0解析当a =0时,f (x )=2x -3在定义域R 上是单调递增的,故在(-∞,4)上单调递增;当a ≠0时,二次函数f (x )的对称轴为x =-1a,因为f (x )在(-∞,4)上单调递增,所以a <0,且-1a ≥4,解得-14≤a <0.综上,实数a 的取值范围是-140.9.记min{a ,b },a ≤b ,,a >b ,若f (x )=min{x +2,10-x }(x ≥0),则f (x )的最大值为________.答案6解析由题意知,f (x )+2,0≤x ≤4,-x ,x >4,易知f (x )max =f (4)=6.10.设函数f (x )x 2+4x ,x ≤4,2x ,x >4.若函数y =f (x )在区间(a ,a +1)上单调递增,则实数a的取值范围是__________________.答案(-∞,1]∪[4,+∞)解析作函数f (x )的图象如图所示,由图象可知f (x )在(a ,a +1)上单调递增,需满足a ≥4或a +1≤2,即a ≤1或a ≥4.11.已知f (x )=x x -a(x ≠a ).(1)若a =-2,试证f (x )在(-∞,-2)上单调递增;(2)若a >0且f (x )在(1,+∞)上单调递减,求a 的取值范围.(1)证明当a =-2时,f (x )=x x +2.设x 1<x 2<-2,则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2=2(x 1-x 2)(x 1+2)(x 2+2).因为(x 1+2)(x 2+2)>0,x 1-x 2<0,所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),所以f (x )在(-∞,-2)上单调递增.(2)解设1<x 1<x 2,则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a=a (x 2-x 1)(x 1-a )(x 2-a ).因为a >0,x 2-x 1>0,所以要使f (x 1)-f (x 2)>0,只需(x 1-a )(x 2-a )>0恒成立,所以a ≤1.综上所述,0<a ≤1.12.(2018·河南南阳一中月考)设函数f (x )=ax 2+bx +1(a ,b ∈R ),F (x )x ),x >0,f (x ),x <0.(1)若f (-1)=0,且对任意实数x 均有f (x )≥0成立,求F (x )的解析式;(2)在(1)的条件下,当x ∈[-2,2]时,g (x )=f (x )-kx 是单调函数,求实数k 的取值范围.解(1)∵f (-1)=0,∴b =a +1.由f (x )≥0恒成立,知a >0且方程ax 2+bx +1=0中Δ=b 2-4a =(a +1)2-4a =(a -1)2≤0,∴a =1.从而f (x )=x 2+2x +1.∴F (x )x +1)2,x >0,(x +1)2,x <0.(2)由(1)可知f (x )=x 2+2x +1,∴g (x )=f (x )-kx =x 2+(2-k )x +1,由g (x )在[-2,2]上是单调函数,知-2-k 2≤-2或-2-k 2≥2,得k ≤-2或k ≥6.即实数k 的取值范围为(-∞,-2]∪[6,+∞).13.已知函数f (x )3,x ≤0,(x +1),x >0,若f (2-x 2)>f (x ),则实数x 的取值范围是()A .(-∞,-1)∪(2,+∞)B .(-∞,-2)∪(1,+∞)C .(-1,2)D .(-2,1)答案D 解析∵当x =0时,两个表达式对应的函数值都为0,∴函数的图象是一条连续的曲线.又∵当x ≤0时,函数f (x )=x 3为增函数,当x >0时,f (x )=ln(x +1)也是增函数,∴函数f (x )是定义在R 上的增函数.因此,不等式f (2-x 2)>f (x )等价于2-x 2>x ,即x 2+x -2<0,解得-2<x <1.14.已知f (x )2-4x +3,x ≤0,x 2-2x +3,x >0,不等式f (x +a )>f (2a -x )在[a ,a +1]上恒成立,则实数a 的取值范围是________.答案(-∞,-2)解析二次函数y 1=x 2-4x +3的对称轴是x =2,∴该函数在(-∞,0]上单调递减,∴x 2-4x +3≥3,同样可知函数y 2=-x 2-2x +3在(0,+∞)上单调递减,∴-x 2-2x +3<3,∴f (x )在R 上单调递减,∴由f (x +a )>f (2a -x )得到x +a <2a -x ,即2x <a ,∴2x <a 在[a ,a +1]上恒成立,∴2(a +1)<a ,∴a <-2,∴实数a 的取值范围是(-∞,-2).15.已知函数f (x )=2020x +ln(x 2+1+x )-2020-x +1,则不等式f (2x -1)+f (2x )>2的解集为____________.答案解析由题意知,f (-x )+f (x )=2,∴f (2x -1)+f (2x )>2可化为f (2x -1)>f (-2x ),又由题意知函数f (x )在R 上单调递增,∴2x -1>-2x ,∴x >14,∴16.已知定义在区间(0,+∞)上的函数f (x )是增函数,f (1)=0,f (3)=1.(1)解不等式0<f (x 2-1)<1;(2)若f (x )≤m 2-2am +1对所有x ∈(0,3],a ∈[-1,1]恒成立,求实数m 的取值范围.解(1)2-1>0,x 2-1<3,得2<x <2或-2<x <- 2.∴原不等式的解集为(-2,-2)∪(2,2).(2)∵函数f (x )在(0,3]上是增函数,∴f (x )在(0,3]上的最大值为f (3)=1,∴不等式f (x )≤m 2-2am +1对所有x ∈(0,3],a ∈[-1,1]恒成立转化为1≤m 2-2am +1对所有a ∈[-1,1]恒成立,即m 2-2am ≥0对所有a ∈[-1,1]恒成立.设g (a )=-2ma +m 2,a ∈[-1,1],∴(-1)≥0,(1)≥0,m +m 2≥0,2m +m 2≥0,解该不等式组,得m ≤-2或m ≥2或m =0,即实数m 的取值范围为(-∞,-2]∪{0}∪[2,+∞).。
2024年高考数学总复习第二章《函数与基本初等函数》函数的奇偶性与周期性

2024年高考数学总复习第二章《函数与基本初等函数》§2.3函数的奇偶性与周期性最新考纲1.结合具体函数,了解函数奇偶性的含义.2.学会运用函数图象理解和研究函数的奇偶性.3.了解函数周期性、最小正周期的含义,会判断、应用简单函数的周期性.1.函数的奇偶性奇偶性定义图象特点偶函数一般地,如果对于函数f (x )的定义域内任意一个x ,都有f (-x )=f (x ),那么函数f (x )就叫做偶函数关于y 轴对称奇函数一般地,如果对于函数f (x )的定义域内任意一个x ,都有f (-x )=-f (x ),那么函数f (x )就叫做奇函数关于原点对称2.周期性(1)周期函数:对于函数y =f (x ),如果存在一个非零常数T ,使得当x 取定义域内的任何值时,都有f (x +T )=f (x ),那么就称函数y =f (x )为周期函数,称T 为这个函数的周期.(2)最小正周期:如果在周期函数f (x )的所有周期中存在一个最小的正数,那么这个最小正数就叫做f (x )的最小正周期.概念方法微思考1.如果已知函数f (x ),g (x )的奇偶性,那么函数f (x )±g (x ),f (x )·g (x )的奇偶性有什么结论?提示在函数f (x ),g (x )公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.2.已知函数f (x )满足下列条件,你能得到什么结论?(1)f (x +a )=-f (x )(a ≠0);(2)f (x +a )=1f (x )(a ≠0);(3)f (x +a )=f (x +b )(a ≠b ).提示(1)T =2|a |(2)T =2|a |(3)T =|a -b |题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)函数y =x 2,x ∈(0,+∞)是偶函数.(×)(2)偶函数的图象不一定过原点,奇函数的图象一定过原点.(×)(3)若函数y =f (x +a )是偶函数,则函数y =f (x )关于直线x =a 对称.(√)题组二教材改编2.已知函数f (x )是定义在R 上的奇函数,且当x >0时,f (x )=x (1+x ),则f (-1)=________.答案-2解析f (1)=1×2=2,又f (x )为奇函数,∴f (-1)=-f (1)=-2.3.设f (x )是定义在R 上的周期为2的函数,当x ∈[-1,1)时,f (x )-4x 2+2,-1≤x <0,x ,0≤x <1,则f 32______.答案1解析f 32=f -124×-122+2=1.4.设奇函数f (x )的定义域为[-5,5],若当x ∈[0,5]时,f (x )的图象如图所示,则不等式f (x )<0的解集为________.答案(-2,0)∪(2,5]解析由图象可知,当0<x <2时,f (x )>0;当2<x ≤5时,f (x )<0,又f (x )是奇函数,∴当-2<x <0时,f (x )<0,当-5≤x <-2时,f (x )>0.综上,f (x )<0的解集为(-2,0)∪(2,5].题组三易错自纠5.已知f (x )=ax 2+bx 是定义在[a -1,2a ]上的偶函数,那么a +b 的值是()A .-13 B.13C.12D .-12答案B 解析∵f (x )=ax 2+bx 是定义在[a -1,2a ]上的偶函数,∴a -1+2a =0,∴a =13.又f (-x )=f (x ),∴b =0,∴a +b =13.6.偶函数y =f (x )的图象关于直线x =2对称,f (3)=3,则f (-1)=________.答案3解析∵f (x )为偶函数,∴f (-1)=f (1).又f (x )的图象关于直线x =2对称,∴f (1)=f (3).∴f (-1)=3.题型一函数奇偶性的判断例1判断下列函数的奇偶性:(1)f (x )=36-x 2+x 2-36;(2)f (x )=ln (1-x 2)|x -2|-2;(3)f (x )2+x ,x <0,x 2+x ,x >0.解(1)-x 2≥0,2-36≥0,得x 2=36,解得x =±6,即函数f (x )的定义域为{-6,6},关于原点对称,∴f (x )=36-x 2+x 2-36=0.∴f (-x )=-f (x )且f (-x )=f (x ),∴函数f (x )既是奇函数又是偶函数.(2)-x 2>0,-2|≠2,得定义域为(-1,0)∪(0,1),关于原点对称.∴x -2<0,∴|x -2|-2=-x ,∴f (x )=ln (1-x 2)-x.又∵f (-x )=ln[1-(-x )2]x =ln (1-x 2)x =-f (x ),∴函数f (x )为奇函数.(3)显然函数f (x )的定义域为(-∞,0)∪(0,+∞),关于原点对称.∵当x <0时,-x >0,则f (-x )=-(-x )2-x =-x 2-x =-f (x );当x >0时,-x <0,则f (-x )=(-x )2-x =x 2-x =-f (x );综上可知,对于定义域内的任意x ,总有f (-x )=-f (x ),∴函数f (x )为奇函数.思维升华判断函数的奇偶性,其中包括两个必备条件:(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域;(2)判断f (x )与f (-x )是否具有等量关系.在判断奇偶性的运算中,可以转化为判断奇偶性的等价关系式f (x )+f (-x )=0(奇函数)或f (x )-f (-x )=0(偶函数)是否成立.跟踪训练1(1)下列函数中,既不是奇函数也不是偶函数的是()A .f (x )=x +sin 2xB .f (x )=x 2-cos xC .f (x )=3x -13xD .f (x )=x 2+tan x答案D解析对于选项A ,函数的定义域为R ,f (-x )=-x +sin 2(-x )=-(x +sin 2x )=-f (x ),所以f (x )=x +sin 2x 为奇函数;对于选项B ,函数的定义域为R ,f (-x )=(-x )2-cos(-x )=x 2-cos x =f (x ),所以f (x )=x 2-cos x 为偶函数;对于选项C ,函数的定义域为R ,f (-x )=3-x-13-x =-x f (x ),所以f (x )=3x -13x 为奇函数;只有f (x )=x 2+tan x 既不是奇函数也不是偶函数.故选D.(2)(2018·石景山模拟)下列函数中既是奇函数,又在区间(0,+∞)上单调递减的函数为()A .y =xB .y =-x 3C .y =12log xD .y =x +1x答案B解析由题意得,对于函数y =x 和函数y =12log x 都是非奇非偶函数,排除A ,C.又函数y=x +1x 在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,排除D ,故选B.题型二函数的周期性及其应用1.(2018·抚顺模拟)已知f (x )在R 上是奇函数,且满足f (x +4)=f (x ),当x ∈(0,2)时,f (x )=2x 2,则f (7)=________.答案-2解析f (7)=f (-1)=-f (1)=-2.2.已知定义在R上的函数f(x)满足f(2)=2-3,且对任意的x都有f(x+2)=1-f(x),则f(2020)=________.答案-2-3解析由f(x+2)=1-f(x),得f(x+4)=1-f(x+2)=f(x),所以函数f(x)的周期为4,所以f(2020)=f(4).因为f(2+2)=1-f(2),所以f(4)=-1f(2)=-12-3=-2- 3.故f(2020)=-2- 3.3.(2017·山东)已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x,则f(919)=________.答案6解析∵f(x+4)=f(x-2),∴f((x+2)+4)=f((x+2)-2),即f(x+6)=f(x),∴f(x)是周期为6的周期函数,∴f(919)=f(153×6+1)=f(1).又f(x)是定义在R上的偶函数,∴f(1)=f(-1)=6,即f(919)=6.4.设定义在R上的函数f(x)同时满足以下条件:①f(x)+f(-x)=0;②f(x)=f(x+2);③当0≤x<1时,f(x)=2x-1,则f(1)+f(2)+________.答案2-1解析依题意知:函数f(x)为奇函数且周期为2,则f(1)+f(-1)=0,f(-1)=f(1),即f(1)=0.∴f(1)+f(2)+=0+f(0)+=f(0)+=f(0)=122-1+20-1=2-1.思维升华利用函数的周期性,可将其他区间上的求值、求零点个数、求解析式等问题,转化到已知区间上,进而解决问题.题型三函数性质的综合应用命题点1求函数值或函数解析式例2(1)设f (x )是定义在R 上周期为4的奇函数,若在区间[-2,0)∪(0,2]上,f (x )=ax +b ,-2≤x <0,ax -1,0<x ≤2,则f (2021)=________.答案-12解析设0<x ≤2,则-2≤-x <0,f (-x )=-ax +b .因为f (x )是定义在R 上周期为4的奇函数,所以f (-x )=-f (x )=-ax +1=-ax +b ,所以b =1.而f (-2)=f (-2+4)=f (2),所以-2a +b =2a -1,解得a =12,所以f (2021)=f (1)=12×1-1=-12.(2)已知f (x )为偶函数,当x ≤0时,f (x )=e -x -1-x ,则f (x )=________.答案e-x -1-x ,x ≤0,e x -1+x ,x >0解析∵当x >0时,-x <0,∴f (x )=f (-x )=e x -1+x ,∴f (x )e -x -1-x ,x ≤0,e x -1+x ,x >0.命题点2求参数问题例3(1)若函数f (x )=x ln(x +a +x 2)为偶函数,则a =__________.答案1解析∵f (-x )=f (x ),∴-x ln(a +x 2-x )=x ln(x +a +x 2),∴ln[(a +x 2)2-x 2]=0.∴ln a =0,∴a =1.(2)设f (x )是定义在R 上且周期为2的函数,在区间[-1,1]上,f (x )ax +1,-1≤x <0,bx +2x +1,0≤x ≤1,其中a ,b ∈R .若f 12=f 32,则a +3b 的值为________.答案-10解析因为f (x )是定义在R 上且周期为2的函数,所以ff (-1)=f (1),故从而12b +212+1=-12a +1,即3a +2b =-2.①由f (-1)=f (1),得-a +1=b +22,即b =-2a .②由①②得a =2,b =-4,从而a +3b =-10.(3)已知函数f (x )是定义在R 上的奇函数,且当x >0时,f (x )=-x 2+ax -1-a ,若函数f (x )为R 上的减函数,则a 的取值范围是____________.答案[-1,0]解析因为函数f (x )是R 上的奇函数,所以f (0)=0,若函数f (x )为R 上的减函数,则满足当x >0时,函数为减函数,且-1-a ≤0-a -2=a 2≤0,1-a ≤0,≤0,≥-1,即-1≤a ≤0.命题点3利用函数的性质解不等式例4(1)(2018·聊城模拟)已知函数f (x )=|x |(10x -10-x ),则不等式f (1-2x )+f (3)>0的解集为()A .(-∞,2)B .(2,+∞)C .(-∞,1)D .(1,+∞)答案A解析由于f (-x )=-f (x ),所以函数为奇函数,且为单调递增函数,故f (1-2x )+f (3)>0等价于f (1-2x )>-f (3)=f (-3),所以1-2x >-3,x <2,故选A.(2)设函数f (x )=ln(1+|x |)-11+x2,解不等式f (x )>f (2x -1).解由已知得函数f (x )为偶函数,所以f (x )=f (|x |),由f (x )>f (2x -1),可得f (|x |)>f (|2x -1|).当x>0时,f(x)=ln(1+x)-11+x2,因为y=ln(1+x)与y=-11+x2在(0,+∞)上都单调递增,所以函数f(x)在(0,+∞)上单调递增.由f(|x|)>f(|2x-1|),可得|x|>|2x-1|,两边平方可得x2>(2x-1)2,整理得3x2-4x+1<0,解得13<x<1.所以符合题意的x思维升华解决周期性、奇偶性与单调性结合的问题,通常先利用周期性转化自变量所在的区间,再利用奇偶性和单调性求解.跟踪训练2(1)定义在R上的奇函数f(x)满足f(x),当x ,12时,f(x)=12log(1)x ,则f(x)()A.减函数且f(x)>0B.减函数且f(x)<0 C.增函数且f(x)>0D.增函数且f(x)<0答案D解析当x ,12时,由f(x)=12log(1-x)可知,f(x)单调递增且f(x)>0,又函数f(x)为奇函数,所以在区间-12,f(x)<0.由f(x)知,函数的周期为32,f(x)<0.故选D.(2)(2018·烟台模拟)已知偶函数f(x)在[0,+∞)上单调递增,且f(1)=-1,f(3)=1,则满足-1≤f(x-2)≤1的x的取值范围是()A.[3,5]B.[-1,1]C.[1,3]D.[-1,1]∪[3,5]答案D解析由偶函数f(x)在区间[0,+∞)上单调递增,则在区间(-∞,0)上单调递减,又f(1)=-1,f(3)=1,则f(-1)=-1,f(-3)=1,要使得-1≤f(x-2)≤1,即1≤|x-2|≤3,即1≤x-2≤3或-3≤x-2≤-1,解得-1≤x≤1或3≤x≤5,即不等式的解集为[-1,1]∪[3,5],故选D.(3)已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),函数f(x)3,x≤0,(x),x>0,解不等式f(6-x2)>f(x).解∵g(x)是奇函数,∴当x>0时,g(x)=-g(-x)=ln(1+x),易知f(x)在R上是增函数,由f(6-x2)>f(x),可得6-x2>x,即x2+x-6<0,∴-3<x<2.函数的性质函数的奇偶性、周期性及单调性是函数的三大性质,在高考中常常将它们综合在一起命题,解题时,往往需要借助函数的奇偶性和周期性来确定另一区间上的单调性,即实现区间的转换,再利用单调性解决相关问题.一、函数性质的判断例1(1)(2017·全国Ⅰ)已知函数f(x)=ln x+ln(2-x),则()A.f(x)在(0,2)上单调递增B.f(x)在(0,2)上单调递减C.y=f(x)的图象关于直线x=1对称D.y=f(x)的图象关于点(1,0)对称答案C解析f(x)的定义域为(0,2).f(x)=ln x+ln(2-x)=ln[x(2-x)]=ln(-x2+2x).设u=-x2+2x,x∈(0,2),则u=-x2+2x在(0,1)上单调递增,在(1,2)上单调递减.又y=ln u在其定义域上单调递增,∴f(x)=ln(-x2+2x)在(0,1)上单调递增,在(1,2)上单调递减.∴选项A,B错误;∵f(x)=ln x+ln(2-x)=f(2-x),∴f(x)的图象关于直线x=1对称,∴选项C正确;∵f(2-x)+f(x)=[ln(2-x)+ln x]+[ln x+ln(2-x)]=2[ln x+ln(2-x)],不恒为0,∴f(x)的图象不关于点(1,0)对称,∴选项D错误.故选C.(2)定义在R上的函数f(x)满足f(x)=f(-x),且f(x)=f(x+6),当x∈[0,3]时,f(x)单调递增,则f(x)在下列哪个区间上单调递减()A.[3,7]B.[4,5]C.[5,8]D.[6,10]答案B解析依题意知,f(x)是偶函数,且是以6为周期的周期函数.因为当x∈[0,3]时,f(x)单调递增,所以f(x)在[-3,0]上单调递减.根据函数周期性知,函数f(x)在[3,6]上单调递减.又因为[4,5]⊆[3,6],所以函数f(x)在[4,5]上单调递减.(3)定义在实数集R上的函数f(x)满足f(x)+f(x+2)=0,且f(4-x)=f(x).现有以下三个命题:①8是函数f(x)的一个周期;②f(x)的图象关于直线x=2对称;③f(x)是偶函数.其中正确命题的序号是________.答案①②③解析由f(x)+f(x+2)=0可得f(x+4)=-f(x+2)=f(x),∴函数f(x)的最小正周期是4,①对;由f(4-x)=f(x),可得f(2+x)=f(2-x),f(x)的图象关于直线x=2对称,②对;f(4-x)=f(-x)且f(4-x)=f(x),∴f(-x)=f(x),f(x)为偶函数,③对.二、函数性质的综合应用例2(1)(2018·全国Ⅱ)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)等于()A.-50B.0C.2D.50答案C解析∵f(x)是奇函数,∴f(-x)=-f(x),∴f(1-x)=-f(x-1).∵f(1-x)=f(1+x),∴-f(x-1)=f(x+1),∴f(x+2)=-f(x),∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),∴函数f(x)是周期为4的周期函数.由f(x)为奇函数且定义域为R得f(0)=0,又∵f(1-x)=f(1+x),∴f(x)的图象关于直线x=1对称,∴f(2)=f(0)=0,∴f(-2)=0.又f(1)=2,∴f(-1)=-2,∴f(1)+f(2)+f(3)+f(4)=f(1)+f(2)+f(-1)+f(0)=2+0-2+0=0,∴f(1)+f(2)+f(3)+f(4)+…+f(49)+f(50)=0×12+f(49)+f(50)=f(1)+f(2)=2+0=2.故选C.(2)已知定义在R 上的奇函数f (x )满足f (x -4)=-f (x ),且在区间[0,2]上是增函数,则()A .f (-25)<f (11)<f (80)B .f (80)<f (11)<f (-25)C .f (11)<f (80)<f (-25)D .f (-25)<f (80)<f (11)答案D解析因为f (x )满足f (x -4)=-f (x ),所以f (x -8)=f (x ),所以函数f (x )是以8为周期的周期函数,则f (-25)=f (-1),f (80)=f (0),f (11)=f (3).由f (x )是定义在R 上的奇函数,且满足f (x -4)=-f (x ),得f (11)=f (3)=-f (-1)=f (1).因为f (x )在区间[0,2]上是增函数,f (x )在R 上是奇函数,所以f (x )在区间[-2,2]上是增函数,所以f (-1)<f (0)<f (1),即f (-25)<f (80)<f (11).(3)设偶函数f (x )满足f (x )=2x -4(x ≥0),则满足f (a -2)>0的实数a 的取值范围为__________.答案{a |a >4或a <0}解析∵偶函数f (x )满足f (x )=2x -4(x ≥0),∴函数f (x )在[0,+∞)上为增函数,f (2)=0,∴不等式f (a -2)>0等价于f (|a -2|)>f (2),即|a -2|>2,即a -2>2或a -2<-2,解得a >4或a <0.1.下列函数中,既是偶函数又在区间(1,2)内单调递减的是()A .f (x )=xB .f (x )=1x 2C .f (x )=2x +2-xD .f (x )=-cos x答案B解析函数f (x )=1x2是偶函数,且在(1,2)内单调递减,符合题意.2.已知f (x )为定义在R 上的奇函数,当x ≥0时,f (x )=2x +m ,则f (-2)等于()A .-3B .-54C.54D .3答案A 解析由f (x )为R 上的奇函数,知f (0)=0,即f (0)=20+m =0,解得m =-1,则f (-2)=-f (2)=-(22-1)=-3.3.已知y =f (x )是定义在R 上的奇函数,则下列函数中为奇函数的是()①y =f (|x |);②y =f (-x );③y =xf (x );④y =f (x )+x .A .①③B .②③C .①④D .②④答案D解析由奇函数的定义f (-x )=-f (x )验证,①f (|-x |)=f (|x |),为偶函数;②f (-(-x ))=f (x )=-f (-x ),为奇函数;③-xf (-x )=-x ·[-f (x )]=xf (x ),为偶函数;④f (-x )+(-x )=-[f (x )+x ],为奇函数.可知②④正确,故选D.4.已知函数f (x )是定义在R 上的周期为2的奇函数,当0<x <1时,f (x )=4x ,则f (1)等于()A .-2B .0C .2D .1答案A解析∵函数f (x )为定义在R 上的奇函数,且周期为2,∴f (1)=-f (-1)=-f (-1+2)=-f (1),∴f (1)=0,124=-2,∴f (1)=-2.5.(2018·惠州调研)已知定义域为R 的偶函数f (x )在(-∞,0]上是减函数,且f (1)=2,则不等式f (log 2x )>2的解集为()A .(2,+∞)(2,+∞)(2,+∞)D .(2,+∞)答案B解析f (x )是R 上的偶函数,且在(-∞,0]上是减函数,所以f (x )在[0,+∞)上是增函数,所以f (log 2x )>2=f (1)⇔f (|log 2x |)>f (1)⇔|log 2x |>1⇔log 2x >1或log 2x <-1⇔x >2或0<x <12.6.(2018·海南联考)已知函数f (x )是定义在R 上的偶函数,f (x )=f (12-x ),当x ∈[0,6]时,f (x )=log 6(x +1),若f (a )=1(a ∈[0,2020]),则a 的最大值是()A .2018B .2010C .2020D .2011答案D解析由函数f (x )是定义在R 上的偶函数,f (x )=f (12-x ),可得f (-x )=f (12+x ),即f (x )=f (12+x ),故函数的周期为12.令log 6(a +1)=1,解得a =5,∴在[0,12]上f (a )=1的根为5,7;又2020=12×168+4,∴a 的最大值在[2004,2016]上,即2004+7=2011.故选D.7.若f (x )=ln(e 3x +1)+ax 是偶函数,则a =________.答案-32解析函数f (x )=ln(e 3x +1)+ax 是偶函数,故f (-x )=f (x ),即ln(e-3x+1)-ax =ln(e 3x +1)+ax ,化简得ln 1+e 3x e 3x +e 6x =2ax =ln e 2ax,即1+e 3x e 3x +e 6x =e 2ax ,整理得e 3x +1=e 2ax +3x (e 3x +1),所以2ax +3x =0恒成立,所以a =-32.8.已知函数f (x )是奇函数,当x >0时,f (x )=ln x ,则f ________.答案-ln 2解析由已知可得ln 1e2=-2,所以f (-2).又因为f (x )是奇函数,所以f (-2)=-f (2)=-ln 2.9.奇函数f (x )在区间[3,6]上是增函数,且在区间[3,6]上的最大值为8,最小值为-1,则f (6)+f (-3)的值为________.答案9解析由于f (x )在[3,6]上为增函数,所以f (x )的最大值为f (6)=8,f (x )的最小值为f (3)=-1,因为f (x )为奇函数,所以f (-3)=-f (3)=1,所以f (6)+f (-3)=8+1=9.10.若函数f (x )是定义在R 上的偶函数,且在区间[0,+∞)上是单调递增的.如果实数t 满足f (ln t )+2f (1),那么t 的取值范围是________.答案1e,e 解析由于函数f (x )是定义在R 上的偶函数,所以f (ln t )=由f (ln t )+2f (1),得f (ln t )≤f (1).又函数f (x )在区间[0,+∞)上是单调递增的,所以|ln t |≤1,即-1≤ln t ≤1,故1e≤t ≤e.11.已知函数f (x )x 2+2x ,x >0,,x =0,2+mx ,x <0是奇函数.(1)求实数m 的值;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.解(1)设x <0,则-x >0,所以f (-x )=-(-x )2+2(-x )=-x 2-2x .又f (x )为奇函数,所以f (-x )=-f (x ),于是x <0时,f (x )=x 2+2x =x 2+mx ,所以m =2.(2)要使f (x )在[-1,a -2]上单调递增,结合f (x )的图象(如图所示)-2>-1,-2≤1,所以1<a ≤3,故实数a 的取值范围是(1,3].12.设f (x )是定义在R 上的奇函数,且对任意实数x ,恒有f (x +2)=-f (x ).当x ∈[0,2]时,f (x )=2x -x 2.(1)求证:f (x )是周期函数;(2)当x ∈[2,4]时,求f (x )的解析式.(1)证明∵f (x +2)=-f (x ),∴f (x +4)=-f (x +2)=f (x ).∴f (x )是周期为4的周期函数.(2)解∵x ∈[2,4],∴-x ∈[-4,-2],∴4-x ∈[0,2],∴f (4-x )=2(4-x )-(4-x )2=-x 2+6x -8.∵f (4-x )=f (-x )=-f (x ),∴-f (x )=-x 2+6x -8,即f (x )=x 2-6x +8,x ∈[2,4].13.若定义在R 上的偶函数f (x )满足f (x )>0,f (x +2)=1f (x )对任意x ∈R 恒成立,则f (2023)=________.答案1解析因为f (x )>0,f (x +2)=1f (x ),所以f (x +4)=f [(x +2)+2]=1f (x +2)=11f (x )=f (x ),即函数f (x )的周期是4,所以f (2023)=f (506×4-1)=f (-1).因为函数f (x )为偶函数,所以f (2023)=f (-1)=f (1).当x =-1时,f (-1+2)=1f (-1),得f (1)=1f (1).由f (x )>0,得f (1)=1,所以f (2023)=f (1)=1.14.(2018·天津河西区模拟)设f (x )是定义在R 上的偶函数,且当x ≥0时,f (x )=x 2+1,0≤x <1,-2x ,x ≥1,若对任意的x ∈[m ,m +1],不等式f (1-x )≤f (x +m )恒成立,则实数m的最大值是()A .-1B .-13C .-12D.13答案B解析易知函数f (x )在[0,+∞)上单调递减,又函数f (x )是定义在R 上的偶函数,所以函数f (x )在(-∞,0)上单调递增,则由f (1-x )≤f (x +m ),得|1-x |≥|x +m |,即(1-x )2≥(x +m )2,即g (x )=(2m +2)x +m 2-1≤0在x ∈[m ,m +1]上恒成立,当m =-1时,g (x )=0,符合要求,当m ≠-1(m )=(3m -1)(m +1)≤0,(m +1)=(m +1)(3m +1)≤0,解得-1<m ≤-13,所以-1≤m ≤-13,即m 的最大值为-13.15.已知函数f (x )=sin x +x ,对任意的m ∈[-2,2],f (mx -2)+f (x )<0恒成立,则x 的取值范围为______________________________.答案2解析易知f (x )在R 上为单调递增函数,且f (x )为奇函数,故f (mx -2)+f (x )<0等价于f (mx -2)<-f (x )=f (-x ),则mx -2<-x ,即mx +x -2<0对所有m ∈[-2,2]恒成立,令h (m )=mx +x -2,m ∈[-2,2](-2)<0,(2)<0即可,解得-2<x <23.16.已知f (x )是定义在R 上的奇函数,f (x +1)是偶函数,当x ∈(2,4)时,f (x )=|x -3|,求f (1)+f (2)+f (3)+f (4)+…+f (2020)的值.解因为f (x )为奇函数,f (x +1)为偶函数,所以f (x +1)=f (-x +1)=-f (x -1),所以f (x +2)=-f (x ),所以f (x +4)=-f (x +2)=f (x ),所以函数f(x)的周期为4,所以f(4)=f(0)=0,f(3)=f(-1)=-f(1).在f(x+1)=f(-x+1)中,令x=1,可得f(2)=f(0)=0,所以f(1)+f(2)+f(3)+f(4)=0.所以f(1)+f(2)+f(3)+f(4)+…+f(2020)=0.。
基本初等函数知识总结

基本初等函数1.根式的运算性质:①当n 为任意正整数时,(n a )n =a②当n 为奇数时,nna =a ;当n 为偶数时,nna =|a|=⎩⎨⎧<-≥)0()0(a a a a2.分数指数幂的运算性质:)()(),()(),(Q n b a ab Q n m a a Q n m a a a n n n mn n m n m n m ∈⋅=∈=∈=⋅+ 3.指数式与对数式的互化:log b a a N N b =⇔=4.重要公式: 01log =a ,1log =a a 对数恒等式N aNa =log5.对数的运算法则:如果0,1,0,0a a N M >≠>>有log ()log log a a a MN M N =+;log log log aa a MM N N=-;log log n a a M n M = 6.对数换底公式:aNN m m a log log log =( a > 0 ,a ≠ 1 ,m > 0 ,m ≠ 1,N>0)7.指数函数)1,0(≠>=a a a y x与对数函数)1,0(log ≠>=a a x y a的图象与性质x=1x=1y=1y=1在(0,+∞)内是 减函数在(0,+∞)内是 增函数在(- ∞,+∞)内是 减函数在(- ∞,+∞)内是 增函数0<x<1时,y<0;x>1时,y>0.0<x<1时,y>0;x>1时,y<0.x<0时,0<y<1;x>0时,y>1.x<0时,y>1;x>0时,0<y<1.(1,0),即x=1时,y=0.(0,1),即x =0时,y=1.(0,+∞)(0,+∞)(- ∞,+∞)(- ∞,+∞) 单调性y 值区域过定点值 域定义域图象a>10<a<1a>10<a<1a y=log a xy=a x函数11O O OO1axy1a xy1axy1a xy8.同底的指数函数)1,0(≠>=a a a y x与对数函数)1,0(log ≠>=a a x y a 互为反函数,其图象关于直线x y =对称9.幂函数y x α=的概念、图像和性质:结合函数y=x,y=x 2 ,y=x 3,y=12,y x y x--==,y=12x 的图像,了解它们的变化情况.①α>0时,图像都过(0,0)、(1,1)点,在区间(0,+∞)上是增函数; 注意α>1与0<α<1的图像与性质的区别.②α<0时,图像都过(1,1)点,在区间(0,+∞)上是减函数;在第一象限内,图像向上无限接近y 轴,向右无限接近x 轴.③当x>1时,指数大的图像在上方.幂 函 数 复 习一、幂函数定义:形如)(R x y ∈=αα的函数称为幂函数,其中x 是自变量,α是常数。
2024年高考数学总复习第二章《函数与基本初等函数》模考卷及答案解析

2024年高考数学总复习第二章《函数与基本初等函数》模考卷(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.函数y =ln x +1-x 的定义域是()A .(0,1)B .[0,1)C .(0,1]D .[0,1]答案C解析>0,-x ≥0,解得0<x ≤1,所以函数f (x )的定义域为(0,1].故选C.2.下列函数中,既是奇函数,又在区间(0,1)上递减的函数是()A .y =cos xB .y |C .y =tan xD .y =x-3答案D解析由于y =cos x 是偶函数,故A 不是正确选项.由于y |是偶函数,故B 不是正确选项.由于y =tan x 在(0,1)上为增函数,故C 不是正确选项.D 选项中y =x -3既是奇函数,又在(0,1)上递减,符合题意.故选D.3.设函数y =log 3x 与y =3-x 的图象的交点为(x 0,y 0),则x 0所在的区间是()A .(0,1)B .(1,2)C .(2,3)D .(3,4)答案C解析因为方程log 3x =-x +3的解,就是m (x )=log 3x +x -3的零点,因为m (x )=log 3x +x -3单调递增且连续,m (x )=log 3x +x -3在(1,2)上满足m (1)m (2)>0,m (x )=log 3x +x -3在(2,3)上满足m (2)m (3)<0,所以m (x )=log 3x +x -3的零点在(2,3)内,可得方程log 3x +x -3=0的解所在的区间是(2,3),即则x 0所在的区间是(2,3),故选C.4.若a =π82=1πlog b ,c =log ()A .b >c >aB .a >b >cC .c >a >bD .b >a >c答案B解析a =π82>20=1,∵0<1π<1,1πlog b >0,∴0<b <1,c =log log 232<log 21=0,∴a >b >c .故选B.5.(2019·山师大附中模拟)函数f (x )-2a )x +3a (x <1),x (x ≥1)的值域为R ,则实数a 的取值范围是()A .(-∞,-1) B.12,1C.-1答案C解析因为函数f (x )-2a )x +3a (x <1)x (x ≥1),的值域为R -2a >0,1-2a )+3a ≥0,解得-1≤a <12,故选C.6.函数y =2xln|x |的图象大致为()答案B解析采用排除法,函数定义域为{x |x ≠0且x ≠±1},排除A ;当x >1时,ln|x |>0,y =2xln|x |>0,排除D ;当x <-1时,ln|x |>0,y =2x ln|x |<0,排除C ,故选B.7.(2019·山师大附中模拟)函数f (x )是R 上的偶函数,且f (x +1)=-f (x ),若f (x )在[-1,0]上单调递减,则函数f (x )在[3,5]上是()A.增函数B.减函数C.先增后减的函数D.先减后增的函数答案D解析已知f(x+1)=-f(x),则函数周期T=2,因为函数f(x)是R上的偶函数,在[-1,0]上单调递减,所以函数f(x)在[0,1]上单调递增,即函数在[3,5]上是先减后增的函数.故选D.8.(2019·新乡模拟)设函数f(x)=e-x-e x-5x,则不等式f(x2)+f(-x-6)<0的解集为() A.(-3,2)B.(-∞,-3)∪(2,+∞)C.(-2,3)D.(-∞,-2)∪(3,+∞)答案D解析由f(x)=e-x-e x-5x,得f(-x)=e x-e-x+5x=-f(x),则f(x)是奇函数,故f(x2)+f(-x-6)<0⇔f(x2)<-f(-x-6)=f(x+6).又f(x)是减函数,所以f(x2)<f(x+6)⇔x2>x+6,解得x<-2或x>3,故不等式f(x2)+f(-x-6)<0的解集为(-∞,-2)∪(3,+∞),故选D.9.(2019·广东六校模拟)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(2019)等于()A.-2018B.2C.0D.50答案C解析f(x)是定义域为(-∞,+∞)的奇函数,可得f(-x)=-f(x),f(1-x)=f(1+x)即有f(x+2)=f(-x),即f(x+2)=-f(x),进而得到f(x+4)=-f(x+2)=f(x),f(x)为周期为4的函数,若f(1)=2,可得f(3)=f(-1)=-f(1)=-2,f(2)=f(0)=0,f(4)=f(0)=0,则f(1)+f(2)+f(3)+f(4)=2+0-2+0=0,可得f(1)+f(2)+f(3)+…+f(2019)=504×0+2+0-2=0.故选C.10.(2019·衡水中学摸底)已知函数f(x)e x,x≤0,x,x>0(e为自然对数的底数),若关于x 的方程f(x)+a=0有两个不相等的实根,则a的取值范围是()A .a >-1B .-1<a <1C .0<a ≤1D .a <1答案C解析画出函数f (x )的图象如图所示,若关于x 的方程f (x )+a =0有两个不相等的实根,则函数f (x )与直线y =-a 有两个不同交点,由图可知-1≤-a <0,所以0<a ≤1.故选C.11.(2019·新疆昌吉教育共同体月考)若关于x 的不等式1+a cos x ≥23sin 2R 上恒成立,则实数a 的最大值为()A .-13 B.13C.23D .1答案B解析1+a cos x ≥23sin 2=23cos 2x =23(2cos 2x -1),令cos x =t ∈[-1,1],并代入不等式,则问题转化为不等式4t 2-3at -5≤0在t ∈[-1,1]+3a -5≤0,-3a -5≤0,所以-13≤a ≤13.所以实数a 的最大值为13.12.(2019·沈阳东北育才学校模拟)设函数f (x )+1|,x ≤0,4x |,x >0,若关于x 的方程f (x )=a 有四个不同的解x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则x 3(x 1+x 2)+1x 23x 4的取值范围是()1,721C .(-1,+∞)-∞,72答案A解析画出函数f (x )的图象如图所示,根据对称性可知,x 1和x 2关于x =-1对称,故x 1+x 2=-2.由于|log 4x |=|log 41x |,故1x 3=x 4,x 3·x 4=1.令log 41x =1,解得x =14,所以x 3∈14,x 3(x 1+x 2)+1x 23x 4=-2x 3+1x 3,由于函数y =-2x +1x 在区间14,减函数,故-2x 3+1x 3∈1,72,故选A.二、填空题(本大题共4小题,每小题5分,共20分)13.函数f (x )=ln x -2的定义域为________.答案[e 2,+∞)解析∵函数f (x )=ln x -2,∴ln x -2≥0,即ln x ≥ln e 2,∴x ≥e 2,∴函数f (x )=ln x -2的定义域为[e 2,+∞).14.(2019·浏阳六校联考)f (x )是定义在R 上的周期为3的奇函数,当0<x <1时,f (x )=4x ,则f (6)=________.答案-2解析由题意得-72+=-124=-2,又f (6)=f (0)=0,∴f (6)=-2.15.(2019·青岛调研)已知函数f (x )3(x +1),x >0,-x ,x ≤0,f (m )>1,则m 的取值范围是____________.答案(-∞,0)∪(2,+∞)解析若f (m )>1>0,3(1+m )>log 33≤0,-m >1,>0,+1>3≤0,m >0,解得m >2或m <0.16.已知函数f (x )2+3a ,x <0,a (x +1)+1,x ≥0(a >0且a ≠1)在R 上单调递减,且关于x 的方程|f (x )|=2-x 恰好有两个不相等的实数解,则a 的取值范围是________.答案13,23∪解析画出函数y =|f (x )|的图象如图,由函数y =f (x )是单调递减函数可知,0+3a ≥log a (0+1)+1,即a ≥13,由log a (x 0+1)+1=0得,x 0=1a -1≤2,所以当x ≥0时,y =2-x 与y =|f (x )|图象有且仅且一个交点.所以当2≥3a ,即13≤a ≤23时,函数y =|f (x )|与函数y =2-x 图象恰有两个不同的交点,即方程|f (x )|=2-x 恰好有两个不相等的实数解,结合图象可知当直线y =2-x 与函数y =x 2+3a 相切时,得x 2+x +3a -2=0.由Δ=1-4(3a -2)=0,解得a =34,此时也满足题意.综上,所求实数a 的取值范围是13,23∪三、解答题(本大题共70分)17.(10分)(2019·酒泉敦煌中学诊断)求下列函数的解析式:(1)已知2f (x -1)-f (1-x )=2x 2-1,求二次函数f (x )的解析式;(2)已知f (x -1)=x ,求f (x )的解析式.解(1)设f (x )=ax 2+bx +c (a ≠0),则f (x -1)=a (x -1)2+b (x -1)+c ,f (1-x )=a (1-x )2+b (1-x )+c ,所以2f (x -1)-f (1-x )=2ax 2-4ax +2a +2bx -2b +2c -(ax 2-2ax +a +b -bx +c )=ax 2-(2a -3b )x +a -3b +c =2x2-1,=2,a -3b =0,-3b +c =-1,=2,=43,=1,所以f (x )=2x 2+43x +1.(2)令t =x -1,t ≥-1,则x =(t +1)2,∴f (t )=(t +1)2(t ≥-1).∴f (x )的解析式为f (x )=(x +1)2,x ≥-1.18.(12分)(2019·廊坊省级示范高中联考)已知函数f (x )=log 3(ax 2-x +3).(1)若函数f (x )的定义域为R ,求a 的取值范围;(2)已知集合M =[1,3],方程f (x )=2的解集为N ,若M ∩N ≠∅,求a 的取值范围.解(1)因为函数的定义域为R ,所以ax 2-x +3>0恒成立,当a =0时,-x +3>0不恒成立,不符合题意;当a ≠0>0,=1-12a <0,解得a >112.综上所述a >112.(2)由题意可知,ax 2-x +3=9在[1,3]上有解.即a =6x 2+1x 在[1,3]上有解,设t =1x,t ∈13,1,则a =6t 2+t ,因为y =6t 2+t 在13,1上单调递增,所以y ∈[1,7].所以a ∈[1,7].19.(12分)函数f (x )对任意的a ,b ∈R 都有f (a +b )=f (a )+f (b )-1,并且当x >0时,f (x )>1.(1)判断函数f (x )是否为奇函数;(2)证明:f (x )在R 上是增函数;(3)解不等式f (3m 2-m -2)<1.(1)解当a =b =0时,解得f (0)=1,显然函数不可能是奇函数.(2)证明任取x 1,x 2∈R ,且x 1<x 2,则f (x 2)-f (x 1)=f [(x 2-x 1)+x 1]-f (x 1)=f (x 2-x 1)+f (x 1)-1-f (x 1)=f (x 2-x 1)-1,∵x 2-x 1>0,∴f (x 2-x 1)>1,∴f (x 2)-f (x 1)>0,∴f (x )在R 上是增函数.(3)∵f (0)=1,∴f (3m 2-m -2)<1=f (0),又f (x )在R 上递增,所以3m 2-m -2<0,解得-23<m <1,∴-23,20.(12分)已知定义在R 上的函数f (x )是偶函数,当x ≥0时,f (x )=x 2-4x +1.(1)求函数f (x )在R 上的解析式;(2)若方程m =f (x )有4个根x 1,x 2,x 3,x 4,求m 的取值范围及x 1+x 2+x 3+x 4的值.解(1)设x <0⇒-x >0⇒f (-x )=(-x )2-4(-x )+1=x 2+4x +1,由函数f (x )是偶函数,则f (x )=f (-x )=x 2+4x +1,综上f (x )2-4x +1,x ≥0,2+4x +1,x <0或f (x )=x 2-4|x |+1.(2)作出函数f (x )的图象如图所示,由图可知,当-3<m <1时,方程m =f (x )有4个根.令x 1<x 2<x 3<x 4,由x 1+x 22=-2,x 3+x 42=2,得x 1+x 2=-4,x 3+x 4=4,则x 1+x 2+x 3+x 4=0.21.(12分)(2019·荆州质检)为响应国家提出的“大众创业,万众创新”的号召,小李同学大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为5万元,每年生产x 万件,需另投入流动成本为C (x )万元,且C (x )=2+4x ,0<x <8,x +49x -35,x ≥8,每件产品售价为10元.经市场分析,生产的产品当年能全部售完.(1)写出年利润P (x )(万元)关于年产量x (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?解(1)因为每件产品售价为10元,则x 万件产品销售收入为10x 万元,依题意得,当0<x <8时,P (x )=10x 2+45=-12x 2+6x -5,当x ≥8时,P (x )=10x x +49x -5=30所以P (x )-12x 2+6x -5,0<x <8,x ≥8.(2)当0<x <8时,P (x )=-12(x -6)2+13,当x =6时,P (x )取得最大值P (6)=13,当x ≥8时,P ′(x )=-1+49x 2<0,所以P (x )为减函数,当x =8时,P (x )取得最大值P (8)=1278,因为13<1278,故当年产量为8万件时,小李在这一产品的生产中所获利润最大,最大利润为1278万元.22.(12分)(2019·佛山禅城区调研)已知f (x )是定义在(-1,1)上的奇函数,当x ∈(0,1)时,f (x )=2x 4x +1.(1)求f (x )在(-1,1)上的解析式;(2)若g (x )是周期为2的函数,且x ∈(-1,1)时g (x )=f (x ),求x ∈(2n ,2n +1),n ∈N 时函数g (x )的解析式.解(1)当x ∈(-1,0)时,-x ∈(0,1),因为函数f (x )为奇函数,所以f (x )=-f (-x )=-2-x4-x +1=-2x1+4x .因为f (x )是定义在(-1,1)上的奇函数,所以f (0)=0,故当x ∈(-1,1)时,f (x )的解析式为f (x )∈(0,1),x ∈(-1,0).(2)设x ∈(2n ,2n +1),则x -2n ∈(0,1),g (x -2n )=2x-2n4x -2n +1.因为g (x )周期为2,n ∈N ,所以2n 也是周期,g (x -2n )=g (x ),所以x ∈(2n,2n +1)时,g (x )=2x -2n 4x-2n+1.。
基本初等函数经典复习题+答案
必修1根本初等函数复习题求函数的定义域时列不等式组的主要依据是:⑴偶次方根的被开方数不小于零;(2)对数式的真数必须大于零;⑶分式的分母不等于零;[4〕指数、对数式的底必须大于零且不等于1.4、函数单调区间与单调性的判定方法(八)定义法:①任取xι,X 2∈D,且XKX2;Q)作差千(xι)—fa);(3)变形〔通常是因式分解和配方];④定号[即判断差千(x∣)-f(x2)的正负〕;@下结论[指出函数f(x)在给定的区间D 上的单调性].(B)图象法(从图象上看升降)⑹复合函数的单调性:复合函数Hg"]的单调性与构成它的函数u=g(x),y 二人。
的单调性密切相关,其规律:"同增异减〃 1、以下函数中,在区间(0,÷oo)不是增函数的是()1、暴的运算性质 〔1〕a r ∙a s = a r+s (r,5 ∈ R); 〔3〕a r ∙b r = (ab)r (r ∈ R) 2对数的运算性质 如果 α>0,且 awl, M >0, ① Iog“(M ・N)= Iogq M +log” N ; ③ IOg“M" =〃Iog"M,(Y ∈R). 换底公式:log” b = l°g 。
■ 〔 a IogC α(1)log b n= —log rt ⅛ ; [2 〃7 〔2〕S)' =α" ; (r,StR)(4)a" =yja n, (a>0,m,n E N ∖n> 1) a' = N Q IOga N = x N>0,那么:② log 噂=log” M Tog” N ;④ IOgQl= O, bg" = lO,且 awl ; c>0,且 CW1; b>0〕 log” b =; ---- ∙log/y = a x a>1 0<a<1 y = Iog tj X a>1 II0<a<1定义域R 值域y>0 在R 上单调递增 非奇非偶函数 函数图象都过定点[0, 1〕 3、定义域: 定义域R 值域y>0 在R 上单调递减 非奇非偶函数 函数图象都过定点〔〕 定义域x>0 值域为R在R 上递增 非奇非偶函数 函数图象都过定点定义域x>0值域为R 在R 上递减 非奇非偶函数 函数图象都过定点[1, 能使函数式有意义的实数X 的集合称为函数的定义域。
基本初等函数复习
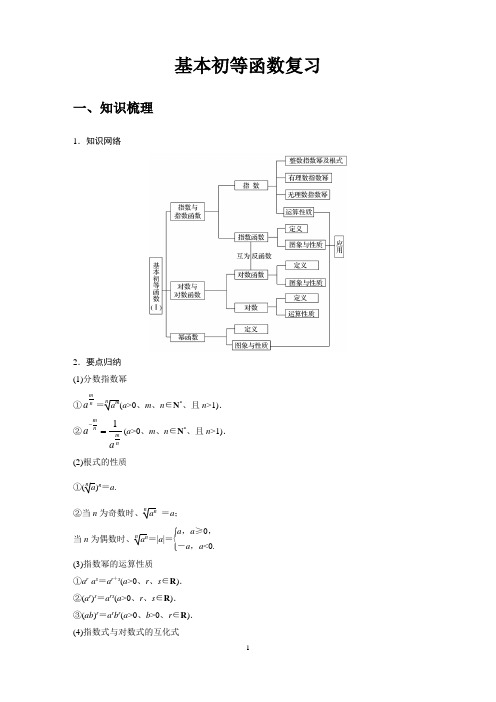
基本初等函数复习一、知识梳理1.知识网络2.要点归纳 (1)分数指数幂①m na =na m (a >0、m 、n ∈N *、且n >1). ②1m n m naa-=(a >0、m 、n ∈N *、且n >1).(2)根式的性质 ①(na )n =a .②当n 为奇数时、na n =a ;当n 为偶数时、na n =|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0.(3)指数幂的运算性质 ①a r ·a s =a r +s (a >0、r 、s ∈R ). ②(a r )s =a rs (a >0、r 、s ∈R ). ③(ab )r =a r b r (a >0、b >0、r ∈R ). (4)指数式与对数式的互化式log a N =b ⇔a b =N (a >0、且a ≠1、N >0). (5)对数的换底公式log a N =log m Nlog m a(a >0、且a ≠1、m >0、且m ≠1、N >0).推论:log m na b =n m log a b (a >0、且a ≠1、m 、n >0、且m ≠1、n ≠1、b >0).(6)对数的四则运算法则若a >0、且a ≠1、M >0、N >0、则 ①log a (MN )=log a M +log a N ; ②log a MN =log a M -log a N ;③log a M n =n log a M (n ∈R ). (7)指数函数①理解指数函数概念及单调性.②会画具体指数函数图象并掌握图象通过的特殊点. (8)对数函数①理解对数函数概念及单调性.②会画具体对数函数图象并掌握图象通过的特殊点. ③了解y =a x 、y =log a x (a >0、且a ≠1)互为反函数. (9)幂函数①了解幂函数的概念.②结合y =x α、α=-1、12、1、2、3的图象、了解它们的性质.二、专题讲解1、 指数、对数的运算1、化简:(1)2932)-⨯ (2)2log 32-log 3329+log 38-5log 325.2、已知22(xxa a -+=为常数、)x Z ∈、求88x x -+的值3、计算80.25×42+(32×3)6+log 32×log 2(log 327)的值为________.4、22(lg 2)(lg 5)2lg 2lg 5++⋅= 5、设,,a b c 都是正数、且346a b c ==、则下列正确的是( )111.A c a b =+ 221.B c a b =+ 122.C c a b =+ 212.D c a b =+ 6、已知1414log 7,log 5,a b ==则用,a b 表示35log 28=2、函数的解析式1、函数()xa a a 33y 2+-=是指数函数、求a 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数总复习【知识点回顾】一、指数与指数幂的运算 (1)根式的概念①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 次方根用符号n 是偶数时,正数a 的正的n n 次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.n a =;当n a =;当n 为偶数时, (0)|| (0) a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈ 二、指数函数及其性质 (4)指数函数定义域R值域(0,+∞)过定点图象过定点(0,1),即当x=0时,y=1.奇偶性非奇非偶单调性在R上是增函数在R上是减函数函数值的变化情况y>1(x>0), y=1(x=0), 0<y<1(x<0)y>1(x<0), y=1(x=0), 0<y<1(x>0)a变化对图象的影响在第一象限内,a越大图象越高,越靠近y轴;在第二象限内,a越大图象越低,越靠近x轴.在第一象限内,a越小图象越高,越靠近y轴;在第二象限内,a越小图象越低,越靠近x轴.【考点链接】考点一、指数的运算xay=xy(0,1)O1y=xay=xy(0,1)O1y=例1.化简:1114424111244()a b b a a b --=- .例2. 根据下列条件求值:已知32121=+-xx ,求23222323-+-+--x x x x 的值;练习1:计算:(1)1020.5231(2)2(2)(0.01)54--+⋅-(2)120.750311(0.064)()16()2322----÷+-.(3) 2433221)(---⋅÷⋅a b b a(4)211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭考点二、定义域例3. 求下列函数的定义域:21(1).2-=x y 31(2).3-⎛⎫= ⎪⎝⎭xy练习2.求下列函数的定义域:(1)1x 21y ()2-= (2)2x 3y 5-=考点三、值域例4. 函数11x x e y e -=+的值域练习3、(1)求函数2(0)21xxy x =>+的值域.(2)求下列函数的定义域、值域: (1)1218x y -= (2)11()2x y =-(3)3x y -=考点四、指数型函数例5. 已知函数3234+⋅-=x x y 的定义域为[0,1],则值域为 。
练习4.若方程0)21()41(=++a x x 有正数解,则实数a 的取值范围是考点五、函数的奇偶性与解析式例6.(1)函数()f x 是奇函数,且当0x ≥时,()1x f x e =-,则x R ∈ 时,()f x =_____.(2)设0,()x x e aa f x a e>=+是R 上的偶函数,则a =________________.练习5.(1)定义在R 上的函数()f x 是奇函数,且当0x >时,()1x f x e =+,则x R ∈ 时,()f x =__________. (2)已知函数1()21xf x a =-+,若()f x 为奇函数,则a =________________. (3)已知)1,0(1)1()(≠>+-=a a a a x x f xx ,试判定)(x f 的奇偶性。
考点五、函数的单调性例7.(1)比较下列各组数的大小:(1)0.1-和 0.24-; (2)163()4和154()3-; (3)2(0.8)-和125()3- .(2)试比较8.08.0=a ,8.09.02.1,8.0==c b 三者之间的大小关系。
例8. 已知函数5213222)21()(,)21()(-++-==x x x x x g x f ,(1)求使)()(x g x f >成立的x 值;(2)求使)(x f 、)(x g 均为增函数的单调区间; (3)求)(x f 和)(x g 的值域。
练习6.(1)比较下列各组数的大小:(1)0.73-和0.33-; (2)133()2和142()3-; (3)5(0.6)-和154()3- .(2)设10<<a ,1>>n m ,试确定aa n m n m a a ,,,的大小关系。
考点六、综合应用例9.已知函数1()(1,0)1x xa f x a a a -=>≠+且. (1)求()f x 的定义域和值域;(2)讨论()f x 单调性.例10.已知函数)(2)(2xx a a a a x f ---=,其中1,0≠>a a ,是R 上的增函数,求a 的取值范围。
练习7. 已知函数31()(1,0)31+=>≠-x xf x a a . (1)求()f x 的定义域和值域;(2)讨论()f x 单调性.练习8. 设)2()(,111)(||x f x g x x f =-+=。
(1)写出函数)(x f 与)(x g 的定义域。
(2)函数)(x f 与)(x g 是否具有奇偶性,并说明理由。
(3)求出函数)(x g 的单调递减区间。
【课后练习】 一、选择题:1.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个)。
经过3个小时,这种细菌由1个可繁殖成( )511.A 个 512.B 个 1023.C 个 1024.D 个2.在统一平面直角坐标系中,函数ax x f =)(与x a x g =)(的图像可能是( )3.设d cb a ,,,都是不等于1的正数,x x x x d y c y b ya y ====,,,在同一坐标系中的图像如图所示,则d c b a ,,,的大小顺序是( )d c b a A <<<. c d b a B <<<. c d a b C <<<. d c a b D <<<.4. 函数c bx x x f +-=2)(满足)2()(x f x f -=且3)0(=f ,则)(x b f 与)(x c f 的大小关系是( )A. )()(x x c f b f ≤B. )()(x x c f b f ≥C. )()(x x c f b f >D. 不能确定5.若01<<-x ,那么下列各不等式成立的是( )x x x A 2.022.<<- x x x B -<<22.02. x x x C 222.0.<<- x x x D 2.022.<<-6.函数x a x f )1()(2-=在R 上是减函数,则a 的取值范围是( )1.>a A2.<a B 2.<a C 21.<<a D 7.函数121-=x y 的值域是( ) )1,.(-∞A ),0()0,.(+∞-∞ B ),1.(+∞-C ),0()1,.(+∞--∞ D8.当1>a 时,函数11-+=x x a a y 是( ).A 奇函数 .B 偶函数 .C 既奇又偶函数 .D 非奇非偶函数 9.函数0.(12>+=-a a y x 且)1≠a 的图像必经过点( ))1,0.(A )1,1.(B )0,2.(C )2,2.(D10.某厂1998年的产值为a 万元,预计产值每年以n %递增,则该厂到2010年的产值(单位:万元)是( )n a A +1(.%13) n a B +1(.%12) n a C +1(.%11) n D -1(910.%12) 二、填空题:1.已知)(x f 是指数函数,且255)23(=-f ,则=)3(f2.设10<<a ,使不等式531222+-+->x xx xa a 成立的x 的集合是3.函数x x y 28)13(0-+-=的定义域为 4.函数xx y -=22的单调递增区间为三、解答题:1.设20≤≤x ,求函数523421+•-=-x x y 的最大值和最小值。
2函数0()(>=a a x f x 且)1≠a 在区间]2,1[上的最大值比最小值大2a,求a 的值。
3.设R a ∈,)(,1222)(R x a a x f xx ∈+-+•=试确定a 的值,使)(x f 为奇函数。
4.已知函数1762)21(+-=x x y (1)求函数的定义域及值域;(2)确定函数的单调区间。
5.已知函数3)21121()(x x f x +-= (1)求函数的定义域; (2)讨论函数的奇偶性; (3)证明:0)(>x f对数函数总复习【知识点回顾】 一、对数与对数运算 (1)对数的定义①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式: log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数:常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a M M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a NaN =⑤log log (0,)b na a n M Mb n R b=≠∈ ⑥换底公式:log log (0,1)log b a b N N b b a =>≠且 二、对数函数及其性质 (5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y f x -=. (7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=; ③将1()x f y -=改写成1()y f x -=,并注明反函数的定义域. (8)反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域. ③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上. ④一般地,函数()y f x =要有反函数则它必须为单调函数.【考点链接】 考点一、对数的运算例1、(1)计算: 9log 27, 625.(2)求 x 的值:①33log 4x =-; ②()2221log 3211x x x ⎛⎫ ⎪⎝⎭-+-=.(3)求底数:①已知48log 2=x ,求x 的值 ②7log 28x =,求x 的值 (4)已知0)](lg [log log 25=x ,求x 的值 例2、计算: (1)lg14-21g 18lg 7lg 37-+; (2)9lg 243lg ; (3)2.1lg 10lg 38lg 27lg -+.练习1、计算:(1) 0.21log 35-; (2)492log 3log 2log ⋅+练习2、已知18log 9a =,185b =,求36log 45(用 a , b 表示).练习3、设1643>===t z y x ,求证:yx z 2111=-.练习4、若8log 3p =,3log 5q =,求lg 5.考点二、函数的定义域 例3、求下列函数的定义域:(1)2log x y a =; (2))4(log 2x y -=; (3))9(log 2x y a -=.练习5、求下列函数的定义域:(1))1,0(1log ≠>-=a a x y a (2))12(log 2+=x y(3)11lg -=x y (4))1(log )(31-=x x f (5))3(log )()1(x x f x -=-考点三、函数的值域 例4、求下列函数的值域:(1)2log (3)y x =+;(2)22log (3)y x =-;(3)2log (47)a y x x =-+(0a >且1a ≠).练习6、求下列函数的值域(1) )1lg(2+=x y (2))8(log 25.0+-=x y考点五、对数函数的单调性例5、比较下列各组数中两个值的大小:(1)2log 3.4,2log 8.5; (2)0.3log 1.8,0.3log 2.7; (3)log 5.1a ,log 5.9a .例6、已知log 4log 4m n <,比较m ,n 的大小。
