电场强度与电势梯度-精选
电势梯度和电场强度的关系

电势梯度和电场强度的关系
电势梯度和电场强度是电学中两个非常重要的概念,它们之间存在着密切的关系。
电势梯度是指电势在空间中的变化率,而电场强度则是指单位电荷在电场中所受到的力的大小。
在电学中,电势梯度和电场强度的关系是非常紧密的,它们之间的关系可以用以下公式来表示:
E = -∇V
其中,E表示电场强度,V表示电势,∇表示梯度运算符。
这个公式告诉我们,电场强度的大小与电势梯度的大小成反比。
也就是说,当电势梯度越大时,电场强度就越小;反之,当电势梯度越小时,电场强度就越大。
这个公式的意义可以通过一个简单的例子来说明。
假设我们有一个电荷为Q的点电荷,它在空间中产生了一个电势场。
如果我们想知道在某一点P处的电场强度,我们可以通过以下步骤来计算:
1. 首先,我们需要计算出点P处的电势V。
2. 然后,我们需要计算出点P处的电势梯度∇V。
3. 最后,我们可以通过公式E = -∇V来计算出点P处的电场强度E。
这个例子告诉我们,电势梯度和电场强度之间的关系是非常密切的。
在电学中,我们经常使用这个公式来计算电场强度,从而更好地理解电场的性质和行为。
电势梯度和电场强度是电学中两个非常重要的概念,它们之间存在着密切的关系。
电场强度的大小与电势梯度的大小成反比,这个关系可以用公式E = -∇V来表示。
在电学中,我们可以通过这个公式来计算电场强度,从而更好地理解电场的性质和行为。
8.5电场强度与电势梯度的关系

E
ds
等势面——规定、性质、梯度
gradU
U n
n
三、 q、E、U 三者关系网
1、 q E
E
1
4 0
dq r3
r
sE
ds
1
0
vdv
2、 q U
U
1
4 0
dq r
U LE dl
3 E U
U LE dl
势面2,电场力做功
dA qE dl
qEdl cos
en
1
2
P1
en P2
P3
qEdn
V V+dV
上页 下页 返回 退出
电场力做功等于电势能的减少量 dA q dU
E dU dn
场强也与等势面垂直,但指向电势降低的方向。
E Een 写成矢量形式
E
第一章 真空中静电场小结
一、理论体系:
出发点
:叠 库加 仑原 定理 律
高斯定理 环路定理
电场为有源场 电场是有势场
二、内容:
1、一个定律 : 2、两个定理 :
F
q1q2
4 0
r r3
E
ds
1
dv
s
0 v
l E dl 0
上页 下页 返回 退出
则 dn dl cos
dU dU cos
dl dn
2
P1
en P2
P3
U U+dU
上页 下页 返回 退出
定义电势梯度
高二物理竞赛课件:电场强度与电势梯度

40a(a l )
Q
Q a l
(2)球在 x 处电势 V 4 0 x
ln 40 a
2
电场强度和电势梯度 d V:两等位面电势之差。
E
dl
nˆ
d l:两等位面间在P1点处的最短距离。 P1
P2
(等位面间在P1点处的法向距离)
nˆ :P1点处法线方向上的单位矢量,
V V dV
指向电势升高的方向。
r
dr
2 0
4 0
(
R2
r2
)
0
外电场对电偶极子的力矩和取向作用
解:电偶极子受 力偶的作用
F qE F qE
合力: F F F
电矩
0
p ql
l
F
q
q
F E
故偶极子不平动。 合力矩:
M 的方向
M
M
2F
P
l 2
sin qEl
E
M使 p
sin
转向
E
pE
sin
2
电荷在外电场中的静电势能 任何电荷在静电场中都具有势能,叫的静电势能。
E R2
若令V= 0 则
rR V
R2
E dl
r
2 0 r
r
R2 dr 2 0 r
ln 电势发散,无意义!
20 r
R
只能取有限远处电势为零。
r
若令柱面 处 VR=0,则
r > R:V R R2 dr R2 ln R 0
r 20r
20 r
r
r < R:V
R r
W q0 (Vb Va )
2
例、长为L 的均匀带电导线,电荷线密度为 。
电势梯度和电场强度的关系

电势梯度和电场强度的关系电势梯度与电场强度是电学中两个重要的概念,它们之间存在着密切的联系和相互依赖关系。
本文将从电势梯度和电场强度的定义、计算方法以及它们之间的关系等方面展开阐述。
我们来了解一下电势梯度和电场强度的定义。
电势梯度是指电势在空间中变化的快慢程度,表示为电势的变化率。
电场强度是指单位正电荷所受的力的大小和方向,表示为电场力的大小。
电势梯度的计算方法是通过对电势函数沿着某一方向求偏导数,即电势梯度等于电势函数在某一方向上的偏导数。
电场强度的计算方法是通过库仑定律得到的,即电场强度等于单位正电荷所受力的大小。
接下来,我们来探讨电势梯度和电场强度之间的关系。
根据定义可知,电场强度是电势梯度的负梯度,即电场强度与电势梯度具有相反的方向。
这是因为电势梯度表示电势的变化率,而电场强度表示单位正电荷所受的力的大小和方向,二者之间存在着直接的关系。
进一步地,我们可以通过电势梯度和电场强度的性质来理解它们之间的关系。
首先,电势梯度的方向指向电势变化率最快的方向,而电场强度的方向指向力的作用方向。
由于力的方向是电势下降最快的方向,所以电势梯度的方向与电场强度的方向相反。
电势梯度的大小与电场强度的大小成正比。
根据电势梯度的定义可知,电势梯度的大小等于电势函数在某一方向上的偏导数。
而根据电场强度的定义可知,电场强度的大小等于单位正电荷所受力的大小。
由于电场力与电势梯度具有相反的方向,所以电场强度的大小与电势梯度的大小成正比。
我们可以通过具体的例子来进一步说明电势梯度和电场强度之间的关系。
假设有一个点电荷位于原点,我们要计算该点电荷在距离原点某一点的电场强度。
首先,我们可以通过库仑定律计算出该点电荷在距离原点某一点的电势。
然后,我们可以通过计算电势在该点的梯度得到该点电荷在该点的电场强度。
根据电势梯度和电场强度的关系可知,电场强度的大小与电势梯度的大小成正比,方向与电势梯度的方向相反。
电势梯度和电场强度之间存在着密切的关系。
高中物理 电场强度与电势梯度

电场中电势相等的点所构成的面.
电荷沿等势面移动时,电场力做功为零.
b
WAB
q(VA
VB
)
a
qE dl
0
E dl
电场线与等势面垂直并指向电势降低的方向.
1
规定:任意两相邻等势面间的电势差相等. 等势面越密的地方,电场强度越大.
点电荷的电场线与等势面
-
2
两平行带电平板的电场线和等势面
E
电偶极子处于非稳定平衡位置。
q
F qE
q
F qEE
q F qE
r0
E
q
F qE
F qE
q r0 q E
F qE
结论:电偶极子总具有 p // E 的趋势。
13
x Px
7Leabharlann 例2 求电偶极子电场中任意一点A的电势
和电场强度.
1q
解
V 4πε0 r
V
1 4πε0
q r
y
A
r
r r
V
V
V
q 4πε0
r r r r
- +x
r0
8
r0 r r r r0 cosθ
V
V
V
q 4πε0
y2 )1/ 2 y2 )2
y0 x0
E
2p 4πε0
1 x3
p1 E 4πε0 y3
y
A
r
r r
- +x
r0
11
§5-9 静电场中的电偶极子
5-5 电场强度与电势梯度的关系
2
2
P 2 2 4 x y 4 0 ( x 2 y 2 ) 2
P(0,y) y E -q
-L/2
讨论:
1. 在X轴上,y=0,则
Ex P 20 x 3 P 40 y
Ey 0
3
2. 在Y轴上,x=0,则
Ex
+q
O
L/2
P(x,0)
Ey 0
E
x
与用叠加原理得到的结果一致。
1 1
E
en
P2
P1
P3
V
V+dV
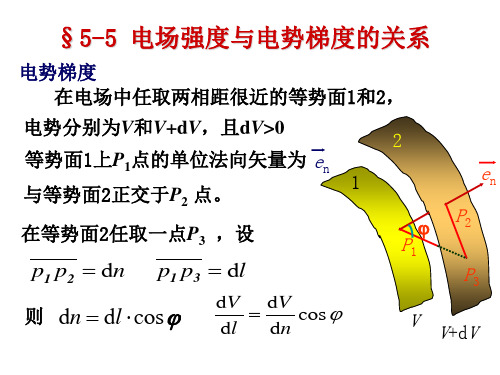
例1 试由电偶极子的电势分布求其的电场强度。 解: 在直角坐标系中先写出电势的表达式,
1 q 1 q q r r V 40 r 40 r 40 r r
L cos P cos 2 2 40 r 4 0 r Px 40 ( x 2 y 2 ) 3 / 2 q
P3
V
则 dn dl cos
V+dV
定义电势梯度
dV grad V en dn
单位:V/m
其量值为该点电势增加率的最大值。 方向与等势面垂直,并指向电势升高的方向。 电势梯度与电场强度的关系 2
en
电荷q从等势面1移动到等 势面2,电场力做功
1
en P1
dA qE dl qE dl cos qE den
例2 将半径为R2 的圆盘在盘心处挖去半径为R1的小孔,并 使盘均匀带电.试通过用电势梯度求电场强度的方法,计算这 个中空带电圆盘轴线上任一点P处的电场强度.
解:设圆盘上的电荷 面密度为 轴线上任一点p 到中空圆盘的 距离为x,在圆 盘上取半径为r 宽为dr的圆环 ,环上所带电 z 荷为
1.5.2电场强度与电势梯度的关系
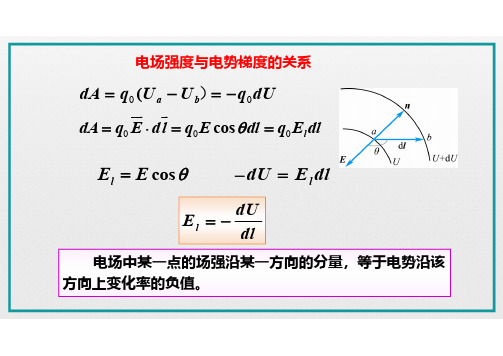
00(a b dA q U U q dU )cos l E E l dU E dl
电场中某一点的场强沿某一方向的分量,等于电势沿该方向上变化率的负值。
000cos l dA q E dl q E dl q E dl
l dU E dl
电场强度与电势梯度的关系
或
U 的梯度
:
一般
所以
的方向与U的梯度反向,即指向U 降落的方向物理意义:电势梯度是一个矢量,它的大小为电势沿等势面法线方向的变化率,它的方向沿等势面法线方向且指向电势增大的方向。
例1、利用场强与电势梯度的关系,计算均匀带电细圆环轴线上一点的场强。
解:
例2、利用场强与电势梯度的关系,求半径为R ,面电荷密度为σ的均匀带电圆盘轴线上的场强。
220
2[]U R x x 解:22012()x U x E x R x
0y U E y
0z U E z 即轴线上一点的场强为22012()x E i R x。
电场强度与电势梯度
ε0
S
+
+
+
++
+ E0
+
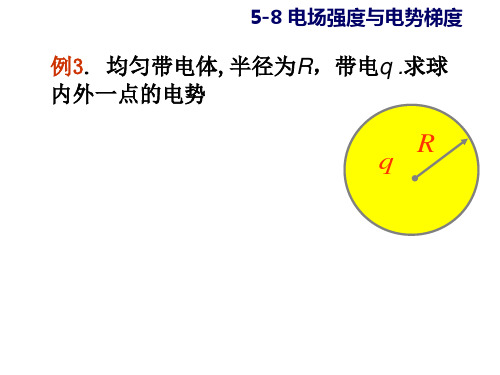
导体表面电荷分布规律
E σ ε0
σ E ;σ , E
++ + ++
++++
注意:导体表面电荷分布与导体形状以 及周围环境有关.
四.静电屏蔽
静电场中的导体的一个重要结论: 导体外表面及其以外空间的电荷,在导 体外表面以内的空间产生的场强处处为零。
导体达到静电平衡
E 感
E内 E外 E感 0
+ + + + +
+ E外
+ + + +
感应电荷
2 静电平衡
+
E0 +
+
E'
+ + +
E0
E0 +
+
静电平衡条件:
(1)导体内部任何一点处的电场强度为零; (2)导体表面处电场强度的方向,都与导 体表面垂直.
推论:导体为等势体
E
二. 静电平衡时导体上电荷的分布
R2 R1
( 1 1 )q Q q
R2 R3
R1
V壳
Q q
4 0R1
例2:.导体板A,带电量QA,在其旁边放入
导体板B,带电量QB ,面积均为S。 求:
(1) A、B上的电荷分布及空间的电场分布
(2) 将B板接地,求电荷分布 1 A 2 3 B 4
a点
1 2 3 4 0 2 0 2 0 2 0 2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y0 x0
2p 1 E 4πε0 x3
E p 4πε0
1 y3
y
A
r
r r
- +x
r0
第五章 静电场
12
物理学
第五版
选择进入下一节:
本章目录
5-0 教学基本要求
5-1 电荷量子化 电荷守恒定律
5-2 库仑定律
5-3 电场强度
5-4 电场强度通量 高斯定理
*5-5 密立根测定电子电荷的实验
第五章 静电场
物理学
第五版
5-8 电场强度与电势梯度
一 等势面
电场中电势相等的点所构成的面.
电荷沿等势面移动时,电场力做功为零.
b
W A Bq (V A V B )aq E d l 0
Edl
某点的电场强度与通过该点的等势面垂直.
第五章 静电场
1
物理学
第五版
5-8 电场强度与电势梯度
用等势面的疏密表示电场的强弱. 任意两相邻等势面间的电势差相等. 等势面越密的地方,电场强度越大.
点电荷的电场线与等势面
-
第五章 静电场
2
物理学
第五版
5-8 电场强度与电势梯度
两平行带电平板的电场线和等势面
++++++++++++
一对等量异号点电荷的电场线和等势面
-
+
第五章 静电场
3
物理学
第五版
5-8 电场强度与电势梯度
二 电场强度与电势梯度
V E l
V
Elcoθs
EcoθsEl
El
VVV4πqε0
rr rr
q 4πε0
r0
cosθ r2
1
4πε0
pcosθ r2
y
A
r
θ 0
V
1 4πε0
p r2
r r
θπ
θπ 2
V
1 4πε0
p r2
V 0
- +x
r0
第五章 静电场
10
物理学
第五版
5-8 电场强度与电势梯度
V 1 4πε0
pcosθ r2
p 4πε0
(x2
x y2)3/2
Ro
xP x
第五章 静电场
8
物理学
第五版
5-8 电场强度与电势梯度
例2 求电偶极子电场中任意一点A的电势
和电场强度.
解
V
1 4πε0
q r
V
1 4πБайду номын сангаас0
q r
y
A
r
r r
VVV
q 4πε0
r r rr
- +x
r0
第五章 静电场
9
物理学
第五版
5-8 电场强度与电势梯度
r0 r rrr0coθs rr r2
Ex
V x
p 4πε0
y2 2x2 (x2 y2)5/2
V Ey y
p 3xy 4πε0 (x2 y2)5/2
y
A
r
r r
E Ex2 Ey2
p (4x2 y2)1/2
4πε0
(x2 y2)2
- +x
r0
第五章 静电场
11
物理学
第五版
5-8 电场强度与电势梯度
E p 4πε0
(4x2y2)1/2 (x2y2)2
El
dV dl
dl dln
En
dV dln
En El
E
dV dln
en
大小
E
dV
dln
V
VV
E
en
dl
dln
低高 电电 势势
方向 由高电势处指向低电势处
第五章 静电场
6
物理学
第五版
5-8 电场强度与电势梯度
电场强度等于电势梯度的负值
E ( Vi V j Vk ) grVa dV x y z
V l
El ll im 0Vl ddVl
VV
l A
El
B
E
I
II
第五章 静电场
4
物理学
第五版
5-8 电场强度与电势梯度
El
dV dl
电场中某一点
的电场强度沿任一
方向的分量,等于
这一点的电势沿该
方向单位长度上电
势变化率的负值.
V
VV
l A
El
B
E
I
II
第五章 静电场
5
物理学
第五版
5-8 电场强度与电势梯度
13
求电场强度的三种方法
利用电场强度叠加原理 利用高斯定理 利用电势与电场强度的关系
第五章 静电场
7
物理学
第五版
5-8 电场强度与电势梯度
例1 用电场强度与电势的关系,求均匀 带电细圆环轴线上一点的电场强度.
解
q V4πε0(x2 R2)12
EEx
V x
x4πε0(x2qR2)12 4πε0(xq2 xR2)32
