武汉理工大学结构力学
结构力学辅导书和各个学校[修改版]
![结构力学辅导书和各个学校[修改版]](https://img.taocdn.com/s3/m/15c8742d2bf90242a8956bec0975f46527d3a796.png)
第一篇:结构力学辅导书和各个学校本人参加了12年研究生入学考试,并且成功考上了结构工程专业,由于本人比较喜好结构力学,现把我学习的过程中的一些心得和知道的信息写出来以方便以后的广大研友们。
下面先谈谈结构力学教材和辅导书,然后再讲各个学校真题的风格和复习建议。
一、结构力学教材现存市面上《结构力学》教材版本还是挺多的,每个学校都有自己固定的教材,每本教材又有自己固有的特点。
1、龙驭球版《结构力学》这应该是用的最多的教材,也是最常见的版本,龙驭球是清华老院士,这本教材的另一个作者袁驷也是龙驭球的学生,教材后边还附有一个结构力学求解器,非常好用!这个教材比较基础,什么知识都有来龙去脉,讲的很细,难度不是很大,作为本科生教学和考研前期准备还行,但是光做这上面的题目对付考研还是不够的。
是华南理工大学考研指定的教材之一。
其他一些没自编教材的院校一般都是这本教材。
2、李廉锟版《结构力学》李廉锟老师也是清华的毕业生,是国内最早写结构力学教材的一批老先生之一,这本教材第 5 版了,这本教材也是比较基础,但相对于龙驭球版的教材,要相对简练一些。
课后习题也不是很难,是中南大学和北京交通大学和华工桥隧考研的指定教材。
3、王焕定版《结构力学》王焕定老师是哈工大结构力学的教学带头人,教材内容不错,课后习题也不错,天大连续好几年的静定结构位移计算都是出自这本教材的课后习题原题,最近两年没遇到了,但其课后习题作为前期的一本习题集还是不错的。
4、杨茀康、李家宝版《结构力学》湖南大学的指定教材,内容也很朴实,也算国内比较早的教材之一。
李家宝老先生(曾是湖南大学副校长)1951 年考入的广西大学土木系,1956 年就参与了最早的结构力学教材的编辑,所以同龙驭球,李廉锟的版本内容(包括模式和讲解方式)都是差不多的,作为湖南大学指定的教材,考湖大的同学可以看看。
洪范文老师写的教材,也是湖南大学结构力学教研室编的。
湖南大学最近两年的出题老师变了,题型风格当然也就变了,11 年变化就挺大的了(但还是能找到原题,11 年的力法跟天大考的一个题,西南交大05 年考过,结构动力学是北京工业06 年的原题,题都不难,但对于没复习到一定境界的同学,或多或少会有些不适应),12 年更是全部大题,考湖大的同学注意复习的方向了,貌似跟华南理工类似。
结构力学英文课件 Chapter1

Introduction
③ Combination Joint
A
B
A:Rigid joint
C
D
B、D:Hinge joint C:Combination joint BF、CD Hinge joint,
E
F
G
BC、CF Rigid joint
3. Simplification of supports
长江三峡工程
Introduction
Introduction
上海南浦大桥
Introduction
Introduction
现代桥梁欣赏
Introduction
现代桥梁欣赏
Introduction
Introduction
中国民航飞机
Introduction
宇宙飞船
Introduction
Summary
Two words:
Simplification
Classification
Introduction
Fig.1 Main Teaching Building
Introduction
Fig.2
Introduction
Introduction
Introduction
Introduction
Introduction
Introduction
荷兰拦海大坝
Introduction
(1)、beam (2)、arch
(3)、truss (4)、rigid frame (5)、composite structure
梁
拱
桁架
刚架
组合结构
Introduction
结构力学2019武汉理工网络答案

一、单选(共计100分,每题2.5分)1、力矩分配法中的传递弯矩等于()。
A.固端弯矩B.分配弯矩乘以传递系数C.固端弯矩乘以传递系数D.不平衡力矩乘以传递系数错误:【B】2、图4结构超静定次数为()。
图4A.2次B.3次C.4次D.5次错误:【B】3、等截面直杆的转角位移方程是表示单跨超静定梁()。
A.荷载、杆端位移等外因与杆端力之间的关系B.荷载与杆端位移之间的关系C.荷载与杆端力之间的关系D.杆端力与杆端位移之间的关系4、图6结构,用矩阵位移法计算时,结点C的综合结点荷载是()。
图6A.B.C.D.错误:【C】5、等直杆件AB的弯矩传递系数C AB()。
A.与B端支承条件及杆件刚度有关B.只与B端的支承条件有关C.与A、B两端的支承条件有关D.只与A端支承条件有关错误:【B】6、已知某单元的杆端位移向量为,则单元类型为()。
A.梁单元B.桁架单元C.一般单元D.其他单元错误:【B】7、图3结构超静定次数为()。
图3A.6次B.7次C.8次D.9次错误:【C】8、图2结构,对QC的影响线描述正确的是()。
图2A.AC不为零,CD为斜线B.AC为零,CD为水平线C.AC为零,CD为斜线D.AC为零,CD为零错误:【B】9、力矩分配法计算得出的结果()。
A.一定是近似解B.不是精确解C.是精确解D.可能为近似解,也可能是精确解错误:【D】10、机动法作静定结构内力影响线的依据是()。
A.刚体体系虚力原理B.刚体体系虚力原理C.刚体体系的虚位移原理D.变形体虚位移原理错误:【C】11、图2结构当桁架高度增加时,杆I的内力()。
图2A.增大B.减小C.不变D.不确定错误:【C】12、用图乘法求位移的必要条件之一是()。
A.单位荷载下的弯矩图为一直线B.结构可分为等截面直杆段C.所有杆件EI为常数且相同D.结构必须是静定的错误:【B】13、用位移法求图5结构时,若不考虑杆件的轴向变形,且各杆件的EI相同,且为有限值,则独立的结点角位移和线位移未知数数目分别为()。
10第十章-结构力学位移法
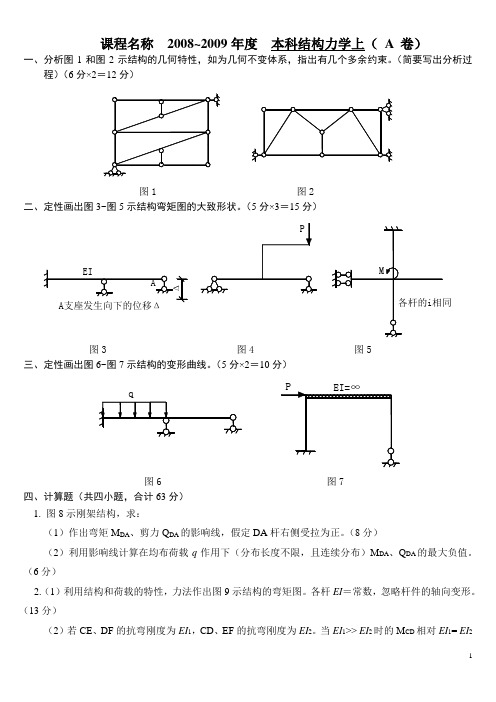
i
j
rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
根据反力互等定理: ij r ji j r i
T12 r ji T21 rij
i
j
T12 T21 r ji rij
第十章 位移法 §10-4 位移法的典型方程及计算步骤 副系数 —— 可正、可负、可为零 刚度系数 主系数 —— 恒为正 自由项 —— 可正、可负、可为零 位移法——刚度法
3
R1P 60
6i l
F AB M BA 0
F M BA
M AB 3i( A
AB l
2i
)
F AB
)M
1 2
F M BA 3i ( A
AB l
)M
F AB
M AB
AB F 3i ( A ) M AB l
— 该梁转角位移方程
表 11-1 等直梁杆端弯矩和剪力。
——典型方程
个附加约束中的反力(矩)。
r11 ——单位位移 Z1 1单独作用引起的第一
第十章 位移法 §10-4 位移法的典型方程及计算步骤 当有n个基本未知量时:
r11Z1 r12 Z 2 r1n Z n R1P 0
r21Z1 r22 Z 2 r2n Z n R2 P 0
M 21 1 8
56
,
2 EI l Z1 56
pl
9 pl
图
作M图:
第十章 §10-1 概论
位移法
归纳出位移法解题的基本思路: ⑴ 依据几何条件(支、变形),确定某些结 点位移为基本未知数。 ⑵ 视各杆为单跨超静定梁,建立内力和位移 的关系。 ⑶ 由基本方程(平衡方程)求位移。 ⑷ 求结构内力。
图乘法

y0 o A
MM P 1 ∆ = ∑∫ ds = ωy 0 EI EI
武汉理工大学土木工程与建筑学院 结构力学教研室 李保德副教授
MM P 1 ds = ∑ ωy 0 ∆ = ∑∫ EI EI
1 1 2 ω 3 = × qL 2 8 3 y3 = L 4
C
B L/2
1 L 1 2 ω1 = × × qL 3 2 8
1 L 1 2 ω 2 = × × y2 = L 6
∆B =
1 (ω1 y1 + ω 2 y 2 + ω 3 y3 ) EI
41qL4 = 384 EI
武汉理工大学土木工程与建筑学院
结构力学教研室
李保德副教授
3. 常见图形的面积和形心
武汉理工大学土木工程与建筑学院
结构力学教研室
李保德副教授
注意: 注意:
标准抛物线
武汉理工大学土木工程与建筑学院
结构力学教研室
李保德副教授
4. 图乘的一般方法
两图均是直线图形,y0可取其中的任一图形
ω
y0
y0
ω
武汉理工大学土木工程与建筑学院
武汉理工大学土木工程与建筑学院
C
B L/2
∆B =
1 ωM P y EI
1 1 2 PL3 = × L × PL × L = EI 2 3 EI
B
MP
或
1 ∆B = ωM y EI
1 1 2 PL3 = × L × L × PL = EI 2 3 EI
M
结构力学教研室
李保德副教授
武汉理工大学土木工程结构力学本科期末考试题资料
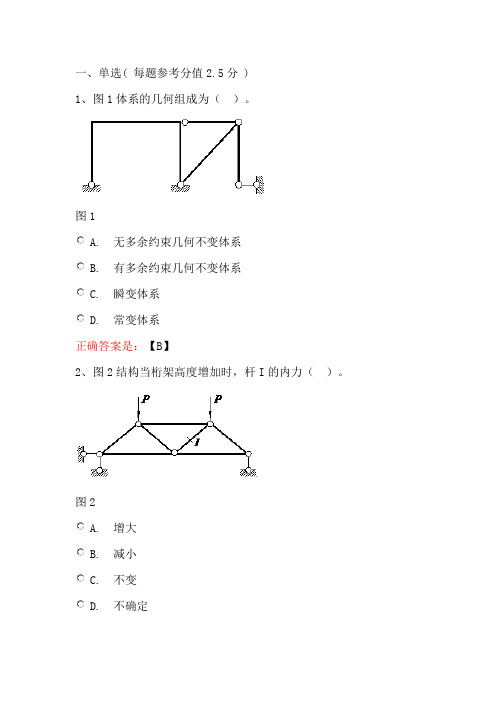
课程名称 2008~2009年度 本科结构力学上( A 卷)一、分析图1和图2示结构的几何特性,如为几何不变体系,指出有几个多余约束。
(简要写出分析过程)(6分×2=12分)图1 图2 二、定性画出图3~图5示结构弯矩图的大致形状。
(5分×3=15分)A支座发生向下的位移Δ图3 图4 图5 三、定性画出图6~图7示结构的变形曲线。
(5分×2=10分)q图6 图7 四、计算题(共四小题,合计63分) 1. 图8示刚架结构,求:(1)作出弯矩M DA 、剪力Q DA 的影响线,假定DA 杆右侧受拉为正。
(8分)(2)利用影响线计算在均布荷载q 作用下(分布长度不限,且连续分布)M DA 、Q DA 的最大负值。
(6分)2.(1)利用结构和荷载的特性,力法作出图9示结构的弯矩图。
各杆EI =常数,忽略杆件的轴向变形。
(13分)(2)若CE 、DF 的抗弯刚度为EI 1,CD 、EF 的抗弯刚度为EI 2。
当EI 1>> EI 2时的M CD 相对EI 1= EI 2时的是变大还是变小;反之,当EI1<< EI2时的M CD又如何变化。
(4分)图8 图93. 位移法计算图10示超静定结构,各杆i=常数。
(1)判断图示结构位移法的独立基本未知量。
(2分)(2)写出杆端弯矩表达式。
(6分)(3)列出位移法基本方程(不需求解)。
(8分)(备注:也可采用位移法基本体系进行求解。
)4.力矩分配法计算图11示结构,各杆i=常数。
内力值保留到小数点后一位。
(1)绘出弯矩图(12分)(2)求出C支座反力。
(4分)图10 图11试题标准答案课程名称2008~2009年度本科结构力学上( A 卷)一、分析图1和图2示结构的几何特性,如为几何不变体系,指出有几个多余约束。
(简要写出分析过程)图1. 无多余约束的几何不变体系;分析过程如下,此处仅给出一种分析方法,只要说明合理均给分。
结构力学(专科)——武汉理工大学
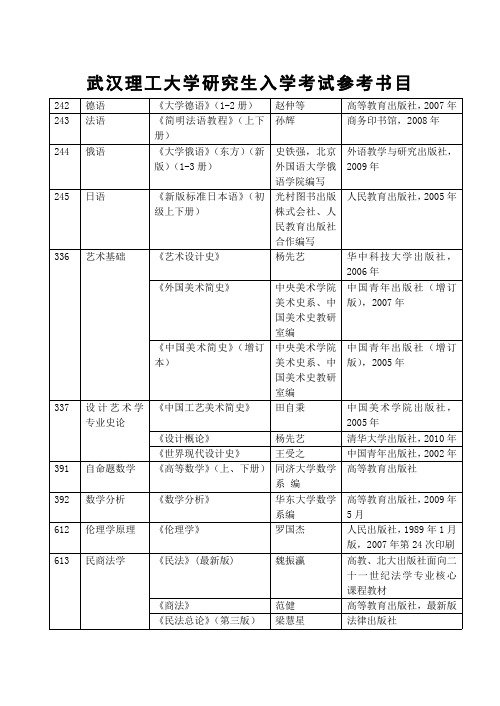
一、单选( 每题参考分值2.5分 )1、图1体系的几何组成为()。
图1A. 无多余约束几何不变体系B. 有多余约束几何不变体系C. 瞬变体系D. 常变体系正确答案是:【B】2、图2结构当桁架高度增加时,杆I的内力()。
图2A. 增大B. 减小C. 不变D. 不确定正确答案是:【C】3、当杆件刚度系数SAB=3i时,杆的B端为()。
A. 自由端B. 固定端C. 铰支承D. 定向支承正确答案是:【C】4、图3结构超静定次数为()。
图3A. 6次B. 7次C. 8次D. 9次正确答案是:【C】5、图1体系的多余约束的个数为()。
图1A. 0个B. 1个C. 2个D. 3个正确答案是:【B】6、拱轴线为合理拱轴线,其横截面上内力为零的是()。
A. 弯矩B. 扭矩C. 轴力D. 支座反力正确答案是:【A】7、图2梁受到三角形荷载作用,A端竖向支座反力的大小为()。
图2A. ql/2B. ql/3C. ql/4D. ql/6正确答案是:【A】8、在力法方程中()。
A.B.C.D. 前三种答案都有可能正确答案是:【D】9、拱的突出持点是竖向荷载下有()。
A. 轴力B. 弯矩C. 竖向力D. 水平推力正确答案是:【D】10、力法典型方程的物理意义是()。
A. 结构的平衡条件B. 结点的平衡条件C. 结构的变形协调条件D. 结构的平衡条件及变形协调条件正确答案是:【C】11、绘制任一量值的影响线时,假定荷载是()。
A. 一个方向不变的单位荷载B. 移动荷载C. 动力荷载D. 可动荷载正确答案是:【A】12、力矩分配法计算得出的结果()。
A. 一定是近似解B. 不是精确解C. 是精确解D. 可能为近似解,也可能是精确解正确答案是:【D】13、图3桁架零杆的个数为()。
图3A. 3个B. 4个C. 5个D. 6个正确答案是:【D】14、图3a结构,EI=常数,取图3b为力法基本体系,则中的和分别等于()。
图3A. Δ,Δ/4B. -Δ,Δ/4C. Δ,-Δ/4D. -Δ,-Δ/4正确答案是:【D】15、叠加原理用于求解静定结构时,需要满足的条件是()。
武汉理工大学专业课考研参考书目
武汉理工大学研究生入学考试参考书目242德语《大学德语》(1-2册)赵仲等高等教育出版社,2007年243法语《简明法语教程》(上下册)孙辉商务印书馆,2008年244俄语《大学俄语》(东方)(新版)(1-3册)史铁强,北京外国语大学俄语学院编写外语教学与研究出版社,2009年245日语《新版标准日本语》(初级上下册)光村图书出版株式会社、人民教育出版社合作编写人民教育出版社,2005年336艺术基础《艺术设计史》杨先艺华中科技大学出版社,2006年《外国美术简史》中央美术学院美术史系、中国美术史教研室编中国青年出版社(增订版),2007年《中国美术简史》(增订本)中央美术学院美术史系、中国美术史教研室编中国青年出版社(增订版),2005年337设计艺术学专业史论《中国工艺美术简史》田自秉中国美术学院出版社,2005年《设计概论》杨先艺清华大学出版社,2010年《世界现代设计史》王受之中国青年出版社,2002年391自命题数学《高等数学》(上、下册)同济大学数学系编高等教育出版社392数学分析《数学分析》华东大学数学系编高等教育出版社,2009年5月612伦理学原理《伦理学》罗国杰人民出版社,1989年1月版,2007年第24次印刷613民商法学《民法》(最新版)魏振瀛高教、北大出版社面向二十一世纪法学专业核心课程教材《商法》范健高等教育出版社,最新版《民法总论》(第三版)梁慧星法律出版社614经济法学《经济法学》漆多俊高等教育出版社615马克思主义基本原理及其发展《马克思主义发展史》顾海良武汉大学出版社,2006年《回到文本——马克思主义经典文献解读》朱喆、杨金洲武汉理工大学出版社,2009年616传播学原理《传播学教程》郭庆光中国人民大学出版社《传播学引论》(增补版)李彬新华出版社,2003.8617体育教育专业综合《运动生理学》王瑞元人民体育出版社,2003.6《运动训练学》田麦久高等教育出版社,2006.7618教育学《新编教育学教程》叶澜华东师范大学出版社,2006年619基础英语《新编英语教程》1-6册李观仪上海外语教育出版社,2008年620设计艺术学专业史论《中国工艺美术简史》田自秉中国美术学院出版社,2005年《艺术设计史》杨先艺华中科技大学出版社,2006年《世界现代设计史》王受之中国青年出版社。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
F ( e )
结点位移 结点力
单元杆端力
K F
F FP 0
K FP 0
位移法基本方程
(1) 0 结点位移
FP
结点约束力
(2)
F
结点位移 结点力
☻等效结点荷载的概念
(1) 0 结点位移
FP
结点约束力
K FP 0
K -FP
等效结点荷载
P -FP
K P
(2)
F
以等效结点荷载表示的位移法基本方程
合成为整体结构的等效结点荷载。
FPe 反号-FPe Pe集合 P
FP ( e)
FP
FP e
FP
实际过程还有一个坐标变换问题:
由局部坐标下单元的固端约束力
F P e=(F xP1
F xP2
F yP1 F yP2
M P1 M P2 )T
(1)
反号,即得局部坐标下单元的等效结点荷载:
P e - FP e
Pe TT P e=-TT FP e
得整体坐标下单元等效结点荷载{P}e ,
再由它们集合成结构整体等效结点荷载。
0
FP
结点约束力
F (e) P
固端约束力 (单元杆端力)
FP ( e)
FP
FP e
单元集成法求整体等效结点荷载的步骤
集成结构
整体坐标系下单元
整体等效
x
等效结点荷载 P e
9-6 Equivalent Nodal Load
等效结点荷载
☻Nodal Load and General Load
结点荷载与非结点荷载
☺ Continuous Beam
F1 ①
F2 ②
1
2
Assembled Stiffness Matrix
3 F3
FF12 F3
K11 K21 K31
3 1
4 ①
解:各种编号已经于例10-2中完成
(1)局部坐标系下固端约束力FP e
8kN ②
(查表10-1)
FP 1 F xP1 F yP1 M P1 F xP2 F yP2
0 12 10 0 12 10T
T
M P2
FP 2 F xP1
F yP1
M P1
F xP2
F yP2
T
M P2
K12 K22 K32
K13 K23 K33
12 3
F K
☺ Frame
x
y F2 F3
F4
F4
①
Assembled Stiffness Matrix
②
F1 K11 K12 K13 K14 1
F2 F3
K
21
K31
K22 K32
K23 K33
K24 K34
2 3
2
0
0
4
0
P(2) T (2)T FP (2) 00
0 0
1 0
0 0
0 1
0 0
5 0
5
4
0 0 0 1 0 0 4 0
0
0
00
0
1 5
5
(3)求刚架的等效结点荷载
2 4.8kN/m
P
3 1
4 ①
(1) 1 2 3 0 0 4T 8kN ②
(2) 1 2 3 0 0 0T
12 →0
0 →0
10 →4
5
→0
集合过程
0
P
0 0
集合单元1
P
0 12 10
0
10
集合单元2 0 (4) 4
P
12 (0) 10 (5)
12 5
10 10
思考:
x y 当结构上同时存在非结点荷
载和结点荷载时如何处理?
小结
K11 K12
结点位移 结点力
☻单元集成法求等效结点荷载
P -FP
是由结点约束状态的结点约束力{FP} 又是由各单元的固端约束力{FP}(e) 集 (1) 合而成(注意在结点处有多个杆端)。
FP e
集合
FP
反号
-FP
P
FP
0
FP
结点约束力
F (e) P
固端约束力 (单元杆端力)
将单元固端约束力的反号值-{FP}e 定 义为单元等效结点荷载{P}e ,由它们集
0 4 5 0 4 5T
(单位略)
(2)各单元在整体坐标系下等效结点荷载 2 4.8kN/m
3
4
1
①
单元1、2的倾角分别为:
1 0,2 90
8kN ②
P1 T 1T FP(1) I FP(1) FP(1) 0 12 10 0 12 10T
0 1 0 0 0 0 0 4
1
0
00
3
F4 K41 K42 K43 K44 4 1
①
0 4 0
F K
仅受到结点荷载作用
② 坐标变换
0
0
单元集成
0
定位向量
☻ 当有非结点荷载作用
时
(1)
结点位移
结点力 0
单元杆端力 F (e)
F FP 0 结点力
F(e) F(e)
单元杆端力
(2)
0
FP F ( e )
结点位移
结点约束力 固端约束力
对号
结点荷载 y
①
入座
{P}
②
坐标变换
局部坐标系下的单元
e
等效结点荷载 P
反
符号
号
规则
单元的固端
约束力
e
FP
(表10-1)
杆件的
固端约束力 (表8-1)
☺ 结构结点位移与杆端内力的解 FP
求得结构整体的等效结点荷载{P}后,位
移法基本方程可求解:
K P
即可得到状态(2)的结点位移 ,也就
0 →1
12
→2
P1
Байду номын сангаас
10 0
→3 →0
12 →0
10 →4
4 →1
0
→2
P(2)
5 →3
4
→0
0 →0
5
→0
2 4.8kN/m
0 →1
12
→2
4 →1
0
→2
3 1
4 ①
P1
10 0
→3 →0
P(2)
5
4
→3 →0
8kN ②
符号
号
规则
单元的 e
固端约束力 F P
(表10-1)
杆件的
固端约束力 (表8-1)
矩阵位移法的基本方程
K P
各杆的杆端内力
Fe k e e FPe
是原结构的结点位移。
求出后,按照位移思想,该状态下的
所有单元杆端内力即可解出。将它与结点 约束状态(1)下的固端力相叠加,即得到 原结构的单元杆端力(后面详细讲)。
(1) (2)
0
FP 结点约束力
+ FP
(e) 固端约束力 (单元杆端力)
P
P FP F ( e )
2 4.8kN/m
例10-3 求图示刚架等效结点荷载。
刚架的总体刚度矩阵
K
K
21
K 22
K
n1
Kn2
坐标
k e 变换
k e 换码 累加
刚架的总体刚度方程
K1n
K
2
n
K
nn
F K
单元集成法求整体等效结点荷载
集成结构
整体坐标系下单元
整体等效
等效结点荷载 P e
对号
结点荷载
入座
{P}
x
y
①
②
坐标变换
局部坐标系下的单元
等效结点荷载
e
P
反
