理论力学复习题(武汉理工大学)
理论力学复习题(含答案)
《理论力学》复习题A一、填空题1、二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是 二力平衡是作用在一个物体上,作用效果能抵消、作用力与反作用力是作用在两个物体上,作用效果不能抵消。
2、平面汇交力系平衡的几何条件是顺次将表示各个力Fi 的有向线段首尾相接,可以构成闭合n 边形;平衡的解析条件是 ∑Fxi=0;且∑Fyi=o 。
3、静滑动摩擦系数与摩擦角之间的关系为 tanφ=fs 。
4、点的切向加速度与其速度的 方向 变化率无关,而点的法向加速度与其速度 大小 的变化率无关。
5、点在运动过程中,满足0,0=≠n a a 的条件,则点作 牵连 运动。
6、动点相对于的 定系 运动称为动点的绝对运动;动点相对于 动系 的运动称为动点的相对运动;而 动系 相对于 定系 的运动称为牵连运动。
7、图示机构中,轮A (只滚不滑)作 平面 运动;杆DE 作 定轴转动 运动。
题7图 题8图8、图示均质圆盘,质量为m ,半径为R ,则其对O 轴的动量矩为 。
9、在惯性参考系中,不论初始条件如何变化,只要质点不受力的作用,则该质点应保持 静止或等速直线 运动状态。
10. 任意质点系(包括刚体)的动量可以用 其质心 的动量来表示。
二、选择题1. 在下述公理、规则、原理和定律中,对所有物体都完全适用的有( D )。
A.二力平衡公理B.力的平行四边形规则C.加减平衡力系原理D.力的可传性2. 分析图中画出的5个共面力偶,与图(a )所示的力偶等效的力偶是(B )。
A. 图(b ) B. 图(c ) C.图(d ) D. 图(e )题2图3. 平面力系向点1简化时,主矢0='RF ,主矩01≠M ,如将该力系向另一点2简化,则( D )。
A. 12,0M M F R≠≠' B. 12,0M M F R ≠='C. 12,0M M F R=≠' D. 12,0M M F R ==' 4. 将大小为100N 的力F 沿x 、y 方向分解,若F 在x 轴上的投影为86.6 N ,而沿x 方向的分力的大小为115.47 N ,则F 在y 轴上的投影为( B )。
理论力学试卷武汉理工大学
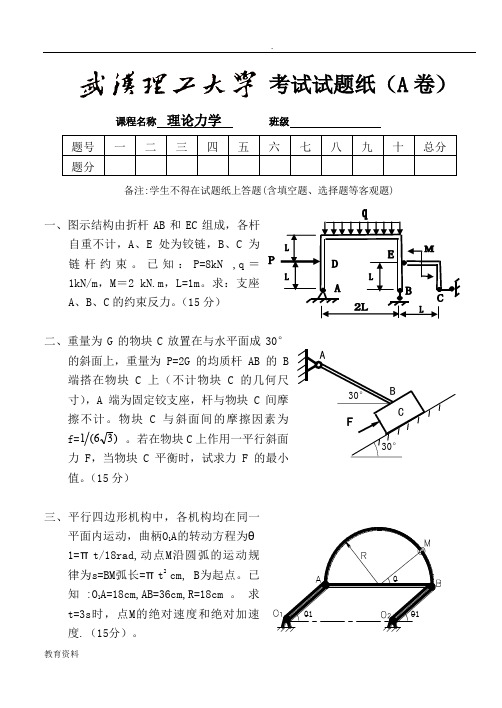
考试试题纸(A 卷)课程名称理论力学班级备注:学生不得在试题纸上答题(含填空题、选择题等客观题)一、图示结构由折杆AB 和EC 组成,各杆自重不计,A 、E 处为铰链,B 、C 为链杆约束。
已知:P=8kN ,q =1kN/m ,M =2 kN.m ,L=1m 。
求:支座A 、B 、C 的约束反力。
(15分)二、重量为G 的物块C 放置在与水平面成30°的斜面上,重量为P=2G 的均质杆AB 的B 端搭在物块C 上(不计物块C 的几何尺寸),A 端为固定铰支座,杆与物块C 间摩擦不计。
物块C 与斜面间的摩擦因素为f=)36(1 。
若在物块C 上作用一平行斜面力F,当物块C平衡时,试求力F 的最小值。
(15分)三、平行四边形机构中,各机构均在同一平面内运动,曲柄O 1A 的转动方程为θ1=πt/18rad,动点M 沿圆弧的运动规律为s=BM 弧长=πt 2 cm, B 为起点。
已知:O 1A=18cm,AB=36cm,R=18cm 。
求t=3s 时,点M 的绝对速度和绝对加速度.(15分)。
四、曲柄滑块机构中,曲柄AB=L ,连杆BC=3L ,在某瞬时,90=∠ABC , 60=∠BAC ,滑块的速度为V ,加速度为 a 。
求:在该瞬时,曲柄AB 的角速度与角加速度。
(15分)五、如图机构所示,已知:沿地面作纯滚动的均质轮A 质量为1.5m ,半径为R ,其上作用有一常力偶矩M=2mgR ;均质轮C 质量为m ,半径为r ;重物B 质量为m ;动滑轮D 的质量、绳的质量及轴承处的摩擦不计。
与轮A 相连的绳段与水平面平行。
试求:1)重物B 上升的加速度;2)EH 段绳索张力。
(15分)六、AB 杆长为L ,重为P ,用两根等长的绳子挂于O 点,设绳与杆间的夹角为θ=450,求:当突然剪断绳OB 时,AB 杆的角加速度和绳子OA 的张力。
(12分)七、五根长度相同的柱形匀质连杆,各重W ,与固定边AB 形成正六边形,如图所示,设在水平连杆EF 的中点施加力F ,以维持平衡,试用虚位移原理求力F 的大小。
武汉理工大学——工程力学复习练习题

C
m=2qa2
B
布如图 的约束
A 2a
7、图 2 所示结构, AB 杆是钢杆且垂直于墙面,其横截面面 积 A1=6cm2,许用应力[]=140MPa;BC 杆是木杆,横 截面面积 A2 =300cm2 ,许用压应力 [c]=3.5MPa 。已知 P=5kN,试 校核 AB 杆和 BC 杆的强度。 A
6qa a 5a A 6a B q
水平 集中 B 的约束
3、水平梁的支承和载荷如图示。已知: 100N , 力偶矩 M = 200mN , 分布载 40 N/m , 长度 a=1米 。求 :铰 A 、 B 的约束反力。
q A a a
力P =
M B a a P
荷 q = 支 座
4 、曲杆 DOC 和直杆 BA 在 OC 段的中 点 B 铰接,各杆自重 不计。已知: AD =DB= DO =OB=BC,P = 1500N。 求支座 O 及光滑面 C 处的约束反力 和铰 B 对 OC 杆的作用力。
C 2m A 3m B
P
18、圆柱同时受拉力和扭矩作用。若力 P=40KN,扭矩 T=500 N·m,直径 d=50 mm。 (1) 画出 A 点处的应力状态 ; (2) 求出 A 点处各截面上的应力; (3) 求出 A 点处的主应力的大小
2
ζ 1、 ζ
和 ζ3。
19、图示托架,AB
为刚性杆。CD 杆为两端铰支的空心圆截面杆,外
6m
4
3m
三、铸铁梁,截面惯性矩 IZ=3000cm , y1=42mm,y2=98mm, P=15kN,l=1m。许用拉应力为 [t]=40MPa,许用压应力[C]=90MPa,校核梁的弯曲正应力强度。 (14 分) P B A
大学理论力学期末考试题库及答案

大学理论力学期末考试题库及答案1. 题目:简述牛顿三定律的内容。
答案:牛顿第一定律(惯性定律)指出,物体在没有受到外力作用时,将保持静止或匀速直线运动状态;牛顿第二定律(加速度定律)表明,物体的加速度与作用在物体上的合外力成正比,与物体质量成反比,方向与合外力方向相同;牛顿第三定律(作用与反作用定律)说明,对于任何两个相互作用的物体,它们之间的力是大小相等、方向相反的。
2. 题目:什么是角动量守恒定律?答案:角动量守恒定律是指在没有外力矩作用的情况下,一个系统的总角动量保持不变。
3. 题目:请解释达朗贝尔原理。
答案:达朗贝尔原理是将动力学问题转化为静力学问题的一种方法。
它基于牛顿第二定律,通过引入惯性力,将动力学方程转化为平衡方程。
4. 题目:什么是虚功原理?答案:虚功原理是分析力学中的一个基本原理,它指出,一个保守系统中,如果系统从一个平衡位置发生微小的虚位移,那么系统内所有力对这些虚位移所做的虚功之和为零。
5. 题目:简述拉格朗日方程的一般形式。
答案:拉格朗日方程的一般形式为:\( \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}_i}) -\frac{\partial L}{\partial q_i} = Q_i \),其中 \( L \) 是拉格朗日量,\( q_i \) 是广义坐标,\( \dot{q}_i \) 是广义速度,\( Q_i \) 是广义力。
6. 题目:请解释什么是哈密顿原理。
答案:哈密顿原理,也称为最小作用量原理,它指出在所有可能的路径中,实际发生的过程是使作用量取极小值的路径。
作用量是拉格朗日量 \( L \) 对时间的积分。
7. 题目:什么是刚体的转动惯量?答案:刚体的转动惯量是衡量刚体对旋转运动的抵抗程度的物理量,它与刚体的质量分布和旋转轴的位置有关。
8. 题目:请解释什么是势能。
答案:势能是物体由于其位置或状态而具有的能量形式,它与物体的位形有关,通常与保守力相关。
理论力学1 期末考试试题及参考答案

理论力学复习题1一、是非题(正确用√,错误用×)1:作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
( )2:作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
( ) 3:刚体的运动形式为平动,若刚体上任一点的运动已知,则其它各点的运动随之确定。
( )4: 瞬时速度中心点的速度等于零,加速度一般情况下不等于零。
( )5:一个质点只要运动,就一定受到力的作用,而且运动的方向就是它受力的方向。
( )二、选择题(单选题)1. 一重W 的物体置于倾角为α的斜面上,若摩擦系数为f ,且tg α<f ,若增加物体重量,则物体会 () 。
A: 静止不动; B: 向下滑动; C: 运动与否取决于平衡条件。
2. 一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量( ) 。
A :平行;B :夹角随时间变化;C :垂直;D :不能确定3. 牵连运动是指( )A.动系相对于静系的运动B.牵连点相对于动系的运动C.静系相对于动系的运动D.牵连点相对于静系的运动4. 图示均质杆OA 质量为m 、长度为l ,则该杆对O 轴转动惯量为( )A .12m lB .12m 2lC .3mlD .3m 2l5.质点系动量守恒的条件是( )。
A :作用于质点系的内力主矢恒等于零;B :作用于质点系的外力主矢恒等于零;C :作用于质点系的约束反力主矢恒等于零;D :作用于质点系的主动力主矢恒等于零;三、已知图示结构中的F 、a ,试求结构A 、B 的约束反力。
理论力学复习题(武汉理工大学)

p y - 0 y = ∑I (e ) y
( pz - p0 z = ∑I ze )
(2)质点系的动量守恒定理
若 ∑Fi 若 ∑Fi
(e ) (e )
= 0, 则 p = p0 = 恒矢量 = 0, 则 p = p0 = 恒矢量
4
(3)质心运动定理
dvC (e ) ∑ i m = F dt
maC = ∑ i F
应用时,前一式取其投影式。
e maCy Fy e J C M C ( F ) maCx Fx
e
n e maC Fn e J C M C ( F ) ma Ft
t C
7
e
四 动能定理 (1)质点系的动能定理 (2)功率方程 (3)机械能守恒定律
mg
a
B
mg
14
(1): M 0
P
2 FEH m( 4a 3g ) 0
K
C E 1 2mR 2 FEH 2 R 3maR 3mgR 0 2 FEH m( 4a g ) 0 (2): M 0 A H D 1 2mR 2 2 FEHR m( g 2a ) R 0 2 2 FCy B 1 R a FCx 2mR 2 C 2 1 1 得: a g aA 2a g 2mg FEH 6 12 2a A FEH 2ma F 4 FEH mg mg 1 2mR 3 2 D P 2ma 2mg ma a B mg 15
M IO M IZ J z
(1) (2)
0
FIR
M IO
简化为一主失
FIR maC
惯性力系简化为一主矩 则
理论力学试卷 武汉理工大学解析

考试试题纸(A 卷)课程名称理论力学班级题号 一 二 三 四 五 六 七 八 九 十 总分 题分备注:学生不得在试题纸上答题(含填空题、选择题等客观题)一、图示结构由折杆AB 和EC 组成,各杆自重不计,A 、E 处为铰链,B 、C 为链杆约束。
已知:P=8kN ,q =1kN/m ,M =2 kN.m ,L=1m 。
求:支座A 、B 、C 的约束反力。
(15分)二、重量为G 的物块C 放置在与水平面成30°的斜面上,重量为P=2G 的均质杆AB 的B 端搭在物块C 上(不计物块C 的几何尺寸),A 端为固定铰支座,杆与物块C 间摩擦不计。
物块C 与斜面间的摩擦因素为f=)36(1 。
若在物块C 上作用一平行斜面力F ,当物块C 平衡时,试求力F 的最小值。
(15分)三、平行四边形机构中,各机构均在同一平面内运动,曲柄O 1A 的转动方程为θ1=πt/18rad,动点M 沿圆弧的运动规律为s=BM 弧长=πt 2 cm, B 为起点。
已知:O 1A=18cm,AB=36cm,R=18cm 。
求t=3s 时,点M 的绝对速度和绝对加速度.(15分)。
ACB F30°30°0101四、曲柄滑块机构中,曲柄AB=L ,连杆BC=3L ,在某瞬时,90=∠ABC , 60=∠BAC ,滑块的速度为V ,加速度为 a 。
求:在该瞬时,曲柄AB 的角速度与角加速度。
(15分)五、如图机构所示,已知:沿地面作纯滚动的均质轮A 质量为1.5m ,半径为R ,其上作用有一常力偶矩M=2mgR ;均质轮C 质量为m ,半径为r ;重物B 质量为m ;动滑轮D 的质量、绳的质量及轴承处的摩擦不计。
与轮A 相连的绳段与水平面平行。
试求:1)重物B 上升的加速度;2)EH 段绳索张力。
(15分)六、AB 杆长为L ,重为P ,用两根等长的绳子挂于O 点,设绳与杆间的夹角为θ=450,求:当突然剪断绳OB 时,AB 杆的角加速度和绳子OA 的张力。
武汉理工大学――工程力学复习练习题.

三、将上题T字型铸铁梁换成工字形截面梁,材料为Q235钢,许用应力[]=140MPa, I Z=2540cm ,试按第四强度理论对危险 4 10 100 5 z a 100 截面上的a点(翼板和腹板的交点作强度校核。
(15分) 100 10 四、画梁的剪力图和弯矩图。
A、B支座反力为RA= RB=qa/2。
(13 分) RA q qa 2 m 2 RB B A a C a 五、如图所示圆截面杆,Q235 钢,d = 30mm,P=50kN,m=300N·m,材料的E=200GPa, = 0.3, 试求:杆表面 K 点沿主应力 1 方向的线应变。
(14 分) m P K 附: 10 号槽钢的截面几何量 A=12.75cm2 Ix=198cm4 Iy=25.6 cm4六、混凝土立柱,a=550mm,b=250mm,e=600mm,A=181×10 mm2,截面惯性矩 I Z=13.7 9 ×10 mm4,许用拉应力 [t]=2.8MPa, 许用压应力[c]=8.5MPa,已知: P=160kN。
校核立柱柱身的强度。
(不考虑稳定性)。
(15 分) 3 P z a b C y e m m 七、图示压杆为 10 号槽钢,符合钢结构设计规范中实腹式 b 类截面中心受压杆的要求,A 端约束为球铰,材料为 3 号钢,已知:l=3m , P=100kN,[]=176 MPa,问该杆是否安全?(14 分) P y A l b y 一、图示桁架,已知:AB 杆子的直径 d=50mm,[]=160MPa, F=100kN,校核 AB 杆的强度。
(12 分) A 45° B C F t h x x二、阶梯圆轴如图所示,已知外力偶矩MA=3000N•m,MB=1800N•m,MC=1200N•m,AB 段直径 d1=75mm, BC 段直径 d2=50mm。
[]=80MPa,校核圆轴的强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
(4)冲量
t
I 0 Fdt
(5)力矩 MO (F) rF
(6)力的功 W sFcosds 0
W
M1 M1
F
dr
M M 1 2(F xd x F yd y F zd)z
1.重力的功
W m z g z W m z g z
12
12
12
C1 C2
2.弹性力的功
W12k2(12 22)
3.转动刚体上作用力的功
(2)动量矩守恒定律 M O(F i(e))0 LO 常矢量。
M x(Fi(e))0 Lx 常量。
(3)刚体绕定轴转动微分ห้องสมุดไป่ตู้程。
JZ
d n
dt i1
MZ(Fi)
n
JZ MZ(Fi)
i1
JZ
d2
dt2
n i1
MZ(Fi )
6
(5)质点系对于质心的动量矩定理。
dLC dt
n
MC(Fi(e))
W12
2 1
MZd
4. 平面运动刚体上力系的功
W12
C2 C1
FR drC
2 1
M Cd
2
(7)势能
V
M0 Fdr
M
M M0(Fxd xFyd yFzd)z
1.重力场 质点 Vzz0mgd m(zzgz0)
质点系 Vm(g zczc0)
2.弹性力场
V
k (2
2
02)
V k2
12
§13-6 普遍定理的综合应用举例
(3)取梁KC为研究对象。
MK
FKy FKx
FCy′
K
C FCx′
Fx 0
Fy 0
FF 0
Kx
Cx
F F 0
Ky
Cy
M K(F)0
M3R F0
K
C y
解方程得
FKx 0
FKy 4.m 5 g
一 基本计算
(1)质点系的动量:
p
=
∑mi vi
mv C
(2)质点系的动量矩
n
LO MO(mivi) i1
L Z M Z (m i v i )
(3)质点系的动能
T
1 2
mivi2
1.平移刚体的动能
T
1 2
mv
2 c
2.转动刚体的动能
T
1 2
JZ2
3.平面运动刚体的动能 TT1212mJ cPv2212JC2
M C (F
e
) 7
四 动能定理 (1)质点系的动能定理 (2)功率方程 (3)机械能守恒定律
T2T1 Wi
dT n dt i1
Wi n
dt i1
Pi
T1V1T2V2
8
达朗贝尔原理
一 质点的达朗贝尔原理 F+ FN+ FI =0 FI= – m a
二 质点系的达朗贝尔原理 F i(e) F I i0
aA 2a1g 6
11
§13-6 普遍定理的综合应用举例
(2)取研究对象如图: dLC MC(F)
C
C
FCy C FCx
dt
d(12 m2 C R m A R )v (F E Hm )R gVA A 2mg FEH
d2 t
得:
FEH 4 mg
aA mg
3
由动量定理,得
得: FCx0
0FCx m A F C a y 2 m m g F E g H FCy4.m 5 g
m C= a tm d d= v t∑ F i(e t),m C= a n m v ρ C 2= ∑ F i(e n ),∑ F i(e b )= 0 。
(4) 质心运动守恒定律
若 ∑Fi(e)= 0 ,则 aC = 0,质心作匀速直线运动;若开始
时系统静止,即 vC0 0, 则质心位置始终保持不变。
2
(8)转动惯量
n
J mr2
Z
i1 i i
3
二 动量定理
(1)动量定理
dp F ∑ (e)
dt
i
dp x dt
=
∑ F x (e)
dp y dt
=
∑ F y(e)
dp z dt
=
∑ F z(e)
p - p0 = ∑Ii(e)
px
-
p0 x
=
∑
I
(e x
)
py
-
p0 y
=
∑
I
(e y
)
pz
-
p0z
MMJ
IO
IZ
z
F (1)
M
IR
IO
(2)
0 简化为一主失
Fma
IR
C
(3) 转轴过质心时 a 0 惯性力系简化为一主矩 MJ
C
IO
z
(4) 轴过质心,且
0
则
F 0 IR
M 0 IO
惯性力系向质心简化:Fma MJ
3.刚体平面运动
IR
C
IC
C
Fma MJ
IR
C
IC
C
9
【题1】图示机构中,物块A,B的质量均为m,两均质圆轮C 和D的质量均为2m,半径均为R。轮C铰接于无重悬臂梁CK上, D为动滑轮,梁的长度为3R,绳与轮间无滑动,系统由静止开 始运动。求:(1)A物块上升的加速度;(2)HE段绳索的拉 力;(3)固定端K处的约束力。
三 刚体惯性力系的简化 M O (F i(e )) M O (F I) i 0
1.刚体作平移
Fma
IR
C
合力通过质心
2.刚体定轴转动
J J Fma
IR
C
M ( 2 ) i ( J J 2 ) j ( J ) k
IOxz yz
yz xz
z
刚体有质量对称平面且该平面与转轴Z垂直,简化中心O取此平面与转轴z的交点。则
若Fix(e)0, 则 aCx = 0 ,质心沿x方向速度不变;若开始 vCx0=0 ,则质心在x 轴的位置坐标保持不变。
5
三 动量矩定理
(1)质点系的动量矩定理
d
dtLO
n i1
MO(Fi(e))
ddtLx
n
i1
Mx(Fi(e))
ddtLy
n
i1
My(Fi(e))
ddtLz
n
i1
Mz(Fi(e))
K CE
A
H
D
B
10
§13-6 普遍定理的综合应用举例
解(1)取整体为研究对象。
T1m(2v)2 112mR2(2)2
2
22
132mR22 1mv26m2v
22
2
P 3 m m g 2 v v g m gv
K
2V A
由功率方程 dT P,得: 12mvamgv dt
2
CE
H
D
B
V
得: a 1 g 12
=
∑
I
( z
e
)
(2)质点系的动量守恒定理
若∑Fi(e) =0, 则 p= p0 =恒矢量 若∑Fi(e) =0, 则 p= p0 =恒矢量
4
(3)质心运动定理
mdvC dt
= ∑Fi (e)
maC =∑Fi(e)
质心运动定理投影形式:
m C = m x a x C = ∑ F i ( e ) x ,m C = m y a y C = ∑ F i ( e ) y ,m C = m z a z C = ∑ F i ( e ) z 。
i1
(6)平面运动微分方程。
m aC F(e)
md2rC F(e) dt2
d d(tJC )JC M C(F(e))
JCdd22t MC(F(e))
应用时,前一式取其投影式。
maCx Fxe maCy Fye
JC M C (F e)
maCt Fte maCn Fne
J C
