第五章 对流换热解析
合集下载
传热学第5章讲解
A qxdA
A
hx
tw
tf
x
dA
tw tf
A hxdA
等壁温，tw
tf
x
tw
tf
常数
对照式 = A h( tw－tf ) 可得
h 1 A
A hxdA
如何确定表面传热系数的大小是对流换热计算的
核心问题，也是本章讨论的主要内容。
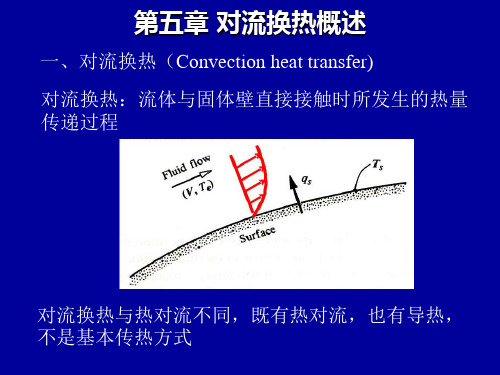
5－1 对流换热概述
h t tw t y y0
上面两式建立了对流换热表面传热系数与温度场 之间的关系。而流体的温度场又和速度场密切相关， 所以对流换热的数学模型应该包括描写速度场和温度 场的微分方程。
5-2.对流换热过程的数学描述
一、连续性微分方程（质量守恒） y
u v 0
dy
x y
(2) 流动的状态 层流 ：流速缓慢，流体分层地平行于壁面方 向流动，垂直于流动方向上的热量传递 主要靠分子扩散（即导热）。
6
紊流
：流体内存在强烈的脉动和旋涡，使各 部分流体之间迅速混合，因此紊流对流 换热要比层流对流换热强烈，表面传热 系数大。
7
(3) 流体有无相变 沸腾换热 凝结换热
(4) 流体的物理性质
q = h( tw－tf ) =h tm
h—整个固体表面的平均 表面传热系数;
tw—固体表面的平均温度 ; tf —流体温度，对于外部绕流，tf 取远离壁面的 主流温度；对于内部流动，tf 取流体的平均温度。
tm—平均换热温差。
对于局部对流换热，
qx
hx
tw
tf
x
4
ut 0
dx cp x dxdy
第5章-对流换热分析
二、连续性方程(质量守恒方程) A
流体的连续流动遵循质量守恒定律 从流场中 (x, y) 处取出边长为 dx、dy 、1的微元体，对进出 微元体的流量进行分析 （流入的质量=流出的质量)。
Mx M x dx x
M y vdx
二维、不可压缩ρ=C 、稳态流动时：
u v 0 x y
4个假设：（1）体积力(重力)作的功、表面力作的功， 流体不可压缩，流体不做功 W＝0
（2）流体的热物性均为常量，热力学能变化由温度引起 （3）一般工程问题，流速低 ΔU动能=0
（4）无化学反应等qv
Φ内热源=0
能量微分方程式
y
Φ 导热 + Φ 对流 = U热力学能
2t 2t 1 ） 导热 2 dxdy＋ 2 dxdy x y 2）单位时间,左侧面,进入的流体热量: x udycp t cp t udy
t hx ( ) t x y
w ,x
2 W m K
对流换热过程 微分方程式 D
对流换热过程微分方程
t hx ( ) t x y
梯度。
w,x
W m 2 K ( 5 2a )
hx 取决于流体λ、温度差Δt=（ tw – tf ）、贴壁流体的温度
( tu ) ( tv ) c p dxdy c p dxdy x y
由于对流进入 单元的净热量
t t u t v t u v c p u t v t dxdy c p u v t( ) dxdy y y y x y x x x t t u v c p u v dxdy ( 应用连续性方程: 0 ) y x y x
《传热学》第五章 对流换热分析PPT演示课件
4个方程,4个未知数(h,u,v,t)， 理论上存在唯一解， 可通过数学方法进行求解
24
求解结果 局部表面传热系数：
或可写成：
其中：
——准则方程
——无量纲流速 ——无量纲物性 ——无量纲换热强度
准则方程的意义——
把微分方程所反映的众多因素间的规律用少数几个准则来概括， 从而减少变量个数，以便于进行对流换热问题的分析、实验研究 和数据处理。
将上式在x,y两个方向代入牛顿第二定律，得到Navier-Stokes方程： 对于不可压缩流体：
11
将其代入Navier-Stokes方程，并采用连续方程化简，得到：
对稳态流动：
惯性力
体积力 压强梯度 黏滞力
当只有重力场作用时：
12
四、能量微分方程式
推导依据—— 内能增量＝导热热量＋对流热量 1.导热热量：
外掠平板全板长平均换热准则方程：
29
第六节 相似理论基础
相似原理的意义——通过实验寻找现象的规律以及指导推广应用实验。
一、物理相似的基本概念
1.几何相似
LA、LB——几何相似准则
30
2.物理现象相似
以管内流动为例，当两管各r之比满足下列 关系时：
若： 则速度场相似。 以外掠平板为例，当x,y坐标满足下列关系时：
《传热学》
1
第五章 对流换热分析
研究对象——流体与固体壁面之间的传热过程
研究目的——确定牛顿冷却定律
中的h
对流表面 传热系数
局部对流表面传热系数hx 平均对流表面传热系数
Isaac Newton(1642-1727)
确定对流表面传热系数的四种方法
分析法
类比法 数值法 实验法
24
求解结果 局部表面传热系数：
或可写成：
其中：
——准则方程
——无量纲流速 ——无量纲物性 ——无量纲换热强度
准则方程的意义——
把微分方程所反映的众多因素间的规律用少数几个准则来概括， 从而减少变量个数，以便于进行对流换热问题的分析、实验研究 和数据处理。
将上式在x,y两个方向代入牛顿第二定律，得到Navier-Stokes方程： 对于不可压缩流体：
11
将其代入Navier-Stokes方程，并采用连续方程化简，得到：
对稳态流动：
惯性力
体积力 压强梯度 黏滞力
当只有重力场作用时：
12
四、能量微分方程式
推导依据—— 内能增量＝导热热量＋对流热量 1.导热热量：
外掠平板全板长平均换热准则方程：
29
第六节 相似理论基础
相似原理的意义——通过实验寻找现象的规律以及指导推广应用实验。
一、物理相似的基本概念
1.几何相似
LA、LB——几何相似准则
30
2.物理现象相似
以管内流动为例，当两管各r之比满足下列 关系时：
若： 则速度场相似。 以外掠平板为例，当x,y坐标满足下列关系时：
《传热学》
1
第五章 对流换热分析
研究对象——流体与固体壁面之间的传热过程
研究目的——确定牛顿冷却定律
中的h
对流表面 传热系数
局部对流表面传热系数hx 平均对流表面传热系数
Isaac Newton(1642-1727)
确定对流表面传热系数的四种方法
分析法
类比法 数值法 实验法
第五章对流换热分析
wton’s law of cooling:−=W/m 2dxdtq λ−=Contents第一节对流换热概述Analysis on Convection第二节对流换热微分方程组The Convection Heat Transfer Equations第三节边界层换热微分方程组Convection Differential Equations of Boundary Layer 第四节边界层换热积分方程(自学)第五节动量传递和热量传递的类比(自学)第六节相似理论基础Basis of similarity theoryConvection is the mode of energy transfer between a solid surface and the adjacent liquid or gas that is in motion, and it involves the combined effects of conduction and fluid motion.(流体与固体壁直接接触时所发生的热量传递过程，称为对流换热)The faster the fluid motion, the greater the convection heat transfer.We will study how to calculate the convection heat-transfer coefficient h in Chapter 5 and Chapter 6.5-1 Analysis on Convection(对流换热概述) Convection transfer problemHeat exchangers Tubes in steamboiler (蒸汽锅炉的管束)Tube-shell heat exchanger (管壳式换热器)Condenser ofrefrigerator Tubes withfins (翅片管束)图5-1几种常见的换热设备示意图Factors influencing convection heat transfer ：Flow causes of fluid (流体流动的起因)、flow states ( 流动状态)、properties of fluid (流体物性)、change of phase of fluid (流体物相变化)、geometry parameters (壁面的几何参数),and so on 。
传热学第5章-对流换热的理论基础
沿热竖壁的自然对流局部传热系数变换规律受多种因素影响。首先，自然对流是由于流体内部密度差产生的流动，其流速和温度分布与强迫对流不同，导致传热规律有差异。其次，流动状态（层流或湍流）对传热有显著影响。层流时，流体沿壁面规则分层流动，热量传递主要靠导热；而湍流时，流体内部存在强烈脉动和旋涡运动，热量传递主要靠对流。此外，流体的热物理性质如导热系数、密度、比热容、粘度和体积膨胀系数等也影响传热过程。例如，导热系数越大，对流换热越强烈；粘度影响速度分布与流态，高粘度流体多处于层流状态，传热系数较小。最后，换热表面的几何形状、尺寸、相对位置和表面状态等因素也会对传热产生影响。综作用的结果。
第5章对流换热分析2讲
和热量扩散的深度
t Pr 1 3
( 层 流 、 0.6 Pr 50 )
第五章 对流换热 （李琼主讲） 20
δt<<L； 边界层内温度梯度变化显著，用能量微分方程描述； 边界层外温度梯度约为零，传热忽略不计。
因为膝盖处的热边界层很薄(相当 于外掠物体的前驻点),换热能力较 强，该处与空气的热交换量较大。 摩托车手的膝盖需要特别的保温, 你知道为什么吗?
u u u p 2u 2u （ u v ) X ( 2 2 ) x y x x y v v v p 2v 2v （ u v ) Y ( 2 2 ) x y y x y
2 2t t t t t c p u v 2 2 x y y x
这就是关于udydudy第五章对流换热李琼主讲39边界层积分方程组求解在常物性情况下动量积分方程可以独立求解即先求出然后求解能量积分方程获得dycy第五章对流换热李琼主讲40dydure64dydure323第五章对流换热李琼主讲41在工程中场使用局部切应力与流体动压头之比这个无量纲量并称之为范宁摩擦系数简称摩擦系数re646re292平均摩擦系数
第五章 对流换热 （李琼主讲） 21
三 数量级分析与边界层换热微分方程
1.数量级分析：比较方程中各量或各项的量级的相对大小；保 留量级较大的量或项；舍去那些量级小的项，方程大大简化 例：二维、稳态、强制对流、层流、忽略重力
u ~ 0(1); 5个基本量的数量级： 主流速度：
温度：t ~ 0(1); 边界层厚度： 壁面特征长度：l ~ 0(1);
边界层概念也可以用于分析其他情况下的流动和换热： 如：流体在管内受迫流动、流体外掠圆管流动、流体 在竖直壁面上的自然对流等
t Pr 1 3
( 层 流 、 0.6 Pr 50 )
第五章 对流换热 （李琼主讲） 20
δt<<L； 边界层内温度梯度变化显著，用能量微分方程描述； 边界层外温度梯度约为零，传热忽略不计。
因为膝盖处的热边界层很薄(相当 于外掠物体的前驻点),换热能力较 强，该处与空气的热交换量较大。 摩托车手的膝盖需要特别的保温, 你知道为什么吗?
u u u p 2u 2u （ u v ) X ( 2 2 ) x y x x y v v v p 2v 2v （ u v ) Y ( 2 2 ) x y y x y
2 2t t t t t c p u v 2 2 x y y x
这就是关于udydudy第五章对流换热李琼主讲39边界层积分方程组求解在常物性情况下动量积分方程可以独立求解即先求出然后求解能量积分方程获得dycy第五章对流换热李琼主讲40dydure64dydure323第五章对流换热李琼主讲41在工程中场使用局部切应力与流体动压头之比这个无量纲量并称之为范宁摩擦系数简称摩擦系数re646re292平均摩擦系数
第五章 对流换热 （李琼主讲） 21
三 数量级分析与边界层换热微分方程
1.数量级分析：比较方程中各量或各项的量级的相对大小；保 留量级较大的量或项；舍去那些量级小的项，方程大大简化 例：二维、稳态、强制对流、层流、忽略重力
u ~ 0(1); 5个基本量的数量级： 主流速度：
温度：t ~ 0(1); 边界层厚度： 壁面特征长度：l ~ 0(1);
边界层概念也可以用于分析其他情况下的流动和换热： 如：流体在管内受迫流动、流体外掠圆管流动、流体 在竖直壁面上的自然对流等
第五章对流换热分析
程，简称N-S方程，又称不可压缩粘性流体的运动微分方
程）
据牛顿第二定律：F=ma及相关流体力学知识推出。
第二节 对流换热的数学描写
一、运动微分方程
2.动量微分方程
u
u
u x
u y
X
p x
2u x2
2u 2 y
u
边界层的形成、发及区域划分
u∞
u∞
o
u∞=f（x,u,）
紊流核心层
o
缓冲层
u c
xc
层流底层
层流边界层 过渡段
紊流边界层
自O点开始边界层逐渐加厚，并随着粘滞力对外影响的减弱， 在某处开始层流开始不稳定起来。
临界距离xc：O点距层流向紊流过渡点的水平距离； 临界雷诺数Rec：层流向紊流过渡点的雷诺数值。Rec=u∞·xc/
b.粘滞力项：<3>式粘滞力可略去，且<2>中只须保留第二项；
c.压力梯度：<3>式中可略去，此时说明压力仅沿x方向发生变 化，故可将P/x改写成dP/dx，其值可由伯努利方程得出：
-dP/dx=u∞du∞/dx
N-S方程可写成：
u
u x
u y
1
dp dx
2u 2y
<2>.能量微分方程的简化：可忽略式右侧第一项，即沿x向
第三节 边界层换热微分方程组的解
一、流动边界层
6.流体受迫横掠圆管时的边界层
发生绕流脱体 形成卡门涡街
第三节 边界层换热微分方程组的解
传热学 第五章 对流原理.
层流边界层 紊流核心区
过渡区 紊流边界层 层流底层 主流区 速度边界层厚度 临界距离
层流
过渡流
湍流
u
y
x
xc
层流底层 缓冲层
根据流体力学知识，层流边界层厚度 xv 5x 5x 5 vf vf x Re x
在层流边界层内的速度分布线为抛物线型； 在紊流边界层内，层流底层部分的速度 分布较陡，接近于直线，而在底层以外 的区域，由于流体微团的紊流运动，动 量传递被强化了，速度变化趋于平缓。
如果流体的流动是由于流体冷热部分的密度不同 引起的浮升力造成的，则称为自然对流。暖气 片的散热，蒸汽或其他热流体输送管道的热量 损失，都与这类换热有关。 一般来讲：强迫对流 换热优于自然对流。
二、 在分析对流换热时，还应分清流体的流态。 流体力学告诉我们，流体受迫在流道内流 动时可以有两种不同性质的流态。流体分 层地平行于流道的壁面流动，呈现层流状 态。但当流动状态到超过某一临界值时， 流体的流动出现了旋涡，而且在不断地发 展和扩散，引起不规则的脉动，使流动呈 现紊流状态。
α ＝q/（tf－tw） W
对流换热系数 α表征着对流换热的强弱 。
在数值上，它等于流体和壁面之间的温度 差为 1℃时，通过对流换热交换的热流密 度。单位为W/(m２·℃)。 对流换热量以及相应的换热系数的大小，将 更多地取决于流体的运动性质和情况。
一、速度边界层
流体力学指出，具有粘性且能湿润固 体壁面的流体，流过壁面会产生粘性力。 根据牛顿粘性（内摩擦）定律，流体粘性 力 τ 与垂直于运动方程速度梯度 (dv/dy ） 成正比，即: τ＝μ（dv/dy） Ｎ／m２ （5-2） 式中，μ 称为流体的动力粘度，单位为Pa· s 或kg/(m· s）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c. 流场的划分
从分析速度边界层中知，在边界层外，法向速度已接近 或达到来流速度，粘性已不起作用，称主流区（自由 区），可看作理想流体。
流场可以化分为边界层和主流区
d. 流动状态
流体的流动可分为层流和紊流，在边界层内，流型也 可以分为层流和紊流。
在紊流边界层中，又可以人为地划分成三个区域：
层流底层
管外凝结 管内凝结
5. 影响对流换热的影响因素
（1）流体流动的起因：强制对流换热和自然对流换 热流动的成因不同，流体中的速度场也有差别，换热 规律不一样。
（2）流体有无相变：无相变—显热；有相变—潜热
（3）流体的流动状态：层流、湍流
（4）换热表面的几何因数：换热表面的形状、大小、 换热表面与流体运动方向的相对位置以及换热表面的 状态（光滑或粗糙）
根据质量守恒定律：对于不可压缩的流体，从各个方向上流 入、流出为控制体质量流量差值的总和等于零。
y
dy dz
z dx x
二、动量微分方程 根据动量定理：作用与微元体表面和内部的所有
外力的总和，等与微元体中流体动量的变化率。
先考虑x方向微元体中流体动量的变化率。由三部 分组成：
来自面积为dydz的微元体 来自面积为dxdz的微元体 微元体内部
l/d
边界层示意图表示了近壁处流速的变化。贴壁处这层薄层 的流体层相对于壁面是不流动的，壁面与流体间的热量传 递必须穿过这个流体层，而穿过不流动的流体层的热量传 递方式只能是导热。因此，对流换热量就等于贴壁流体层 的导热量。将傅里叶定律应用与贴壁流体层，可得：
将牛顿冷却公式与上式联立，即得以下关系式：
（5）流体的物理性质：流体密度、动力粘度、导热 系数及定压比热容等
6. 边界层（附面层）的概念
由于流体都存在着粘性，所以流体流过壁面时，在 壁面附近的区域流体的温度和速度均发生了很大的变 化。实验研究表明，表面传热系数的大小主要取决于 这一区域内流体的流动情况，这一区域称边界层。
（1）速度边界层
如果流体为没有粘性流体，流体流过平板时，流 速在截面上一直保持不变。
第五章 对 流 换 热
第一节 对流换热概述
1. 定义：
流体流过与其温度不同的固体壁时所发生的热量传 递称对流换热。对流换热是由热对流与热传导两部分 组成的。
2. 牛顿冷却公式 对流换热的换热量由牛顿冷却公式计算。
从公式可知，要计算换热量，温度、面积比较容 易得到，主要任务是如何求得对流换热系数h。 3. 求换热系数h的两种基本途径
y
dy dz
z dx x
同理：在y方向上的动量变化率为
微元体所受外力的作用有二类：
与体积成正比的体积力Fx，Fy
与面积成正比的表面力（流体压力引起的粘性应力引 起的）法向应力、切向应力。
流体无粘性时
u∞
面之间产生一粘滞力，粘滞
u∞
力使得靠近壁面处的速度逐
渐下降，最后使壁面上的流
体速度降为零，流体质点在 流体有粘性时
u∞
壁面上产生一薄层。随着流
体的流动，粘滞力向内传递， 形成的薄层又阻碍邻近流体
u∞
层中微粒运动的作用，依此
类推，形成的薄层又阻碍邻
近流体层微粒运动，以至到
一定程度，粘滞力不再起作 用。
第二节 对流换热微分方程
由换热微分方程可知，要求h需先知道温度分布（能量方 程），而速度分布影响温度分布；要求速度分布，需连续性方 程和动量微分方程。下面就逐个建立这三个方程。先作假设：
（1）仅考虑二维问题； （2）流体为不可压缩的牛顿流体，稳定流动； （3）常物性，无内热源； （4）忽略由粘性摩擦而产生的耗散热。 一、连续性方程 取一控制体
（3）两者的联系和区别（理论分析法和实验研究 方法）
两种方法在解决对流换热问题上起相辅相成的作用。虽然解 析解不能求解各种各样对流换热问题，但能深刻地揭示出各 个物理量对换热系数的影响，而且也是评价其它方法所得结 果的标准和依据，而实验研究方法可以得到具体的表达方式， 而且是设计计算的主要计算式，是必须掌握的内容。
4. 对流换热问题的分类
内部流动
圆管内强制对流换热 其它形式截面管道内的对流换热
无ห้องสมุดไป่ตู้变
强制对流
外部流动
外掠平板的对流换热 外掠单根圆管的对流换热 外掠圆管管束的对流换热 外掠其它截面形状柱体的对流换热 射流冲击换热
对流换热
自然对流
大空间自然对流 有限空间自然对流
混合对流
沸腾换热 有相变
凝结换热
大容器沸腾 管内沸腾
形象说明边界层的形成过程
b. 两个概念：速度（流动）边界层和边界层厚度
速度边界层：近壁处有一法向速度梯度的薄层。
边界层厚度：从速度为零的壁面到速度达到u∞的99 ％处的法向距离，用δ表示。
边界层厚度是随x的增加而增加的，但是一个很小 的量。
为定量地说明它的大小，下面举例说明：
20 ℃的空气以u ∞ =10m/s流过平板时，在 x=100mm处，δ=1.8mm；x=200mm处，δ=2.5mm。 从这个例子可以看出， δ<< x(l)，在这样薄的流体内， 速度从零变化到接近来流速度u ∞ ，可见平均速度是 很大的。为定性地说明速度的变化，人为地把边界层 夸大了。
如果流体为粘性流体，情况会如何呢？我们用一测 速仪来测量壁面附近的速度分布。测量发现在法面 方向上，即y方向上，壁面上速度为零，随着y方向 的增加，流速急剧增加，到达一薄层后，流速接近 或等于来流速度，普朗特研究了这一现象，并且在 1904年第一次提出了边界层的概念。
a. 边界层产生原因： 由于粘性的作用，流体与壁
缓冲层
紊流核心
层流 u
过渡流
湍流
y
x
xc
层流底层 缓冲层
e. 边界层发展过程（见上图） f. 判别依据（流态） 用xc（临界长度）行不通，因为xc随流体的性质、流速、壁 面情况及扰动情况有关，可以用雷诺数来判断。
物理意义： 惯性力与粘滞力之比的相对大小。
g. hx 的变化趋势 (见上图) hx
h. 对流换热微分方程式：
（1）分析法（解析解，理论分析法） a 建立边界层内的微分方程组求解h
思路：取控制体，利用能量守恒和动量守恒建立微 分方程组结合单值性条件。
b. 建立边界层的积分方程组求解h （近似解法）
c. 利用动量和能量的比拟方法（类比法）
（2）实验研究方法：
用相似原理或量纲分析法，将众多的影响因素归纳 成为数不多的几个无量纲的准则，通过实验确定h的 具体关系式。