拉普拉斯变换及反变换.

合集下载

拉普拉斯变换和反变换

F (s)s(s2s 2 1 s 5 )1 5 [1 ss2 s 2 s3 5 ]
L 1 [(s 1 s ) 2 3 4 ] L 1 [(s ( 1 s ) 2 1 )4 ] L 1 [(s 1 4 )2 4 ]
0
s
t
L[ 0
t 0
f(t)dnt]s1nF(s)
第16页
黄河科技学院
控制工程基础
（7）初值定理
lim f(t)lim sF (s)
t 0
s
f(0)lim sF(s) s
（8）终值定理
lim f(t)lim sF (s)
t
s 0
f()lim sF(s)
Fssp1
Ns sp2 .......spn
k1 k2 .........kn
sp1 sp2
spn
其中 k i [F s(s p i)s ]p i
第23页
黄河科技学院
控制工程基础
例
F(s)s2
s1 5s6
解：（1）F（s）的极点
s25s60 s1 2 s2 3
Fs 的原函数；L是表示进行拉氏变换的
符号。
第2页
黄河科技学院
控制工程基础
F(s)L[f(t)]
f(t)L1[F(s)]
拉氏变换是这样一种变换，即在一定的条件下，它能把一实数域中的实变函数
f t 变换为一个在复数域内与之等价的
复变函数 Fs。
第3页
黄河科技学院
控制工程基础
1）、典型函数的拉氏变换
式中 L1 表示拉普拉斯反变换的符号
第20页
黄河科技学院
控制工程基础

022第五章-3拉普拉斯变换反变换

§5.5 拉普拉斯反变换一、部分分式展开法(Haviside Theorem)
Ⅰ. F(s)单极点情况
(1) F (s)有n个单极点s1, s2
sn , 且n m,即F (s)为真分式
ki ki e si t (t ) s si
(2) F ( s)有n个单极点，但 n m 即 F ( s) 为假分式
则应将F(s)化为多项式和真分式之和，真分式部分用“部分分式展开法”求反变换，多项式的反变换为冲激函数及其导数
(t ) 1 (t ) s
s 例3、 F ( s) 2 求 f (t ) s 2s 5
真分式、共轭极点
e t sin t (t ) e t cos t (t )
k1 ( s 2 ) k2 ( s 2 ) 解： F (s) 2 2 s 3 s 2s 5
2 4 4 3 s 1 2 s 1 k1 ( s ) 2 s s 1 1 ss22 s 2 s 5 s 2 3 0 1 3 04
p
( s sn ) K11 s s1

K1 p 1 ( s s1 )
p 1

K1i i ( s s1 )
Kn s sn
p i
1 d p 其中：K1i [(s s1 ) F (s) ] s s p i 1 ( p i) ! ds
P231 式（5-26C）
0 2 s 0 2
s
2 s 0 2
解：极点 s1,2 1 j 2
s 1 1 2 s F ( s) 2 2 2 ( s 1) 2 2 ( s 1) 2 22 ( s 1) 4

常用拉普拉斯变换及反变换

419附录A 拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质齐次性)()]([s aF t af L =1线性定理叠加性)()()]()([2121s F s F t f t f L ±=±一般形式=−=][′−ٛ−=−=−−−−=−∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n n n dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L M ）（ 2微分定理初始条件为0时)(])([s F s dtt f d L n nn =一般形式 }}∑∫∫∫∫∫∫∫∫∫∫∫==+−===+=++=+=nk t n n k n n n n t t t dt t f ss s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共L L M3积分定理初始条件为0时}nnn s s F dt t f L )(]))(([=∫∫个共L4 延迟定理（或称t 域平移定理）)()](1)([s F e T t T t f L Ts−=−− 5 衰减定理（或称s 域平移定理）)(])([a s F e t f L at +=−6 终值定理 )(lim )(lim 0s sF t f st →∞→=7 初值定理 )(lim )(lim 0s sF t f s t ∞→→=8 卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =−=−∫∫τττττ4202．表A-2 常用函数的拉氏变换和z 变换表序号拉氏变换E(s)时间函数e(t) Z 变换E(z)1 1δ(t)12 Ts e −−11∑∞=−=0)()(n T nT tt δδ 1−z z3 s1 )(1t 1−z z 421s t2)1(−z Tz5 31s 22t32)1(2)1(−+z z z T6 11+n s!n t n )(!)1(lim 0aTn n n a e z z a n −→−∂∂− 7 as +1ate −aTe z z−− 8 2)(1a s + atte− 2)(aT aT e z Tze −−−9 )(a s s a +ate−−1 ))(1()1(aT aT e z z z e −−−−− 10 ))((b s a s ab ++− btate e−−−bTaT e z z e z z −−−−− 11 22ωω+st ωsin 1cos 2sin 2+−T z z Tz ωω12 22ω+s st ωcos1cos 2)cos (2+−−T z z T z z ωω 13 22)(ωω++a s t eatωsin −aTaT aT eT ze z T ze 22cos 2sin −−−+−ωω 14 22)(ω+++a s a st e at ωcos −aTaT aTe T ze z T ze z 222cos 2cos −−−+−−ωω15aT s ln )/1(1−T t a/az z −4213．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

(完整版)拉普拉斯变换表

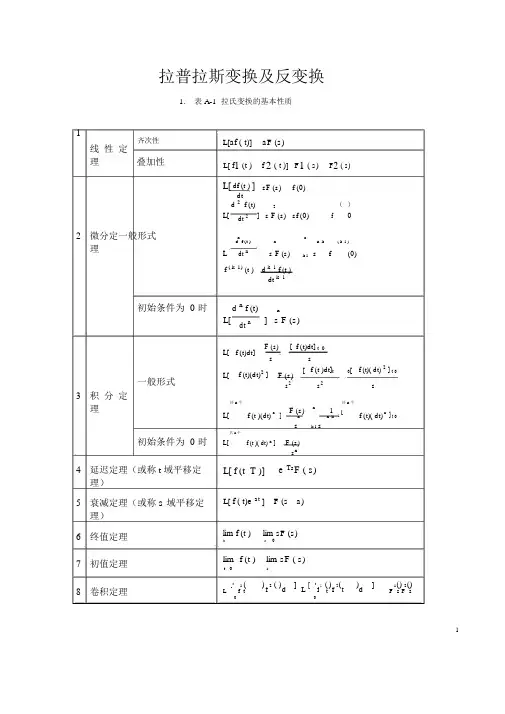
拉普拉斯变换及反变换1. 表 A-1 拉氏变换的基本性质1齐次性线性定理叠加性2微分定一般形式理L[af ( t)] aF (s)L[ f1 (t ) f 2 ( t )] F1 ( s) F2 ( s) L[ df (t ) ] sF (s) f (0)dtL[d 2 f (t) 2f（）dt 2 ] s F (s) sf (0) 0n nd f (t ) n n k ( k 1 )L dt n s F (s) k 1 s f (0) f ( k 1) (t ) d k 1 f (t )dt k 1初始条件为 0 时一般形式3积分定理初始条件为 0 时4延迟定理（或称 t 域平移定理）5衰减定理（或称 s 域平移定理）6终值定理7初值定理8卷积定理L[d n f (t) ndt n ] s F (s)L[ f (t)dt]F (s) [ f (t)dt] t 0s sL[ f (t)(dt)2 ] F (s)[ f (t )dt]t 0[ f (t)( dt) 2 ] t 0s2 ss2共 n个n共 n个nF (s) 1 nL[ f (t )(dt) ] 1 [ f (t)( dt) ] t 0nk 1 sn ks共 n个F (s)L[ f (t )( dt) n ]s nL[ f (t T )] e Ts F ( s)L[ f ( t)e at ] F (s a)lim f (t ) lim sF (s)t s0lim f (t ) lim sF ( s)t 0 st 1 ( ) 2 ( ) ] [ t 1 ( ) 2 ( ) ] 1() 2()[ f d L f f t dL f t t F s F s0 012．表 A-2 常用函数的拉氏变换和z 变换表拉氏变换E(s)111 e Ts1s12s13s1s n 11s a1( s a) 2as( s a)b a( s a)(s b)s2 2ss2 2( s a) 2 2s a( s a)2 21s (1 / T ) ln a 时间函数 e(t)δ(t)T (t )(t nT )n01(t )tt 22ntn!e atte at1 e ate at e btsin tcos te at sin te at cos ta t / T23．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

拉普拉斯变换及反变换1

方法一：方法一：利用拉氏反变换定义求
——不常用解
方法二：方法二：查拉氏变换表求解 ——对简单的象函数适用方法三：方法三：部分分式法——象函数为有理分式函数时适用
第21页页
黄河科技学院
控制工程基础
应用部分分式展开式计算拉氏逆变换的一般步骤：的极点；（1）计算有理分式函数F（s）的极点；（2）根据极点把F（s）的分母多项式进行因式分解、展开成部分分式；式分解、并进一步把F（s）展开成部分分式；（3）对F（s）的部分分式展开式两边同时进行拉氏逆变换。行拉氏逆变换。
（11）卷积定理 11）
f (t ) * g (t ) = ∫
+∞
−∞
f (τ ) g (t − τ )dτ
= ∫ f (τ ) g (t − τ )dτ
0
t
L[ f (t ) * g (t )] = F ( s ) ⋅ G ( s ) = G ( s ) F ( s )
第19页页
黄河科技学院
控制工程基础
s +1 c2 = ( s + 3) ( s + 2)( s + 3)
s = −3
（2）对F（s）的分母多项式进行因式分解、并把（s）展开）（）的分母多项式进行因式分解、并把F（）成部分分式
=2
第24页页
黄河科技学院
控制工程基础
s +1 1 2 F ( s) = 2 =− + s + 5s + 6 s+2 s+3
− st
单位阶跃函数，记作单位阶跃函数，记作1( t )
t<0 t≥0
1 L[1(t )] = s

拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表
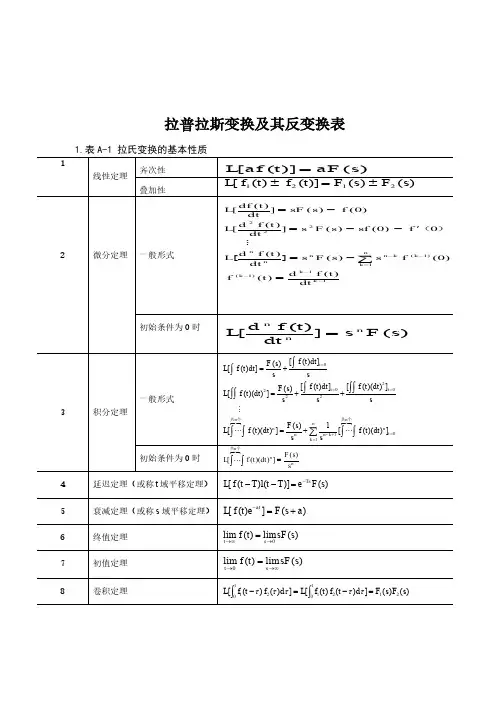
1.表 A-1 拉氏变换的基本性质
1 线性定理齐次性叠加性
L[ af (t )] aF ( s )
L[ f 1 (t ) f 2 (t )] F1 ( s ) F2 ( s )
df (t ) ] sF ( s ) f (0) dt d 2 f (t ) L[ ] s 2 F ( s ) sf (0) f （ 0 ） dt 2 L[
1(t )
z z 1
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1) 3
1 s n 1
1 sa
tn n!
lim
( 1) n n z ( ) n a 0 n! a z e aT
z z e aT
e at te
at
1 n 1 n 0 1 m 1 m
代数定理可将 F ( s ) 展开为部分分式。分以下两种情况讨论。 ① A( s) 0 无重根这时，F(s)可展开为 n 个简单的部分分式之和的形式。
c c c c c F (s ) ss ss ss ss ss
1 2 i n n i i 1 1 2 i n
r 1 r 1 n r 1 1 r 1 i n r 1
c c c c c c (s s ) (s s ) (s s ) s s ss ss
r 1 1 1 r 1 i
n
式中， s1 为 F(s)的 r 重根， s r 1 ，…, sn 为 F(s)的 n-r 个单根；其中， c r 1 ，…, cn 仍按式(F-2)或(F-3)计算， cr ， cr 1 ，…, c1 则按下式计算：

拉普拉斯变换及逆变换

第十二章拉普拉斯变换及逆变换拉普拉斯(Laplace)变换就是分析与求解常系数线性微分方程得一种简便得方法,而且在自动控制系统得分析与综合中也起着重要得作用。

我们经常应用拉普拉斯变换进行电路得复频域分析。

本章将扼要地介绍拉普拉斯变换(以下简称拉氏变换)得基本概念、主要性质、逆变换以及它在解常系数线性微分方程中得应用。

第一节拉普拉斯变换在代数中,直接计算328.957812028.6⨯⨯=N 53)164.1(⨯就是很复杂得,而引用对数后,可先把上式变换为164.1lg 53)20lg 28.9lg 5781(lg 3128.6lg lg ++-+=N然后通过查常用对数表与反对数表,就可算得原来要求得数N 。

这就是一种把复杂运算转化为简单运算得做法,而拉氏变换则就是另一种化繁为简得做法。

一、拉氏变换得基本概念定义12、1 设函数()f t 当0t ≥时有定义,若广义积分()pt f t e dt +∞-⎰在P 得某一区域内收敛,则此积分就确定了一个参量为P 得函数,记作()F P ,即dte tf P F pt ⎰∞+-=)()( (12、1)称(12、1)式为函数()f t 得拉氏变换式,用记号[()]()L f t F P =表示。

函数()F P 称为()f t 得拉氏变换(Laplace) (或称为()f t 得象函数)。

函数()f t 称为()F P 得拉氏逆变换(或称为()F P 象原函数),记作)()]([1t f P F L =-,即)]([)(1P F L t f -=。

关于拉氏变换得定义,在这里做两点说明:(1)在定义中,只要求()f t 在0t ≥时有定义。

为了研究拉氏变换性质得方便,以后总假定在0t <时,()0f t =。

(2)在较为深入得讨论中,拉氏变换式中得参数P 就是在复数范围内取值。

为了方便起见,本章我们把P 作为实数来讨论,这并不影响对拉氏变换性质得研究与应用。

拉普拉斯Laplace变换

f (t) = 2e − t − e −2t
例2
2s + 12 k1 k2 F(s) = 2 = + s + 2s + 5 s + 1 + 2 j s + 1 − 2 j
2s + 12 k1 = 2 (s + 1 + 2 j) s + 2s + 5
5 k2 = 1− j 2
s =−1− 2 j
5 = 1+ j 2
[a1s + a2 ]s =− p1 B( s) =[ ( s + p1 )( s + p2 )]s =− p1 A( s)
c. F(s)含有多重极点时，可展开为
an br br −1 b1 ar +1 F ( s) = + + ⋅⋅⋅ + + + ⋅⋅⋅ + r r −1 ( s + p1 ) ( s + p1 ) ( s + p1 ) ( s + pr +1 ) ( s + pn )
s =−1
=2
d s 2 + 2s + 3 a12 = [ (s + 1)3 ] s=−1 = 0 ds (s + 1)3 1 d 2 s 2 + 2s + 3 a13 = [ (s + 1)3 ] s =−1 = 1 2! ds 2 (s + 1)3
所以:
2 1 f (t) = L [ + ] = t 2e − t + e − t = (t 2 + 1)e − t (s + 1)3 s + 1
线性定理位移定理延迟定理终值定理

拉氏变换与拉氏反变换

e
at
e dt
st
1 ( s a )t e sa

j t
1 ] s j
0
1 sa
拉普拉斯变换及反变换
3. f (t ) (t ) （单位脉冲函数）
0 (t 0) (t ) (t 0)
δ(t) t

(t )dt 1
t
拉普拉斯变换及反变换二、微分定理
设 ℒ [ f ( t )] F ( s )
d n f (t ) n n 1 n2 ( n 1) ] s F ( s ) s f（0 ） s f （0 ） ... f （0 ） ℒ[ n dt
例1
df ( t ) 则 ℒ[ ] sF ( s ) f (0 ) dt 2 d f (t ) 2 ] s F ( s ) sf ( 0 ) f ( 0 ) ℒ [ 2 dt
s s
1 s 1 sa
由终值定理得
f () lim sF ( s) lim
s 0 s 0
1 s 0 sa
拉普拉斯变换及反变换七、时域卷积性 8 时域卷积性：
L 若f1 (t ) F1 ( s ), f 2 (t ) F2 ( s ) L 则f1 (t ) f 2 (t ) F1 ( s ) F2 ( s )
t
f ( ) lim f ( t ) lim sF ( s )
t s 0
拉普拉斯变换及反变换例1
例2
1 u (t ) t 0 lim s 1 s s 5 2 I ( s) s1 s 2
5 2 5 2 i (0 ) l i ms( ) lim ( )3 s s s1 s 2 1 1/ s 1 2/ s

拉普拉斯变换性质及反演

b p a
p f( ) a
数学物理方法
（7）卷积定理
若 f1 ( p) L[ f1 (t )] ， f 2 ( p) L[ f 2 (t )]
t
则 L[ f1 (t )* f 2 (t )] f1 ( p) f 2 ( p) ，其中积。在傅里叶变换中我们定义了两个函数的卷积： f1 (t ) * f 2 (t ) f1 ( ) f 2 (t )d
a y ( p) y ( p) 2 2 p p 1
1 1 解得 y ( p ) a ( 2 4 ) p p
1 3 从而 y (t ) a (t t ) 6
数学物理方法
（三）黎曼－梅林反演公式* 在上两种方法都不能求出原函数时，原则上总是可以采用
n
数学物理方法
（4）相似性定理
1 p L[ f (at )] f ( ) a a
（5）位移定理 L[ e t f( t) f ( ] p 请大家仿照傅里叶积分变换验证。
)
计算 eat cos t ， e at sin t ， eat cht ， eat sht 的拉普拉斯变换函数。解：略。例 6.2.6
e ap 1 解：由于的原函数为 H (t ) ，应用延迟定理有 p p 1 的原函数为 H (t a) ，又由位移定理有的原函 pb bt 数为 e 。应用卷积定理，有
t e ap 1 L [ ] H ( a)e b (t ) d 0 p ( p b)
t 1 1 L [ 2 ] ( )et d t 1 et 0 p p 1 1
6.3 拉普拉斯变换的反演
数学物理方法

常用拉普拉斯变换及反变换

常用拉普拉斯变换及反变换拉普拉斯变换在工程和数学中是个非常实用的工具。

它不仅能帮助我们解决微分方程，还能简化许多复杂的问题。

今天我们就来聊聊常用的拉普拉斯变换和反变换，看看它们是如何发挥作用的。

一、拉普拉斯变换的基本概念1.1 定义拉普拉斯变换是一个积分变换，它将时间域的函数转换为复频域的函数。

简单来说，它把一个函数从“时间的世界”带到了“频率的世界”。

公式上，拉普拉斯变换可以表示为：\[ \mathcal{L}\{f(t)\} = F(s) = \int_0^{\infty} e^{-st} f(t) dt \]这里的 \( s \) 是复数变量，\( f(t) \) 是我们要变换的时间域函数，\( F(s) \) 则是变换后的结果。

1.2 性质拉普拉斯变换有几个重要的性质，比如线性性、时间延迟和微分等。

这些性质使得在实际应用中，可以灵活地对待不同类型的函数。

例如，线性性让我们可以把两个函数的变换简单相加，这对于解决复杂问题很有帮助。

二、常用的拉普拉斯变换2.1 单位阶跃函数单位阶跃函数 \( u(t) \) 是拉普拉斯变换中最常用的函数之一。

它的变换结果是：\[ \mathcal{L}\{u(t)\} = \frac{1}{s} \]这个简单的公式为很多工程应用奠定了基础，因为很多信号和系统可以用阶跃函数来描述。

2.2 指数函数另一个常见的函数是指数函数 \( e^{at} \)。

它的拉普拉斯变换结果为：\[ \mathcal{L}\{e^{at}\} = \frac{1}{s - a} \]这在处理自然衰减或增长的过程时特别有用，比如在电子电路中，我们经常会遇到这种情况。

2.3 正弦和余弦函数正弦和余弦函数的拉普拉斯变换也很重要。

它们分别为：\[ \mathcal{L}\{\sin(\omega t)\} = \frac{\omega}{s^2 + \omega^2} \] \[ \mathcal{L}\{\cos(\omega t)\} = \frac{s}{s^2 + \omega^2} \]这些变换结果在振动分析和控制系统中应用广泛，帮助我们理解系统的频率响应。

拉普拉斯变换的基本性质变换及反变换

拉普拉斯变换的基本性质变换及反变换The following text is amended on 12 November 2020.拉普拉斯变换的基本性质、变换及反变换3．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >）式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算：)()(lim s F s s c i s s i i-=→ （F-2）或iss i s A s B c ='=)()(（F-3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝t s n i i ie c -=∑1(F-4)② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1(（F-6）。

拉普拉斯变换及反变换

路漫漫其修远兮, 吾将上下而求索
路漫漫其修远兮, 吾将上下而求索
路漫漫其修远兮, 吾将上下而求索
路漫漫其修远兮, 吾将上下而求索
• 作业
1 写出拉普拉斯变换定义式、 2 、
路漫漫其修远兮, 吾将上下而求索
路漫漫其修远兮, 吾将上下而求索
__
1
(s-1)2
路漫漫其修远兮, 吾将上下而求索
F(s)= ℒ ℒ
路漫漫其修远兮, 吾将上下而求索
（单位脉冲函数） δ(t)
0
t
ℒ
=1
路漫漫其修远兮, 吾将上下而求索
（单位斜坡函数） f(t) t
0
F(s)=L[f(t)]=
路漫漫其修远兮, 吾将上下而求索
（幂函数）
ℒ
ℒ
路漫漫其修远兮, 吾将上下而求索
ℒ
ℒ
ℒ ℒ
ℒ
路漫漫其修远兮, 吾将上下而求索
路漫漫其修远兮, 吾将上下而求索
三、积分定理
ℒ
ℒ
例
路漫漫其修远兮, 吾将上下而求索
四、时域平移
ℒ
平移
f(t)
f(t-t0)
路漫漫其修远兮, 吾将上下而求索
五、复频域平移
ℒ ℒ 例1 ℒ
例2 ℒ 例3 ℒ
路漫漫其修远兮, 吾将上下而求索
六、初值定理和终值定理初值定理若ℒ [f(t)]=F(s)，且 f(t)在t = 0处无冲激，
f1(t)
f2(t)
1 e-t
1 e-t
0
t 0
t
解由于定义的拉氏变换积分上限是0－，两个函数的拉氏变换式相同
当取上式的反变换时，只能表示出区间的函数式
ℒ -1

拉普拉斯变换和逆变换讲课文档

如何求k2?
对原式两设法边使乘部(以分s 分1)式2 s只s 2 保2留(ks2 ，1其)2它sk 分12式为k20(s1)k3 令 s1时 ,只能 k3 求 1,若出 k2 求 ,两边再求右边 d d s (s1)2sk 12(s1)k2k3
2(s1)s( (s2 )k 2 1) 2k1(s1)2k20
4 点是( , 0)，比曲线 y A sin x
4 的起点滞后了个单位，相当
4 于像函数乘以指数因子e as ，因此这个性质叫做延滞性质．如图 14-2 所示．
f (t)
O
a
图14-2
f (t) f (t a)
t
现在二十八页，总共五十页。
例3
求函数u
t
a
0, t 1, t
a a
函数F (s)也可叫做 f (t)的像函数．
现在十八页，总共五十页。
若 F (s)是 f (t)的拉氏变换，则称 f (t)是 F (s)的拉氏逆变换（或叫做 F ( s ) 的像原函数），记作
f (t) L1[ f (s)]．注意 1．在拉氏变换中，只要求 f (t) 在 [0, ) 内有定义即可．为了研究方便，以后总假定在 ( ,0) 内， f (t) 0 ．在以后的研究中，规定所研究的 t 均属于 [0, )； 2．在此我们规定只讨论 s 是实数的情况； 3．拉氏变换的作用是通过建立 f (t)的一个新的函数，来化繁为简．
第二种情况：包含共轭复数极点

拉普拉斯变换及反变换

初值定理若ℒ [f(t)]=F(s)，且 f(t)在t = 0处无冲激，
则 f (0 ) lim f (t) lim sF (s)
t 0
s
终值定理 f(t)及其导数f (t)可进行拉氏变换，且
lim f (t)存在时
t
f () lim f (t) lim sF(s)
t
s0
例1
u(t)t0
k2(2 ss1)52(s1)2S13 k1dds(2s5)S12
f(t)L1[F(s])2et3tet t0
例2
F(s)
s2 2s2 (s2)3
k1 (s2)
(s k22)2(s k32)3
等式两边乘 (s 2)3
F(s)(s 2)3 k1(s 2)2 k2 (s 2) k3
k3s2(s22 s)32(s2)3S22
lims11 s s
例2 I(s) 5 2 s1 s2
i( 0 ) lis ( m 52) li(m 52) 3 s s 1s 2s 1 1 /s1 2 /s
例3
I(s)ℒ [1e-t]1 1 s s1
11 i(t)t ls i0m s(ss1)1
例4：已知F(s)= 1 ，求f(0)和f(∞) sa
拉普拉斯变换的基本性质表
本讲小结：拉普拉斯变换定义常用函数的拉普拉斯变换
拉普拉斯变换的基本性质
(1)
利用 ℒ
• 作业
1、写出拉普拉斯变换定义式 2、
__
1
(s-1)2
二、拉普拉斯反变换
1、由象函数求原函数 f(t)=L-1[F(s)]
（1）利用公式
f(t) 1 2πj
（S2+a1S+a0）R(S)-(S+a1)r(0-)-r/(0-)=(Sb1+b0)E(s)-b1×0

拉氏变换和反变换

式中：s=σ+jω（σ，ω均为实数） F(s)称为函数f(t)旳拉普拉氏变换或象函数; f(t)称为F(s)旳原函数； L为拉氏变换旳符号。
拉氏反变换旳定义
其中L－1为拉氏反变换旳符号。
序号
1 2 3 4 5 6 7
常见时间函数拉氏变换表
f(t)
F(s)
单位脉冲函数:d(t)
单位阶跃函数:1(t) 单位速度函数：t
由线性性质可得
假如 f (t) 旳拉普拉斯变换 F (s) 可分解为 F (s) F1 (s) Fn (s)
并假定 Fi (s) 旳拉普拉斯变换轻易求得，即
Fi (s) L[ fi (t)]
则 L1[F (s)] L1[F1(s)] L1[Fn (s)]
f1(t) fn (t)
例1 求
F(s) s 3 s 2 3s 2
旳Laplace 反变换
解
F (s)
s2
s
3 3s
2
(s
s3 1)(s
2)
2 1 s 1 s 2
f (t) L1[F (s)] L1[ 2 ] L1[ 1 ]
s 1
s2
2et e2t t 0
例2 求
旳Laplace 反变换
解 F (s) 1 1 s 1 (s 2)2
线性定理
叠加定理
百分比定理
多重微分原函数旳高阶导数像函数中s旳高次代数式
积分定理
多重积分原函数旳n重积分像函数中除以sn
位移定理原函数乘以指数函数e-at像函数d在复数域中作位移a
延时定理原函数平移像函数乘以 e-s
终值定理
原函数f(t)旳稳态性质
sF(s)在s=0邻域内旳性质

拉普拉斯变换及反变换ppt课件

补充拉普拉斯变换及反变换重点知识
一、拉氏变换及其特性 1、拉氏变换定义
如果有一个以时间 t为自变量的实变函数 f t ，它的定义域是 t 0 ，那么 f t 的拉普
拉斯变换定义为
F
s
L
f
t
0
f
t estdt
式中，s是复变数，s j（、
均为实数）， est 称为拉普拉斯积分；F s 0
>> p=[1 -120 25 126
用num和den分别表示F(s)的分子和分母多项式，即：num = [b0 b1 … bm]
den = [a0 a1 … an] MATLAB提供函数residue用于实现部分分式展开，其句法为：
[r, p, k] = residue(num, den)
f (t) L1(F (s)) 1
c
j
F
(s)e
st
ds
2j c j
式中 L1 表示拉普拉斯反变换的符号
2、拉氏反变换的计算方法由象函数求原函数的方法：
方法一：利用拉氏反变换定义求 ——不常用解
方法二：查拉氏变换表求解——对简单的象函数适用方法三：部分分式法——象函数为有理分式函数时适用
p1)r ]}s p1
br j
1 dj
{ j!
ds
j
[F
s
(s
p1)r ]}s p1
b1
1
d r1
(r
{ 1)!
ds
r
1
[
F
s
(s
p1)r ]}s p1
例
F(s)
(s
s 1 2)3 ( s
3)
解：F (s)