8.4位移法的基本结构及位移法方程
合集下载
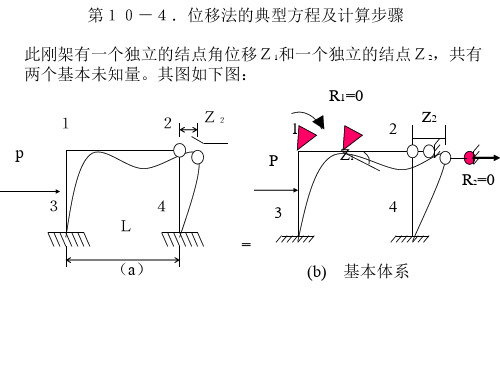
结构力学-位移法的典型方程及计算步骤
(e)
依题意可知并根据叠加原理上述条件可写为:
R1=R11+R12+R1P=r11 Z1+r12 Z2+R1P=0 R2=R21+R22+R2P=r21 Z1+r22 Z2+R2P=0
上述方程称为位移法基本方程,也称为位移法的典型方程。
为了求出典型方程的系数和自由项,可借助于表10-1,绘出基本
结构图,如下图10-7a,b, 和c所示。然后求出各系数和自由项。
r11 1 3i 4i
r12 6i1 0
R1P PL1 0
l
8
Z1=1
4i 1
2
6i 1l
2
Z2=1 1
2
3i M
3 2i 4
(a)
6i 3 l
3i 4 l
(b)
p
MP
PL 3
4
8
(C)
T10-7
1
2
r21 1
2
r22 1
6i l
0
12i
L2
3i
P
L2
2
2
R2P
0
系数和自由项可分为两类,分别由力矩平衡方程 M1=O求得为:
0
6 2 6 9 12 2 11 l Z1 l 2 Z2 16 P 0
Z1 0.02218 Pl Z2 0.02859 Pl 2
M M1Z1 M 2Z2 M P
转到下一节
者的原理有所不同。
§10-7 有侧移的斜柱刚架
B
B’
C’ C
C”
C
A
D
O A,D
B 结点位移图
O为极点,各结点位移前的位置
位移法的基本结构及位移法方程

C D F1P C
b) M 1 图
D Z 1=1 k 11
c)
C
M图(kN· m)
D
(90) A -90 B C
F FQ CA = 45
(90) A EI 12 C EI 72 EI 12 D EI 72 k 11 B 225 A 135 B
D
F FQ DB=0
F1P
分别在MP图和 M 1 图中,截取两柱顶端以上部分为隔离体, F 0 如图8-17所示。由剪力平衡条件 ,得 x
Z
三、位移法方程
l/2 A Z1 FP l/2
l/2
FP l/2
C
F1=0
A
Z1 Z 1
C
Z1
EI =常数
l
FP F1=0 FP Z1 Z1 C A A Z 1Z Z1 Z1 1
F1P
P F1P
F
FP
C
C
A
A
C
EI =常数
B
l
B
B
B
B
B
c)
A
基本体系
F11 Z1
d)
F11 Z1 A Z1
C
锁住结点
M图
4i
重庆大学土木工程学院®
A
4i
C C EA =∞ D 例如,图8-16a所示刚架的基本未知量为结点 C、D D的水 平线位移Z1。在结点D加一附加支座链杆,就得到基本结构 EI EI (图8-16b)。其相应的基本体系如图8-16c所示,它的变形 和受力情况与原结构完全相同。 A B A B
k Z F 0 11 1 1P
这就是求解基本未知量Z1的位移法基本方程,其实质是平 衡条件 。 为了求出系数k11和自由项F1P,可利用表8-2和表8-1,在 基本结构上分别作出荷载作用下的弯矩图(MP图)和 Z1=1引起的弯矩图( M 1 图)。
b) M 1 图
D Z 1=1 k 11
c)
C
M图(kN· m)
D
(90) A -90 B C
F FQ CA = 45
(90) A EI 12 C EI 72 EI 12 D EI 72 k 11 B 225 A 135 B
D
F FQ DB=0
F1P
分别在MP图和 M 1 图中,截取两柱顶端以上部分为隔离体, F 0 如图8-17所示。由剪力平衡条件 ,得 x
Z
三、位移法方程
l/2 A Z1 FP l/2
l/2
FP l/2
C
F1=0
A
Z1 Z 1
C
Z1
EI =常数
l
FP F1=0 FP Z1 Z1 C A A Z 1Z Z1 Z1 1
F1P
P F1P
F
FP
C
C
A
A
C
EI =常数
B
l
B
B
B
B
B
c)
A
基本体系
F11 Z1
d)
F11 Z1 A Z1
C
锁住结点
M图
4i
重庆大学土木工程学院®
A
4i
C C EA =∞ D 例如,图8-16a所示刚架的基本未知量为结点 C、D D的水 平线位移Z1。在结点D加一附加支座链杆,就得到基本结构 EI EI (图8-16b)。其相应的基本体系如图8-16c所示,它的变形 和受力情况与原结构完全相同。 A B A B
k Z F 0 11 1 1P
这就是求解基本未知量Z1的位移法基本方程,其实质是平 衡条件 。 为了求出系数k11和自由项F1P,可利用表8-2和表8-1,在 基本结构上分别作出荷载作用下的弯矩图(MP图)和 Z1=1引起的弯矩图( M 1 图)。
结构力学 位移法典型方程、计算举例
r11 B r12 CH
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
8-3、8-4位移法的基本未知量和基本结构__典型方程及计算步骤解析

§8.3 位移法的基本未知量和基本结构
确定独立的结点线位移另种一方法
( 1)不考虑轴向变形 长度不变 (2) 弯曲变形微小,受弯矩
把原结构的所有刚结点和固定支座均改为铰结点→铰结体系,如图b。 此铰结体系为几何不变,原结构无结点线位移。 此铰结体系为几何可变或瞬变,添加最少的支座链杆保证其几何不变, 添加的链杆数目既是原结构独立的结点线位移数目。如图b,加一个水 平支座链杆,体系成为几何不变的。
上一章复习
等截面直杆的杆端弯矩和剪力
1 A
B A
2i
B
A B
4i
M AB 4i M BA 2i
A B 1 A
6i/l
FQ 6i / l
6i/l
B A
12i/l2
B
6i/l
M AB 6i / l M BA 6i / l
FQ 12i / l 2
等截面直杆的杆端弯矩和剪力
1 A A B A
+
2 EI i 2l
EI A l
1
B
3i/l
3i/l 3i/l
1
1
EI 2l
1
=
6
+
EI 3i 2 (2l ) 2l 6 EI 3i 2 (2l ) 2l
1
q A EI l B
ql 2 3
ql 2 6
1 1 q (2l ) 2 ql 2 8 2
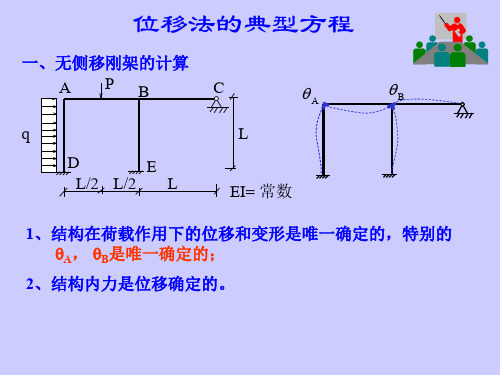
§8.3 位移法的基本未知量和基本结构
附加刚臂: 阻止刚结点的转动,但不能阻止结点的移动。 附加支座链杆:阻止结点的线位移。
图a所示刚架,在刚结点1、3处分别加上刚臂,在结点3处加上一根 水平支座链杆,则原结构的每根杆件都成为单跨超静定梁。
[工学]位移法
![[工学]位移法](https://img.taocdn.com/s3/m/8f40a05c1711cc7931b7167e.png)
[ e ] B
(b)
b M F Q B A
单元刚度方程——单元杆端力和杆 端位移的关系式。
推导单元刚度方程思 路及方法:
方法1
已知梁的两端固定支座发生位移A、 B、,求杆端力FQAB、MAB、FQBA、 MBA。推导是求超静定梁在支座移动 时的支座反力(杆端力)的过程,直 接由力法计算。
方法 2
已知简支梁两端作用有集中外力偶 MAB、MBA,同时B支座有支座位移, 用单位荷载法求位移A、B,然后将 杆端力FQAB、MAB、FQBA、 MBA表示成 位移的函数形式。推导是对静定梁在 荷载和支座移动下,求梁两端转角位 移的过程。
按方法2建立单元刚度方程
M A B A M B A B B `
FQAB FQBA
6 EI 6 EI 12 EI 2 A 2 B 3 L L L
(9-2-1a)
4)当考虑典型单元上同时也作用荷 载时的单元刚度方程
M A B A
A E IL
(a)
[e]
B B `
F Q A B
F M B A
F M A B
B
(b)
4 EI 2 EI 6 EI F M AB A B 2 M AB L L L 2 EI 4 EI 6 EI F M BA A B 2 M BA L L L
EI0=
L
EI
EI
(a)
L
z1 EI0=
z1
EI
EI
(b)
解 1)确定位移法基本未知量
6i 2) M AB M BA z1 L 2 6i qL M CD z1 L 12 2 6i qL M DC z1 L 12
8-3、8-4位移法的基本未知量和基本结构__典型方程及计算步骤

§6.2.1 位移法的基本未知量
3
2
1
结点转角的数目:7个
独立结点线位移的数目:3个
§8.3 位移法的基本未知量和基本结构
图a所示刚架,结点线位移数目=2
图b所示刚架,结点角位移数目=2 结点线位移数目=2
§8.3 位移法的基本未知量和基本结构
确定角位移6个
确定线位移2个
§8.3 位移法的基本未知量和基本结构
图a所示刚架,结点角位移数目=4(注意结点2)
结点线位移数目=2
加上4个刚臂,两根支座链杆,可得基本结构如图b。
§6.2.1 位移法的基本未知量
1
2
1
1
2
3
§6.2.1 位移法的基本未知量
例1.
B
C
例2.
B
C
A 只有一个刚结点B,由于忽 略轴向变形,B结点只有 B
A
只有一个刚结点B, 由于忽略轴向变形及C 结点的约束形式,B结 点有一个转角和水平位 移 B BH
2kN/m 16kN
A
i
6m
B
3m
i
3m 16kN
Z1
C
2kN/m
A
B
C
解 (1)选取基本体系。
(2)建立位移法典型方程。
r11Z1 R1 0
(3)求系数和自由项。
4i
Z1=1
r11
A
2i
B
3i 18 6
M 1图
C
4i
3i
6
R1P
A
B
MP图(kN.m)
C
6
18
r11 4i 3i 7i
典型方程
位移法典型方程计算举例

n
n
rijZj , 为 消 去 该 处 的 约 束 力 , 令 : R iP rijZj=0即 可 。 写 成 方 程 组 的 形 式 为 :
j 1
j 1
r11Z1 r12Z2 r1n Zn R1P 0
r21
Z1
r22Z2
r2n
Zn
R2P
0
rn1Z1 rn2 Z2 rnnZn RnP 0
这就是位移法的典型方程。
R2P +
MP图
r11R1 A
r2R12A
+
rr2111AArr12
2B 2B
R1 R2
r12B r22B
rr2111AArr1222B BR R12PP00 这就是位移法方程,解出θA,θB
5)ri j的求法
2i 4i
r11 8i r212i
2i
M
图
1
4i 4i 2i r12 2i 3ir22 11i
2i
M
图
2
求r11,r12的研究对象
求r21,r22的研究对象
6)弯矩图的作法
qL2/12
q
P R1P
PL/8
R2P
MP图
++
r11R1 A
r2R12A
+
r12B r22B
即 M M P M 1A M 2B
qL2/12
q
P R1P
PL/8
R2P
4i
+ A•
MP图
2i + B•
2i
r11
r21
2i
M
图
1
4i
4i
r12
结构力学 第8章 位移法

6
杆端内力、位移的符号规定: 杆端内力、位移的符号规定:
●
杆端弯矩: 表示AB杆 端的弯矩 绕杆端顺时针 端的弯矩。 顺时针为正 杆端弯矩: MAB表示 杆A端的弯矩。绕杆端顺时针为正 杆端剪力:绕隔离体顺时针转为正(同前) 杆端剪力:绕隔离体顺时针转为正(同前)。 顺时针转为正 结点转角: 顺时针转为正。 结点转角:以顺时针转为正。 转为正 杆端的相对线位移:使杆件弦转角顺时针转动为正。 杆端的相对线位移:使杆件弦转角顺时针转动为正。 弦转角顺时针转动为正
1 2 3
杆14, 36: 两端固定
4 5 6
基本未知量3个。 基本未知量 个
杆12, 23, 25: 一端固定 一端铰结
23
又例:
m m
原结构
次超静定) (4次超静定) 次超静定
基本结构
次超静定) (5次超静定) 次超静定
24
§8—4 位移法的典型方程及计算步骤 4
基本未知量为: 基本未知量为:Z1、Z2 。 基本结构如图。 基本结构如图。 R1—附加刚臂上的反力矩 附加刚臂上的反力矩 F R2—附加链杆上的反力 附加链杆上的反力 l 据叠加原理, 则有 据叠加原理, 2 R1=R11+R12+R1P=0 R2=R21+R22+R2P=0
EI
可见, 不独立, 代入第一式: 可见,B=f (A、△AB), 不独立 代入第一式 MAB=3iA 式中 (转角位移方程) 转角位移方程) (固端弯矩) 固端弯矩)
l
t2
16
§8—3 位移法的基本未知量和基本结构 3
1.位移法的基本未知量 1.位移法的基本未知量
位移法的基本未知量是各结点的角位移和线位移, 位移法的基本未知量是各结点的角位移和线位移, 计算时应 各结点的角位移 独立的角位移和 数目。 首先确定独立的角位移 线位移数目 首先确定独立的角位移和线位移数目。 (1) 独立角位移数目 同一刚结点,各杆端转角相等一个独立的角位移未知量。 一个独立的角位移未知量 同一刚结点,各杆端转角相等一个独立的角位移未知量。 固定支座处,转角=0,已知量; =0,已知量 固定支座处,转角=0,已知量; 铰结点或铰支座各杆端的转角不独立,不必作为基本未知量。 铰结点或铰支座各杆端的转角不独立,不必作为基本未知量。 独立角位移数目= 独立角位移数目=结构刚结点的数目
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.4 位移法的基本结构及位移法方程
一、位移法的基本结构
位移法的基本结构就是通过增加附加约束(包括附 加刚臂和附加支座链杆)后,得到的三种基本超静定杆 的综合体。
所谓附加刚臂,就是在每个可能发生独立角位移的 刚结点和组合结点上,人为地加上的一个能阻止其角位 移(但并不阻止其线位移)的附加约束,用黑三角符号 “ ”表示。
D Z1=1 k11 C
D
(90)
(90)
A -90
B
A
B
A
B
EI 12
EI 12
225
135
C
D
F1P
C
D
k11
FQFCA=45
FQFDB=0
EI 72
EI 72
分别在MP图和 M 1 图中,截取两柱顶端以上部分为隔离体,
如图8-17所示。由剪力平衡条件
Fx ,0得
F1P
FF QCA
FF QDB
45 0 45 kN
k11 8i
F1P
1 8
FP l
k11Z1 F1P 0
将k11和F1P的值代入上式,解得
Z1
F1P k11
FP l 64i
结果为正,表示Z1的方向与所设相同。结构的最后弯矩可由 叠加公式计算,即
M M1Z1 M P
M BA 2i
0 5FPl / 32
M
M
M
AB AC CA
所谓附加支座链杆,就是在每个可能发生独立线 位移的结点上沿线位移的方向,人为地加上的一个能 阻止其线位移的附加约束。
All Rights Reserved
重庆大学土木工程学院®
Z1 Z4
F
G
H
F
Z2
Z3 Z3
C
D
E
C
Z3
A
B
A
G
H
D
E
B
a) 原结构及其基本未知量
b) 基本结构
All Rights Reserved
B
B
l l
l
l/2 FP l/2
A
C
Z1
Z1
F1=0
A
ZA1
A
FP l/2
FP l/2
CC C
F1P A
Z1
ZZ11 Z1
F1F=P0
FP
Z1 C
C
A
Z1
Z1
FF111P Z1 AA Z1
EI =常数
EI =常数
B
BB B
B
B
BB
aA) 原结构C
All Rights Reserved
b) 基本结构F11
2i
16
16
FP l
C
16 A
C
9FP l 64
B
B 2i
B FPl 32
F1P
A
FP l 8
k11 A 4i
4i
在图 M1 中取结点A为隔离体,由 M A 0 ,得
在MP图中取结点A为隔离体,由 M A 0 ,得
刚臂内之反力矩以顺时针为正
All Rights Reserved
重庆大学土木工程学院®
Z1
1620 EI
结构的最后弯矩图可由叠加公式M M1Z1 M P 计算后绘 制,如图c所示。
A
C
Z1
A
Z1
Z1
重庆大学土木工程学院®
c)
基本体系 F11C源自Z1AZ1Z
三、位移法方程
l/2 FPl/l2/2 FP l/2
AA
C
C
Z1
ZZ11
Z1
EI =常数EI =常数
l l
F1=0 F1=0FP
FP F1P
Z1
Z1 C
C
A
A
A
Z1
Z 1Z 1
Z1
FF1PP
FP
C
C
A
B
B
B
B
B
B
c) 基本体系
重庆大学土木工程学院®
二、位移法的基本体系
l/2 FP l/2
F1=0
FP
F1P
图a所示刚架的基本Z1A未知Z1 量为结C 点A的转Z1角A ZZ1Z11。在结C 点 A
A加一附加刚臂,就得到位移EI法=常的数 基本结构(图b)。同力
法一样,受荷载和基本未知量共同作用的基本结构,称为
B
基本体系(图c)。
4i 4i 2i
FPl 64i
0
FFPPl
l /
/ 8
8
FPl /16
5FFPPll//3126
All Rights Reserved
重庆大学土木工程学院®
M BA 2i
0 5FPl / 32
M
M
M
AB AC CA
4i 4i 2i
FPl 64i
0
FFPPl
l /
A
B
Z1
Z1
C
EA=∞ D
EI
EI
C
D
C
D
Z1 F1=0
6m 20kN/m
20kN/m
A
B
位移法方程
All Rights Reserved
A
B
基本结构
A
B
基本体系
C
D
Z1 F1=0
k11Z1 F1P 0
20kN/m
重庆大学土木工程学院®
A
B
a) MP图(kN·m)
C
D
F1P
b) M 1图
C
c) M图(kN·m)
C
9FP l 64
B FPl 32
M图
例如,图8-16a所示C刚Z1 架EA的=∞ 基D 本Z1 未知量为C结点C、DD的水
20kN/m 6m
平线位移Z1。在结点D加E一I 附加E支I 座链杆,就得到基本结构 (图8-16b)。其相应的基本体系如图8-16c所示,它的变形
和受力情况与原结构完全A 相同。B
/ 8
8
FPl /16
5FFPPll//3126
FP l F1P 8
A
FP l
FP
8
C
FP l 8
B
FM1P P图
All
Rights
A
Reserved
FP l 8
k11 Z1=1
2i
A
4i
C
4i
B 2i
M 图 k11 1 重庆大学土A木工程学4i院®
4i
FP l
FP l
16
16
FP l
16 A
式中,Fij表示广义的附加反力矩(或反力),其中第一个 下标表示该反力矩所属的附加约束,第二个下标表示引起 反力矩的原因。设k11表示由单位位移Z1=1所引起的附加刚 臂上的反力矩,则有 F11=k11Z1,代入上式,得
k11Z1 F1P 0
这就是求解基本未知量Z1的位移法基本方程,其实质是平 衡条件 。
为了求出系数k11和自由项F1P,可利用表8-2和表8-1,在 基本结构上分别作出荷载作用下的弯矩图(MP图)和
Z1=1引起的弯矩图( M1 图)。
All Rights Reserved
重庆大学土木工程学院®
FP l F1P 8
A
FP l
FP
8
C
FP l 8
k11 Z1=1 A
4i
4i
FP l
FP l
All Rights Reserved
重庆大学土木工程学院®
C
D
F1P
C
D Z1=1 k11 C
D
(90)
(90)
A -90
B
A
B
A
B
EI 12
EI 12
225
135
C
D
F1P
C
D
k11
FQFCA=45
FQFDB=0
EI 72
EI 72
k11
EI 72
EI 72
EI 36
将k11和F1P的值代入位移法方程式,解得
d)
F11
A
C
基本A 结构在结C 点位移Z1和荷载
共同作用下,刚臂上的反力矩F1必
Z1 A
F11 Z1 C
Z1
Z1 A
Z1
Z1
锁住结点
C
定为零(图c)。
B B
F1 F11 F1P 0
B B
e) 放松结点
All Rights Reserved
重庆大学土木工程学院®
F1 F11 F1P 0
一、位移法的基本结构
位移法的基本结构就是通过增加附加约束(包括附 加刚臂和附加支座链杆)后,得到的三种基本超静定杆 的综合体。
所谓附加刚臂,就是在每个可能发生独立角位移的 刚结点和组合结点上,人为地加上的一个能阻止其角位 移(但并不阻止其线位移)的附加约束,用黑三角符号 “ ”表示。
D Z1=1 k11 C
D
(90)
(90)
A -90
B
A
B
A
B
EI 12
EI 12
225
135
C
D
F1P
C
D
k11
FQFCA=45
FQFDB=0
EI 72
EI 72
分别在MP图和 M 1 图中,截取两柱顶端以上部分为隔离体,
如图8-17所示。由剪力平衡条件
Fx ,0得
F1P
FF QCA
FF QDB
45 0 45 kN
k11 8i
F1P
1 8
FP l
k11Z1 F1P 0
将k11和F1P的值代入上式,解得
Z1
F1P k11
FP l 64i
结果为正,表示Z1的方向与所设相同。结构的最后弯矩可由 叠加公式计算,即
M M1Z1 M P
M BA 2i
0 5FPl / 32
M
M
M
AB AC CA
所谓附加支座链杆,就是在每个可能发生独立线 位移的结点上沿线位移的方向,人为地加上的一个能 阻止其线位移的附加约束。
All Rights Reserved
重庆大学土木工程学院®
Z1 Z4
F
G
H
F
Z2
Z3 Z3
C
D
E
C
Z3
A
B
A
G
H
D
E
B
a) 原结构及其基本未知量
b) 基本结构
All Rights Reserved
B
B
l l
l
l/2 FP l/2
A
C
Z1
Z1
F1=0
A
ZA1
A
FP l/2
FP l/2
CC C
F1P A
Z1
ZZ11 Z1
F1F=P0
FP
Z1 C
C
A
Z1
Z1
FF111P Z1 AA Z1
EI =常数
EI =常数
B
BB B
B
B
BB
aA) 原结构C
All Rights Reserved
b) 基本结构F11
2i
16
16
FP l
C
16 A
C
9FP l 64
B
B 2i
B FPl 32
F1P
A
FP l 8
k11 A 4i
4i
在图 M1 中取结点A为隔离体,由 M A 0 ,得
在MP图中取结点A为隔离体,由 M A 0 ,得
刚臂内之反力矩以顺时针为正
All Rights Reserved
重庆大学土木工程学院®
Z1
1620 EI
结构的最后弯矩图可由叠加公式M M1Z1 M P 计算后绘 制,如图c所示。
A
C
Z1
A
Z1
Z1
重庆大学土木工程学院®
c)
基本体系 F11C源自Z1AZ1Z
三、位移法方程
l/2 FPl/l2/2 FP l/2
AA
C
C
Z1
ZZ11
Z1
EI =常数EI =常数
l l
F1=0 F1=0FP
FP F1P
Z1
Z1 C
C
A
A
A
Z1
Z 1Z 1
Z1
FF1PP
FP
C
C
A
B
B
B
B
B
B
c) 基本体系
重庆大学土木工程学院®
二、位移法的基本体系
l/2 FP l/2
F1=0
FP
F1P
图a所示刚架的基本Z1A未知Z1 量为结C 点A的转Z1角A ZZ1Z11。在结C 点 A
A加一附加刚臂,就得到位移EI法=常的数 基本结构(图b)。同力
法一样,受荷载和基本未知量共同作用的基本结构,称为
B
基本体系(图c)。
4i 4i 2i
FPl 64i
0
FFPPl
l /
/ 8
8
FPl /16
5FFPPll//3126
All Rights Reserved
重庆大学土木工程学院®
M BA 2i
0 5FPl / 32
M
M
M
AB AC CA
4i 4i 2i
FPl 64i
0
FFPPl
l /
A
B
Z1
Z1
C
EA=∞ D
EI
EI
C
D
C
D
Z1 F1=0
6m 20kN/m
20kN/m
A
B
位移法方程
All Rights Reserved
A
B
基本结构
A
B
基本体系
C
D
Z1 F1=0
k11Z1 F1P 0
20kN/m
重庆大学土木工程学院®
A
B
a) MP图(kN·m)
C
D
F1P
b) M 1图
C
c) M图(kN·m)
C
9FP l 64
B FPl 32
M图
例如,图8-16a所示C刚Z1 架EA的=∞ 基D 本Z1 未知量为C结点C、DD的水
20kN/m 6m
平线位移Z1。在结点D加E一I 附加E支I 座链杆,就得到基本结构 (图8-16b)。其相应的基本体系如图8-16c所示,它的变形
和受力情况与原结构完全A 相同。B
/ 8
8
FPl /16
5FFPPll//3126
FP l F1P 8
A
FP l
FP
8
C
FP l 8
B
FM1P P图
All
Rights
A
Reserved
FP l 8
k11 Z1=1
2i
A
4i
C
4i
B 2i
M 图 k11 1 重庆大学土A木工程学4i院®
4i
FP l
FP l
16
16
FP l
16 A
式中,Fij表示广义的附加反力矩(或反力),其中第一个 下标表示该反力矩所属的附加约束,第二个下标表示引起 反力矩的原因。设k11表示由单位位移Z1=1所引起的附加刚 臂上的反力矩,则有 F11=k11Z1,代入上式,得
k11Z1 F1P 0
这就是求解基本未知量Z1的位移法基本方程,其实质是平 衡条件 。
为了求出系数k11和自由项F1P,可利用表8-2和表8-1,在 基本结构上分别作出荷载作用下的弯矩图(MP图)和
Z1=1引起的弯矩图( M1 图)。
All Rights Reserved
重庆大学土木工程学院®
FP l F1P 8
A
FP l
FP
8
C
FP l 8
k11 Z1=1 A
4i
4i
FP l
FP l
All Rights Reserved
重庆大学土木工程学院®
C
D
F1P
C
D Z1=1 k11 C
D
(90)
(90)
A -90
B
A
B
A
B
EI 12
EI 12
225
135
C
D
F1P
C
D
k11
FQFCA=45
FQFDB=0
EI 72
EI 72
k11
EI 72
EI 72
EI 36
将k11和F1P的值代入位移法方程式,解得
d)
F11
A
C
基本A 结构在结C 点位移Z1和荷载
共同作用下,刚臂上的反力矩F1必
Z1 A
F11 Z1 C
Z1
Z1 A
Z1
Z1
锁住结点
C
定为零(图c)。
B B
F1 F11 F1P 0
B B
e) 放松结点
All Rights Reserved
重庆大学土木工程学院®
F1 F11 F1P 0
