结构力学位移法整理.
【精品】结构力学--6、清华--位移法

综上所述,位移法的基本思路是:
1. 在原结构产生位移的结点上设置附加约束,使结点固定,
从而得到基本结构,然后加上原有的外荷载;
2. 人为地迫使原先被“固定”的结点恢复到结构原有的位移。
通过上述两个步骤,使基本结构与原结构的受力和变形完全相
4i
9FP l
8
64
B
MP图F1P
A
FP l 8
B 2i
M图 1k11
A 4i
B FPl
3M2 图
20kN/m 6m 20
20kN/m 20kN/m
(二)只有侧移结A构—以B一个基本未知量A 为例 B
Z1
Z1
C
EA=∞ D
EI
EI
A
B
C
D
基本结构
A
B
C
D
Z1 F1=0
基本体系
A
B
基本结构在结点位移Z1和C荷载共同作D 用下Z1 ,F1=链0 杆上的反力F1 必定为零(图c)由此建立位移法方程 :
BB
l l
F1=0 F1=0 FP FP
Z1
Z1
C
AA
Z1
ZZ11
Z1
F1P C
A
F1P FP
FP
C
C
A
BB
c) 基本体系B
B
基本结构在结点位移Z1和荷载共同作用F11下,F1刚1 臂
上的A反A力矩F1C为零C :
Z1 A
Z1 C
C
F1 F11 F1P 0
Z1
Z1 A
Z1
结构力学6-位移法

7i 1 6 0
解得
(4)将结点位移代回杆端弯矩表达式。
6 M AB 2i 15 16.72kN m 7i 6 M BA 4i 15 11.57 kN m 7i 6 M BC 3i 9 11.57kN m 7i
M图(kNm)
§7-4
位移法Ⅱ——典型方程法
一、超静定结构计算的总原则:
欲求超静定结构先取一个基本结构,然 后让基本结构在受力方面和变形方面与原 结构完全一样。
力法的特点: 基本未知量——多余未知力; 基本结构——静定结构; 基本方程——位移条件 (变形协调条件)
位移法的特点: 基本未知量—— 独立结点位移 一组单跨超静定梁 基本结构—— ? 基本方程—— 平衡条件
2
F FQ AB 5ql / 8 F FQ BA 3ql / 8
FP A l/2 l/2 B
3FP l/16 A B A
11FP/16 B 5FP/16
M
F AB
3FP l / 16
F FQ AB 11FP l / 16 F FQ BA 5FP l / 16
A
t1 t2 l
A
B
F FQ AB ql F FQ BA 0
FP
A
l/2 l/2
B
3FPl/8
A FP l/8
F M AB 3 FP l / 8 F M BA FP l / 8
FP
B
A
B
F FQ AB FP F FQ BA 0
FP A l B
FPl/2 A FPl/2
F M AB FP l / 2 F M BA FP l / 2
结构力学第8章位移法

结构力学第8章位移法位移法是结构力学中一种常用的分析方法。
它基于结构物由刚性构件组成的假设,通过计算结构在外力作用下产生的位移和变形,进而推导出结构的反力和应力分布。
位移法的基本思想是将结构的局部位移组合成整体位移,通过建立位移和反力之间的关系,解决结构的力学问题。
位移法的分析步骤通常包括以下几个方面:1.建立结构的整体位移函数。
位移函数是位移法分析的基础,通过解结构的运动方程建立结构的位移与自由度之间的关系。
2.应用边界条件。
根据边界条件,确定结构的支座的位移和转角值。
支座的位移和转角值可以由结构的约束条件和外力产生的位移计算得出。
3.构建位移方程组。
将结构的整体位移函数带入到结构的平衡方程中,得到位移方程组。
位移方程组是未知反力系数的线性方程组。
4.解位移方程组。
通过解位移方程组,求解未知反力系数。
可以使用高斯消元法、克拉默法则或矩阵方法等解方程的方法求解。
5.求解反力和应力分布。
通过已知的位移和未知的反力系数,可以计算出结构的反力和应力分布。
这些反力和应力分布可以进一步用于结构的设计和评估。
位移法的优点是适用范围广泛,适合复杂结构的分析。
它可以处理线性和非线性的结构,包括静力学和动力学的分析。
同时,位移法具有较高的精度和准确度,在结构的分析和设计中得到广泛应用。
然而,位移法也存在一些限制。
首先,位移法假设结构是刚性的,忽略了结构的变形和位移过程中的非线性效应。
其次,位移法需要建立适当的位移函数,对于复杂结构来说,这是一个复杂和困难的任务。
此外,位移法在处理大变形和非线性结构时可能会遭遇困难。
综上所述,位移法是结构力学中一种重要的分析方法。
它通过计算结构的位移和变形,推导出结构的反力和应力分布,为结构的设计和评估提供基础。
然而,位移法也存在一些限制,需要在具体的分析问题中谨慎应用。
01-结构力学 位移法知识点小结
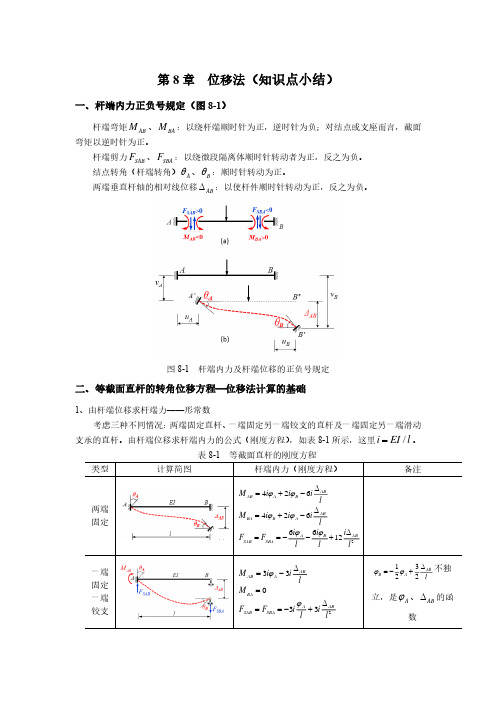
第8章 位移法(知识点小结)一、杆端内力正负号规定(图8-1)杆端弯矩AB M 、BA M :以绕杆端顺时针为正,逆时针为负;对结点或支座而言,截面弯矩以逆时针为正。
杆端剪力SAB F 、SBA F :以绕微段隔离体顺时针转动者为正,反之为负。
结点转角(杆端转角)A θ、B θ:顺时针转动为正。
两端垂直杆轴的相对线位移AB ∆:以使杆件顺时针转动为正,反之为负。
图8-1 杆端内力及杆端位移的正负号规定二、等截面直杆的转角位移方程—位移法计算的基础1、由杆端位移求杆端力——形常数考虑三种不同情况:两端固定直杆、一端固定另一端铰支的直杆及一端固定另一端滑动支承的直杆。
由杆端位移求杆端内力的公式(刚度方程),如表8-1所示,这里/i EI l =。
由杆端位移求出杆端弯矩后,杆端剪力可由平衡条件求出。
表8-1中,杆端内力是根据图示方向的位移方向求得的,当计算某一结构时,应根据其杆件所受的实际位移方向,判断其杆端内力的正负号及受拉侧。
2、由荷载求固定内力——载常数对三种等截面直杆,在荷载作用、温度改变作用下的杆端弯矩和剪力,称为固端弯矩和固端剪力(载常数)。
常见荷载作用下的载常数可查表所得。
3、等截面直杆的转角位移方程对等截面直杆,既有已知荷载作用,又有已知的杆端位移,可根据叠加原理,写出其杆端力的一般表达式,这即为等截面直杆的转角位移方程。
三、位移法的基本未知量包括独立的结点角位移和独立的结点线位移。
独立的结点角位移数目等于刚结点(包括组合结点、弹性抗转弹簧)的数目。
结点线位移的数目可通过增设支杆法(或铰化体系法)来确定。
铰化体系法就是将原结构中所有刚结点和固定支座均改为铰结点形成铰接体系,此铰接体系的自由度数就是原结构的独立结点线位移数。
然后分析该铰接体系的几何组成:如果它是几何不变的,说明结构无结点线位移;相反,如果铰接体系是几何可变的,再看最少需要增设几根附加支杆才能确保体系成为几何不变,或者说使此铰接体系成为几何不变而需添加的最少支杆数就等于原结构的独立结点线位移数目。
结构力学位移法

M=1 C
M=1
若求结构两个截面的相对角位移 在两个截面上加两个方向相反单 位力偶
1 d
1 d
A
求结构两个截面的相对角位移 B
d
C 求AB杆的角位移 杆的角位移
若求桁架中AB杆的角位移,应 加一单位力偶,构成这一力偶 的两个集中力取 1/d,垂直作 用于杆端
1 d1
1 d1
A
B 求AB、AC杆的角位移 、 杆的角位移
式中k—考虑剪应力沿截面分布不均匀的修正系数, 考虑剪应力沿截面分布不均匀的修正系数, 式中k 考虑剪应力沿截面分布不均匀的修正系数 与截面形状有关
∆ = ∑∫
FQ FQP FN FNP MMP ds + ∑ ∫ ds + ∑ ∫ k ds EI EA GA
式中 F N FQ M ——虚设单位荷载引起的内力 虚设单位荷载引起的内力
l
q
A B
L
∆Q ∆M
∆Q ∆M
EI = 4.8 GAl 2
= 4.8
E 8 = 2(1 + µ ) = G 3
I h2 = A 12
EI h = 1.067( ) 2 GAl 2 l
∆Q ∆M h = 1.067( ) 2 = 1.067% l
当 h= 1 时 l 10 h 1 当 = 时 l 2
FN FQ FQ
ds ds
M
M
ds dθ=κds
γ0 dη= γ0 ds dλ=εds
ds微段 微段 整根杆 变形体系
dwi12=FN εds+FQ γ0ds +M κds w’i12= ∫ (FN εds+FQ γ0ds +M κds) wi12= ∑∫(FN εds+FQ γ0ds +M κds)
结构力学位移法

例:求图示悬臂梁C 点的竖向位移。
(a) 54 C MP (c) 24 C 3kN/m (d) 30 3kN/m (b) 4 C M1 3kN/m F =1
4m
2m
6 M P2 C
M P1
解 在C点施加竖向单位力,作出M1图和MP图,再 用图乘法求位移。但图乘结果不能直接得出,需要采用 叠加法, 将MP图分解为MP1和MP2叠加,见图c、图d, 然后令MP1 和MP2 图分别与M1图图乘后再相加。
4. 图乘法及其应用
(Graphic Multiplication Method and its Applications)
已有基础: 1. 静定结构的内力计算; 2. 利用位移计算公式求静定结构的位移;
3. 杆件结构在荷载作用下的位移计算公式,即:
kFQ FQds FN FNds MM P ds P EI EA GA
Dy
3 1 FP a 2 2a ( 1 2 2 ) F a 4 F a P ( FP a 2 a ) P () E2 I 2 2 3 E1 A1 3 E2 I 2
例 7. 已知 EI 为常数,求 Cy 。
解:作荷载和单位荷载的内力图
返回
MP
分解
M
Cy
1 1 ql l 3l 1 ql l [( ) ( l) EI 3 8 2 8 2 8 3 2 ql 2 l ql 4 ( l) ] () 温 3 8 4 128 EI 度
ql 4
ql 2 M 8 2
ql 2 8
解法二、
ql 2 2
ql 2 8
ql 2 2
A
ql 2 32
ql 2 8
1 1 l ql l Cy [( ) EI 2 2 2 3 A 2 1 l ql l ( ) 2 2 8 6 2 4 2 l ql l 17ql ( )] () 3 2 32 4 384 EI
结构力学 第8章 位移法

6
杆端内力、位移的符号规定: 杆端内力、位移的符号规定:
●
杆端弯矩: 表示AB杆 端的弯矩 绕杆端顺时针 端的弯矩。 顺时针为正 杆端弯矩: MAB表示 杆A端的弯矩。绕杆端顺时针为正 杆端剪力:绕隔离体顺时针转为正(同前) 杆端剪力:绕隔离体顺时针转为正(同前)。 顺时针转为正 结点转角: 顺时针转为正。 结点转角:以顺时针转为正。 转为正 杆端的相对线位移:使杆件弦转角顺时针转动为正。 杆端的相对线位移:使杆件弦转角顺时针转动为正。 弦转角顺时针转动为正
1 2 3
杆14, 36: 两端固定
4 5 6
基本未知量3个。 基本未知量 个
杆12, 23, 25: 一端固定 一端铰结
23
又例:
m m
原结构
次超静定) (4次超静定) 次超静定
基本结构
次超静定) (5次超静定) 次超静定
24
§8—4 位移法的典型方程及计算步骤 4
基本未知量为: 基本未知量为:Z1、Z2 。 基本结构如图。 基本结构如图。 R1—附加刚臂上的反力矩 附加刚臂上的反力矩 F R2—附加链杆上的反力 附加链杆上的反力 l 据叠加原理, 则有 据叠加原理, 2 R1=R11+R12+R1P=0 R2=R21+R22+R2P=0
EI
可见, 不独立, 代入第一式: 可见,B=f (A、△AB), 不独立 代入第一式 MAB=3iA 式中 (转角位移方程) 转角位移方程) (固端弯矩) 固端弯矩)
l
t2
16
§8—3 位移法的基本未知量和基本结构 3
1.位移法的基本未知量 1.位移法的基本未知量
位移法的基本未知量是各结点的角位移和线位移, 位移法的基本未知量是各结点的角位移和线位移, 计算时应 各结点的角位移 独立的角位移和 数目。 首先确定独立的角位移 线位移数目 首先确定独立的角位移和线位移数目。 (1) 独立角位移数目 同一刚结点,各杆端转角相等一个独立的角位移未知量。 一个独立的角位移未知量 同一刚结点,各杆端转角相等一个独立的角位移未知量。 固定支座处,转角=0,已知量; =0,已知量 固定支座处,转角=0,已知量; 铰结点或铰支座各杆端的转角不独立,不必作为基本未知量。 铰结点或铰支座各杆端的转角不独立,不必作为基本未知量。 独立角位移数目= 独立角位移数目=结构刚结点的数目
结构力学-位移法

DA柱:
MA 0
FQDA
1 4
(M DA
M
AD )
D C
FQDA
MDA
1 4
(3i D
1.5i EH
)
MAD
0.75iD 0.375iEH
A
E
FQEB
MBE
B 28
2kN/m
EB柱 MB 0
FQEB
1 4
M BE
242 4
1 4
(1.5i EH
4)
4
0.375iEH 3
14kN
D C
M BA
3i1 h1
M DC
3i2 h2
M FE
3i3 h3
32
3)建立位移法方程并求解
求各柱剪力。
FQAB
M BA h1
3i1 h12
k1
FQCD
M DC h2
3i2 h22
k2
FQEF
M FE h3
3i3 h32
k3
FP A
h1
E
C
FQAB
FQCD
FQEF
h2 h3
MBA
ql 2 8
M
F AB
ql 2 8
q
BA
B
l
M
F BA
ql 2 8
BB
q
M
F AB
ql 2 8
AA
杆端弯矩顺时针方向为正!
21
§7-3 无侧移刚架的计算
刚架内部结点无线位移,只有角位移。 基本未知量:内部结点的角位移。
8kN/m
Bi
i
A
4m
Di
i
C
4m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同济大学朱慈勉 结构力学 第7章 位移法习题答案 7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c) EI EI EI
2EI 2EI
1个角位移 3个角位移,1个线位移 4个角位移,3个线位移
(d) (e) (f) EI1=∞ EA EI
EI1=∞
3个角位移,1个线位移 2个线位移 3个角位移,2个线位移
(g) (h) (i) k
一个角位移,一个线位移 一个角位移,一个线位移 三个角位移,一个线位移 7-5 试用位移法计算图示结构,并绘出其内力图。 (a)
解:(1)确定基本未知量和基本结构 有一个角位移未知量,基本结构见图。
11r1
1Z3i
4i
2iii
1M图
1pR213ql
216ql
pM图 (2)位移法典型方程 11110prZR (3)确定系数并解方程
iqlZqliZqlRirp24031831,821212111 (4)画M图
2724ql
2524ql
M图
218ql
216ql
l l
l A B C D i i i
q (b)
解:(1)确定基本未知量 1个角位移未知量,各弯矩图如下
11r11Z
1M图3
2EI
EI12EI
590
pM图 (2)位移法典型方程 11110prZR (3)确定系数并解方程 1115,352prEIR 1
53502EIZ 1
14ZEI
(4)画M图
()KNmM图2640
147
(c)
4m 4m
4m A C D B 10kN EI 2EI 2.5kN/m EI 解:(1)确定基本未知量 一个线位移未知量,各种M图如下
11r
1M图
11Z27EI227EI
27
EI
1243EI2
243EI1
243EI p
M图
pF1p
R
(2)位移法典型方程 11110prZR(3)确定系数并解方程 1114,243pprEIRF 140243pEIZF
1
243
4ZEI
(4)画M图
94pF9
4pF9
2pF
M图
6m 6m
9m A B
C
EA=∞ FP 4×
2EI EI EI
D E F EA=∞ (d)
解:(1)确定基本未知量 一个线位移未知量,各种M图如下 11Z2/25EAa4/25EAa
11r
1M图 2
5EA
11r
1M图
2/25EAa
2
/25EAa
简化
图1pRpFpF
4
5a3
5a
1
5a
pM
(2)位移法典型方程 11110prZR(3)确定系数并解方程
11126/,55pprEAaRF 126055p
EAZFa 1
3aZEA
(4)画M图
图M0.6pFap
Fa
1.2pF0.6pF
a 2a a 2a a EA EA A B C D
E F
FP FP
EI1=∞ (e)
解:(1)确定基本未知量 两个线位移未知量,各种M图如下 图11Z 11r
21r
1121
2142 4EArlEArl
1M2EAl
EAl
图21Z
12r22
r
22214EArl
2M2EAl
EAl
图 12 0ppp
RFR
pM
1pRpF000
图 M
122212pF
2212pF
1
212pF
(2)位移法典型方程 1111221211222200pp
rZrZRrZrZR
(3)确定系数并解方程1112212212221,44214,0pppEAEArrrllEArlRFR代入,解得
121222121212p
p
lZFEAlZFEA
l l EA
A B
C D
EA EA
FP
4×2a 7-6 试用位移法计算图示结构,并绘出M图。
(a)
解:(1)确定基本未知量 两个角位移未知量,各种M图如下 23EI13EI23EI
23EI
13EI
1121
21 3rEIrEI
图1M
23EI
23EI
13EI
22116rEI
图2M
13EI1
3EI
1130 0pp
RR
图pM
3035.16 图M19.69
9.38
10.313.27
1.871.40
(2)位移法典型方程 1111221211222200pp
rZrZRrZrZR
(3)确定系数并解方程
111221221212,311630,0pp
rEIrrEIrEIRR
代入,解得1215.47,2.81ZZ
(4)画最终弯矩图
10kN/m A C
B E
D F
6m 6m
6m
6m EI=常数 (b) 解:(1)确定基本未知量 两个位移未知量,各种M图如下
4i2i3i
4i
2i11
r
21r图1M
iii
12r
22r图2M
i/2
1pR2pR图p
M
3030
图M75.45
20.9129.09
34.558.18
20
(2)位移法典型方程1111221211222200pprZrZRrZrZR (3)确定系数并解方程 111221
221211,03430,30pp
rirrirRKNRKN
代入,解得 123011,4011ZZii
(4)画最终弯矩图
A C E D EI=常数
6m 6m
6m B 10kN/m
