结构力学位移法讲解学习
合集下载
结构力学 位移法
6i
12i
3i
l
l2
l
6i
θ=1
3i
1
0 0
3i
l
3i
l2
A
θ=1
i
B i
i
－i
0
10
§7-2 等截面直杆的刚度方程
四、说明：
⑴杆件的线刚度应为杆件的抗弯刚度EI除以杆件长度l。 ⑵转角位移方程中杆端位移若为负应以负值代入以获得杆端弯矩。 ⑶固端弯矩表在应用时，应随实际杆件所受荷载，其固端弯矩作相应变化。
B
ql2/16
EI l
q
A
EI=C
l
l
A
EI l
B EI
C l 3ql2/32
中点
5
§7-2 等截面直杆的刚度方程
一、两端固定杆件的转角位移方程 ⑴杆端位移和杆端弯矩的正负规定 MAB P
①角位移θA、θB顺时针为正。
②Δ=vB-vA A、B两点的相对侧移，使杆件 产生顺时针方向旋转角βAB=Δ/l 的Δ为正。 ③杆端弯矩规定顺时针为正。 ⑵两端固定杆件的转角位移方程 M1AB
1
A
原结构有两个基本未知量 B
1
14
§7-2 等截面直杆的刚度方程
⑷位移法基本结构的构成。 位移法的附加约束法构造基本结构时，在刚结点角位移处加入附加刚臂， 在结点独立线位移处沿线位移方向加入附加链杆。 Δ1 基本结构 Δ3 Δ2 Δ4 Δ5 Δ6
B
Δ2
Δ1 C
基本结构 A
B
Δ3 C
Δ4
A
3
§7-1 位移法基本概念
三、位移法的基本思路（补充说明） 一给定结构在外因作用下，分析其内力和变形（位移）所采用途径有二：
结构力学(I)结构静力分析篇(位移法)@@
l
EI
正对称
q q q
h
反对称
q
哈工大 土木工程学院
29 / 65
q
q
q
对称结构在对称荷载作 用下内力、反力和变形皆对 称，故取半结构计算。由半 结构特点采用位移法较好。
哈工大 土木工程学院
30 / 65
q
q
q
对称结构在反对称荷载 作用下内力、反力和变形皆 反对称，故取半结构计算。 而此半结构仍具有对称结构 特点。继续分解。
A 2EI
l
B
EI c
l
C
原始结构
C
A
Z1
B c
基本结构 基本体系
k R 0 1Z 11 1 C
哈工大 土木工程学院
基本方程
33 / 65
4i
Z1 1
3i
8i
k 11
3i
8i
12 i l 12 i l
M1
1 2 i l
k i 1111
R 1C
3i l
c
3i l
MC
9i R1C c l
哈工大 土木工程学院
15 / 65
3i
Z1 1
k 11
4i
3i
1 Z1 FPl 56i
2i
1 FPl 8 1 FPl 8
M1
4i k i 117
R1P
1 FPl 8
M Z M M 1 1 P
3 FPl 56 8 FPl 56 9 FPl 56
FP
MP
1 R 1P F Pl 8
哈工大 土木工程学院
21 / 65
Z1 1
EI
正对称
q q q
h
反对称
q
哈工大 土木工程学院
29 / 65
q
q
q
对称结构在对称荷载作 用下内力、反力和变形皆对 称，故取半结构计算。由半 结构特点采用位移法较好。
哈工大 土木工程学院
30 / 65
q
q
q
对称结构在反对称荷载 作用下内力、反力和变形皆 反对称，故取半结构计算。 而此半结构仍具有对称结构 特点。继续分解。
A 2EI
l
B
EI c
l
C
原始结构
C
A
Z1
B c
基本结构 基本体系
k R 0 1Z 11 1 C
哈工大 土木工程学院
基本方程
33 / 65
4i
Z1 1
3i
8i
k 11
3i
8i
12 i l 12 i l
M1
1 2 i l
k i 1111
R 1C
3i l
c
3i l
MC
9i R1C c l
哈工大 土木工程学院
15 / 65
3i
Z1 1
k 11
4i
3i
1 Z1 FPl 56i
2i
1 FPl 8 1 FPl 8
M1
4i k i 117
R1P
1 FPl 8
M Z M M 1 1 P
3 FPl 56 8 FPl 56 9 FPl 56
FP
MP
1 R 1P F Pl 8
哈工大 土木工程学院
21 / 65
Z1 1
结构力学 7.位移法
也称“先拆后搭”
§7-1 位移法的基本概念
2 位移法计算刚架的基本思路
（1）基本未知量——A 和。
（2）建立位移法基本方程 ■刚架拆成杆件，得出杆件的刚度方程。 ■杆件合成刚架，利用刚架平衡条件，建立位移法基本方程。
§7 – 2 等截面直杆的刚度方程 正负号规定
结点转角 A 、 B 、弦转角（ = / l ) 和杆端弯矩M AB
0
0
6
5ql
3ql
3l / 8
8
8
9ql2 / 128
（↑） （↑）
2ql
ql
7
5
10
（↑） （↑）
8
9ql
11ql
40
40
（↑） （↑）
§7-2 等截面杆件的刚度方程
表1：载常数表（续）
序号 计算图及挠度图
弯矩图及固端弯矩
9
10
5FPl / 32
11
12
固端剪力
FQAB
FQBA
FPb(3l 2 b2 ) 2l 3
M AB
4i A
2i B
6i
l
M BA
2i A
4i B
6i
l
（1）B端为固定支座 B 0
FQ AB FQ BA
6i l
A
6i l
B
12i l2
（2）B端为铰支座 MBA 0
M AB
4i A
6i
l
M BA
2i A
6i
l
M AB
3i A
3i
l
§7-2 等截面杆件的刚度方程
M AB
24
25
26
27
固端剪力
§7-1 位移法的基本概念
2 位移法计算刚架的基本思路
（1）基本未知量——A 和。
（2）建立位移法基本方程 ■刚架拆成杆件，得出杆件的刚度方程。 ■杆件合成刚架，利用刚架平衡条件，建立位移法基本方程。
§7 – 2 等截面直杆的刚度方程 正负号规定
结点转角 A 、 B 、弦转角（ = / l ) 和杆端弯矩M AB
0
0
6
5ql
3ql
3l / 8
8
8
9ql2 / 128
（↑） （↑）
2ql
ql
7
5
10
（↑） （↑）
8
9ql
11ql
40
40
（↑） （↑）
§7-2 等截面杆件的刚度方程
表1：载常数表（续）
序号 计算图及挠度图
弯矩图及固端弯矩
9
10
5FPl / 32
11
12
固端剪力
FQAB
FQBA
FPb(3l 2 b2 ) 2l 3
M AB
4i A
2i B
6i
l
M BA
2i A
4i B
6i
l
（1）B端为固定支座 B 0
FQ AB FQ BA
6i l
A
6i l
B
12i l2
（2）B端为铰支座 MBA 0
M AB
4i A
6i
l
M BA
2i A
6i
l
M AB
3i A
3i
l
§7-2 等截面杆件的刚度方程
M AB
24
25
26
27
固端剪力
01-结构力学 位移法知识点小结
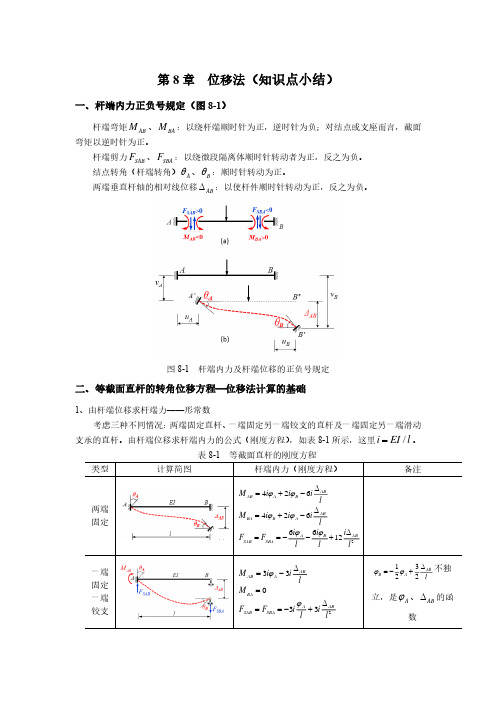
第8章 位移法（知识点小结）一、杆端内力正负号规定（图8-1）杆端弯矩AB M 、BA M ：以绕杆端顺时针为正，逆时针为负；对结点或支座而言，截面弯矩以逆时针为正。
杆端剪力SAB F 、SBA F ：以绕微段隔离体顺时针转动者为正，反之为负。
结点转角（杆端转角）A θ、B θ：顺时针转动为正。
两端垂直杆轴的相对线位移AB ∆：以使杆件顺时针转动为正，反之为负。
图8-1 杆端内力及杆端位移的正负号规定二、等截面直杆的转角位移方程—位移法计算的基础1、由杆端位移求杆端力——形常数考虑三种不同情况：两端固定直杆、一端固定另一端铰支的直杆及一端固定另一端滑动支承的直杆。
由杆端位移求杆端内力的公式（刚度方程），如表8-1所示，这里/i EI l =。
由杆端位移求出杆端弯矩后，杆端剪力可由平衡条件求出。
表8-1中，杆端内力是根据图示方向的位移方向求得的，当计算某一结构时，应根据其杆件所受的实际位移方向，判断其杆端内力的正负号及受拉侧。
2、由荷载求固定内力——载常数对三种等截面直杆，在荷载作用、温度改变作用下的杆端弯矩和剪力，称为固端弯矩和固端剪力（载常数）。
常见荷载作用下的载常数可查表所得。
3、等截面直杆的转角位移方程对等截面直杆，既有已知荷载作用，又有已知的杆端位移，可根据叠加原理，写出其杆端力的一般表达式，这即为等截面直杆的转角位移方程。
三、位移法的基本未知量包括独立的结点角位移和独立的结点线位移。
独立的结点角位移数目等于刚结点（包括组合结点、弹性抗转弹簧）的数目。
结点线位移的数目可通过增设支杆法（或铰化体系法）来确定。
铰化体系法就是将原结构中所有刚结点和固定支座均改为铰结点形成铰接体系，此铰接体系的自由度数就是原结构的独立结点线位移数。
然后分析该铰接体系的几何组成：如果它是几何不变的，说明结构无结点线位移；相反，如果铰接体系是几何可变的，再看最少需要增设几根附加支杆才能确保体系成为几何不变，或者说使此铰接体系成为几何不变而需添加的最少支杆数就等于原结构的独立结点线位移数目。
结构力学第五章位移法.ppt
NDA
NDB
2
2
NDC FNDB 2 FNDC 2 FNDA FP
建立力的 平衡方程
D Fp
EA(2 2L
2) FP
由方程解得： 2PL
(2 2)EA
位移法方程
把△回代到杆端力的表达式中就可得到各杆的轴力 ：
FNDB
2FP 2 2
FNDA
FNDC
P 2
发生一个顺时针的转角 A。
A
A EI,L B
由力法求得：
MAB
MBA
M AB
3
EI L
B
3iB
M BA 0
§8-3 杆端力与杆端位移的关系
5、一端固定一端铰结单元，在B端
发生一个向下的位移 。
A MAB
EI,L
B
△
由力法求得：
M
AB
3EI L2
3i L
MBA
M BA 0
两端固定单元在荷载、支座位移共同作用下的杆端
弯矩表达式：
M AB
4i A
2iB
6i
L
M
F AB
M BA
4iB
2i A
6i
L
M
F BA
§8-3 杆端力与杆端位移的关系
一端固定一端铰结单元在荷载、支座位移共同作用下 的杆端弯矩表达式：
M AB
3iA
6EI L2
BC
qL2 12
M AB
结构力学位移法
M=1 C
M=1
若求结构两个截面的相对角位移 在两个截面上加两个方向相反单 位力偶
1 d
1 d
A
求结构两个截面的相对角位移 B
d
C 求AB杆的角位移 杆的角位移
若求桁架中AB杆的角位移，应 加一单位力偶，构成这一力偶 的两个集中力取 1/d，垂直作 用于杆端
1 d1
1 d1
A
B 求AB、AC杆的角位移 、 杆的角位移
式中k—考虑剪应力沿截面分布不均匀的修正系数， 考虑剪应力沿截面分布不均匀的修正系数， 式中k 考虑剪应力沿截面分布不均匀的修正系数 与截面形状有关
∆ = ∑∫
FQ FQP FN FNP MMP ds + ∑ ∫ ds + ∑ ∫ k ds EI EA GA
式中 F N FQ M ——虚设单位荷载引起的内力 虚设单位荷载引起的内力
l
q
A B
L
∆Q ∆M
∆Q ∆M
EI = 4.8 GAl 2
= 4.8
E 8 = 2(1 + µ ) = G 3
I h2 = A 12
EI h = 1.067( ) 2 GAl 2 l
∆Q ∆M h = 1.067( ) 2 = 1.067% l
当 h= 1 时 l 10 h 1 当 = 时 l 2
FN FQ FQ
ds ds
M
M
ds dθ=κds
γ0 dη= γ0 ds dλ=εds
ds微段 微段 整根杆 变形体系
dwi12=FN εds+FQ γ0ds +M κds w’i12= ∫ (FN εds+FQ γ0ds +M κds) wi12= ∑∫(FN εds+FQ γ0ds +M κds)
结构力学位移法课件
r11
3i
R1P
r11=6i
3i R1Pql2/8
ql 2 Z1ql2/48i
8 MM 1Z1M P
ql2 /16
Z1
M
位移法基本未知数 ----结点位移.
位移法的基本结构 ----单跨梁系.
=
=
Z1
q
EI
EI
Z1
R1
q
EI
EI
ql 2 / 8
R1P
q
位移法的基本方程 ----平衡方程.
+
MP
Z1=1
三.位移法基本结构与基本未知量 无侧移结构(刚架与梁不计轴向变形)
位移法计算, 1个基本未知量
R1=r11 Z1+ R1P =0
基本未知量:独立的 结点位移.包括角位移和线位移 如果把所有的刚结点(包括固定支座)都改为铰结点，则此铰结体系的自由度数就是原结构的独立结点线位移的数目.
有侧移结构(刚架与梁不计轴向变形) 杆端单位位移引起的杆端内力称为形常数.
杆端剪力：使所研究的分离体 有顺时针转动趋势为正，有逆 时针转动趋势为负。
2. 杆端位移的正、负号规定
杆端转角（角位移）：以顺时针方向转动为正，反之 为负 。
杆端相对线位移：指杆件两端垂直于杆轴线方向的相对 线位移，正负号则以使整个杆件顺时针方向转动规定为 正，反之为负。
第八章 位移法
一.单跨超静定梁的形常数与载常数
3. 等截面梁的形常数 杆端单位位移引起的杆端内力称为形常数.
i=EI/l----线刚度
4. 等截面梁的载常数 荷载引起的杆端内力称为载常数.
第八章 位移法
一.单跨超静定梁的形常数与载常数
二.位移法基本概念
结构力学 第8章 位移法
B B
3i
1
0 0
l
3i
l
3i
l2
A
θ=1
B
i
－i
0
二、由外部荷载求固端反力矩
mAB q
EI l
q EI l mBA
mAB
ql 2 8
ql 2 mBA 8
» 在已知荷载及杆端位移的共同作用下的杆端力 一般公式（转角位移方程）： AB 4i A 2i B 6i m AB M
位移法：以某些结点位移基本未知量
用力法求解，有6个未知数。 用位移法求解，未知数=
？个。
5.力法与位移法的适用范围：
力 法: 超静定结构
位移法：超静定结构，也可用于静定结构。 一般用于结点较少而杆件较多的刚架。
位移法正负号规定
★杆端角位移、杆两端相对线位移（侧移）Δ ：顺时针为正 ★ 杆端弯矩：绕杆端顺时针为正、绕结点逆时针为正
综上所述，位移法的基本思路是： 1. 在原结构产生位移的结点上设置附加约束，使结点 固定，从而得到基本结构，然后加上原有的外荷载；
２. 人为迫使原先被“固定”的结点恢复到结构原有的 位移。
通过上述两个步骤，使基本结构与原结构的受力和变 形完全相同，从而可以通过基本结构来计算原结构的内力 和变形。
位移法中需要解决的问题：
2. 回顾力法的解题思路
先求多余未知力 结构内力
结构位移
具体解题过程：
超静定结构 拆成基本结构 加上某些条件
位移条件（力法典型方程）
3. 反推位移法的解题思路
先求某些结点位移 结构内力
具体解题过程：
结 构 拆成单根杆件 的组合体
1.杆端位移协调条件
2.结点平衡条件