结构力学位移法的计算
结构力学-位移法的典型方程及计算步骤
(e)
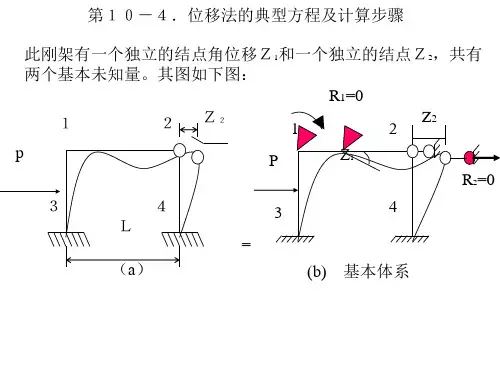
依题意可知并根据叠加原理上述条件可写为:
R1=R11+R12+R1P=r11 Z1+r12 Z2+R1P=0 R2=R21+R22+R2P=r21 Z1+r22 Z2+R2P=0
上述方程称为位移法基本方程,也称为位移法的典型方程。
为了求出典型方程的系数和自由项,可借助于表10-1,绘出基本
结构图,如下图10-7a,b, 和c所示。然后求出各系数和自由项。
r11 1 3i 4i
r12 6i1 0
R1P PL1 0
l
8
Z1=1
4i 1
2
6i 1l
2
Z2=1 1
2
3i M
3 2i 4
(a)
6i 3 l
3i 4 l
(b)
p
MP
PL 3
4
8
(C)
T10-7
1
2
r21 1
2
r22 1
6i l
0
12i
L2
3i
P
L2
2
2
R2P
0
系数和自由项可分为两类,分别由力矩平衡方程 M1=O求得为:
0
6 2 6 9 12 2 11 l Z1 l 2 Z2 16 P 0
Z1 0.02218 Pl Z2 0.02859 Pl 2
M M1Z1 M 2Z2 M P
转到下一节
者的原理有所不同。
§10-7 有侧移的斜柱刚架
B
B’
C’ C
C”
C
A
D
O A,D
B 结点位移图
O为极点,各结点位移前的位置
结构力学 结构的位移计算

k
F Ndu
Md
F Q 0ds
F RC
只有荷载作用
无支座移动
k F Ndu Md FQ 0ds
由材料力学知
du
FNP d s EA
d
M Pds EI
d s
k FQP d s GA
10
1.2
9
k--为截面形状系数
A A1 [Al为腹板截面积]
FP
X
待分析平衡的力状态
(c)
直线
几点说明:
X C (1) 对静定结构,这里实际用的是刚体
虚设协调的位移状态
虚位移原理,实质上是实际受力状态 的平衡方程,即
由外力虚功总和为零,即:
X F 0
X
P
C
M 0 B
(2) 虚位移与实际力状态无关,故可设
1 x
X P b 0 (3) 求解时关键一步是找出虚位移状态的
计算结构的位移,就必须明确广义力与广义位移的对应关系。常见的对应有
以下几种情况:
基本原则
求哪个方向的位移就在要求位移的方向上施加相应的单位力。
A
B
位移方向未知
时无法直接虚
拟单位荷载!
求A点的 水平位移
P=1
m=1 求A截面 的转角
m=1
m=1
求AB两截面 的相对转角
P=1
P=1
求AB两点 的相对位移
位移与约束协调:位移函数在约束处的数值等于约束位移。
§4-2 虚功原理
一、虚功原理的三种形式
1、质点系的虚位移原理
具有理想约束的质点系,其平衡的必要和充分条件是:作用于质点系的主
结构力学 位移法典型方程、计算举例
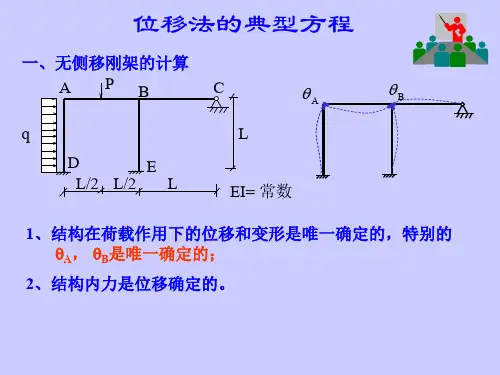
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
结构力学位移法计算步骤
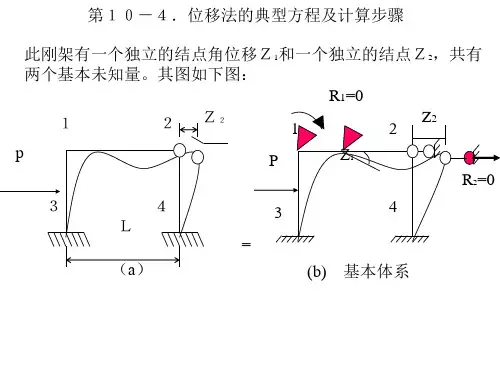
r
R1P=PL/8
R2P=-P/2
r21=-6i/l
r22=15i/l*l
再代入典型方程可得: Z1=9PL/552i Z2=22PL*L/552i 结构的最后弯矩图可由叠加法绘制: M=M1Z1+M2Z2+MP
根据上述的结论可以求出M、Q、N图。这里不再详细画了。 我们可以由上所述,得出位移法的计算步骤如下: (1)、确定原结构的基本未知量,加入附加联系得到基本结构。 (2)、令各附加联系发生与原结构相同的结点位移,再根据附加 联系上的反力矩与反力均为 0的条件下,建立位移法的典型方程。 (3)、绘出基本结构在单位结点位移下的弯矩图和荷载作用下的 的弯矩图,由平衡方程求出各系数和自由项。 (4)、解算典型方程,求出作为基本未知量的各结点位移。 (5)、按叠加法绘出最后弯矩图。 可以看出,位移法与力法在计算上的步骤上是极为相似的,只是两 者的原理有所不同。
M
4 6i l 3 3i 4 l
p PL 3 8
MP 4
(a)
(b)
(C)
T10-7 1 6i l 2 0 r21 1 12i 2 L 2 r22 1 2 P 2 0 R2P
3i 2 L
系数和自由项可分为两类,分别由力矩平衡方程 M1=O求得为:
=7i, r12=-6i/l 然后再由方程 X=0求得为:
Z1 0.02218 Pl
Z 2 0.02859 Pl 2
M M1Z1 M 2 Z 2 M P
转到下一节
第10-4.位移法的典型方程及计算步骤 此刚架有一个独立的结点角位移Z1和一个独立的结点Z2,共有 两个基本未知量。其图如下图: R1=0 z2 Z2 1 2 1 2
结构力学位移法

R2
R1=0 R2=0
ql
C D
Z1 R1
l
四.位移法典型方程
ql
q
l/2 B
ql
C D
ql B
A r22
q
R2 Z1
R1=0
ql C D
Z2=1
l/2 A
EI=常数
R2=0 R1 R1 r11 Z1 r12 Z 2 R1 P 0
l
C
r21
R2 r21 Z1 r22 Z 2 R2 P 0
r11
3i 3i
EI
r
11
=6i
R1P
ql 2 / 8
R1P
q
R1 P ql 2 / 8
Z1 ql / 48i ql 2 8 MM Z M 1 1 P
2
MP
ql2 / 16
r11
3i
Z1=1 3i
M1
Z1
M
位移法求解过程:
1)确定基本体系和基本未知量 2)建立位移法方程 3)作单位弯矩图和荷载弯矩图 4)求系数和自由项 5)解方程 6)作弯矩图
A
Z1
B
Z1
q
B
C
=
A
B
+
B
ቤተ መጻሕፍቲ ባይዱ
C
Z1
q
A
EI
B
Z1
EI
C
----刚臂,限制转动的约束 R1=0 R1=r11 Z1+ R1P =0
R1
q
A
EI
B
EI
C
r11
3i
B B
ql 8
2
3i
r
结构力学位移法

M=1 C
M=1
若求结构两个截面的相对角位移 在两个截面上加两个方向相反单 位力偶
1 d
1 d
A
求结构两个截面的相对角位移 B
d
C 求AB杆的角位移 杆的角位移
若求桁架中AB杆的角位移,应 加一单位力偶,构成这一力偶 的两个集中力取 1/d,垂直作 用于杆端
1 d1
1 d1
A
B 求AB、AC杆的角位移 、 杆的角位移
式中k—考虑剪应力沿截面分布不均匀的修正系数, 考虑剪应力沿截面分布不均匀的修正系数, 式中k 考虑剪应力沿截面分布不均匀的修正系数 与截面形状有关
∆ = ∑∫
FQ FQP FN FNP MMP ds + ∑ ∫ ds + ∑ ∫ k ds EI EA GA
式中 F N FQ M ——虚设单位荷载引起的内力 虚设单位荷载引起的内力
l
q
A B
L
∆Q ∆M
∆Q ∆M
EI = 4.8 GAl 2
= 4.8
E 8 = 2(1 + µ ) = G 3
I h2 = A 12
EI h = 1.067( ) 2 GAl 2 l
∆Q ∆M h = 1.067( ) 2 = 1.067% l
当 h= 1 时 l 10 h 1 当 = 时 l 2
FN FQ FQ
ds ds
M
M
ds dθ=κds
γ0 dη= γ0 ds dλ=εds
ds微段 微段 整根杆 变形体系
dwi12=FN εds+FQ γ0ds +M κds w’i12= ∫ (FN εds+FQ γ0ds +M κds) wi12= ∑∫(FN εds+FQ γ0ds +M κds)
结构力学位移法
例:求图示悬臂梁C 点的竖向位移。
(a) 54 C MP (c) 24 C 3kN/m (d) 30 3kN/m (b) 4 C M1 3kN/m F =1
4m
2m
6 M P2 C
M P1
解 在C点施加竖向单位力,作出M1图和MP图,再 用图乘法求位移。但图乘结果不能直接得出,需要采用 叠加法, 将MP图分解为MP1和MP2叠加,见图c、图d, 然后令MP1 和MP2 图分别与M1图图乘后再相加。
4. 图乘法及其应用
(Graphic Multiplication Method and its Applications)
已有基础: 1. 静定结构的内力计算; 2. 利用位移计算公式求静定结构的位移;
3. 杆件结构在荷载作用下的位移计算公式,即:
kFQ FQds FN FNds MM P ds P EI EA GA
Dy
3 1 FP a 2 2a ( 1 2 2 ) F a 4 F a P ( FP a 2 a ) P () E2 I 2 2 3 E1 A1 3 E2 I 2
例 7. 已知 EI 为常数,求 Cy 。
解:作荷载和单位荷载的内力图
返回
MP
分解
M
Cy
1 1 ql l 3l 1 ql l [( ) ( l) EI 3 8 2 8 2 8 3 2 ql 2 l ql 4 ( l) ] () 温 3 8 4 128 EI 度
ql 4
ql 2 M 8 2
ql 2 8
解法二、
ql 2 2
ql 2 8
ql 2 2
A
ql 2 32
ql 2 8
1 1 l ql l Cy [( ) EI 2 2 2 3 A 2 1 l ql l ( ) 2 2 8 6 2 4 2 l ql l 17ql ( )] () 3 2 32 4 384 EI
结构力学位移法的计算
结构力学位移法的计算一、结构力学位移法的基本原理结构力学位移法基于结构静力学原理,通过分析结构的受力平衡、变形和刚度等特性,计算结构的位移。
其基本原理是建立结构的数学模型,利用力学等效原理将外力转化为内力,进而计算出结构的位移。
其求解过程通常通过数学公式和计算软件来实现。
二、结构力学位移法的计算步骤1.确定结构的边界条件和约束条件。
边界条件指结构在边界上受到的力或位移约束。
约束条件指固定点、支座的位置以及其他限制。
边界条件和约束条件对结构的位移计算具有重要影响。
2.建立结构的数学模型。
数学模型是结构力学位移法的核心,可以通过数学方程或矩阵形式来表示。
常用的模型有刚度矩阵法和有限元法。
刚度矩阵法适用于简单结构,而有限元法适用于复杂结构。
3.计算结构的刚度矩阵。
刚度矩阵描述了结构的刚度特性,可以通过结构的几何和材料性质来计算。
刚度矩阵的计算通常包括杆件的刚度以及节点刚度的组装。
4.应用边界条件和约束条件。
根据结构的边界条件和约束条件,将其转化为数学方程或矩阵形式,然后应用到结构的刚度矩阵上。
一般通过修正刚度矩阵或施加位移限制来实现。
5.求解结构的位移。
通过求解修正后的刚度矩阵和边界条件所构成的方程组,可以得到结构的位移。
通常使用数值方法,如高斯消元法、LU 分解法或迭代法。
6.分析与验证结果。
计算得到的结构位移可用于分析结构的变形、挠度、应力等参数。
还可以与设计要求进行对比和验证,以评估结构的可靠性和稳定性。
三、结构力学位移法的应用1.建筑结构设计。
在建筑结构设计中,利用结构力学位移法可以分析和优化建筑物的静力学特性,确保其稳定性和可靠性。
2.桥梁工程。
结构力学位移法可用于桥梁的设计和分析,帮助工程师评估桥梁的变形、位移和受力状况。
3.航天器设计。
在航天器设计中,结构力学位移法可用于分析航天器的振动、变形和稳定性,确保其在太空中的安全运行。
4.机械工程。
结构力学位移法也可以应用于机械结构的设计和分析,例如汽车、飞机和机器人等。
结构力学第五章 位移计算
M ( x ) x l , M P ( x ) q (l x ) 2 / 2
FP 1 x
MP
例 2:求曲梁B点的竖向位移(EI、EA、GA已知)
FP B FP=1 FP
FQ P M P
A
R
O
θ
R
FN P R
θ
FPF R sin , M k R R R3 M P P , i FP sin, FP R 设 : M Q N
3.变形体的虚功原理 (1)质点系的虚位移原理 具有理想约束的质点系,在某一 位置处于平衡的必要和充分条件 是: 对于任何可能的虚位移,作用 于质点系的主动力所做虚功之 和为零。也即
FP1
FN 1
FP 2
m1 m
2
FN 2
→. → ΣFi δri=0
(2)刚体系的虚位移原理
去掉约束而代以相应 的反力,该反力便可看 成外力。则有:刚体系 处于平衡的必要和充分 条件是:
铁路工程技术规范规定: 桥梁在竖向活载下,钢板桥梁和钢桁梁 最大挠度 < 1/700 和1/900跨度 (2) 超静定、动力和稳定计算
(3)施工要求
3.本章位移计算的假定 (1)
(2) (3)
线弹性 (Linear Elastic),
小变形 (Small Deformation), 理想联结 (Ideal Constraint)。
[
M PM EI
FN P FN EA
]ds
2.桁架
kp FN P FN EA FN P FN l EA ds
3.组合结构
kp
这些公式的适 用条件是什么?
结构力学位移法
r32=r23= –1/2
(5)计算自由项:R1P、R2P、R3P
4m
4m
5m
4m
2m
A
B
C
D
F
E
i=1
i=1
i=1
i=3/4
i=1/2
q=20kN/m
(1/8) × 20×42=40
(1/12) × 20×52=41.7
R1P=40–41.7= –1.7
R2P=41.7
R3P=0
位移法的基本思路概括为,先离散后组合的处理过程。所谓离散,就是把对整体结构的分析转化对单个杆件系在变形协调一致条件下的杆系分析。所谓组合,是要把离散后的结构恢复到原结构的平衡状态,也就是要把各个杆件组合成原结构,组合条件就是要满足原结构的平衡条件。
◆ 确定杆端内力与杆端位移及荷载之间的函数关系
◆确定结构中哪些结点位移作为基本未知量。
(6)建立位移法基本方程:
(7)解方程求结点位移:
(8)绘制弯矩图
A
B
C
D
F
E
M图(kN•m)
18.6
42.8
47.8
26.7
23.8
14.9
5
3.6
8.9
3.97
(9)校核
结点及局部杆件的静力平衡条件的校核。
由于考虑了结点和杆件的联结以及支座约束情况,所以满足了结构的几何条件,即变形连续条件和支座约束条件
位移法基本结构
位移法中采用增加附加约束,以限制原结构的结点位移而得到的新结构,称为位移法的基本结构
● 在刚结点处附加刚臂,只限制刚结点的角位 移,不限制结 点线位移,用符号“▼”表示刚臂
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3i
ql 2 48i
ql 2 16
,
M BC
3i B
ql 2 8
ql 2 16
ql 2 8
ql 2 。 16
ql 2 16
A B
C
M 图 3ql2 32
6
小结:
1)位移法的基本未知量是结构内部刚结点(不包括 支座结点)的转角位移或结点之间的相对线位移。
2)选取内部结点的位移作为未知量就已经满足了结 构的变形协调条件:位移法的典型方程是力(其中 包括力矩)的平衡方程,满足了结构中力的平衡条 件。
A AB
l
AB
l
B
AB
AB A
B
14
二.等截面直杆的刚度(转角位移)方程
1. 两端固定的梁:( i EI )
l
A
EI
B
A
AB
l B
M AB 4i A M BA 2i A
A
i
B
A
M AB 2iB M BA 4iB
MAB EI
MBA
A
B
A
l B
AB
A
i
B
B
A MAB i MBA B
30
3)建立位移法方程,并求解:
由结点B和结点D的平衡条件,可得:
B
MBD
MDB
D MDE
MBA
MB 0,
MBA MBD 0,
8iB 2iD 10.67 0, 1
MDC
MD 0,
M DB M DC M DE 0,
2iB 8iD 32.00 0,2
B 0.356 / i( )。
点之间的相对线位移。此时产生固端弯矩
M
F。
BC
q
锁A 住
B 0
B
C
q
M
F BA
0,
M
F BC
ql2 。 8
B
M
F BC
C
2)令B结点产生转角
(
B
)。此时AB、BC杆类似
于B端为固端且产生转角 B 的单跨超静定梁。 4
B
A
B
放
i
松
3i B
A
i B
BB
3i B
3)杆端弯矩的表达式:
i
B i
Ci EI l C
的确定:
采用增加附加链杆的方法只确限定制独相立对的线结位点移之间的
相对线位移的基本未知量 Z j KL。
从两个不动点(没有线位移的点)引出的两根无 轴向变形的杆件,其交点没有线位移。
若一个结构须要附加 j 根链杆才能使所有内部的
结点成为不动点(没有任何结点之间的相对线位移发 生),则该结构中独立的结点之间的相对线位移的基
1. 位移法的基本未知量
选取结构内部结点的转角位移或结点之间的相 对线位移作为位移法的基本未知量。
q
A
B
C
EI
B
EI
l
l
如上图所示的连续梁,取结点B的转角位移 B作
为基本未知量,这就保证了AB杆与BC杆在B截面的
转角位移的连续协调( B BL BR )。
3
2. 位移法求解的基本步骤
1)在B结点增加附加转动约束(附加刚臂)( )。 附加转动约束只能阻止刚结点的转动,不能阻止结
R1P 10.67
8kN/m 10.67 R2P
B
i
Di
B 10.67 i
42.67 i
0
MP 图
R1P= 10.67A
C
R2P E 21.33
10.67 D
42.67
0
R2P= 32
34
r11
Z1 B 1
r11
r21 Z2 D 0
2i
B
4i 4i
B
4i
i
D i E 2i
4i
i M1图 i
2)典型方程法:利用位移法的基本体系来建立位移 法的典型方程。
25
例8-3-1 采用位移法求作图示刚架的 M 图,已知各杆 的 EI 相同。
B
i
Di E
i
A
4m
i
C
4m
4m i EI
4
解:
1. 直接列方程法:直接利用结点的力矩平衡条件来建 立位移法的一般方程。
1)确定基本未知量为:θB ( )和 θD ( )
未知量: Z1
B 和
Z2
,选取基本体系如下图所
D
示。
Z1 B 0 Z2 D 0
B
i
基本体系
i
Di E i
A
C
33
2)列出位移法的典型方程:
rr1211ZZ11
r12 Z2 r22 Z2
R1P R2 P
0, 0。
3)计算系数和自由项:
i)作出基本体系的
M P 图,M1图,M
图:
2
R1P
因为:
1)为了减少人工计算时基本未知量的数目; 2) 单跨超静定梁的杆端弯矩表达式中已经反映了支座 可能位移(转角位移,相对线位移)的影响,如下图
所示。
q
q
A
BA
B
M
F AB
ql 2 8
,
M
F BA
0。
M
F AB
ql 2 12
,
M
F BA
ql2 。 128
i EI / l
A A
BA
i EI / l B
A
MAB 4iA,
M BA
2i
。
A
M AB 3iA,
MBA 0。
为了减少人工计算时基本未知量的数目,在采用 位移法求解时,确定结构的基本未知量之前,引入如 下的基本假设:对于受弯杆件,忽略其轴向变形和剪 切变形的影响。
亦即假定杆件在轴向是刚性的,杆件在发生弯曲 变形时既不伸长也不缩短。
9
1.刚结点的转角位移的基本未知量 Zi K的确定:
Z4 BH B
A
C
Z5 CH
Z2
B
BH
E A
D
当BD杆: EI无限大
D
?
12
§8-2 等截面直杆的刚度(转角位移)方程
一. 符号规则:
B MBC
MCB C
1.杆端弯矩:
规定杆端弯矩顺时针
MBA
方向为正,逆时针方向为 负。
杆端弯矩具有双重身份: A
1)对杆件隔离体,杆端弯矩是外力偶,顺时针方向 为正,逆时针方向为负。
23
四.正确判别固端弯矩的正负号:
q
q
A
l
M
F AB
ql 2 8
q
M
F AB
ql 2 8
BA
B
B
ll
A
A
B
l
M
F BA
ql 2 8
q
M
F AB
ql 2 8
24
§8-3 无侧移刚架和有侧移刚架的计算
一. 采用位移法求解无侧移的刚架 有两种建立位移法方程的方法:
1)直接列方程法:直接利用平衡条件建立位移法的 典型方程。
D 3.911/ i( )。
31
4)作弯矩图:
将求得的 θB,θD 代入杆端弯矩表达式,得:
M AB 0.71KN m MBA 1.42KN m MBD 1.42KN m
MDB 27.02KN m MDC 11.73KN m MDE 38.76KN m
MED 25.24KN m
16
2. 一端固定,一端滚轴支座的梁:
A M AB EI
A
l
i EI l
B
AB
A
M AB 3i A
i
B
A
A
i
3i M AB l
B AB
M AB
3i A
3i l
AB ;
MBA 0。
17
3. 一端固定,一端定向滑动支座的梁:
MAB A
A
EI MBA
B
i EI l
M AB i A ,
3i A
3i l
AB
3) A
MAB
i
EI l
MBA B
A
MAB i EI
l
MBA
B
A
A
M AB i A
MBA i A
20
三. 固端弯矩
单跨超静定梁在荷载作用下产生的杆端弯矩称为 固端弯矩。固端弯矩以顺时针方向为正,逆时针方向 为负。
1. 两端固定的梁:
q
ql 2 12
A
ql 2 24
l
ql 2 12 FP l 8
3)位移法的基本结构可看作为单跨超静定梁的组合 体系。为了顺利求解,必须首先讨论单跨超静定梁 在荷载及杆端位移作用下的求解问题。
7
二.位移法的基本未知量的确定
位移法的基本未知量是结构内部的刚结点(不
包括支座结点)的转角 i和独立的结点之间的相对
线位移 j 。 不把支座结点的可能位移作为位移法的未知量是
r12 = r21 = 2i,
R2P= 32.00。
4)回代入方程中,求解得:
82iiZZ11
2iZ 8iZ
2 2
10.67 32.00
0, Z1 0。Z2
B D
0.356 / 3.911 /
8kN/m 27.02 38.76
1.42
B 1.78 i
D
i 11.73 i
i
E 25.24
4m
M 图( KN m) A 0.71
C
4m
4m
