经典位移法习题课
位移法习题解答

8-2、清华8-2c 试用位移法计算图示结构,并作内力图。
题8-2c (a )方法一:列位移法典型方程解:(1)D 处定向支座与AD 段不平行,视为固定端。
AB 段剪力、弯矩是静定的,弯矩图、剪力图直接可以画出来,DA 杆D 端支座与杆轴线不平行,视为固定端。
结构只有一个转角位移法基本未知量。
基本结构如图(b)。
(2)建立典型方程:11110P k z R ⋅+=(3)画基本结构的P M 、1M 的弯矩图:如图(c) 、(d) 所示。
(4)利用结点的力矩平的平衡求系数:1110;k i =1P R P l =-⋅(5)将系数,自由项代入典型方程得z 1。
110P lz i⋅=(6)利用叠加法求各杆端的最后弯矩,如图(f ):11P M M M z =+⋅30.3()1040.4()20.2()101030.3()10AC AD DA AEP lM i Pl i P l P lM i Pl M i Pl i iP l M i Pl i⋅=+⋅=⋅⋅=+⋅==+⋅=⋅=+⋅=左拉上拉下拉右拉 方法二:转角位移法(c)ACMAB(d)(b)(e)Q ABF Q解:(1)确定结构的基本未知量。
有一个角位移z1,如图所示(b)。
(2)列杆端的转角位移方程:AB段剪力和弯矩静定,DA杆D端支座与杆轴线不平行,视为固定端。
C1111,,3,3,4,2 FAB AB A AE AD DAM Pl M Pl M i z M i z M i z M i z =-=-=⋅=⋅=⋅=⋅(3)根据刚结点的力矩平衡,列位移方程,求未知量z1:111100343010AB AC AD AEPl M M M M M Pl i z i z i z zi =→+++=→-+⋅+⋅+⋅=→=∑(4)将所求位移代回转角位移方程求各杆端力,并作结构的弯矩图,如图(c)所示。
C1111,,330.3,330.3,1010440.4,220.21010FAB ABA AEAD DAM Pl M PlPl PlM i z i Pl M i z i Pli iPl PlM i z i Pl M i z i Pli i=-=-=⋅=⨯==⋅=⨯==⋅=⨯==⋅=⨯=讨论;本题将D处的滑动支座改为与杆轴线平行。
位移法习题

结构力学-位移法习题1.确定用位移法计算下图所示结构的基本未知量数目,并绘出基本结构。
2.判断题1)位移法基本未知量的个数与结构的超静定次数无关。
()2)位移法可用于求解静定结构的内力。
()3)用位移法计算结构由于支座移动引起的内力时,采用与荷载作用时相同的基本结构。
()4)位移法只能用于求解连续梁和钢梁,不能用于求解桁架。
()3.已知下图所示钢架的结点B产生转角,试用位移法概念求解所作用外力偶M。
4.若下图所示结构结点B向右产生单位位移,试用位移法概念求解应施加的力。
5.已知钢架的弯矩图如下图所示,各杆常数,杆长,试用位移法概念直接计算结点B的转角。
6.用位移法计算下图所示的连续梁,作弯矩图和剪力图。
EI=常数。
7.用位移法计算下图所示结构,作弯矩图。
常数。
8.用位移法计算下图所示各结构,并作弯矩图。
常数。
9.利用对称性计算下图所示结构,作弯矩图。
常数。
10.下图所示等截面连续梁,,已知支座C下沉,用位移法求作弯矩图。
11.下图所示的刚架支座A下沉,支座B下沉,求结点D的转角。
已知各杆。
12.试用位移法计算下图所示结构,并绘出其内力图。
13.试用位移法计算下图所示结构,并绘出其内力图。
14.试用位移法计算图示结构,并绘出M图。
15.试用位移法计算图示结构,并绘出M图。
16.试利用对称性计算图示刚架,并绘出M图。
6m 6m9ml lq(a)4m 4m4m(b)10kN/m6m6m 6m 6m6m(a)8m 4m 4m 4m 4m20kN/m17. 试计算图示结构在支座位移作用下的弯矩,并绘出M 图。
18. 试用位移法计算下图所示结构,并绘出其内力图。
19. 试用位移法求作下列结构由于温度变化产生的M 图。
已知杆件截面高度h =0.4m ,EI =2×104kN ·m 2,α=1×10-5。
20.试计算图示具有牵连位移关系的结构,并绘出M 图。
3EI lA D CB l EI EIϕl Δ=ϕa 2aa 2aaF P6m 4m A B C +20℃0℃ +20℃0℃ 20kN8m 8m 6m 3m A C D EB F G EI 1=∞EI 1=∞ 3EI3EI 3EI EI。
高中物理必修一 位移 习题课

3、物体(质点)在同一直线上运动时(可以是单 、物体(质点) 同一直线上运动时( 向也可以是往返),我们就用数学的正负代表方向 ),我们就用 向也可以是往返),我们就用数学的正负代表方向 具体的方法如下: 、先确定(假设) 具体的方法如下:1、先确定(假设)正方向 2、若位移方向与正方向一致则位移为正数,否则 一致则位移为正数, 、若位移方向与正方向一致则位移为正数 为负数。 或可以这样表达 或可以这样表达: 位移为正数, 为负数。(或可以这样表达:若位移为正数,则方向 与正方向相同,否则相反) 与正方向相同,否则相反) 思考:用正负代表方向有什么局限性? 思考:用正负代表方向有什么局限性?
ห้องสมุดไป่ตู้ 思考
1、为什么前4s位移会是 ?那是不是说明物 、为什么前 位移会是 位移会是0? 体在4s内没有运动 内没有运动? 体在 内没有运动? 2、由思考 你能不能说说位移这个物理量对 你能不能说说位移 、由思考1你能不能说说位移这个物理量对 描述物体的运动有什么优势 不足? 优势和 描述物体的运动有什么优势和不足? 能确切表示出某时间段的初位置和末位置, 能确切表示出某时间段的初位置和末位置, 但无法具体描述物体在这段时间的每时每刻 的运动情况
位移习题课
领悟1: 领悟 :
1、位移的大小的运算不能简单用算术运算法 、 则 但用什么呢? 但用什么呢? 2、位移是有大小又有方向的量,只求出大小 有大小又有方向的量 、位移是有大小又有方向的量, 而不说明方向是不完整的答案。 而不说明方向是不完整的答案。
领悟2: 领悟 :
1、求位移要先确定是哪段时间内的,因为在 、求位移要先确定是哪段时间内的 哪段时间内 不同时间段内物体的初、 不同时间段内物体的初、末位置不同 2、求位移必须确定物体在所求时间段内的初 、 位置( 初时刻对应在什么位置) 位置(及初时刻对应在什么位置)和末位置 末时刻对应在什么位置), ),因为只有确 (及末时刻对应在什么位置),因为只有确 定初、末位置才可以确定位移( 定初、末位置才可以确定位移(包括大小和 方向) 方向)
位移法习题
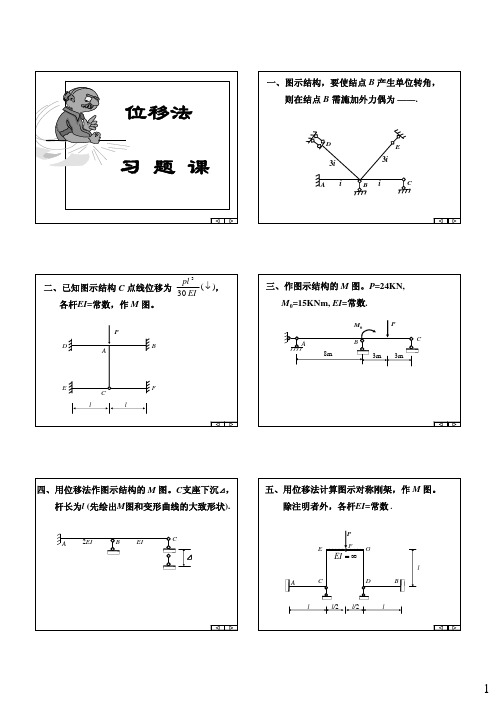
一、图示结构,要使结点 B 产生单位转角, 则在结点 B 需施加外力偶为 ——.
D
3i Ai
E
3i
Bi
C
二、已知图示结构 C 点线位移为 pl 3 ( ↓ ), 30 EI
各杆EI=常数,作 M 图。
P
D
B
A
E
F
C
l
l
三、作图示结构的 M 图。P=24KN, M0=15KNm, EI=常数.
P
k
l/ 2 l/ 2 l
3
P
A
BC
D
பைடு நூலகம்
E
七、作图示结构弯矩图 。
E
F
I
P C
D
l/2 B
l
A
G
H
l
l/2
l/2
八、用 位 移 法 作 图 示 结 构 M 图 。 E I = 常数,
EI1= ∞
q
A EI1 C EI D EI1 B
l/3
l/3
l/3
九、作图示结构M图, EI=常数
A l
q
B
C
F l
G l
D
E
l
H
I
l
十、如图n1, n2均为比例系数,当 n1>n2时,则有: (1) MA> MB , (2) MA<MB , (3) MA= MB , (4)不定
aP
A EI
n1EI
n1EI
h
l
aP
B EI
n2EI
n2EI
h
l
十一、试用位移法求解图示刚架,各杆EI相同。
qa
F
q
位移法习题课

6i
6i
1
Pl
lC
lD
8C
D
i
i
k13
6i k23
6i
l
l 3 k331
A
21i2i
B 12i
l
l
2i
2i
Pi
i
F1P 1
1 Pl F2 P 8
F3 P
8 Pl A
2i
B
P
2i
2i
12i E
12i
F
l
l
E
1 Pl 8
F
k 33
72i l2
F1P 0 F2 P 0 F3P P
(3)列经典方程:20i1
M BA
1 2
ql 2
q
F 0.5l
i ql
0.5l
M BC 4i1 2i 2 M BD 4i1
M CB 2i1 4i 2
M CE
3i 2
3 ql 2 16
A iB
i
C 0.5l
i
i ql 0.5l
D
E
M CF
i 2
3 ql 2 8
l
l
(3)基本方程:
M B 0 M BA M BC M BD 0 MC 0 M CB M CE M CF 0
位移法习题课
1、超静定构造
力法:多出未知力,变形协调条件 位移法:结点位移,静力平衡条件
相对每一种独立旳结点角位移,可列一种结点力矩平衡方程 相对每一种独立旳结点线位移,可列一种截面力矩平衡方程
2、基本未知量鉴定
结点角位移:构造内部刚结点数;支座位移不作为基本未知量。
结点线位移:将构造中全部结点均改为铰结(点弹(性涉支及座固除定外端)),
结构力学(5.1.2)--位移法习题及参考答案
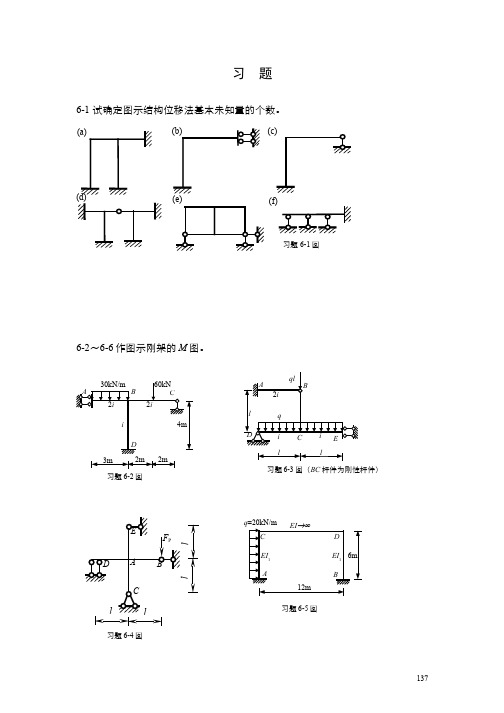
习 题6-1 试确定图示结构位移法基本未知量的个数。
6-2~6-6作图示刚架的M 图。
(a)(f)习题6-1图(d)习题6-2图习题6-5图习题6-3图(BC 杆件为刚性杆件)习题6-4图6-6 试用位移法计算图示结构,并作内力图。
6-7 试用位移法计算图示结构,并作内力图。
6-8 试用位移法计算图示结构,并作内力图。
EI 为常数。
6-9试用位移法计算图示结构,并作弯矩图。
EI 为常数。
6-10 试用位移法计算图示结构,并作弯矩图(提示:结构对称)。
习题6-9图习题6-7图6-11作图示刚架的体系内力图。
6-12 设支座 B 下沉0.5cm B D =,试作图示刚架的M 图。
6-13如图所示连续梁,设支座C 下沉淀1cm ,试作M 图。
6-14图示等截面正方形刚架,内部温度升高+t°C ,杆截面厚度h ,温度膨胀系数为 ,试作M 图。
10 kN/m( a )( b)40 kN习题6-10图BGH习题6-11图(a )(b )q6-15试作图示有弹性支座的梁的弯矩图,332EIk l=,EI =常数。
6-16 试用弯矩分配法计算图示连续梁,并作M 图。
6-176-18 用力矩分配法计算图示结构,并作M 图。
6-19 已知图示结构的力矩分配系数1238/13,2/13,3/13,A A A m m m ===作M 图。
6-20 求图示结构的力矩分配系数和固端弯矩。
已知q=20kN/m,各杆EI 相同。
习题6-17图习题6-13图习题6-14图6-21~6-22 用力矩分配法计算图示连续梁,作M 图,并计算支座反力。
EI=常数。
6-23~6-25用力矩分配法计算图示刚架,作M 图。
EI=常数。
参考答案6.1 (a) 2 (b) 1 (c) 2 (d) 3 (e) 6 (f) 26.2 15BD M =kN·m (右侧受拉)20kN/m 40kN习题6-22图习题6-21图15kN/m习题6-23图F P =10kN 习题6-24图习题6-25图6.321112AB M ql =(上侧受拉)6.4P 0.4AD M F l =(上侧受拉)6.5150AC M =kN·m (左侧受拉)6.651.3AB M =kN·m (左侧受拉)6.780AB M =kN·m (上侧受拉)6.816.9AB M =kN·m (左侧受拉)6.9 (a) 10.43CA M =kN·m (左侧受拉) (b) 56.84CE M =kN·m (下侧受拉)6.10 (a) 8.5AB M =kN·m (上侧受拉) (b) 34.3AC M =kN·m (左侧受拉)6.11 (a) 20.794DC M ql =(右侧受拉) (b) 6.14GD M q =(右侧受拉)6.1223.68AC M =kN·m (右侧受拉)6.1359.3310BA M =ᅲkN·m (上侧受拉)6.142/M EIt h a =(外侧受拉)6.152/32BA M ql =(下侧受拉)6.1617.5CB M =kN·m (下侧受拉)6.1778.75CD M =kN·m (上侧受拉)6.1827/12AB M ql =(上侧受拉)6.191117.95A M =kN·m (上侧受拉)6.200.34AD m =,13.33AD M =kN·m 6.2142.3BA M =kN·m (上侧受拉)6.2217.35BA M =kN·m (上侧受拉)6.2357.4BA M =kN·m (上侧受拉)6.2428.5BA M =kN·m (上侧受拉)6.2573.8BD M =kN·m (左侧受拉)。
位移法习题

习题8-1 图示梁杆端弯矩=ABM, 侧受拉;杆端剪力Q AB F = 。
题8-1图 题8-2图8-2图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
8-3图示梁杆端弯矩ABM= ,侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
2EI AB题8-3图 题8-4图 8-4图示梁杆端弯矩ABM= , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
8-5图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q AB F = 。
Q B A F = 。
题8-5图 题8-6图8-6 图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
Q AB F = 。
8-7图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
题8-7图 题8-8图 8-8 图示梁杆端弯矩ABM= , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
8-9 图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
题8-9图 题8-10图8-10 图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
8-11 图示梁杆端弯矩ABM = , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
6EI AB1题8-11图 题8-12图 8-12 试作图示梁弯矩图,并求B 支座的反力。
8-13 图示梁的跨度为l ,若使A 端截面的转角为零,在A 端施加的弯矩=ABM。
1M1Δ题8-13图 题8-14图8-14 已知图示结构的柱端水平位移为EIlF Δ93P 1=,试作弯矩图。
8-15 试用位移法计算图示结构,作弯矩图。
(a ) (b)题8-15图8-16 试用位移法计算图示结构,作弯矩图。
(a) (b) (c)题8-16图8-17 用位移法解图示结构,基本未知量最少为2个的结构是( )。
A.(a)、(b)B.(b)、(c)C.(c)、(a)D.(a)、(b)、(c)(a)(b) (c)题8-17图8-18 用位移法解图示结构,基本未知量最少为3个的结构是()。
位移法例题

r21=- 24i/l 2
0
6i/l 6i/l
r12= -24i/l 2
r12
Z2=1
-12i/l 2 -12i/l 2 12i/l 2
-12i/l 2 -12i/l 2 r22=48i/l 2 12i/l 2
r22
6i/l
M 2图
FP
说明:水平杆的M图没画,并不是其M=0,而 是EI无穷大的杆能平衡任何弯矩。
R1P FP
R1P=-FP
0 0 0 0 0
FP
R2P FP MP图
R2P=-FP
0
作用在结点上的外力相当于 支座,故杆件无弯矩。 解得
3FP l 2 Z1 = 24i FP l 2 Z2 = 12i
FPl /4 FPl /4 FPl / 2
FPl / 2
M图
(4) 利用叠加法作出弯矩图
例4:用位移法计算图示结构 ,并作弯矩图.EI= 常数. 4:
l
A l
D
(同济大学,2004年考研题)
Z1 = 1
B 4i A 4i 2i l
C 2i l D
Z2 = 1
6i/l
2i/l
B
C
4i/l
M1 图
A
6i/l
D
l
M2 图
l
Z1 = −ql / ( 84i )
2
Z 2 = ql / ( 3i )
3
M 图(× ql )
2
例2: 位移法求解图示结构。
P
P /2
l A EA = B
Z1
l
l
P
l
注意: M 1图和 M P图的正确作图
例3:用位移法作图示结构的 M 图。EI=常数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角位移数目: 6 个 线位移数目: 4 个
位移法计算10个未知量 力法计算2个未知量
角位移数目: 4 个 线位移数目: 6 个
B
aβ
l
A
Δ
斜杆 AB
al
角位移数目:
t°C
因为温度轴向变形产生的位移不能忽略不计,
所以该结构有 4 个独立的结点线位移。( ×)
MC2 16kN.m
44
↑↑↑↑↑↑
12 24
12
(f)
28
M
(kN.m)
16
用位移法计算图示结构,并绘弯矩图.
40
10kNA/m↓↓↓↓↓↓
10kN/m
↓↓↓↓↓↓↓↓↓↓↓
80
30kN
30kN
EI=C 25 5
25
20
M (kN.m)
10
4m 4m 4m 4m
4m 4m
30kN
B
80kN.m
温度轴向变形引起结点C、D发生水平和竖向位移。但温度 轴向变形产生故端力可事先求出来,该结构只有1个独立结点 线位移。
P
B
A
l/2
l1 l/2
q=3kN/m
a
↓↓↓↓↓↓
Δ
A
B
(a)
q=3kN/m ↓↓↓↓↓↓
(b)
题8-29图
题8-30图
题8-31图
1-29、图示单跨超静定梁的固端弯矩MBA=
√ A -3Pl/16
M本BC未=知4θ量B+)2。θC - 16 =-18
A
D
E1I
E1I
E
MCB=2θB+ 4θC +16 =18
4m
4m
MCE=θC -64 =-63 MEC= - θC -32 =-34
3)由平衡条件列位移法方程;
1B8 18
M24BC 18 63 C 45
MBA
24
MBC MCE34
1M0θBB+2MθCB+A 8+=M0 BC 0
ED
3i l
D
+
ql 2 8
7iqC -M3lCi DMCB0+MCD + MCA(1) 0
QDC
QDE
QDC
-
M3li qDCCl
+ +
0l32i-q2Dl
-
3ql 8
解方程(1)(2):
QDE
-
3-i l2
M DDEl++380ql+
ql 2
-
3i l
qYC
+Ql62iDC-D
Q- D3Eql0 4
A 位移法方程的系数= 0
C R1P= 0
√ E R2P= 0
√ B MP= 0
D 各杆端弯矩= 0
F 结点位移= 0
1-42、图示结构在荷载作用下,下列答案正确的是
A r11= 0
√ B R1P= 0
√ C A点位移= 0
√ √ D AB杆的弯矩= 0
E AB杆的剪力= 0
2-7、图示单跨超静定梁,已知θA,则Δ=__QB_A _-
√ A M相同
√ B Q相同
C N相同
D 反力相同
√ E 结点位移相同
BΔ
A
a
MP A
i i
θA θB
A
aa
题2-6图
题1-38图
题1-39图
1-38、下列关于图示结构位移法基本未知量的论述,正确的是
A 三个基本未知量θA,θB,Δ B 两个基本未知量θA=θB,Δ
√ C θA=θB= 0,只有一个未知量Δ D θA=θB=Δ/a,只有一个未知量Δ 1-39、欲使结点A的转角= 0,应在结点A施加的力偶M=
12kN/m
↓↓↓↓↓↓
i 2i
(k)
5.6 2.3
M反对称 34.6
M对称
计算图示结构,并绘弯矩图。
P
A
B
6i M AB M BA - l
-
2Pl QB9A
2,12i l2
,
EI
M CD
M DC
- 6i l
-
Q2PD9Cl
2
,
12i l2
,
C EI D l
EI E l
M DE
3i l
PQl 2D.E 9
I
I
A
B
4m
I
(a) C
4m
M B1 2iq - 3i 2 MC2 -3i 4
M13
M12
Q3 A
-
M A3 4
+ Q30A
3i 16
-
21
Q1B
-
M1B
+ 4
M B1
- 3i
2q
+ 3i 4
M1B
Q2C
-
3i 16
③列平衡方程:取结点及截面分离体如图
Q3A
Q1B
Q2C
M1 M13 + M1B + M12 0
B 3.4
24.5 14.7
62.5
C
190.803.7D
A
B 80
C
D
50.7 M图(kN4.5M.2)
4m 2m
E E
4m
12..715 4.9F Q图5(mkN) F
2.15 4m
3.7 D
NDE=0 3.7
29.3
A
45.2 C 3.7
NCB
0
2.15
NCF
NCB=-2.15
NCF=-48.9
1 2 i
2
64 3i
⑥校核: M1 12 +12 - 24 0
X Q3A + Q1B + Q2C -17 +13 + 4 0
r22=9i/8
3i / 2
M2
3i / 4
44
↑↑↑↑↑↑
12 24
12
(f)
28
M
(kN.m)
16
Q3A
Q1B
Q2C
Q3 A
-
-44 4
+
(- 14 2
43)4 解方程,求结点M位(移kN;.m)
2MθB+C 5θMC -CB3+=0MCE + 45 0
θC=1, θB= - 1,
5)mB将A 结3点 13位62 移 4代回24杆, m端CB弯 矩-m表BC达式12,124求2 出 1杆6,端弯矩;
6)mC校E 核-
12
3
4
2MB-641, m8E-C 18-
B
M EB - M BE 2EI
l
D B由得单M4位BiC 荷载法求
MBC 4iB + 2iC
14kN/m 4m
↑↑↑↑↑↑ ↑↑↑↑↑↑
例题8-5 用位移法按两种方法计算图8-13a示刚架并绘制弯矩图。 解法1:①基本未知量Z1,Z2及基本体系如图8-13b。②位移法典型方程 ③画单位弯矩图荷载弯矩图求系数和自由项
q4l02kN2.m0•42 --84q1l 2.7k-N82.m0•5
12 12
2
MBA
m 41.7kN.m
EE 300I..77355.M59图(kN.M300)I..55 MCB
MCD
3.9FF7 MCF
4m
5m
4m
MBC
M BE =3θB - 1.125Δ =5.0
CB
M M
M M
BA BC CB
6iq A l
+
12i l2
0
q Al 2
l
↓↓↓↓↓↓ ↓
C
D
B
已知结构弯 A
矩图如图,求结
点 B的转角。
E
F
l
l
l
√A
B
M BA 3i
mBA
√C
MB BA
M3BiEB 4i
+
mBA
√E
MB BE
2M4iBCB 6i
MCB
M BC 4i B + 2iC M CB 2i B + 4iC
√B
1
R2P=0
↑↑↑↑↑↑
2I
I
I
2I
I (a) C
(b) 基本体系
(c)
R2P=21
MP
4m
4m
28
6i r11=16i r21=-3i/2 4i
6i
(d)
M1
2i
3i / 4
r12=-3i/2
(e)
3i / 2
④ 16i1 - 3i 2 2 0
- 3i 2 1 + 9i 8 2 - 21 0
⑤叠加M图如图.
0
(2)
qC
3ql 2 44i
,
D
7ql3 44i
单元练习
2m 2m
位移法的计算步骤:
12kN/m 45kN.m
12))(M定确列B铰A向=定杆结支6位端θ点座B+移弯、的2法4矩铰侧的表支移基=达座不1本8式的作未;转为知角基量,θBθC;32kN↓↓B↓22↓E↓I↓Ei↓=I↓1↓↓↓↓↓C↓
1
D
EI
E
QDE - 9 P
2Pl Pl l
99
q
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
BC
D
解:1、基本未知量θC,ΔD
E
2、列杆端弯矩表达式
l
EI=C
