流体力学泵与风机 蔡增基 第五版 下 答案
泵与风机课后习题参考答案(完整版)(基础教育)
泵与风机（课后习题答案）第五章5-1 水泵在n=1450r/min 时的性能曲线绘于图5-48中，问转速为多少时水泵供给管路中的流量为Hc=10+17500q v 2（q v 单位以m 3/s 计算）？已知管路特性曲线方程Hc=10+8000q v 2（q v 单位以m 3/s 计算）。
2q v (L/s) 0 10 20 30 40 50 q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 Hc （m ） 10 10.8 13.2 17.2 22.8 30同一水泵，且输送流体不变，则根据相似定律得：5-2 某水泵在管路上工作，管路特性曲线方程Hc=20+2000q v 2（q v 单位以m 3/s 计算），水泵性能曲线如图5-49所示，问水泵在管路中的供水量是多少？若再并联一台性能相同的水泵工作时，供水量如何变化？ 【解】绘出泵联后性能曲线2q v (L/s) 0 10 20 30 40 50 60 q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 0.06Hc （m ） 20 20.2 20.8 21.8 23.2 25 27.2 管路特性曲线与泵并联后性能曲线交于M 点（56L/s ，25m ）.5-3为了增加管路中的送风量，将No.2风机和No.1风机并联工作，管路特性曲线方程为p =4 q v 2（q v 单位以m 3/s 计，p 以p a 计），No.1 及No.2风机的性能曲线绘于图5-50中，问管路中的风量增加了多少？2q v (103m 3/h) 0 5 10 15 20 25 q v (m 3/s) 0 1.4 2.8 4.2 5.6 7p （p a ）0 7.84 31.36 70.56 125.44 196 ×103m 3/h ，700p a ）于单独使用No.1风机相比增加了33×103-25×103=8 m 3/h5-4 某锅炉引风机，叶轮外径为1.6m ，q v -p 性能曲线绘于图5-51中，因锅炉提高出力，需改风机在B 点（q v =1.4×104m 3/h ，p =2452.5p a ）工作，若采用加长叶片的方法达到此目的，问叶片应加长多少？min /r 114246145030m m p m p =⨯==v v v q n n q q ，【解】锅炉引风机一般为离心式，可看作是低比转速。
第五版 流体力学习题答案完整版
《流体力学》答案1-6．当空气温度从00C 增加至020C 时，ν值增加15%，容重减少10%，问此时μ值增加多少？⎡⎤⎣⎦解0000000000(115%90%)()()0.035 3.5%gggγγννμμρνρνμρνγν⨯---====1-7．图示为一水平方向运动的木板，其速度为1m s ，平板浮在油面上，油深 1mm δ=，油的0.09807Pa s μ=，求作用于平板单位面积上的阻力？⎡⎤⎣⎦解10.0980798.070.001du Pa dy τμ==⨯= 1-9．一底面积为4045cm ⨯，高为1cm 的木板，质量为5kg ，沿着涂有润滑油的斜面等速向下运动，已知1m v s =，1mm δ=，求润滑油的动力粘滞系数？⎡⎤⎣⎦解0T GSin α-= 55255131313T GSin G g g α==⋅=⨯⨯=所以 10.400.451800.001du T A dy μμμ==⨯=但 259.8070.10513180Pa s μ⨯==⋅⨯所以1-10．一个圆锥体绕其铅直中心轴等速旋转，锥体与固定壁的间距为δ＝1mm ，全部为润滑油充满，μ＝0.1Pa.s ，当旋转角速度ω＝16s －1，锥体底部半径R ＝0.3m,高H ＝0.5m 时，求：作用于圆锥的阻力矩。
解： 取微元体， 微元面积：阻力矩为：阻力： 阻力矩51213GVδ22cos 0dhdA r dl r du r dy dT dA dM dT rππθωτμμδτ=⋅=⋅-====⋅0333012cos 12()cos 12cos HHHM dM rdT r dAr r dh r dh r tg h tg h dhττπθωμπθδθωμπθδθ====⋅⋅=⋅⋅⋅=⋅=⋅⋅⋅⋅⎰⎰⎰⎰⎰⎰1-14．图示为一采暖系统图，由于水温升高引起水的体积膨胀，为了防止管道及暖气片胀裂，特在顶部设置一膨胀水箱，使水的体积有自由膨胀的余地，若系统内水的总体积38V m =，加热前后温度差050t C =，水的热胀系数0.0005α=，求膨胀水箱的最小容积？⎡⎤⎣⎦解因为 dV V dt α=所以 30.00058500.2dV Vdt m α==⨯⨯=2-2．在封闭管端完全真空的情况下，水银柱差250Z mm =，求盛水容器液面绝对压强1p 及测压管中水面高度1Z ？⎡⎤⎣⎦解312013.6109.80.056664a p Z p γ=+=⨯⨯⨯=11 6.6640.686809.8p Z m mm γ==== 2-6．封闭容器水面的绝对压强20107.7KNp m =，当地大气压强298.07a KNp m =，试求（1）水深0.8h m =的A 点的绝对压强和相对压强？（2）若容器水面距基准面高度5Z m =，求A 点的测压管高度和测压管水头。
流体力学泵与风机 蔡增基 第五版 下 答案讲解学习
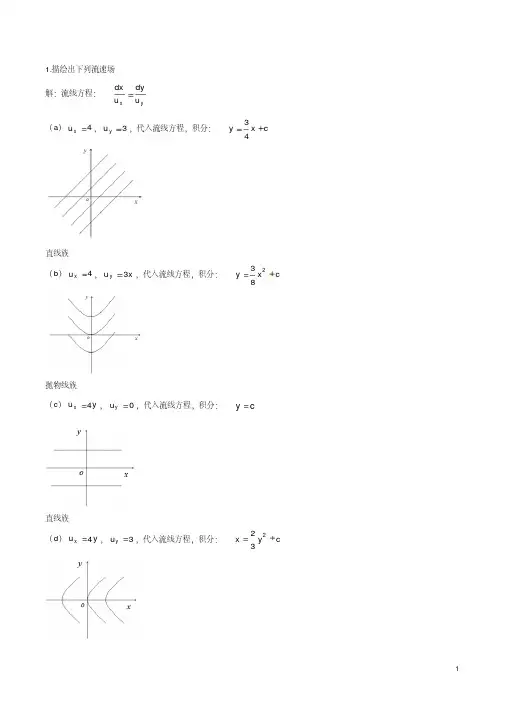
流体力学泵与风机蔡增基第五版下答案1.描绘出下列流速场解：流线方程： yx u dy u dx = （a ）4=x u ，3=y u ，代入流线方程，积分：c x y +=43直线族（b ）4=x u ，x u y 3=，代入流线方程，积分：c x y +=283抛物线族（c ）y u x 4=，0=y u ，代入流线方程，积分：c y =直线族（d ）y u x 4=，3=y u ，代入流线方程，积分：c y x +=232抛物线族（e ）y u x 4=，x u y 3-=，代入流线方程，积分：c y x =+2243椭圆族（f ）y u x 4=，x u y 4=，代入流线方程，积分：c y x =-22双曲线族（g ）y u x 4=，x u y 4-=，代入流线方程，积分：c y x =+22同心圆（h ）4=x u ，0=y u ，代入流线方程，积分：c y =直线族（i ）4=x u ，x u y 4-=，代入流线方程，积分：c x y +-=22抛物线族（j ）x u x 4=，0=y u ，代入流线方程，积分：c y =直线族（k ）xy u x 4=，0=y u ，代入流线方程，积分：c y =直线族（l ）rc u r =，0=θu ，由换算公式：θθθsin cos u u u r x -=，θθθcos sin u u u r y +=220y x cx r xr c u x +=-=，220y x cyr y r c u y +=+=代入流线方程积分：c y x=直线族 （m ）0=r u ，r c u =θ，220y x cy r yr c u x +-=-=，220y x cxr x r c u y +=+=代入流线方程积分：c y x =+22同心圆2.在上题流速场中，哪些流动是无旋流动，哪些流动是有旋流动。
如果是有旋流动，它的旋转角速度的表达式是什么？解：无旋流有：x uy u yx ∂∂=∂∂（或r ru u r∂∂=∂∂θθ）（a ），（f ），（h ），（j ），（l ），（m ）为无旋流动，其余的为有旋流动对有旋流动，旋转角速度：)(21y ux u xy ∂∂-∂∂=ω（b ）23=ω （c ）2-=ω （d ）2-=ω （e ）27-=ω（g ）4-=ω （i ）2-=ω （k ）x 2-=ω3.在上题流速场中，求出各有势流动的流函数和势函数。
工程流体力学泵与风机课后答案
⼯程流体⼒学泵与风机课后答案第1章绪论1.1 试从⼒学分析的⾓度，⽐较流体与固体对外⼒抵抗能⼒的差别。
答：固体在承受⼀定的外⼒后才会发⽣形变;⽽流体只要承受任何切⼒都会发⽣流动，直到切⼒消失;流体不能承受拉⼒，只能承受压⼒。
1.2 何谓连续介质模型？为了研究流体机械运动的规律，说明引⽤连续介质模型的必要性和可能性。
答：把流体当做是由密集质点构成的、内部⽆空隙的连续体来研究，这就是连续介质模型。
建⽴连续介质模型，是为了避开分⼦运动的复杂性，对流体物质的结构进⾏简化，建⽴连续介质模型后．流体运动中的物理量都可视为空间坐标和时间变址的连续函数．这样就可⽤数学分析⽅法来研究流体运动。
1.3 按作⽤⽅式的不同，以下作⽤⼒：压⼒、重⼒、引⼒、摩擦⼒、惯性⼒，哪些是表⾯⼒？哪些是质量⼒？答：压⼒、摩擦⼒是表⾯⼒；重⼒、引⼒、惯性⼒是质量⼒。
1.4 为什么说流体运动的摩擦阻⼒是内摩擦阻⼒？它与固体运动的摩擦⼒有何不同？答：上平板带动与其相邻的流层运动，⽽能影响到内部各流层运动，说明内部各流层间存在切向⼒，即内摩擦⼒，这就是黏滞性的宏观表象。
也就是说，黏滞性就是流体的内摩擦特性。
摩擦阻⼒存在于内部各流层之间，所以叫内摩擦阻⼒。
固体运动的摩擦⼒只作⽤于固体与接触⾯之间，内摩擦阻⼒作⽤于流体各流层之间。
1.5 什么是流体的粘滞性？它对流体流动有什么作⽤？动⼒粘滞系数µ和运动粘滞系数v有何区别及联系？答：黏滞性的定义⼜可表⽰为流体阻抗剪切变形的特性。
由于流体具有黏性,在流动时存在着内摩擦⼒,便会产⽣流动阻⼒，因⽽为克服流动阻⼒就必然会消耗⼀部分机械能。
消耗的这部分机械能转变为热，或被流体吸收增加了流体的内能,或向外界散失，从⽽使得推动流体流动的机械能越来越⼩。
运动黏滞系数是动⼒黏滞系数与密度的⽐。
1.6 液体和⽓体的粘度随着温度变化的趋向是否相同？为什么？答：⽔的黏滞系数随温度升⾼⽽减⼩，空⽓的黏滞系数则随温度升⾼⽽增⼤。
流体力学泵与风机 蔡增基 第五版 下 答案
1.描绘出下列流速场 解：流线方程： y x u dy u dx = （a ）4=x u ，3=y u ，代入流线方程，积分：c x y +=43直线族（b ）4=x u ，x u y 3=，代入流线方程，积分：c x y +=283抛物线族（c ）y u x 4=，0=y u ，代入流线方程，积分：c y =直线族（d ）y u x 4=，3=y u ，代入流线方程，积分：c y x +=232抛物线族（e ）y u x 4=，x u y 3-=，代入流线方程，积分：c y x =+2243椭圆族（f ）y u x 4=，x u y 4=，代入流线方程，积分：c y x =-22双曲线族（g ）y u x 4=，x u y 4-=，代入流线方程，积分：c y x =+22同心圆（h ）4=x u ，0=y u ，代入流线方程，积分：c y =直线族（i ）4=x u ，x u y 4-=，代入流线方程，积分：c x y +-=22抛物线族（j ）x u x 4=，0=y u ，代入流线方程，积分：c y =直线族（k ）xy u x 4=，0=y u ，代入流线方程，积分：c y =直线族（l ）r c u r =，0=θu ，由换算公式：θθθsin cos u u u r x -=，θθθcos sin u u u r y += 220y x cx r x r c u x +=-=，220y x cy r y r c u y +=+= 代入流线方程积分：c y x =直线族（m ）0=r u ，r c u =θ，220y x cy r y r c u x +-=-=，220y x cx r x r c u y +=+= 代入流线方程积分：c y x =+22同心圆2.在上题流速场中，哪些流动是无旋流动，哪些流动是有旋流动。
如果是有旋流动，它的旋转角速度的表达式是什么？解：无旋流有：x u y u y x ∂∂=∂∂（或rr u u r ∂∂=∂∂θθ） （a ），（f ），（h ），（j ），（l ），（m ）为无旋流动，其余的为有旋流动对有旋流动，旋转角速度：)(21yu x u x y ∂∂-∂∂=ω （b ）23=ω （c ）2-=ω （d ）2-=ω （e ）27-=ω （g ）4-=ω （i ）2-=ω （k ）x 2-=ω3.在上题流速场中，求出各有势流动的流函数和势函数。
新版流体力学泵与风机蔡增基第五版下答案-新版.pdf
xa
ux
y 2 ( y2 ( x a) 2 y 2 ( x a) 2 )
Q
y
y
uy
ห้องสมุดไป่ตู้
x 2 ( y 2 (x a)2 y 2 ( x a) 2 )
4 ydy
3xdx 2 y2 3 x2 2
（g）积分路径可以选
0,0 x,0 : dy 0, y 0
x,0 x, y : dx 0, x x
4ydy ( 4x)dx 2 y 2 2x 2
（L ）积分路径可以选 0,0 x,0 : dy 0, y 0
x,0 x, y : dx 0, x x
ux ur cos u sin
1.描绘出下列流速场 解：流线方程： dx dy
ux uy
（a） u x 4 ， u y 3 ，代入流线方程，积分：
3 y xc
4
直线族 （b） u x 4 ， u y 3x ，代入流线方程，积分：
y 3 x2 c 8
抛物线族
（c） u x 4y ， uy 0 ，代入流线方程，积分： y c
直线族 （d） u x 4 y ， uy 3 ，代入流线方程，积分：
xa
6
驻点在 y 0, x
l 处，由 l 2
2,b
0.5 得椭圆轮廓方程：
x2 1
y2 (0.25) 2
1
即： x2 16 y2 1
8. 确定绕圆柱流场的轮廓线，主要取决于哪些量？已知
R 2 m ，求流函数和势函数。
解：需要流速 v0 ，柱体半径 R
v0 (r ∵R 2
R2 ) sin
r ∴ v0(r
4) sin r
R2
v0 (r
) cos
流体力学泵与风机(第五版)蔡增基课后习答案(一)
流动阻力和能量损失1.如图所示：（1）绘制水头线；（2）若关小上游阀门A ，各段水头线如何变化？若关小下游阀门B ，各段水头线又如何变化？（3）若分别关小或开大阀门A 和B ，对固定断面1-1的压强产生什么影响？解：（1）略（2）A 点阻力加大，从A 点起，总水头线平行下移。
由于流量减少，动能减少，使总水头线与测压管水头线之间的距离减小，即A 点以上，测压管水头线上移。
A 点以下，测压管水头线不变，同理讨论关小B 的闸门情况。
（3）由于1—1断面在A 点的下游，又由于A 点以下测压管水头线不变，所以开大或者关小阀门对1—1断面的压强不受影响。
对B 点，关小闸门，B 点以上测压管水头线上移，使1—1断面压强变大，反之亦然。
2.用直径的管道，输送流量为的水，如水温为mm d 100=s kg /105℃，试确定管内水的流态。
如用这样管道输送同样质量流量的石油，已知石油密度，运动粘滞系数3850m kg =ρ，试确定石油的流态。
s cm 214.1=υ解：（1）5℃时，水的运动粘滞系数sm 2610519.1−×=υ，=Av Q Q ρρ==v()231.0410110×××π20008386310519.1)1.0(41011.010Re 623>=××××××==−πυvd 故为紊流（2）200013141014.1)1.0(48501.010Re 42<=×××××=−π故为层流3.有一圆形风道，管径为300mm ，输送的空气温度20℃，求气流保持层流时的最大流量。
若输送的空气量为200kg/h ，气流是层流还是紊流？解：20℃时,空气的运动粘滞系数sm v 26107.15−−×=3205.1m kg =ρ2000Re ==υvdsm v 105.03.0107.1520006=××=−hkg s kg vA Q m 32109.83.04105.0205.132=×=×××==−πρ故，为紊流h kg 2004.水流经过一渐扩管，如小断面的直径为，大断面的直径1d 为，而，试问哪个断面雷诺数大？这两个断面的雷2d 221=d d 诺数的比值是多少？21Re Re 解：；2211A v A v Q ==4)(2122121===d dA A v v2214Re Re 221121=×==d v d v 故直径为的雷诺数大1d 5.有一蒸汽冷凝器，内有250根平行的黄铜管，通过的冷却水总流量为8L/s ，水温为10℃，为了使黄铜管内冷却水保持为紊流（紊流时黄铜管的热交换性能比层流好），问黄铜管的直径不得超过多少？解：0℃时,水的运动粘滞系数υ=1.31×10−6m 2/s24250d Q v ⋅⋅=π要使冷却水保持紊流,则4000Re ≥，4000≥υvd mm vd 61031.14000−××≤即：mmd 67.7≤若最小Re 取2000时，mmd 3.15≤6.设圆管直径，管长，输送石油的流量mm d 200=m L 1000=运动粘滞s L Q /40=系数，求沿程水头损失。
《流体力学及泵与风机》习题解答
= −2 x − y
＝－1
ε zz =
∂v z =0 ∂z
ϖz =
∂v 1 ∂ (rvθ ) − r 2r ∂r ∂θ
∴ϖ z =
r02 r02 1 − v 1 − sin θ + v ( 1 − ) sin θ ∞ =0 ∞ 2 2 2r r r
H = z 2 − z1 +
v2 1.7 2 + hw = 0.2 + + 3.25 = 3.6m 2g 2 × 9.8
2
1
－9 解 由题意可知：在 y 方向 z 方向上速度可近似为 0,即： v
y
= vz = 0 ∂v x =0 ∂x ∂v x =0 ∂z
流 动 为 定 常 流 动 、 在 z 方 向 为 无 穷 大 故 ： ∂∂t = 0 根据公式（1－37）得
1 6
－解
令被测管道的体积流量为 Q ， 则
A1v1 = A2 v 2 = Q v1 = v 2 A2 A1 p1 + ρg ( z1 − z 2 + h) = p 2 + ρ m gh p1 − p 2 = ( ρ m − ρ ) gh − ρg ( z1 − z 2 )
（1） （2） （3）
易知：
f y = − g cos θ
fz = 0
0 = g sin θ −
∂ 2vx 1 ∂p +υ ρ ∂x ∂y 2
（1）
0 = − g cos θ −
0=
1 ∂p ρ ∂y
（2） （3）
显然 p = p( x, y) 同 1－9 题一样，由（2）得 p ( x, y ) = − ρg cos θy + c( x) 代入（1）式并积分
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、描绘出下列流速场解:流线方程: y x u dy u dx=(a)4=x u ,3=y u ,代入流线方程,积分:c x y +=43直线族(b)4=x u ,x u y 3=,代入流线方程,积分:c x y +=283抛物线族(c)y u x 4=,0=y u ,代入流线方程,积分:c y =直线族(d)y u x 4=,3=y u ,代入流线方程,积分:c y x +=232抛物线族(e)y u x 4=,x u y 3-=,代入流线方程,积分:c y x =+2243椭圆族(f)y u x 4=,x u y 4=,代入流线方程,积分:c y x =-22双曲线族(g)y u x 4=,x u y 4-=,代入流线方程,积分:c y x =+22同心圆(h)4=x u ,0=y u ,代入流线方程,积分:c y =直线族(i)4=x u ,x u y 4-=,代入流线方程,积分:c x y +-=22抛物线族(j)x u x 4=,0=y u ,代入流线方程,积分:c y =直线族(k)xy u x 4=,0=y u ,代入流线方程,积分:c y =直线族 (l)r c u r =,0=θu ,由换算公式:θθθsin cos u u u r x -=,θθθcos sin u u u r y +=220y x cx r x r cu x +=-=,220y x cyr y r c u y +=+=代入流线方程积分:c y x=直线族(m)0=r u ,r c u =θ,220y x cy r y r c u x +-=-=,220y x cx r x r c u y +=+= 代入流线方程积分:c y x =+22同心圆2、在上题流速场中,哪些流动就是无旋流动,哪些流动就是有旋流动。
如果就是有旋流动,它的旋转角速度的表达式就是什么？解:无旋流有:x u y u y x ∂∂=∂∂(或rr u u r ∂∂=∂∂θθ) (a),(f),(h),(j),(l),(m)为无旋流动,其余的为有旋流动对有旋流动,旋转角速度:)(21yu x u x y ∂∂-∂∂=ω (b)23=ω (c)2-=ω (d)2-=ω (e)27-=ω (g)4-=ω (i)2-=ω (k)x 2-=ω3、在上题流速场中,求出各有势流动的流函数与势函数。
解:势函数⎰+=dy u dx u y x ϕ流函数⎰-=dx u dy u y x ψ(a)⎰+=+=y x dy dx 3434ϕy x dx dy 4334+-=-=⎰ψ(积分;路径可以选择)(d)积分路径可以选0,0:0,0,0==→y dy xx x dx y x x ==→,0:,0,x y dx ydy dx ydy 3234342-=-=-=⎰⎰⎰ψ(e)⎰⎰⎰⎰-+=-+=yy x x xdy dx y xdy ydx 0034340ϕ 取),(00y x 为)0,0(则积分路线可选其中0,0:0,0,0==→y dy xx x dx y x x ==→,0:,0,2223234x y xdx ydy +=--=⎰⎰ψ (g)积分路径可以选0,0:0,0,0==→y dy xx x dx y x x ==→,0:,0,2222)4(4x y dx x ydy +=--=⎰ψ (L)积分路径可以选0,0:0,0,0==→y dy xx x dx y x x ==→,0:,0,其中均可以用上图作为积分路径图4、流速场为r cu u a r ==θ,0)(,r u u b r 2,0)(ωθ==时,求半径为1r 与2r 的两流线间流量的表达式。
解:ψd dQ = ⎰⎰-=dr u rd u r θθψ⎰-=-=r c dr r ca ln )(ψ∴211212ln )ln (ln r r c r c r c Q =---=-=ψψ⎰-=-=2)(222r rdr b ωωψ∴)(22221212r r Q -=-=ωψψ5、流速场的流函数就是323y y x -=ψ。
它就是否就是无旋流动？如果不就是,计算它的旋转角速度。
证明任一点的流速只取决于它对原点的距离。
绘流线2=ψ。
解:xy x 6=∂∂ψ y x622=∂∂ψ 2233y x y-=∂∂ψ y y 622-=∂∂ψ ∴+∂∂22x ψ022=∂∂y ψ 就是无旋流 2233y x y u x -=∂∂=ψ xy xu y 6-=∂∂-=ψ ∴222223)(3r y x u u u y x =+=+= 即任一点的流速只取决于它对原点的距离流线2=ψ即2332=-y y x用描点法:2)3(22=-y x y(图略)6、确定半无限物体的轮廓线,需要哪些量来决定流函数。
要改变物体的宽度,需要变动哪些量。
以某一水平流动设计的绕流流速场,当水平流动的流速变化时,流函数就是否变化？解:需要水平流速0v ,半无限物体的迎来流方向的截面A,由这两个参数可得流量A v Q 0=。
改变物体宽度,就改变了流量。
当水平流速变化时,ψ也变化 xy arctg Q y v πψ20+= 7、确定朗金椭圆的轮廓线主要取决于哪些量？试根据指定长度m l 2=,指定宽度m b 5.0=,设计朗金椭圆的轮廓线。
解:需要水平流速0v ,一对强度相等的源与汇的位置a ±以及流量Q 。
)(20ax y arctg a x y arctg Q y v --++=πψ驻点在2,0l x y ±==处,由5.0,2==b l 得椭圆轮廓方程:1)25.0(1222=+y x 即:11622=+y x8、确定绕圆柱流场的轮廓线,主要取决于哪些量？已知m R 2=,求流函数与势函数。
解:需要流速0v ,柱体半径R θψsin )(20rR r v -= ∵2=R ∴θψsin )4(0rr v -= θϕcos )(20rR r v += ∵2=R ∴θϕcos )(20rR r v += 9、等强度的两源流,位于距原点为a 的x 轴上,求流函数。
并确定驻点位置。
如果此流速场与流函数为vy =ψ的流速场相叠加,绘出流线,并确定驻点位置。
解:叠加前)(2ax y arctg a x y arctg Q -++=πψ ))()((22222a x y a x a x y a x Q y u x -+-++++=∂∂=πψ ))()((22222a x y y a x y y Q x u y -++++=∂∂-=πψ 当0=x )(22a y Qy u y +=π 0=x u 0=y )11(2ax a x Q u x -++=π 0=y u ∴驻点位置)0,0( 叠加后)(2ax y arctg a x y arctg Q vy -+++=πψ 流速为零的条件:0)(2)(20=-+++=∂∂==a x Q a x Q v y u y x ππψ解得:⎥⎦⎤⎢⎣⎡+±-=22)2(21v a Q Q v x ππ 即驻点坐标:⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+--0,)2(2122v a Q Q v ππ⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡++-0,)2(2122v a Q Q v ππ 10、强度同为s m /602的源流与汇流位于x 轴,各距原点为m a 3=。
计算坐标原点的流速。
计算通过)4,0(点的流线的流函数值,并求该点流速。
解:)(2ax y arctg a x y arctg Q --+=πψ s m a x a x y a x a x y Q y u a Q y x /37.61111112223,60,0=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛++-+⎪⎭⎫ ⎝⎛++=∂∂====πψ 0=y u)4,0(的流函数:34)3434(2arctg Q arctg arctg Q ππψ=--= s m a x a x y a x a x y Q y u a y x Q x /25180)1)(111)(11(2223,4,0,60ππψ=-++-+++=∂∂===== 0=y u11、为了在)5,0(点产生10的速度,在坐标原点应加强度多大的偶极矩？过此点的流函数值为何？ 解:202R v M π=将5,100==R v 代入得:π500=MrM πθψ2sin -= 将5,1sin ,500====R r M θπ代入得:50-=ψ 12、强度为s m /2.02的源流与强度为s m /12的环流均位于坐标原点,求流函数与势函数,求)5.0,1(m m 的速度分量。
解:r Q ln 22πΓπθψ+=,θπΓπϕ2ln 2+=r Q ,rQ u r π2= 将225.01,2.0+==r Q 代入得:s m u r /0284.0=ru πΓθ2-= 将225.01,1+==r Γ代入得:s m u /142.0-=θ1、弦长为3m 的飞机机翼以300km/h 的速度,在温度为20℃,压强为1at (n )的静止空气中飞行,用比例为20的模型在风洞中作试验,要求实现动力相似。
(a) 如果风洞中空气温度、压强与飞行中的相同,风洞中的空气速度应该怎样？(b) 如果在可变密度的风洞中作实验,温度为20℃, 压强为30at(n), 则速度为多少？(c) 如果模型在水中作实验,水温20℃,则速度为多少？解:雷诺准数相等 (a)=υnn L v υmm L v=m v n v mn L L =300⨯20=6000km/h 不可能达到此速度,所以要改变实验条件(b) ∵等温c P =ρ,μ不变,μμρυpvl vl vl →==Re 得n m v v =m n L L m n P P =300⨯20⨯301=200km/h (c)由气υn n L v =水υmm L v 得m n n m L L v v 水气υυ==300⨯20×7.15007.1=384km/h 2、长1、5m,宽0、3m 的平板在20℃的水内拖曳,当速度为3m/s 时,阻力为14N,计算相似板的尺寸,它的速度为18m/s,绝对压强101、4kN/m 2,温度15℃的空气气流中形成动力相似条件,它的阻力为多少？解:由雷诺准数相等:222111υυL v L v =⇒水υλl 3=υ18⇒l λ=0、4 且v l λλλυ=m L =lnL λ=4051..=3、75m (长) m L =l n L λ=4.03.0=0、75m (宽) F mF λ=14=226.12.998)2.15007.1(2222==ρυρλλλλλl v 解得:N F m 92.3=3、当水温为20℃、平均速度为4、5m/s 时,直径为0、3m 水平管线某段的压强降为68、95kN/m 2,如果用比例为6的模型管线,以空气作为工作流体,当平均速度为30m/s 时,要求在相应段 产生55、2kN/m 2的压强降。