材料力学课后答案第12章 习题解答PPT课件
合集下载
浙江工业大学材料力学第12章答案
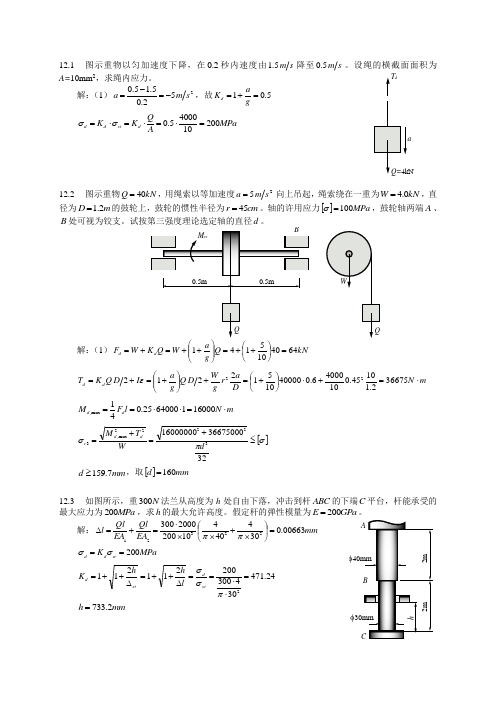
12.1 图示重物以匀加速度下降，在2.0秒内速度由s m 5.1降至s m 5.0。
设绳的横截面面积为A=10mm 2，求绳内应力。
解：（1）252.05.15.0s m a -=-=，故5.01=+=g a K dMPa A Q K K d st d d 2001040005.0=⋅=⋅=⋅=σσ12.2 图示重物kN Q 40=，用绳索以等加速度25s m a =向上吊起，绳索绕在一重为kN W 0.4=，直径为m D 2.1=的鼓轮上，鼓轮的惯性半径为cm r 45=。
轴的许用应力[]MPa 100=σ，鼓轮轴两端A 、B解：（1）kN Q g a W Q K W F d d 6440105141=⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=+= m N D a r g W D Q g a I D Q K T d d ⋅=+⋅⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+=+=366752.11045.01040006.0400001051221222ε m N l F M d d ⋅=⋅⋅==1600016400025.041max , []σπσ≤+=+=32366750001600000032222max ,3d WT M d d rmm d 7.159≥，取[]mm d 160=12.3 如图所示，重N 300法兰从高度为h 处自由下落，冲击到杆ABC 的下端C 平台，杆能承受的最大应力为MPa 200，求h 的最大允许高度。
假定杆的弹性模量为E 200=解：mm EA Ql EA Ql l 00663.030440410200200030022321=⎪⎭⎫ ⎝⎛⨯+⨯⨯⋅=+=∆ππ MPa K st d d 200==σσ24.4713043002002112112=⋅⋅==∆++=∆++=πσσst d st d l h h K mm h 2.733=12.4 如图所示，重N 100物体从mm h 500=位置自由下落到铝制梁AB 上的C 点，求截面C 的位移和梁上的最大应力。
材料力学第十二章
寸系数。 1.弯曲时的有效应力集中系数和尺寸系数
D 50 1.25 d 40
f50
f40
r 5 0.125 d 40
由图表查有效应力集中系数 r=5
当 : b 1000 MPa 时 ,K 1.55
当 : b 900MPa 时 ,K 1.55
当 : b 920MPa 时 ,K 1.55
的有效应力集中系数和尺寸系数。
10、简述影响构件持久极限的主要因素
11、交变应力的平均应力为σm＝20MPa，应力 幅为σa＝50MPa，其循环特性中的 最大应力 σmax ＝ ，最小应力σmin＝ ，循环特性r ＝ 。
12、最大弯曲正应力相等的三根材料相同的梁，承受交变应力。 （A）是对称循环；
（B）是脉动循环；
（C）是∣σmin∣<∣σmax∣的不对称循环。 则以 种循环的梁的疲劳强度最低。
α B
18、 火车轮轴受力情况如图所示。a=500mm，
l=1435mm，轮轴中段直径d=15cm。若P=50kN， 试求轮轴中段截面边缘上任一点的最大应力，最 小应力，循环特征，并作出曲线。
19、阶梯轴如图所示。材料为铬镍合 b 920MPa 金， 1 420MPa ， 1 250MPa 。轴的尺寸是： d=40mm，D=50mm，r=5mm。求弯曲和扭转时
③ 强度校核
0 1 1
max 1
安全
1、构件在临近疲劳断裂时，其内部： A：无应力集中；
。
B：无明显的塑性变形；
C：不存在裂纹； D：不存在应力；
2、塑性较好的材料在交变应力的作用下，当危险点的最 大应力低于屈服极限时： A：既不可能有明显的塑性变形，也不可能发生断裂； B：虽可能有明显的塑性变形，但不可能发生断裂； C：不仅可能有明显的塑性变形，而且可能发生断裂；
D 50 1.25 d 40
f50
f40
r 5 0.125 d 40
由图表查有效应力集中系数 r=5
当 : b 1000 MPa 时 ,K 1.55
当 : b 900MPa 时 ,K 1.55
当 : b 920MPa 时 ,K 1.55
的有效应力集中系数和尺寸系数。
10、简述影响构件持久极限的主要因素
11、交变应力的平均应力为σm＝20MPa，应力 幅为σa＝50MPa，其循环特性中的 最大应力 σmax ＝ ，最小应力σmin＝ ，循环特性r ＝ 。
12、最大弯曲正应力相等的三根材料相同的梁，承受交变应力。 （A）是对称循环；
（B）是脉动循环；
（C）是∣σmin∣<∣σmax∣的不对称循环。 则以 种循环的梁的疲劳强度最低。
α B
18、 火车轮轴受力情况如图所示。a=500mm，
l=1435mm，轮轴中段直径d=15cm。若P=50kN， 试求轮轴中段截面边缘上任一点的最大应力，最 小应力，循环特征，并作出曲线。
19、阶梯轴如图所示。材料为铬镍合 b 920MPa 金， 1 420MPa ， 1 250MPa 。轴的尺寸是： d=40mm，D=50mm，r=5mm。求弯曲和扭转时
③ 强度校核
0 1 1
max 1
安全
1、构件在临近疲劳断裂时，其内部： A：无应力集中；
。
B：无明显的塑性变形；
C：不存在裂纹； D：不存在应力；
2、塑性较好的材料在交变应力的作用下，当危险点的最 大应力低于屈服极限时： A：既不可能有明显的塑性变形，也不可能发生断裂； B：虽可能有明显的塑性变形，但不可能发生断裂； C：不仅可能有明显的塑性变形，而且可能发生断裂；
材料力学第2版 课后习题答案 第12章 变形能法
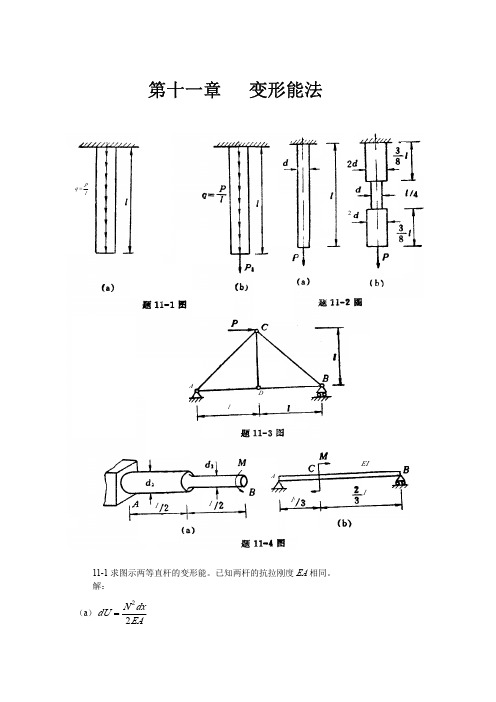
3 d1 ； 2
(b) 梁的抗弯刚度EI，略去剪切变形的影响。 解： （a） M n1 = m
M n2 = m U2 = J P2 =
9.6m 2 l Gπd14
U1 = J P1 =
m 2l 4GJ P1 π 4 d1 32
m 2l 4GJ P2 π 4 5.06π 4 d2 = d1 32 32
故
U a 16 = Ub 7
11-3 图示桁架各杆材料相同，截面面积相等，试求在 P 力作用下，桁架的变形能。 解：
支反力
R Ax = P R Ay = R B =
各杆的轴力和变形能如表所示 杆号 1 内力 Ni 杆长 各杆的变形能 Ui
P 2
2P 2
2l
2 P 2 l (4 EA)
2
− 2P 2
求 θA
M 0 ( x1 ) = −1 M 0 ( x 2 ) = −1
θA =
1 EJ
⎡ ⎛L ⎤ 1 ⎞ − P⎜ + x2 ⎟(− 1)⎥ dx 2 ∫0 (− Px1 )(− 1)dx1 + 2EJ ∫0 2 ⎢ ⎠ ⎣ ⎝2 ⎦
2
L
L
1 L2 1 = ⋅P⋅ + EJ 8 2 EJ =
求 δB
0
2l
l l l
2 P 2 l (4 EA)
0
3 4 5ຫໍສະໝຸດ P 2 P 2P 2 l (8EA) P 2l (8 EA)
故珩架的变形能为
5
U = ∑ Ui =
i =1
2 2 + 1 P 2l P 2l = 0.957 4 EA EA
11-4 试计算图示各杆的变形能。 (a) 轴材料的剪切弹性模量为G， d 2 =
压杆稳定《材料力学》ch-12课件
实验设备与步骤
实验设备：压杆实验装置、压力表、砝码、各 种不同材料和截面形状的细长杆。
01
1. 准备不同材料和截面形状的细长杆，将 其固定在压杆实验装置上；
03
02
实验步骤
04
2. 在杆的一端施加砝码，逐渐增加压力， 观察压杆在不同压力下的失稳现象；
3. 记录不同条件下（如不同材料、截面形 状、长度、直径等）压杆的失稳载荷；
析。
欧拉公式与临界应力
欧拉公式是计算细长压杆临界应力的公式，其形式为： Pcr = π²EI/L²。
输标02入题
其中，Pcr是临界力，E是弹性模量，I是压杆横截面的 惯性矩，L是压杆长度。
01
03
临界应力是衡量压杆稳定性的重要指标，当压杆所受 应力小于临界应力时，压杆处于稳定状态；当所受应
力大于临界应力时，压杆将发生屈曲失稳。
04
通过欧拉公式可以计算出不同长度和形状的细长压杆 的临界应力。
不同长度压杆的稳定性分析
对于不同长度的压杆，其稳定性分析方法有所不同。
对于细长压杆，可以采用欧拉公式进行计算；对于短粗杆，需要考虑剪切变形和弯 曲变形的影响，可以采用能量法或有限元法进行分析。
在进行稳定性分析时，需要考虑压杆的实际工作条件和载荷情况，以确定合理的分 析方法和参数。
起重机的吊臂、支腿等部位需要承受 较大的压力和弯矩，压杆稳定问题直 接关系到设备的安全性和稳定性。
发动机支架
发动机支架需要承受较大的振动和压 力，压杆稳定问题对于保证发动机的 正常运行至关重要。
其他领域的压杆稳定问题
航空航天
飞机和火箭的结构需要承受较大的气动压力和加速度，压杆稳定问题直接关系到飞行器的安全性和稳定性。
材料力学12(1)
（二）斜弯曲时的强度条件 a. 中性轴与z轴的夹角
tan Iz M y 12 1
Iy Mz
以图12-2为例，此时中性轴位置的表达式为：
图12-2
tan
Iz Iy
P sin l P cos l
x x
Iz Iy
tan
12 1
tan
Iz Iy
P sin l P cos l
例3图
例3图
受力简图
解（一）外力分析
将各力向圆轴的 截面形心简化， 画出受力简图。
（二）内力分析
画出内力图如图， 从内力图分析，B截面 为危险截面。B截面上 的内力为：
扭矩： Mn 1KN m
弯矩：
M M
z y
0.364KN 1KN m
m
总弯矩为：
MB
M
2 z
M
2 y
1.06KN
m
i
2 y
ez
12
4
式(12-4)中ay, az为中性轴在直角坐标轴上的截距（图12-3）； ey, ez为偏心力P的作用点的位置（图中E点），iy, iz为惯性半径， 其计算式为：
i
y
Iy A
iz
Iz A
b. 正应力强度条件 最大正应力和最小正应力发生在离中性轴最远的点，危
险点的应力状态是单向应力状态，建立的强度条件为：
若圆杆受扭转与拉伸（压缩）的联合作用，危险点的应
力状态与图12-4相同，只是正应力为
N
N A
，强度条
件用式 (12-6) 和式(12-7)来计算，式中 M以 N 代替。
图12-4 若圆杆受拉伸（压缩）、弯曲和扭转的联合作用，
危险点应力状态还是图12-4所示的单元体，此时正应
材料力学ppt(刘鸿文第四版含课后答案)
l1
A' l3
(3) 物理关系
A
l1
N1l
E1A1 cos
l1 l2 A' l3
(1) 静平衡方程
N1 N2
(1)
N3 2N1 cos P 0 (2)
(2) 变形协调方程 l1 l源自 l3 cos (3)(3) 物理关系
l1
N1l
E1A1 cos
0.52 104 (m)
AB杆的变形
lAB lBD lCD lAC 1.05104(m)
例 2 (书例2. 7) 已知： BC杆: d=20mm, BD杆: 8号槽钢。[]= 160 MPa, E=200GPa, P=60kN。 求：校核强度及B点位移。 解：(1) 求轴力
Al
l Nl Pl 胡克定律的
EA EA
另一种形式
EA 抗拉(或抗压)刚度
注意：上式只在应力不超过比例极限时成立。
推广: (1) 阶梯轴
l Nili
Ei Ai
(2) 变截面轴
l
l
N ( x) EA(x)
dx
l1
l2
l3
A1
A2
A3
x
N(x)+dN(x)
N(X)
应力 A2 1024.8106 m2
1
N1 A1
143MPa
[ ] 160MPa
2
N2 A2
73.2 MPa
[ ] 160MPa
(3) 计算杆的变形
BC杆变形
l1
BB1
N1l1 EA1
材料力学第十二章
设 R0 为轴线的曲率半径，e 为截面形心到中性轴的距离，由图 12-2 可 知
e R0 r 将式（12-1）代入式（d），得
（12-3）
M y
E
(d) d
yz dA 0
A
由于 y 轴是横截面的对称轴，有
A
yz
dA
0
所以式（d）便自动满足了。
将式（12-1）代入式（e），得
M
y dA E (d)
若材料的许用拉、压力应分别为[1] 和[ y ]，则曲杆正应力强度条件为
lmax [l ] | ymax | [ y ]
一般来说，由剪力 FS 引起的剪应力很小，可以不予考虑。
例 12-2 起重机吊钩上的载荷 P 100 kN （见图 12-13）。截面 m n 的尺 寸为 b1 40 mm ， b2 60 mm ， h 140 mm ， R1 260 mm ， R2 120 mm 。材 料的许用应力[ ] 160 MPa 。试校核吊钩的强度。
力 FN 叠加，得出截面内侧边缘处的最大拉应力为 A
l
M (R2 r) SR2
FN A
143.5
100 103 7 000 106
MPa
158 MPa
截面外侧边缘处的最大压应力为
y
M (R1 r) SR1
FN A
97.6
100 103 7 000 106
MPa
83.3 MPa
或写为
E y (d) r y d
（b）
由于对任一横截面上的不同点来说，E (d) 及中性层的曲率半径 r 都是常数， d
所以各点的正应力 只与坐标 y 有关。式（b）表明 沿截面高度按双曲线规
律变化（见图 12-3）。
材料力学(I)答案课件
弯曲
材料在受到外力作用时，会发生 弯曲变形。弯曲变形是指材料在 平面内发生弯曲，而其轴线仍然 为直线。
弯曲的分类
根据弯曲形状的不同，可以分为 简支梁弯曲、悬臂梁弯曲和外伸 梁弯曲等。
弯曲的应力分布
在弯曲变形中，材料内部的应力 分布不均匀，最大应力出现在中 性轴附近，且方向垂直于中性轴 。
弯曲的应力分析
03
失效与断裂的关系
材料的失效和断裂是两个不同的概念，但它们之间存在一定的联系。材
料的失效可能是由于内部损伤或外部因素引起的，而断裂则是失效的一
种形式。
04
轴向拉伸与压缩
轴向拉伸与压缩的概念
轴向拉伸
物体在轴向受到拉伸力作用，产生伸 长变形。
轴向压缩
物体在轴向受到压缩力作用，产生缩 短变形。
轴向拉伸与压缩的应力分析
强度与塑性
强度
材料在受到外力作用时所能承受的最大应力 。
塑性
材料在受到外力作用时发生不可逆变形的性质。
强度与塑性的关系
材料的强度和塑性是相互关联的，强度高的 材料通常塑性也较好，但不同材料之间存在 差异。
材料的失效与断裂
01
失效
材料在受到外力作用时发生的变形或破坏。
02
断裂
材料在受到外力作用时发生的突然破裂或开裂。
剪切应力=剪切力/剪切面面积。
剪切应力的分布
03
剪切应力在剪切面上分布不均匀，最大剪切应力发生在剪切面
的边缘。
剪切的应变分析
剪切应变
是指物体在剪切力作用下发生的形状改变。
剪切应变的计算公式
剪切应变=剪切位移/原长。
剪切应变的影响因素
剪切力的大小和材料的性质影响剪切应变的 大小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章 绪论
1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴
线且大小均为M 的力偶作用。试问在杆件的任一横截面m-m何 种内力分量，并确定其大小。
x
Mx 解：（1）将杆沿mm切开，并选择切开后的左段为研究 对象。设
此时在截面m-m扭矩 Mx。 （2）根据右手法则及法线方向并由平衡方程可得:
规定x方向为正，分别在1、2、3处切开杆得：
AB段
▕
FN 1
FN1 2kN （压缩）
BC段 CD段 F N 3
FN 2 FN2 1kN （拉伸）
FN3 3kN （ 拉 伸 ）
最大拉应力
t,m axF 拉 A m ax50 3 1 1 0 0 3 6 N m 260M P a
最大压应力
c,m a xF 压 A m a x5 0 2 1 1 0 0 3 6 N m 24 0 M P a
解：1.问题分析
由于横截面上仅存在沿截面高度线
性分布的正应力，因此，在横截面上
不可能存在剪力与扭矩，且不可能存
在矢量沿坐标轴y的弯矩My,只存在轴
力FN和弯矩Mz。
2020/12/10
3
2.内力计算
方法一：以C点为原点建立坐标系
b
根据题意，设 kya代入数据得：
k109Pa/m a50106Pa
2020/12/10
9
45
0
45 解：杆件横截面上的正应力为 0F A N101 00 0 1 10 03N 6m 210M Pa
由于斜截面的方位角 450
得该斜截面上的正应力和切应力分别为
4 5 0 c o s 2 1 0 c o s 2 4 5 0 M P a 5 M P a
强度极限
b 445MPa
伸长率 ll10 % 0 ma x2% 8 由于 28，00故5该00材料属于塑性材料。
11
解：（1）由图得 弹性模量 E0 2.13011006 3700GPa 比例极限 p 230MPa
屈服极限 0.2 325MPa
………
A
…………
（2）当 350M Pa时
p
e
正应变 0 .7 6 1 0 3 0 .0 0 0 7 6
因此 (y)109y50106
A
则：
h
F N(y)d A A （ ky a ） d A -2 h(ky a )b d y2 0 0k N
A
2
z
h
M z(y)y d A 2 h(kya)yd A 3 .3 3k N m
A
2
2020/12/10
y
4
• 方法二
先计算分布力的合力，然后向形心平移，求出轴力 和弯矩
0s in 2 1 1 0 s in 9 0 0 M P a 5 M P a
4 5 2
2
2020/12/10
10
2020/12/10
b s
解：由题图可近似确定所求各量：
弹性模量 E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
屈服极限 s 240MPa
m-m
x
x
FN
轴力图
7
(b)以截面C 的形心为坐标原 点，沿杆建立坐标轴x。
x
2
1
B C 段，利用截面法得平衡方程：
FN1 qx0
FN1 qx
A B 段承受载荷的反作用力因此
FN 2
FN2 qa0
FN2 qa
因此： FN，maxqa
FN1
x
a
轴力图
2020/12/10
8
1
2 →x 3
AB C D
相应的弹性应变 e 0.00046塑性应变 p 0.0003
2020/12/10
12
解：根据题意及已知数据可知
延伸率
l0 1% 0 0 l1l0 1% 0 0 2.4 6 %
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 =26.4%5%故属于塑性材料。
2020/12/10
Fx 0
FN1-FN2co4s50
Fy 0
FN2si4n5-F0
得
FN1 F
FN2 2F
15
2.确定 d 与 b
由
=F 4F A d2
s
A1
d2
4
FN1
s
d
4FN1
s
20mm
取 d20mm
A2
b2
FN 2
b
FN2
84.1mm
取2020/12/10b84.1mmFN1 FN2
16
得截面m-m
M =0 Mx M0
Mx M
其真实方向与假设 的方向一致。
2020/12/10
1
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
n
α
解：应力p与斜截面m-m的法线的夹角 α=90 º-60 º- θ =10°， 故
13
解：求外径D 面积A 材料能安全使用则 材料的许用应力为
杆件上的正应力为
应力σ [σ]
= s
ns
F
A
4F D2 -d2
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
2020/12/10
14
2020/12/10
FN1 FN2
解：1. 轴力分析 设杆1轴向受拉，杆2轴向受压，其轴力分 别为 F N 1 和 F N 2 ，根据节点A的平衡方程：
F N 1 2 m a x b h 1 2 b h m a x 1 2 4 0 1 0 3 1 0 0 1 0 3 1 0 0 1 0 6 N 2 0 0 K N
而其作用点到坐标轴z轴的距离d h h
23
所以： M z F N h 2 h 3 1 6 F N h 3 .3 3 1 0 3N 3 .3 3 K N
2020/12/10
5
解：微元直角改变量称为切应变。
Aa
0
22
Ab222-2
2020/12/10
6
第二章 轴向拉伸与压缩
解：(a)以截面A的形心为坐标点，沿杆
建立坐标轴x。在x处将杆切开，得到平
衡方程： FN2qaqx0
F N2qaqxq(2ax)
因此，在x=0 时 FN,max 2qa
2020/12/10
FN1
p c o s 1 2 0 c o s 1 0 1 1 8 .2 M P a
p s in 1 2 0 s in 1 0 2 0 .8 M P a
2020/12/10
2
1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布， 截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正 应力均为零。试问杆件横截面上存在何种内力分量，并确定其 大小。图中之C点为截面形心。
1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴
线且大小均为M 的力偶作用。试问在杆件的任一横截面m-m何 种内力分量，并确定其大小。
x
Mx 解：（1）将杆沿mm切开，并选择切开后的左段为研究 对象。设
此时在截面m-m扭矩 Mx。 （2）根据右手法则及法线方向并由平衡方程可得:
规定x方向为正，分别在1、2、3处切开杆得：
AB段
▕
FN 1
FN1 2kN （压缩）
BC段 CD段 F N 3
FN 2 FN2 1kN （拉伸）
FN3 3kN （ 拉 伸 ）
最大拉应力
t,m axF 拉 A m ax50 3 1 1 0 0 3 6 N m 260M P a
最大压应力
c,m a xF 压 A m a x5 0 2 1 1 0 0 3 6 N m 24 0 M P a
解：1.问题分析
由于横截面上仅存在沿截面高度线
性分布的正应力，因此，在横截面上
不可能存在剪力与扭矩，且不可能存
在矢量沿坐标轴y的弯矩My,只存在轴
力FN和弯矩Mz。
2020/12/10
3
2.内力计算
方法一：以C点为原点建立坐标系
b
根据题意，设 kya代入数据得：
k109Pa/m a50106Pa
2020/12/10
9
45
0
45 解：杆件横截面上的正应力为 0F A N101 00 0 1 10 03N 6m 210M Pa
由于斜截面的方位角 450
得该斜截面上的正应力和切应力分别为
4 5 0 c o s 2 1 0 c o s 2 4 5 0 M P a 5 M P a
强度极限
b 445MPa
伸长率 ll10 % 0 ma x2% 8 由于 28，00故5该00材料属于塑性材料。
11
解：（1）由图得 弹性模量 E0 2.13011006 3700GPa 比例极限 p 230MPa
屈服极限 0.2 325MPa
………
A
…………
（2）当 350M Pa时
p
e
正应变 0 .7 6 1 0 3 0 .0 0 0 7 6
因此 (y)109y50106
A
则：
h
F N(y)d A A （ ky a ） d A -2 h(ky a )b d y2 0 0k N
A
2
z
h
M z(y)y d A 2 h(kya)yd A 3 .3 3k N m
A
2
2020/12/10
y
4
• 方法二
先计算分布力的合力，然后向形心平移，求出轴力 和弯矩
0s in 2 1 1 0 s in 9 0 0 M P a 5 M P a
4 5 2
2
2020/12/10
10
2020/12/10
b s
解：由题图可近似确定所求各量：
弹性模量 E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
屈服极限 s 240MPa
m-m
x
x
FN
轴力图
7
(b)以截面C 的形心为坐标原 点，沿杆建立坐标轴x。
x
2
1
B C 段，利用截面法得平衡方程：
FN1 qx0
FN1 qx
A B 段承受载荷的反作用力因此
FN 2
FN2 qa0
FN2 qa
因此： FN，maxqa
FN1
x
a
轴力图
2020/12/10
8
1
2 →x 3
AB C D
相应的弹性应变 e 0.00046塑性应变 p 0.0003
2020/12/10
12
解：根据题意及已知数据可知
延伸率
l0 1% 0 0 l1l0 1% 0 0 2.4 6 %
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 =26.4%5%故属于塑性材料。
2020/12/10
Fx 0
FN1-FN2co4s50
Fy 0
FN2si4n5-F0
得
FN1 F
FN2 2F
15
2.确定 d 与 b
由
=F 4F A d2
s
A1
d2
4
FN1
s
d
4FN1
s
20mm
取 d20mm
A2
b2
FN 2
b
FN2
84.1mm
取2020/12/10b84.1mmFN1 FN2
16
得截面m-m
M =0 Mx M0
Mx M
其真实方向与假设 的方向一致。
2020/12/10
1
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
n
α
解：应力p与斜截面m-m的法线的夹角 α=90 º-60 º- θ =10°， 故
13
解：求外径D 面积A 材料能安全使用则 材料的许用应力为
杆件上的正应力为
应力σ [σ]
= s
ns
F
A
4F D2 -d2
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
2020/12/10
14
2020/12/10
FN1 FN2
解：1. 轴力分析 设杆1轴向受拉，杆2轴向受压，其轴力分 别为 F N 1 和 F N 2 ，根据节点A的平衡方程：
F N 1 2 m a x b h 1 2 b h m a x 1 2 4 0 1 0 3 1 0 0 1 0 3 1 0 0 1 0 6 N 2 0 0 K N
而其作用点到坐标轴z轴的距离d h h
23
所以： M z F N h 2 h 3 1 6 F N h 3 .3 3 1 0 3N 3 .3 3 K N
2020/12/10
5
解：微元直角改变量称为切应变。
Aa
0
22
Ab222-2
2020/12/10
6
第二章 轴向拉伸与压缩
解：(a)以截面A的形心为坐标点，沿杆
建立坐标轴x。在x处将杆切开，得到平
衡方程： FN2qaqx0
F N2qaqxq(2ax)
因此，在x=0 时 FN,max 2qa
2020/12/10
FN1
p c o s 1 2 0 c o s 1 0 1 1 8 .2 M P a
p s in 1 2 0 s in 1 0 2 0 .8 M P a
2020/12/10
2
1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布， 截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正 应力均为零。试问杆件横截面上存在何种内力分量，并确定其 大小。图中之C点为截面形心。