计量经济学第六章课后作业
计量经济学课后答案第六章 自相关

第六章课后答案6.1(1)收入—消费模型为Se = (2.5043) (0.0075)t = (-3.7650) (125.3411)R2 = 0.9978,F = 15710.39,d f = 34,DW = 0.5234(2)对样本量为36、一个解释变量的模型、5%显著水平,查DW统计表可知,d L=1.411,d U= 1.525,模型中DW<d L,显然消费模型中有自相关。
(3)采用广义差分法查5%显著水平的DW统计表可知d L = 1.402,d U = 1.519,模型中DW= 2.0972>d U,说明广义差分模型中已无自相关。
同时,判定系数R2、t、F统计量均达到理想水平。
由差分方程式可以得出:所以最终的消费模型为:6.2(1)给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中不存在自相关。
(2)自相关可能由于模型6.1的误设,因为它排除了趋势的平方项。
(3)虚假自相关是由于模型的误设造成的,因此就要求对可能的函数形式有先验知识。
真正的自相关是可以通过广义差分法等方法来修正。
6.3(1)收入—消费模型为(2)DW=0.575,取,查DW上下界,说明误差项存在正自相关。
(3)采用广义差分法使用普通最小二乘法估计的估计值,得DW=1.830,已知,模型中因此,在广义差分模型中已无自相关。
由差分方程式可以得出:因此,修正后的回归模型应为6.4(1)回归结果如下:(2)模型检验:从回归结果可以看出,参数均显著,模型拟和较好。
异方差的检验:通过white检验可以得知模型不存在异方差。
DW检验:给定n=25, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
(3)采用广义差分法修正模型中存在的自相关问题:给定n=24,,在的显著水平下,查DW统计表可知,。
计量经济学第六章部分课后题(庞皓(第三版))

计量经济学第六章作业思考题:6.1 如何使用DW统计量来进行自相关检验?该检验方法的前提条件和局限性有哪些?答:(1)DW 检验是J.Durbin(杜宾)和G.S.Watson(沃特森)于1951年提出的一种适用于样本容量大于等于15的检验自相关的方法,许多计量经济学和统计学计算机软件都可以计算出DW 值。
给定显著水平α,依据样本容量n和解释变量个数k’(不包括常数项),查D.W.分布表可得临界值(d统计量的上界d U和下界d L),当0<DW<d L时,表明存在一阶正自相关,而且正自相关的程度随DW向0的靠近而增强。
当d L<DW<d U时,表明为不能确定是否存在自相关。
当d U<DW<4-d U时,表明不存在一阶自相关。
当4-d U<DW<4-d L时,表明不能确定是否存在自相关。
当4-d L<DW<4时,表明存在一阶负自相关,而且负自相关的程度随DW向4的靠近而增强。
(2)DW检验的前提条件:<1>解释变量是非随机的(因此与随机扰动项不相关);<2>随机扰动项是一阶自回归形式,即u t=ρu t-1 +v t (v t满足古典假定);<3>线性模型的解释变量中不包含滞后的被解释变量,如不应出现下列形式:Y t =β1 +β2 X t +β 3 Y t-1 +u t;<4>截距项不为零,即只适用于有常数项的回归模型;<5>数据序列无缺失项,样本比较大。
(3)DW检验的局限性:<1>DW检验有两个不能确定的区域,一旦DW值落在这两个区域,就无法判断。
这时,只有增大样本容量或选取其他方法;<2>DW统计量的上、下界表要求n≥15, 这是因为样本如果再小,利用残差就很难对自相关的存在性做出比较正确的诊断;<3> DW检验不适应随机误差项具有高阶序列相关的检验;<4> DW检验有运用的前提条件,只有符合这些条件DW检验才是有效的。
新《计量经济学》第6章 计量练习题

《计量经济学》第6章习题一、单项选择题1.当模型存在严重的多重共线性时,OLS 估计量将不具备( ) A .线性 B .无偏性 C .有效性 D .一致性2.如果每两个解释变量的简单相关系数比较高,大于( )时则可认为存在着较严重的多重共线性。
A .0.5B .0.6C .0.7D .0.83.方差扩大因子VIF j 可用来度量多重共线性的严重程度,经验表明,VIF j ( )时,说明解释变量与其余解释变量间有严重的多重共线性。
A .小于5B .大于1C .小于1D .大于104.对于模型01122i i i i Y X X u βββ=+++,与r 23等于0相比,当r 23等于0.5时,3ˆβ的方差将是原来的( )A .2倍B .1.5倍C .1.33倍D .1.25倍 5.无多重共线性假定是假定各解释变量之间不存在( )A .线性关系B .非线性关系C .自相关D .异方差 二、多项选择题1.多重共线性包括( )A .完全的多重共线性B .不完全的多重共线性C .解释变量间精确的线性关系D .解释变量间近似的线性关系E .非线性关系2.多重共线性产生的经济背景主要由( )A .经济变量之间具有共同变化趋势B .模型中包含滞后变量C .采用截面数据D .样本数据自身的原因E .模型设定误差 3.多重共线性检验的方法包括( )A .简单相关系数检验法B .方差扩大因子法C .直观判断法D .逐步回归法E .DW 检验法 4.修正多重共线性的经验方法包括( ) A .剔除变量法 B .增大样本容量C .变换模型形式D .截面数据与时间序列数据并用E .变量变换 5.严重的多重共线性常常会出现下列情形( ) A .适用OLS 得到的回归参数估计值不稳定 B .回归系数的方差增大C .回归方程高度显著的情况下,有些回归系数通不过显著性检验D .回归系数的正负号得不到合理的经济解释E .预测精度降低一、单项选择题1.C2.D3.D4.C5.A 二、多项选择题1.AB2.ABCD3.ABCD4.ABCDE5.ABCDE三、简答题1.什么是多重共线性?产生多重共线性的经济背景是什么?所谓多重共线性(Multicollinearity )是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。
第六章计量经济学

第六章 虚拟变量的回归模型第一部分 学习目标和要求本章主要介绍虚拟变量的基本概念及其应用。
需要掌握并理解以下内容:(1) 虚拟变量的基本概念、虚拟变量分别作为解释变量和被解释变量的情形、虚拟变量回归模型的类型和解释变量个数选取规则; (2) 定量变量与不同数量定性变量(一对一、一对多和多对多)虚拟变量模型; (3) 应用虚拟变量改变回归直线的截距或斜率; (4) 分段线性回归;(5) 应用虚拟变量检验回归模型的结构稳定性、传统判别结构稳定性的方法及存在的缺陷、虚拟变量法比较两个回归方程的结构方法。
第二部分 练习题一、解释下列概念:1.虚拟变量2.方差分析模型(ANOV A ) 3.协方差模型(ANOCV A ) 4.基底5.级差截距系数 6.虚拟变量陷阱二、简要回答下列问题:1.虚拟变量在线性回归模型中的作用是什么?举例说明。
2.回归模型中虚拟变量个数的选取原则是什么?为什么?3.如果现在有月度数据,在对下面的假设进行检验时,你将引入几个虚拟变量? A) 一年中的每月均呈现季节性波动趋势;B) 只有双数月份呈现季节性波动趋势。
4.如果现在让你着手检验上海和深圳两个股票市场在过去5年内的收益率是否有显著差异,如何使用虚拟变量进行?三、考虑如下模型:12i i i Y D u ββ=++其中,i D 对前20个观察值取0,对后30个观察值取1。
已知2()300i Var u =。
(1) 如何解释1β和2β? (2) 这两组的均值分别是多少?(3) 已知12()15Cov ββ∧∧+=-。
如何计算12()ββ∧∧+的方差?四、考虑如下模型:12i i i i Y D X u ααβ=+++ 其中Y 代表一位大学教授的年薪; X 为从教年限; D 为性别虚拟变量。
考虑定义虚拟变量的三种方式:(1)D 对男性取值1,对女性取值0; (2)D 对女性取值1,对男性取值2; (3)D 对女性取值1,对男性取值-1;对每种虚拟变量定义解释上述回归模型。
伍德里奇---计量经济学第6章部分计算机习题详解(STATA)
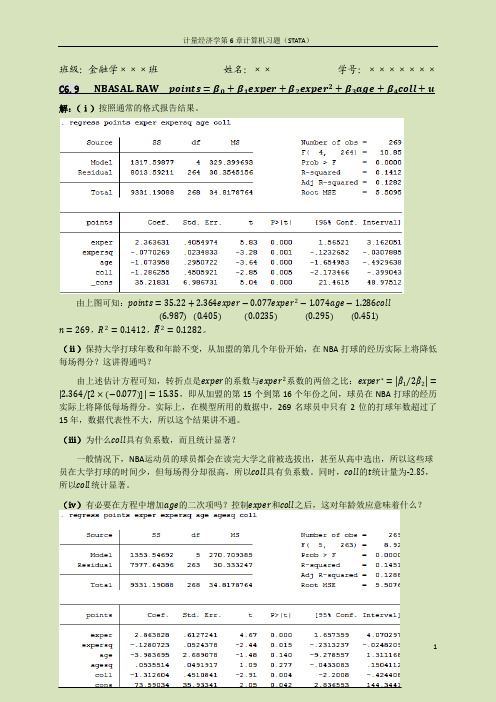
班级:金融学×××班姓名:××学号:×××××××C6.9 NBASAL.RAW points=β0+β1exper+β2exper2+β3age+β4coll+u 解:(ⅰ)按照通常的格式报告结果。
由上图可知:points=35.22+2.364exper−0.077exper2−1.074age−1.286coll6.9870.4050.02350.295 (0.451)n=269,R2=0.1412,R2=0.1282。
(ⅱ)保持大学打球年数和年龄不变,从加盟的第几个年份开始,在NBA打球的经历实际上将降低每场得分?这讲得通吗?由上述估计方程可知,转折点是exper的系数与exper2系数的两倍之比:exper∗= β12β2= 2.364[2×−0.077]=15.35,即从加盟的第15个到第16个年份之间,球员在NBA打球的经历实际上将降低每场得分。
实际上,在模型所用的数据中,269名球员中只有2位的打球年数超过了15年,数据代表性不大,所以这个结果讲不通。
(ⅲ)为什么coll具有负系数,而且统计显著?一般情况下,NBA运动员的球员都会在读完大学之前被选拔出,甚至从高中选出,所以这些球员在大学打球的时间少,但每场得分却很高,所以coll具有负系数。
同时,coll的t统计量为-2.85,所以coll统计显著。
(ⅳ)有必要在方程中增加age的二次项吗?控制exper和coll之后,这对年龄效应意味着什么?增加age的二次项后,原估计模型变成:points=73.59+2.864exper−0.128exper2−3.984age+0.054age2−1.313coll35.930.610.05 2.690.05 (0.45)n=269,R2=0.1451,R2=0.1288。
计量经济学练习题答案(第六章)
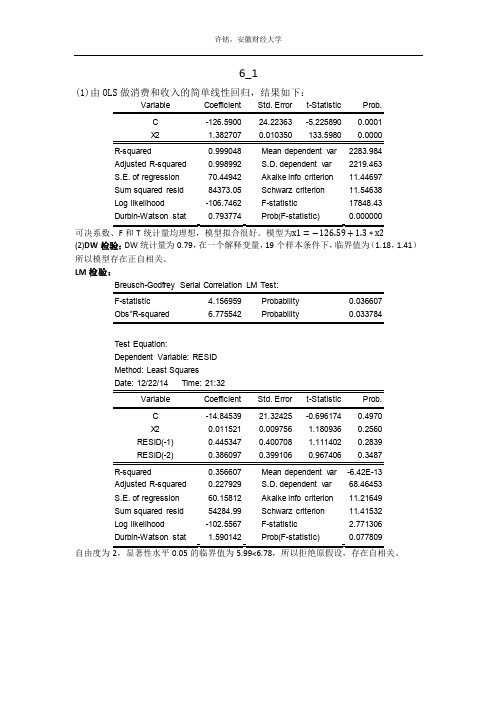
6_1(1)由OLS做消费和收入的简单线性回归,结果如下:Variable Coefficient Std. Error t-Statistic Prob.C -126.5900 24.22363 -5.225890 0.0001R-squared 0.999048 Mean dependent var 2283.984Adjusted R-squared 0.998992 S.D. dependent var 2219.463S.E. of regression 70.44942 Akaike info criterion 11.44697Sum squared resid 84373.05 Schwarz criterion 11.54638Log likelihood -106.7462 F-statistic 17848.43Durbin-Watson stat 0.793774 Prob(F-statistic) 0.000000可决系数、F和T统计量均理想,模型拟合很好。
模型为x1=−126.59+1.3∗x2(2)DW检验:DW统计量为0.79,在一个解释变量,19个样本条件下,临界值为(1.18,1.41)所以模型存在正自相关。
LM检验:F-statistic 4.156959 Probability 0.036607Test Equation:Dependent Variable: RESIDMethod: Least SquaresDate: 12/22/14 Time: 21:32C -14.84539 21.32425 -0.696174 0.4970X2 0.011521 0.009756 1.180936 0.2560RESID(-1) 0.445347 0.400708 1.111402 0.2839RESID(-2) 0.386097 0.399106 0.967406 0.3487R-squared 0.356607 Mean dependent var -6.42E-13Adjusted R-squared 0.227929 S.D. dependent var 68.46453S.E. of regression 60.15812 Akaike info criterion 11.21649Sum squared resid 54284.99 Schwarz criterion 11.41532Log likelihood -102.5567 F-statistic 2.771306Durbin-Watson stat 1.590142 Prob(F-statistic) 0.077809自由度为自相关分析:解释变量和被解释变量有显著二阶自相关。
安徽财经大学计量经济学 第六章练习题及参考解答
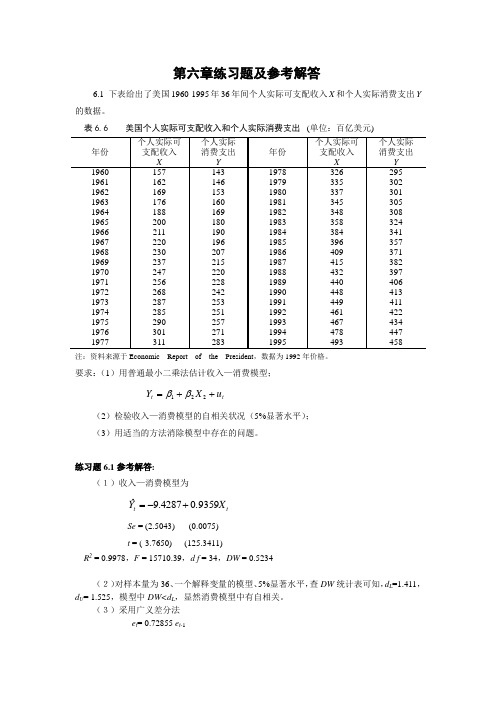
第六章练习题及参考解答6.1 下表给出了美国1960-1995年36年间个人实际可支配收入X 和个人实际消费支出Y 的数据。
表6.6 美国个人实际可支配收入和个人实际消费支出 (单位:百亿美元)注:资料来源于Economic Report of the President ,数据为1992年价格。
要求:(1)用普通最小二乘法估计收入—消费模型;t t u X Y ++=221ββ(2)检验收入—消费模型的自相关状况(5%显著水平); (3)用适当的方法消除模型中存在的问题。
练习题6.1参考解答:(1)收入—消费模型为 tt X Y 0.93594287.9ˆ+-=Se = (2.5043) (0.0075)t = (-3.7650) (125.3411)R 2 = 0.9978,F = 15710.39,d f = 34,DW = 0.5234(2)对样本量为36、一个解释变量的模型、5%显著水平,查DW 统计表可知,d L =1.411,d U = 1.525,模型中DW<d L ,显然消费模型中有自相关。
(3)采用广义差分法e t = 0.72855 e t-1**9484.07831.3ˆtt X Y +-=)8710.1(=Se (0.0189)t = (-2.0220) (50.1682)R 2 = 0.9871 F = 2516.848 d f = 33 DW = 2.0972查5%显著水平的DW 统计表可知d L = 1.402,d U = 1.519,模型中DW = 2.0972> d U ,说明广义差分模型中已无自相关。
同时,可决系数R 2、t 、F 统计量均达到理想水平。
9366137285501783131...ˆ=--=β最终的消费模型为 Y t = 13.9366+0.9484 X t6.2 在研究生产中劳动所占份额的问题时,古扎拉蒂采用如下模型模型1 t t u t Y ++=10αα模型2 t t u t t Y +++=2210ααα其中,Y 为劳动投入,t 为时间。
计量经济学第六章课后作业.doc
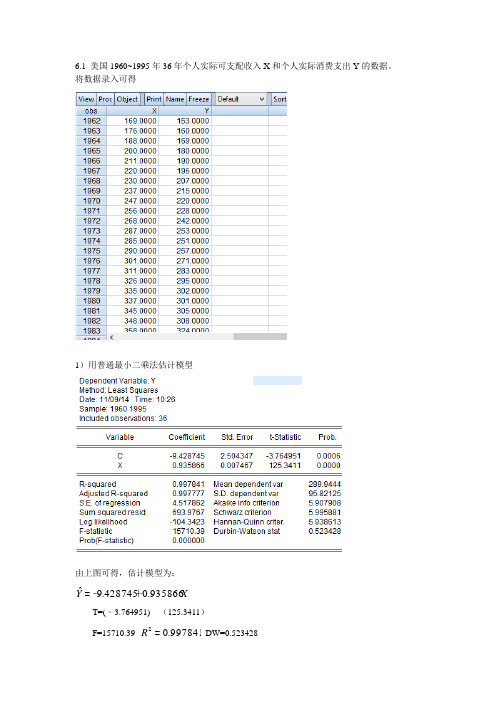
6.1 美国1960~1995年36年个人实际可支配收入X 和个人实际消费支出Y 的数据。
将数据录入可得1)用普通最小二乘法估计模型由上图可得,估计模型为:X Y 935866.0428745.9ˆ+﹣=T=(﹣3.764951) (125.3411)F=15710.39 997841.02=R DW=0.5234282)检验自相关问题-------DW 检验根据DW=0.523428<411.1=L d ,可知此回归模型中误差项1μ,2μ......n μ间存在正相关关系。
3)用适当的方法消除模型中的问题----------广义差分法 首先得到t e 和1-t e 的回归结果。
如下图所示:由上图回归结果可知,回归方程为1721594.0ˆ﹣t t e e =故721594.0ρˆ=,对原模型进行广义差分,得到广义差分方差为 t t t t t X X Y Y υβ721594.01β1211)+-()+-(---= 对广义差分方程进行回归,。
可得以下回归结果:可得回归方程为:••=t t X Y 948215.0858791.3ˆ+﹣Se= (1.868548) (0.018453)t= (﹣2.065129) (51.38528)987656.02=R F=2640.445 DW=2.082177通过查表可知DW=1.255999>1.195,故可以判断不存在自相关关系。
画出t e 和1-t e 的散点图由图形可知,随机误差项之间不存在相关性。
6.3北京市连续19年城镇居民家庭人均收入与人均支出的数据1)为了消除价格变动因素对城镇居民人均收入和人均支出的影响,不宜直接采用现价的人均纯收入和现价的人均消费支出的数据,而需要采用经消费价格指数进行调整后的基期的可比价格计的人均纯收入和人居消费支出的数据作回归分析。
根据表中的数据,使用普通最小二乘法估计消费模型得:根据上图分析结果可知:21690488.093004.79ˆX X += Se= (12.39919) (0.012877) t= (6.446390) (53.62068)994122.02=R 178.2875=F 574663.0=DW该方程的可决系数较高,回归系数显著,对于样本容量为19、一个解释变量的模型、1%的显著性水平,查DW 统计表可得,928.0=L d ,132.1=U d ,模型中DW<928.0=L d ,显然模型中存在自相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1 美国1960~1995年36年个人实际可支配收入X 和个人实际消费支出Y 的数据。
将数据录入可得
1)用普通最小二乘法估计模型
由上图可得,估计模型为:
X Y 935866.0428745.9ˆ+﹣=
T=(﹣3.764951) (125.3411)
F=15710.39 997841.02
=R DW=0.523428
2)检验自相关问题-------DW 检验
根据DW=0.523428<411.1=L d ,可知此回归模型中误差项1μ,2μ......n μ间存在正相关关系。
3)用适当的方法消除模型中的问题----------广义差分法 首先得到t e 和1-t e 的回归结果。
如下图所示:
由上图回归结果可知,回归方程为
1721594.0ˆ﹣t t e e =
故721594.0ρ
ˆ=,对原模型进行广义差分,得到广义差分方差为 t t t t t X X Y Y υβ721594.01β1211)+-()+-(---=
对广义差分方程进行回归,。
可得以下回归结果:
可得回归方程为:
••=t t X Y 948215.0858791.3ˆ+﹣
Se= (1.868548) (0.018453)
t= (﹣2.065129) (51.38528)
987656.02=R F=2640.445 DW=2.082177
通过查表可知DW=1.255999>1.195,故可以判断不存在自相关关系。
画出t e 和1-t e 的散点图
由图形可知,随机误差项之间不存在相关性。
6.3北京市连续19年城镇居民家庭人均收入与人均支出的数据
1)为了消除价格变动因素对城镇居民人均收入和人均支出的影响,不宜直接采用现价的人均纯收入和现价的人均消费支出的数据,而需要采用经消费价格指数进行调整后的基期的可比价格计的人均纯收入和人居消费支出的数据作回归分析。
根据表中的数据,使用普通最小二乘法估计消费模型得:
根据上图分析结果可知:
2
1690488.093004.79ˆX X += Se= (12.39919) (0.012877) t= (6.446390) (53.62068)
994122.02=R 178.2875=F 574663.0=DW
该方程的可决系数较高,回归系数显著,对于样本容量为19、一个解释变量的模型、1%的显著性水平,查DW 统计表可得,928.0=L d ,132.1=U d ,模型中DW<928.0=L d ,
显然模型中存在自相关。
喝一点也可以从残差图中可以看出。
如图所示,残差的变化有系统模式,连续为正和连续为负,表明残差项存在一阶正自相关。
故需要对模型进行改进。
2)自相关问题的补救--------广义差分法
如图所示,可得回归方程:1657352.0ˆ﹣t t e e
=。
则可得自相关系数657352.0ρˆ= 对原模型进行广义差分,得到广义差分方程为:
t t t t t X X Y Y υ657352.0β657352.01β657352.01-211-)+-()+-(-=
(此处t Y 为X1,1-t Y 代表X1的滞后一期;t X 代表X2,1-t X 代表X2的滞后一期。
)
对广义差分方程进行回归,可得如下图所示:
如上图所示:可得回归方程为:
••=2
1174038.077625.11ˆX X + Se= (21.66267) (0.013289) T= (0.543620) (13.09619)
F=171.5102 914671.02
=R DW=1.504466
在显著性水平为1%的情况下,通过查DW 统计表可以知道,902.0=L d ,118.1=U d ,由于DW=1.504466>118.1=U d ,故可知修改后的模型中的随机误差项已不存在自相关关系。
3)对模型进行经济意义的解释: 根据调整后的回归模型可得,当去除价格变动因素的影响的情况下,每增加一个单位的收入,消费支出就会增加0.174038个单位。
6.4日本工薪家庭实际消费支出与可支配收入数据(部分截图)
1)建立日本工薪家庭的收入--消费函数
利用普通最小二乘法进行回归,可得如下图所示:
由上图回归结果可得回归方程为:
X Y
637437.087454.50ˆ+= )021242.0)(291058.8(=Se )00846.30)(136073.6(=t
975095.02=R 5078.900=F 35276
2.0=DW 该方程的可决系数较高,回归系数均显著。
对样本为25,一个解释变量模型,1%显著性水平,查DW 统计表可得055.1=L d ,211.1=U d 又因为352762.0=DW <055.1=L d ,故此模型的随机误差项之间存在自相关关系。
由残差图可知,图形系统变动,连续为正和连续为负,故可知存在正自相关关系。
残差图如下:
2)自相关问题的解决---------广义差分法
由上图回归结果可得回归方程为:
1-850961.0ˆt t e e
= 则自相关系数的估计值为850961.0ρˆ= 则对原模型进行广义差分,可得广义差分方程为:
t t t t t X X Y Y υ850961.0β850961.0-1β850961.01211-)+-()+(-﹣=
对广义差分方程进行回归,可得如下图所示:
由上图的回归结果可得回顾方程如下:
••=t
t X Y 535125.097334.13ˆ+ 699417.02=R 19110.51=F 377660.2=DW
此时样本为24,解释变量为1,在1%的显著性水平的情况下,查DW 统计表可得
037.1=L d 199.1=U d 。
又因为DW>199.1=U d ,则可知利用广义差分法调整后的回归
模型中的随机误差项之间已经不存在自相关关系。
3)经济意义的解释
日本工薪家庭的实际可支配收入每增加一个单位,则其个人实际消费支出就会增加0.535125个单位。
6.5某地区1980~2000年的地区生产总值(Y )与固定资产投资额(X )的数据
1)由题意可知,对原数据进行取对数变换。
后利用OLS 进行回归分析,并检验其自相关性。
回归结果如下图所示:
由回归结果可得回归方程为:
t t
X Y 953107.0160588.2ˆ+= Se= (0.242884)(0.039211) T= (8.895563)(24.30694)
968844.02=R 8272.590=F 181802.1=DW
该模型回归系数显著,样本为21,解释变量为1,5%显著性水平下,查DW 统计表可得
221.1=L d 420.1=U d 又因为181802.1=DW <221.1=L d ,故此模型中随机误差项之
间存在自相关关系。
2)采用广义差分法处理自相关问题
由回归结果可知回归方程为:
1-388201.0ˆt t e e
= 故自相关系数的估计值为388201.0ρˆ=,对原模型进行广义差分变换。
可得广义差分方程为:
t t t t t X LNX LNY Y LN υLN -β388201.0-1β388201.0ˆ1-211-)+()+(-=
对广义差分方程进行回归分析,可得:
又回归结果可得回归方程为:
••=t
t LNX Y LN 909178.0495437.1ˆ+ 又因为此时样本容量为20,在5%的显著性水平下,查得DW 统计表,可得411.1=U d <DW=1.499525,故可知模型中已经不存在自相关关系。
3)由题意可得
此模型的样本为20,解释变量为1,1%显著性水平下查DW 统计表,可得952.0=L d 147.1=U d ,因为DW=1.195153>147.1=U d ,故此模型中随机误差项之间不
存在自相关关系。
在5%显著性水平下,201.1=L d 411.1=U d ,又因为DW=1.195153>201.1=L d ,故此时此模型中随机误差项之间存在自相关关系。
从残差图中可以看出,残差图形呈现规律变动,连续上升和连续下降,故可以看出此模型中随机误差项之间存在不显著的自相关关系。
可用广义差分法进行修正。
修正具体过程参照以上题目的解法,此处省略。
计量经济学作业
-------------------第六章课后习题
姓名:李曼丽
专业:统计学
班级:统计一班
学号:20121701310013
完成时间:2014年11月10日。
