离散时间信号与系统
信号与系统-离散时间域分析
滤波器性能评估
分析滤波器的幅频响应、 相频响应、群延迟等性能 指标，以评估滤波器的性 能。
数字调制与解调技术
ASK调制与解调
通过改变载波的振幅来 传递数字信息，实现 ASK调制，并通过相干 或非相干解调方法恢复 原始信号。
FSK调制与解调
利用不同频率的载波表 示不同的数字信息，实 现FSK调制，通过鉴频 器或锁相环等实现FSK 信号的解调。
分类
根据信号的性质和特征，离散时间信 号可分为周期信号和非周期信号、确 定信号和随机信号等。
离散时间系统定义及性质
定义
离散时间系统是一种对离散时间输入 信号进行变换或处理的系统，其输出 也是离散时间信号。
性质
离散时间系统具有线性、时不变性、 因果性、稳定性等性质，这些性质对 于系统的分析和设计具有重要意义。
离散时间信号处理重要性
数字信号处理基础
理论分析基础
离散时间信号处理是数字信号处理的 基础，对于数字通信、音频视频处理、 雷达声呐等领域具有重要意义。
离散时间信号和系统分析的理论和方法 可以推广到连续时间信号和系统，为信 号处理和分析提供统一的理论框架。
计算机处理方便
离散时间信号适合计算机处理，可以 通过算法实现各种复杂的信号处理和 变换。
06 实验：离散时间信号处理 实践
实验目的和要求
理解和掌握离散时间 信号的基本概念和性 质
培养实验操作能力和 分析解决问题的能力
熟悉离散时间信号的 处理方法和实现过程
实验内容和步骤
01
实验内容
02
生成离散时间信号
对信号进行基本运算（如加减、乘除、平移、翻转等）
03
实验内容和步骤
01
对信号进行频谱分析，观察信号 的频谱特性
离散时间信号和系统理论知识介绍
离散时间信号和系统理论知识介绍离散时间信号和系统理论是信号与系统理论领域的重要分支，用于描述和分析在离散时间点上的信号及其相应的系统行为。
离散时间信号是在离散时间集合上定义的函数，通常由离散采样得到。
离散时间系统则是对输入离散时间信号进行操作和处理得到输出信号的过程。
离散时间信号是时间的一个离散序列，可以通过对连续时间信号进行采样得到。
最常见的离散时间信号是离散时间单位脉冲信号，其在一个时间点的值为1，其他时间点的值为0。
其他常见的离散时间信号包括阶跃信号、正弦信号、方波信号等。
每个离散时间信号都有其特定的频谱和幅度特性。
离散时间系统是对离散时间信号进行处理和操作的载体。
离散时间系统可以是线性系统或非线性系统。
线性系统可以通过线性时不变（LTI）系统模型来描述，即系统的输入和输出之间存在线性时不变关系。
LTI系统可以用巴特沃斯（Bartow）方程式或其它传输方程式来表示，并可以通过离散时间卷积来分析系统的响应。
非线性系统则不满足线性性质的要求，其描述和分析方法更为复杂。
离散时间信号和系统理论的基本概念包括线性性、时不变性、因果性和稳定性等。
线性性要求系统对输入信号的加法性和乘法性具有反应；时不变性要求系统的性质不随时间变化而改变；因果性要求系统的响应仅依赖于过去和当前的输入信号；稳定性要求系统的输出有界且有限。
离散时间信号和系统的分析方法包括时域分析和频域分析。
时域分析主要关注信号和系统在时间域上的行为，如脉冲响应、单位样本响应、单位阶跃响应等；频域分析则关注信号和系统在频域上的特性，如频谱分析、频率响应等。
离散时间信号和系统在实际应用中有广泛的应用。
例如，它们可以用于数字音频处理、数字图像处理、通信系统、控制系统等领域中。
在这些应用中，离散时间信号和系统的理论方法可以帮助我们分析和设计系统，优化信号处理算法，并提高系统的性能。
总而言之，离散时间信号和系统理论是信号与系统理论中重要的一部分，用于描述和分析离散时间信号和系统的特性。
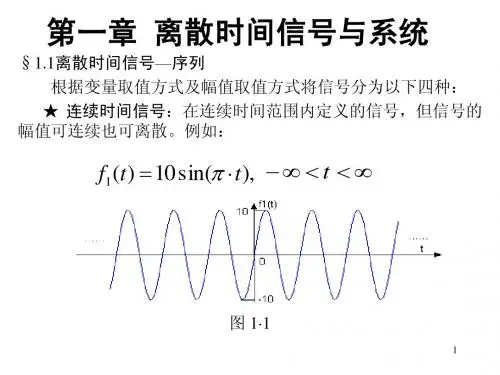
第一章 离散时间信号与系统
k =−∞
∑ δ (k )
n
u (n )
1
1
1
1 L n
-1
0
1
2
3
单位阶跃序列示意图
3. 矩形序列
• 矩形序列又称门函数序列，定义如下：
1 (0 ≤ n ≤ N −1) Rn (n) = 0 (n < 0 orn ≥ N) = u(n) −u(n − n0 )
R (n )
k
1
1
1
1
卷积和计算的步骤
•置换： z(n) →z(m) •翻转：x(m) ，z(m) →z(-m) 翻转： • 移位：z(-m) → z(n-m) 移位： •相乘：z(n-m) • x(m) （m值相同） 相乘： 相加： =∑ • 相加：y(n) =∑{z(n-m) • x(m)}
图解法举例
• 设两离散信号如图，求卷积和
四、用单位抽样序列表示 任意序列
• 任意序列都可以表示成单位抽样序列的加 ∞ 权和。 x(n) = ∑ x(m)δ (n − m)
m = −∞
x ( n) x(n)δ (n − m) = 0
m=n 其他
五、序列的能量
• 序列的能量为：序列各序列值的平方和：
∞
E=
n = −∞
∑ x ( n)
L
-1 0 1 2 k −1 k n
矩形序列示意图
4. 斜变序列
单位斜变序列R(n)可以看成是单位斜变信号 R(t)的抽样信号，如下图所示，表示为：
n R (n) = nu ( n) = 0
n
0
n<0
R (n) 2 1
3
L n -1 0 1 2 3
离散时间信号与系统
若要
2
2 若要 为有理数（N/k），则： T0 2 N NT k T
为整数，T0应为T的整数倍；
kT 0
即N个抽样间隔应等于连续正弦信号的k 个周期.
25
四、序列的能量 x(n)的能量定义为序列各样本的平方和，即：
E
n
x ( n)
2
26
1.3
连续时间信号的采样
采样器可以看成是一个电子开关，开关每隔T秒闭
合一次，（理想采样闭合时间无穷短，实际采样闭
合时间τ秒，）对输入信号进行采样。
采样过程可以看成脉冲调幅， xa(t)为调制信号，被 调脉冲载波是周期为T的周期性脉冲串。当脉冲宽 度为τ时，实际采样，τ→0时，理想采样。
29
实际采样：
T
p(t)为脉冲 序列 …
n
a为实数，当
a 1时, 收敛 a 1时, 发散
17
5.复指数序列 complex exponent sequence
① 实、虚部
x(n) Ae
( j ) n
x(n) Ae jn
为数字域频率。
② 极坐标
x(n) Ae jn | x(n) | e j arg[ x ( n)]
X a ( j) xa (t )e
jt
dt
33
s (t )
n
(t nT )
s (t ) Ak e jk s t
周期函数
利用傅立叶级数展开，可得：
k
s=2/T，s称为采样角频率 fs=1/T，fs为采样频率
1 T2 其中： Ak T s (t )e jk s t dt T 2 1 T2 T (t nT )e jk s t dt T 2 n 1 T2 1 jk s t T (t )e dt 2 T T
第1章 离散时间信号和系统
第1章 思考题参考解答1．变化规律已知的信号称之为确定信号，反之，变化规律不确定的信号称之为随机信号。
以固定常数周期变化的信号称之为周期信号，否则称之为非周期信号。
函数随时间连续变化的信号称之为连续时间信号，也称之为模拟信号。
自变量取离散值变化的信号称之为离散时间信号。
离散信号幅值按照一定精度要求量化后所得信号称之为数字信号。
2．对于最高频率为f c 的非周期信号，选取f s ＝2f c 可以从采样点恢复原来的连续信号。
而对于最高频率为f c 的非周期信号，选取f s ＝2f c 一般不能从采样点恢复原来的连续信号的周期信号，通常采用远高于2f c 的采样频率才能从采样点恢复原来的周期连续信号。
3．被采样信号如果含有折叠频率以上的高频成分，或者含有干扰噪声，这些频率成分将不满足采样恢复定理的条件，必然产生频率混叠，导致无法恢复被采样信号。
4．线性时不变系统的单位脉冲响应h (n )满足n <0，h (n )=0，则系统是因果的。
若∞<=∑∞-∞=P n h n |)(|，则系统是稳定的。
5．ω表示数字角频率，Ω表示模拟角频率。
ω=ΩT (T 表示采样周期)。
6．不一定。
只有当周期信号的采样序列满足x (n )= x (n +N )时，才构成一个周期序列。
7．常系数差分方程描述的系统若满足叠加原理，则一定是线性时不变系统。
否则，常系数差分方程描述的系统不是线性时不变系统。
8．该说法错误。
需要增加采样和量化两道工序。
9．受采样频率、有限字长效应的约束，与模拟信号处理系统完全等效的数字系统不一定找得到。
因此，数字信号处理系统的分析方法是先对采样信号及系统进行分析，再考虑幅度量化及实现过程中有限字长效应所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
10、只有当系统是线性时不变时，有y (n )= h (n )*x (n )。
11、时域采样在频域产生周期延拓效应。
12．输入信号x a (t )先通过一个前置低通模拟滤波器限制其最高频率在一定数值之内，使其满足采样频率定理的条件。
第一章 离散时间信号与系统1
根据定义
n y ( n ) 1 ( 1 ) k , n 1 2 2 k 1 y ( n) 0, n 1
14
我们计算几个值，画出图形。显然，
n 2 n 1 n0 n 1 n2
y(2) 0
1 3 2 2 3 1 7 y(1) y(0) x(1) 2 4 4 7 1 15 y(2) y(1) x(2) 4 8 8
j 0 n
0 ：复正弦的数字域频率 用欧拉公式将复指数序列展开： n n n x(n) e (cos0 n j sin 0 n) e cos0 n j e sin 0 n
用极坐标表示 其中 x(n)
x(n) x (n)
n
e
j arg[ x ( n )]
f2 (t )
0 1 1 0
, t 1 , 1 t 1 , 1 t 3 , t 3
定义域是连续的（-∞，∞），但是函数值只取-1，0，1三个离 散的值。（在间断点-1，1，3处一般不定义其函数值） f 以上两例中，1 (t ) 我们也称为模拟信号。
8
2 n , n 1 1 1 1 1 z (n) x(n) y(n) 2 ( 2 ) 2 3 , n 1 2 1 1 n 2 ( 2 ) n 1, n 0
图 1· 9 在求序列的和的时候要注意：相同序列 (n) 的序列值相加。
9
4．积（相乘） 两序列的积指相同序号 (n) 的序列值逐项对应相乘： z (n) x(n) y(n) 0.5, n 1 1.5, n 0 例1.1.4已知序列 x(n) = 1, n 1 求 y(n) x(n) 2 x(n) x(n 2) 0.5, n 2 0, n为其它值
离散时间信号与系统教程
离散时间信号与系统教程离散时间信号与系统教程离散时间信号与系统是数字信号处理领域中的重要内容之一。
离散时间信号是在离散时间点上取值的信号，而离散时间系统则是对这些信号进行处理和变换的设备或算法。
本文将介绍离散时间信号与系统的基本概念、性质以及常用的变换方法和应用。
一、离散时间信号离散时间信号是在离散时间点上取值的函数，离散时间点一般用整数表示。
例如，对于一个音频信号，可以按照每秒采集多少个样本来表示离散时间点。
离散时间信号可以表示为x(n)，其中n为离散时间点。
离散时间信号有许多重要的性质，例如周期性、能量与功率、线性性等。
周期性是指信号具有重复的特征，可以表示为x(n)=x(n+N)，其中N为周期。
能量与功率是用来描述信号的能量和功率大小的，能量表示信号的总能量，功率表示单位时间内信号的平均功率。
线性性是指信号满足线性叠加原理，即若有两个信号x1(n)和x2(n)，则对应的线性组合也是一个信号。
二、离散时间系统离散时间系统是对离散时间信号进行处理和变换的设备或算法。
离散时间系统可以表示为y(n)=T[x(n)]，其中T为系统的变换操作。
常见的离散时间系统有线性时不变系统(LTI系统)、卷积系统和差分方程系统等。
LTI系统是指具有线性性和时不变性的系统，线性性表示系统满足线性叠加原理，时不变性表示系统的输入与输出之间的关系不随时间变化。
卷积系统是通过卷积操作实现信号的处理和变换的系统，可以将输入信号与系统的冲击响应进行卷积运算得到输出信号。
差分方程系统是通过差分方程描述系统的输入与输出之间的关系，可以通过求解差分方程得到输出信号。
三、离散时间变换离散时间变换是将离散时间信号从一个表示域转换到另一个表示域的方法。
常见的离散时间变换有傅里叶变换、Z变换和小波变换等。
傅里叶变换是将离散时间信号从时间域转换到频率域的方法，可以将信号分解成一系列不同频率的正弦和余弦波的叠加。
Z变换是将离散时间信号从时间域转换到复平面的方法，可以得到离散时间系统的频率响应。
离散时间的信号和系统(实验报告)
实验二、离散时间的信号和系统（实验报告）一、 实验目的：1、复习离散时间的信号和系统，复习离散时间重要类型的信号和它们的运算的实现。
2、复习离散时间信号理论中一些重要的结果，它们在数字信号处理中很有用。
二、 实验原理：1、典型序列单位采样序列；单位阶跃序列；实数指数序列；复数指数序列；正余弦序列；随机序列：MATLAB 可用rand(1,N)和randn(1,N)来生成；周期序列。
2、序列的运算 信号加；信号乘；改变比例 ；移位；折叠：fliplr(x)；取样和：sum(x(n1:n2)) 取样积：prod(x(n1:n2))；信号能量：sum(abs(x)^2)； 信号功率：sum(abs(x)^2)/length(x)3、一些有用的结果 单位采样合成：奇偶合成：几何级数：序列相关：卷积运算：差分方程：在Matlab 中：三、 实验内容1、 单位阶跃响应clear all;clf;t=-4:4;t0=0;y=stepfun(t,t0);stem(t,y,'filled'); title('单位阶跃序列')xlabel('时间(t)');ylabel('幅值f(t)');axis([-4.5,4.5,-0.5,1.5]);∑∞-∞=-=k k n k x n x )()()(δ)()()(n x n x n x o e +=1||,110<-→∑∞=a aan n对∑∞-∞=-=n y x l l ny n x l r 称为移位),()()(,),(y x conv ∑∑==---=Mm Nk k m k n y a m n x b n y 01)()()(),,()(x a b filter n y =-4-2024-0.500.511.5单位阶跃序列时间(t)幅值f (t )2、实数指数序列 clf;k1=-1;k2=10; k=k1:k2; a=0.6; A=1; f=A*a.^k;stem(k,f,'filled'); title('指数序列')xlabel('时间(k)');ylabel('幅值f(k)');指数序列时间(k)幅值f (k )3、复数指数序列 clf;c = -(1/12)+(pi/6)*i; K = 2; n = 0:40;x = K*exp(c*n);subplot(2,1,1); stem(n,real(x)); ylabel('幅值f(k)'); title('实部'); subplot(2,1,2); stem(n,imag(x));xlabel('时间（k ）');ylabel('幅值f(k)'); title('虚部');010203040幅值f (k )实部010203040时间（k ）幅值f (k )虚部4、正余弦序列clf;k1=-20;k2=20; k=k1:k2; f=sin(k*pi/6); f1=cos(k*pi/6); subplot(2,1,1); stem(k,f,'filled'); title('正弦序列')xlabel('时间(k)');ylabel('幅值(k)'); subplot(2,1,2); stem(k,f1,'filled'); title('余弦序列')xlabel('时间(k)');ylabel('幅值(k)');正弦序列时间(k)幅值f (k )余弦序列时间(k)幅值f (k )5、随机序列 clf;R = 51;d = rand(1,R) % m = 0:R-1;stem (m,d','b');title('随机序列')xlabel('k');ylabel('f(k)');1020304050随机序列kf (k )clf;R = 51;d = randn(1,R) % m = 0:R-1; stem (m,d','b');title('随机序列')xlabel('k');ylabel('f(k)');1020304050随机序列kf (k )6、序列的运算给定序列x1=[1 2 3 4 5 6 7 8 9], ns1=-4; x2=[9 8 7 6 5 4 3 2 1], ns2=4求：1) x1+x2; 2) y3=x1×x2； 3) y1=0.5×x1+0.8×x2； 4) y2=0.3×x1(n)×δ(n-6)+0.8×δ(n-5)×x2(n); 5) x1和x2的反折序列; 6) x1(n)和x2(n)的功率； 7) y3=x1*x2 (线性卷积)；(1) x1=[1 2 3 4 5 6 7 8 9]; x2=[9 8 7 6 5 4 3 2 1]; c=x1+x2; n=-4:1:4; stem(n,c);xlabel('n'); ylabel('幅度');-4-224c =10 10 10 10 10 10 10 10 10 (2) clc;f1=[1 2 3 4 5 6 7 8 9];f2=[9 8 7 6 5 4 3 2 1]; y3=f1.*f2; k=-4:4; stem(k,f);-4-224y3 =9 16 21 24 25 24 21 16 9(3)clc;f1=[1 2 3 4 5 6 7 8 9]; f2=[9 8 7 6 5 4 3 2 1]; k=-4:4;y1=0.5*f1+0.8*f2; stem(k,y);-4-2024y 1 =7.7000 7.4000 7.1000 6.8000 6.5000 6.2000 5.9000 5.6000 5.3000(4)clc;f1=[1 2 3 4 5 6 7 8 9]; f2=[9 8 7 6 5 4 3 2 1]; k1=-4;k2=4;k=k1:k2; n=5;f=[(k-n)==0]; n1=6;f3=[(k-n1)==0];y2=0.3*f3.*f1+0.8*f2.*f; stem(k,y);-4-2024y 2 = 0 0 0 0 0 0 0 0 0（5）clc;f1=[1 2 3 4 5 6 7 8 9]; f2=[9 8 7 6 5 4 3 2 1]; k=-4:4y=Fliplr(f1); subplot(2,1,1); stem(k,y); y1=Fliplr(f2); subplot(2,1,2); stem(k,y1);-4-2024-4-2024y =9 8 7 6 5 4 3 2 1 y1 =1 2 3 4 5 6 7 8 9（6）clc;f1=[1 2 3 4 5 6 7 8 9]; f2=[9 8 7 6 5 4 3 2 1]; n=length(f1);n1=length(f2);y=sum((abs(f1).^2))/n; subplot(2,1,1); stem(y);y1=sum((abs(f2).^2))/n1; subplot(2,1,2); stem(y1);0.511.520204000.511.5202040y = 31.6667 y1 = 31.6667（7）f1=[1 2 3 4 5 6 7 8 9];f2=[9 8 7 6 5 4 3 2 1]; y=conv(f1,f2); k=0:16; stem(k,y);05101520y =9 26 50 80 115 154 196 240 285 240 196 154 115 80 50 26 9。
离散时间信号与离散时间系统
§7-1 概述一、 离散时间信号与离散时间系统离散时间信号：只在某些离散的时间点上有值的信号。
离散时间系统：处理离散时间信号的系统。
混合时间系统：既处理离散时间信号，又处理连续时间信号的系统。
二、 连续信号与离散信号连续信号可以转换成离散信号，从而可以用离散时间系统（或数字信号处理系统）进行处理：三、 离散信号的表示方法：1、 时间函数：f(k)<——f(kT)，其中k 为序号，相当于时间。
例如：)1.0sin()(k k f =2、 （有序）数列：将离散信号的数值按顺序排列起来。
例如：f(k)={1,0.5,0.25,0.125,……,}时间函数可以表达任意长（可能是无限长）的离散信号，可以表达单边或双边信号，但是在很多情况下难于得到；数列的方法表示比较简单，直观，但是只能表示有始、有限长度的信号。
四、 典型的离散时间信号1、 单位样值函数：⎩⎨⎧==其它001)(k k δ下图表示了)(n k -δ的波形。
连续信号离散信号 数字信号 取样量化这个函数与连续时间信号中的冲激函数)(t δ相似，也有着与其相似的性质。
例如：)()0()()(k f k k f δδ=， )()()()(000k k k f k k k f -=-δδ。
2、 单位阶跃函数：⎩⎨⎧≥=其它001)(k k ε这个函数与连续时间信号中的阶跃函数)(t ε相似。
用它可以产生（或表示）单边信号（这里称为单边序列）。
3、 单边指数序列：)(k a k ε比较：单边连续指数信号：)()()(t e t e t a at εε=，其底一定大于零，不会出现负数。
4、 单边正弦序列：)()cos(0k k A εφω+(a) 0.9a = (d) 0.9a =-(b) 1a = (e) 1a =-(c) 1.1a = (f) 1.1a =-双边正弦序列：)cos(0φω+k A五、 离散信号的运算1、 加法：)()()(21k f k f k f +=<—相同的k 对应的数相加。
第1章离散时间信号与系统
右移n；当n为负数时，左移n。 (3)相乘：将h(n-k)和x(k)的对应取样值相乘。 (4)相加：把所有的乘积累加起来，即得y(n)。 上图为：
与
的线性卷积。
计算线性卷积时，一般要分几个区间分别加以考虑，下面 举例说明。
y[k] x[n]h[k n] n
例：已知x1[k] * x2[k]= y[k]，试求y1[k]= x1[kn] * x2[km]。
结论： y1[k]= y[km+n)]
例：x[k] 非零范围为 N1 k N2 ， h[k] 的非零范围为 N3 k N4
求： y[k]=x[k]* h[k]的非零范围。
单位脉冲响应（Impulse response）
定义： h[k ] T{ [k ]}
例：累加器:
k
y[k] x[n]
n
h[k ] u[k ]
LTI系统对任意输入的响应
T{x[k]} T{ x[n][k n]}
n
x[n]T{[k n]}
n
x[n]h[k n]
n
x[k]* h[k]
第1章离散时间信号与系 统
2021年8月29日星期日
离散信号(序列)的表示
2 x[k]
1
1
1
2
k
-1
0
1
3
-1
x[k] {1,1, 2,1,1}
x [k]={1, 1, 2, -1, 1;k=-1,0,1,2,3}
离散序列的产生
▪ 对连续信号抽样 x[k]=x(kT) ▪ 信号本身是离散的 ▪ 计算机产生
离散时间信号和系统理论知识介绍
离散时间信号和系统理论知识介绍离散时间信号和系统是数字信号处理领域中的重要分支，其研究对象是以离散时间为变量的信号和系统。
在离散时间信号和系统理论中，信号的变量只在离散时间点上取值，而系统对信号的处理也是在离散时间点上进行的。
离散时间信号和系统的研究为数字信号处理提供了理论基础和工具。
离散时间信号可以表示为x(n)，其中n是一个整数，代表信号的时间变量。
离散时间信号可以是有限长度的序列，也可以是无限长度的序列。
离散时间信号的幅度可以是实数或复数，表示信号在不同时间点上的取值。
离散时间信号可以用图形表示，横轴表示时间变量n，纵轴表示信号的幅度。
离散时间信号有几个重要的性质。
1. 周期性：如果对于某个正整数N，有x(n) = x(n+N)，那么离散时间信号是周期性的，其最小周期是N。
2. 偶对称性：如果对于任意的n，有x(n) = x(-n)，那么离散时间信号是偶对称的。
3. 奇对称性：如果对于任意的n，有x(n) = -x(-n)，那么离散时间信号是奇对称的。
4. 单位冲激响应：单位冲激响应是一个离散时间信号h(n)，在n=0时为1，其他时间点为0。
单位冲激响应在离散时间系统中起着重要的作用，可以用来表示系统对单位冲激信号的响应。
离散时间系统是对离散时间信号进行处理的数学模型。
离散时间系统可以是线性系统或非线性系统。
线性系统具有叠加性和比例性质，即对于系统的输入信号x1(n)和x2(n)，系统的输出信号y1(n)和y2(n)，有以下关系：1. 叠加性：系统对输入信号的响应是可叠加的，即y(n) = y1(n) + y2(n)。
2. 比例性：系统对输入信号的响应是可比例的，即y(n) =k1y1(n) = k2y2(n)，其中k1和k2是常数。
离散时间系统可以用差分方程表示：y(n) = a0x(n) + a1x(n-1) + ... + an-1x(1) + anx(0)，其中ai是系统的系数。
离散时间系统的输入和输出信号也可以用离散时间卷积进行描述：y(n) = x(n) * h(n)，其中*表示离散时间卷积运算，h(n)是系统的单位冲激响应。
离散时间信号与系统(最全)word资料
第一章 离散时间信号与系统1.1数字信号处理系统的基本组成我们来讨论模拟信号的数字化处理系统，此系统先把模拟信号变化为数字信号，然后用数字技术进行处理，最后再还原成模拟信号。
这一系统的方框图见图所示。
数字信号处理系统的简单方框图当然实际的系统并不一定要包括它的所有框图，例如有些系统只需数字输出，可直接以数字形式显示或打印，那么就不需要D/A 变换器。
另一些系统，其输入就是数字量，因而就不需要A/D 变换器。
对于纯数字系统，则只需要数字信号处理器这一核心部分就行了。
从图中来区别几种信号：1） 连续时间信号，也常称为模拟信号：)(),(t Y t X z z2） 离散时间信号：在一些离散时刻点有定义的信号。
是数值的序列。
离散时间信号可以由一个连续时间信号的采样来表示，如)(),(nT Y nT X a a ，也可以直接由一个离散时间过程产生。
3） 数字信号：时间和幅度上都离散的信号。
)(),(n Y n X 。
和离散时间信号进行区别。
1.2本章重点内容本章先认识一些常用离散时间序列，重点是线性时不变离散时间系统，掌握如何判断某系统是否为LTI 离散时间系统，判断系统的稳定性、因果性。
1.3离散时间信号：序列离散时间信号在数学上表示成数值的序列。
用)(n x 来表示序列的第n个数，其中n 为整数。
这里不涉及时间，只涉及次序。
连续信号经采样后变成离散时间信号，存储在存储器中。
这样序列表示为{)(n x }，为方便，用)(n x 表示序列。
（)(),(),(k p n y k x 都可以用来表示序列，只要变量是离散即可）这里注意：)(n x 仅仅在n 为整数时才有定义，认为)(n x 在n 不为整数时就是零是不正确的。
见书上图1-1。
1．序列的基本运算方式和、积、移位（或延迟）、翻折、累加、卷积和移位：)(n x ----)(m n x -，m 正则右移。
若是)(m x ----)(m n x -，n 正则右移。
离散时间信号和系统的频域分析
离散时间信号和系统的频域分析离散时间信号与系统是研究数字信号与系统的频域分析，其中离散时间信号是对连续时间信号进行采样得到的，而离散时间系统是对连续时间系统进行离散化得到的。
频域分析是对信号与系统在频率域上的特性进行研究和分析。
对于离散时间信号，其离散化的过程是将连续时间信号在时间轴上进行均匀采样，得到指定的采样间隔，得到离散时间序列。
在频域上，其频谱是周期性的，并且频谱是以单位圆为单位周期的。
频域分析的目的是研究离散时间信号在频率域上的特性，包括频谱范围、频率分辨率、功率谱密度等。
离散时间信号的频域分析可以通过离散时间傅里叶变换（DTFT）来实现。
DTFT是信号在频域上的完全变换，将一个离散时间信号映射到一个连续的频率域函数。
DTFT是一个复数函数，表示信号在不同频率上的振幅和相位。
频谱的振幅可以表示信号在该频率上的能量大小，相位可以表示信号在该频率上的相对位置。
除了DTFT之外，还可以使用离散傅里叶变换（DFT）进行频域分析。
DFT是DTFT的一种计算方法，可以将离散时间信号转换为有限的频域信号。
DFT的计算是通过对离散时间信号进行有限长的时间窗口进行采样，并进行频域变换得到的。
DFT的结果是一个离散的频域信号，也称为频谱。
DFT通常使用快速傅里叶变换（FFT）算法来快速计算。
离散时间系统的频域分析主要是通过系统的频率响应函数来实现。
频率响应函数是系统在不同频率上对信号的响应情况的描述。
对于线性时不变系统，其频率响应函数是系统的传递函数的傅里叶变换。
频率响应函数拥有类似信号的频谱特性，可以描述系统对不同频率的信号的增益和相位。
频域分析在离散时间信号与系统中有着广泛的应用。
首先，频域分析可以帮助我们理解信号的频率构成和能量分布情况，有助于对信号进行合理的处理和分析。
其次，频域分析可以快速计算离散时间系统的响应，能够有效地评估系统的性能和稳定性。
此外，频域分析还可以进行滤波器设计、信号压缩、信号重构等应用。
[离散时间信号处理学习笔记]1.离散时间信号与离散时间系统
![[离散时间信号处理学习笔记]1.离散时间信号与离散时间系统](https://img.taocdn.com/s3/m/a014da215b8102d276a20029bd64783e09127dd5.png)
[离散时间信号处理学习笔记]1.离散时间信号与离散时间系统本⽂给出了离散时间信号与离散时间系统的基本定义，建⽴符号注释。
离散时间信号的定义离散时间信号在数学上表⽰成数的序列。
如果以连续时间信号（函数）来进⾏对⽐，有：⼀个函数f，该函数中的某⼀点k上的值记作f(k)。
⼀个数的序列x，该序列中的第n个数记作x[n]。
正规地可写作x={x[n]},n∈Z不过实际上，序列往往可以通过周期采样⼀个模拟（连续时间）信号x a(t)来得到x[n]=x a(nT),n∈Z其中T为采样周期，其倒数1T为采样频率。
离散时间信号的表⽰x[n]指的序列中的第n个数，即序列的第n个样本。
在表⽰整个序列时，如果⽤x={x[n]},n∈Z则会过于繁琐，因此我们通常⽤“序列x[n]”来进⾏称呼。
基本序列在讨论离散时间信号与系统理论时，有⼏个基本序列是特别重要的。
单位样本序列Unit sample定义为δ[n]=1,n=0 0,n≠0单位样本序列在离散时间信号与系统中的作⽤就如同单位脉冲函数δ(t)在连续时间信号与系统中所起的作⽤，⽬的是⽤于采样。
为了⽅便起见，我们通常称之为离散时间脉冲，或者简单称为脉冲。
我们注意到只要中括号内的值为0，则该点的值为1。
因此如果有⼀延迟的单位样本序列δ[n−2]，则表明在n=2处的值为1，表现为单位样本信号δ[n]向右移动了两个单位。
如此⼀来，我们可以发现任何序列都可以⽤⼀组幅度加权的延迟单位样本序列的和来表⽰x[n]=⋅⋅⋅+a−2δ[n+2]+a−1δ[n+1]+a0δ[0]+a1δ[n−1]+⋅⋅⋅即任何序列均可表⽰为x[n]=∞∑k=−∞x[k]δ[n−k]单位跃阶序列Unit step定义为{u [n ]=1,n ⩾00,n <0观察前⾯的图UnitStep 与Delta ，可以发现单位跃阶序列在n 时刻点的值就等于单位样本序列在n 点以及该点以前的全部值的累加和，即（此处u [n ]为单位跃阶序列上的第n 点）u [n ]=n∑k =−∞δ[k ]此外，序列u [n ]也可表⽰成⼀组延迟的单位样本序列之和u [n ]=δ[n ]+δ[n −1]+δ[n −2]+⋅⋅⋅=∞∑k =0δ[n −k ]指数序列 Exponential指数序列的⼀般形式为x [n ]=A αn如果A ,α都为实数的话，则x [n ]为实指数序列。
第一章 离散时间信号和系统
30
一、线性时不变系统
1.线性系统
y1 ( n) T [ x1 ( n)]
y2 ( n) T [ x2 ( n)]
（1）可加性 （2）奇次性
y1 (n) y2 (n) T [ x1 (n) x2 (n)]
u( n) ( n m )
m 0
(n)
1
0 u(n)
1
0 1
n
…
n
22
(3). 矩形序列
1, 0 n N 1 R N ( n) 0 , 其他n
RN (n) 和 (n) 、 (n) 的关系为： u
RN (n)
RN (n) u(n) u(n N )
取和
11
例1 - 1 - 2 已知x(n) h(n) 1 ， 3，求x(n) h(n)。 2， n 0
x(m)
解：
（1）翻褶 (2) 移位、相乘、累加
n<0, y(n)=0 n＝0, y(n)=1 n=1, y(n)=1•2+2•1=4 n=2, y(n)=1•3+2•2+ 1•3 =10
(n 1) 2 (n) (n 2) 0.5 (n 3) 1.5 (n 4) 28
1.2 离散时间系统
29
离散时间系统定义: 离散时间系统是将输入序列变换成输出序列的一种运算。
x(n)
T[.]
y(n)
y(n)=T[x(n)]
例如 理想时延系统 : y ( n) x( n n0 )
2
离散时间信号与系统
离散时间信号与系统离散时间信号与系统是数字信号处理领域中的重要概念。
离散时间信号是在离散时间点上取值的信号，而离散时间系统则是对离散时间信号进行处理或操作的系统。
在本文中，我们将详细探讨离散时间信号与系统的基本概念、特性和应用。
一、离散时间信号的定义和表示离散时间信号是在离散时间点上取值的信号，通常用序列表示。
离散时间序列可以用数学公式或图形方式表示。
其中，数学公式表示常用的形式是$x[n]$，而图形表示则可以通过绘制离散时间序列的点来展示。
离散时间信号可以分为有限长序列和无限长序列。
有限长序列在某一区间上有值，而在其他区间有值或为零。
无限长序列在整个时间轴上有值，通常会满足某些性质，如周期性或衰减性。
二、离散时间系统的定义和分类离散时间系统是对离散时间信号进行处理或操作的系统。
离散时间系统可以通过输入输出关系来定义。
输入为离散时间信号，输出为对输入信号进行处理或操作后得到的信号。
离散时间系统可以分为线性系统和非线性系统、时不变系统和时变系统、因果系统和非因果系统、稳定系统和非稳定系统等不同类别。
不同类别的系统具有不同的特性和性质，对信号的处理方式也会有所不同。
三、离散时间信号与系统的特性离散时间信号与系统具有许多特性。
其中一些重要的特性包括时域特性、频域特性和稳定性。
时域特性描述了信号或系统在时间上的行为，频域特性描述了信号或系统在频率上的行为，而稳定性则描述了系统的输出是否受到输入的限制。
离散时间信号的时域特性可以通过序列的幅值、相位和频率来描述。
离散时间系统的时域特性可以通过系统的冲激响应、单位样值响应和单位阶跃响应来描述。
频域特性则可以通过离散时间信号和系统的傅里叶变换来描述。
四、离散时间信号与系统的应用离散时间信号与系统在数字信号处理中有广泛的应用。
其中一些常见的应用包括音频处理、图像处理、通信系统和控制系统等。
在音频处理中，离散时间信号与系统用于音频信号的录制、编码和解码。
它可以通过滤波和均衡等方式改善音频信号的质量。
第1章离散时间信号与系统
2 (a)若： N ，N为整数，则序列的最小周期为N
0
(b)若： 2 N S L ，N为有理数但不是整数，L、S 0
为整数，则序列的最小周期为S。
2 0 N , 不是有理数，则序列是非周期性的 (c)若：
所以 x(n) 的周期N是 N1 , N2的最小公倍数30
(2) 1 2 1 , N1 8 ; 4 14
2
4
, N2
2 8; 4
13
N1/N2是无理数，所以x(n)是非周期的。
n0 n0
u(n-n0),n0>0
…
-1
…
0 1
(a)
2
3
n
… … -1
u(-n0-n),n0>0
…
0 1 (b) n0
… …
n
… … 图1.1.2
-n0
…
-1
… 0 1 …
n
思考： u(n+n0),n0>0; 的图形。
4
(c)
单位脉冲序列与单位阶跃序列的相互关系：
(n) u (n) u (n 1)
u(n) (n) (n 1) (n 2) (n m)
m 0
5
（３）矩形序列 (Rectangle sequence)
1, RN (n) 0,
0 n N 1 n 0, n N
RN ( n )
1
…
0 1
-3 -2 -1
第1章 离散时间信号与系统
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验：离散时间信号与系统的时域分析一、实验目的1、熟悉和掌握常用的用于信号与系统时域仿真分析的MA TLAB函数；2、掌握离散时间信号的MATLAB产生，掌握用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号的MA TLAB编程；3、牢固掌握系统的单位序列响应的概念，掌握MATLAB描述LTI系统的常用方法及有关函数，并学会利用MATLAB求解LTI系统响应，绘制相应曲线。
基本要求：掌握用MATLAB描述离散时间信号的方法，能够编写MATLAB程序，实现各种信号的时域变换和运算，并且以图形的方式再现各种信号的波形。
掌握线性时不变离散系统的时域数学模型用MATLAB描述的方法，掌握线性常系数差分方程的求解编程。
二、实验原理信号（Signal）一般都是随某一个或某几个独立变量的变化而变化的，例如，温度、压力、声音，还有股票市场的日收盘指数等，这些信号都是随时间的变化而变化的，还有一些信号，例如在研究地球结构时，地下某处的密度就是随着海拔高度的变化而变化的。
一幅图片中的每一个象素点的位置取决于两个坐标轴，即横轴和纵轴，因此，图像信号具有两个或两个以上的独立变量。
在《信号与系统》课程中，我们只关注这种只有一个独立变量（Independent variable）的信号，并且把这个独立变量统称为时间变量（Time variable），不管这个独立变量是否是时间变量。
在自然界中，大多数信号的时间变量都是连续变化的，因此这种信号被称为连续时间信号（Continuous-Time Signals）或模拟信号（Analog Signals），例如前面提到的温度、压力和声音信号就是连续时间信号的例子。
但是，还有一些信号的独立时间变量是离散变化的，这种信号称为离散时间信号。
前面提到的股票市场的日收盘指数，由于相邻两个交易日的日收盘指数相隔24小时，这意味着日收盘指数的时间变量是不连续的，因此日收盘指数是离散时间信号。
而系统则用于对信号进行运算或处理，或者从信号中提取有用的信息，或者滤出信号中某些无用的成分，如滤波，从而产生人们所希望的新的信号。
系统通常是由若干部件或单元组成的一个整体（Entity）。
系统可分为很多不同的类型，例如，根据系统所处理的信号的不同，系统可分为连续时间系统（Continuous-time system）和离散时间系统（Discrete-time system），根据系统所具有的不同性质，系统又可分为因果系统（Causal system）和非因果系统（Noncausal system）、稳定系统（Stable system）和不稳定系统（Unstable system）、线性系统（Linear system）和非线性系统（Nonlinear system）、时变系统（Time-variant system）和时不变系统（Time-invariant system）等等。
然而，在信号与系统和数字信号处理中，我们所分析的系统只是所谓的线性时不变系统，这种系统同时满足两个重要的基本性质，那就是线性性和时不变性，通常称为线性时不变（LTI）系统。
1. 信号的时域表示方法1.1将信号表示成独立时间变量的函数例如x(t)=sin(ωt) 和x[n]=n(0.5)n u[n]分别表示一个连续时间信号和一个离散时间信号。
在MA TLAB中有许多内部函数，可以直接完成信号的这种表达，例如：sin()：正弦信号cos()：余弦信号exp()：指数信号1.2用信号的波形图来描述信号用函数曲线表示一个信号，图1.1就是一个连续时间信号和一个离散时间信号的波形图。
图1.1 连续时间信号与离散时间信号的波形图1.3将信号用一个数据序列来表示对于离散时间信号，还可以表示成一个数的序列，例如：x[n]={...., 0.1, 1.1, -1.2, 0, 1.3, ….}↑n=0在《信号与系统》和《数字信号处理》课程中，上述三种信号的描述方法是经常要使用的。
2 用MATLAB仿真离散时间信号在MATLAB中，无论是连续时间信号还是离散时间信号，MATLAB都是用一个数字序列来表示信号，这个数字序列在MATLAB中叫做向量(vector)。
通常的情况下，需要与时间变量相对应。
如前所述，MA TLAB有很多内部数学函数可以用来产生这样的数字序列，例如sin()、cos()、exp()等函数可以直接产生一个按照正弦、余弦或指数规律变化的数字序列。
2.1离散时间信号的仿真程序Program1_2用来产生离散时间信号x[n]=sin(0.2πn)。
% Program1_2% This program is used to generate a discrete-time sinusoidal signal and draw its plotclear, % Clear all variablesclose all, % Close all figure windowsn = -10:10; % Specify the interval of timex = sin(0.2*pi*n); % Generate the signalstem (n,x) % Open a figure window and draw the plot of x[n]title ('Sinusoidal signal x[n]') xlabel ('Time index n')请仔细阅读该程序，比较程序Program1_1和Program1_2中的不同之处，以便自己编程时能够正确使用这种方法方针连续时间信号和离散时间信号。
程序Program1_3用来仿真下面形式的离散时间信号： x[n]={...., 0.1, 1.1, -1.2, 0, 1.3, ….} ↑n=0% Program1_3% This program is used to generate a discrete-time sequence % and draw its plotclear, % Clear all variablesclose all, % Close all figure windowsn = -5:5; % Specify the interval of time, the number of points of n is 11. x = [0, 0, 0, 0, 0.1, 1.1, -1.2, 0, 1.3, 0, 0]; % Generate the signalstem(n,x,'.') % Open a figure window and draw the plot of x[n] grid on,title ('A discrete-time sequence x[n]') xlabel ('Time index n')由于在程序的stem(n,x,'.') 语句中加有'.'选项，因此绘制的图形中每根棒条线的顶端是一个实心点。
如果需要在序列的前后补较多的零的话，可以利用函数zeros()，其语法为： zeros(1, N)：圆括号中的1和N 表示该函数将产生一个一行N 列的矩阵，矩阵中的所有元素均为零。
利用这个矩阵与序列x[n]进行组合，从而得到一个长度与n 相等的向量。
例如，当 x[n]={ 0.1, 1.1, -1.2, 0, 1.3} 时，为了得到程序Program1_3中的序列， ↑n=0可以用这个MA TLAB 语句x = [zeros(1,4) x zeros(1, 2)] 来实现。
用这种方法编写的程序如下：% Program1_4% This program is used to generate a discrete-time sinusoidal signal % and draw its plotclear, % Clear all variablesclose all, % Close all figure windows n = -5:5; % Specify the interval of timex = [zeros(1,4), 0.1, 1.1, -1.2, 0, 1.3, zeros(1,2)]; % Generate the sequence stem (n,x,'.') % Open a figure window and draw the plot of x[n] grid on,title ('A discrete-time sequence x[n]') xlabel ('Time index n')离散时间单位阶跃信号u[n]定义为⎩⎨⎧<≥=0,00,1][n n n u 2.1离散时间单位阶跃信号u[n]除了也可以直接用前面给出的扩展函数来产生，还可以利用MATLAB 内部函数ones(1,N) 来实现。
这个函数类似于zeros(1,N)，所不同的是它产生的矩阵的所有元素都为1。
值得注意的是，利用ones(1,N) 来实现的单位阶跃序列并不是真正的单位阶跃序列，而是一个长度为N单位门(Gate)序列，也就是u[n]-u[n-N]。
但是在一个有限的图形窗口中，我们看到的还是一个单位阶跃序列。
在绘制信号的波形图时，有时我们需要将若干个图形绘制在图一个图形窗口中，这就需要使用MATLAB的图形分割函数subplot()，其用法是在绘图函数stem或plot之前，使用图形分割函数subplot(n1,n2,n3)，其中的参数n1，n2和n3的含义是，该函数将把一个图形窗口分割成n1×n2个子图，即将绘制的图形将绘制在第n3个子图中。
2.2信号的时域变换2.2.1 信号的时移信号的时移可用下面的数学表达式来描述：设一个连续时间信号为x(n)，它的时移y(n) 表示为：y(n) = x(n - n0) 2.2其中，n0为位移量。
若n0为正数，则y(n)等于将x(n)右移n0秒之后的结果。
反之，若n0为负数，则y(n)等于将x(n)左移n0秒之后的结果。
在MA TLAB中，时移运算与数学上习惯表达方法完全相同。
2.2.2 信号的时域反褶对一个信号x[n]的反褶运算在数学上表示为y[n] = x[-n] 2.3 这种反褶运算，用MATLAB实现起来也是非常简单的。
有多种方法可以实现信号的反褶运算。
方法一，修改绘图函数plot(t,x)和stem(n,x)中的时间变量t和n，即用-t和-n替代原来的t和n，这样绘制出来的图形，看起来就是原信号经时域反褶后的版本。