小升初数学讲义第1讲计算专题
六年级下册数学讲义-小升初培优:第01讲 乘法分配律之速算巧算(上)(解析版)全国通用

第01讲乘法分配律之速算巧算(上)教学目标:1、引导学员能运用乘法分配律进行一些简便运算,掌握能用乘法分配律进行简便计算的式题的特点;2、运用乘法分配律的速算和巧算进行相关应用题题型的解决;3、使学员感受数学与现实生活的联系,能用所学知识解决简单的实际问题。
教学重点:使学员掌握乘法分配律并用于简便计算。
教学难点:使学员理解并掌握乘法分配律的转化及应用。
教学过程:【环节一:预习讨论,案例分析】【知识回顾——温故知新】(参考时间-2分钟)涉及时间方面的统筹安排,如何考虑?①要做哪些事情;②每件事情需要多少时间;③弄清所做事情的程序,即先做什么,后做什么,哪些工作可以同时做,从而根据题意找出最佳方案。
涉及最优方案选择方面的统筹安排,如何考虑?可以将所有的方案一一枚举,再根据问题的要求去分析每个方案,从而选择出满足条件的方案或者几个方案的组合;如果可供选择的方案过多,我们可以调整法进行解答,即先对条件进行假设,再由此进行分析并调整,这样可帮助我们快速将问题解决。
【知识回顾——上期巩固】(参考时间-3分钟)某工地A有20辆卡车,要把60车渣土从A运到B,把40车砖从C运到D(工地道路图如下所示)。
问如何调运最省汽油(最后卡车还要回到A处)?解析部分:把渣土从A运到B或把砖从C运到D,都无法节省汽油,只有设法减少跑空车的距离,才能省汽油。
给予新学员的建议:对于图形尽可能画的更为精确,并强调基础计算能力。
哈佛案例教学法:引导学员多多进行纸上的动手操作演练,鼓励积极的课堂发言。
参考答案:如果各派10辆车分别运渣土和砖,那么每运一车渣土要空车跑回300米,每运一车砖则要空车跑回360米,这样到完成任务总共空车跑了:300×60+360×40=32400(米)。
如果一辆从从A→B→C→D→A跑一圈,那么每运一车渣土,运一车砖要空车跑:240+90=330(米)。
因此,先派20辆车都从A开始运渣土到B,再空车开往C运砖到D后空车返回A,这样每辆车跑两圈就完成了运砖任务。
小升初冲刺专题之计算专题

第1弹 凑整与分组法计算是我们学习数学知识基础中的基础,所以关于计算的重要性我们就不多说了。
计算可以分为硬算和巧算,本讲义主要介绍一些巧算方法,但是在做计算题目的时候也需要一些硬算基本功。
1. 凑整凑整指的是在混合运算中想办法凑出整数,通常可以先计算能够得到整数或整百整千的两个数。
例如在四则运算中先算 6436+,28128-,8125⨯,37111÷。
2. 分组分组指在计算中对某些数分成一组,通常分成一组的目的是凑整,也有把一个周期放在一组,如例3。
【例 1】 计算:9109...991...199919919个++++.【例 2】 计算:14.2020142014.2014⨯÷.精选例题知识简介【例 3】 计算:1234...4344454647484950++--+--++--+.1. 计算: 4116.025.452-++.2. 计算:125328325⨯⨯⨯.小试牛刀3. 计算: )2072()318431326413(-⨯+++ .4. 计算: 371391222÷⨯÷5. 计算:999988889999999888999998899989+++.6. 计算:)200198...642()201199...531(+++++-+++++.第2弹提取公因数法知识简介提取公因数是乘法分配律的逆运算,也是巧算中常用的方法,很多题目提取公因数后括号部分可以凑整。
同时,你可以发现,每提取一次公因数就可以少算一次乘法。
提取公因式法可以细分为以下三类:1.直接提取公因数2.部分提取公因数3.分组提取公因数下面三道例题分别对应上述三类提取方法。
当然这样分类只是一种区分不同问题的手段,关键还是对问题的理解和掌握。
精选例题【例1】计算:445633562256⨯+⨯+⨯.计算专题【例2】计算:20092008200820092008200920092009-⨯-⨯.【例3】计算:122334...96979798989999100⨯+⨯-⨯++⨯-⨯+⨯-⨯.小试牛刀1.计算:22241112225111⨯-⨯.2.计算:556444445555⨯-⨯.3.计算17451511217161654⨯+⨯+⨯. 4.计算:122123124123123123123⨯-+⨯.5.计算:.7.53125.08.6487548.637.525537.08.64⨯⨯⨯-⨯⨯+⨯⨯6.计算:85111125473244537⨯+⨯+⨯+⨯.计算专题第3弹数列与数表知识简介数列指的是一列数,数表指的是一个表格的数。
小升初 数学 暑假课14讲 第1讲 四则运算及运算定律 讲义
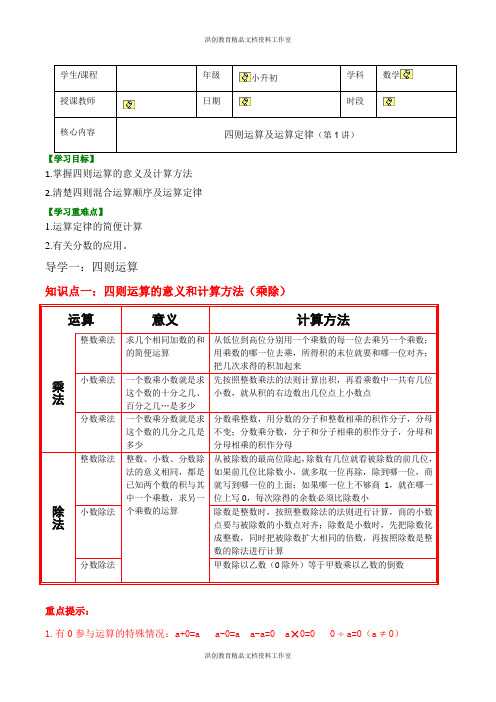
1.掌握四则运算的意义及计算方法2.清楚四则混合运算顺序及运算定律【学习重难点】1.运算定律的简便计算2.有关分数的应用。
导学一:四则运算知识点一:四则运算的意义和计算方法(乘除)运算 意义 计算方法乘法 整数乘法 求几个相同加数的和的简便运算 从低位到高位分别用一个乘数的每一位去乘另一个乘数;用乘数的哪一位去乘,所得积的末位就要和哪一位对齐;把几次求得的积加起来小数乘法 一个数乘小数就是求这个数的十分之几、百分之几…是多少 先按照整数乘法的法则计算出积,再看乘数中一共有几位小数,就从积的右边数出几位点上小数点分数乘法 一个数乘分数就是求这个数的几分之几是多少 分数乘整数,用分数的分子和整数相乘的积作分子,分母不变;分数乘分数,分子和分子相乘的积作分子,分母和分母相乘的积作分母除法整数除法 整数、小数、分数除法的意义相同,都是已知两个数的积与其中一个乘数,求另一个乘数的运算从被除数的最高位除起,除数有几位就看被除数的前几位,如果前几位比除数小,就多取一位再除,除到哪一位,商就写到哪一位的上面;如果哪一位上不够商1,就在哪一位上写0,每次除得的余数必须比除数小小数除法 除数是整数时,按照整数除法的法则进行计算,商的小数点要与被除数的小数点对齐;除数是小数时,先把除数化成整数,同时把被除数扩大相同的倍数,再按照除数是整数的除法进行计算分数除法甲数除以乙数(0除外)等于甲数乘以乙数的倒数重点提示:1.有0参与运算的特殊情况:a+0=a a-0=a a-a=0 a ×0=0 0a=0(a 0)学生/课程 年级 小升初 学科 数学授课教师日期时段核心内容 四则运算及运算定律(第1讲)2.有1参与运算的特殊情况:a×1=a a 1=a a a=1(a0)知识点二:四则运算中各部分间的关系运算各部分间的关系加法加数十加数=和一个加数=和一另一个加数减法被减数一减数=差减数=被减数一差被减数=减数+差乘法乘数×乘数=积一个乘数=积另一个乘数除法没有余数的除法商=被除数除数除数=被除数商被除数=除数×商有余数的除法被除数÷除数=商……余数被除数=商×除数+余数商=(被除数-余数)除数除数=(被除数-余数)商余数=被除数-商×除数1.小数乘法转化为整数乘法,除数为小数的除法转化为除数为整数的除法,分数除法转化为分数乘法,都体现了转化的数学思想。
小升初数学专题选讲

第一讲计数原理知识纵横:如果完成一件事情,有几类不同的方法,而且每类方法中又有几种可能的方法,那么求完成这件事的方法总数,即各类方法的总和,就是我们要掌握的加法原理。
加法原理:完成某件事情,如果有几类方法,而在第一类方法中有m1种方法,第二类方法中有m2种方法……第n类有m n种,那么完成这件事的方法总数可以表示为m1+ m2+ m3+…+m n。
完成一件事,需要分几个步骤来完成,而完成每步又有几种不同的方法,要求完成这件事的方法的总数,应当将各步骤方法总数相乘,这就是我们应掌握的乘法原理。
乘法原理:完成一件事需要分成几个步骤,第一步有m1种方法,第二步有m2种方法,第三步有m3种方法……第n步有m n种方法,那么完成这件事共有m1×m2×m3×…×m n种不同的方法。
例题求解:【例1】 10个人进行乒乓球比赛,每两个人之间比赛一场,问:一共要比赛多少场?【例2】一天有6节不同的课,这一天的课表有多少种排法?【例3】 1000至1999这些自然数中,个位数大于百位数的有多少个?【例4】 4只鸟飞入4个不同的笼子里,每只小鸟都有自己的一个笼子(不同的鸟,笼子也不同),每个笼子只能进一只鸟。
若都不飞进自己的笼子里去,有种不同的飞法。
【例5】如果组成三位数abc的三个数字a,b,c中,有一个数字是另外两个数字的乘积,则称它为“特殊数”。
在所有的三位数中,共有个“特殊数”。
【例6】如下图所示,用红、绿、蓝、黄四种颜色,涂编号为1、2、3、4的长方形,使任何相邻的两个长方形的颜色都不相同,一共有多少种不同的涂法?【例7】恰有两位数字相同的三位数共有多少个?基础夯实1、一件工作可以用3种方法完成,有5人会用第1种方法完成,有4人会用第2种方法完成,有6人会用第3种方法完成。
选出一个人来完成这项工作共有多少种选法?2、一件工序可以分3步方法完成,有5人会做第1步,有4人会做第2步,有6人会做第3步,每个人只会做一步。
小升初专题:第一讲:整数与小数的巧算

小升初专题:第一讲:整数与小数的巧算小升初专题:第一讲:整数与小数的巧算第一讲:整数与小数的巧算一、训练目标:在日常生活和答疑数学问题时,经常必须展开排序,在数学课里我们自学了一些方便快捷排序的方法,但如果擅于观测、勤于思考,排序中还能够找出更多的精妙的计算方法,不仅并使你能算得不好、算得快,还可以使你显得精明和机智。
巧算也就是简便运算,在四则运算中,可以根据数的特点,通过数的分解、合并改变原来的运算顺序,从而达到简便计算的目的。
一道计算题的简便算法常常不止一种,有时也运用四则运算的定律、性质或利用和、差、积、商的变化规律,使计算简便。
二、巧算常用的方法:1凑整2发生改变运算顺序3分拆4设数(换元)三、巧算方法的根据:1四则运算的定律2和差积商的变化规律3数的性质。
一、整数的巧算准备题:口算①4356+1287-356=②44×79÷4=③1457-(185+457)=④237×97+237×5-237×2=例1①999+998+997+1003+1002+1001②77×132+255×999+510③1994×19931994-1993×19941994④2021×20212021-2021×20212021出色的成绩源自我们共同的不懈努力------------徐老师1基准2排序2021×2021×202120212021-2021×2021×202120212021例3计算99999×77778+33333×66666基准4排序1+2-3+4+5-6+7+8-9+…+97+98-99例5计算(100+621+739+458)×(621+739+458+378)-(100+621+739+458+378)×(621+739+458)稳固练:1.计算2001×20002002000-2000×2001200120012.排序78787878×88888888÷1010101÷22222222优异的成绩来自我们共同的努力------------徐老师23.计算9999×2222+3333×33344.排序1+2-3-4+5+6-7-8+…+1997+1998-1999-2000+2001+2002-2021-2021+20215计算(2+23+234)×(23+234+2345)-(2+23+234+2345)×(23+234)课后作业:1.计算2021×20212021-2021×202120212.排序8888×77771+4444×666663.计算2021+2021-2021-2002+2001+2000-1999-1998+…+5+4-3-2+1出色的成绩源自我们共同的不懈努力------------徐老师34.排序(1+12+23)×(12+23+34)-(1+12+23+34)×(12+23)二、小数的巧算例题1用方便快捷算法排序以下各题:①4.25-1.64+8.75-9.36=②45.3×8.77-45.3+2.23×45.3=③0.9+0.99+0.999+0.9999④27.26-(4.5-2.74)练习:1计算3.18+4.57+2.82+5.43=2排序3.14×6.5+4.5×3.14-3.14=3计算0.9+9.9+99.9+999.9=例题2用方便快捷算法排序以下各题:①4.84×2.25÷1.21=②88.8÷31.4×62.8×24.3÷8÷8.1=③1240×3.8+124×51+1.24×1400+760×9.6+0.76×700=优异的成绩来自我们共同的努力------------徐老师4④(12×21×45×10.2)÷(15×4×0.7×51).?68.?068.=练:①99②6.49×0.22+258×0.0649+5.3×6.49+64.9×0.19=③23.75×3.987+6.013×92.07+6.832×39.87=例题3用简便算法计算下列各题:①1.25×32×2.5=②0.999×0.7+0.111×3.7=③11.8×43-860×0.09=④2222×0.29+6666×0.09-3333×0.04练1排序2.5×128×125×5=2排序6.25×1.25×6.4=例题4计算:(1+0.12+0.23)×(0.12+0.23+0.34)-(1+0.12+0.23+0.34)×(0.12+0.23)优异的成绩来自我们共同的努力------------徐老师5。
2022-2023学年小升初数学精讲精练专题汇编讲义 第1讲 整数和小数第1讲 整数和小数(原卷)

提高版(通用)2022-2023学年小升初数学精讲精练专题汇编讲义第1讲整数和小数知识精讲知识点一:整数1.整数的意义和分类:像-3,-2,-1,0,1,2,3,…这样的数统称为(整数)。
整数分为正整数、0、负整数(整数也可以分为自然数和负整数)【提示】0既不是正数,也不是负数2.整数的读法:读一个多位数,从高级到低级,一级一级地读。
每级都按照个级的读法来读,读亿级、万级时,必须加上“亿”字或“万”字。
每级末尾的“0"都不读,其他数位有一个或连续几个“0"的都只读一个零。
(读数时,可以先画出分级线,再读数,这样可以快速、准确地读出一个多位数3.整数的写法:写数时,按从高位到低位的顺序,一级一级地写。
亿级和万级都按个级的写法来写。
哪个数位上一个单位也没有,就在那一位上写0(写完后,画上分级线检查,每一级都只能写四位,不要多写或少写0)4.整数的大小比较:○1比较两个整数的大小,首先数一下多位数的位数,位数多的大于位数少的○2如果位数相同,就比较最高位,最高位上的数大的那个数就大;最高位上的数相同,次高位上的数大那个数就大,如果还相同,则继续依次比较,直到比较出大小为止。
5.整数的改写和近似数一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
(1)数的改写:①把整万、整亿数改写成用“万”或“亿”作单位的数:把万位或亿位后面的4个0或个0去掉,换成一个“万”字或“亿”字就可以了②把非整万、整亿数改写成用“万”或“化”作单位的数:先把原数的小数点向左移动4位或8位(小数部分末尾是0的要划掉),再在数的后面写上“万”字或“亿”字,中间用“=”连接(2)近似数:省略尾数改写成近似数:先用“四舍五入”法省略万位或亿位后面的尾数,再在数的后面写上“万”或“亿”字,中间用约等号连接【提示】近似数常用词:精确到哪位小数、保留几位小数等。
六年级小升初数学寒假培优 第1讲 简便运算
第1讲简便运算专题简析:根据算式的结构和数的特征,灵活运用运算法则、定律、性质和某些公式,可以把一些较复杂的四则混合运算化繁为简,化难为易。
简便运算解题关键点总结四个字:“凑整好算”。
(二)重要性质:(1)减法:a-b-c=a-(b+c)(2)除法:a÷b÷c=a÷(b×c)(一)结合运算律简算【例题1】10.26-(3.28+5.26)【同步训练1】2723+378-723+622【例题2】1999+999×999 【同步训练2】99999×7778+3333×6666【例题3】125×32×25 【同步训练3】25×64×2.5×0.5【例题4】(12.5+60)×8 【同步训练4】57×15+43×15【例题5】58×102 【同步训练5】54×98【例题6】745×101-745 【同步训练6】101×46-46【例题7】0.8+63×54+36×0.8 【同步训练7】141×7.3+3.7×1.25-1.25【例题8】77.5×53+530×2.25 【同步训练8】0.888×125×73+889×73 【例题9】9999×7778+3333×6666 【同步训练9】9999×2222+3333×3334 【例题10】2019÷12.5÷8 【同步训练10】1600÷25÷4【例题11】(4.5×11.1×4.8)÷(3.33×0.8×0.9)【同步训练11】(9.1×7.5×4.6)÷(1.3×2.5×2.3)【例题12】374-183+273-1.625 【同步训练12】465—2.63+561—0.37【例题13】99998+9998+998+31 【同步训练13】99987+9943+921+87【例题14】12.5%×157+37.5%×157+21÷715【同步训练14】50%×18+41×144—0.25×179【例题15】26×28×(2827127261⨯+⨯) 【同步训练15】7721×53+530×241【例题16】(4035+20161)×20171 【同步训练16】(6052—20181)×20171【例题17】211421+531531⨯⨯ 【同步训练17】2519×317+257×316【例题18】33×20192019—2019×330033【同步训练18】2019×20182018—2018×20192019【例题19】20012-20002【同步训练19】19912-19902(二)结合约分简算 【例题1】(1—21)(1+21)(1—31)(1+31)(1—41)(1+41)...(1—1001)(1+1001)【同步训练1】(1+21)(1+41)(1+61)(1+81)(1—31)(1—51)(1—71)【例题2】2009÷200920102009 【同步训练2】2016÷(2016+20152016)【例题3】999555666222777333⨯⨯-⨯ 【同步训练3】201620142015120162015⨯+-⨯(二)结合裂项法简算【例题1】211⨯+321⨯+431⨯+......100991⨯ =(1—21)+(21—31)+(31—41)+......+(991—1001)=1—21+21—31+31—41+ (991)1001=1—1001= 1001【同步训练1】311⨯+531⨯+751⨯+.....+101991⨯【同步训练2】422⨯+642⨯+862⨯+.....+100982⨯。
第1课时《数的认识—整数的认识》-小升初数学第一轮总复习讲练专题讲义
小升初第一轮总复习讲练专题
专题一:数的认识
第1课时:整数的认识
复习提纲
经典案例 ❒ 考点1:整数的读写
【例1】一个数是由6个亿、8个千万、4个十万、5个千和2个百组成的,这个数写作:
(
),读作(
)。
【解析】根据数的组成写数时,可以先简写一个数位顺序表,再对应各数位写计数单位 的个数,即6个亿、8个千万、4个十万、5个千、2个百 分别对应亿位、千万位、十万位 、千位、百位写6,8,4,5,2,其他数位上一个计数单位也没有,都写0占位。读数时,先分级 ,6⋮8040⋮5200分成了三级,再从高位读起,亿级上是6就读作六亿,万级上是8040,就读 作八千零四十万,个级上是5200,就读作五千二百。
)。
【解答】 1. 3006000080 2. 万 4个万 3. 9 5
三十亿零六百万零八十 30 百 4个百 个 4个一
实战演练 ❒ 重点题型解答
4.你知道下面的 ▢ 里可以填哪些数吗? (1)1. 29894<29 ▢ 00 (2) 2975300>2 ▢ 90000 (3) 124 ▢ 940≈124万 (4) 68 ▢ 6840000≈69亿
(2)478000和487000
【解析】
第(1)题中,因为98989是五位数,而101010是六位数,在自然数范围内,五位数小于六
位数,即98989<101010;
第(2)题中,478000和487000都是六位数,且最高位十万位上的数字相同,但一个数万
位上是7,另一个数万位上是8,所以478000<487000。
经典案例 ❒ 考点4:负数的认识
强化训练4:
1. -1.5读作:(
),+3读作(
1第一讲 速算与巧算
第一讲速算与巧算知识导航:计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领.准确.快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率.节省计算时间,更可以锻炼记忆力,提高分析.判断能力,促进思维和智力的发展.1.要认真观察算式中数的特点,算式中运算符号的特点.2.掌握基本的运算定律:乘法交换律.乘法结合律.乘法分配律.3.掌握速算与巧算的方法:如等差数列求知.凑整.拆数等等.例1.19199199919999199999++++解析:运用凑整法来解十分方便,也不容易出错误.解:原式=)1)1+(−20−−−+−+200020000((200000)()1200)1(1=5222220−=222215【巩固】898998999899998999998+++++=解析:个位数都是8,加2正好可以凑整得10,每个数加2就会多出12,所以还要在最后减12.解:原式=12++++10−+1000000100000100001000100=1111098例2.539540541542543544545++++++解析:这七个数均差1,且个数为7,是单数,所以中间数就是七个数的平均数.解:原式5427=×=3794【巩固】(445443440439433434)6+++++÷解析:这6个数相差并不均匀,但是可以看出都比较接近440,采用移多补少的方法求和.解:原式=6−×+(÷)440146=439例3.482594115932359×+×−×解析:先改变运算顺序,带着符号搬家,把4159×与×与32359×交换位置,4825932359×都有公共因数59,用乘法分配律将48259×与32359×的差算出再与41159×求和.解:原式482593235941159=×−×+×59(482323)41159=×−+×5915941159=×+×159(5941)=×+159100=×15900=【巩固】9999222233333334×+×解析:数虽然比较大,但是仔细观察就能发现有共同之处,可以进行拆数找到相同的因数,再利用乘法分配律进行计算.解:原式=33343333222233333×+××=)33346666(3333+×=100003333×=33330000例4.10099989796321+−+−++−+⋯解析:仔细观察就会发现:符号是交替出现的,这是一个等差数列,从后向前看从1到100一共是100个数,从前向后看不管100和1,中间部分两数相减的差都是1,中间部分是98个,两个一组有98÷2=49个1.解:原式100(9998)(9796)(32)1=+−+−++−+⋯100491=++150=【巩固】989796959493929190894321+−−++−−++−−−++⋯解析:加减交替出现,观察可知两加两减结果是98+97-96-95=4,最后的2和1不算在内,可知四个一组有244)298(=÷−个4.解:原式=12)3456(...)91929394()95969798(++−−+++−−++−−+=3244+×=99例5.200920102010201020092009×−×解析:仔细观察每一个数,找出它们的共同特点,20102010可分解成201010001×这是四位数的复写如10001,abcd abcdabcd ×=三位数的复写1001,abcabc ×=abc 二位数的复写101,ab abab ×=这个规律在简便运算中常用到.解:原式20092010100012010200910001=××−××0=【巩固】9898989899999999101010111111111×÷÷解析:因为abababab ab =×1010101,aaaaaaaa a =×11111111.解:原式=111111111010101111111119101010198÷÷×××=998×=882例6.(11637)(163756)(1163756)(1637)++×++−+++×+解析:设数法.可将某些括号内的数用字母代替,设163756a ++=,1637b +=,这样就达到简便的目的.也可用口诀来解答.解:方法一:设163756a ++=1637b+=(11637)(163756)(1163756)(1637)++×++−+++×+=(1)(1)b a a b+×−+×=a ab b ab+−−=a b −(,a b 分别用原式代入)=1637561637++−−=56方法二:观察算式,记口诀:有头无尾,无头有尾,有头有尾,无头无尾,结果头乘尾.算式中1为头,56为尾.原式=561×=56【巩固】(31735)(173549)(3173549)(1735)++×++−+++×+解:设a =++35173,b=+3517原式=ba b a ×+−+×)49()49(=bab a ab 4949−−+=)(49b a −×=)351735173(49−−++×=349×=147课后作业1.(1351989)(2461988)++++−++++=⋯⋯解析:按照等差数列的分组求和方法,前括号从第二项开始每项的数比后面括号中的相应的数大1,可以进行分组,此为方法1;另一方法,按照等差数列求和公式分别求出两者之和再相减.解:法1:原式=1+++−⋯3(+−−1988)21989)(5()4=1×÷21+1988=995法2:求项公式:(末项-首项)÷公差+1;前括号有:9952-2+÷(项)11988=)12−项;后括号有:99419891÷+(=原式=2+−×+(÷×÷1988994)19892(2)1995=989030990025−=9952.389387383385384386388++++++=解析:找基准数,这几个数都和385接近,采用多加,少减的方法解:原式=3−+++×+−711385+242=27023.777777777777777++++=解析:将7按照所在的数位来计算,解:原式=70000+××××++527+37000470700=70000+++21001400028035+=864154.999995++++998997996解析:凑整法解:原式=1+−−+−+−+10001000210001000−3541000=155000−=49855.2008++++++2005(÷2006)20102011200720082009解析:括号里的数移多补少正好都能凑成2008共有7个,所以是2008的7倍.解:原式=2008×72008÷=76.12345×+×−999899991234512345×解析:数比较大,但是仍然符合乘法分配律的情况解:原式=)+×(12345−9998999=1000012345×=1234500007.1234314243212413+++解析:数字1、2、3、4,在个位.十位.百位.千位上均各出现一次.解:原式1111222233334444=+++1111(1234)=×+++111110=×11110=8.�100100100111222333÷⋯⋯⋯������个个个的结果解:�100100100111222333÷⋯⋯⋯������个个个��10010010099099311122211131000233334=÷÷=÷=⋯⋯⋯���⋯�����⋯�����个个个个个9.计算889899899989999++++解析:观察题目的特点发现:8可以看作19−,可以看作190−,899可以看作1900−……,又是连加的算式.根据这个特点,可以看作9,90,900,9000与90000的和再减去5个1的和.解:899998999899898++++=19000019000190019019−+−+−+−+−=51)900009000900909(×−++++=599999−=99994还可以这样想:889899899989999++++=)189999()18999()1899()189(4++++++++=900009000900904++++=9999410.486250480375×+×解:原式=480625480375×+×)625375(480+×=1000480×=480000=。
小升初数学衔接课讲义(160页)(衔接版)(含答案)
小升初数学衔接课讲义(160页)(衔接版)(含答案)目录第一讲巧算 (1)第二讲行程和工程问题 (9)第三讲和差倍鸡兔同笼 (14)第四讲几何专题 (20)第五讲整数和整除 (54)第六讲素数合数分解素因数 (59)第七讲最大公因数与最小公倍数 (64)第八讲分数的意义和性质 (70)第九讲分数的运算 (75)第十讲分数与小数的互化 (81)第十一讲分数混合运算及应用 (85)第十二讲比的意义和性质 (96)第十三讲比例 (100)第十四讲百分比的意义 (108)第十五讲百分比的应用及等可能事件 (114)答案 (130)第一讲巧算一、【考点解读】测量物体时往往会得不到整数,于是就用小数来补充整数。
小数是十进制分数的一种特殊表现形式。
分母是10 ,100,1000……的分数也可以用小数表示。
二、【知识讲解】加法运算定律加法交换律加法交换律的概念为:两个加数交换位置,和不变。
同时从字母公式:a+b+c=(b+a)+c加法结合律加法结合律的概念为:先把前两个数相加,或者先把后两个数相加,和不变。
字母公式:a+b+c=a+(b+c)乘法运算定律乘法交换律乘法交换律的概念为:两个因数交换位置,积不变。
字母公式:a×b=b×a乘法结合律乘法结合律的概念为:先乘前两个数,或者先乘后两个数,积不变。
字母公式:a×b×c=a×(b×c)乘法分配律乘法分配律的概念为:两个数与一个数相乘,可以先把它们与这个数分别相乘,再相加。
字母公式:(a+b)×c=a×c+b×c减法性质减法性质的概念为:一个数连续减去两个数,可以先把后两个数相加,再相减。
字母公式:A-B-C=A-(B+C)差不变的规律字母公式:A-B=(AN)-(BN)=(A-B)/N (N≠0 B≠0)除法的性质除法性质的概念为:一个数连续除以两个数,可以先把后两个数相乘,再相除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲 计算专题在小升初的分数计算中,掌握一些实用的简便方法,可以提高同学们的计算能力,达到速算、巧算的目的。
(1)约分法:在分数乘除的过程中可以巧妙的拆分,从而达到先约分再计算,可以使计算过程更加简便。
(2)设数法:根据算式中数字的特点,用字母代表数字或算式,可以化繁为简,达到简算的目的。
(3)拆分法:根据算式的特点,通过拆分方便约分,从而达到简便运算。
(4)乘积不变的规律,商不变的规律。
计算:15 × 27 + 35 × 41【解析】:在分数的计算的过程中,可以巧妙的拆分,从而使计算的过程更加简便。
原式=35 × 9 + 35 × 41=35 ×(9 + 41)=35 × 50=301、用简便方法计算:16.205.20115.207.201⨯-⨯【解析】:原式2、用简便方法计算:15 × 27 + 35 × 41【解析】: 原式=35 × 9 + 35 × 41=35 ×(9 + 41)015.201.05.2015.201)16.2017.20=⨯=⨯-=(=35 × 50=30把纯循环小数化分数:【解析】:1、.将下列循环小数化为分数【解析】:(2)先看小数部分335.02、请将算式•••++100.010.01.0的结果写成最简分数 【解析】:原式11110010111137990900900900300++=++===计算:(1 + 12 + 13 + 14 )×(12 + 13 + 14 + 15 )-(1+ 12 + 13 + 14 + 15 )×(12 + 13 + 14 )【解析】:观察算式,直接算会很麻烦,这时巧用字母代替算式中的某个算式,即令1 + 12 + 13 + 14 =a , 12 + 13 + 14 =b ,化繁为简,从而达到简算。
设1 + 12 + 13 + 14 =a 12 + 13 + 14 =b原式=a ×(b + 15 )-(a + 15 )× b=ab + 15 a - ab - 15 b=15 (a -b )=151、用简便方法计算:)201612015120141()201712016120151201411()20171201612015120141()2016120151201411(++⨯++++-+++⨯+++ 【解析】:设 则原式=2、用简便方法计算:)4332)(5443321()544332)(43321(++++-++++【解析】:设则原式=计算:12×4 + 14×6 + 16×8 +…..+ 148×50b 20171201612015120141,a 201612015120141=+++=++==+-+=a-b a)b 1(b )a 1(20171b 544332,a 4332=++=+==+-+=a -b a)b 1(b )a 1(54【解析】:在遇到这样的分数求和时,肯定不能去通分求和,这里要用到的也是拆分法,即对算式里的分数进行拆分,和例题一中不同的是把算式里的每一项进行拆分后都扩大了2倍,所以在最后要乘以21,这样就是我们要求的结果。
25621251221501-2121501-48181-6161-4141-212150482862642422=⨯=⨯=⨯++++=⨯⨯++⨯+⨯+⨯= L L 1、计算:113 -712 +920 -1130 +1342 -1556 【解析】:则原式=878776766565545443433131⨯+-⨯++⨯+-⨯++⨯+-⨯+ =)8171()7161()6151()5141()4131(311+-+++-+++-+ =811- =87 2、计算:12 + 14 + 18 + 116 + 132 + 164【解析】: 6463641-1641-641641321161814121==++++++=)(原式观察:,,3⊗1.5=3×5+1.5×3=19.5,…(1)m ⊗n=m × 5 +n × 3(2)若,请求出x . 【解析】:(1)m ⊗n=m ×5+n ×3;故答案为:5;3.(2),x×5+×3=2,5x+=2,5x=2﹣,5x=,x=÷5,x=×,x=.1、如果m,n表示两个数,那么规定:m¤n=4n-(m+n)÷2。
求3¤(4¤6)¤12的值。
【解析】:3¤(4¤6)¤12=3¤[4×6-(4+6)÷2]¤12=3¤19¤12=[4×19-(3+19)÷2]¤12=65¤12=4×12-(65+12)÷2=9.52、如果a※b=3a﹣2b,当x※5比5※x大5时,x= 6 .【解析】:x※5=3x﹣2×5=3x﹣10,5※x=3×5﹣x×2=15﹣2x,而x※5﹣5※x=5,即3x﹣10﹣(15﹣2x)=5,3x﹣10﹣15+2x=5,5x=5+25,5x=30,x=6,故答案为:6.用简便方法计算:245 ×23.4+11.1×57.6+6.54×28【解析】:原式用简便方法计算:(927 +729 )÷(57 +59 )【解析】:原式12 + 14 + 18 + 116 + 132 + 164【解析】: 6463641-1641-641641321161814121==++++++=)(原式888801.116.574.221.16.571.111.1188.26.571.118.888.26.571.114.654.238.26.571.114.658.24.238.2=⨯=+⨯=⨯+⨯⨯=⨯+⨯=⨯++⨯=⨯+⨯+⨯=)()(13)9171()9171(565)9575()965765(=⎥⎦⎤⎢⎣⎡+÷+⨯÷=+÷+=【解析】:原式计算: •••⨯800.2400.2(结果用最简分数表示)【解析】:原式=481804200636188249047065606224900999900999899100224775224775⨯=⨯===解简易方程:如果我们规定:a ☆b=a+2b ,则方程x ☆2=3☆(2☆3)的解.【解析】:x ☆2=3☆(2☆3),x+2×2=3☆(2+3×2),x+4=3☆8,x+4=3+8×2,x+4=19,x=19﹣4,x=15.用简便方法计算:59 ×791617 +50×19 +19 ×517【解析】:原式用简便方法计算:1993×1994-11993+1992×1994 3029201912116521++++614655)6151514141313121211(565115411431132112111=-=-+-+-+-+--=⨯-+⨯-+⨯-+⨯-+⨯-=5090951711017167995=⨯=++⨯=)(【解析】:原式用简便方法计算:(18 +19 +110 +111 )×(19 +110 +111 +112 )-(18 +19 +110 +111 +112 )×(19 +110 +111 )【解析】:设,则原式计算: 14 + 128 + 170 + 1130 + 1208 【解析】:原式····110.150.2180.3111⎛⎫+⨯⨯ ⎪⎝⎭; ⑵ ()2.2340.9811-÷ (结果表示成循环小数) 【解析】:⑴原式1512182311909909111--⎛⎫=+⨯⨯ ⎪⎝⎭371111123456790.01234567999311181999999999=⨯⨯=== ⑵23422322.23422990990-==,980.9899=,所以23298242222.2340.982119909999090-=-==, ()22122.2340.98111110.090.020.113901190-÷=÷=+=+= 119941992199319931994199219941992199311994)11992(=⨯++⨯=⨯+-⨯+=b 12111110191,a 11110191=+++=++96112181)a -b (81b)a 81(-b )a 81(=⨯==++=165161531161-131131-101101-7171-4141-13116131131011071741411=⨯=++++⨯=⨯+⨯+⨯+⨯+⨯=)(“△”是一种新的运算规则,先观察下面的式子,再按规则计算.3△5=(3+5)÷2=4,12△2=(12+2)÷2=7,△=(+)÷2=问:试求5.5△x=7的未知数x.【解析】:5.5△x=7,(5.5+x)÷2=7,5.5+x=14,x=14﹣5.5,x=8.5,答:5.5△x=7的未知数x的值是8.5.。
