2012年东城初三二模数学试题及答案
2012年北京市中考数学二模试题中几何压轴题汇编

2012年北京市中考数学二模试题中几何压轴题汇编(2012东城二模24.) 已知:等边ABC ∆中,点O 是边AC,BC 的垂直平分线的交点,M,N 分别在直线AC , BC 上,且60MON ∠= .(1) 如图1,当CM=CN 时, M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN三者之间的数量关系;(2) 如图2,当CM ≠CN 时,M 、N 分别在边AC 、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3) 如图3,当点M 在边AC 上,点N 在BC 的延长线上时,请直接写出线段AM 、CN 、MN 三者之间的数量关系.(2012丰台二模24.)在△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P 作PE ⊥AC 于点E ,PF ⊥AB 于点F .(1)如图1,当AB =AC 时,判断的DE 与DF 的数量关系,直接写出你的结论;(2)如图2,当AB ≠AC ,其它条件不变时,(1)中的结论是否发生改变?请说明理由.图1 图2(2012大兴二模23.)在△ABC 中,AB =AC ,点P 为△ABC 所在平面内一点,过点P 分别作PE ∥AC 交AB 于点E ,PF ∥AB 交BC 于点D ,交AC 于点F .AEFPB D CCE AD F P(1)如图1,若点P 在BC 边上,此时PD =0,易证PD ,PE ,PF 与AB 满足的数量关系是PD +PE +PF =AB ;当点P 在△ABC 内时,先在图2中作出相应的图形,并写出PD ,PE ,PF 与AB 满足的数量关系,然后证明你的结论;(2)如图3,当点P 在△ABC 外时,先在图3中作出相应的图形,然后写出PD ,PE ,PF 与AB 满足的数量关系.(不用说明理由)(2012密云二模25.)已知菱形ABCD 的边长为1,60ADC ∠=,等边△AEF 两边分别交DC 、CB 于点E 、F .(1)特殊发现:如图1,若点E 、F 分别是边DC 、CB 的中点,求证:菱形ABCD 对角线AC 、BD 的交点O 即为等边△AEF 的外心;(2)若点E 、F 始终分别在边DC 、CB 上移动,记等边△AEF 的外心为P . ①猜想验证:如图2,猜想△AEF 的外心P 落在哪一直线上,并加以证明;②拓展运用:如图3,当E 、F 分别是边DC 、CB 的中点时,过点P 任作一直线,分别交DA 边于点M ,BC 边于点G ,DC 边的延长线于点N ,请你直接写出11DM DN+的值.(2012平谷二模24.)如图1,若四边形ABCD 、GFED 都是正方形,显然图中有AG =CE ,AG ⊥CE .(1)当正方形GFED 绕D 旋转到如图2的位置时,AG =CE 是否成立?若成立,请给出证明,若不成立,请说明理由;(2)当正方形GFED 绕D 旋转到B ,D ,G 在一条直线 (如图3)上时,连结CE ,设CE 分别交AG 、AD 于P 、H .① 求证:AG ⊥CE② 如果AD =4,DGCE 的长.ADEF G AD EFGA(2012延庆二模24.) (1)如图1:在△ABC 中,AB=AC ,当∠ABD =∠ACD=60°时,猜想AB 与BD+CD 数量关系,请直接写出结果 ;(2)如图2:在△ABC 中,AB=AC ,当∠ABD =∠ACD=45°时,猜想AB 与BD+CD 数量关系并证明你的结论; (3)如图3:在△ABC 中,AB=AC ,当∠ABD =∠ACD=β(20°≤β≤70°)时,直接写出AB 与BD+CD 数量关系(用含β的式子表示)。
2012年北京东城区中考二模数学试卷

2012年北京东城中考二模数 学2012年6月一、选择题(本题共 32 分,每小题 4 分)下面各题均有四个选项,其中只有一个是符合题意的 1.9的算术平方根是A .-9B .9C .3D .±32.如图,由几个小正方体组成的立体图形的俯视图是3.下列运算正确的是A .532a a a B .532a a a C .3332)(ba ab D .5210a a a 4.抛掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点数为奇数的概率为 A .16B .14C .13D .125.如果一个多边形的内角和是其外角和的2倍,那么这个多边形是A .六边形B .五边形C .四边形D .三角形6.在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调查.四个城市5个月香蕉价格的平均值均为3.50元,方差分别为2S 甲=18.3,2S 乙=17.4,2S 丙=20.1,2S 丁=12.5.一至五月份香蕉价格最稳定的城市是 A .甲B .乙C .丙D .丁7.如图,在平行四边形ABCD 中,E 为AD 的中点,DEF △的周长为1,则BCF △的周长为A .1B .2C .3D .48.如右图,正方形ABCD 的顶点A ,B ,顶点C D 、位于第一象限,直线:(0l x t t 将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为S ,则S 关于t 的函数图象大致是二、填空题(本题共16分,每小题4分)9.x 的取值范围是.10.一个扇形的圆心角为120°,半径为1,则这个扇形的弧长为.11.观察下列等式: 1=1,2+3+4=9, 3+4+5+6+7=25, 4+5+6+7+8+9+10=49,……照此规律,第5个等式为.12.如图,正方形ABCD 内接于⊙O ,⊙O 的半径为2,以圆心O 为顶点作 ∠MON ,使∠MON =90°,OM 、ON 分别与⊙O 交于点E 、F ,与正方形ABCD 的边交于点G 、H , 则由OE 、OF 、EF ⌒及正方形ABCD 的边围成的图形(阴影部分)的面积S= .三、解答题(本题共30分,每小题5分)13.0(4)6cos302 o .14.解方程组212x y x y,.15.已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线.求证:AB =DC .16.先化简,再求值:2212111x x x x,其中2x .17.列方程或方程组解应用题:小明家有一块长8m 、宽6m 的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的x 值.18.如图,在平面直角坐标系xOy 中,直线AB 与反比例函数k y x的图像交于点A(-3,4),AC ⊥x 轴于点C.(1)求此反比例函数的解析式;(2)当直线AB 绕着点A 转动时,与x 轴的交点为B(a,0), 并与反比例函数ky x图象的另一支还有一个交点的情形下,求△ABC 的面积S 与a 之间的函数关系式.并写出自变量a 的取值范围.四、解答题(本题共20分,每小题5分)19.在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:(1)a= ,b= ;(2)在扇形统计图中,B 组所占圆心角的度数为 ;(3)全校共有1000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?20. 如图,在平行四边形ABCD 中,5AB ,8BC ,AE BC 于点E ,53cos B ,求tan CDE 的值.21.如图,在矩形ABCD 中,点O 在对角线AC 上,以OA 长为半径的O ⊙与AD ,AC 分别交于点E ,F ,∠ACB =∠DCE .(1)请判断直线CE 与O ⊙的位置关系,并证明你的结论;(2)若 DE:EC=1 2BC ,求⊙O 的半径.22.阅读并回答问题:小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程21x 时,突发奇想:21x 在实数范围内无解,如果存在一个数i ,使21i ,那么当21x 时,有x i ,从而x i 是方程21x 的两个根.据此可知:(1) i 可以运算,例如:i 3=i 2·i =-1×i =-i ,则i 4=,i 2011=______________,i 2012=__________________;(2)方程2220x x 的两根为(根用i 表示)五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的方程2(1)(4)30m x m x .(1) 若方程有两个不相等的实数根,求m 的取值范围;(2) 若正整数m 满足822m ,设二次函数2(1)(4)3y m x m x 的图象与x 轴交于A B、两点,将此图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线3y kx 与此图象恰好有三个公共点时,求出k 的值(只需要求出两个满足题意的k 值即可).24.已知:等边ABC中,点O 是边AC,BC 的垂直平分线的交点,M,N 分别在直线AC , BC 上,且60MON o .(1) 如图1,当CM=CN 时, M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN 三者之间的数量关系;(2) 如图2,当CM ≠CN 时,M 、N 分别在边AC 、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3) 如图3,当点M 在边AC 上,点N 在BC 的延长线上时,请直接写出线段AM 、CN 、MN 三者之间的数量关系.25.如图,在平面直角坐标系xOy 中,已知二次函数2+2y ax ax c 的图像与y 轴交于点(0,3)C ,与x轴交于A、B两点,点B的坐标为(-3,0)(1)求二次函数的解析式及顶点D的坐标;(2)点M是第二象限内抛物线上的一动点,若直线OM把四边形ACDB分成面积为1:2的两部分,求出此时点M的坐标;(3)点P是第二象限内抛物线上的一动点,问:点P在何处时△CPB的面积最大?最大面积是多少?并求出此时点P的坐标.数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3.评分参考中所注分数,表示考生正确做到此步应得的累加分数.一、选择题(本题共32分,每小题4分)二、填空题(本题共16分,每小题4分)三、解答题:(本题共30分,每小题5分)13.解:原式=164L L分=1……5分14.解:①②得:23x x1x .……2分将1x 代入②得:12y,1y ……4分11xy……5分15.证明:∵AC平分BCD BC∠,平分ABC∠,∴ACB DBC∠∠……2分在ABC△与DCB△中,A B C D C B A C B D B C B C B C∠∠∠∠ ABC △DCB ≌△……4分AB DC .……5分16.解:原式=22111111111x x x x x x x x x x x x ·……3分当2x时,原式=211.22……5分 17.解:据题意,得1(8)(6)862x x .解得12122x x ,.1x 不合题意,舍去.2x .18.解: (1)∵4=3k12k ∴12y x……2分(2)∵BC =a -(-3)=a +3AC =4,∴14(3)2ACB S a……4分=2a +6 (a >-3)……5分四、解答题(本题共20分,每小题5分) 19.解:(1) 15,0.16;……2分(2)144 ;……3分(3)271000[(1584)50]100054050(人)……5分 答:该校平均每周做家务时间不少于4小时的学生约有540人 20.解: 在△ABE 中,AE BC ,5AB ,53cosB∴BE=3,AE=4. ∴EC=BC-BE =8-3=5.∵平行四边形ABCD,∴CD=AB=5.∴△CED 为等腰三角形.……2分 ∴∠CDE =∠CED . ∵ AD//BC, ∴∠ADE =∠CED . ∴∠CDE =∠ADE .在Rt △ADE 中,AE =4,AD=BC =8,41tan .82CDE21.解:(1)直线CE 与O ⊙相切证明:∵矩形ABCD , ∴BC//AD ,∠ACB =∠DAC . ∵,ACB DCE ∴.DAC DCE ……1分连接OE,则.DAC AEO DCE 90,90.90.2DCE DEC AEO DEC OEC o ooQ L L 分∴直线CE 与O ⊙相切.22222AB(2)tan2,tan3,tan Dtan D 1.,4,CO3,54ACB BCBCAB BC ACB ACACB DCECEDE DC CERt CDE CEO Rt CE OCE EOr rQL LQLL L分在中分设⊙的半径为r, 则在中即解得分22.解:(1)4i 1,2011i -i 20121i ……3分(2)方程2220x x的两根为1+i和1-i……5分五.解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.解:(1)2(4)12(1)m m2(2)m.……2分由题意得,2(2)m >0且10m.∴符合题意的m的取值范围是21m m且的一切实数.……3分(2)∵正整数m满足822m,∴m可取的值为1和2.又∵二次函数2(1)(4)3y m x m x,∴m=2.……4分∴二次函数为2-23y x x.∴A点、B点的坐标分别为(-1,0)、(3,0).依题意翻折后的图象如图所示.由图象可知符合题意的直线3y kx经过点A、B.A可求出此时k 的值分别为3或-1.……7分注:若学生利用直线与抛物线相切求出k =2也是符合题意的答案.24.解: (1) AM CN MN ……2分(2)AM CN MN ……3分证明:过点O 作,,OD AC OE BC 易得,120,OD OE DOE o在边AC 上截得DN’=NE ,连结ON ’, ∵ DN ’=NE , OD =OE , ∠ODN ’=∠OEN'.DON EON ……4分∴ON’=OE. ∠DON ’=∠NOE .120,DOE oQ 60,MON o∴∠MOD +∠NOE=600.∴∠MOD +∠DON ’=600.易证'MON MON .……5分∴MN’=MN.'.,,()(),.MN MD DN MD NE MD AM AD AM CE NE CE CN MN AM CE CE CN AM CN AM CN MN (3) .MN CN AM ……7分25.解:(1)由题意,得:3,9-60.c a a c…解得:-1,3.a c所以,所求二次函数的解析式为:2--23y x x ……2分顶点D 的坐标为(-1,4).……3分 (2)易求四边形ACDB 的面积为9. 可得直线BD 的解析式为y=2x+6设直线OM 与直线BD 交于点E ,则△OBE 的面积可以为3或6. ①当1=9=33OBE S 时,易得E 点坐标(-2,-2),直线OE 设M 点坐标(x ,-x ),212---2 3.-122x x x x x (舍),∴-1-1(22M , ……4分②当1=9=63OBE S 时,同理可得M ∴ M 点坐标为(-1,4)……5分(3)连接OP ,设P 点的坐标为 ,m n ,因为点P 在抛物线上,所以所以PB PO OPB OB S S S S △C △C △△C ……6分111()222OC m OB n OC OB 339332222m n n m 22333273.2228m m m……7分因为3<0m,所以当32m 时,154n . △CPB 的面积有最大值27.8 ……8分所以当点P 的坐标为315(,)24 时,△CPB 的面积有最大值,且最大值为27.8。
2012年北京市东城区、西城区、海淀区初三数学二模试题及答案
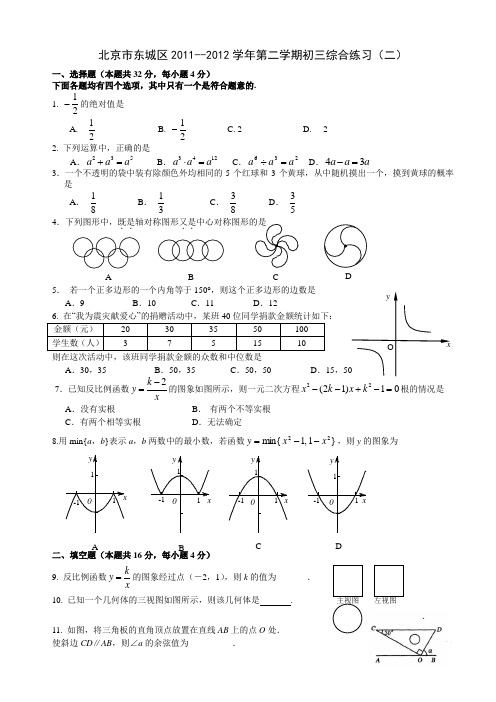
北京市东城区 2011--2012 学年第二学期初三综合练习(二)一、选择题(本题共 32 分,每小题 4 分) 下面各题均有四个选项,其中只有一个是符合题意的. 1. 1 2的绝对值是1 2A.B. 1 2C. 2D.-22. 下列运算中,正确的是 A. a a a B. a a a C. a a a D. 4 a a 3 a 3.一个不透明的袋中装有除颜色外均相同的 5 个红球和 3 个黄球,从中随机摸出一个,摸到黄球的概率 是2 3 5 3 4 12632A.1 8B.1 3C.3 8D.3 54.下列图形中,既是轴对称图形又是中心对称图形的是 .. ..D B C A 5. 若一个正多边形的一个内角等于 150° ,则这个正多边形的边数是 A.9 B.10 C.11 D.12 6. 在“我为震灾献爱心”的捐赠活动中,某班 40 位同学捐款金额统计如下: 金额(元) 学生数(人) 20 3 30 7 35 5 50 15 100 10 D.15,502 2y则在这次活动中,该班同学捐款金额的众数和中位数是 A.30,35 B.50,35 C.50,50 7.已知反比例函数 y A.没有实根 C.有两个相等实根k2 xOx的图象如图所示,则一元二次方程 x ( 2 k 1) x k 1 0 根的情况是 B. 有两个不等实根 D.无法确定2 28.用 min{a,b}表示 a,b 两数中的最小数,若函数 y min{ x 1, 1 x } ,则 y 的图象为y1 1 xy1y1y1 1 x -1-1 0-1 01 x-1 001 xA B 二、填空题(本题共 16 分,每小题 4 分)CD9. 反比例函数 y k x的图象经过点(-2,1) ,则 k 的值为_______. .主视图 俯视图 左视图10. 已知一个几何体的三视图如图所示,则该几何体是 11. 如图,将三角板的直角顶点放置在直线 AB 上的点 O 处. 使斜边 CD∥AB,则∠a 的余弦值为__________.12. 如图, R t △ A B C 中, A C B 9 0 , C A B 3 0 , B C 2 ,O, H 分别为边 A B, A C 的中点,将 △ A B C 绕点 B 顺时针旋A1转 1 2 0 到 △ A1 B C 1 的位置,则整个旋转过程中线段 O H 所扫过 部分的面积(即阴影部分面积)为 三、解答题(本题共 30 分,每小题 5 分)2 13. 先化简,再求值: (2 x 1) ( x 2)( x 2) 4 x ( x 1) ,其中 x H A OC B.O1H1 C13 3 2.14. 解分式方程:x 1 x 21 2 x 3.15. 如图, A、 、 的坐标分别为 点 B C (3, 、 3) (2, 、 1) (5, , 1) 将△ABC 先向下平移 4 个单位, 得△A1B1C1; 再将△A1B1C1 沿 y 轴翻折,得△A2B2C2. (1)画出△A1B1C1 和△A2B2C2; A (2)求线段 B2C 长. B O C x y16. 如图,点 D 在 A B 上, D F 交 A C 于点 E , C F ∥ A B , A E E C . 求证: A D C F . A D B E FC17. 列方程或方程组解应用题 为了配合学校开展的“爱护地球母亲”主题活动,初三(1)班提出“我骑车我快乐”的口号. “五一”之后小 明不用父母开车送,坚持自己骑车上学. 五月底他对自己家的用车情况进行了统计,5 月份所走的总路程 比 4 月份的4 5还少 100 千米,且这两个月共消耗 93 号汽油 260 升. 若小明家的汽车平均油耗为 0.1 升/千米,求他家 4、5 两月各行驶了多少千米.18.如图,矩形 ABCD 的边 AB 在 x 轴上,AB 的中点与原点 O 重合,AB=2,AD=1,点 Q 的坐标为(0,2). (1)求直线 QC 的解析式; (2)点 P(a,0)在边 AB 上运动,若过点 P、Q 的直线将矩形 ABCD 的周长分成 3∶1 两部分,求出此时 a 的值.四、解答题(本题共 20 分,每小题 5 分) 19. 如图,在梯形 ABCD 中,AD//BC,BD 是∠ABC 的平分线. (1)求证:AB=AD;A D(2)若∠ABC=60° ,BC=3AB,求∠C 的度数BC20. 如图,四边形 ABCD 是平行四边形,以 AB 为直径的⊙O 经过点 D,E 是⊙O 上一点,且AED=45. (1) 试判断 CD 与⊙O 的位置关系,并证明你的结论; (2) 若⊙O 的半径为 3,sinADE=5 6,求 AE 的值.21.某商店在四个月的试销期内,只销售 A,B 两个品牌的电视机,共售出 400 台.试销结束后,将决定 经销其中的一个品牌.为作出决定,经销人员正在绘制两幅统计图,如图 l 和图 2. (1)第四个月销量占总销量的百分比是_______; (2)在图 2 中补全表示 B 品牌电视机月销量的折线图; (3)经计算,两个品牌电视机月销量的平均水平相同,请你结合折线的走势进行简要分析,判断该商店 应经销哪个品牌的电视机.图1图222. 如图 1 是一个三棱柱包装盒, 它的底面是边长为 10cm 的正三角形, 三个侧面都是矩形. 现将宽为 15cm 的彩色矩形纸带 AMCN 裁剪成一个平行四边形 ABCD(如图 2) ,然后用这条平行四边形纸带按如图 3 的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分) ,纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图 3 中,将三棱柱沿过点 A 的侧棱剪开,得到如图 4 的 侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究. (1)请在图 4 中画出拼接后符合条件的平行四边形; (2)请在图 2 中,计算裁剪的角度(即∠ABM 的度数).A MDNB图2C图1D F A图4C E B五、解答题(本题共 22 分,第 23 题 7 分,第 24 题 7 分,第 25 题 8 分) 23. 已知关于 x 的一元二次方程 x 2 ax b 0 , a 0 , b 0 .2 2(1)若方程有实数根,试确定 a,b 之间的大小关系;(2)若 a∶b=2∶ 3 ,且 2 x1 x 2 2 ,求 a,b 的值; (3)在(2)的条件下,二次函数 y x 2 a x b 的图象与 x 轴的交点为 A、C(点 A 在点 C 的左侧) ,2 2与 y 轴的交点为 B,顶点为 D.若点 P(x,y)是四边形 ABCD 边上的点,试求 3x-y 的最大值.24. 如图 1,在△ ABC 中,AB=BC=5,AC=6. △ ECD 是△ ABC 沿 CB 方向平移得到的,连结 AE,AC 和 BE 相交于点 O. (1)判断四边形 ABCE 是怎样的四边形,并证明你的结论; (2) 如图 2, 是线段 BC 上一动点 P (不与点 B、C 重合) 连接 PO 并延长交线段 AE 于点 Q, , QR⊥BD, 垂足为点 R.①四边形 PQED 的面积是否随点 P 的运动而发生变化?若变化,请说明理由;若不变,求出四边 形 PQED 的面积; ②当线段 BP 的长为何值时,以点 P、Q、R 为顶点的三角形与△ BOC 相似?E Q AEAOODC 图1BDC R 图2PB25. 如图,已知在平面直角坐标系 xOy 中,直角梯形 OABC 的边 OA 在 y 轴的正半轴上,OC 在 x 轴的正半 轴上,OA=AB=2,OC=3,过点 B 作 BD⊥BC,交 OA 于点 D.将∠DBC 绕点 B 按顺时针方向旋转, 角的两边分别交 y 轴的正半轴、x 轴的正半轴于点 E 和 F. (1)求经过 A、B、C 三点的抛物线的解析式; (2)当 BE 经过(1)中抛物线的顶点时,求 CF 的长; (3)在抛物线的对称轴上取两点 P、Q(点 Q 在点 P 的上方) ,且 PQ=1,要使四边形 BCPQ 的周长最 小,求出 P、Q 两点的坐标. y E A D O F C x B北京市东城区 2010--2011 学年第二学期初三综合练习(二) 数学试卷参考答案一、选择题(本题共 32 分,每小题 4 分)题 号 答 案 题 号 答 案1 A 9 -22 D3 C 10 圆柱4 B5 D 111 26 C7 A 12 π8 A二、填空题(本题共 16 分,每小题 4 分)三、解答题: (本题共 30 分,每小题 5 分) 13. (本小题满分 5 分) 解: 原式 4 x 4 x 1 x 4 4 x 4 x2 2 2„„„„„„3 分 „„„„„„4 分 x 3 .2当x 3 3 2时 , 27 15 3 . 3 4 4 23 3 原式 2 „„„„„„5 分14. (本小题满分 5 分) 解:x 1 x2 1 x2 3„„„„„„1 分去分母得 x-1+1=3(x-2) 解得 x=3. 经检验:x=3 是原方程的根. 所以原方程的根为 x=3.„„„„„„4 分 „„„„„„5 分15. (本小题满分 5 分) 解: (1)A1 点的坐标为(3,-1) 1 点的坐标为(2,-3) 1 点的坐标为(5,-3) ,B ,C ; A2 点的坐标为(-3,-1) 2 点的坐标为(-2,-3) ,B , C2 点的坐标为(-5,-3). 图略,每正确画出一个三角形给 2 分. (2)利用勾股定理可求 B2C= 16. (本小题满分 5 分) 证明:∵ C F ∥ A B , ∴ ∠A=∠ACF, ∠ADE=∠CFE. 在△ADE 和△CFE 中, ∠A=∠ACF, ∠ADE=∠CFE, AE EC , ∴ △ADE≌△CFE. ∴ AD CF . -------2 分 A D --------4 分 ------5 分 B E F65 .„„„„„„5 分C17. (本小题满分 5 分) 解:设小刚家 4、5 两月各行驶了 x、y 千米.--------------------------1 分4 y x 100 , 依题意,得 5 0 . 1 x 0 . 1 y 260 . ----------------------------3 分解得, x 1 5 0 0 . y 1100-------------------------------4 分答:小刚家 4 月份行驶 1500 千米,5 月份行驶了 1100 千米. -----------5 分18. (本小题满分 5 分) 解: (1)由题意可知 点 C 的坐标为(1,1) . „„„„„„„„„„„„„1 分 设直线 QC 的解析式为 y kx b . ∵ 点 Q 的坐标为(0,2), ∴ 可求直线 QC 的解析式为 y x 2 .„„„„„„„„„„„„„2 分 (2)如图,当点 P 在 OB 上时,设 PQ 交 CD 于点 E,可求点 E 的坐标为( 则 AP AD DE 2 由题意可得 2 5 2 5 2 a 3(3 3 2 a) . a ,CE BC BP 3 3 2 a.a 2,1) .∴ a 1. „„„„„„„„„„„„„4 分 由对称性可求当点 P 在 OA 上时, a 1 ∴ 满足题意的 a 的值为 1 或-1. „„„„„„„„„„„„„5 分四、解答题(本题共 20 分,每小题 5 分) 19.(本小题满分 5 分) 解: (1)证明:∵BD 是∠ABC 的平分线, ∴ ∠1=∠2. ∵ AD//BC,∴∠2=∠3. ∴ ∠1=∠3. ∴AB=AD. ---------------------2 分1AD3B2EFC(2)作 AE⊥BC 于 E,DF⊥BC 于 F. ∴ EF=AD=AB. ∵ ∠ABC=60° ,BC=3AB, ∴ ∠BAE=30° . ∴ BE=1 2AB.BA∴ BF =23AB=21BC .∴ BD=DC . ∴ ∠C =∠2.∵ BD 是∠ABD 的平分线, ∴ ∠1=∠2=30°.∴ ∠C =30°. -------------------------5分20.(本小题满分5分)解:(1)CD 与圆O 相切. …………………1分 证明:连接OD ,则∠AOD =2∠AED =2⨯45︒=90︒. …………………2分 ∵四边形ABCD 是平行四边形,∴AB //DC .∴∠CDO =∠AOD =90︒.∴OD ⊥CD . …………………3分 ∴CD 与圆O 相切.(2)连接BE ,则∠ADE =∠ABE .∴sin ∠ADE =sin ∠ABE =65. …………………4分∵AB 是圆O 的直径,∴∠AEB =90︒,AB =2⨯3=6. 在Rt △ABE 中,sin ∠ABE =ABAE =65.∴AE =5 .21.(本小题满分5分)解:(1)30%; ……………………2分 (2)如图所示. ……………………4分(3)由于月销量的平均水平相同,从折线的走势看,A 品牌的月销量呈下降趋势,而B 品牌的月销量呈上升趋势.所以该商店应经销B 品牌电视机. …………………5分 22.(本小题满分5分)解:(1)将图4中的△ABE 向左平移30cm ,△CDF 向右平移30cm ,拼成如图下中的平行四边形,此平行四边形即为图2中的□ABCD .…………………2分(2)由图2的包贴方法知:AB 的长等于三棱柱的底边周长,∴AB =30.∵ 纸带宽为15,∴ sin ∠ABM =151302A M A B==.∴∠AMB =30°. …………………5分五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分)23.(本小题满分7分) 解:(1) ∵ 关于x 的一元二次方程2220x ax b ++=有实数根,∴ Δ=,04)2(22≥-b a 有a 2-b 2≥0,(a+b )(a-b )≥0. ∵ 0,0>>b a , ∴ a+b >0,a-b ≥0.∴ b a ≥. …………………………2分(2) ∵ a ∶b =2,∴ 设2,a k b ==.解关于x 的一元二次方程22430x kx k ++=,得 -3x k k =-或.当12,= -3x k x k =-时,由1222x x -=得2k =. 当123,= -x k x k =-时,由1222x x -=得25k =-(不合题意,舍去).∴ 4,a b ==. …………………………5分(3) 当4,a b ==时,二次函数2812y x x =++与x 轴的交点为、C 的交点坐标分别为A (-6,0)、(-2,0),与y 轴交点坐标为(0,12),顶点坐标D 为(-4,-4). 设z =3x -y ,则3y x z =-.画出函数2812y x x =++和3y x =的图象,若直线3y x =平行移动时,可以发现当直线经过点C 时符合题意,此时最大z 的值等于-6 ……………7分 24. (本小题满分7分)解:(1)四边形ABCE 是菱形.证明:∵ △ECD 是△ABC 沿BC 方向平移得到的,∴ EC ∥AB ,EC =AB .∴ 四边形ABCE 是平行四边形. 又∵ AB =BC ,∴四边形ABCE 是菱形. ……………2分(2)①四边形PQED 的面积不发生变化,理由如下: 由菱形的对称性知,△PBO ≌△QEO , ∴ S △PBO = S △QEO321GRQPOEDC BA∵ △ECD 是由△ABC 平移得到的, ∴ ED ∥AC ,ED =AC =6. 又∵ BE ⊥AC , ∴BE ⊥ED∴S 四边形PQED =S △QEO +S 四边形POED =S △PBO +S 四边形POED =S △BED=12×BE ×ED =12×8×6=24. ……………4分②如图,当点P 在BC 上运动,使以点P 、Q 、R 为顶点的三角形与△COB 相似. ∵∠2是△OBP 的外角, ∴∠2>∠3.∴∠2不与∠3对应 . ∴∠2与∠1对应 .即∠2=∠1,∴OP =OC =3 .过O 作OG ⊥BC 于G ,则G 为PC 的中点 . 可证 △OGC ∽△BOC . ∴ CG :CO =CO :BC . 即 CG :3=3:5 . ∴ CG =95.∴ PB =BC -PC =BC -2CG =5-2×95=75 .∴ BD =PB +PR +RF +DF =x +185+x +185=10.∴ x =75∴ BP =75. ……………7分25.(本小题满分8分) 解:(1)由题意得A (0,2)、B (2,2)、C (3,0).设经过A ,B ,C 三点的抛物线的解析式为y=ax 2+bx +2. 则⎩⎨⎧=++=++02390224b a b a解得 ⎪⎪⎩⎪⎪⎨⎧=-=3432b aH∴ 224233y x x =-++.……………2分(2)由224233y x x =-++=228(1)33x --+.∴ 顶点坐标为G (1,83).过G 作GH ⊥AB ,垂足为H . 则AH =BH =1,GH =83-2=23.∵ EA ⊥AB ,GH ⊥AB ,∴ EA ∥GH .∴GH 是△BEA 的中位线 . ∴EA =3GH =43.过B 作BM ⊥OC ,垂足为M . 则MB =OA =AB .∵ ∠EBF =∠ABM =90°,∴ ∠EBA =∠FBM =90°-∠ABF . ∴ R t △EBA ≌R t △FBM . ∴ FM =EA =43.∵ CM =OC -OM =3-2=1, ∴ CF =FM +CM =73.……………5分(3)要使四边形BCGH 的周长最小,可将点C 向上 平移一个单位,再做关于对称轴对称的对称点C 1,得点C 1的坐标为(-1,1). 可求出直线BC 1的解析式为1433y x =+.直线1433y x =+与对称轴x =1的交点即为点H ,坐标为(1,53).点G 的坐标为(1,23).……………8分海淀区九年级第二学期期末练习数 学 2012. 6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. -5的倒数是A .15B .15- C .5- D .52. 2012年4月22日是第43个世界地球日,中国国土资源报社联合腾讯网发起“世界地球日”微话题,共有18 891 511人次参与了这次活动,将18 891 511用科学记数法表示(保 留三个有效数字)约为A. 18.9⨯106B. 0.189⨯108C. 1.89⨯107D. 18.8⨯106 3. 把2x 2− 4x + 2分解因式,结果正确的是A .2(x − 1)2B .2x (x − 2)C .2(x 2− 2x + 1) D .(2x −2)24. 右图是由七个相同的小正方体堆砌而成的几何体, 则这个几何体的俯视图是A BCD 5.从1, -2, 3这三个数中,随机抽取两个数相乘,积为正数的概率是A .0B .13C.23D .16. 如图,在△ABC 中,∠C =90°,BC =3,D ,E 分别在 AB 、AC 上,将△ADE 沿DE翻折后,点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为 A.21 B. 3C. 2D. 1A'EDABCA. 极差是40B. 平均数是60C. 中位数是51.5D. 众数是588.如图,在梯形ABCD 中,AD //BC ,∠ABC =60°,AB = DC =2, AD =1, R 、P 分别是BC 、CD 边上的动点(点R 、B 不重合, 点P 、C 不重合),E 、F 分别是AP 、RP 的中点,设BR=x ,EF=y ,则下列 图象中,能表示y 与x 的函数关系的图象大致是A B C D二、填空题(本题共16分,每小题4分)9. 若二次根式23-x 有意义,则 x 的取值范围是 .10.若一个多边形的内角和等于540︒,则这个多边形的边数是 .11. 如图,在平面直角坐标系xOy 中,已知点A 、B 、C 在双曲线xy 6=上,BD ⊥x 轴于D , CE ⊥ y 轴于E ,点F 在x 轴上,且AO =AF , 则图中阴影部分的面积之和为 .12.小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:按表中规律,当所得分数为71分时,则挪动的珠子数为 颗; 当挪动n 颗 珠子时(n 为大于1的整数), 所得分数为 (用含n 的代数式表示).三、解答题(本题共30分,每小题5分) 1311|5|()3tan 604---+︒.14.解方程:6123x x x +=-+.15. 如图,AC //EG , BC //EF , 直线GE 分别交BC 、BA 于P 、D ,且AC=GE , BC=FE . 求证:∠A =∠G .FE R P B C DA GF E D CBAP16.已知2220a a --=,求代数式221111121a a a a a --÷--++的值.17. 如图,一次函数的图象与x 轴、y 轴分别交于点A (-2, 0)、B (0, 2). (1)求一次函数的解析式; (2)若点C 在x 轴上,且OC =23, 请直接写出∠ABC 的度数.18. 如图,在四边形ABCD 中,∠ADB =∠CBD =90︒,BE//CD 交AD 于E , 且EA=EB .若AB=54,DB =4,求四边形ABCD 的面积.四、解答题(本题共20分,第19题、第20题各5分,第21题6分,第22题4分) 19. 某街道办事处需印制主题为“做文明有礼的北京人,垃圾减量垃圾分类从我做起”的宣传单. 街道办事处附近的甲、乙两家图文社印制此种宣传单的收费标准如下: 甲图文社收费s (元)与印制数t (张)的函数关系如下表:乙图文社的收费方式为:印制2 000张以内(含2 000张),按每张0.13元收费;超过 2 000张,均按每张0.09元收费.(1)根据表中给出的对应规律,写出甲图文社收费s (元)与印制数t (张)的函数关系式; (2)由于马上要用宣传单,街道办事处同时在甲、乙两家图文社共印制了1 500张宣传单,印制费共179元,问街道办事处在甲、乙两家图文社各印制了多少张宣传单? (3)若在下周的宣传活动中,街道办事处还需要加印5 000张宣传单,在甲、乙两家EDA图文社中选择 图文社更省钱.20.如图,AC 、BC 是⊙O 的弦, BC //AO , AO 的延长线与过点C 的射线交于点D , 且∠D =90︒-2∠A .(1)求证:直线CD 是⊙O 的切线;(2)若BC=4,1tan 2D =,求CD 和AD 的长.21. 李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了 为期半个月的跟踪调查,他将调查结果分为四类,A :很好;B :较好;C :一般;D : 较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:(1)李老师一共调查了多少名同学?(2)C 类女生有 名,D 类男生有 名,将上面条形统计图补充完整; (3)为了共同进步,李老师想从被调查的A 类和D 类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.22.阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC .图1 图2小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对E 3 E 1P 1 P 2 N 1N 2 AFH 类别50%25%15%D C B A称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题: 如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点,P 1、P 2, M 1、M 2, N 1、N 2分别为 AB 、BC 、CA 的三等分点.(1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹);(2)若△ABC 的面积为a ,则图3中△FGH 的面积为 .五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线 2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点.(1)求m 的取值范围;(2)若m >1, 且点A 在点B 的左侧,OA : OB =1 : 3, 试确定抛物线的解析式;(3)设(2)中抛物线与y 轴的交点为C ,过点C 作直线l //x 轴, 将抛物线在y 轴左侧的部分沿直线 l翻折, 抛物线的其余部分保持不变,得到一个新图象. 请你结合新图象回答: 当直线13y x b=+与新图象只有一个公共点P (x 0, y 0)且 y 0≤7时, 求b 的取值范围.24. 如图, 在平面直角坐标系xOy 中,抛物线xx m y 222-=与x 轴负半轴交于点A , 顶点为B , 且对称轴与x 轴交于点C .(1)求点B 的坐标 (用含m 的代数式表示);(2)D 为BO 中点,直线AD 交y 轴于E ,若点E 的坐标为(0, 2), 求抛物线的解析式; (3)在(2)的条件下,点M 在直线BO 上,且使得△AMC 的周长最小,P 在抛物线上,Q 在直线 BC 上,若以A 、M 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐 标.备用图25. 在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系及BMCE 的值, 并证明你的结论;(2)如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在(1)中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3海淀区九年级第二学期期末练习数学试卷答案及评分参考 2012. 6说明: 与参考答案不同, 但解答正确相应给分. 一、选择题(本题共32分,每小题4分)1. B2. C3. A4. C5. B6. D7. D8. C 二、填空题(本题共16分,每小题4分)9.23x ≥10. 5 11. 12 12.8; 21n n +- (每空各 2分)三、解答题(本题共30分,每小题5分) 13115()3tan 604---+︒=54-+ …………………………………………………4分=1. …………………………………………………5分14.解:去分母,得 ()()()()63223x x x x x ++-=-+. ………………………………2分2261826x x x x x ++-=+-. ……………………………………………………3分整理,得 324x =-.解得 8x =-. ………………………………………………………………4分F A ( M ) D N D C E N M B F E C B F NM E C B A经检验,8x =-是原方程的解.所以原方程的解是8x =-. ……………………………………………………5分15.证明:∵ AC //EG ,∴ C C PG ∠=∠. …………1分 ∵ BC //EF ,∴ C P G F E G ∠=∠.∴ C F E G ∠=∠. …………………………………………2分在△ABC 和△GFE 中,,,,AC G E C FEG BC FE =⎧⎪∠=∠⎨=⎪⎩∴ △ABC ≌△GFE . …………………………………………………4分∴A G ∠=∠. …………………………………………………5分 16. 解:原式=()()()21111111a a a a a +-⋅-+-- ……………………………………………2分=()21111a a a +--- …………………………………………………3分=22.(1)a -- …………………………………………………4分由2220a a --=,得 2(1)3a -=.∴ 原式=23-. …………………………………………………5分17.解:(1)依题意设一次函数解析式为2y kx =+. …………………………………1分 ∵ 点A (2,0-)在一次函数图象上, ∴022k =-+.∴ k =1. ……………………………………………………2分 ∴ 一次函数的解析式为2y x =+. …………………………………3分 (2)A B C ∠的度数为15︒或105︒. (每解各1分) ……………………5分 18.解: ∵∠ADB =∠CBD =90︒, ∴ DE ∥CB . ∵ BE ∥CD ,∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE . 在Rt △ABD 中,由勾股定理得8AD ===. ………2分设D E x =,则8EA x =-. ∴8EB EA x ==-.在Rt △BDE 中,由勾股定理得 222D E B D E B +=.∴ 22248x x +=-(). ……………………………………………………3分 ∴ 3x =.∴ 3BC D E ==. ……………………………………………………4分 ∴1116622.22ABD BD C ABCD S S S BD AD BD BC ∆∆=+=⋅+⋅=+=四边形 ………… 5分四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分) 19.解:(1)甲图文社收费s (元)与印制数t (张)的函数关系式为0.11s t =. ……1分GFE DCB AP D ECA(2)设在甲、乙两家图文社各印制了x 张、y 张宣传单, 依题意得{1500,0.110.13179.x y x y +=+= ………………………………………… 2分解得800,700.x y =⎧⎨=⎩ ……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分 (3) 乙 . ……………………………………………………… 5分20.(1)证明:连结OC .∴ ∠DOC =2∠A . …………1分∵∠D = 90°2A -∠, ∴∠D +∠DOC =90°. ∴ ∠OCD =90°. ∵ OC 是⊙O 的半径,∴ 直线CD 是⊙O 的切线. ………………………………………………2分(2)解: 过点O 作OE ⊥BC 于E , 则∠OEC =90︒.∵ BC =4,∴ CE =12BC =2.∵ BC //AO , ∴ ∠OCE =∠DOC .∵∠COE +∠OCE =90︒, ∠D +∠DOC =90︒,∴ ∠COE =∠D . ……………………………………………………3分 ∵tan D =12,∴tan C O E ∠=12.∵∠OEC =90︒, CE =2, ∴4tan CE O E CO E==∠.在Rt △OEC 中, 由勾股定理可得O C ==在Rt △ODC 中, 由1tan 2O C D CD==,得CD =, ……………………4分由勾股定理可得10.O D =∴10.AD OA OD OC OD =+=+= …………………………………5分 21.解:(1)(64)50%20+÷=. 所以李老师一共调查了20名学生. …………………1分(2)C 类女生有 3 名,D 类男生有 1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分(3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种.从D 类中选取从A 类中选取女女男男女女男女男所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分解法二:由题意列表如下:………………………5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分22.解:(1)画图如下:(答案不唯一) …………………………………2分图3(2)图3中△FGH 的面积为7a. …………………………………4分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 解:(1)∵ 抛物线2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点,∴210,(2)4(1)0.m m m ì- ïïíïD =-+->ïî由①得1m¹, 由②得0m ¹,∴ m 的取值范围是0m ¹且1m ¹. ……………………………………………2分 (2)∵ 点A 、B 是抛物线2(1)(2)1y m x m x =-+--与x 轴的交点,∴ 令0y =,即 2(1)(2)10m x m x -+--=. 解得 11x =-,211x m =-.∵1m >, ∴10 1.1m >>--∵ 点A 在点B 左侧,∴ 点A 的坐标为(1,0)-,点B 的坐标为1(,0)1m -. …………………………3分∴ OA=1,OB =11m -.∵ OA : OB =1 : 3,①② …………………………………………1分∴131m =-.∴ 43m =.∴ 抛物线的解析式为212133y x x =--. ………………………………………4分(3)∵ 点C 是抛物线212133y x x =--与y 轴的交点,∴ 点C 的坐标为(0,1)-.依题意翻折后的图象如图所示. 令7y =,即2121733x x --=.解得16x =, 24x =-.∴ 新图象经过点D (6,7). 当直线13y x b =+经过D 点时,可得5b =. 当直线13y x b =+经过C 点时,可得1b =-. 当直线1(1)3y x b b =+<-与函数2121(33y x x x =-->的图象仅有一个公共点P (x 0, y 0)时,得20001121333x b x x +=--.整理得 2003330.x x b ---=由2(3)4(33)12210b b D =----=+=,得74b =-结合图象可知,符合题意的b 的取值范围为15b -<≤或4b <-. ……………7分24.解:(1)∵22222221212112()()4422y x x x m x m m x m m mmm m=-=-+-⋅=--,∴抛物线的顶点B 的坐标为11(,)22m m -. ……………………………1分(2)令2220x x m-=,解得10x =, 2x m =.∵ 抛物线xx m y 222-=与x 轴负半轴交于点A ,∴ A (m , 0), 且m <0. …………………………………………………2分 过点D 作DF ⊥x 轴于F .由 D 为BO 中点,DF //BC , 可得CF =FO =1.2C O ∴ DF =1.2BC由抛物线的对称性得 AC = OC .∴ AF : AO =3 : 4. ∵ DF //EO ,∴ △AFD ∽△AOE . ∴.FD AF O EAO=由E (0, 2),B 11(,)22m m -,得OE =2, DF =14m -.∴134.24m -=∴ m = -6.∴ 抛物线的解析式为2123y x x =--. ………………………………………3分(3)依题意,得A (-6,0)、B (-3, 3)、C (-3, 0).可得直线OB 的解析式为x y -=,直线BC 为3x =-. 作点C 关于直线BO 的对称点C '(0,3),连接AC '交BO 于M ,则M 即为所求. 由A (-6,0),C ' (0, 3),可得 直线AC '的解析式为321+=x y .由13,2y x y x⎧=+⎪⎨⎪=-⎩解得2,2.x y =-⎧⎨=⎩ ∴ 点M 的坐标为(-2, 2). ……………4分由点P 在抛物线2123y x x =--上,设P (t ,213t - (ⅰ)当AM 为所求平行四边形的一边时. 如右图,过M 作MG ⊥ x 轴于G , 过P 1作P1H ⊥ BC 于H , 则x G = x M =-2, x H = x B =-3.由四边形AM P 1Q 1为平行四边形, 可证△AMG ≌△P 1Q 1H . 可得P 1H = AG =4. ∴ t -(-3)=4. ∴ t =1.∴17(1,)3P -. ……………………5分如右图,同 方法可得 P 2H=AG =4. ∴ -3- t =4. ∴ t =-7.∴27(7,)3P --. ……………………6分(ⅱ)当AM 为所求平行四边形的对角线时, 如右图,过M 作MH ⊥BC 于H , 过P 3作P 3G ⊥ x 轴于G , 则x H = x B =-3,x G =3P x =t .由四边形AP 3MQ 3为平行四边形, 可证△A P 3G ≌△MQ 3H . 可得AG = MH =1. ∴ t -(-6)=1. ∴ t =-5. ∴35(5,)3P -. ……………………………………………………7分综上,点P 的坐标为17(1,)3P -、27(7,)3P --、35(5,)3P -.25. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;C E B M2证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC ,∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°.∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD , ∴ GF =DG =11.22DF CD =∴ 1.2G E CD =∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD =∴ GE =AN , NG=ND+DG=ND+AN=AD=AB . ……………………………2分 ∴ △NGE ≌△BAN . ∴ ∠1=∠2. ∵ ∠2+∠3=90°, ∴ ∠1+∠3=90°. ∴ ∠BNE =90°.∴ BN ⊥NE . ……………………………………………………………3分 ∵ ∠CDF =90°, CD =DF , 可得 ∠F =∠FCD =45°,CF CD=.于是122CFCECECEBM BA CD CD ====……………………………………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .∵ 四边形ABCD 是矩形, ∴ AB ∥CG .∴ ∠MBN =∠DGN ,∠BMN =∠GDN . ∵ N 为MD 的中点, ∴ MN =DN .∴ △BMN ≌△GDN . ∴ MB =DG ,BN =GN .HGABCDEMNF321GFEA (M )CDNB∵ BN =NE ,∴ BN =NE =GN .∴ ∠BEG =90°. ……………………………………………5分 ∵ EH ⊥CE , ∴ ∠CEH =90°. ∴ ∠BEG =∠CEH . ∴ ∠BEC =∠GEH . 由(1)得∠DCF =45°. ∴ ∠CHE =∠HCE =45°. ∴ EC=EH , ∠EHG =135°. ∵∠ECB =∠DCB +∠HCE =135°, ∴ ∠ECB =∠EHG . ∴ △ECB ≌△EHG . ∴ EB =EG ,CB =HG . ∵ BN =NG ,∴ BN ⊥NE. ……………………………………………6分∵ BM =DG= HG -HD= BC -HD =CD -HD =CH=CE ,∴CE BM=2……………………………………………7分(3)BN ⊥NE ;CE BM2.………………………………………………8分北京市西城区2012年初三二模试卷数 学 2011. 6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.3-的倒数是A .3B .13-C .3-D .132.2010年,我国国内生产总值(GDP )为58 786亿美元,超过日本,成为世界第二大经济体.58 786用科学记数法表示为 A .45.878610⨯ B .55.878610⨯ C .358.78610⨯ D .50.5878610⨯ 3.⊙O 1的半径为3cm ,⊙O 2的半径为5cm ,若圆心距O 1O 2=2 cm ,则这两圆的位置关系是A .内含B .外切C .相交D .内切 4.若一个多边形的内角和是它的外角和的2倍,则这个多边形是A .四边形B .五边形C .六边形D .八边形 5.某鞋店试销一种新款女鞋,销售情况如下表所示:鞋店经理最关心的是哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是A .平均数B .众数C .中位数D .方差6.小明的爷爷每天坚持体育锻炼,一天他步行到离家较远的公园,打了一会儿太极拳后跑步回家.下面的四个函数图象中,能大致反映当天小明的爷爷离家的距离y 与时间x 的函数关系的是7.下图的长方体是由A ,B ,C ,D 四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是8.在平面直角坐标系xOy 中,点P 在由直线3+-=x y,直线4y =和直线1x =所围成的区域内或其边界上,点Q 在x 轴上,若点R 的坐标为(2,2)R ,则QP QR +的最小值为A .B .25+C .D .4 二、填空题(本题共16分,每小题4分) 9.分解因式 m 3 – 4m = . 10.函数21-=x y 中,自变量x 的取值范围是 .11.如图,两同心圆的圆心为O ,大圆的弦AB 与小圆相切,切点为P .若两圆的半径分别为2和1,则弦长AB =;若用阴影部分围成一个圆锥(OA 与OB 重合),则该圆锥的底面半径长为 . 12.对于每个正整数n ,抛物线2211(1)(1)n n n n n yx x +++=-+与x 轴交于A n ,B n 两点,若n n A B 表示这两点间的距离,则n n A B = (用含n 的代数式表示);11222011A B A B A B +++ 的值为 .三、解答题(本题共30分,每小题5分) 13.计算:2273181---⎪⎭⎫ ⎝⎛--- .14.已知:如图,直线AB 同侧两点C ,D 满足CAD DBC ∠=∠, AC =BD ,BC 与AD 相交于点E .求证:AE =BE .15.已知:关于x 的一元二次方程2420x x k ++=有两个不相等的实数根. (1)求k 的取值范围;(2)当k 取最大整数值时,用公式法求该方程的解.16.已知 122=+xy x ,215xy y +=,求代数式()22()x y y x y +-+的值.17.如图,一次函数y kx b =+()0≠k 的图象与反比例函数m y x=()0≠m 的图象交于(3,1)A -,(2,)B n 两点.(1)求反比例函数和一次函数的解析式;(2)求△AOB 的面积.18.今年3月12日,某校九年级部分学生参加植树节活动,以下是根据本次植树活动的有关数据制作的统计图的一部分.请根据统计图所提供的有关信息,完成下列问题:(1)参加植树的学生共有 人; (2)请将该条形统计图补充完整;(3)参加植树的学生平均每人植树 棵.(保留整数)四、解答题(本题共20分,每小题5分)19.某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆,已知大型客车每辆62万元,中型客车每辆40万元,设购买大型客车x(辆),购车总费用为y(万元).(1)求y与x的函数关系式(不要求写出自变量x的取值范围);(2)若购买中型客车的数量少于大型客车的数量,请你给出一种费用最省的方案,并求出该方案所需费用.20.如图,在梯形ABC D中,AB∥D C,5AB=,4C D=,连结并延长BD到E,使==,10AD BC=,作EF AB⊥,交BA的延长线于点F.DE BD(1)求tan ABD∠的值;(2)求AF的长.21.已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连结AB.(1)求证:2=⋅;A B A E A D(2)过点D作⊙O的切线,与BC的延长线交于点F,若AE=2,ED=4,求EF的长.22.如图1,若将△AOB绕点O逆时针旋转180°得到△COD,则△AOB≌△COD.此时,我们称△AOB 与△COD为“8字全等型”.借助“8字全等型”我们可以解决一些图形的分割与拼接问题.例如:图2中,△ABC是锐角三角形且AC>AB,E为AC的中点,F为BC上一点且BF≠FC(F不与B,C 重合),沿EF将其剪开,得到的两块图形恰能拼成一个梯形.请分别按下列要求用直线将图2中的△ABC重新进行分割,画出分割线及拼接后的图形.(1)在图3中将△ABC沿分割线剪开,使得到的两块图形恰能拼成一个平行四边形;(2)在图4中将△ABC沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的两块为直角三角形;(3)在图5中将△ABC沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的一块为钝角三角形.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.阅读下列材料:若关于x 的一元二次方程20ax bx c ++=()0≠a 的两个实数根分别为x 1,x 2,则12b x x a+=-,12c x x a⋅=.解决下列问题:已知:a ,b ,c 均为非零实数,且a >b >c ,关于x 的一元二次方程20ax bx c ++=有两个实数根,其中一根为2.(1)填空:42a b c ++ 0,a 0,c 0;(填“>”,“<”或“=”)(2)利用阅读材料中的结论直接写出方程20ax bx c ++=的另一个实数根(用含a ,c 的代数式表示); (3)若实数m 使代数式2am bm c ++的值小于0,问:当x =5m +时,代数式2ax bx c ++的值是否为正数?写出你的结论并说明理由.。
2012北京东城中考二模数学(word解析)

2012年东城区中考二模数学试卷一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1.9的算术平方根是()A .-9B .9C .3D .±32.如图,由几个小正方体组成的立体图形的俯视图是()3.下列运算正确的是()A .235+a a a =B .235a a a ⋅=C .2333()ab a b =D .1025a a a ÷=4.抛掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点奇数的概率为() A .16B .14C .13D .125.如果一个多边形的内角和是其外角和的2倍,那么这个多边形是()A .六边形B .五边形C .四边形D .三角形6.在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调查.四个城市5个月香蕉价格的平均值均为3.50元,方差分别为2=18.3S 甲,2=17.4S 乙,2=20.1S 丙,2=12.5S 丁.一至五月份香蕉价格最稳定的城市是()A .甲B .乙C .丙D .丁7.如图,在平行四边形ABCD 中,E 为AD 的中点,DEF △的周长为1,则BCF △的周长为()A .1B .2C .3D .48.如右图,正方形ABCD 的顶点2(0,)2A ,2(,0)2B ,顶点C 、D 位于第一象限,直线:(02)l x t t =≤≤将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为S ,则S 关于t 的函数图象大致是()二、填空题(本题共16分,每小题4分)9.使二次根式41x-有意义的x的取值范围是.10.一个扇形的圆心角为120°,半径为1,则这个扇形的弧长为.11.观察下列等式:1=1,2+3+4=9,3+4+5+6+7=25,4+5+6+7+8+9+10=49,……照此规律,第5个等式为.12.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、弧EF及正方形ABCD的边围成的图形(阴影部分)的面积S=.三、解答题(本题共30分,每小题5分)13.计算:027(4π)6cos30+2---︒-.14.解方程组:212x yx y+=⎧⎨-=⎩.15.已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC.16.先化简,再求值:22121(1)1x x x x -+-÷-,其中2x =-.17.列方程或方程组解应用题:小明家有一块长8m 、宽6m 的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的x 值.18.如图,在平面直角坐标系xOy 中,直线AB 与反比例函数ky x=的图像交于点(3,4)A -,AC x⊥轴于点C .(1)求此反比例函数的解析式;(2)当直线AB 绕着点A 转动时,与x 轴的交点为(,0)B a ,并与反比例函数ky x=图象的另一支还有一个交点的情形下,求ABC △的面积S 与a 之间的函数关系式.并写出自变量a 的取值范围.四、解答题(本题共20分,每小题5分)19.在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题: (1)a=,b=;(2)在扇形统计图中,B 组所占圆心角的度数为;(3)全校共有1000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?20.如图,在平行四边形ABCD 中,5AB =,8BC =,AE BC ⊥于点E ,3cos 5B =,求t a n C D E ∠的值.21.如图,在矩形ABCD 中,点O 在对角线AC 上,以OA 长为半径的⊙O 与AD ,AC 分别交于点E ,F ,ACB DCE ∠=∠.(1)请判断直线CE 与⊙O 的位置关系,并证明你的结论; (2)若:1:2DE EC =,2BC =,求⊙O 的半径.组别 做家务的时间 频数 频率 A 1≤t <23 0.06 B 2≤t <4 20 c C 4≤t <6 a 0.30 D 6≤t <88 b E t ≥8 40.0822.阅读并回答问题:小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程21x =-时,突发奇想:21x =-在实数范围内无解,如果存在一个数i ,使21i =-,那么当21x =-时,有x i =±,从而x i =±是方程21x =-的两个根.据此可知:(1)i 可以运算,例如:321i i i i i =⋅=-⨯=-,则4=i , 2011=i ___________,2012i =____________;(2)方程2220x x -+=的两根为.(根用i 表示).五.解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的方程2(1)(4)30m x m x -+-+=. (1)若方程有两个不相等的实数根,求m 的取值范围;(2)若正整数m 满足822m ->,设二次函数2(1)(4)3y m x m x =-+-+的图象与x 轴交于A 、B两点,将此图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线3y kx =+与此图象恰好有三个公共点时,求出k 的值(只需要求出两个满足题意的k 值即可).24.已知:等边ABC△中,点O是边AC,BC的垂直平分线的交点,M,N分别在直线AC,BC 上,且60MON∠=︒.(1)如图1,当CM CN=时,M、N分别在边AC、BC上时,请写出AM、CN、MN三者之间的数量关系;(2)如图2,当CM CN≠时,M、N分别在边AC、BC上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3)如图3,当点M在边AC上,点N在BC的延长线上时,请直接写出线段AM、CN、MN三者之间的数量关系.25.如图,在平面直角坐标系xOy 中,已知二次函数22y ax ax c =++的图像与y 轴交于点,与x 轴交于A 、B 两点,点B 的坐标为(3,0)-. (1)求二次函数的解析式及顶点D 的坐标;(2)点M 是第二象限内抛物线上的一动点,若直线OM 把四边形ACDB 分成面积为1:2的两部分,求出此时点M 的坐标;(3)点P 是第二象限内抛物线上的一动点,问:点P 在何处时CPB △的面积最大?最大面积是多少?并求出此时点P 的坐标.2012年东城区中考二模数学试卷答案一、选择题(本题共32分,每小题4分)题号 1 2 3 4 5 6 7 8 答案CDBDADBC二、填空题(本题共16分,每小题4分)题号 9 10 1112答案14x ≥23π 567891011121381++++++++=2π-三、解答题:(本题共30分,每小题5分) 13.解:原式=33316+22--⨯=1.14.解:①+②得:23x x +=1x =.将1x =代入②得:12y -=, 1y =- ∴11x y =⎧⎨=-⎩.15.证明:∵AC 平分BCD ∠,BC 平分ABC ∠, ∴ACB DBC =∠∠ 在ABC △与DCB △中, ABC DCB ACB DBC BC BC =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴ABC DCB ≌△△ ∴AB DC =.16.解:原式()()()()()()22111111=111x x x x x x x x x x x x -+---+÷==+--· 当2x =-时,原式211=22-+=-.17.解:据题意,得1(8)(6)862x x --=⨯⨯.解得112x =,22x =. 1x 不合题意,舍去.∴2x =.18.解:(1)∵4=3k-12k =- ∴12y x-=(2)∵(3)3BC a a =--=+4AC =, ∴14(3)2ACB S a ∆=⨯⨯+26(3)a a =+>-四、解答题(本题共20分,每小题5分) 19.解:(1)15,0.16; (2)144︒;(3)271000[(1584)50]100054050⨯++÷=⨯=(人) 答:该校平均每周做家务时间不少于4小时的学生约有540人.20.解:在ABE △中,AE BC ⊥,5AB =,3cos 5B =∴3BE =,4AE =∴835EC BC BE =-=-=. ∵平行四边形ABCD , ∴5CD AB ==∴CED △为等腰三角形. ∴CDE CED ∠=∠. ∵AD BC ∥, ∴ADE CED ∠=∠. ∴CDE ADE ∠=∠.在Rt ADE △中,4AE =,8AD BC ==, ∴41ta n 82CDE ∠==.21.解:(1)直线CE 与⊙O 相切 证明:∵矩形ABCD , ∴BC AD ∥,ACB DAC ∠=∠. ∵ACB DCE ∠=∠, ∴DAC DCE ∠=∠.连接OE ,则DAC AEO DCE ∠=∠=∠. ∵90DCE DEC ∠+∠=︒, ∴90AEO DEC ∠+∠=︒, ∴90OEC ∠=︒. ∴直线CE 与⊙O 相切.(2)∵ AB 2tan 2BC ACB =∠=,2BC =, ∴tan 2AB BC ACB =⋅∠=,6AC =. ∵ACB DCE ∠=∠,∴2tan D 2CE ∠=,∵tan D 1DE DC CE =⋅∠=. 在Rt CDE ∆中,3CE =.设O ⊙的半径是r ,则在Rt CEO ∆中, 222CO CE EO =+,即22(6)3r r -=+,解得64r =.22.解:(1)4222=()(1)1i i =-=,201120101i i i i i =⋅=-⨯=-,20121i =; (2)2220x x -+=2(1)1x -=- 1x i -=±11x i =+,21x i =-方程2220x x -+=的两根为1i +和1i -.五.解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.解:(1)2(4)12(1)m m ∆=---2(2)m =+.由题意得,2(2)0m +>且10m -≠.∴符合题意的m 的取值范围是2m ≠-且1m ≠的一切实数. (2)∵正整数m 满足822m ->, ∴m 可取的值为1和2.又∵二次函数2(1)(4)3y m x m x =-+-+, ∴2m =.∴二次函数为2-23y x x =++.∴A 点、B 点的坐标分别为(1,0)-、(3,0). 依题意翻折后的图象如图所示.由图象可知符合题意的直线3y kx =+经过点A 、B . 可求出此时k 的值分别为3或1-.注:若学生利用直线与抛物线相切求出2k =也是符合题意的答案.24.解:(1)AM CN MN =+. (2)AM CN MN =+.证明:过点O 作OD AC ⊥,OE BC ⊥,易得OD OE =,120DOE ∠=︒, 在边AC 上截得'DN NE =,连结'ON ,OED BC AM N N'E M xy O A BCD ∵'DN NE =, OD OE =, 'ODN OEN ∠=∠∴'DON EON ≅△△∴'ON OE =.'DON NOE ∠=∠. ∵120DOE ∠= ,60,MON ∠= ∴60MOD NOE ∠+∠=︒. ∴'60MOD DON ∠+∠=︒. 易证'MON MON ∆≅∆. ∴'MN MN =.∴'MN MD DN MD NE =+=+. MD AM AD AM CE =-=-, NE CE CN =-.∴()()MN AM CE CE CN AM CN =-+-=- ∴AM CN MN =+. (3)MN CN AM =+.25.解:(1)由题意,得:3,9-60.c a a c =⎧⎨+=⎩解得:1,3.a c =-⎧⎨=⎩所以,所求二次函数的解析式为:223y x x =--+ 顶点D 的坐标为(1,4)-.(2)易求四边形ACDB 的面积为9. 可得直线BD 的解析式为26y x =+.设直线OM 与直线BD 交于点E ,则OBE △的面积可以为3或6. ① 当1=9=33OBE S ∆⨯时,易得E 点坐标(2,2)--,直线OE 的解析式为y x =-.设M 点坐标(,)x x -, 223x x x -=--+11132x --=(舍),21132x -+=∴113113()22M -+-+, ② 当1=9=63OBE S ∆⨯时,同理可得M 点坐标.∴M 点坐标为(1,4)-.(3)连接OP ,设P 点的坐标为(),m n ,因为点P 在抛物线上,所以232n m m =-+-,xy O AB CDM所以PB PO OPB OB S S S S =+-△C △C △△C 111()222OC m OB n OC OB =⋅-+⋅-⋅ ()339332222m n n m =-+-=--()223332732228m m m ⎛⎫=-+=-++⎪⎝⎭. 因为3<0m -<,所以当32m =-时,154n =.CPB △的面积有最大值278.所以当点P 的坐标为315(,)24-时,CPB △的面积有最大值,且最大值为278.2012年东城区中考二模数学试卷部分解析一、选择题 1. 【答案】C【解析】9的算术平方根是3,故选C .2. 【答案】D【解析】该立体图的俯视图是,故选D .3. 【答案】B 【解析】2336()ab a b =,1028a a a ÷=,235a a a ⋅=,故选B .4. 【答案】D【解析】骰子的六个面1到6共6个点数,奇数有3个,故选中奇数的概率为12,故选D .5. 【答案】A【解析】多边形外角和为360︒,该多边形内角和为720︒,内角和公式为(2)180720n -⨯︒=︒,解得6n =,故选A .6. 【答案】D【解析】平均数相同的情况下,方差越小,波动越小,越稳定,故选D .7. 【答案】B【解析】依题可知DEF BFC ∽△△,12DE BC =,由相似三角形的性质可知,相似三角形周长之比等于相似比,DEF △的周长为1,所以BCF △的周长为2,故选B .8. 【答案】C【解析】当l 在BC 的左侧,阴影部分的面积2S t =;当l 在BC 的右左侧,阴影部分的面积21(2)S t =--,故选C .二、填空题 9. 【答案】14x ≥【解析】二次根式41x -有意义,被开方数大于等于0,所以410x -≥,14x ≥.故答案为:14x ≥.10. 【答案】23π【解析】扇形的弧长为π180n r l =︒,所以120π12π1803l ︒⨯==︒. 故答案为23π.11. 【答案】567891011121381++++++++=【解析】根据前几项找规律可知,第一行从1开始一个数,第二行从2开始连续的三个自然数的和,第三行从3开始连续的五个自然数的和,第四行从4开始连续的七个自然数的和,第五行从5开始连续的九个自然数的和,L 第n 行从n 开始连续的(21)n -个自然数的和. 故答案为:567891011121381++++++++=.12. 【答案】2π-【解析】由题可知,阴影部分的面积等于扇形EOF 的面积减去四边形BHOG 的面积,而四边形BHOG 的面积等于正方形ABCD 面积的14,正方形面积为144=82⨯⨯,所以阴影部分的面积为290π218π23604︒⨯-⨯=-︒.故答案为:2π-.。
03.2012年北京市东城区中考二模数学试题(word版含答案)-推荐下载

C.3 D.±3
C. (ab 2 )3 a3b3
4. 抛掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有 1 到 6 的点数,掷得朝上
一面的点数为奇数的概率为
1
A.
6
1
B.
4
5. 如果一个多边形的内角和是其外角和的 2 倍,那么这个多边形是
A.六边形
B.五边形
1
C.
3
6. 在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调
1
D.
2
C.四边形
C.丙
D. a10 a 2 a 5
D.三角形
D.丁
7. 如图,在平行四边形 ABCD 中, E 为 AD 的中点, △DEF 的周长为 1,则 △BCF 的
周长为 A.1 B.2 C.3 D.4
8. 如右图,正方形 ABCD 的顶点 A(0,
顶点 C、D 位于第一象限,直线 l : x t(0 t 2) 将正
(2)当直线 AB 绕着点 A 转动时,与 x 轴的交点为 B(a,0), 并与反比例函数 y k 图象的另一支还有一个交点的情形 x 下,求△ABC 的面积 S 与 a 之间的函数关系式.并写出自变 量 a 的取值范围.
四、解答题(本题共 20 分,每小题 5 分)
19.在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在
学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分
布表和扇形统计图:
组别 A B C D E
做家务的时间 1≤t<2 2≤t<4 4≤t<6 6≤t<8 t≥8
频数 3 20 a 8 4
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
北京东城区2011-2012学年中考数学模拟试卷(含答案)

14.一连串分数,共有 6 个,是按照一种简单规律排成的 . 由于抄写的人笔头较慢,别人抄下来前 3 个,
他只抄了前两个,把第 3 个空着;别人把后面 3 个也抄好了,他才抄了第 4 个和第 5 个,把第 6 个也空
着 . 请你帮他补上:
1、 1、 20 10
、1、1、
.
54
15.如图,该图形经过折叠可以围成一个正方体,折好以后,与“静”字相对的字是
( 6 分)
( 8 分) ( 9 分) ( 10 分)
25.(本题 10 分)
- 11 - / 14
. ⑴ r =5 (3 分) ⑵ CF= 20 ( 3 分) ⑶ tan ∠BAD= 6 (4 分)
3
17
26.(本题 10 分)
解:( 1)政府没出台补贴政策前,这种蔬菜的收益额为
3000 800 2400000(元). ·················· 2 分
上,小圆在正方形的外部且与 CD切于点 N,则正方形 ABCD的边长为
▲.
三、解答题: ( 本大题共 10 小题,共 96 分,解答应写出必要的计算过程、推演步骤或文字说明
)
19. ( 本小题满分 8 分 ) 计算
(
2)0
1 tan 600
1 ()
1
6
2
3
20. ( 本小题满分 8 分 ) 请先将下式化简,再选择一个适当的无理数...代入求值.
7260000 元.
································
10 分
注:本卷只在第 26 题中,学生若出现答题时未写单位或未答分别扣除
1 分.
27.(本题 10 分)
-北京市东城区2012年中考数学二模(真题无答案)

北京市东城区2011--2012学年第二学期初三综合练习(二)数 学 试 卷考生须知1.本试卷共5页,共五道大题,25道小题,满分120分.考试时间120分钟.2.在试卷和答题卡上认真填写学校名称、姓名和准考证号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.5.考试结束,请将本试卷、答题卡一并交回. 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1. 9的算术平方根是A .-9B .9C .3D .±3 2. 如图,由几个小正方体组成的立体图形的俯视图是3. 下列运算正确的是A .532a a a =+B .532a a a =⋅C .3332)(b a ab =D .5210a a a =÷4. 抛掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点数为奇数的概率为 A .16B .14C .13D .125. 如果一个多边形的内角和是其外角和的2倍,那么这个多边形是 A .六边形B .五边形C .四边形D .三角形6. 在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调查.四个城市5个月香蕉价格的平均值均为3.50元,方差分别为2S 甲=18.3,2S 乙=17.4,2S 丙=20.1,2S 丁=12.5.一至五月份香蕉价格最稳定的城市是 A .甲B .乙C .丙D .丁7. 如图,在平行四边形ABCD 中,E 为AD 的中点,DEF △的周长为1,则BCF △的周长为 A .1 B .2 C .3 D .48. 如右图,正方形ABCD 的顶点2(0,)2A ,2(,0)2B , 顶点CD 、位于第一象限,直线:(02)l x t t =≤≤将正 方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面 积为S ,则S 关于t 的函数图象大致是二、填空题(本题共16分,每小题4分)9. 使二次根式41x -有意义的x 的取值范围是 .10. 一个扇形的圆心角为120°,半径为1,则这个扇形的弧长为 . 11. 观察下列等式: 1=1,2+3+4=9, 3+4+5+6+7=25, 4+5+6+7+8+9+10=49,……照此规律,第5个等式为 . 12. 如图,正方形ABCD 内接于⊙O ,⊙O 的半径为2,以圆心O 为顶点作 ∠MON ,使∠MON =90°,OM 、ON 分别与⊙O 交于点E 、F ,与正方形ABCD 的边交于点G 、H , 则由OE 、OF 、EF ⌒及正方形ABCD 的边围成的图形(阴影部分)的面积S= . 三、解答题(本题共30分,每小题5分)13. 计算:027(4)6cos302--π-+-.314. 解方程组212x y x y +=⎧⎨-=⎩,.15. 已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线.求证:AB =DC .16. 先化简,再求值:2212111x x x x -+⎛⎫-÷ ⎪-⎝⎭,其中2x =-.17. 列方程或方程组解应用题:小明家有一块长8m 、宽6m 的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的x 值.BCEA D 18. 如图,在平面直角坐标系xOy 中,直线AB 与反比例函数ky x =的图像交于点A(-3,4),AC ⊥x 轴于点C.(1)求此反比例函数的解析式;(2)当直线AB 绕着点A 转动时,与x 轴的交点为B(a,0), 并与反比例函数ky x=图象的另一支还有一个交点的情形下,求△ABC 的面积S 与a 之间的函数关系式.并写出自变量a 的取值范围.四、解答题(本题共20分,每小题5分)19.在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:(1)a= ,b= ;(2)在扇形统计图中,B 组所占圆心角的度数为 ;(3)全校共有1000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?组别 做家务的时间频数 频率 A 1≤t <2 3 0.06 B 2≤t <4 20 c C 4≤t <6 a 0.30 D 6≤t <8 8 b Et ≥840.08520. 如图,在平行四边形ABCD 中,5AB =,8BC =,AE BC ⊥于点E ,53cos =B ,求tan CDE ∠的值.21.如图,在矩形ABCD 中,点O 在对角线AC 上,以OA 长为 半径的O ⊙与AD ,AC 分别交于点E ,F ,∠ACB =∠DCE .(1)请判断直线CE 与O ⊙的位置关系,并证明你的结论; (2)若 DE:EC=1:2, 2BC =,求⊙O 的半径.22. 阅读并回答问题:小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程21x =-时,突发奇想:21x =-在实数范围内无解,如果存在一个数i ,使21i =-,那么当21x =-时,有x =±i ,从而x =±i 是方程21x =-的两个根.据此可知:(1) i 可以运算,例如:i 3=i 2·i =-1×i =-i ,则i 4= , i 2011=______________,i 2012=__________________;(2)方程2220x x -+=的两根为 (根用i 表示).五.解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 已知关于x 的方程2(1)(4)30m x m x -+-+=. (1) 若方程有两个不相等的实数根,求m 的取值范围;(2) 若正整数m 满足822m ->,设二次函数2(1)(4)3y m x m x =-+-+的图象与x 轴交于A B 、两点,将此图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线3y kx =+与此图象恰好有三个公共点时,求出k 的值(只需要求出两个满足题意的k 值即可).724. 已知:等边ABC ∆中,点O 是边AC,BC 的垂直平分线的交点,M,N 分别在直线AC , BC上,且60MON ∠=.(1) 如图1,当CM=CN 时, M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN 三者之间的数量关系; (2) 如图2,当CM ≠CN 时,M 、N 分别在边AC 、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3) 如图3,当点M 在边AC 上,点N 在BC 的延长线上时,请直接写出线段AM 、CN 、MN 三者之间的数量关系.25.如图,在平面直角坐标系xOy 中,已知二次函数2+2y ax ax c =+的图像与y 轴交于点(0,3)C ,与x 轴交于A 、B 两点,点B 的坐标为(-3,0)(1) 求二次函数的解析式及顶点D 的坐标;(2) 点M 是第二象限内抛物线上的一动点,若直线OM 把四边形ACDB 分成面积为1:2的两部分,求出此时点M的坐标;(3) 点P 是第二象限内抛物线上的一动点,问:点P 在何处时△CPB 的面积最大?最大面积是多少?并求出 此时点P 的坐标.。
2012北京市东城区中考二模数学试题及答案(真题)

北京市东城区2011--2012学年第二学期初三综合练习(二)数 学 试 卷 2012.6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1. 9的算术平方根是A .-9B .9C .3D .±3 2. 如图,由几个小正方体组成的立体图形的俯视图是3. 下列运算正确的是A .532a a a =+B .532a a a =⋅C .3332)(b a ab =D .5210a a a =÷4. 抛掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点数为奇数的概率为 A .16B .14C .13D .125. 如果一个多边形的内角和是其外角和的2倍,那么这个多边形是 A .六边形B .五边形C .四边形D .三角形6. 在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调查.四个城市5个月香蕉价格的平均值均为3.50元,方差分别为2S 甲=18.3,2S 乙=17.4,2S 丙=20.1,2S 丁=12.5.一至五月份香蕉价格最稳定的城市是 A .甲B .乙C .丙D .丁7. 如图,在平行四边形ABCD 中,E 为AD 的中点,DEF △的周长为1,则BCF △的周长为A .1B .2C .3D .48. 如右图,正方形ABCD 的顶点A ,B ,顶点C D 、位于第一象限,直线:(0l x t t =≤将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为S ,则S 关于t 的函数图象大致是二、填空题(本题共16分,每小题4分)9.x 的取值范围是 .10. 一个扇形的圆心角为120°,半径为1,则这个扇形的弧长为 . 11. 观察下列等式: 1=1,2+3+4=9, 3+4+5+6+7=25, 4+5+6+7+8+9+10=49,……照此规律,第5个等式为 . 12. 如图,正方形ABCD 内接于⊙O ,⊙O 的半径为2,以圆心O 为顶点作 ∠MON ,使∠MON =90°,OM 、ON 分别与⊙O 交于点E 、F ,与正方形ABCD 的边交于点G 、H , 则由OE 、OF 、EF ⌒及正方形ABCD 的边围成的图形(阴影部分)的面积S= .三、解答题(本题共30分,每小题5分) 13.0(4)6cos302-π-+-.14. 解方程组212x y x y +=⎧⎨-=⎩,.15. 已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线.求证:AB =DC .16. 先化简,再求值:2212111x x x x -+⎛⎫-÷ ⎪-⎝⎭,其中2x =-.17. 列方程或方程组解应用题:小明家有一块长8m 、宽6m 的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的x 值.18. 如图,在平面直角坐标系xOy 中,直线AB 与反比例函数ky x =的图像交于点A(-3,4),AC ⊥x 轴于点C.(1)求此反比例函数的解析式;(2)当直线AB 绕着点A 转动时,与x 轴的交点为B(a,0),并与反比例函数ky x=图象的另一支还有一个交点的情形下,求△ABC 的面积S 与a 之间的函数关系式.并写出自变量a 的取值范围.四、解答题(本题共20分,每小题5分)19.在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:(1)a= ,b= ;(2)在扇形统计图中,B 组所占圆心角的度数为 ;(3)全校共有1000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?20. 如图,在平行四边形ABCD 中,5AB =,8BC =,AE BC ⊥于点E ,53cos =B ,求tan CDE ∠的值.21.如图,在矩形ABCD 中,点O 在对角线AC 上,以OA 长为 半径的O ⊙与AD ,AC 分别交于点E ,F ,∠ACB =∠DCE .(1)请判断直线CE 与O ⊙的位置关系,并证明你的结论;(2)若 DE:EC=1 2BC =,求⊙O 的半径.22. 阅读并回答问题:小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程21x =-时,突发奇想:21x =-在实数范围内无解,如果存在一个数i ,使21i =-,那么当21x =-时,有x =±i ,从而x =±i 是方程21x =-的两个根.据此可知:(1) i 可以运算,例如:i 3=i 2·i =-1×i =-i ,则i 4= , i 2011=______________,i 2012=__________________;(2)方程2220x x -+=的两根为 (根用i 表示).五.解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 已知关于x 的方程2(1)(4)30m x m x -+-+=. (1) 若方程有两个不相等的实数根,求m 的取值范围;(2) 若正整数m 满足822m ->,设二次函数2(1)(4)3y m x m x =-+-+的图象与x 轴交于A B 、两点,将此图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线3y kx =+与此图象恰好有三个公共点时,求出k 的值(只需要求出两个满足题意的k 值即可).24. 已知:等边ABC ∆中,点O 是边AC,BC 的垂直平分线的交点,M,N 分别在直线AC , BC上,且60MON ∠=.(1) 如图1,当CM=CN 时, M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN 三者之间的数量关系;(2) 如图2,当CM ≠CN 时,M 、N 分别在边AC 、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3) 如图3,当点M 在边AC 上,点N 在BC 的延长线上时,请直接写出线段AM 、CN 、MN 三者之间的数量关系.25.如图,在平面直角坐标系xOy 中,已知二次函数2+2y ax ax c =+的图像与y 轴交于点(0,3)C ,与x轴交于A 、B 两点,点B 的坐标为(-3,0) (1) 求二次函数的解析式及顶点D 的坐标;(2) 点M 是第二象限内抛物线上的一动点,若直线OM 把四边形ACDB 分成面积为1:2的两部分,求出此时点M 的坐标;(3) 点P 是第二象限内抛物线上的一动点,问:点P 在何处时△CPB 的面积最大?最大面积是多少?并求出 此时点P 的坐标.2012北京市东城区中考二模数学试题及答案11。
