曲线的凹凸性与拐点
高等数学(上) 第3版教学课件3-4 曲线的凹凸性与拐点

答案
x
y
y
(, 1 ) 2
1
( 1 , )
2
2
0
1
练一练
例4 求曲线 y e x2 的凹凸区间与拐点.
答案
x
,
2 2
2 2
2, 2
2 2
y
0
y
1
e
2 2
2 2
,
0
1
e
《高等数学》
谢谢观看
基础课教学部
若曲线弧 AB 位于此曲线每一点的切 线的下方,则称曲线 (函数的图形)在区间 (a, b)内是凸的.称(a, b)为凸区间.
连续曲线上凹弧与凸弧的分界点称为曲线的拐点. 如图
2.凹凸性的判别方法
设函数 f (x) 在(a, b)内有二阶导数,
(1) 若在区间(a, b)内,f ( x) 0,则曲线 f ( x) 在(a, b)内是凹的.
《高等数学》
第四节 曲线的凹凸性 与拐点
基础课教学部
第四节 曲线的凹凸性与拐点
目
1 曲线凹凸性、拐点定义
录 2 曲线凹凸性、拐点判定
1.凹凸性的定义
y
C
B
如图
A
D
oa
b
x
若曲线弧 AB 位于此曲线每一点的切 线的上方,则称曲线 (函数的图形)在区间 (a, b)内是凹的 .称(a, b)为凹区间.
(2) 若在区间(a, b)内,f ( x) 0,则曲线 f ( x) 在(a, b)内是凸的.
注意 判定曲线 f (x) 的凹凸性的一般步骤是:
(1)确定函数 f ( x)的定义域; (2)求出函数f ( x)的二阶导数f (x); (3)在定义区间内求出使f ( x) 0的点
曲线的凹凸性与拐点【一元分析学经典讲义】

上页
返回
下页
例1 判断曲线 y = x 3 的凹凸性 . 解 ∵ y′ = 3 x 2 , y′′ = 6x ,
当x < 0时, y′′ < 0,
∴ 曲线 在(−∞ ,0]为上凸的; −∞ 为上凸的;
当x > 0时, y′′ > 0, ∴曲线 在[0,+∞ )为凸的;
注意到, 注意到 点( 0,0 )是曲线由凹变凸的分界 点.
则 f ′′( x ) = [ f ′( x )]′在x0两边变号 ,
∴ f ′( x )在x0取得极值 ,由可导函数取得极值的 条件,
∴ f ′′( x0 ) = 0.
方法1: 方法1:设函数 f ( x )在x0的邻域内二阶可导 , 且f ′′( x0 ) = 0,
(1) x0两近旁 f ′′( x )变号,点( x0 , f ( x0 ))即为拐点; ( 2) x0两近旁 f ′′( x )不变号,点( x0 , f ( x0 ))不是拐点.
x2 x
o
x1
x2
x
图形上任意弧段位 于所张弦的下方
上页 返回
图形上任意弧段位 于所张弦的上方
下页
I , 定义 设f ( x)在区间 上有定义 若∀x1 , x2 ∈ I和∀λ ∈(0,1) 恒有 f (λx1 + (1 − λ)x2 ) ≤ λf ( x1 ) + (1 − λ) f ( x2 ), 那末称 f ( x)为I上的下凸函数 简称凸函数 ; ,
( 理2 定 2 如 f (x)在 x0 − δ , x0 + δ )内 在 阶 理 果 存 二 导
( x0 , f ( x0 ))是拐点的必要条件是f "( x0 ) = 0. 数则 , 点
4.5 曲线的凹凸性与拐点
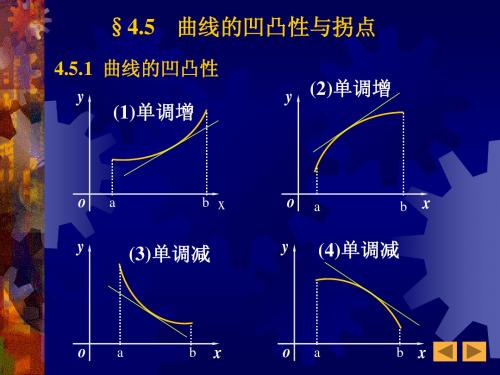
4.5.1 曲线的凹凸性
y y
(2)单调增
(1)单调增
o
y
a
b x
o
y
a
b
x
(3)单调减
(4)单调减
o
a
b
x
o
a
b
x
定义 设函数y=f (x) 在[a , b]上连续,在(a , b)内导, (1) 若对任意x0 (a,b), 曲线 y=f (x)在点 (x0, f (x0)) 处的切线总位于曲线的下方, 则称该曲线 在 [a,b] 上是凸的 (2) 若对任意 x0 (a,b),曲线 y = f (x)在点 (x0, f (x0)) 处的切线总位于曲线的上方, 则称该曲线在 [a,b] 上是凹的 从定义可知: 图(1)、图(3)所示的曲线在[a,b]上是凸的; 图(2)、图(4)所示的曲线在[a,b]上是凹的
拐点的求法: (1)求出使函数 f (x)的二阶导数 f ' ' (x) 0的点以及二阶 不可导的点;
(2)若在 x 0两旁f (x)变号, 则点(x 0 , f (x 0 ))即为拐点;
(3) 若在x 0两近旁f (x)不变号, 则点(x 0 , f (x 0 )) 不是拐点.
例4 求曲线 y 3x4 4x 3 1 的拐点及凹、凸的区间 .
(2) f ( x ) 0, 则 曲线y f ( x ) 在 [a , b] 上是凹的 .
例1 判断曲线 y=lnx 的凹凸性
解 函数的定义域(0, +) 1 1 y' , y '' 2 0 x x 故由上述定义知,曲线 y = lnx 在 (0, +) 内是凹的
《曲线凹凸与拐点》课件

曲线凹凸的计算方法
定义法
通过定义凹凸性,利用二阶导数正负来判断。如果二阶导数大于0,则曲线在相 应区间内是凹的;如果二阶导数小于0,则曲线在相应区间内是凸的。
切线法
通过切线斜率判断。在某点处做切线,如果切线斜率在相邻两点之间由负变正, 则该点为拐点。
拐点的计算方法
定义法
根据拐点的定义,即函数在某点的左 右极限不相等,来确定拐点。
具体应用
在气候学中,通过研究气候数据的曲线凹凸性,可以更好地理解气候变化的规律和趋势 。在金融学中,通过研究股票价格的拐点,可以更好地把握股票市场的变化和趋势。
导数符号变化法
通过判断函数在某点附近左右两 侧导数的符号变化来确定是否为
拐点。
二阶导数测试法
通过判断二阶导数的符号变化来确 定是否为拐点。如果二阶导数在某 点处从正变为负或从负变为正,则 该点为拐点。
切线方向变化法
通过观察曲线在某点处的切线方向 是否发生变化来确定是否为拐点。 如果切线方向发生改变,则该点为 拐点。
导数法
通过求函数的二阶导数,并令其为0 ,解出相应的x值,再判断该点是否为 拐点。
曲线凹凸与拐点计算中的注意事项
初始判断
在计算前应先大致判断 函数的形态,以便选择
合适的计算方法。
精确度要求
对于实际应用,应考虑 计算结果的精确度,选 择合适的数学工具和算
法。
拐点判断
在确定拐点时,应同时 考虑左右极限,避免误
拐点是曲线上的一个点,在该点处曲线的切线方向发变符号
在拐点处,曲线的导数由正变负或由 负变正。
拐点处凹凸性改变
拐点处切线方向变化
在拐点处,曲线的切线方向发生变化 ,由上升变为下降或由下降变为上升 。
曲线的凹凸性与拐点

一、曲线凹凸的定义
观察:
y y
o
x
o
x
都是上升的曲线,但是上升的方式不一样; 红色曲线上升的速度在增加,蓝色曲线上升速度减少; 呈现出来的不同的弯曲方式。
一、曲线凹凸的定义
观察:
y y
o
凹
x
o
x
弦在曲线上方
凸
弦在曲线下方
一、曲线凹凸的定义
凹
y f ( x1 )
凸
f ( x)
y
f ( x)
f ( x2 )
f ( x1 )
f ( x2 )
x1 x 2 x x 2 2
o
x1 x1 x 2 2
x2 x
o
x1
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
一、曲线凹凸的定义
对 I 上任意两点x1 , x2, 定义1:若函数 f ( x)在区间 I上连续,
x1 x2 f ( x1 ) f ( x2 ) (1)如果恒有 f ( 2 ) 2 那么称 f ( x)在 I 上的图形是凸的。
_
(2)如果恒有 那么称
x1 x2 f ( x1 ) f ( x2 ) f( ) 2 2
f ( x )的极值点. 拐点:
凹
f ( x) 0
凸
f ( x) 0
f ( x )
f ( x )
拐点可能是二阶导数等于0的点,和二阶导数不存在的 点.
四、计算凹凸区间与拐点的步骤
1)求函数的定义域; 2)求 f ( x); 3)求出 f ( x) 0的点,和 f ( x) 不存在的点;
曲线的凹凸性与拐点

曲线的凹凸性与拐点在数学中,曲线的凹凸性以及拐点对于研究曲线的性质和变化具有重要的意义。
凹凸性可以帮助我们理解曲线的弯曲程度以及变化趋势,而拐点则是曲线上的一个特殊点,表示曲线在该处发生方向的变化。
本文将介绍曲线的凹凸性与拐点的概念,以及它们在数学和其他实际应用中的重要性。
一、凹凸性的定义与判断凹凸性是描述曲线在某一区间上的弯曲程度的性质。
我们有以下两个定义来判断曲线的凹凸性:1. 凹曲线:如果曲线上的任意两点连线的下方部分都在曲线上方,则称该曲线为凹曲线。
换句话说,如果对于曲线上的任意两点A和B,A和B连线的下方不与曲线相交,则该曲线为凹曲线。
2. 凸曲线:如果曲线上的任意两点连线的下方部分都在曲线下方,则称该曲线为凸曲线。
换句话说,如果对于曲线上的任意两点A和B,A和B连线的下方不与曲线相交,则该曲线为凸曲线。
凹凸性的判断可以通过曲线的二阶导数来进行。
如果曲线的二阶导数大于0,则曲线为凹曲线;如果二阶导数小于0,则曲线为凸曲线。
而当二阶导数恰好为0时,需要考虑其他方法。
二、拐点的定义与判断拐点是曲线上的一个特殊点,表示曲线在该点处方向发生改变。
我们有以下定义来判断曲线是否存在拐点:1. 拐点:如果曲线在某一点处既没有切线也没有二阶切线(即曲线在该点处没有明确的方向),则称该点为拐点。
判断曲线是否存在拐点可以通过曲线的三阶导数来进行。
如果曲线的三阶导数存在不连续的点,则该点即为拐点。
值得注意的是,如果曲线的三阶导数的符号在该点的左右两侧不同,也可以判断该点为拐点。
三、凹凸性与拐点的应用与意义凹凸性和拐点不仅仅在数学领域中有重要性,还被广泛应用于其他学科和实际问题中,如物理学、经济学等。
在物理学中,凹凸性可以帮助解释某一物体的形状和弯曲程度,例如在光学中,曲率半径越小的曲面会导致光线的弯曲程度越大。
因此,通过研究光线在曲面上的传播可以利用凹凸性来分析光的折射和反射现象。
在经济学中,凹凸性可以用来描述供需曲线的变化趋势。
曲线的凹凸性与拐点

曲线上的
七、作业
知识回顾 Knowledge Review
若函数上连续在内具有一二阶导数则1若果在内有2若果在内有拐点三拐点拐点
曲线的凹凸性与拐点
一、曲线凹凸的定义
观察:
y
yoxFra bibliotekox
都是上升的曲线,但是上升的方式不一样; 红色曲线上升的速度在增加,蓝色曲线上升速度减少; 呈现出来的不同的弯曲方式。
一、曲线凹凸的定义
观察:
y
y
o
x
凹
弦在曲线上方
o
x
凸
弦在曲线下方
那么称 f (x)在 I上的图形是凹的。
二、曲线凹凸的判定
观察:
y
y
o
x
凹:切线的的斜率递增 f (x) 递增,即 f (x) 0
o
x
凸:切线的的斜率递减 f (x) 递减,即 f (x) 0
二、曲线凹凸的判定
定理:若函数f (x)在[a,b]上连续,在(a,b)内具有一、 二阶导数,则
(1)若果在(a, b)内有 f (x) 0, 那么 f (x)在[a,b]内图像是凸的.
(2)若果在(a, b)内有 f (x) 0, 那么 f (x)在[a,b]内图像是凹的.
三、拐点
拐点:连续曲线凹弧与凸弧的分界点称为拐点。 拐点
凸凹
凸
f (x) 0 f (x) 0 f (x) 0
4)判断二阶导数在上述点左右两侧的符号,确定曲 线的凹凸区间和拐点。
五、应用举例
例判断函数 f (x) 2x3 3x2 36x 25的凹凸区间与拐点.
六、小结
1.凹凸的定义:曲线与弦的位置关系 点和弦上点的位置关系 2.凹凸的判定:二阶导数的符号;
经济数学3.3曲线的凹向与拐点
ESC
二. 曲线凹凸与拐点的求法
例5 与拐点. 求曲线 y 2 ( x 4) 的凹凸区间
1 3
, 解 函数的连续区间为(, ) 2 5 1 2 ( x 4) 3 ( x 4) 3 y y 3 9 y 在 (,) 内恒不为零,但 x 4 时, y 不存在. x 在4的左侧邻近时, y 0 ; 在4的右 侧邻近时, y 0 .即 y在 x 4两侧异号,所 以 (4,2)是曲线的拐点. ESC
二. 曲线凹凸与拐点的求法
4) (, 曲线的凹区间是( , ,凸区间是 4 )
练习:
1、求曲线
y (x 1)31 的拐点。
2、 确定曲线
y x x 的凹凸区间与拐点.
3
ESC
内容小结
本节重点讲了: 一. 曲线凹凸与拐点的定义 二.曲线凹凸与拐点的求法 求拐点的一般步骤: ①求函数定义域; ②求函数的二阶导数 f (x) ; ③令 f ( x) 0,解出全部根,并求出所 有二阶导数不存在的点;
二. 曲线凹凸与拐点的求法
例2 (续)
结论: 在区间 (0, b)内,曲线凹; 2 在区间 ( b ,) 内, 曲线凸; 2 曲线的拐点是 ( b , Ae2).
设一消费品的需求 Q 是消费者的收入 x 的函数
Q Ae
b x
(A 0, b 0).
Q
试讨论该需求收入曲线的凹凸区间与拐点.
(3)判定:在各个部分区间内讨论导 数 (x) 的符号:设, b) I 的一个 是 f (a 部分区间,当 (a, b) 时,若(x) 0, x f (2)求二阶导数 (a (1)确定 f (x), 解方程 求其 则曲线在区间, b) 内凹;若 函数的 f (a 根.(x) 0, 其根将 (x) 0, 则曲线在区间, b) 内凸 f 连续区间; 又假设 I, 且有(x ) 0, 若在 x0 f 0 函数连续区间 分成 I 点 的左右邻近(x) 的符号相反, f 0 若干个部分区间; 则曲线上的点, f (x0)) 是曲线的拐 (x0 点; 若在点 的左右邻近(x) 的符 f 0 号相同,则在 处,曲线没有拐点. 0 ESC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
4
注意: 若 f ( x0 ) 不存在,点 ( x0 , f ( x0 )) 也可能 是连续曲线 y f ( x)的拐点.
例5 求曲线 y 3 x 的拐点.
解
当x
0时,
y
1
x
2 3
,
y
4
5
x3
,
3
9
x 0是不可导点, y, y均不存在.
但在(,0)内, y 0, 曲线在(,0]上是凹的; 在(0,)内, y 0, 曲线在[0,)上是凸的.
(2) f (x) 0,则 f (x) 在[a,b] 上的图形是凸的.
例1 判断曲线 y x3 的凹凸性. 解 y 3x2, y 6x, 当x 0时, y 0,
曲线 在(,0]为凸的; 当x 0时, y 0, 曲线 在[0,)为凹的; 注意到, 点(0,0)是曲线由凸变凹的分界点.
方法1:
设函数f (x)在x0的邻域内二阶可导 ,且f (x0 ) 0,
(1) x0两近旁f ( x)变号,点( x0, f ( x0 ))即为拐点;
(2) x0两近旁f ( x)不变号,点( x0, f ( x0 ))不是拐点.
例3 求曲线 y 3x4 4x3 1的拐点及
(2) lim f ( x) a 存在,但 lim[ f ( x) ax] 不存在,
x x
x
可以断定 y f ( x) 不存在斜渐近线.
例1 求 f ( x) 2( x 2)( x 3) 的渐近线. x1
解 D : (,1) (1,).
lim f ( x) , x1
2 2
1
0.8
0.6
0.4
0.2
-2
-1
1
2
x0 f ( x) 0
(0, 2 2 )
2 2
2e12
f ( x) 2
0
f (x)
凸、降 拐点
( 2 2 ,)
凹、降
x
f ( x)
f ( x) fБайду номын сангаас(x)
0 ( 2 2 ,0)
0
2
极大 凸、 值升
2 2
2e
那么 y b 就是 y f (x) 的一条水平渐近线 .
例如 y arctan x,
有水平渐近线两条:
y , y .
2
2
3.斜渐近线 如果 lim [ f (x) (ax b)] 0
x
或 lim [ f (x) (ax b)] 0 (a,b 为常数) x
f
(
x)
4(
x x3
2)
,
f
(
x)
8(
x x4
3)
.
令 f ( x) 0, 得驻点 x 2,
令 f ( x) 0, 得特殊点 x 3.
lim
x
f (x)
lim[4(
x
x x2
1)
2]
2,
得水平渐近线
y
2;
lim
x0
f
(x)
4( x 1)
注:利用凹凸性也可以证明一些不等式。
例2 试证:对 x 0、y 0,x y 及 1,有
1 ( x y ) ( x y ) .
2
2
解 令 f (t ) t , 则 f (t ) ( 1)t 2 ,
在 t 0时有 f (t) 0 , 在 t 0时 f 是凹的。
第四步 确定函数图形的水平、铅直渐近线、斜渐 近线以及其他变化趋势;
第五步 描出与方程 f '( x) 0 和 f "( x) 0 的根对 应的曲线上的点,有时还需要补充一些点,再综 合前四步讨论的结果画出函数的图形.
二、作图举例
例2
作函数
f
(
x)
4(
x x2
1)
2
的图形.
解 D : x 0, 非奇非偶函数,且无对称性.
0
f (x)
凸、降 拐点
( 2 2 ,)
凹、降
x
f ( x)
f ( x) f (x)
0 ( 2 2 ,0)
0
2
极大 凸、 值升
2 2
2e
1 2
0
拐点
(, 2 ) 2
凹、 升
例3
作函数 ( x)
二、曲线凹凸的判定
y
y f (x) B
y y f (x)
B
A A
oa
bx
f ( x) 递增 y 0
oa
bx
f ( x) 递减 y 0
定理1 如果 f (x) 在 [a,b] 上连续,在 (a,b)内具有
一阶和二阶导数 ,若在 (a,b)内
(1) f (x) 0,则 f (x) 在[a,b] 上的图形是凹的;
间 断 点
补充点: (1 3,0), (1 3,0);
A (1,2), B (1,6), C (2,1).
作图
y
6B
1
C
3 2 1 o 1 2
x
2
A
3
f
(
x)
4(
x x2
1)
2
例3、设y f ( x) e x2 ,求f ( x)增减的区间 和 极 值 点 , 以 及 凹 凸 区间 和 拐 点.
5
5
5
0
(0 , )
f ( x)
0
不存在
f (x)
拐点
非拐点
此函数在(, 1/ 5]上是凸的、在[1/ 5, 0] 及 [0, ) 上是凹的,拐点为 1/ 5。 (曲线 y y( x) )
问:此函数在[1/ 5, ) 上是凹的?
4.5.2
第二步 求出方程 f '( x) 0和 f "( x) 0 在函数定义 域内的全部实根,用这些根同函数的间断点或导数 不存在的点把函数的定义域划分成几个部分区间.
第三步 确定在这些部分区间内 f '( x) 和 f "( x) 的符 号,并由此确定函数的增减性与极值及曲线的凹 凸与拐点(可列表进行讨论);
渐近线
定义:
当曲线 y f (x) 上的一动点 P 沿着曲线移向无穷点时,
如果点 P 到某定直线 L的距离趋向于零,
那么直线 L 就称为曲线 y f (x)的一条渐近线.
1.铅直渐近线 (垂直于 x 轴的渐近线)
如果 lim f (x) 或 lim f (x)
x x0
x x0
lim[
x0
x2
2]
,
得铅直渐近线 x 0.
列表确定函数升降区间,凹凸区间及极值点和拐点:
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
对 x、y (0, ) 且 x y , 有
1 ( f (x) f ( y)) f ( x y) ,
2
2
即所证不等式成立。证毕。
三、曲线的拐点及其求法
1、定义 连续曲线上凹凸的分界点称为曲线的拐点. 注意:拐点处的切线必在拐点处穿过曲线. 2、拐点的求法
定理 2 如果 f ( x)在( x0 , x0 )内存在二阶导
那么 y ax b 就是 y f (x) 的一条斜渐近线 .
斜渐近线求法:
lim f ( x) a, lim[ f ( x) ax] b.
x x
x
那么 y ax b 就是曲线 y f ( x) 的一条斜渐近线.
注意: 如果
(1) lim f ( x) 不存在; x x
点(0,0)是曲线 y 3 x的拐点.
例6、设y f (x) ex2 , 求f (x)增减的区间 和极值点,以及凹凸区间和拐点.
解:函数的定义域为( , ),由
y 2xex2及y 0,得驻点x1 0;
y 2e x2 (2 x2 1), 及y 0, 得x2,3
凹的
凹凸区间为 (,0], [0, 2 3], [2 3 ,).
方法2: 设函数 f ( x) 在 x0 的邻域内三阶可导,且 f ( x0 ) 0,而 f ( x0 ) 0,那末 ( x0 , f ( x0 )) 是曲 线 y f ( x)的拐点.
例4 求曲线 y sin x cos x ([0,2]内) 的拐点.
数, 则 点 x0 , f ( x0 ) 是 拐 点 的 必 要 条 件 是
f "( x0 ) 0.
证 f ( x) 二阶可导, f ( x) 存在且连续,
又 ( x0 , f ( x0 ) )是拐点, 则 f ( x) [ f ( x)]在x0两边变号, f ( x)在x0取得极值,由可导函数取得极值的条件, f ( x) 0.
x
x1
y 2x 4 是曲线的一条斜渐近线.
f ( x) 2( x 2)( x 3) 的两条渐近线如图 x1
4.5.3 函数曲线的作图
一 利用函数特性描绘函数图形. 第一步 确定函数 y f ( x) 的定义域,对函数进行奇 偶性、周期性、曲线与坐标轴交点等性态的讨论, 求出函数的一阶导数 f '( x) 和二阶导数 f "( x);
